Optimal Hedging with Options and Futures against Price Risk and Background Risk

Abstract

On the condition that both futures and options exist in the markets for hedging, this paper examines the optimal hedging strategy under price risk and background risk. Compared with the previous research, which has studied options hedging against basis risk and production risk being extended to options and futures hedging against price risk and background risk, we proposed a model and have taken the budget of buying options into consideration. The model is fairly general and some existing models are special cases of it. We firstly derive the necessary and sufficient conditions that guarantee the optimality of an under-hedge, a full-hedge and an over-hedge of futures for the risk-averse utility. Then, sufficient conditions are stipulated under which an over-hedge is optimal. Furthermore, we propose a program minimizing of tail conditional expectation (TCE), which is inherently equivalent to the risk measure of expected shortfall risk (ES) or the conditional VaR (CVaR) under the continuous-time framework. Finally, we find that ES, in our proposed model, is significantly smaller than the one in the model of options hedging only. Therefore, the results emphasize the need for combining futures hedging and options hedging, and it also shows that imposing background risk, whether it be additive or multiplicative, always has a great impact on the hedging efficiency. We also present some sensitivities of the relevant parameters to provide some suggestions for the investors.

1. Introduction

In previous work, Bajo et al. [1] investigated the optimal options hedging strategy for a firm, where the role of production risk and basis risk were taken into account. We provide a further extension by introducing futures as a plus instrument to hedge against price risk and background risk. In fact, the model of Bajo et al. is a special model of our proposed model. There are at least two features of this problem that suggest the need for extension. First, since the firm faces multiple sources of risk, a single hedging instrument cannot completely remove all of the income uncertainty. Possibly, such instruments are both futures and options, which have been proved suitable for hedging linear or nonlinear risk. Second, Frank et al. [2] pointed out that background risk, additive risk or multiplicative, was prevailing, which could not be ignored. Examples of background risks include uncertain labor income, uncertainty about the terminal value of fixed assets and so on. These factors have a great influence on investment decisions.

After the seminal work of Sandmo [3], a large body of research has been focused on the production theory of the competitive firm under price uncertainty. The commonly used approach is confined to choosing only futures for hedging risk, from which two celebrated theorems (separation theorem and full-hedging theorem) emanate, see e.g., [4,5,6]).

The aforementioned studies discussed the establishment of the two theorems under different conditions. It is well-known that linear hedge instruments, such as futures or forwards, are suitable to be used for hedging with linear risk. However, it seems powerless in hedging with nonlinear risk. Nonlinear risk can be hedged using nonlinear instruments such as options, for instance. The conclusions were also supported by Darren [7], Topaloglou et al. [8] and Maciej [9]. To fill the gap of using options as a hedging instrument, Machnes [10] examined the behavior of a competitive firm in the presence of commodity options and price uncertainty. In fact, nonlinear risk is prevailing. For example, if state-dependent variables are considered in the model, it inevitably leads to nonlinear risk. Benninga and Oosterhof [11] showed the role of options hedging under state-dependent preferences. Wong [12] further examined the behavior of the competitive firm under output price uncertainty and state-dependent preferences by establishing a hedging role of options. The multiplied form of two random variables also implies nonlinear risk. Bajo et al. [13] developed a model in which a firm hedged a spot position using options in the presence of both quantity and basis risk. In the real market, however, linear and nonlinear risks exist concurrently. A synthesis of risk management demands both futures and options to be hedge instruments. Sakong et al. [14] dealt with price and production uncertainty using both futures and options hedging. He found that it was optimal for the producer to purchase put options and under-hedge on the futures market. This paper investigates the optimal hedging strategy utilizing both futures and options to hedge against linear and nonlinear risks under a variety of frameworks. We compare our results to the ones of Bajo et al. [1] . Since the investor should pay for option premium when he/she uses options hedging, the budget of buying options can not be ignored. Thus, a budget is considered under the constraints in this paper.

This paper also contributes to extending the existing literature by incorporating additional sources of uncertainty, aggregated into a single source referred to as background risk. Background risk includes additive risk and multiplicative risk. Examples of additive background risk include the firm’s initial wealth that is held in risky assets (Wong [15]) and the firm’s fixed cost that is subject to shocks (Machnes [16]; Wong [17]). Examples of multiplicative background risk include revenue risk (Broll and Wong [18]), credit risk (Wong [19]) and inflation risk (Adam-Müller [20], Battermann and Broll [21]). The previous research has analyzed the separate effects of additive and multiplicative background risk on the derived risk aversion of an agent and hence on risk taking. For example, Gollier and Pratt [22] established conditions for risk vulnerability. Franke et al. [23] proposed conditions for multiplicative risk vulnerability. Furthermore, Franke et al. [24] studied the simultaneous effect of both additive and multiplicative risks and explained some paradoxical choice behavior. In the field of hedging, Adam-Müller and Nolte [25] proposed a model with multiplicative background risk. Wong [26] examined the production and futures hedging decisions of a competitive firm under output price uncertainty and with state-dependent background risk. These above-mentioned pieces of research are the inadequacy of independence assumptions between background risk and price risk. However, the background risk, be it additive or multiplicative, is not necessarily independent of the price risk. In fact, background risk is generally correlated with price risk. Based on these considerations, this paper takes into account both correlated additive and multiplicative risk into the hedging model, and discusses how the background risk affects the optimal decisions. When the background risk is specified, some of the above-mentioned pieces of literature are the exceptions of this paper. For example, Bajo’s model [1] is the special case of only multiplicative risk existing. If the background risk is specialized to be the currency rate in our model, we derive Wong’s condition [17].

In this paper, we study how an investor can optimally choose an options contract and futures position to minimize the risk exposure. Then, it needs to introduce the risk measures. There are many risk measures mentioned in the literature of risk management wherein Value at Risk (VaR) is the maximum potential loss that a financial asset can suffer with a certain probability during a certain holding period. VaR has established its position as one of the standard measures of risk, and it is widely used throughout the field of finance and risk management. The greatest advantage of VaR is that it can summarize risks in a single number. However, as studied in the framework of coherent risk measures, VaR lacks subadditivity, and, therefore, convexity in the general loss distributions. This drawback may cause inconsistency with the well accepted diversification principle, and other negative consequences refer to Artzner et al. [27]. To overcome these problems, scholars have proposed coherent risk measures, such as Conditional VaR (CVaR), which is a supplement to VaR and expected shortfall risk (ES). Various researchers (see, e.g., Acerbi and Tasche [28] and Melnikov and Smirnov [29]) considered coherent risk measures as the objective to be minimized. Bajo et al. [1] employed ES as the risk measure. In this paper, we adopt tail conditional expectation (TCE) or tail VaR as the risk measure based on the consideration of ease calculation. Although the two risk measures of ES and TCE seem different, it does not matter if the advantages of our model compared to the ones of Bajo et al. [1] are evaluated. In fact, we prove out that TCE and ES are equivalent in the continuous-time case.

In this paper, we consider the hedging problem with both options and futures to hedge against price risk and background risk. This paper is an extension of the existing research of Bajo et al. [1]. Several questions are addressed in this paper:

1.

What is the necessity to impose futures hedging?

2.

What is the necessity to consider additive and multiplicative background risk?

3.

How to make informed decisions on futures positions under the budget constraint of options?

4.

What are the predictions of options hedging in the case of a sudden market change compared to the case of only options hedging?

The main contributions of this paper are as follows:

1.

We propose a new hedging model involving both futures and options to hedge against the linear and nonlinear risk.

2.

We present a general model wherein many existing pieces of research are its special conditions by considering different additive and multiplicative background risks.

3.

We draw some conclusions to decide the futures positions under the risk averse utilities and discuss the superiority compared to the existing research.

4.

Some advice, including decisions on budget and the strike price, are provided for the investor.

The rest of this paper is organized as follows: in Section 2, we prove the equivalence of TCE and ES in the continuous case. Section 3 describes the optimal hedging model with the constraints of budget on purchasing options. In this section, we give some results for the general utility function when the investor faces correlated price risk and background risk with futures and options for hedging. 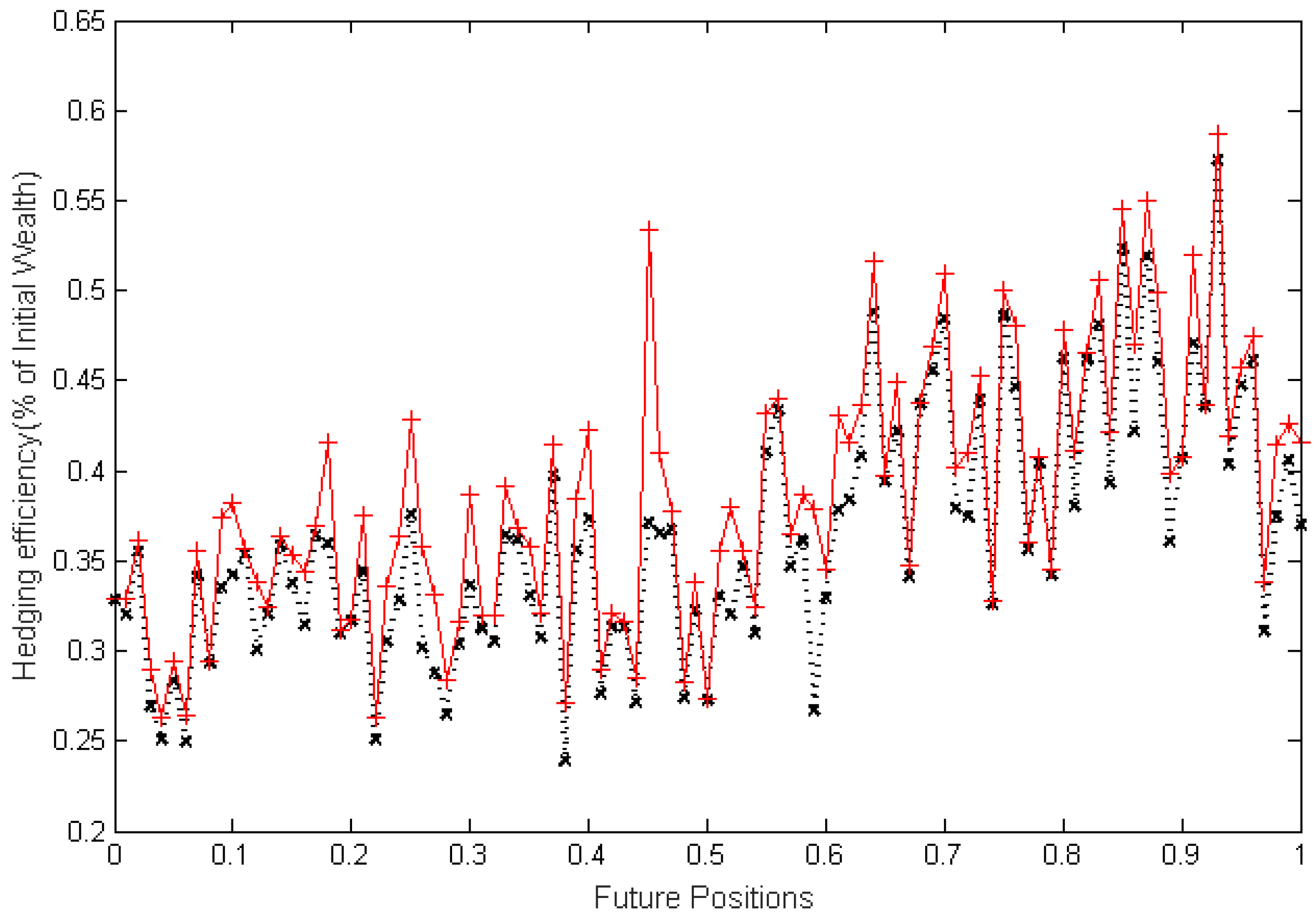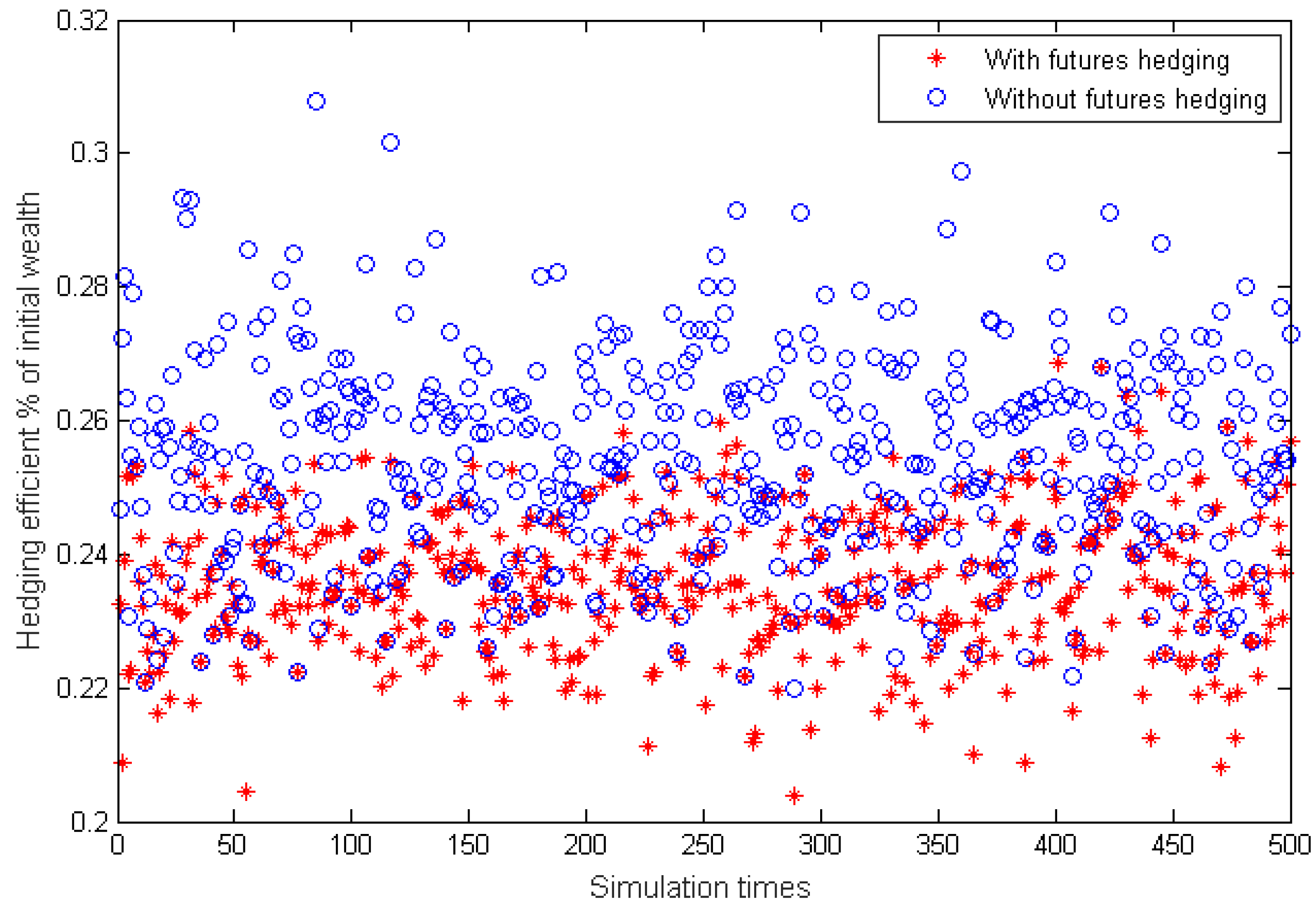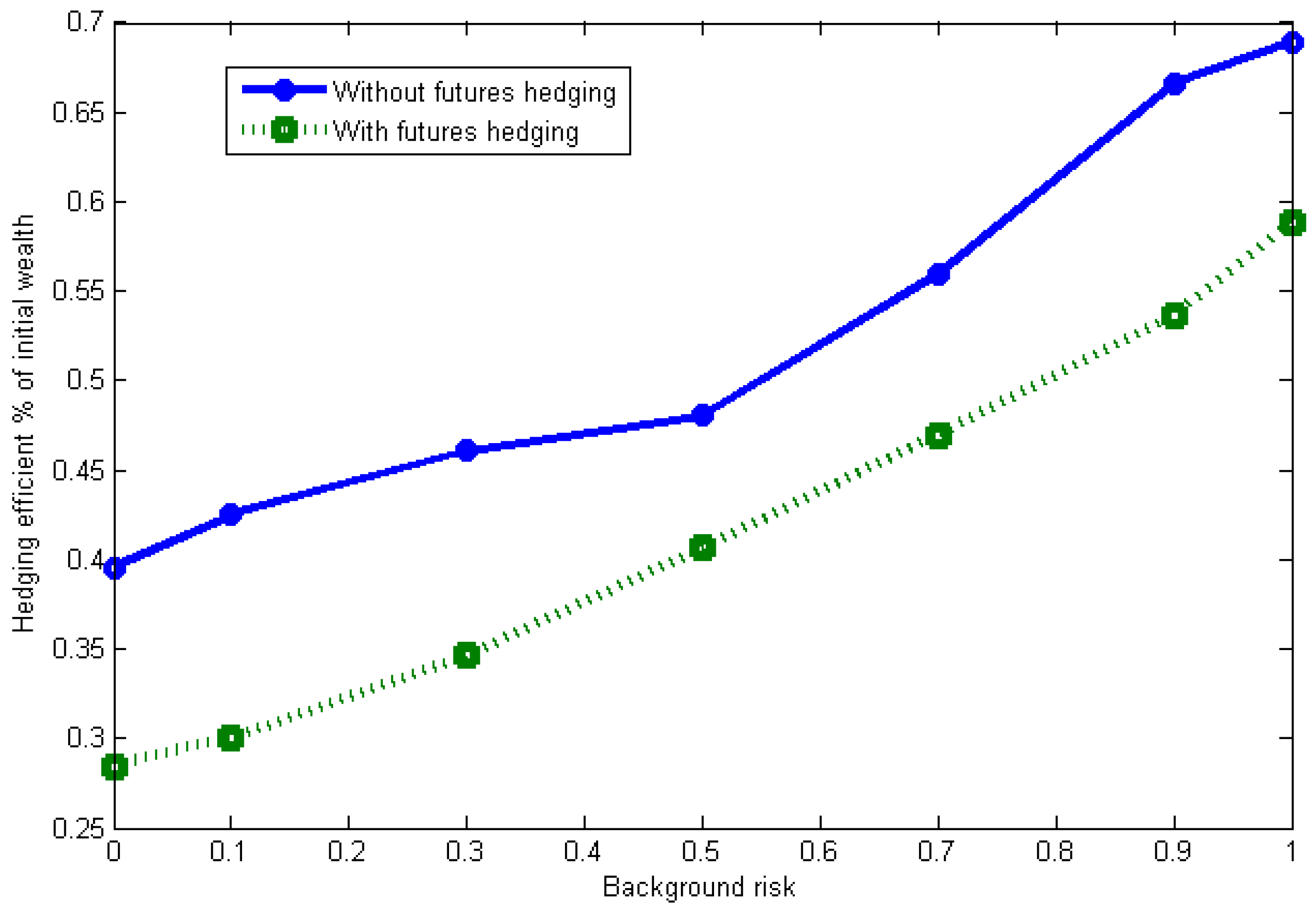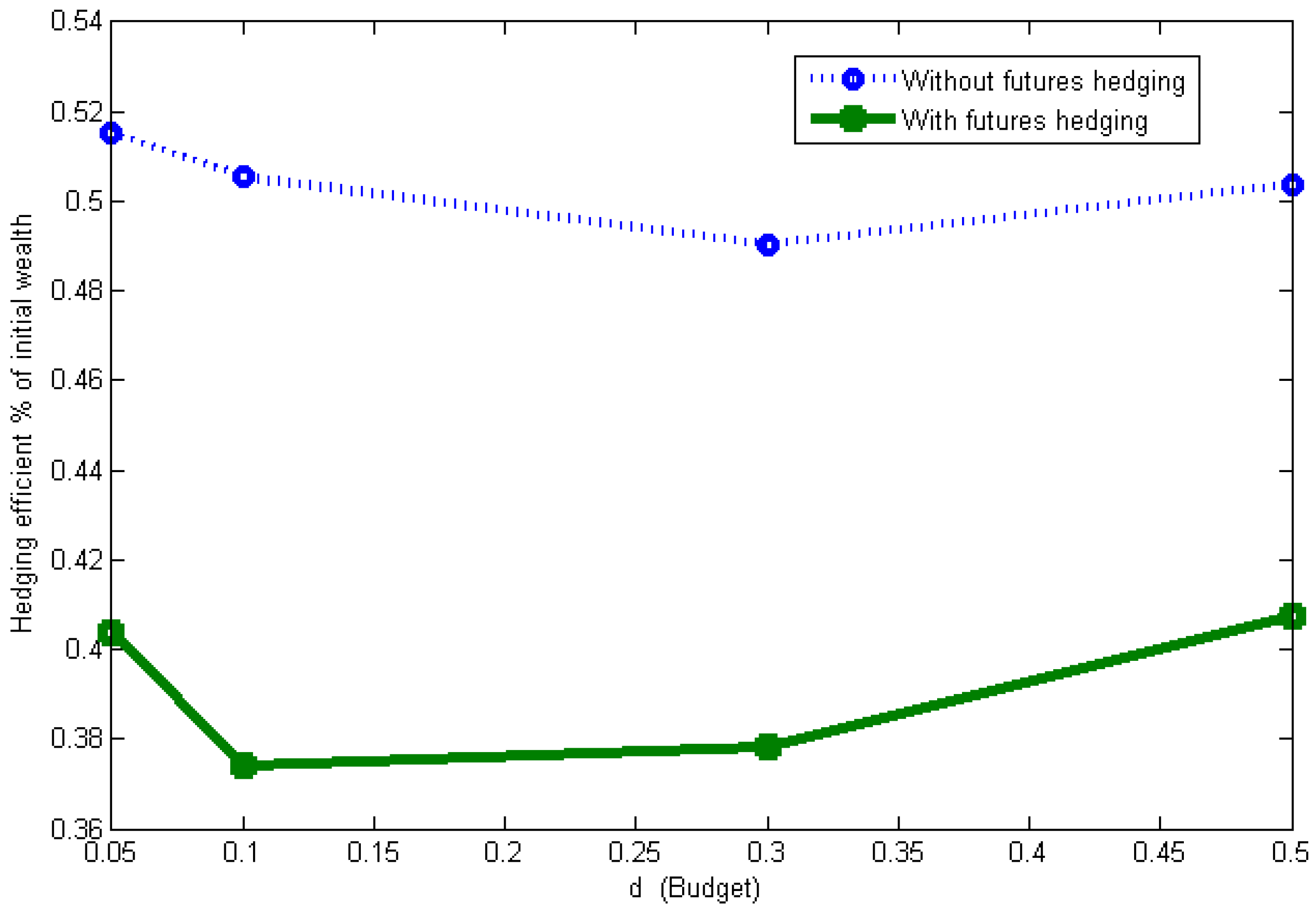In Section 4, we propose a simulation based on data of Shanghai 50 Exchange Traded Funds (SSE 50 ETF). in the Chinese market, and discuss the superiority by mixing futures hedging in minimizing ES. Based on the sensitivities, we provide some decision suggestions for the investors. Finally, Section 5 concludes this paper.

2. Risk Measures

There are four common risk measures, i.e., VaR, CVaR, ES and TCE. For their details, refer to Szegö [30], Rockafellar et al. [31] and Ndarajah et al. [32]. It does not seem reasonable to compare two different risk measures, i.e., ES in the model of Bajo et al. [1] and TCE in this paper. However, Proposition 1 gives the equivalence of TCE and ES with the continuous distribution. We give a proposition to explain the relationships between the different risk measures.

Proposition 1.

(I) 

$Va{R}_{\alpha }\left(X\right)\le TC{E}_{\alpha }\left(X\right)\le E{S}_{\alpha }\left(X\right)$ and $TC{E}_{\alpha }\left(X\right)=\beta E{S}_{\alpha }\left(X\right)+(1-\beta )Va{R}_{\alpha }\left(X\right)$, where $\beta =\alpha P{[X\ge Va{R}_{\alpha }\left(X\right)]}^{-1}$.

(II) 

If $P(X=Va{R}_{\alpha }\left(X\right))=0$, then $TC{E}_{\alpha }\left(X\right)=E{S}_{\alpha }\left(X\right)$.

(III) 

Under the case of continuous distribution function, $Va{R}_{\alpha }\left(X\right)=TC{E}_{\alpha }\left(X\right)=E{S}_{\alpha }\left(X\right)$ holds.

Proof. 

It is obvious that $Va{R}_{\alpha }\left(x\right)\le TC{E}_{\alpha }\left(x\right)\le E{S}_{\alpha }\left(X\right)$ according to their definitions. Then, we have

$$\begin{array}{ccc}& & TC{E}_{\alpha }\left(x\right)=E\left[X\right|X\ge Va{R}_{\alpha }\left(X\right)]\hfill \\ & & =P{[X\ge Va{R}_{\alpha }\left(X\right)]}^{-1}E\left[X{I}_{X\ge Va{R}_{\alpha }\left(X\right)}\right]\hfill \\ & & =P{[X\ge Va{R}_{\alpha }\left(X\right)]}^{-1}\alpha E{S}_{\alpha }\left(X\right)+(P[X\ge Va{R}_{\alpha }\left(X\right)]-\alpha )Va{R}_{\alpha }\left(X\right),\hfill \end{array}$$

i.e., $TC{E}_{\alpha }\left(X\right)$, is the weighted average of $Va{R}_{\alpha }\left(X\right)$ and $E{S}_{\alpha }\left(X\right)$, with the weight $\beta =\alpha P{[X\ge Va{R}_{\alpha }\left(X\right)]}^{-1}$.

For (II), if $P(X=Va{R}_{\alpha }\left(X\right))=0$, then $\beta =1$. According to (I), we have $TC{E}_{\alpha }\left(X\right)=E{S}_{\alpha }\left(X\right)$.

For (III), it is easy to obtain the conclusion according to the results of Acerbi and Tasche [27]. ☐

Based on the discussions above, we can find that TCE, CVaR and ES are equivalent to each other in the case of continuous distribution function. In this paper, we choose TCE as the risk measure, which is inherently equivalent to ES used in Bajo et al. [1]. Notice that we still use ES rather than TCE in the forthcoming sections.

3. Model

At the terminal date, an investor will sell quantity Q of a particular asset at random cash price $P_T$. At the decision date (at time t), the investor can sell a discretionary fraction of Q amount of futures contracts $HQ$ at the future price $F_t$, but she/he must repurchase them at the terminal date at the random future price $F_T$. Simultaneously, the investor buys a discretionary fraction of amount of option contracts with options premium per contract denoted as Φ, and the terminal option value is denoted $V_T$: $V_T=0$ if $F_T\ge K$, and $V_T=K-F_T$ if $F_T<K$.

Besides uncertainty prices of spots and futures, the firm also faces other sources of uncertainty aggregated into additive and/or multiplicative background risk, which is denoted as $Z_T$, with a mean set equal to zero over support $[\underline{Z},\overline{Z}]$, where $\underline{Z}<0<\overline{Z}$. Referring to Wong [4], the terminal wealth is formulated as follows:

$$\begin{array}{c}\hfill {\Pi }_T=(1+\beta Z_T)\{P_{T}Q+[{(K-F_T)}^{+}-\mathsf{\Phi }{e}^{r\tau }]hQ+(F_0{e}^{r\tau }-F_T)HQ+(1-\beta )Z_T\},\end{array}$$

(1)

where $\tau =T-t$, $\beta \in [0,1]$ is a constant such that $-\alpha \underline{Z}<1$. If $\beta =0$ or 1, the background risk becomes purely additive or purely multiplicative, respectively. Some models in existing research are the special cases of this paper. For instance, when we set $Z_T\equiv 0$ and $H=0$, Equation (1) is similar to the model of Bajo et al. [1]. When we let $\beta =1$ and $Z_T\equiv \tilde{S}$, and $\tilde{S}$ is the spot exchange rate, the proposed model becomes the model of Wong [33]; and the model of Wong [34] is the special case when we assume that $\beta =1,H=0$ and $Z_T\equiv \tilde{S}$. When we restrict the budget $C\equiv 0$ and particular background risk forms, there are amounts of special models (see e.g., Broll and Zilcha [35] and Lence [36]). Our results offer new insights in the context of multiple uncertainties. Note that in Equation (1), the option are not necessarily written on the spot, and we choose options on futures due to the higher liquidity of options on futures.

3.1. Optimal Hedging Decisions under the General Utility

Suppose that $L_T$ is the loss of the hedged portfolio, where $L_T=-{\Pi }_T$. The utility function based on the loss satisfies $U^{\prime }\left(L_T\right)<0$ and $U^{″}\left(L_T\right)>0$. Assume that the investor spends C on buying put options. Namely, $\mathsf{\Phi }{e}^{r(T-t)}hQ=C$. Then, the option positions can be calculated as $h=\frac{C}{\mathsf{\Phi }{e}^{r(T-t)}hQ}$. Here, Q and C are known as constants rather than decision variables. Suppose that there is one period with two time instants, 0 and 1. For the sake of simplicity, we do not take the production costs into consideration. Hence, we discuss revenue rather than profit. The objective of the investor is to minimize the expected utility at time 1 under some constraints. It can be expressed by Problem (P1):

$$\begin{array}{cc}& minE\left[U\left(L_T\right)\right],\\ & s.t.C=hQ{P}_t,\\ & 0\le h\le 1.\end{array}$$

In the following, we study the optimal hedging problem under the framework of $\left(P_1\right)$. We first derive the necessary and sufficient conditions that guarantee the optimality of an under-hedge $(H^{*}<1)$, a full-hedge $(H^{*}=1)$ and an over-hedge $(H^{*}>1)$ of the futures in the following Propositions.

Proposition 2.

Assume that there is no arbitrage in the market, if the investor’s utility function based on the loss satisfies $U^{\prime }\left(L_T\right)<0$ and $U^{″}\left(L_T\right)>0$, then the optimal position of futures is smaller than, equal to, or greater than one, if and only if,

$$\begin{array}{c}\hfill Cov{U}^{\prime }[L_T{|}_{H=1}(1+\beta Z_T),F_T]\end{array}$$

is positive, zero, or negative, respectively.

Proof. 

The first-order conditions of Program $\left(P_1\right)$ corresponding to H is given by

$$\begin{array}{c}\hfill E{U}^{\prime }\left(L_T^{*}\right)(1+\beta Z_T)[(F_0{e}^{r(t-T)}-F_T]=0.\end{array}$$

(2)

One the other hand, differentiating $E[U^{\prime }\left(L_T\right]$ with respect to H, and evaluating the resulting derivative at $H=1$ yields

$$\begin{array}{c}\hfill \frac{\partial E\left[U\left(L_T\right)\right]}{\partial H}{|}_{H=1}=-E\left[U^{\prime }\left(L_T\right){|}_{H=1}\right](1+\beta Z_T)(F_0{e}^{r(T-t)}-F_T)Q.\end{array}$$

(3)

Due to no arbitrage in the market, we have $E\left(F_T\right)=F_0{e}^{r(T-t))}$. Then, Equation (3) can be rewritten as follows:

$$\begin{array}{c}\hfill \frac{\partial E\left[U\left(L_T\right)\right]}{\partial H}{|}_{H=1}=QCov(\left[U^{\prime }\left(L_T\right){|}_{H=1}\right](1+\beta Z_T),F_T).\end{array}$$

(4)

It follows from Equations (2) and (4) and the second-order conditions for Program $\left(P_1\right)$ that $H^{*}$ is less than, equal to, or greater than 1 if, and only if, the right-hand side of Equation (4) is negative, zero, or positive, respectively. The following proposition stipulates sufficient condition under which an over-hedge $H^{*}>1$ is optimal. ☐

Proposition 3.

Assume that there is no arbitrage and no basis risk in the market, if the investor’s utility function satisfies $U^{\prime }\left(L_T\right)<0$ and $U^{″}\left(L_T\right)>0$, the investor optimally opts an over-hedge, that is $(H^{*}>1)$, if the random price $F_T$ and the background risk $Z_T$ are independent.

Proof. 

From the results of Proposition 2, we need to prove that the right-hand of Equation (4) is positive under the given conditions. In fact,

$$Cov(\left[U^{\prime }\left(L_T\right){|}_{H=1}\right](1+\beta Z_T),F_T)=Cov(E\left[U^{\prime }\left(L_T\right){|}_{H=1}(1+\beta Z_T)\right|F_T],F_T),$$

(5)

where Equation (5) follows from the properties of the covariance operator $Cov(·,·)$. (For any two random variables, $\tilde{X}$ and, $\tilde{Y}$, $Cov(\tilde{X},\tilde{Y})=Cov[E(\tilde{X}|\tilde{Y}),\tilde{Y}]$) Therefore, the sign of Equation (5) is the same as $\frac{\partial E\left[U^{\prime }\left(L_T\right){|}_{H=1}(1+\beta Z_T)\right|F_T]}{\partial F_T}$. In fact,

$$\begin{array}{c}\hfill \frac{\partial E\left\{U^{\prime }\left(L_T\right){|}_{H=1}(1+\beta Z_T)\right|F_T\}}{\partial F_T}=E\{\left[U^{″}\left(L_T\right){|}_{H=1}\right]{(1+\beta Z_T)}^2\frac{\partial {(K-F_T)}^{+}}{\partial F_T}hQ\}.\end{array}$$

(6)

Then, the strict convex of the utility implies that Equation (6) is indeed negative. Under the same assumptions, Wong [4] gave the result of full-hedge. However, in this paper, the result is over-hedge for futures positions. One of the main reasons is that only futures hedging in the model of Wong [4], and both futures and options are involved in our model. It follows from Proposition 3 that the optimal position of futures is increased because of options hedging.

A natural question is why we add futures into the model of Bajo et al. [1]. The next proposition shows the efficiency of our extension in minimizing the utility based on the loss or in maximizing the utility based on the profit. ☐

Proposition 4.

Assume that there is no arbitrage and no basis risk. Let $E\left[U\left(L_{a=1}^{*}\right)\right]$ and $E\left[U\left(L_{a=0}^{*}\right)\right]$ be the optimal utility corresponding to with and without futures hedging and L is the loss. If the investor’s utility function satisfies with $U^{\prime }\left(L\right)<0$ and $U^{″}\left(L\right)>0$, then $H>1$ implies that $E\left[U\left(L_{a=1}^{*}\right)\right]<E\left[U\left(L_{a=0}^{*}\right)\right]$. In this case, it is always optimal for the risk averse investor to over-hedge futures relative to the case of only with options hedging.

Proof. 

We rewrite the random loss L as $L_a$

$$\begin{array}{c}\hfill {\Pi }_a=(1+\beta Z_T)\{P_{T}Q+[{(K-F_T)}^{+}-\mathsf{\Phi }{e}^{r(T-t)}]hQ+(F_0{e}^{r(T-t)}-F_T)aHQ+(1-\beta )Z_T\},\end{array}$$

(7)

where $a=1$ and 0 denote the cases with and without futures, respectively. The Problem $\left(P_2\right)$ is given by

$$\begin{array}{cc}& minE\left[U\left(L_a\right)\right],\\ & s.t.C=hQ{P}_t,\\ & 0\le h\le 1,\end{array}$$

where $L_a$ is defined in Equation (7). The objective function of Problem $\left(P_2\right)$ is convex due to $U^{\prime }\left(L\right)<0$ and $U^{″}\left(L\right)>0$. Therefore, the first-order condition for Problem $\left(P_2\right)$ is both necessary and sufficient for a unique maximum. Fix $K=K_0^{*}$, where $K_0^{*}$ is the optimal strike price when there is no futures hedging. Treating a as a continuous variable on the real line, it follows from risk aversion that $E\left[U\left(L_a\right)\right|K=K_0^{*}]$ is convex in a. Differentiating $E\left[U\left(L_a\right)\right|K=K_0^{*}]$ with respect to a and evaluating at $a=1$ yields

$$\begin{array}{c}\hfill \frac{\partial E[U\left(L_a\right)|K=K_0^{*}]}{\partial a}{|}_{a=1}=-E\left[U^{\prime }\left(L_{a=1}\right)\right|K=K_0^{*}](1+\beta Z_T)(F_0{e}^{r(T-t)}-F_T)HQ,\end{array}$$

(8)

where

$$\begin{array}{c}\hfill U^{\prime }\left(L_{a=1}\right)|K=K_0^{*}=U^{\prime }(1+\beta Z_T)[{(K-F_T)}^{+}-\mathsf{\Phi }{e}^{r(T-t)}]hQ+(F_0{e}^{r(T-t)}-F_T)HQ+(1-\beta )F_T.\end{array}$$

Returning to Equation (7) and using the assumption of no arbitrage in the market, we see that

$$\begin{array}{c}\hfill \frac{\partial E[U^{\prime }\left(L_a\right)|K=K_0^{*}]}{\partial a}{|}_{a=1}=Cov\{\left(\left[U^{\prime }\left({\Pi }_a\right)\right|K=K_0^{*}]\right)(1+\beta Z_T),-F_T\}HQ.\end{array}$$

(9)

Since $-F_T$ is decreasing with respect to $F_T$,

$$\begin{array}{c}\hfill \frac{\partial E\left[U^{\prime }\left(L_{a=1}\right)\right|K=K_0^{*}](1+\beta Z_T)|F_T}{\partial F_T}=\end{array}$$

$$\begin{array}{c}\hfill E\left[U^{″}\left(L_{a=1}\right)\right|K=K_0^{*}]{(1+\beta Z_T)}^2(1+\frac{\partial {(K_0^{*}-F_T)}^{+}}{\partial F_T}h-H)Q.\end{array}$$

(10)

If the investor chooses over-hedge, i.e., $H>1$, then Equation (10) is negative. Furthermore, Equation (9) is positive. Thus, the convexity of $E\left[U^{\prime }\left(L_{a=1}\right)\right|K=K_0^{*}]$ in a implies that $E\left\{\left[U\left(L_{a=1}\right)\right|K=K_0^{*}]\right\}<E\left\{\left[U\left(L_{a=0}\right)\right|K=K_0^{*}]\right\}=E\left[U\left(L_{a=0}^{*}\right)\right]$. Since $K_1^{*}$ is the optimal solution to Problem $\left(P_2\right)$ for $a=1$, it must be true that $E\left[U\left(L_{a=1}^{*}\right)\right]<E\left[U\left(L_{a=1}\right)\right|K=K_0^{*}]$. It then follows that inequality $E\left[U\left(L_{a=1}^{*}\right)\right]<E\left[U\left(L_{a=0}^{*}\right)\right]$ holds. ☐

In the following, we examine the problem of minimizing ES with lognormal prices.

3.2. Optimal Hedging Decisions under Minimizing Risk of ES

In general, it is not impossible to characterize the explicit solutions without specific assumptions on the utility function and the distributions of the random variables. Thus, similar to Bajo et al. [1], we propose the following assumptions: (i) the utility function of the investor is the risk measure of ES, which is also labelled as $TC{E}_{\alpha }$ in this paper, since we have proved that they are equivalent to each other; (ii) the random variables are used with lognormal dynamics for both the spot and the crossed futures, i.e.,

$$\begin{array}{cc}& P_T=P_{t}exp[(\mu -\frac{1}{2}{\sigma }^2(T-t)+\sigma \epsilon sqrt(T-t)],\\ & F_T=F_{t}exp[({\mu }^{\prime }-\frac{1}{2}{\sigma }^{{}^{\prime }2}(T-t)+{\sigma }^{\prime }{\epsilon }^{\prime }sqrt(T-t)],\end{array}$$

and $\epsilon ,{\epsilon }^{\prime }$ are standard correlated normal random variables with correlation matrix equal to

$$corr\left(\begin{array}{c}\epsilon \hfill \\ {\epsilon }^{\prime }\hfill \end{array}\right)=\left(\begin{array}{cc}1& {\rho }_1\\ {\rho }_1& 1\end{array}\right).$$

$P_t$ is the spot price at current time t, μ and ${\mu }^{\prime }$ are expected return, σ and ${\sigma }^{\prime }$ are volatility. Zero mean normal distribution for the background risk $Z_T$ over support $[\underline{Z},\overline{Z}]$. The correlation coefficient between background risk and spot price is set as ${\rho }_2$.

We investigate how to solve the problem of minimizing $TC{E}_{\alpha }\left(L_T\right),L_T=-{\Pi }_T$. Let C be the budget of the investor to buy put options. Formally, the optimization problem can be written as Problem $\left(P_3\right)$:

$$\begin{array}{cc}& minTC{E}_{\alpha }\left(L_T\right),\\ & s.t.C=hQ{P}_t,\\ & 0\le h\le 1,\end{array}$$

where ${\Pi }_T$ is expressed as Equation (1). In this paper, we study how the investor can optimally choose an option contract to minimize the risk exposure under the constraint of budget using Monte Carlo Simulation to solve the Problem $\left(P_3\right)$.

4. An Illustrative Study and Results

In order to illustrate the derivation of Problem $\left(P_3\right)$ and make a comparison with the previous results, we consider the case of an investor holding an amount of underlying on SSE 50 ETF. He/she is anxious about a down trend of the price, he/she intends to buy put options and sell futures at current time. However, due to the constraints of budget, the investor should make decisions on option strike price and futures positions. Firstly, we present the effect of hedging between two different risk measures, i.e., VaR and ES, wherein the relationship has been be proven in Proposition 1. Secondly, we present the advantages of employing futures in the hedging strategy by comparing with the results of Bajo et al. [1]. Then, we discuss the hedging strategy under different background risk to fully explain the reasons why we take the background risks into consideration. At last, we discuss the outcomes of the sensitivity analysis running on the most relevant parameters.

4.1. Data and Steps

In this section, we first give the basic parameters, and then present the steps to solve the problems. Data of the SSE 50ETF option and China Shanghai 50 fund futures in the Chinese market are derived from the Wind database [37]. spanning from 5 January 2009 to 14 April 2015. Data from 14 April 2015 to 18 September 2015 are the backtesting data. Through Jbtest and Kstest, we find that the log-prices of spot and futures follow the normal distributions, respectively, during the backtesting time interval. Suppose that the current time is 15 April 2015 with an initial spot price 3.145 and an initial futures price 3.2838. By calculating, the expected rate of return and volatility of spot are 0.0142 and 0.15898, and the expected rate of return and volatility of futures are 0.028 and 0.18183, respectively. The correlation coefficient between spot and futures price is ${\rho }_1=0.8$. Let the risk-free interest rate be $r=0.0187$ according to the return of one-year Treasury bills in China. We assume that the investor will sold spot with quantity $Q=1000$ over the next six months $(T-t=0.5)$. Suppose that the investor deduces that the correlation coefficient between spot and background risk is ${\rho }_2=0.8$. The investor spends a proportion $d=0.1$ of the current total value to buy options. Assume that the confidence level is $1-\alpha$. Strike price K is chosen as the current futures price. Next, we give the steps of calculating ES in this paper:

Step 1.

Construct return function under the constraints whose opposite is the loss function.

Step 2.

Given the probability of loss greater than VaR is α, find the α-quantile of the loss, which is known as VaR.

Step 3.

Calculate the mean value of the loss, which is larger than VaR. Since the mean value is expressed as an absolute term, we convert it to a form of percentage relative to the current wealth. Therefore, in this paper, ES means the proportion of mean loss more than VaR.

4.2. Comparison between VaR and ES

Although the relationship is obvious between VaR and ES shown in Proposition 1, we draw the conclusion by simulation in 1. We set $\beta =0.1,\alpha =0,01$.

The intuition of Figure 1 is that VaR is smaller than ES. VaR underestimates the risk, which is detrimental to investor cautious investment. Although the result is obtained under different futures positions, the conclusions still hold in other cases.

4.3. Comparisons on Involving Futures

We explain why we involve futures in the model compared to the model of Bajo et al. [1], which is focused on hedging only with options. The results are shown in Figure 2.

From Figure 2, we can find that ES with futures hedging is smaller than the one without futures hedging. In this sense, it is necessary to employ futures in the hedging model. Furthermore, we discuss the effects with different parameters in the following section.

4.4. Sensitivity Analysis

One of the important factors considered in this paper is the background risk, and we discuss the effect under different background risks. $\beta =0$ means that there is additive background risk and $\beta =1$ means that only multiplied background risk exists. When β is changed in the interval of $(0,1)$, both additive and multiplied background risk are considered in the model. The details are as in Figure 3.

From Figure 3, we can find that ES is increasing with beta increasing, with or without futures hedging. It indicates that ES increases with the increase of components of multiplicative risk. When the background risk is purely additive (i.e., β = 0), ES = 0.3957 or ES = 0.2846 corresponding to the cases of hedging with or without futures. However, when the background risk is purely multiplicative (i.e., β = 1), ES = 0.6888 or ES = 0.5880 corresponding to the cases of hedging with or without futures. Take the case of β= 1 as an example: ES = 0.6888 or ES = 0.5880 implies that without futures hedging, the mean loss is 68.88% with respect to the current total wealth, and 58.80% when the investor uses futures hedging. We can conclude two-fold implications. On one hand, hedging with futures has advantages over without futures hedging. On the other hand, multiplicative background risk has more potential damage to Expected Shortfall than the additive background risk. In this sense, multiplicative risk can not be ignored.

In this paper, we set the budget, marked as C, equal to a proportion d of the current value. Larger d means more budget. We give the effect of budget on the hedging efficiency in Figure 4. We keep the other parameters invariant, and only change d. Let $d=0.01,0.03,0.07,and0.1$. Take $d=0.1$ as an example: it means that the investor spends an amount of cash of 3145 $(3.145\times 1000\times 0.1)$ on options hedging. β is set as 0.5.

From Figure 4, we can find that ES decreases firstly and then increases with respect to budget, with or without futures hedging. This indicates that it is not wise to spend too much from the budget on buying options. For example, if the investor spends 10% of the current total value on buying options, ES is 0.3740 with futures hedging and 0.505 without futures hedging. That is, the average tail loss is the percentage of 37.40% or 50.5% relative to the current total value. We can also conclude that it is necessary to introduce futures hedging. ES decreases after futures are integrated into the hedging model. Furthermore, we compare the results to ones from existing research and find that the conclusions stay consistent with Bajo et al. [1], which claim that the budget affects the optimal strike price. Details are shown in

Table 1. The effect of budget on the strike price.

d	Optimal Strike Price without Futures Hedging	Optimal Strike Price with Futures Hedging
0.05	4.498	4.892
0.1	4.892	2.068
0.3	4.104	2.167
0.5	4.860	2.824

.

Significant level or confidence level has an effect on the decisions and ES intuitively. Sensitivity analysis of a significant level are given in Figure 5.

From Figure 5, we can find that ES increases with respect to confidence level, with or without futures hedging. The investors with more intention to the fatter tail risk face smaller ES. For example, if the investor carries 10% of the tail loss, ES = 0.3386 without futures hedging and ES = 0.2648 with futures hedging. Results in Figure 5 also show the significance of extending the model of Bajo et al. [1] by introducing futures hedging. Investors are more conservative the larger the ES. The results are quite close to reality. If the investor is conservative, then he/she pays more attention to the fat tail loss. The expected loss is larger, thereby ES is larger.

The fundamental motive for the investor is to hedge against risk of the volatility of the spot price. Next, we examine the sensitive analysis of spot volatility expressed as ${\sigma }_1$ in

Table 2. The sensitivity of volatility of the spot.

Volatility of Spot	ES without Futures Hedging	ES with Futures Hedging
0.1	0.3031	0.2115
0.159	0.3247	0.2357
0.2	0.3688	0.2632
0.4	0.562	0.4221
0.6	0.681	0.5367

.

As shown in Table 2, with or without futures hedging, ES increases with respect to the volatility of spot price. As a parallel study, we discuss the impact of the volatility of futures on optimal strategy in

Table 3. The effect of volatility of future.

Volatility of Futures	ES without Futures Hedging	ES with Futures Hedging
0.1	0.344	0.2743
0.1818	0.3422	0.2482
0.2	0.346	0.2454
0.4	0.3475	0.2586
0.6	0.3477	0.2578

. Similarly, the volatility of futures denoted as ${\sigma }_2$ is taken from five values, where 0.159 is the real volatility and the others are artificial ones to make fluctuation and comparison.

As seen from Table 3, ES increases with respect to the volatility of futures, with or without futures hedging. Furthermore, results of Table 2 and Table 3 show that ES, when using futures hedging, is smaller than the one when without futures hedging regardless of volatilities of spot and futures.

There are two correlation coefficients. One is the correlation coefficients between spot and future price, and another is between spot price and background risk.

Table 4. The effect of confidence level.

rho1	rho2	ES without Futures Hedging	ES with Futures Hedging
1	0.8	0.3391	0.1687
0.8	0.8	0.3411	0.2447
0.6	0.8	0.3515	0.2945
0.4	0.8	0.3298	0.3033
0.2	0.8	0.346	0.3372
0	0.8	0.3466	0.3466
0.8	1	0.3624	0.2397
0.8	0.6	0.349	0.26
0.8	0.4	0.3101	0.2443
0.8	0.2	0.2839	0.2139
0.8	0	0.2629	0.217

describes the change process with different correlation coefficients between spot and futures prices and the correlation coefficients between spot price and background risk.

From Table 4, we can find that ES is affected by the coefficients between spot and future prices, spot price and background risk. However, it has no definite function relations.

To summarize Table 2, Table 3 and Table 4, we find that no matter how the parameters change, adding futures into Bajo’s model is beneficial for improving the hedging efficiency. ES is smaller when the investor utilizes both futures and options for hedging. For the investor, we suggest that hedging both with futures and options is advisable and not to ignore the impact of background risk, especially multiplicative background risk.

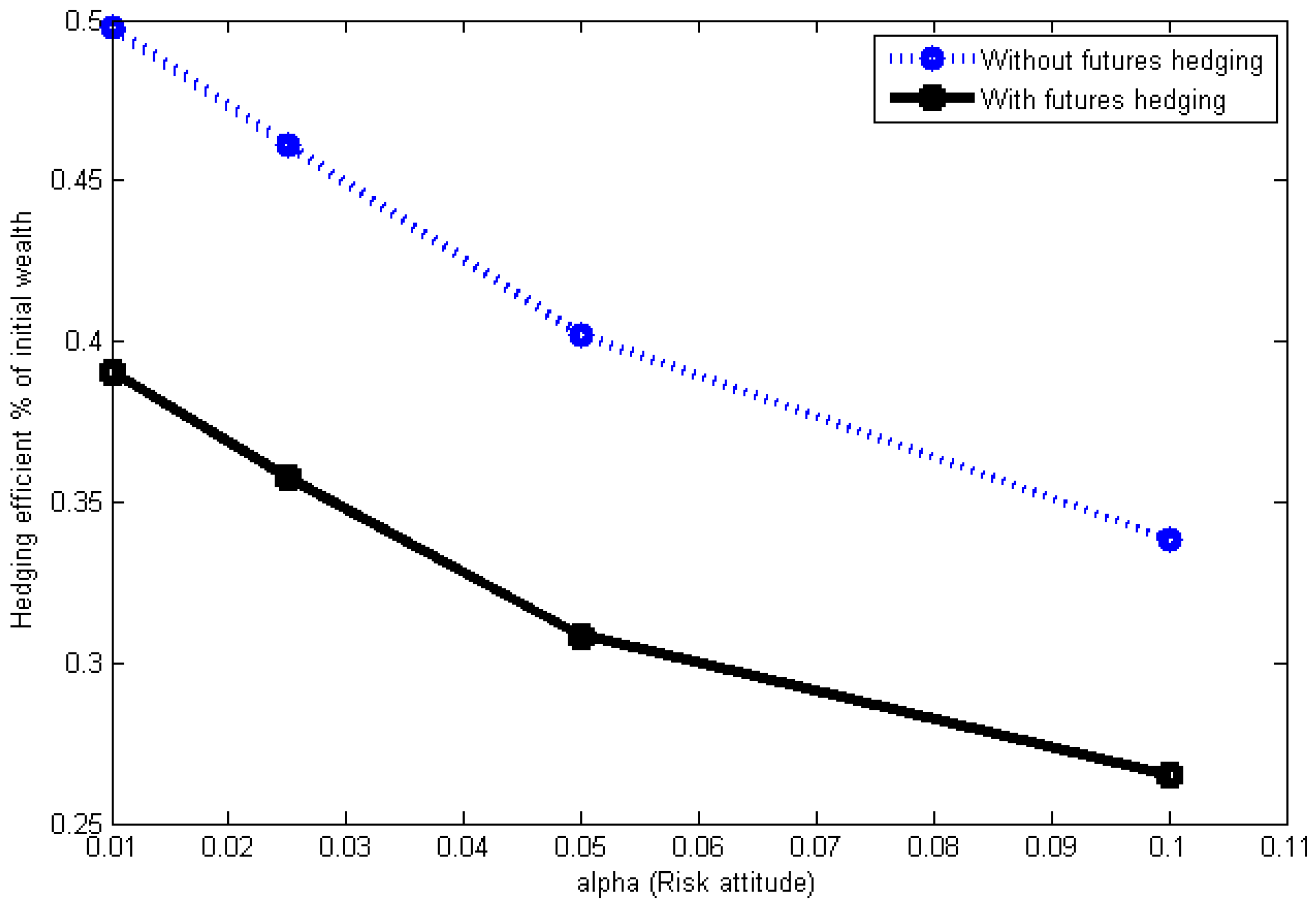
5. Conclusions

In this paper, we investigate the optimal hedging problem with futures and options. In the proposed model, futures hedging, options hedging and background risk are considered. We extend the previous research by allowing the simultaneous hedging choice of futures and options. We show a potentially important role of futures when there are price risks be it additive or multiplicative background risk. Upon comparison, we find that our model performs better than the previous approach in increasing the hedging efficiency. Some interesting results and practical implications are obtained in this paper. Theoretically, we present the necessary and sufficient conditions that guarantee the optimality of an under-hedge, a full-hedge, and an over-hedge. It stipulates sufficient conditions under which an over-hedge is optimal under the assumptions of no basis risk and a general utility. We also give the conditions when it is beneficial to hedge both with futures and options compared to hedging only with options. Practically, hedging with futures combined with options receives remarkable lower ES. The results demonstrate that our intention of adding futures in the model of Bajo et al. [1] is advisable. We find that the optimal contract is affected by the amount of cash spent on the hedging, which is contrary to the existing literature of Ahn et al. [36], but it is consistent with Bajo et al. [1]. Another important factor that we have considered is the background risk. The results show that we especially can not ignore the multiplying background risk.

In futures hedging, we do not consider the opportunity cost and market-to-market risk in futures markets. However, in practice, reserve margin is not always able to maintain the required level, and the need is higher than that stipulated in the exchange level as margin of reserves. Excessive reserve margin restricts the investor from using money, and increases the opportunity cost of investors, while low standby margin may bring losses to investors. Therefore, as future work, we are planning to consider opportunity cost and market-to-market risk.