New Scientific Contribution on the 2-D Subdomain Technique in Polar Coordinates: Taking into Account of Iron Parts
Abstract
:1. Introduction
2. A 2-D Subdomain Technique of the Magnetic Field in Polar Coordinates
2.1. Model Description and Assumptions
- The magnetic vector potential has only one component along the z-axis (i.e., ), and then, the end-effects are not considered;
- All materials are isotropic, and the permeabilities are supposed as constants in both directions (i.e., r- and -axis);
- All electrical conductivities of materials are supposed as nulls (i.e., the eddy-currents induced in the copper/iron are neglected).
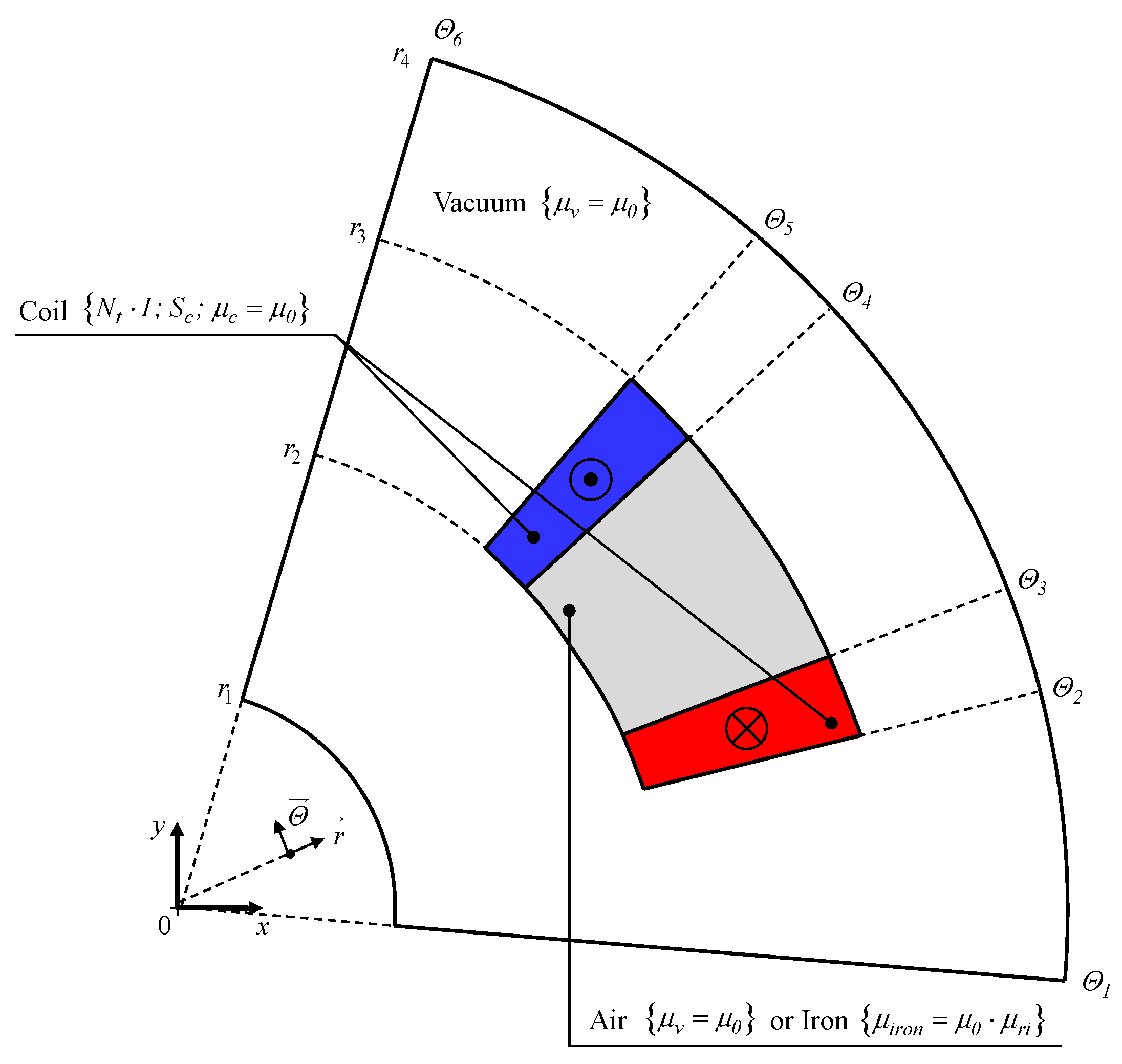
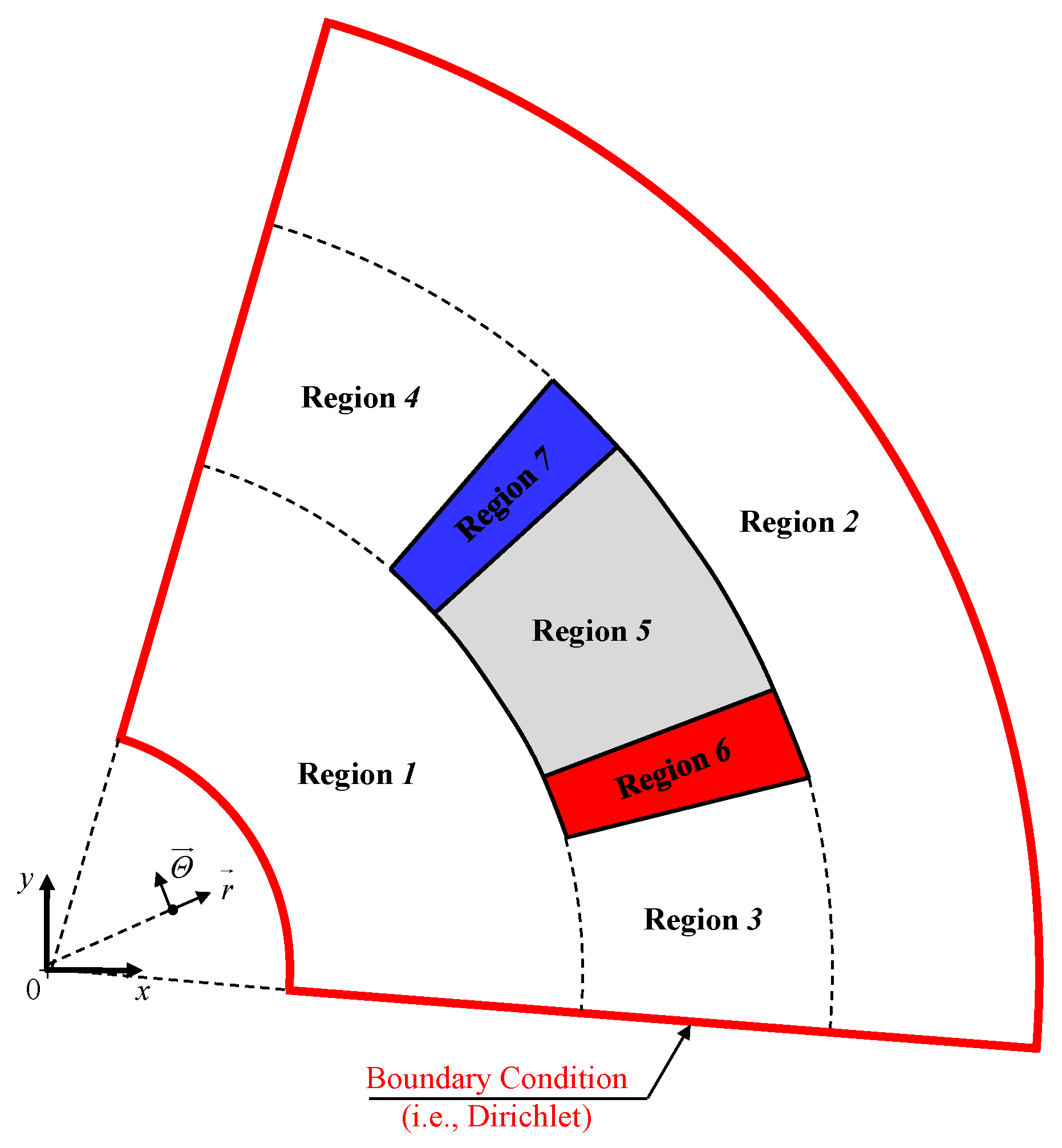
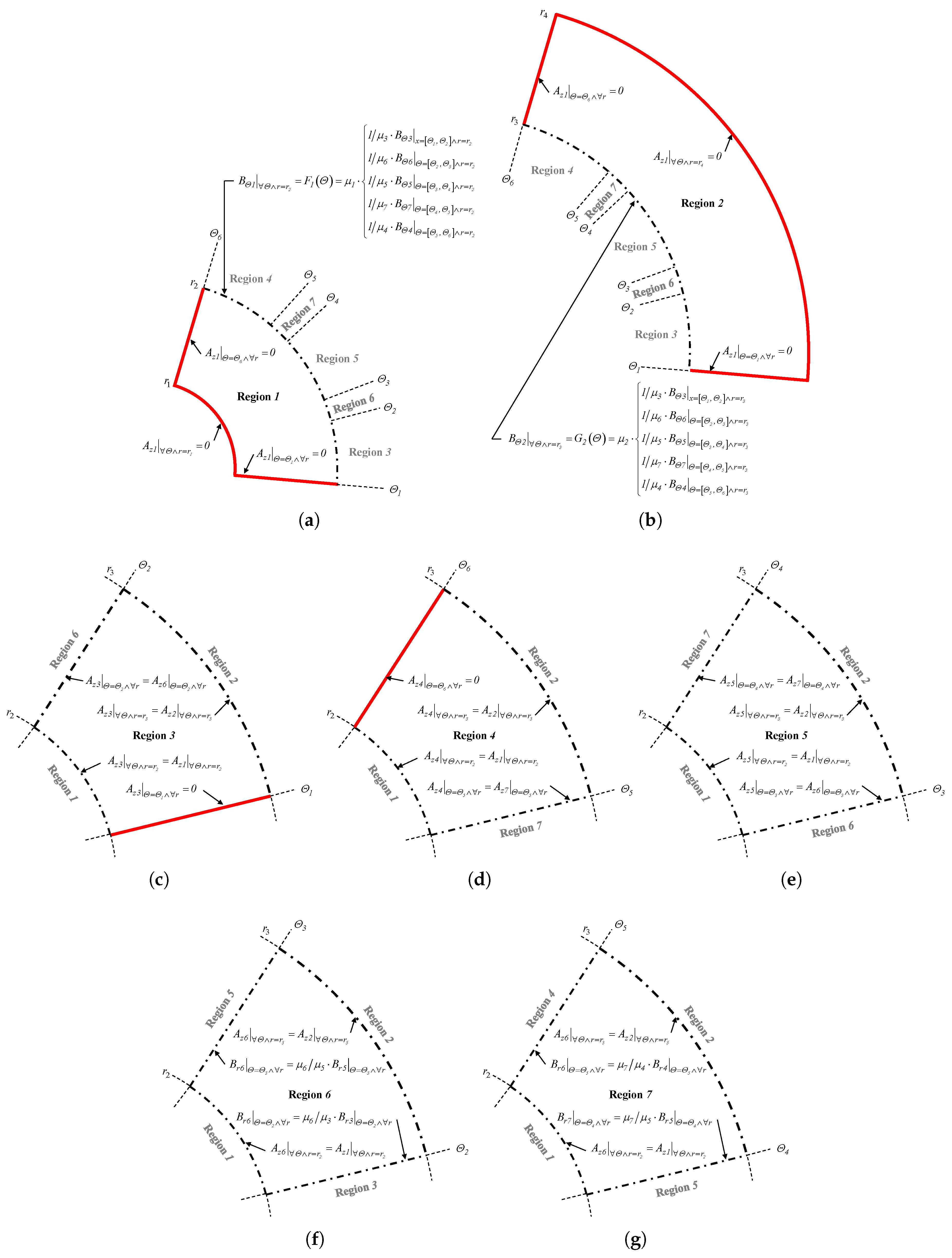
2.2. Problem Discretization in Regions
- Region 1 , with ;
- Region 2 , with ;
- Region 3 , with ;
- Region 4 , with ;
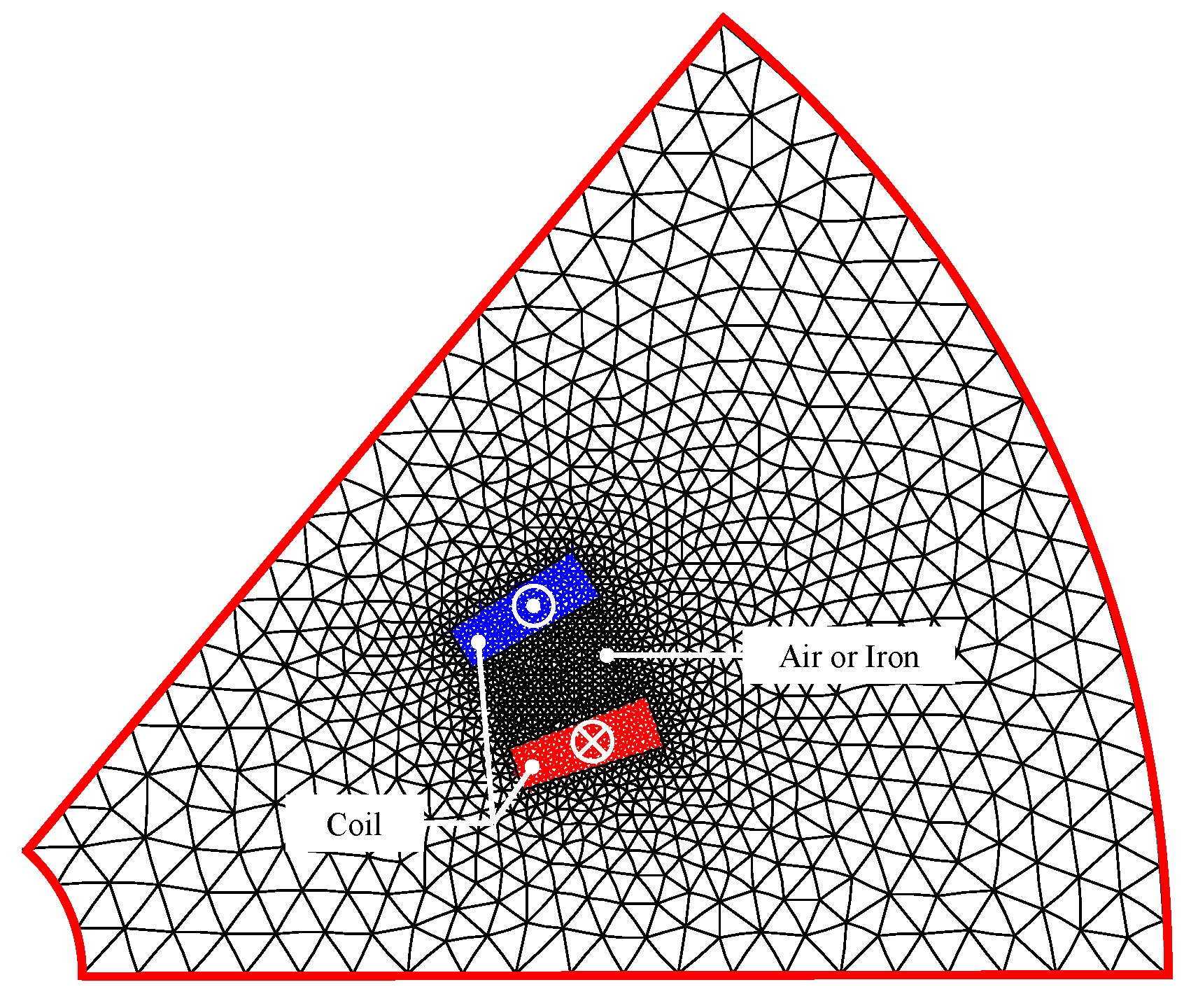
- Region 5 (i.e., the air or iron in the middle of the coil) , with for the air or for the iron;
- Region 6 (i.e., the forward conductor) , with ;
- Region 7 (i.e., the return conductor) , with .
2.3. Governing PDEs in Polar Coordinates: Laplace’s and Poisson’s Equations
2.4. Definition of Boundary Conditions
2.5. General Solutions of Various Regions
2.5.1. Region 1
2.5.2. Region 2
2.5.3. Region 3
2.5.4. Region 4
2.5.5. Region 5
2.5.6. Region 6
2.5.7. Region 7
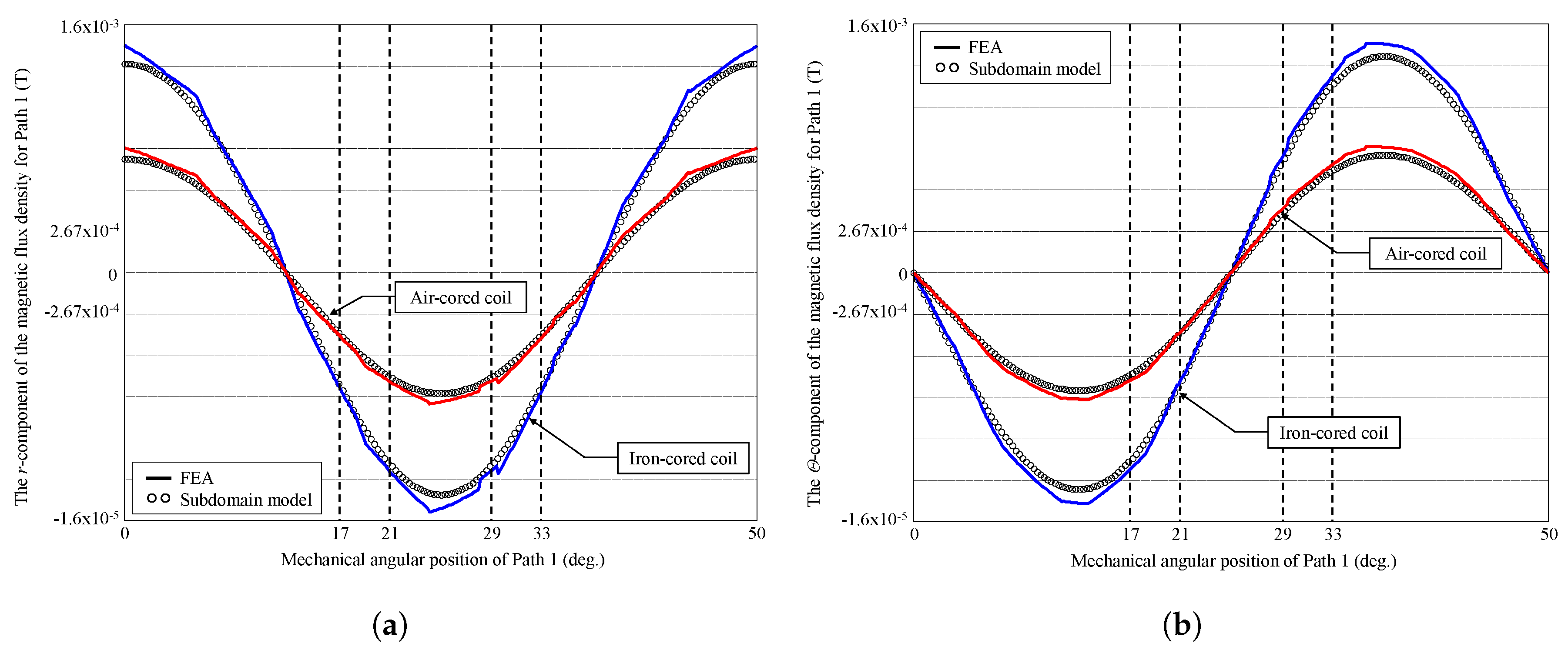
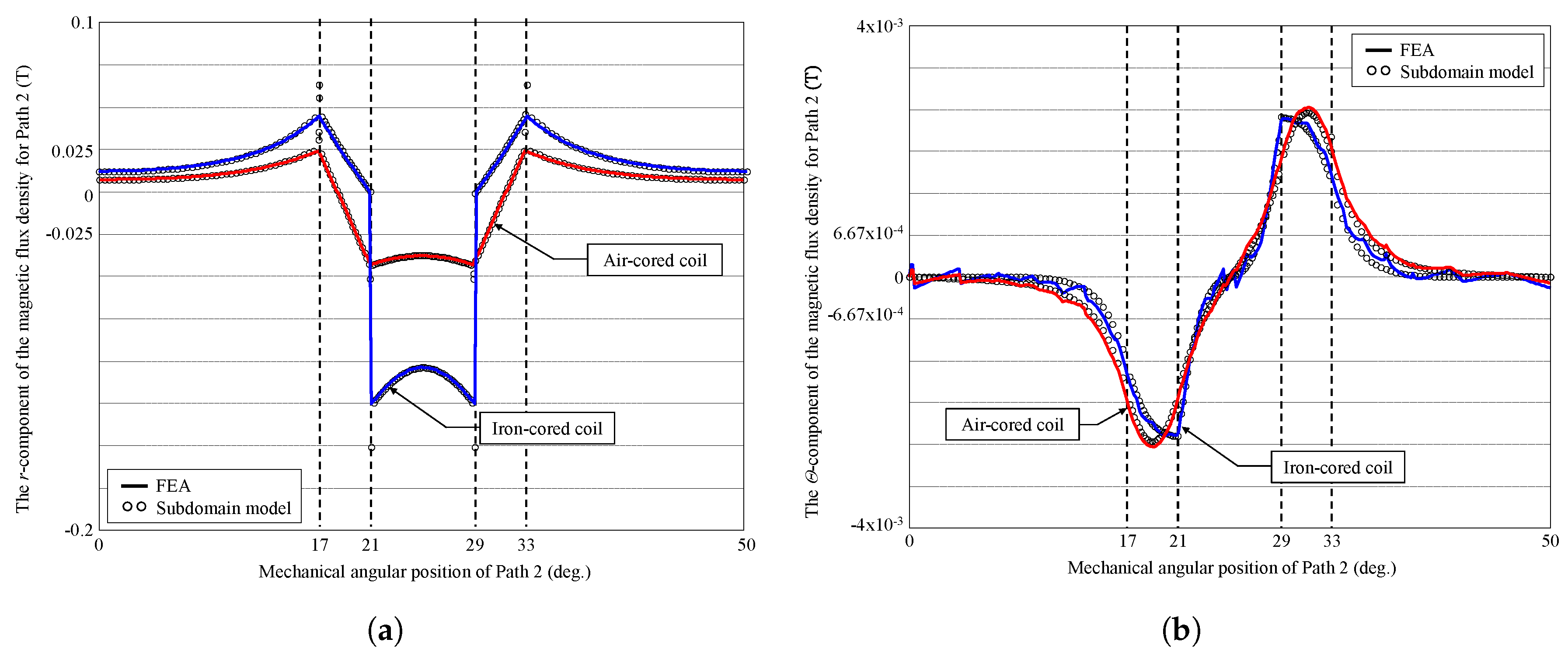
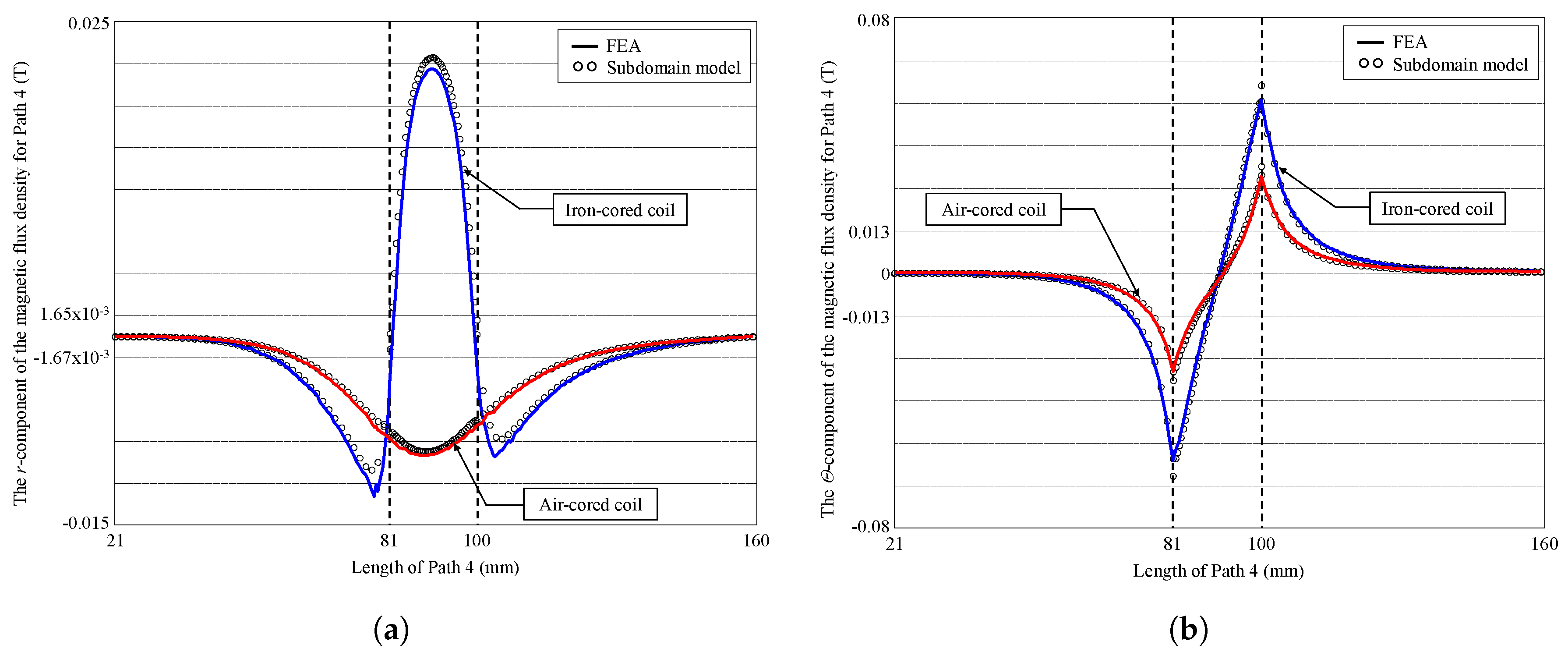
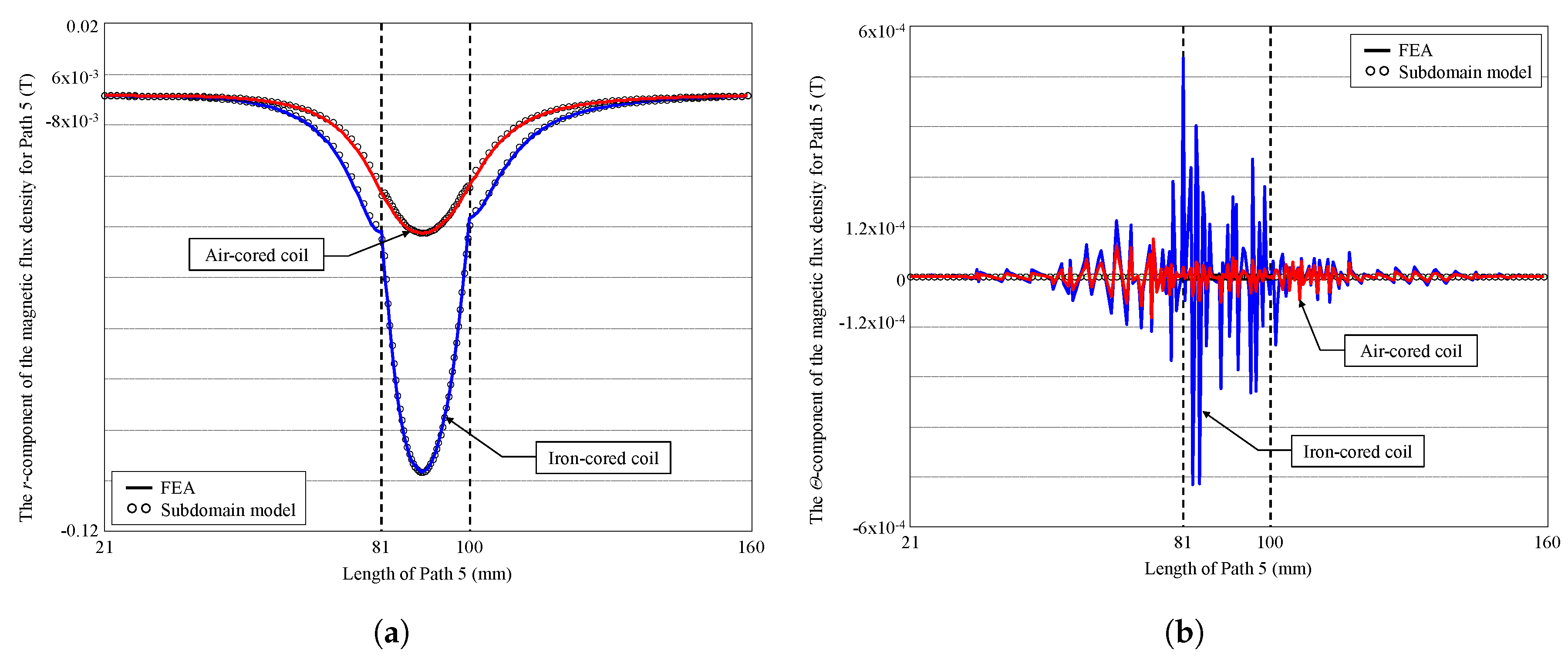
3. Validation of the Semi-Analytic Method with Finite-Element Analysis
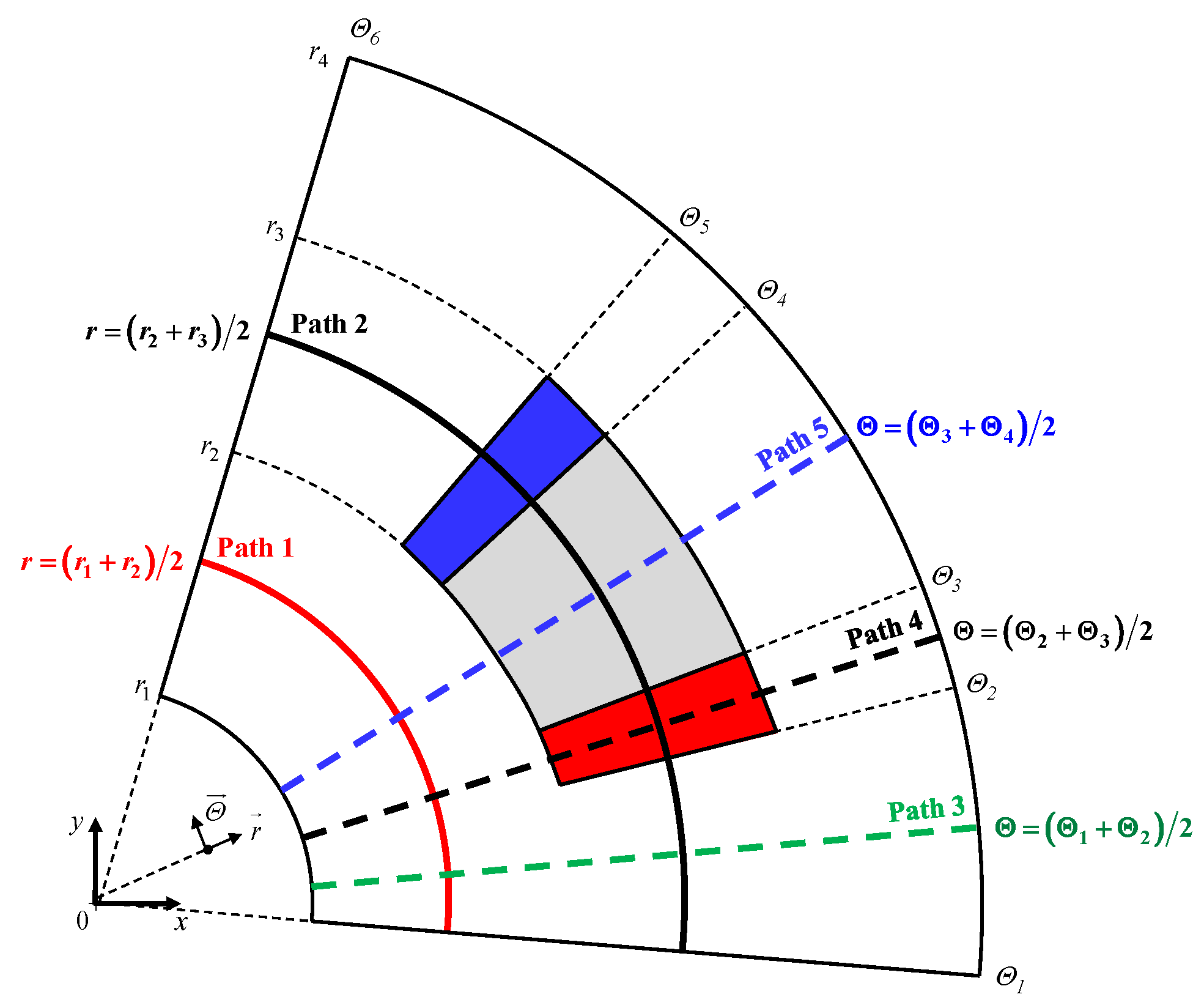
3.1. Introduction
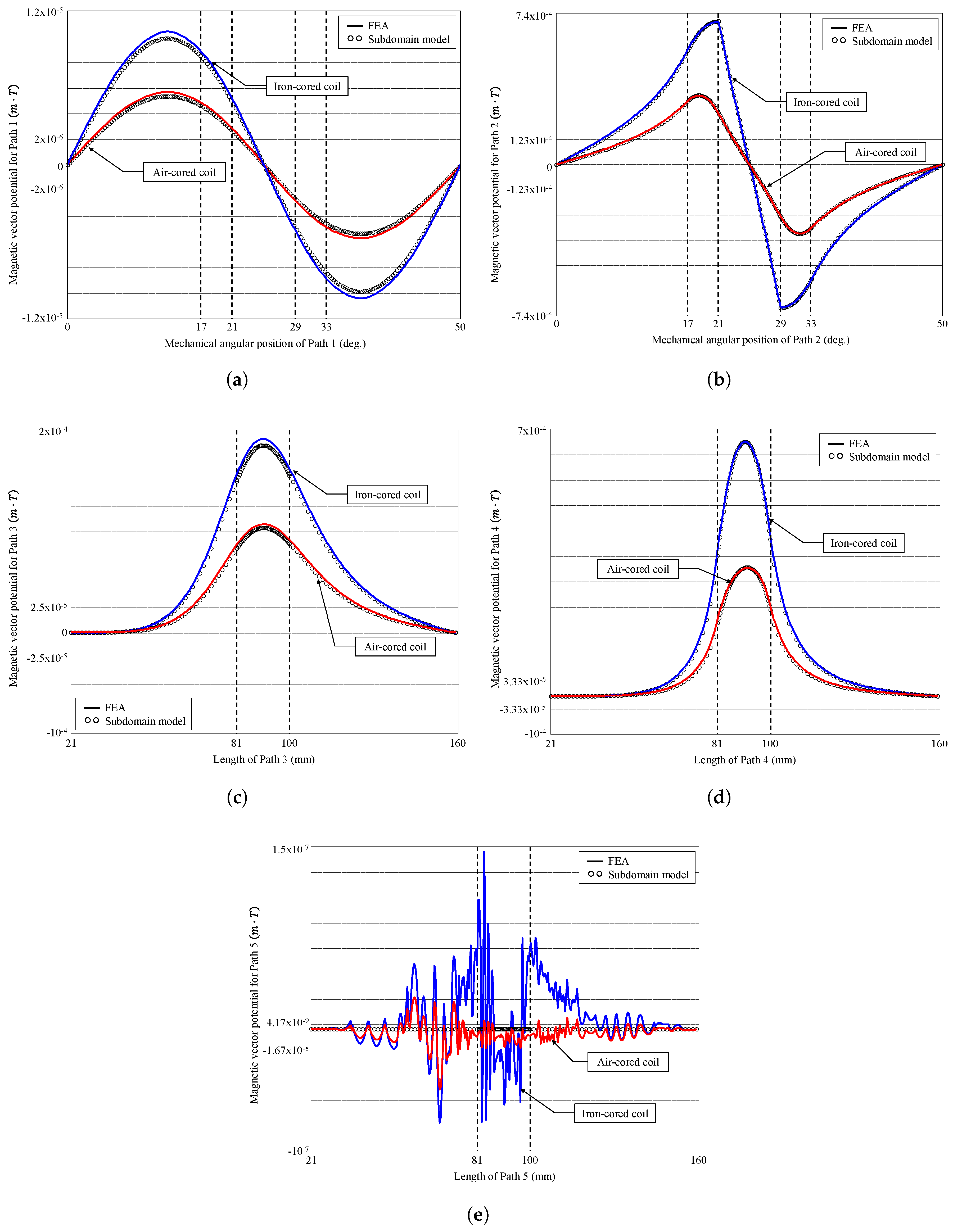
3.2. Results Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. The 2-D General Solution of PDEs (i.e., Laplace’s and Poisson’s Equations) in Polar Coordinates
Appendix B. Simplification of Laplace’s Equations According to Imposed BCs
Appendix B.1. Case-Study No. 1: Imposed on all Edges of a Region

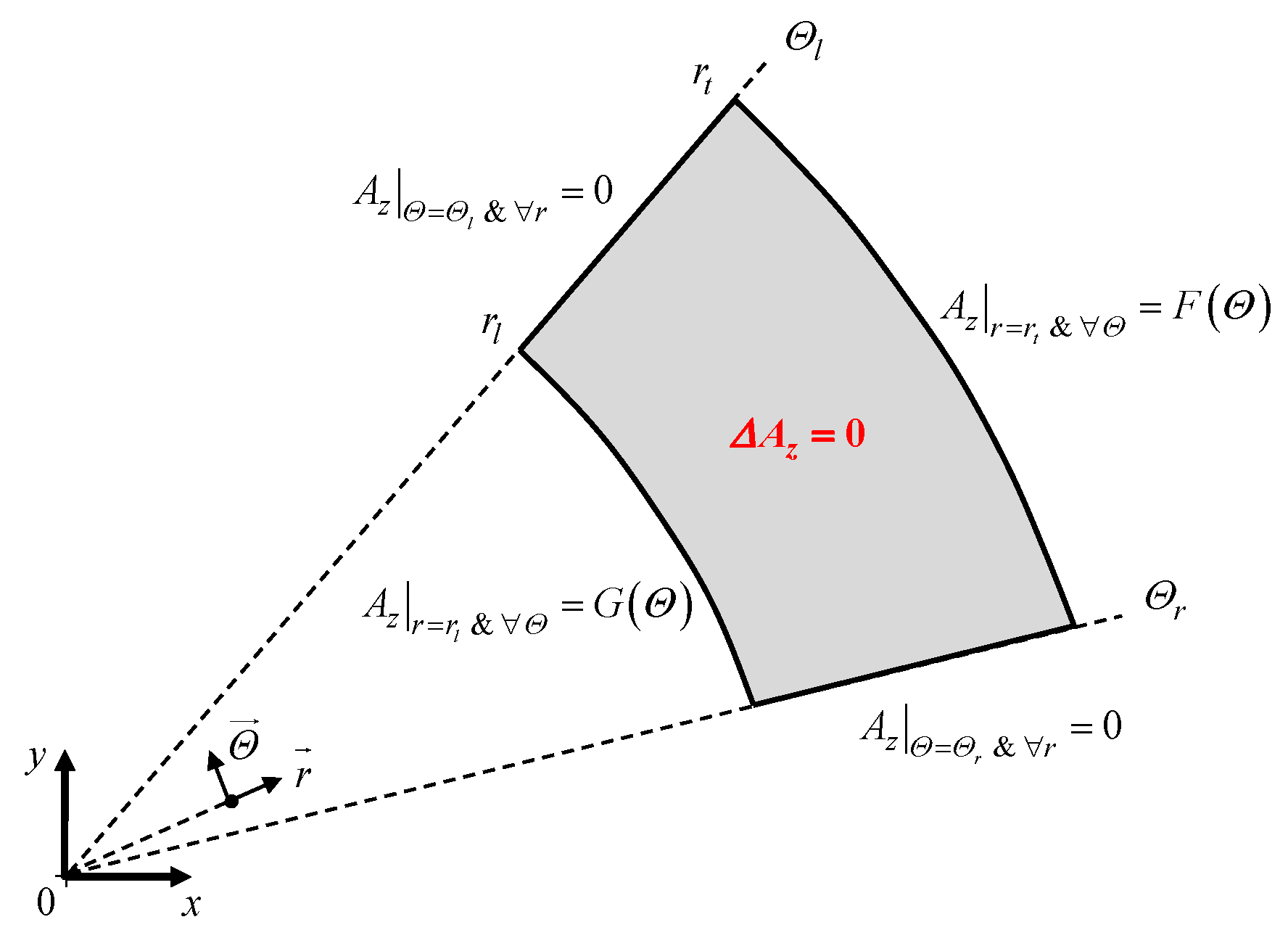
Appendix B.2. Case-Study No. 2: and Are Respectively Imposed on r- and Θ-Edges of a Region
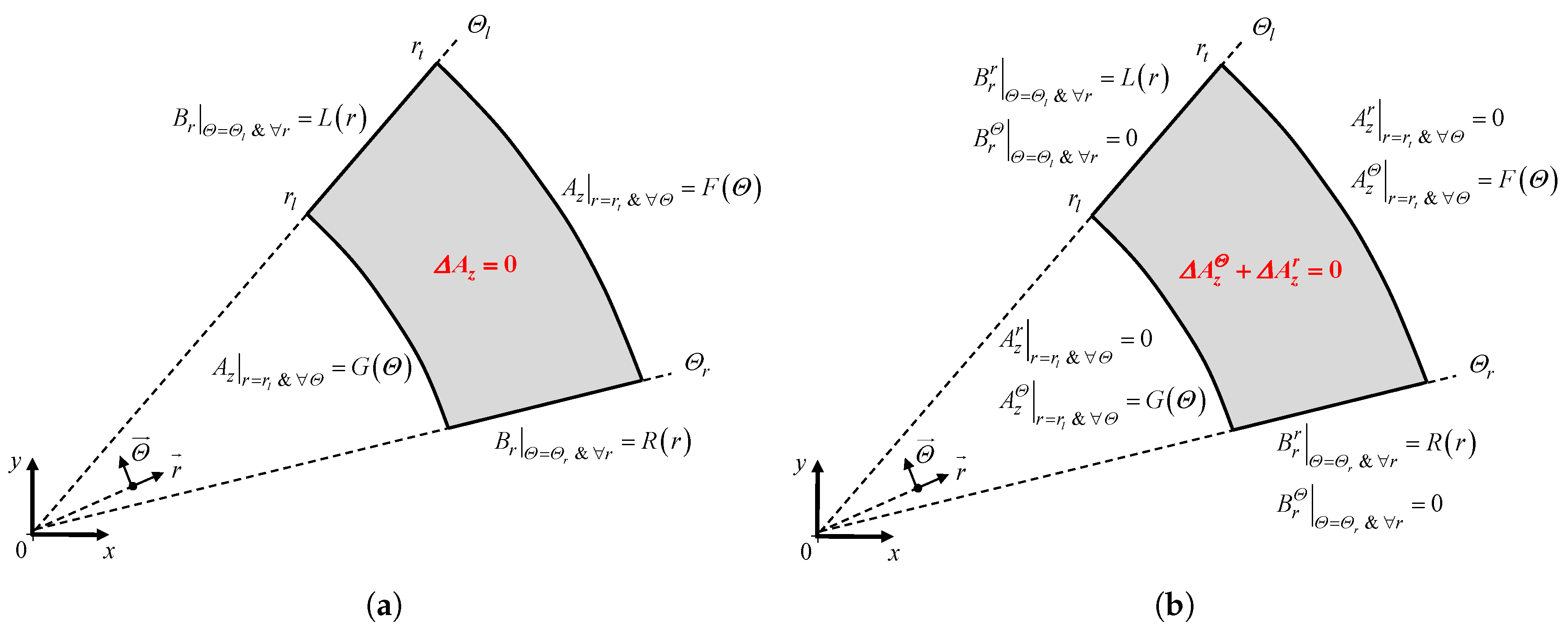
Appendix C. Solving of the Linear System
Appendix C.1. Calculation of General Integrals
Appendix C.2. Determination of Integral Constants
References
- Dubas, F.; Boughrara, K. New scientific contribution on the 2-D subdomain technique in Cartesian coordinates: Taking into account of iron parts. Math. Comput. Appl. 2017, 22. [Google Scholar] [CrossRef]
- Lehmann, T. Méthode graphique pour déterminer le trajet des lignes de force dans l’air. Revue d’Électricité: La Lumière Électrique 1909, 43–45, 103–110, 137–142, 163–168. [Google Scholar]
- Jin, J. The Finite Element Method in Electromagnetic, 2nd ed.; John Wiley and Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods, 3rd ed.; Clarendon Press: Oxford, UK, 1985. [Google Scholar]
- Wrobel, L.C.; Aliabadi, M.H. The Boundary Element Method; John Wiley and Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Kron, G. Equivalent Circuits of Electric Machinery; John Wiley and Sons, Inc.: New York, NY, USA; Chapman and Hall, Ltd.: London, UK, 1951. [Google Scholar]
- Holman, J.P. Heat Transfer, 6th ed.; McGraw-Hill Book Compagny: New York, NY, USA, 1986. [Google Scholar]
- Roters, H.C. Electromagnetic Devices; John Wiley and Sons, Inc.: New York, NY, USA, 1941. [Google Scholar]
- Driscoll, T.A.; Trefethen, L.N. Schwarz-Christoffel Mapping; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Hague, B. Electromagnetic Problems in Electrical Engineering; Oxford University Press: London, UK, 1929. [Google Scholar]
- Sylvester, P. Modern Electromagnetic Fields; Prentice-Hall: London, UK, 1968. [Google Scholar]
- Stoll, R.L. The Analysis of Eddy Currents; Clarendon Press: Oxford, UK, 1974. [Google Scholar]
- Binns, K.J.; Lawrenson, P.J.; Trowbridge, C.W. The Analytical and Numerical Solution of Electric and Magnetic Fields; John Wiley and Sons, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Melcher, J.R. Continuum Electromechanics; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Farlow, S.J. Partial Differential Equations for Scientists and Engineers; Dover, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Dubas, F.; Espanet, C. Analytical solution of the magnetic field in permanent-magnet motors taking into account slotting effect: No-load vector potential and flux density calculation. IEEE Trans. Magn. 2009, 45, 2097–2109. [Google Scholar] [CrossRef]
- Tiegna, H.; Amara, Y.; Barakat, G. Overview of analytical models of permanent magnet electrical machines for analysis and design purposes. Math. Comput. Simul. 2013, 90, 162–177. [Google Scholar] [CrossRef]
- Devillers, E.; Le Besnerais, J.; Lubin, T.; Hecquet, M.; Lecointe, J.P. A review of subdomain modeling techniques in electrical machines: Performances and applications. In Proceedings of the XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016. [Google Scholar]
- Kumar, P.; Bauer, P. Improved analytical model of a permanent-magnet brushless DC motor. IEEE Trans. Magn. 2008, 44, 2299–2309. [Google Scholar] [CrossRef]
- Dalal, A.; Kumar, P. Analytical model for permanent magnet motor with slotting effect, armature reaction, and ferromagnetic material property. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Boules, N. Two-dimensional field analysis of cylindrical machines with permanent magnet excitation. IEEE Trans. Ind. Appl. 1984, IA-20, 1267–1277. [Google Scholar] [CrossRef]
- Berkani, M.S.; Sough, M.L.; Giurgea, S.; Dubas, F.; Boualem, B.; Espanet, C. A simple analytical approach to model saturation in surface mounted permanent magnet synchronous motors. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Mishkin, E. Theory of the squirrel-cage induction machine derived directly from Maxwell’s field equations. Q. J. Mech. Appl. Math. 1954, 7, 472–487. [Google Scholar] [CrossRef]
- Panaitescu, A.; Panaitescu, I. A field model for induction machines. In Proceedings of the International Conference on Electrical Machines (ICEM), Vigo, Spain, 10–12 September 1996. [Google Scholar]
- Madescu, G.; Boldea, I.; Miller, T.J.E. An analytical iterative model (AIM) for induction motor design. In Proceedings of the Conference Record of the I996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996. [Google Scholar]
- Sprangers, R.L.J.; Motoasca, T.E.; Lomonova, E.A. Extended anisotropic layer theory for electrical machines. IEEE Trans. Magn. 2013, 49, 2217–2220. [Google Scholar] [CrossRef]
- Sprangers, R.L.J.; Paulides, J.J.H.; Gysen, B.L.J.; Lomonova, E.A. Magnetic saturation in semi-analytical harmonic modeling for electric machine analysis. IEEE Trans. Magn. 2016, 52. [Google Scholar] [CrossRef]
- Sprangers, R.L.J.; Paulides, J.J.H.; Gysen, B.L.J.; Waarma, J.; Lomonova, E.A. Semi-analytical framework for synchronous reluctance motor analysis including finite soft-magnetic material permeability. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Djelloul, K.Z.; Boughrara, K.; Ibtiouen, R.; Dubas, F. Nonlinear analytical calculation of magnetic field and torque of switched reluctance machines. In Proceedings of the CISTEM, Marrakech-Benguérir, Maroc, 26–28 October 2016. [Google Scholar]
- Djelloul, K.Z.; Boughrara, K.; Dubas, F.; Ibtiouen, R. Nonlinear analytical prediction of magnetic field and electromagnétic performances in switched reluctance machines. IEEE Trans. Magn. 2017, 53. [Google Scholar] [CrossRef]
- Theodoulidis, T.P. Model of ferrite-cored probes for eddy current nondestructive evaluation. J. Appl. Phys. 2003, 93, 3071–3078. [Google Scholar] [CrossRef]
- Theodoulidis, T.P.; Bowler, J. Eddy-current interaction of a long coil with a slot in a conductive plate. IEEE Trans. Magn. 2005, 41, 1238–1247. [Google Scholar] [CrossRef]
- Roubache, L.; Boughrara, K.; Dubas, F.; Ibtiouen, R. Semi-Analytical modeling of spoke-type permanent-magnet machines considering the iron core relative permeability: Subdomain technique and Taylor polynomial. Prog. Electromagn. Res. B 2017, 77, 85–101. [Google Scholar] [CrossRef]
- Roubache, L.; Boughrara, K.; Dubas, F.; Ibtiouen, R. Semi-analytical modeling of spoke-type permanent-magnet machines considering nonlinear magnetic saturation: Subdomain Technique and Taylor polynomial. Math. Comput. Simul. 2017. Under review. [Google Scholar]
- Abdel-Razek, A.A.; Coulomb, J.L.; Feliachi, M.; Sabonnadière, J.C. The calculation of electromagnetic torque in saturated electric machines within combined numerical and analytical solutions of the field equations. IEEE Trans. Magn. 1981, 17, 3250–3252. [Google Scholar] [CrossRef]
- Liu, Z.J.; Bi, C.; Tan, H.C.; Low, T.S. A combined numerical and analytical approach for magnetic field analysis of permanent magnet machines. IEEE Trans. Magn. 1995, 31, 1372–1375. [Google Scholar] [CrossRef]
- Mirzayee, M.; Mehrjerdi, H.; Tsurkerman, I. Analysis of a high-speed solid rotor induction motor using coupled analytical method and reluctance networks. In Proceedings of the 2005 IEEE/ACES International Conference on Wireless Communications and Applied Computational Electromagnetics (ACES), Honolulu, HI, USA, 3–7 April 2005. [Google Scholar]
- Hemeida, A.; Sergeant, P. Analytical modeling of surface PMSM using a combined solution of Maxwell’s equations and magnetic equivalent circuit. IEEE Trans. Magn. 2014, 50. [Google Scholar] [CrossRef]
- Pluk, K.J.W.; Jansen, J.W.; Lomonova, E.A. 3-D hybrid analytical modeling: 3-D Fourier modeling combined with mesh-based 3-D magnetic equivalent circuits. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Flux2D. General Operating Instructions, Version 10.2.1; Cedrat S.A. Electrical Engineering: Grenoble, France, 2008.
- Lee, S.W.; Jones, W.; Campbell, J. Convergence of numerical solution of iris-type discontinuity problems. IEEE Trans. Microw. Theory Tech. 1971, 19, 528–536. [Google Scholar]
- Mittra, R.; Itoh, T.; Li, T.-S. Analytical and numerical studies of the relative convergence phenomenon arising in the solution of an integral equation by the moment method. IEEE Trans. Microw. Theory Tech. 1972, 20, 96–104. [Google Scholar] [CrossRef]
- Rahideh, A.; Korakianitis, T. Analytical calculation of open-circuit magnetic field distribution of slotless brushless PM machines. Electr. Power Energy Syst. 2012, 44, 99–114. [Google Scholar] [CrossRef]
- Dubas, F.; Rahideh, A. Two-dimensional analytical PM eddy-current loss calculations in slotless PMSM equipped with surface-inset magnets. IEEE Trans. Magn. 2014, 50. [Google Scholar] [CrossRef]
- Gysen, B.L.J.; Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. General formulation of the electromagnetic field distribution in machines and devices using Fourier analysis. IEEE Trans. Magn. 2010, 46, 39–52. [Google Scholar] [CrossRef]

| Parameters, Symbols (Units) | Values |
|---|---|
| Number of turns of the coil, (–) | 60 |
| Supply current, I (A) | 20 |
| Conductor surface, (mm) | 120 |
| Current density of the coil, (A/mm) | ±10 |
| Effective axial length, (mm) | 60 |
| Geometrical parameters in the -axis, (deg.) | |
| Geometrical parameters in the r-axis, (mm) | |
| Relative magnetic permeability of the iron, (–) | 1,500 |
| Number of harmonics for Region 1, (–) | 260 |
| Number of harmonics for Region 2, (–) | 260 |
| Number of harmonics for Region 3, (–) | |
| Number of harmonics for Region 4, (–) | |
| Number of harmonics for Region 5, (–) | |
| Number of harmonics for Region 6, (–) | |
| Number of harmonics for Region 7, (–) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubas, F.; Boughrara, K. New Scientific Contribution on the 2-D Subdomain Technique in Polar Coordinates: Taking into Account of Iron Parts. Math. Comput. Appl. 2017, 22, 42. https://doi.org/10.3390/mca22040042
Dubas F, Boughrara K. New Scientific Contribution on the 2-D Subdomain Technique in Polar Coordinates: Taking into Account of Iron Parts. Mathematical and Computational Applications. 2017; 22(4):42. https://doi.org/10.3390/mca22040042
Chicago/Turabian StyleDubas, Frédéric, and Kamel Boughrara. 2017. "New Scientific Contribution on the 2-D Subdomain Technique in Polar Coordinates: Taking into Account of Iron Parts" Mathematical and Computational Applications 22, no. 4: 42. https://doi.org/10.3390/mca22040042






