Acceleration of Neutral Atoms by Strong Short-Wavelength Short-Range Electromagnetic Pulses
Abstract
:1. Introduction
2. Theoretical Method
3. Results and Discussion
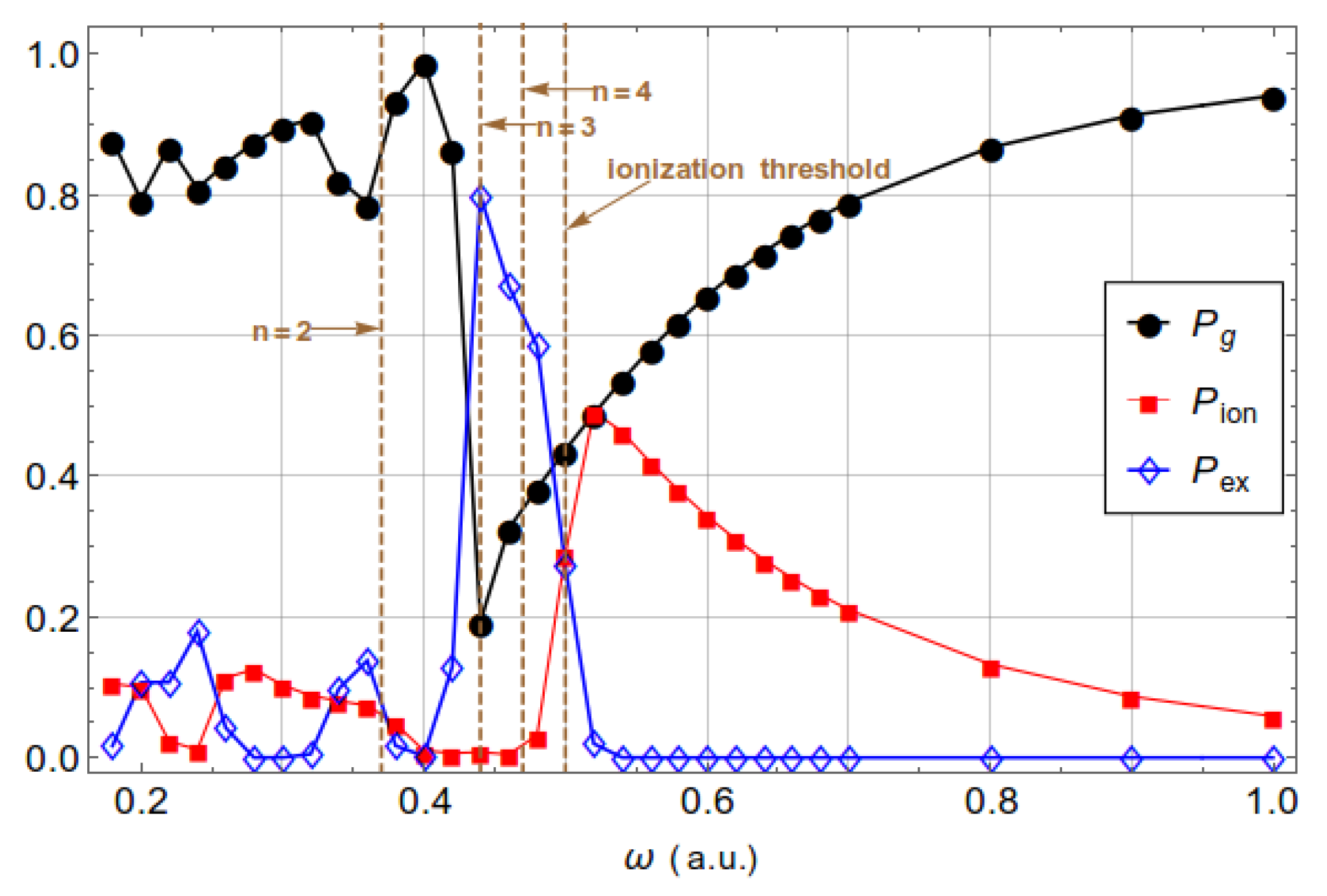
3.1. Excitation and Ionization
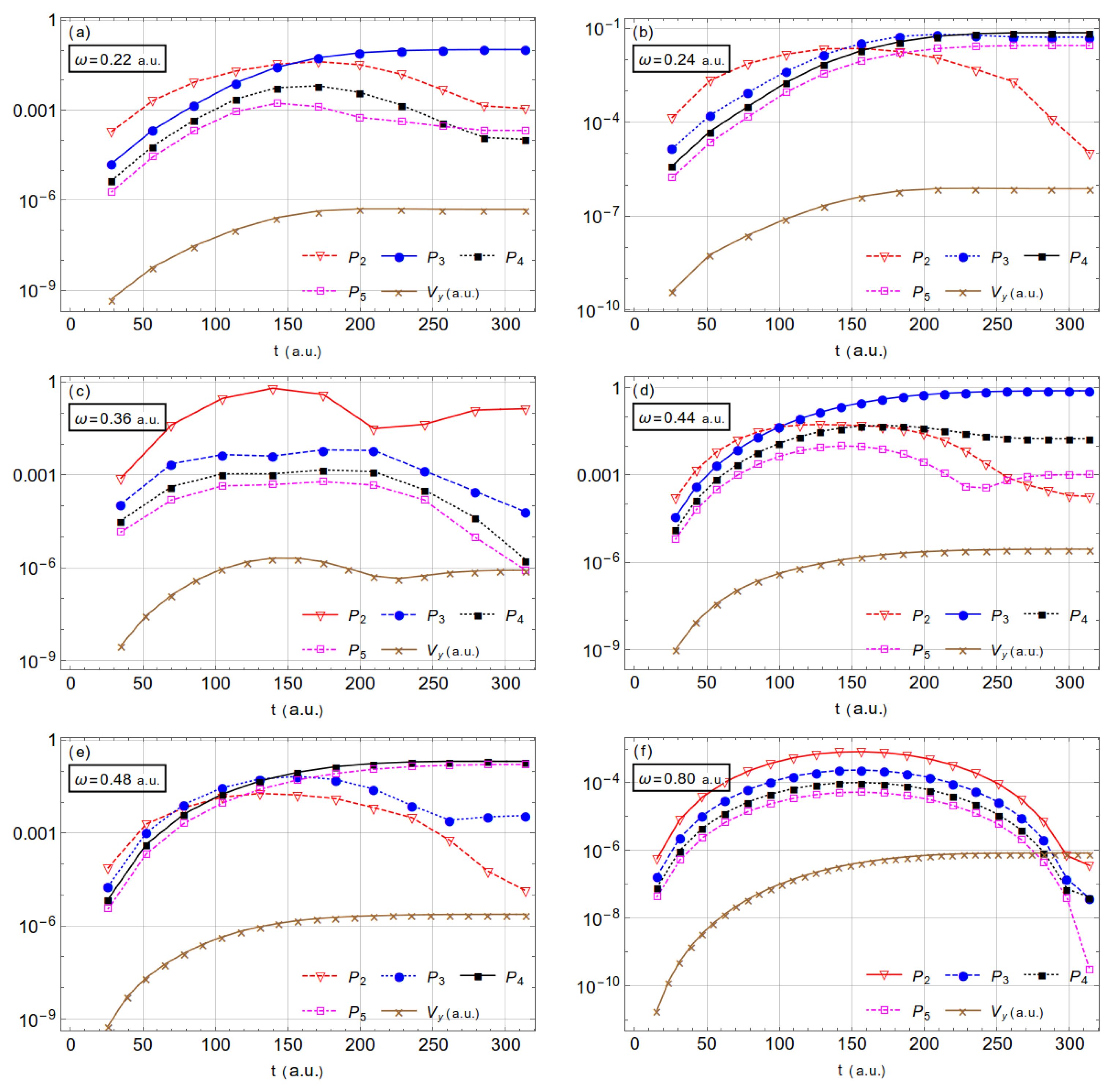
3.2. Acceleration of Neutral Atoms
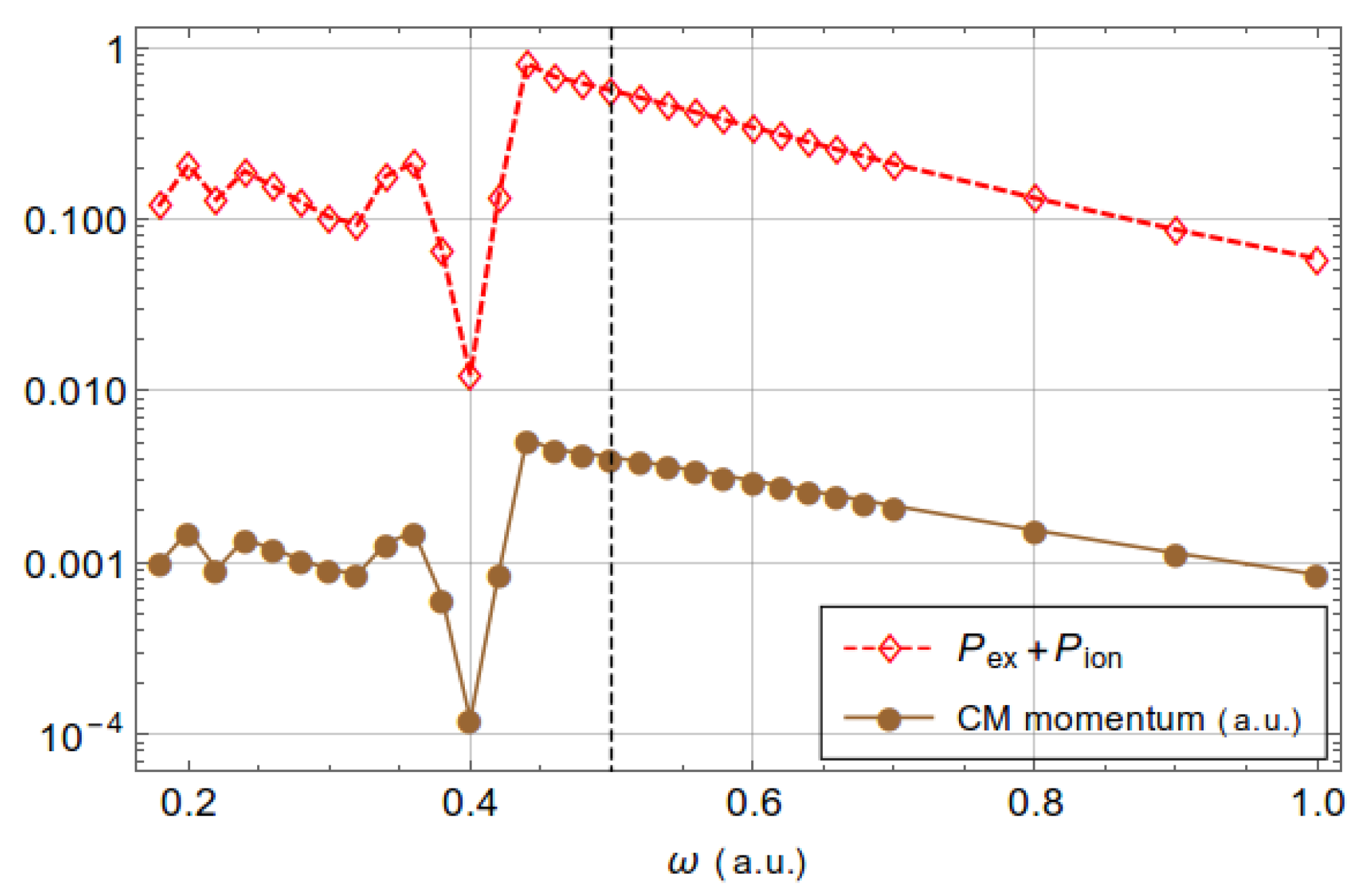
3.3. Influence of Nondipole Effects on Excitation and Ionization Processes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CM | center-of-mass |
| DVR | discrete-variable representation |
References
- Eichmann, U.; Nubbemeyer, T.; Rottke, H.; Sandner, W. Acceleration of neutral atoms in strong short-pulse laser fields. Nature 2009, 461, 1261–1264. [Google Scholar] [CrossRef]
- Kylstra, N.J.; Worthington, R.A.; Patel, A.; Knight, P.L.; De Aldana, J.R.V.; Roso, L. Breakdown of stabilization of atoms interacting with intense, high-frequency laser pulses. Phys. Rev. Lett. 2000, 85, 1835–1838. [Google Scholar] [CrossRef]
- Hemmers, O.; Guillemin, R.; Kanter, E.P.; Krässig, B.; Lindle, D.W.; Southworth, S.H.; Wehlitz, R.; Baker, J.; Hudson, A.; Lotrakul, M.; et al. Dramatic Nondipole Effects in Low-Energy Photoionization: Experimental and Theoretical Study of Xe 5s. Phys. Rev. Lett. 2003, 91, 053002. [Google Scholar] [CrossRef] [PubMed]
- Førre, M.; Hansen, J.P.; Kocbach, L.; Selstø, S.; Madsen, L.B. Nondipole ionization dynamics of atoms in superintense high-frequency attosecond pulses. Phys. Rev. Lett. 2006, 97, 043601. [Google Scholar] [CrossRef]
- Reiss, H.R. Limits on tunneling theories of strong-field ionization. Phys. Rev. Lett. 2008, 101, 043002. [Google Scholar] [CrossRef]
- Smeenk, C.T.L.; Arissian, L.; Zhou, B.; Mysyrowicz, A.; Villeneuve, D.M.; Staudte, A.; Corkum, P.B. Partitioning of the linear photon momentum in multiphoton ionization. Phys. Rev. Lett. 2011, 106, 193002. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, A.; Maurer, J.; Mayer, B.W.; Phillips, C.R.; Gallmann, L.; Keller, U. Breakdown of the dipole approximation in strong-field ionization. Phys. Rev. Lett. 2014, 113, 243001. [Google Scholar] [CrossRef]
- Chelkowski, S.; Bandrauk, A.D.; Corkum, P.B. Photon momentum sharing between an electron and an ion in photoionization: From one-photon (photoelectric effect) to multiphoton absorption. Phys. Rev. Lett. 2014, 113, 263005. [Google Scholar] [CrossRef] [PubMed]
- Førre, M.; Simmonsen, A.S. Nondipole ionization dynamics in atoms induced by intence xuv laser fields. Phys. Rev. A 2014, 90, 053411. [Google Scholar] [CrossRef]
- Klaiber, M.; Hatsagortsyan, K.Z.; Wu, J.; Luo, S.S.; Grugan, P.; Walker, B.C. Limits of strong field rescattering in the relativistic regime. Phys. Rev. Lett. 2017, 118, 093001. [Google Scholar] [CrossRef]
- Ilchen, M.; Hartmann, G.; Gryzlova, E.V.; Achner, A.; Allaria, E.; Beckmann, A.; Braune, M.; Buck, J.; Callegari, C.; Coffee, R.N.; et al. Symmetry breakdown of electron emission in extreme ultraviolet photoionization of argon. Nat. Commun. 2018, 9, 4659. [Google Scholar] [CrossRef] [PubMed]
- Maurer, J.; Keller, U. Ionization in intense laser fields beyond the electric dipole approximation: Concepts, methods, achievements and future directions. J. Phys. B 2021, 54, 094001. [Google Scholar] [CrossRef]
- Førre, M. Nondipole effects and photoelectron momentum shifts in strong-field ionization by infrared light. Phys. Rev. A 2022, 106, 013104. [Google Scholar] [CrossRef]
- Mishra, M.; Kalita, D.J.; Gupta, A.K. Breakdown of dipole approximation and its effect on high harmonic generation. Eur. Phys. J. D 2012, 66, 169. [Google Scholar] [CrossRef]
- Bray, A.W.; Eichmann, U.; Patchkovskii, S. Dissecting strong-field excitation dynamics with atomic-momentum spectroscopy. Phys. Rev. Lett. 2020, 124, 233202. [Google Scholar] [CrossRef]
- Melezhik, V.S. Quantum-quasiclassical analysis of center-of-mass nonseparability in hydrogen atom stimulated by strong laser fields. J. Phys. A Math. Theor. 2023, 56, 154003. [Google Scholar] [CrossRef]
- Maher-McWilliams, C.; Douglas, P.; Barker, P.F. Laser-driven acceleration of neutral particles. Nat. Photonics 2012, 6, 386–390. [Google Scholar] [CrossRef]
- Wang, P.X.; Wei, Q.; Cai, P.; Wang, J.X.; Ho, Y.K. Neutral particles pushed or pulled by laser pulses. Opt. Lett. 2016, 41, 230–233. [Google Scholar] [CrossRef]
- Cai, P.; Zha, J.J.; Xie, Y.J.; Wei, Q.; Wang, P.X. Rydberg-atom acceleration by tightly focused intence laser pulses. Phys. Rev. A 2019, 99, 053401. [Google Scholar] [CrossRef]
- Trabert, D.; Anders, N.; Brennecke, S.; Schöffler, M.S.; Jahnke, T.; Schmidt, L.P.H.; Kunitski, M.; Lein, M.; Dörner, R.; Eckart, S. Nonadiabatic strong field ionization of atomic hydrogen. Phys. Rev. Lett. 2021, 127, 273201. [Google Scholar] [CrossRef]
- Yuan, K.J.; Lefebvre, C.; Chelkowski, S.; Lu, H.; Bandrauk, A.D. Polarization of high-order harmonic generation in oriented molecules with intense ultrashort laser pulses. Phys. Rev. A 2020, 101, 023411. [Google Scholar] [CrossRef]
- Pauly, T.; Bondy, A.; Hamilton, K.R.; Douguet, N.; Tong, X.M.; Chetty, D.; Bartschat, K. Ellipticity dependence of excitation and ionization of argon atoms by short-pulse infrared radiation. Phys. Rev. A 2020, 102, 013116. [Google Scholar] [CrossRef]
- Melezhik, V.S.; Schmelcher, P. Quantum energy flow in atomic ions moving in magnetic fields. Phys. Rev. Lett. 2000, 84, 1870–1873. [Google Scholar] [CrossRef] [PubMed]
- Melezhik, V.S.; Cohen, J.S.; Hu, C.Y. Stripping and excitation in collisions between p and He+(n≤3) calculated by a quantum time-dependent approach with semiclassical trajectories. Phys. Rev. A 2004, 69, 032709. [Google Scholar] [CrossRef]
- Melezhik, V.S.; Idziaszek, Z.; Negretti, A. Impact of ion motion on atom-ion confinement-induced resonances in hybrid traps. Phys. Rev. A 2019, 100, 063406. [Google Scholar] [CrossRef]
- Melezhik, V.S. Improving efficiency of sympathetic cooling in atom-ion and atom-atom confined collisions. Phys. Rev. A 2021, 103, 053109. [Google Scholar] [CrossRef]
- Melezhik, V.S.; Baye, D. Nonperturbative time-dependent approach to breakup of halo nuclei. Phys. Rev. C 1999, 59, 3232–3239. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric numerical integration illustrated by the Störmer–Verlet method. Acta Numerica 2003, 12, 399–450. [Google Scholar] [CrossRef]
- Shadmehri, S.; Melezhik, V.S. A hydrogen atom in strong elliptically polarized laser fields within discrete variable representation. Laser Phys. 2023, 33, 026001. [Google Scholar] [CrossRef]
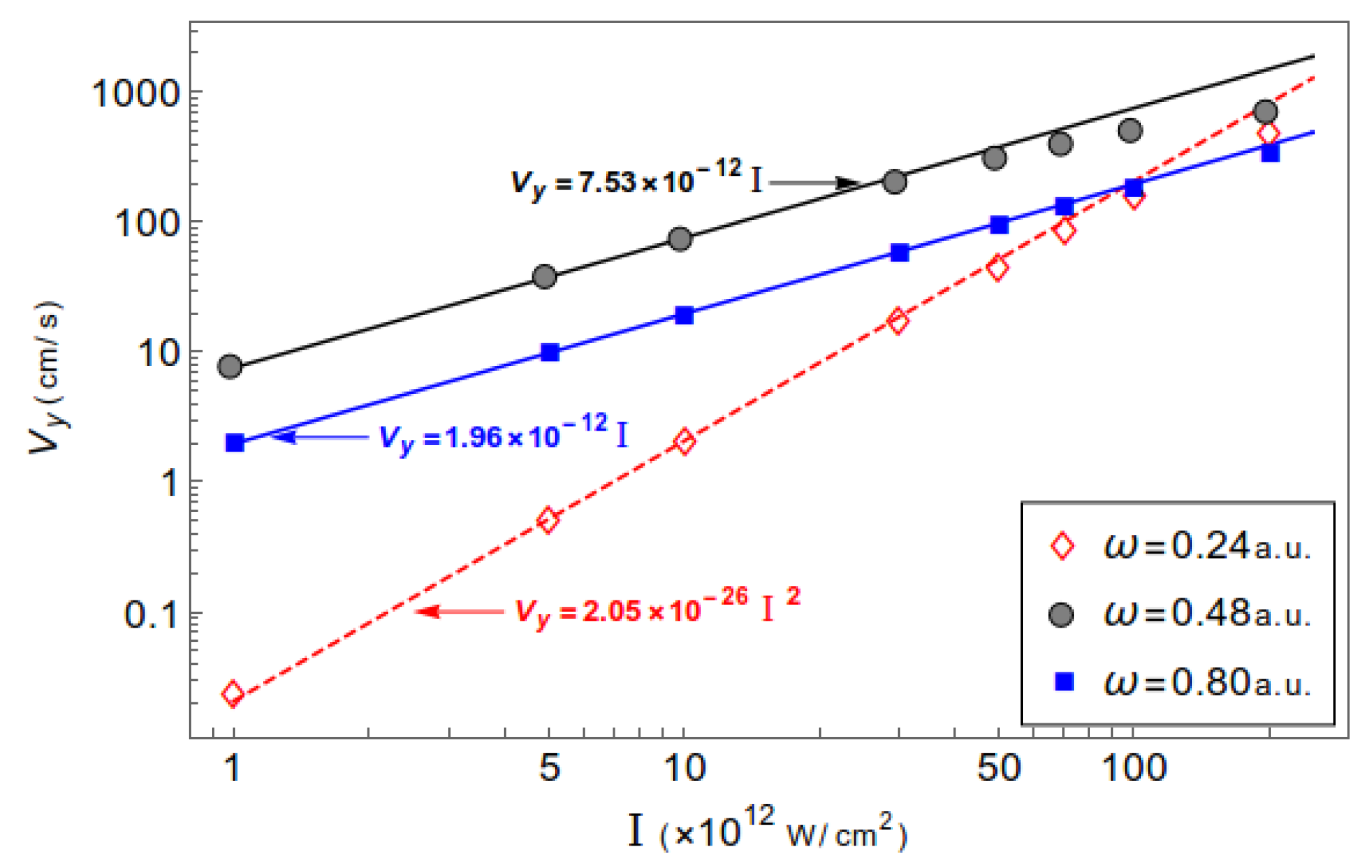
| Vy (cm/s) | |||
|---|---|---|---|
| I (×1012 W/cm2) | ω = 0.80 a.u. | ω = 0.48 a.u. | ω = 0.24 a.u. |
| 1 | 1.97 | 7.90 | 0.024 |
| 10 | 19.6 | 75.7 | 2.06 |
| 50 | 95.2 | 317 | 46.4 |
| 100 | 184 | 517 | 163 |
| 200 | 344 | 722 | 488 |
| Pg | Pex | |||||
|---|---|---|---|---|---|---|
| Dipole | Nondipole | 1 | Dipole | Nondipole | 1 | |
| 0.30 | 0.896815 | 0.896805 | 1.05 × 10 | 6.3410 × 10 | 6.3414 × 10 | 6.59 × 10 |
| 0.40 | 0.987600 | 0.987599 | 1.34 × 10 | 2.3058 × 10 | 2.3052 × 10 | 2.51 × 10 |
| 0.48 | 0.382308 | 0.382294 | 3.54 × 10 | 5.8582 × 10 | 5.8568 × 10 | 2.37 × 10 |
| 0.52 | 0.488483 | 0.488465 | 3.74 × 10 | 1.9974 × 10 | 1.9984 × 10 | 4.84 × 10 |
| 0.80 | 0.867150 | 0.867131 | 2.20 × 10 | 4.6748 × 10 | 4.6756 × 10 | 1.64 × 10 |
| 1.00 | 0.941058 | 0.941045 | 1.39 × 10 | 4.8210 × 10 | 4.8218 × 10 | 1.68 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melezhik, V.S.; Shadmehri, S. Acceleration of Neutral Atoms by Strong Short-Wavelength Short-Range Electromagnetic Pulses. Photonics 2023, 10, 1290. https://doi.org/10.3390/photonics10121290
Melezhik VS, Shadmehri S. Acceleration of Neutral Atoms by Strong Short-Wavelength Short-Range Electromagnetic Pulses. Photonics. 2023; 10(12):1290. https://doi.org/10.3390/photonics10121290
Chicago/Turabian StyleMelezhik, Vladimir S., and Sara Shadmehri. 2023. "Acceleration of Neutral Atoms by Strong Short-Wavelength Short-Range Electromagnetic Pulses" Photonics 10, no. 12: 1290. https://doi.org/10.3390/photonics10121290





