Quantitative Analysis of the Effect of Atmospheric Turbulence on a Bessel–Gaussian Beam
Abstract
:1. Introduction
2. Formulation
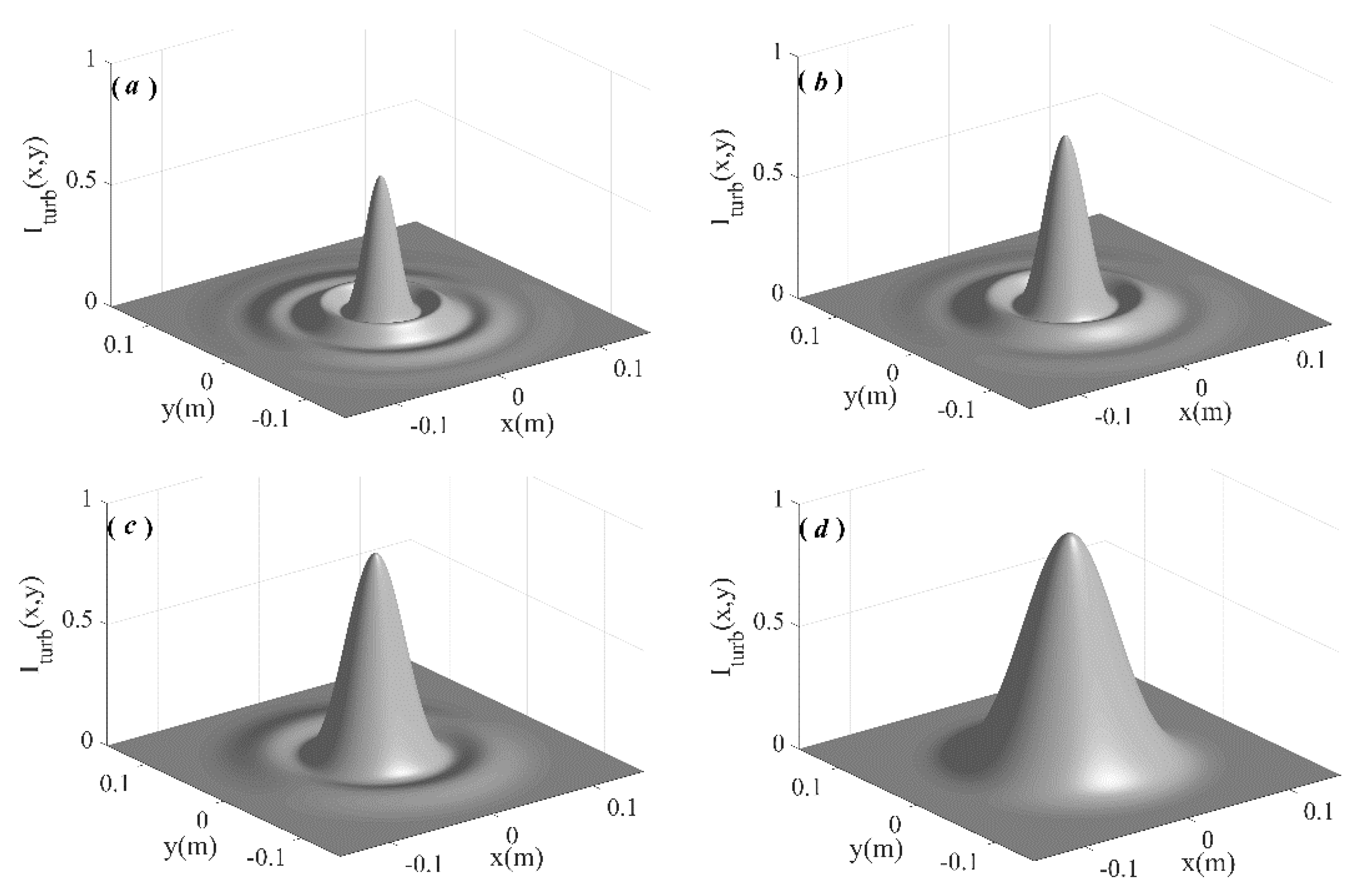
3. Numerical Results and Analysis
4. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Slusher, R.E. Laser technology. Rev. Mod. Phys. 1999, 71, S471–S479. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef] [Green Version]
- Berge, L.; Skupin, S.; Nuter, R.; Kasparian, J.; Wolf, J.P. Ultrashort filaments of light in weakly ionized, optically transparent media. Rep. Prog. Phys. 2007, 70, 1633–1713. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N. Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 1941, 32, 16–18. [Google Scholar]
- Cai, Y.; He, S. Average intensity and spreading of an elliptical Gaussian beam propagating in a turbulent atmosphere. Opt. Lett. 2006, 31, 568–570. [Google Scholar] [CrossRef]
- Chu, X. Evolution of an Airy beam in turbulence. Opt. Lett. 2011, 36, 2701–2703. [Google Scholar] [CrossRef]
- Zhu, X.; Kahn, J.M. Free-space optical communication through atmospheric turbulence channels. IEEE Trans. Commun. 2002, 50, 1293–1300. [Google Scholar]
- Gu, Y.; Gbur, G. Scintillation of Airy beam arrays in atmospheric turbulence. Opt. Lett. 2010, 35, 3456–3458. [Google Scholar] [CrossRef]
- Xu, Y.; Lan, B.; Liu, C.; Chen, M.; Tang, A.; Xian, H. Adaptive optics pre-compensation for orbital angular momentum beams transmitting through simulated atmospheric turbulence. Opt. Express 2023, 31, 13665–13671. [Google Scholar] [CrossRef] [PubMed]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef] [PubMed]
- Weyrauch, T.; Vorontsov, M.A. Free-space laser communications with adaptive optics: Atmospheric compensation experiments. J. Opt. Fiber. Commun. Rep. 2004, 1, 355–379. [Google Scholar] [CrossRef]
- Dayton, D.; Sandven, S.; Gonglewski, J.; Browne, S.; Rogers, S.; McDermott, S. Adaptive optics using a liquid crystal phase modulator in conjunction with a Shack-Hartmann wave-front sensor and zonal control algorithm. Opt. Express 1997, 1, 338–346. [Google Scholar] [CrossRef]
- Belousov, V.N.; Galaktionov, I.V.; Kudryashov, A.V.; Nikitin, A.N.; Otrubyannikova, O.V.; Rukosuev, A.L.; Samarkin, V.V.; Sivertceva, I.V.; Sheldakova, J.V. Adaptive optical system for correction of laser beam going through turbulent atmosphere. Proc. SPIE 2020, 11560, 1156026. [Google Scholar]
- Cox, M.A.; Mphuthi, N.; Nape, I.; Mashaba, N.; Cheng, L.; Forbes, A. Structured light in turbulence. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 7500521. [Google Scholar] [CrossRef]
- Nape, I.; Singh, K.; Klug, A.; Buono, W.; Rosales-Guzman, C.; McWilliam, A.; Franke-Arnold, S.; Kritzinger, A.; Forbes, P.; Dudley, A.; et al. Revealing the invariance of vectorial structured light in complex media. Nat. Photonics 2022, 16, 538–546. [Google Scholar] [CrossRef]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence. J. Opt. Soc. Am. A 2014, 31, 2038–2045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Liang, X.; Goutsoulas, M.; Li, D.; Yang, X.; Yin, S.; Xu, J.; Christodoulides, D.N.; Efremidis, N.K.; Chen, Z. Robust propagation of pin-like optical beam through atmospheric turbulence. APL Photonics 2019, 4, 076103. [Google Scholar] [CrossRef] [Green Version]
- Klug, A.; Peters, C.; Forbes, A. Robust structured light in atmospheric turbulence. Adv. Photonics 2023, 5, 016006. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Chu, X. Quantitative description of turbulence effect on a beam. J. Opt. 2023, 52, 63. [Google Scholar] [CrossRef]
- Yura, H.T.; Hanson, S.G. Optical beam wave propagation through complex optical systems. J. Opt. Soc. Am. A 1987, 4, 1931–1948. [Google Scholar] [CrossRef]
- Hwang, C.Y.; Kim, K.Y.; Lee, B. Bessel-like beam generation by superposing multiple Airy beams. Opt. Express 2011, 19, 7356–7364. [Google Scholar] [CrossRef] [PubMed]
- Chu, X. Analytical study on the self-healing property of Bessel beam. Eur. Phys. J. D 2012, 66, 259. [Google Scholar] [CrossRef]
- Testorf, M.E.; Hennelly, B.M.; Ojeda-Castaneda, J. Phase-Space Optics: Fundamentals and Applications; McGraw-Hill: New York, NY, USA, 2009; ISBN 978-0-07-159799-9. [Google Scholar]
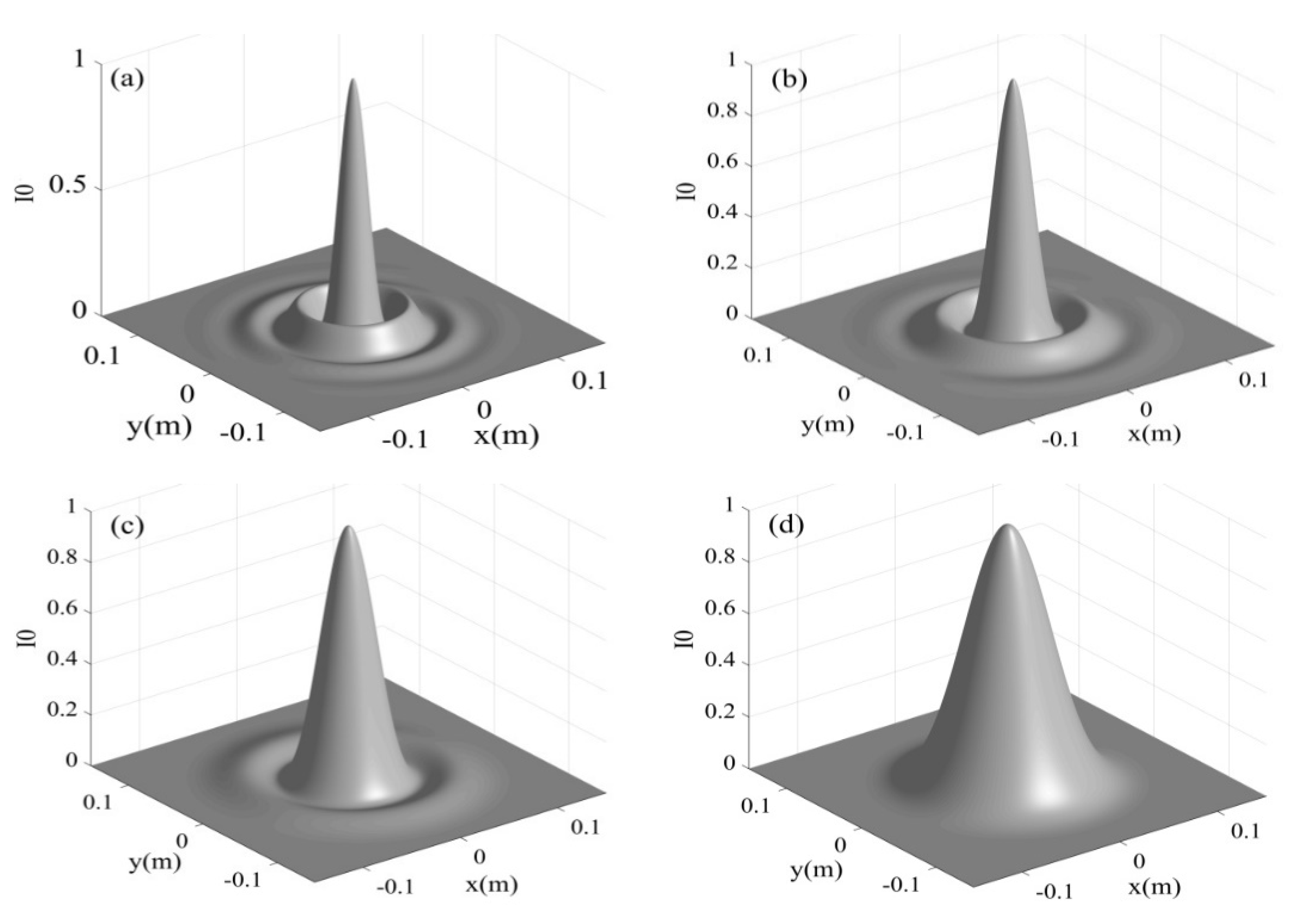
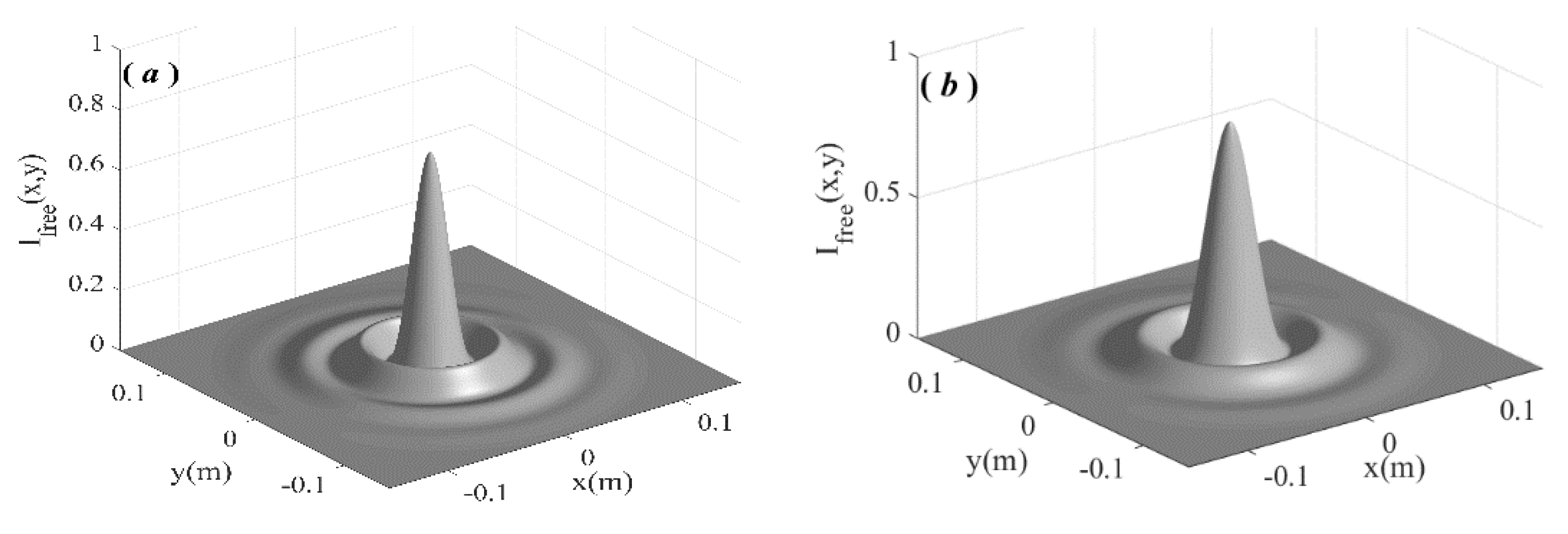
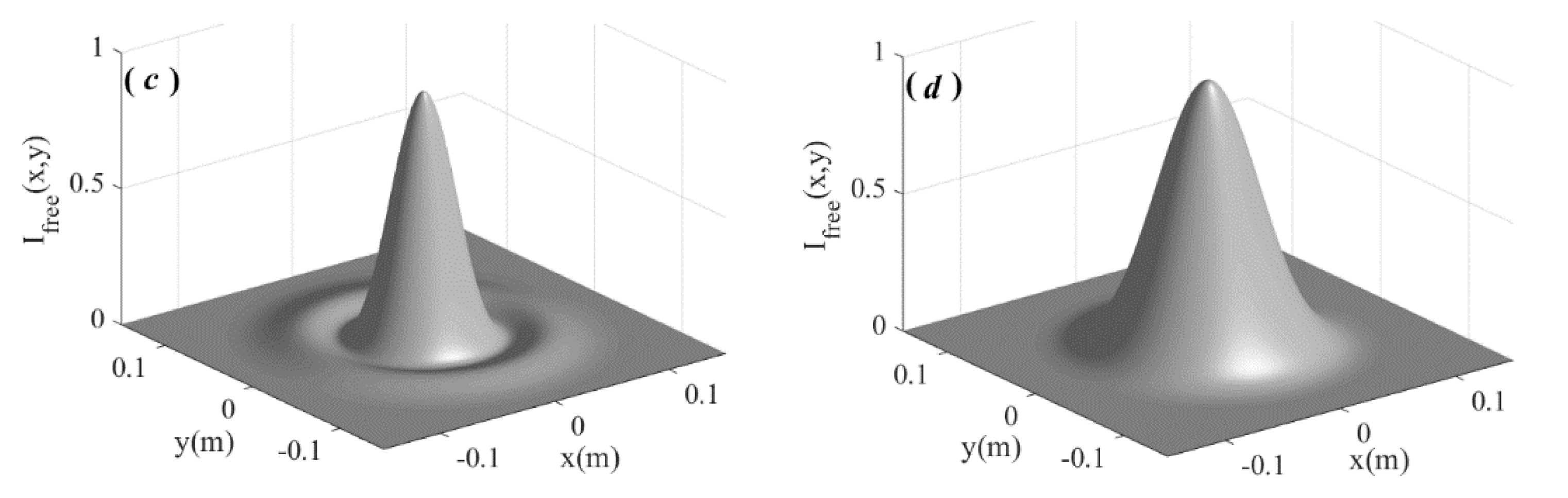
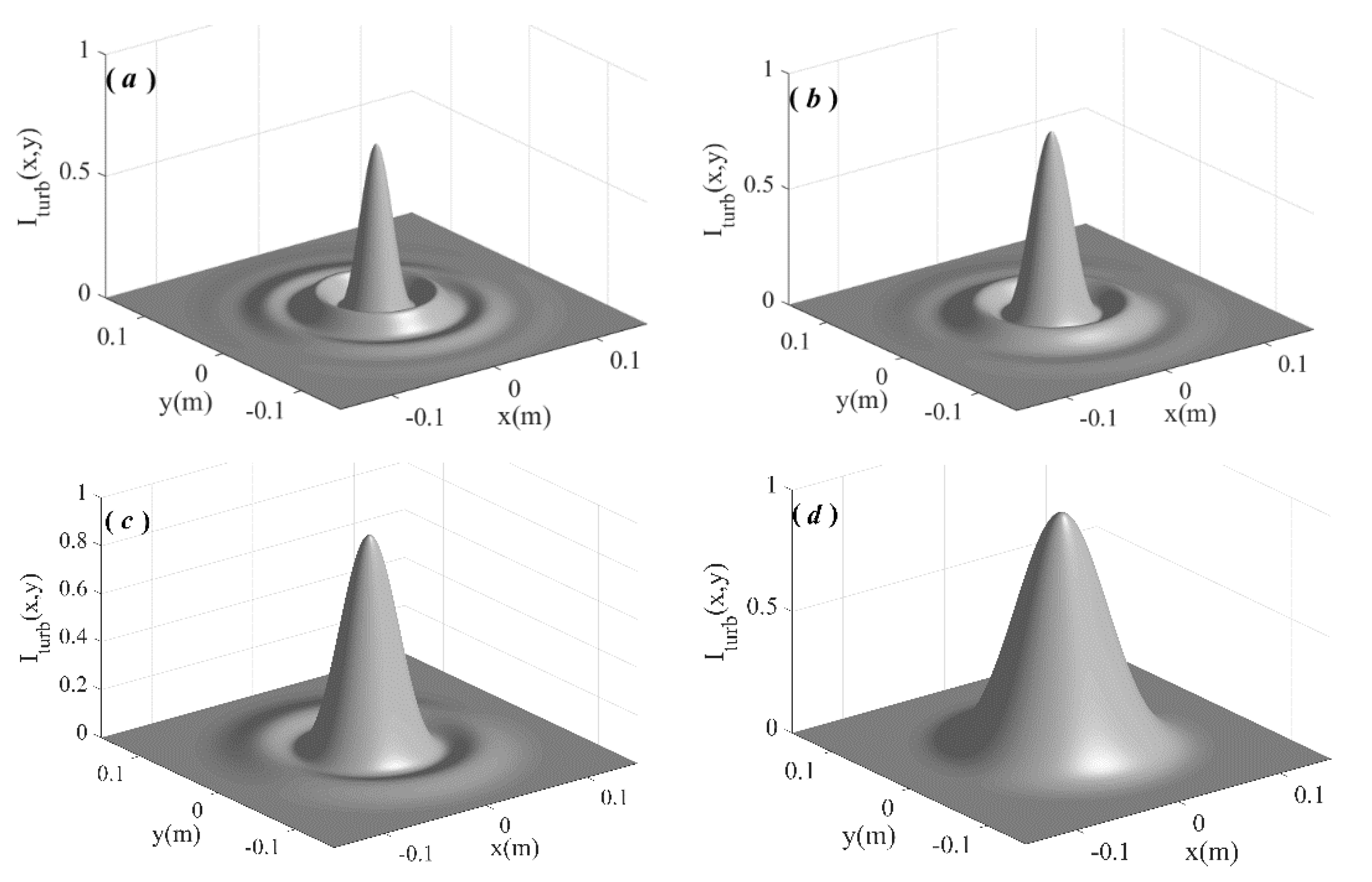

| a (m−1) | rω (m−1) | ρω (m−1) | Τ | S | |
|---|---|---|---|---|---|
| 80 | 81 | 43 | 1.8 | 1.0 | |
| 60 | 62 | 43 | 1.4 | 1.0 | |
| 40 | 44 | 43 | 1.0 | 1.0 | |
| 20 | 27 | 43 | 0.6 | 1.0 | |
| 80 | 81 | 16.6 | 4.9 | 0.993 | |
| 60 | 62 | 16.6 | 3.7 | 0.997 | |
| 40 | 44 | 16.6 | 2.6 | 0.999 | |
| 20 | 27 | 16.6 | 1.7 | 1.0 | |
| 80 | 81 | 11 | 7.4 | 0.977 | |
| 60 | 62 | 11 | 5.7 | 0.991 | |
| 40 | 44 | 11 | 4.0 | 0.997 | |
| 20 | 27 | 11 | 2.6 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, W. Quantitative Analysis of the Effect of Atmospheric Turbulence on a Bessel–Gaussian Beam. Photonics 2023, 10, 932. https://doi.org/10.3390/photonics10080932
Wen W. Quantitative Analysis of the Effect of Atmospheric Turbulence on a Bessel–Gaussian Beam. Photonics. 2023; 10(8):932. https://doi.org/10.3390/photonics10080932
Chicago/Turabian StyleWen, Wei. 2023. "Quantitative Analysis of the Effect of Atmospheric Turbulence on a Bessel–Gaussian Beam" Photonics 10, no. 8: 932. https://doi.org/10.3390/photonics10080932




