The Rating Scale Paradox: An Application to the Solvency 2 Framework
Abstract
:1. Introduction
2. A Rating System with Hybrid Rating Scale
2.1. A Typical Rating System
2.2. A Hybrid Partition Criterion
3. A Credit Insurance Company under the Solvency 2 Regulatory Framework
3.1. Elements of Credit Insurance
3.2. A Credit Insurance RAF in the Solvency 2 Framework
- i.
- The Premium Risk, whose SCR is measured aswhere and are the premiums earned in the last 12 months and the premiums to be earned in the next 12 months, respectively, and are the expected present value of the premiums to be earned after the following 12 months for existing contracts and for contracts whose initial recognition date falls in the following 12 months respectively, and according to the current regulations. We assume the geographical diversification factor is irrelevant in Equation (15).
- ii.
- The Catastrophe Recession Risk, whose SCR is measured as
- iii.
- The Catastrophe Default Risk, whose SCR is measured aswhere () are the first two largest exposures at risk.
4. Benefits of the Hybrid Rating Scale to a Solvency 2 Based RAF
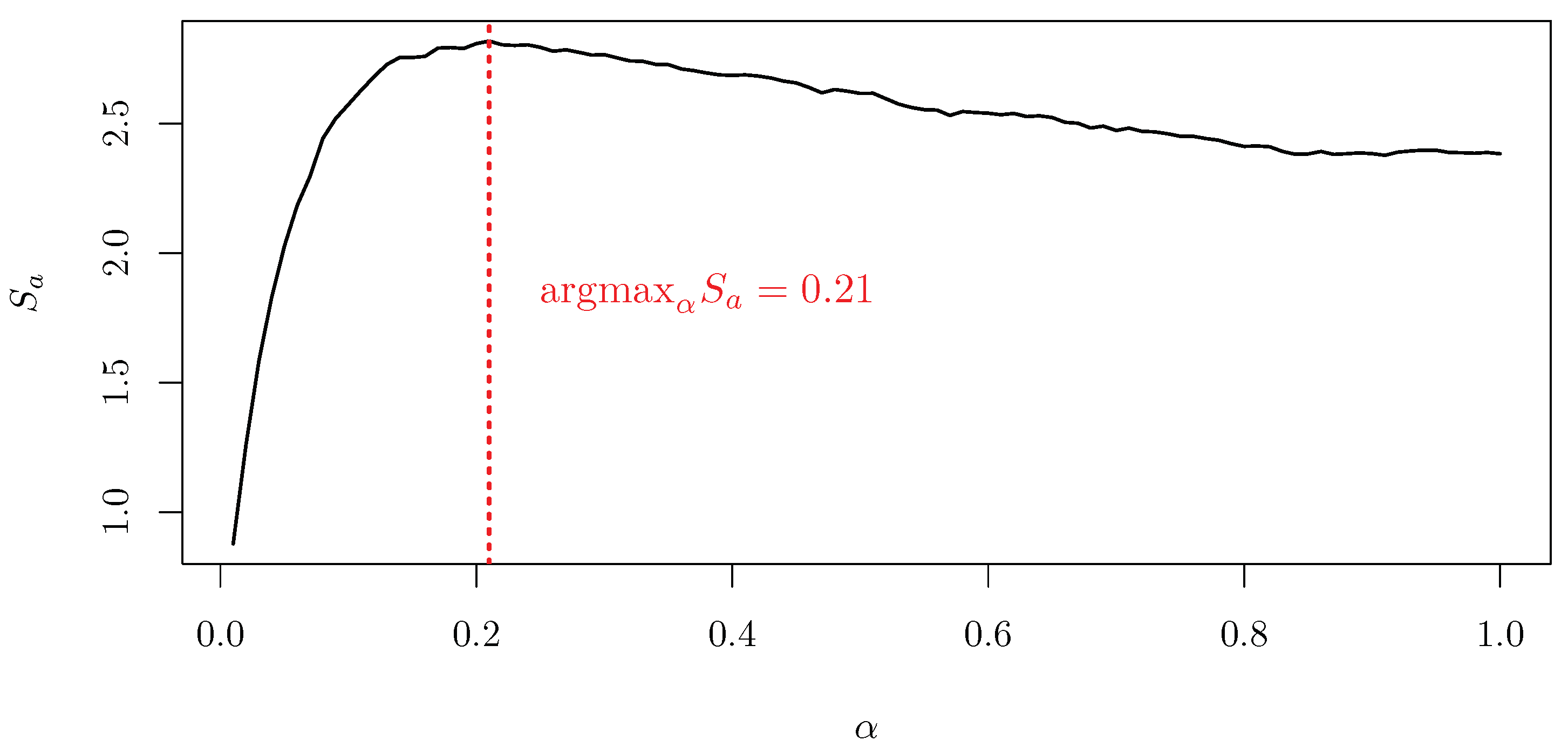
4.1. as the Solution of an Optimization Problem
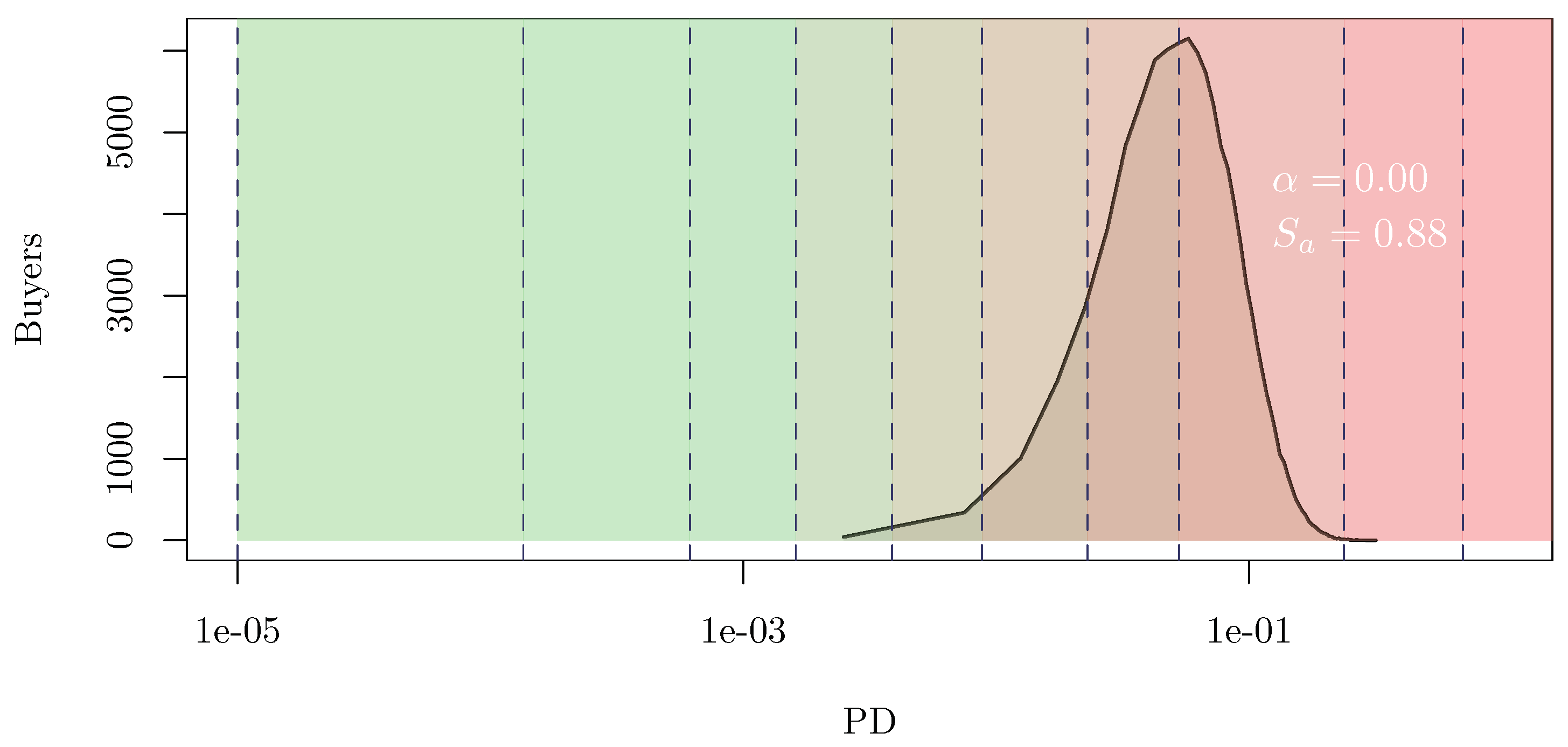
4.2. A Full Working Example
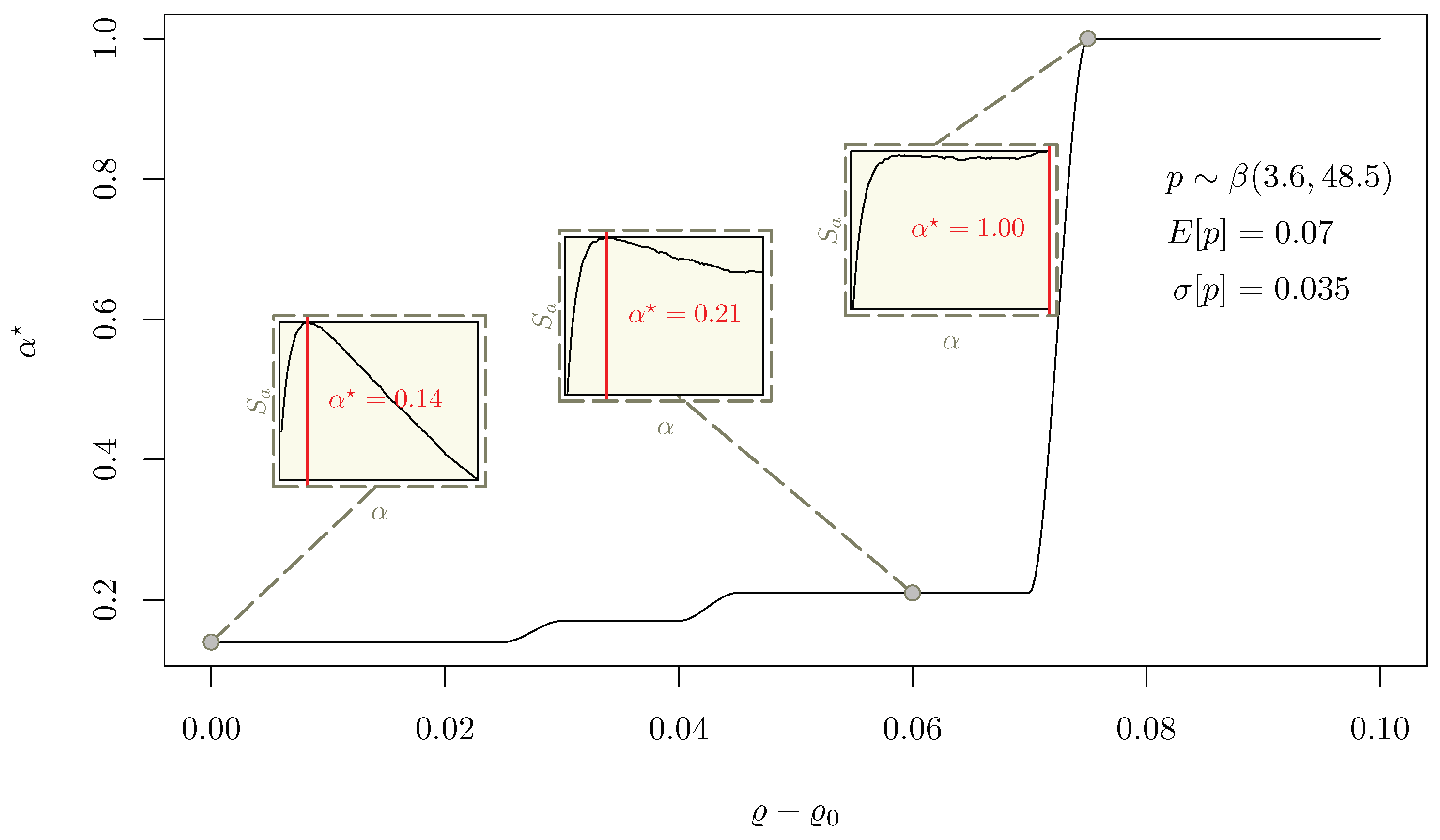
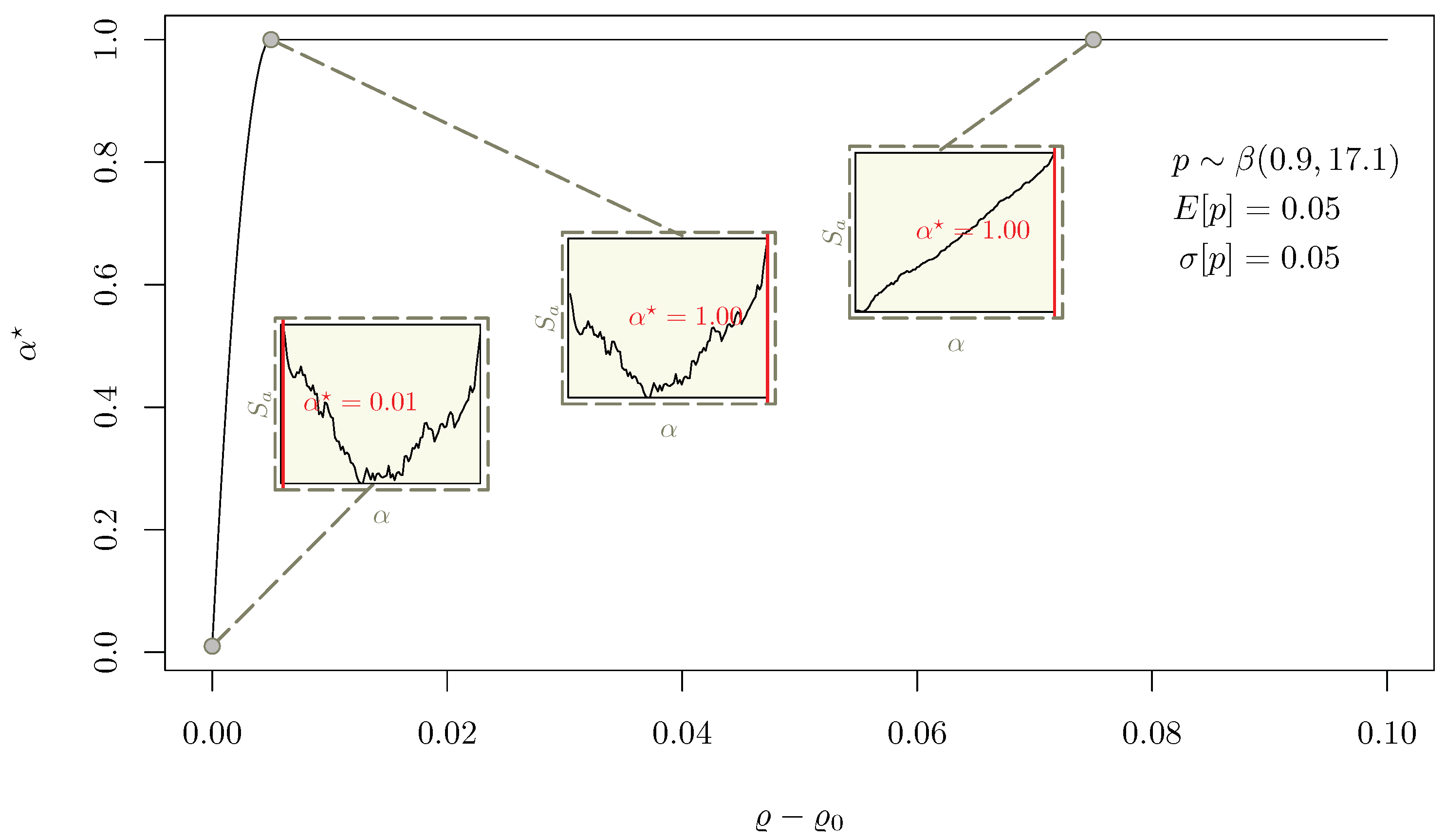
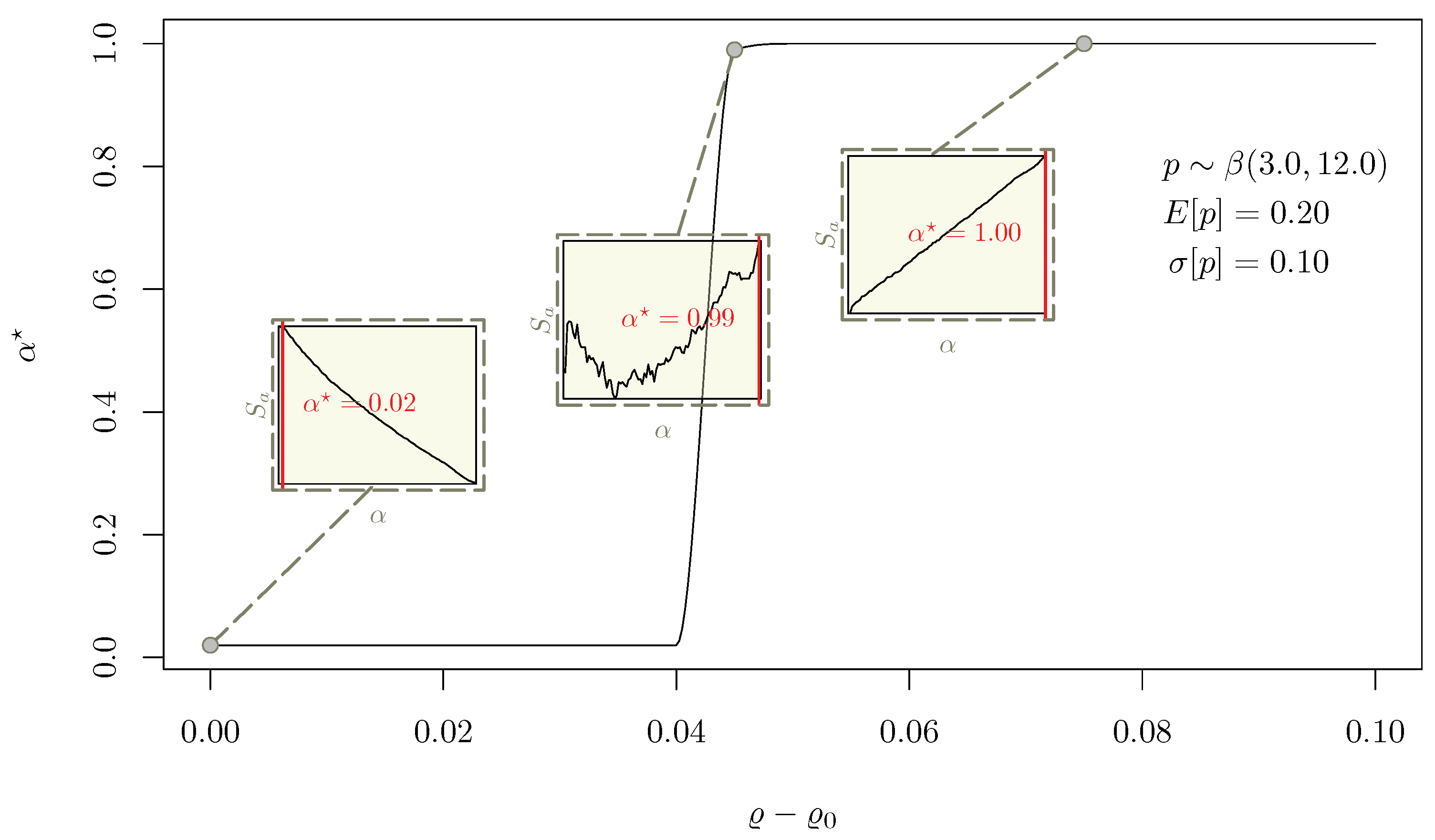
4.3. Sensitivity Analysis
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hodgetts, T.J.; Hall, J.; Maconochie, I.; Smart, C. Paediatric triage tape. Prehosp. Immed. Care 2013, 2, 155–159. [Google Scholar]
- Cross, K.P.; Cicero, M.X. Head-to-head comparison of disaster triage methods in pediatric, adult, and geriatric patients. Ann. Emerg. Med. 2013, 61, 668–676. [Google Scholar] [CrossRef] [PubMed]
- Lerner, E.B.; McKee, C.H.; Cady, C.E.; Cone, D.C.; Colella, M.R.; Cooper, A.; Coule, P.L.; Lairet, J.R.; Liu, J.M.; Pirrallo, R.G.; et al. A consensus-based gold standard for the evaluation of mass casualty triage systems. Prehosp. Emerg. Care 2015, 19, 267–271. [Google Scholar] [CrossRef]
- Elo, A.E. The Proposed USCF Rating System. Chess Life 1967, XXII, 242–247. Available online: http://uscf1-nyc1.aodhosting.com/CL-AND-CR-ALL/CL-ALL/1967/1967_08.pdf (accessed on 6 June 2023).
- Glickman, M.E. Parameter estimation in large dynamic paired comparison experiments. Appl. Stat. 1999, 48, 377–394. [Google Scholar] [CrossRef]
- Veček, N.; Mernik, M.; Črepinšek, M.; Hrnčič, D. A Comparison between Different Chess Rating Systems for Ranking Evolutionary Algorithms. In Proceedings of the 2014 Federated Conference on Computer Science and Information Systems, Warsaw, Poland, 7–10 September 2014. [Google Scholar]
- Thurstone, L.L. Theory of attitude measurement. Psychol. Rev. 1929, 36, 222. [Google Scholar] [CrossRef]
- Likert, R. A technique for the measurement of attitudes. Arch. Psychol. 1932, 22, 55. [Google Scholar]
- Parducci, A. Category ratings and the relational character of judgment. Adv. Psychol. 1983, 11, 262–282. [Google Scholar]
- Menold, N.; Wolf, C.; Bogner, K. Design aspects of rating scales in questionnaires. Math. Popul. Stud. 2018, 25, 63–65. [Google Scholar] [CrossRef]
- Carlsen, L. Rating Potential Land Use Taking Ecosystem Service into Account—How to Manage Trade-Offs. Standards 2021, 1, 79–89. [Google Scholar] [CrossRef]
- Weissova, I.; Kollarb, B.; Siekelova, A. Rating as a Useful Tool for Credit Risk Measurement. Procedia Econ. Financ. 2015, 26, 278–285. [Google Scholar] [CrossRef]
- European Insurance and Occupational Pensions Authority—EIOPA. NLCS 2020 log File A, (V1.1) Updated on 19 July 2021. Available online: https://www.eiopa.europa.eu/consultations/non-life-underwriting-risk-comparative-study-internal-models_en (accessed on 6 June 2023).
- Güttler, A.; Raupach, P. The Impact of Downward Rating Momentum on Credit Portfolio Risk; Discussion Paper Series 2: Banking and Financial Studies No° 16/2008 Deutsche Bundesbank. Available online: https://www.bundesbank.de/resource/blob/704272/d4c8a1578e3122b5cfe696e0553865c3/mL/2008-06-24-dkp-16-data.pdf (accessed on 6 June 2023).
- Rating Symbols and Definitions. Moody’s Investors Service, 2 June 2022. Available online: https://www.moodys.com/researchdocumentcontentpage.aspx?docid=pbc_79004 (accessed on 6 June 2023).
- Oosterveld, B.; Bauer, S. Rating Definitions. FitchRatings Special Report, 21 March 2022. Available online: https://www.fitchratings.com/research/structured-finance/rating-definitions-21-03-2022 (accessed on 6 June 2023).
- Nehrebecka, N. Probability-of-default curve calibration and validation of internal rating systems. In Proceedings of the 8th IFC Conference on “Statistical Implications of the New Financial Landscape”, Basel, Switzerland, 8–9 September 2016; Available online: https://www.bis.org/ifc/publ/ifcb43_zd.pdf (accessed on 6 June 2023).
- Giacomelli, J. The Rating Scale Paradox: Semantics Instability versus Information loss. Standards 2022, 2, 352–365. [Google Scholar] [CrossRef]
- Frei, C. and Wunsch, M. Moment Estimators for Autocorrelated Time Series and Their Application to Default Correlations. J. Credit. Risk 2018, 14, 1–29. Available online: https://ssrn.com/abstract=3141168 (accessed on 30 September 2023). [CrossRef]
- Gordy, M.B. and Howells, B. Procyclicality in Basel II: Can we treat the disease without killing the patient? J. Financ. Intermediation 2006, 15, 395–417. [Google Scholar] [CrossRef]
- Altman, E.I.; Rijken, H.A. How rating agencies achieve rating stability. J. Bank. Financ. 2004, 28, 2679–2714. [Google Scholar] [CrossRef]
- Cantor, R.M.; Mann, C. Analyzing the Tradeoff between Ratings Accuracy and Stability. J. Fixed Income 2006. Available online: https://ssrn.com/abstract=996019 (accessed on 30 September 2023). [CrossRef]
- Giacomelli, J. Parametric estimation of latent default frequency in credit insurance. J. Oper. Res. Soc. 2023, 74, 330–350. [Google Scholar] [CrossRef]
- The International Credit Insurance & Surety Association. A Guide to Trade Credit Insurance; Anthem Press: London, UK, 2015. [Google Scholar]
- The International Credit Insurance & Surety Association. ICISA Catalog of Credit Insurance Terminology—English Edition. 2017. Available online: icisa.org/wp-content/uploads/2019/07/ICISA-Catalogue-of-Credit-Insurance-Terminology-English.pdf (accessed on 6 June 2023).
- Jus, M. Credit Insurance; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Passalacqua, L. A pricing model for credit insurance. G. Dell’Istituto Ital. Degli Attuari 2006, 69, 4. [Google Scholar]
- Passalacqua, L. Measuring effects of excess-of-loss reinsurance on credit insurance risk capital. Giornale Dell’Istituto Ital. Degli Attuari 2007, 70, 81–102. [Google Scholar]
- Commission Delegated Regulation (EU) 2015/35 of 10 October 2014 Supplementing Directive 2009/138/EC of the European Parliament and of the Council on the Taking-Up and Pursuit of the Business of Insurance and Reinsurance. Available online: https://eur-lex.europa.eu/eli/reg_del/2015/35/oj (accessed on 6 June 2023).
- Commission Delegated Regulation (EU) 2019/981 of 8 March 2019 Amending Delegated Regulation (EU) 2015/35 Supplementing Directive 2009/138/EC of the European Parliament and of the Council on the Taking-Up and Pursuit of the Business of Insurance and Reinsurance (Solvency II). Available online: https://eur-lex.europa.eu/eli/reg_del/2019/981/oj (accessed on 6 June 2023).
- Directive 2009/138/EC of the European Parliament and of the Council of 25 November 2009. Available online: https://eur-lex.europa.eu/eli/dir/2009/138/oj (accessed on 6 June 2023).
- Stanghellini, E. Introduzione ai Metodi Statistici per il Credit Scoring, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Konrad, P.M. The Calibration of Rating Models. Estimation of the Probability of Default based on Advanced Pattern Classification Methods, 1st ed.; Tectum Verlag Marburg: Marburg, Germany, 2012. [Google Scholar]
- Gurný, P.; Gurný, M. Comparison of credit scoring models on probability of defaults estimation for US banks. Prague Econ. Pap. 2013, 22, 163–181. [Google Scholar] [CrossRef]
- Fankenstein, E.; Boral, A.; Carty, L.V. RiskCalc for Private Companies: Moody’s Default Model. Moody’s Investor Service Global Credit Research, May 2000. Available online: https://ssrn.com/abstract=236011 (accessed on 6 July 2023).
- Basel Committee on Banking Supervision (BSBC). The Internal Ratings-Based Approach; Bank for International Settlements: Basel, Switzerland, 2001. [Google Scholar]
- Tasche, D. The art of probability-of-default curve calibration. J. Credit. Risk 2013, 9, 63–103. [Google Scholar] [CrossRef]
- Durović, A. Macroeconomic Approach to Point in Time Probability of Default Modeling—IFRS 9 Challenges. J. Cent. Bank. Theory Pract. 2019, 1, 209–223. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Engelmann, B.; Hayden, E.; Tasche, D. Measuring the Discriminative Power of Rating Systems; Discussion Paper Series 2: Banking and Financial Supervision No 01/2003 Deutsche Bundesbank. Available online: https://www.bundesbank.de/resource/blob/704150/b9fa10a16dfff3c98842581253f6d141/mL/2003-10-01-dkp-01-data.pdf (accessed on 6 June 2023).
- Giacomelli, J.; Passalacqua, L. Unsustainability Risk of Bid Bonds in Public Tenders. Mathematics 2021, 9, 2385. [Google Scholar] [CrossRef]
- Giacomelli, J.; Passalacqua, L. Calibrating the CreditRisk+ Model at Different Time Scales and in Presence of Temporal Autocorrelation. Mathematics 2021, 9, 1679. [Google Scholar] [CrossRef]
- Giacomelli, J.; Passalacqua, L. Improved precision in calibrating CreditRisk+ model for Credit Insurance applications. In Mathematical and Statistical Methods for Actuarial Sciences and Finance—eMAF 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Paulusch, J. The Solvency II Standard Formula, Linear Geometry, and Diversification. J. Risk Financ. Manag. 2017, 10, 11. [Google Scholar] [CrossRef]
- Baione, F.; De Angelis, P.; Granito, I. On a Capital Allocation Principle Coherent with the Solvency 2 Standard Formula. IVASS Conference on Insurance Research, 13 July 2017. Available online: https://www.ivass.it/pubblicazioni-e-statistiche/pubblicazioni/att-sem-conv/2017/conf-131407/ (accessed on 6 June 2023).


| Variable | Description | Value |
|---|---|---|
| P | Premiums to be earned during the next 12 months (arbitrary units) | |
| D | SCR associated to Catastrophe Default risk in Solvency 2 Standard Formula framework (arbitrary units) | |
| Risk appetite per risk expressed as the maximum acceptable contribution to the ( units) | 5 | |
| k | Average effect of contractual clauses and conditions | |
| ℓ | Average exposure at default ratio | |
| c | Insurer’s cost ratio | |
| Target return required by the insurer’s stakeholders | ||
| Risk free return | ||
| R | Number of notches belonging to the considered master scale | 10 |
| Notch associated with the minimum acceptable creditworthiness per buyer | 7 | |
| N | Number of risky buyers against whom the insured sellers ask for protection | |
| Expected value of the buyers’ PD distribution | ||
| Standard deviation of the buyers’ PD distribution |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giacomelli, J. The Rating Scale Paradox: An Application to the Solvency 2 Framework. Standards 2023, 3, 356-372. https://doi.org/10.3390/standards3040025
Giacomelli J. The Rating Scale Paradox: An Application to the Solvency 2 Framework. Standards. 2023; 3(4):356-372. https://doi.org/10.3390/standards3040025
Chicago/Turabian StyleGiacomelli, Jacopo. 2023. "The Rating Scale Paradox: An Application to the Solvency 2 Framework" Standards 3, no. 4: 356-372. https://doi.org/10.3390/standards3040025






