Fuzzy Unsteady-State Drainage Solution for Land Reclamation

Abstract

Very well-drained lands could have a positive impact in various soil health indicators such as soil erosion and soil texture. A drainage system is responsible for properly aerated soil. Until today, in order to design a drainage system, a big challenge remained to find the subsurface drain spacing because many of the soil and hydraulic parameters present significant uncertainties. This fact also creates uncertainties to the overall physical problem solution, which, if not included in the preliminary design studies and calculations, could have bad consequences for the cultivated lands and soils. Finding the drain spacing requires the knowledge of the unsteady groundwater movement, which is described by the linear Boussinesq equation (Glover-Dumm equation). In this paper, the Adomian solution to the second order unsteady linear fuzzy partial differential one-dimensional Boussinesq equation is presented. The physical problem concerns unsteady drain spacing in a semi-infinite unconfined aquifer. The boundary conditions, with an initially horizontal water table, are considered fuzzy and the overall problem is translated to a system of crisp boundary value problems. Consequently, the crisp problem is solved using an Adomian decomposition method (ADM) and useful practical results are presented. In addition, by application of the possibility theory, the fuzzy results are translated into a crisp space, enabling the decision maker to make correct decisions about both the drain spacing and the future soil health management practices, with a reliable degree of confidence.

1. Introduction

In general, saturated soils have a negative impact on plant growth and a drainage system could support the land reclamation and the sustainable soil management. For agricultural lands, the definition of subsurface drainage is the artificial removal of water from the land [1]. This process is of vital importance for the soil and plant health and could have also a positive impact in various soil quality indicators such as soil erosion and soil texture. Furthermore, by draining the excessive water on time, it provides aeration and prevents waterlogging and salinization of the plant root zone [2,3].

In subsurface drainage, field drains are used to control the groundwater level. Generally, drainage calculation concerns only the drain spacing and the groundwater level. Drainage equations are based on the Dupuit-Forcheimer assumptions, which reduce the two-dimensional flow to a one dimensional, accepting parallel and horizontal streamlines. Drainage theory can be divided into steady-state theory and non-steady state theory.

For the steady state theory, Hooghoudt (1940) [4] is considered a pioneer. He developed a flow equation assuming that the flow region is divided into two different parts: a part with horizontal flow and a part with radial flow. The rain arrives vertically at the groundwater level, changes direction after and moves horizontally under the drainage system influence. The equipotential lines are assumed vertical, and the hydraulic gradient is approximated with the groundwater gradient. Subsequently, Hooghoudt corrected the simplified assumptions, introducing the concept of the equivalent depth.

Many other solutions consider the case that the water flow into drains takes place through stratified soils (two-layered soils), and the drains are placed above or below the interface of the two layers [5,6,7,8,9]. Kirkham (1958) [10] presented a solution based on the potential flow theory, which takes both the flow above and below the drain level into account, thereby solving the Laplace equation. Ernst (1962) [6] published an approximated method of the drainage problem, extending Hooghoudt’s method, which is applied in the case of stratified soils under certain limitations. Dagan (1964) [11] presented an approximated method, considering radial flow near the drains and horizontal flow at greater distances from the drains. Toksöz and Kirkham (1971) extended the Kirkham (1958) method [10], assuming two-dimensional flow and solving the Laplace equation. Van der Molen and Wesseling (1991) [12] analyzed the flow problem like Hooghoudt and Dagan, by the method of ‘mirror images’, resulting in an exact solution for the equivalent depth. According to Ritzema (1994) [13], the Hooghoudt equation combined with Van der Molen and Wesseling (1991) solutions, provides the best results. Μishra and Singh (2007) [14] modified the Hooghoudt method, improving the groundwater level near the drain region. Recently, Afruzi et al. (2014) [15] presented a two-dimensional Laplace equation solution, using the Schwarz–Christoffel transform and the conformal mapping.

For the case of nonsteady state flow, Glover (Dumm, 1954) [16] provided the fundamental transient drain design equation. Dumm (1954) used this equation to describe the fall of the water table, which after had risen instantaneously to a height above drain level, and his solution was based on an initially horizontal water table. Later Dumm (1960) [17] extended the above solution, considering that the initial water table had the shape of a fourth-degree parabola. This solution is called the Glover-Dumm equation. As in the Hooghoudt analysis, the groundwater gradient was considered a hydraulic gradient in the hole drainage area. The Bureau of Reclamation (1993) [18] estimated drain spacing based on transient flow conditions that relates the behaviour of the water table to time and drain spacing. They have adopted the Glover-Dumm equation with an initially horizontal water table. Further developments enable consideration of an accurate flow net and a more realistic representation of water movement. Tzimopoulos and Terzides (1975) [19] presented numerical solutions for the nonlinear drainage equation, based on implicit computational schemes of the Crank-Nicolson, Laasonen and Douglas types. The MODFLOW [20] computer code includes a model for solving the fundamental equation for saturated flow using the finite difference method. In addition, recent studies [21,22] explored the application of the DRAINMOD process-based model, developed to describe the hydrology of poorly drained and artificially drained soils under different agricultural drainage layouts, fields, weather conditions, and management practices. Nevertheless, these models present many difficulties for engineers and designers, as knowledge of inputs for soil properties, site parameters, weather data, and crop characteristics is required, while for the MODFLOW model, the initial groundwater level in the whole region and the boundary conditions of the problem is required and it is considered awkward for practical problems. For this reason, engineers and designers apply classical models using the Glover—Dumm equation. Interesting studies are also presented regarding the available mathematical models for irrigations and drainage systems [23], for drainage and desorption area analysis [24], for salinization and poor drainage in irrigated areas [25] and for the simulation of water table profile between two parallel sub-surface drains [26]. However, these models refer to classical logic and fuzziness and could not be introduced in the way developed in this work.

The initial groundwater level and the drain depth above the impermeable datum, as well as the hydraulic conductivity and the effective porosity, constitute the variables of the above models. Until today, the parameters were assumed to be well defined, and this assumption is based principally in measurements. Nevertheless, data measurements of these variables present uncertainties and ambiguities which are due to human errors, measuring devices, soil inhomogeneities and anisotropies, etc. The above uncertainties and ambiguities affect significantly the engineers and designers to make accurate decisions in the case of dimensioning a drainage system.

According to the traditional view (classical logic), mathematical models should strive for certainty in all manifestations (precision, specificity, sharpness, consistency, etc.); hence, uncertainty (imprecision, nonspecificity, vagueness, inconsistency, etc.) is regarded as unscientific. According to Klir and Bo Yuan, (1995) [27] uncertainty becomes very valuable when considered in connection to the other characteristics of systems models: in general, allowing more uncertainty tends to reduce complexity and increase credibility of the resulting model. According to Goguen (1967) [28], fuzziness is more the rule than the exception in engineering design problems: usually where there is no well-defined best solution or design.

This research strives to deliver a new solution of the drain spacing, taking into consideration the problem uncertainties, utilizing the fuzzy logic theory and the Adomian decomposition method (ADM) [29,30,31]. Today, the fuzzy set theory provides methods for introducing imprecise information in a possibilistic sense. Zadeh (1965) [32] first introduced the fuzzy set theory for facing imprecision or vagueness, and since then this theory has been applied in different science fields. Fuzzy logic theory is today a powerful tool for many theoretical and applied engineering problems while the Adomian decomposition method (ADM) is a very effective approach for solving broad classes of partial and ordinary differential equations, with important applications in different fields of applied mathematics, engineering, physics and biology [33].

In a more detailed manner, first it is important to highlight that the proposed methodology concerns agricultural irrigated and cultivated lands, considering an unsteady drainage state in the case of homogeneous soil with an initially horizontal ground water level (protected areas by legislation, such as wetlands and ecosystems with unique habitats, are not under consideration). The drainage is obtained by parallel drains, overlined by an impermeable substratum. The linear Boussinesq equation is solved by the ADM and the resulting solution fits perfectly with the Glover–Dumm equation. Subsequently, the crisp solution was fuzzified with respect to the initially phreatic level and the boundary drain conditions. Since the aforementioned problem concerns differential equations, the generalized Hukuhara (gH) derivative [34] was used for total derivatives as well as the extension of this theory concerning partial derivatives [35]. The fuzzy problem is translated to a system of second order of crisp boundary value problems, hereafter called a corresponding system [36] for the fuzzy problem. Therefore, four crisp BVP systems are possible for the fuzzy problem {(1,1), (1,2), (2,1), (2,2)}. We will hereby restrict ourselves to the solution of the (1,1) system, which is described in detail. Finally, an interpretation of numerical results by using the possibility theory is provided [37].

2. Materials and Methods

2.1. Linearized Bousinesq Equation

2.1.1. Classical Case

For the convenience of the reader throughout this work, the following sketch (Figure 1) is provided, in which valuable definitions regarding the drain spacing problem are presented.

The free surface of the groundwater flow to the drains is describing by the Boussinesq equation:

$$\frac{\partial h}{\partial t}=\frac{K}{S}\frac{\partial }{\partial x}(h\frac{\partial h}{\partial x})$$

(1)

with the following boundaries and initial flow conditions:

$$x=0,h(0,t)=d,x=L,h(L,t)=d,t=0,h(x,0)=E$$

(2)

In the above Equation (1), we omit the first derivative squared term and set h equal to the mean value B as follows [13]:

$$\frac{\partial h}{\partial t}=\frac{KB}{S}\frac{{\partial }^{2}h}{\partial x^2}={\alpha }_1\frac{{\partial }^{2}h}{\partial x^2},{\alpha }_1=\frac{KB}{S},$$

Boundary—Initial conditions,

$$h(0,t)=d,h(L,t)=d,h(x,0)=E$$

(3)

where K = hydraulic conductivity, S = specific yield, B = ȳ₀/2 + d, d = the drain distance from the impermeable layer, and ȳ₀ = the drain distance from the initial water table, E = ȳ₀ + d. The boundary conditions and the initial flow condition remain the same as the nonlinear equation. The above equation is the same as the equation derived by Glover, with the difference that the depth h in Glover was from the free surface to the drains. Therefore, Boussinesq’s linear equation coincides with Glover’s equation.

Notation: In this work, the term α₁ was used instead of the term α, because the last term will be used in the fuzzy methodology for the fuzzy α-cuts.

Non dimensional variables

For the parameter α₁, the following non-dimensional variables are introduced:

$$H=\frac{h}{d},\xi =\frac{\pi x}{L},\tau =\frac{{\pi }^2{\alpha }_{1}t}{L^2}$$

(4)

then, the Boussinesq equation is formed as follows:

$$\frac{\partial H}{\partial \tau }=\frac{{\partial }^{2}H}{\partial {\xi }^2}$$

(5)

with the following boundaries and initial flow conditions:

$$\xi =0,H(0,\tau )=1,\xi =\pi ,H(1,\tau )=1,\tau =0,H(\xi ,0)=\frac{E}{d}$$

(6)

Now we set as the main variable $y=H(\xi ,\tau )-1$, and the Boussinesq equation could be written as:

$$\frac{\partial y}{\partial \tau }=\frac{{\partial }^{2}y}{\partial {\xi }^2}$$

(7)

with the following boundaries and initial flow conditions:

$$\xi =0,y(0,\tau )=0,\xi =\pi ,y(\pi ,\tau )=0,\tau =0,y(\xi ,0)=\frac{E}{d}-1={\omega }_1$$

(8)

The linearized Boussinesq equation:

$$\frac{\partial y}{\partial \tau }=\frac{{\partial }^{2}y}{\partial {\xi }^2}$$

(9)

Boundary conditions:

$$\xi =0,y(0,\mathrm{t})=0,\xi =\pi ,\mathrm{y}(\pi ,\tau )=0$$

(10)

Initial flow condition:

$$\tau =0,y(\xi ,0)={\omega }_1$$

(11)

The initial condition ω₁ with the Fourier series is set as follows:

$${\omega }_1=\frac{E}{d}-1={\displaystyle \sum }_{n=0,1,2}^{\infty }{B}_{n}sinn\xi ={\displaystyle \sum }_{n=1,3,5}^{\infty }{B}_{n}sinn\xi$$

(12)

where

$$B_n=\{\frac{2{\omega }_1}{n\pi }[1-(-1{)}^n]\}=\{{ }_{4{\omega }_1/n\pi ,n=2k+1}^{0,n=2k}$$

(13)

Figure 2 presents the straight line E = 3, (L = 14), for n = 2450. At the boundaries, the Gibbs phenomena appeared.

2.1.2. Linearized Boussinesq Solution Based on the ADM

Equation (9) could be written with following form:

$$L\left\{\frac{\partial y}{\partial \tau }-\frac{{\partial }^{2}y}{\partial {\xi }^2}\right\}=0,or L_{\tau }(y)-L_{\xi \xi }(y)=0$$

(14)

$$L_{\tau }^{-1}{L}_{\tau }(y)=L_{\tau }^{-1}{L}_{\xi \xi }(y)$$

where $L_{\tau }=\partial /\partial \tau ,L_{\xi \xi }={\partial }^2/\partial {\xi }^2$ are partial derivative operators. We assume that the operator $L_{\tau }=\partial /\partial \tau ,$ is invertible and is given as follows:

$$L_{\tau }^{-1}(.)={{\displaystyle \int }}_0^{\tau }(.)d\tau$$

(15)

In Equation (14) we have:

$$L_{\tau }{}^{-1}(\frac{\partial y(\xi ,\tau )}{\partial \tau })={{\displaystyle \int }}_0^{\tau }\frac{dy(\xi ,\tau )}{d\tau }d\tau =y(\xi ,\tau )|{ }_0^{\tau }=y(\xi ,\tau )-y(\xi ,0)$$

(16)

$$L_{\tau }^{-1}\{L_{\xi \xi }(y(\xi ,\tau )\}={{\displaystyle \int }}_0^{\tau }(\frac{{\partial }^{2}y(\xi ,\tau )}{\partial {\xi }^2})d\tau$$

(17)

In addition, if we use the invertible operator $L_t^{-1}(.)$, Equation (14) could be written as:

$$y(\xi ,\tau )=y(\xi ,0)+L_{\tau }^{-1}(L_{\xi \xi }y(\xi ,\tau ))$$

(18)

At ADM, the unknown function $y(\xi ,\tau )$ is expressed as an infinite term series as follows:

$$y={\displaystyle \sum }_{n=0}^{\infty }{y}_n$$

(19)

Equation (18) is formed as:

$$y_0+y_1+y_2+\dots ..y_n+\dots =y(\xi ,0)+L_{\tau }^{-1}{L}_{\xi \xi }(y_0+y_1+y_2+\dots ..y_n+\dots )$$

(20)

Based on the above equation we have:

$$y_0=y(\xi ,0)$$

$$y_1=L_{\tau }^{-1}{L}_{\xi \xi }(y_0),$$

$$y_2=L_{\tau }^{-1}{L}_{\xi \xi }(y_1),$$

(21)

$$y_{n+1}=L_{\tau }^{-1}{L}_{\xi \xi }(y_n),$$

Thus, the following iteration equations are formed:

$$y_0(\xi ,\tau )={\omega }_1={\displaystyle \sum }_{n=1}^{\infty }{B}_{n}sinn\xi ,y_{k+1}=L_{\tau }^{-1}(L_{\xi \xi }{y}_k(\xi ,\tau )),k\ge 0$$

(22)

In detail, for the rest of the solutions after the introduction of the $y_0(\xi ,\tau )$ we have:

$$y_1(\xi ,\tau )=L_{\tau }^{-1}(L_{\xi \xi }{y}_0(\xi ,\tau ))=-\tau {\displaystyle \sum }_{n=1}^{\infty }{B}_n{n}^{2}sinn\xi ,$$

(23)

$$y_2=L_{\tau }^{-1}(L_{\xi \xi }{y}_1(\xi ,\tau ))=L_{\tau }^{-1}(L_{\xi \xi }(-\tau {\displaystyle \sum }_{n=1}^{\infty }{B}_n{n}^{2}sin(n\xi )))$$

(24)

$$y_2(\xi ,\tau )=\frac{{\tau }^2}{2!}{\displaystyle \sum }_{n=1}^{\infty }{B}_n{n}^{4}sinn\xi ,$$

(25)

$$y_3(\xi ,\tau )=-\frac{{\tau }^3}{3!}{\displaystyle \sum }_{n=1}^{\infty }{B}_n{n}^{6}sinn\xi ,$$

(26)

Then the solution could be provided by the form of the Fourier series as follows:

$$y(\xi ,\tau )=y_0(\xi ,\tau )+y_1(\xi ,\tau )+y_2(\xi ,\tau )+\cdots$$

(27)

or

$$y(\xi ,\tau )={\displaystyle \sum }_{n=1}^{\infty }{B}_{n}sin(n\xi )\left(1+(-n^2\tau +\frac{{\tau }^2}{2!}{n}^4-\frac{{\tau }^3}{3!}{n}^6+\dots \right),$$

(28)

Finally, we will have the following:

$$y(\xi ,\tau )={{\displaystyle \sum }}_{n=0}^{\infty }{B}_{n}sin(n\xi )e^{-\tau n^2},\xi =\frac{\pi x}{L},\tau =\frac{{\pi }^2{\alpha }_{1}t}{L^2},$$

(29)

or

$$H(\xi ,\tau )=y(\xi ,\tau )+1={\displaystyle \sum }_{n=0}^{\infty }{B}_{n}sin(n\xi )e^{-n^2\tau }+1,$$

or

$$h(\xi ,\tau )=d·H(\xi ,\tau )=d(y(\xi ,\tau )+1)=d({\displaystyle \sum }_{n=0}^{\infty }{B}_{n}sin(n\xi )e^{-n^2\tau }+1)$$

(30)

$$h(x,t)=d({\displaystyle \sum }_{n=1}^{\infty }{B}_{n}sin(n\xi )e^{-n^2\tau }+1)=d({\displaystyle \sum }_{n=1,3,5\dots }^{\infty }\frac{4{\omega }_1}{n\pi }sin(n\xi )e^{-n^2\tau }+1)$$

(31)

Boundary conditions:

$$x=0,\xi =0,h(0,t)=d,x=L,\xi =\pi ,h(L,t)=d$$

(32)

Initial flow condition:

$$\tau =0,h(x,0)=d({\omega }_1+1)=d(\frac{E}{d}-1+1)=E$$

(33)

Therefore, Equation (31) satisfies the boundary conditions and the initial flow condition and is identical to the analytical solution of the linearized Boussinesq equation. In addition, Dumm (1954) [16] developed analogous equation as follows:

$$\overline{h}(x,t)={\displaystyle \sum }_{n=1,3,5\dots }^{\infty }\frac{4{\overline{h}}_0}{n\pi }sin(\frac{n\pi x}{L})e^{-n^2{\alpha }^{\prime }t},{\alpha }^{\prime }=\frac{{\pi }^{2}Kd}{S{L}^2},\tau ={\alpha }^{\prime }t$$

(34)

This equation satisfies the boundary conditions as:

$$x=0,\overline{h}(0,t)=0,x=L,\overline{h}(L,t)=0,$$

(35)

and also satisfies the initial flow condition as:

$$t=0,\overline{h}(x,0)={\overline{h}}_0={\rm E}-d$$

(36)

This equation is known as Glover-Dumm equation and is referring to the x-axis which is at the level of the drains.

2.1.3. Drain Spacing

In Equation (31) we assume that x = L/2 and n = 1. This equation is valid because for n > 1, the error that occurs by omitting the other terms is small, especially for soils with a small S. Equation (31) is formed as follows:

$$h(L/2,t)=d(\frac{4{\omega }_1}{\pi }{e}^{-\tau }+1),n<1,$$

or

$$\frac{h(L/2,t)-d}{d}=\frac{{\overline{y}}_t}{d}=\frac{4(E-d)}{\pi d}{e}^{-\tau }=\frac{4{\overline{y}}_0}{\pi d}{e}^{-\tau }(n<1)\to {\overline{y}}_t=\overline{y}(L/2,t)=\frac{4{\overline{y}}_0}{\pi }{e}^{-\tau },$$

(37)

$$\frac{{\overline{y}}_t}{{\overline{y}}_0}=\frac{4}{\pi }{e}^{-\tau }=1.274e^{-\tau }=1.274e^{{\pi }^2{\alpha }_{1}t/L^2}\to L^2={\pi }^2\frac{KBt/S}{ln\{1.274(\frac{{\overline{y}}_0}{{\overline{y}}_t})\}},$$

(38)

or

$$L_C=\sqrt{\frac{{\pi }^{2}KBt/S}{ln\{1.274(\frac{{\overline{y}}_0}{{\overline{y}}_t})\}}}=\sqrt{\frac{{\pi }^{2}KB/S}{ln\{1.274(\frac{{\overline{y}}_0}{{\overline{y}}_t})\}}}\sqrt{t}$$

(39)

Note: Set as L_C, for the classical case.

Equation (39) could provide the value of the drain spacing as a function of the square root of time and the expression:

$$AA=\sqrt{\frac{{\pi }^{2}KB/S}{ln\{1.274(\frac{{\overline{y}}_0}{{\overline{y}}_t})\}}}.$$

In the expression AA, the parameters K, B, S could be provided by measurements, while the ratio ${\overline{y}}_0/{\overline{y}}_t$ varies between 1 and infinity. Thus, if we choose a value for the ratio ${\overline{y}}_0/{\overline{y}}_t$, and for the time t (d), it is possible to find the drain spacing, when the values of the parameters K, B, S are known. If we apply the Hooghoudt equivalent depth in Equation (39), we can find improved values. Dumm (1960) [17] assumed that the form of the water table is a parabola of 4th order and concluded on the expression:

$$\frac{{\overline{y}}_t}{{\overline{y}}_0}=1.16e^{-\tau }$$

(40)

2.1.4. Fuzzy Case

The Boussinesq equation could be written in the fuzzy form as follows:

$$\frac{\partial \tilde{h}}{\partial \tau }{\Theta }_{\mathrm{gH}}{\alpha }_1\frac{{\partial }^2\tilde{h}}{\partial {\xi }^2}=\tilde{0},{\alpha }_1=\frac{KB}{S}$$

(41)

Boundary conditions:

$$\underset{x=0}{{[\tilde{h}(x,t)]}_{\alpha }}=d\left[1-c(1-\alpha ),1+c(1-\alpha )\right],t\ge 0,$$

(42)

$$\underset{x=L}{{[\tilde{h}(\xi ,\tau )]}_{\alpha }}=d\left[1-c(1-\alpha ),1+c(1-\alpha )\right],t\ge 0,$$

where c is the uncertainty for α = 0, and

Initial flow condition,

$$\underset{t=0}{{[\tilde{h}(x,t)]}_{\alpha }}={\tilde{y}}_0+\tilde{d}=\tilde{E}$$

(43)

New non-dimensional variables are introduced:

$$\tilde{H}(\xi ,\tau )=\frac{\tilde{h}(\mathrm{x},\mathrm{t})}{d},\xi =\frac{\pi x}{L},\tau =\frac{{\pi }^2{\alpha }_{1}t}{L^2}$$

(44)

Thus, the following Boussinesq equation is formed:

$$\frac{\partial \tilde{H}}{\partial \tau }=\frac{{\partial }^2\tilde{H}}{\partial {\xi }^2},$$

(45)

with the following boundary and initial flow conditions:

$$\xi =0,\tilde{H}(0,\tau )={\tilde{1}}_{\ell },\xi =\pi ,\tilde{H}(1,\tau )={\tilde{1}}_{\ell },\tau =0,\tilde{H}(\xi ,0)=\frac{\tilde{E}}{d},$$

(46)

$$[{\tilde{1}}_{\ell }{]}_{\alpha }=[1^{-}{}_{\ell },1^{+}{}_{\ell }]=[1-c(1-\alpha ),1+c(1-\alpha )]$$

Now we set the main variable $\tilde{y}=\tilde{H}(\xi ,\tau )-{\tilde{1}}_{\ell }$, and the Boussinesq equation takes the following form:

$$\frac{\partial \tilde{y}}{\partial \tau }=\frac{{\partial }^2\tilde{y}}{\partial {\xi }^2}$$

(47)

with the following boundary and initial flow conditions:

$$\xi =0,\tilde{y}(0,\tau )=\tilde{0},\xi =\pi ,\tilde{y}(1,\tau )=\tilde{0},\tau =0,\tilde{y}(\xi ,0)=\frac{\tilde{E}}{d}-{\tilde{1}}_{\ell }={\tilde{\omega }}_1$$

(48)

3. Fuzzy Framework and Definitions

Notation: In order to facilitate an understanding for readers unfamiliar with the fuzzy theory, we describe definitions concerning some preliminaries in fuzzy theory and definitions about the differentiability.

Definition 1.

A fuzzy set $\tilde{H}$ on is a universe set X and is mapping $\tilde{H}:X\to \left[0,1\right]$, and assigning to each element $x\in X$ a degree of membership $0\le \tilde{H}\le 1$. The membership function $\tilde{H}(x)$ is also defined as ${\mu }_{\tilde{H}}(x)$ with the properties:

(i) ${\mu }_{\tilde{H}}$is upper semicontinuous, (ii) ${\mu }_{\tilde{H}}(x)$ = 0, is outside of some interval [c, d], (iii) and there are real numbers $c\le a\le b\le d$, such that ${\mu }_{\tilde{H}}$ is monotonic nondecreasing on [c,a], and monotonic nonincreasing on [b, d] and ${\mu }_{\tilde{H}}(x)$ = 1 for each $x\in \left[a,b\right].$ (iv) $\tilde{H}$ is a convex fuzzy set:

$${\mu }_{\tilde{H}}(\lambda x+(1-\lambda )x)\ge min\{{\mu }_{\tilde{H}}(\lambda x),{\mu }_{\tilde{H}}((1-\lambda )x)\}$$

(49)

Definition 2.

Let X be a Banach space and $\tilde{H}$ be a fuzzy set on X. We define the α-cuts of $\tilde{H}$ as:

$${[\tilde{H}]}^{\alpha }=\{\begin{array}{c}x\in X|\tilde{H}(x)\ge \alpha ,\alpha \in (0,1]\hfill \\ \overline{cl(supp(\tilde{H}(x))},\alpha =0\hfill \end{array}$$

(50)

where cl(supp$(\tilde{H}(x))$) denotes the closure of the support of $\tilde{H}(x)$.

Definition 3.

Let Ҡ(X) be the family of all nonempty compact convex subsets of a Banach space. A fuzzy set $\tilde{H}$ on X is called compact if ${[\tilde{H}]}_{\alpha }\in$Ҡ(X), $\forall \alpha \in \left[0,1\right].$ The space of all compact and convex fuzzy sets on X is denoted as Ƒ(X).

Definition 4.

Let $[\tilde{H}]\in$ Ƒ(R). The α-cuts of $\tilde{H}$ are: $[\tilde{H}{]}_{\alpha }=[H_{\alpha }^{-},H_{\alpha }^{+}]$. According to representation theorem of [38] and the theorem of [39], the membership function and the α-cut form of a fuzzy number $\tilde{H}$ are equivalent and, in particular, the α-cuts $[\tilde{H}{]}_{\alpha }=[H_{\alpha }^{-},H_{\alpha }^{+}]$ uniquely represent $\tilde{H}$, provided that the two functions are monotonic ($H_{\alpha }^{-}$ monotonic nondecreasing, $H_{\alpha }^{+}$ monotonic nonincreasing) and$H_{\alpha =1}^{-}\le H_{\alpha =1}^{+}.$

Definition 5.

gH-differentiability [34]. Let $\tilde{H}:[a,b]\to$ R_Ƒ be such that $[\tilde{H}(x){]}_{\alpha }=[H_{\alpha }^{-}(x),H_{\alpha }^{+}(x)]$. Suppose that the functions $H_{\alpha }^{-}(x)$ and $H_{\alpha }^{+}(x)$ are real-valued functions, differentiable w.r.t. x, and uniformly w.r.t. $\alpha \in [0,1]$. Then, the function $\tilde{H}$ is gH-differentiable at a fixed $x\in [a,b]$ if, and only if, one of the following two cases holds:

1. 

${(H_{\alpha }^{-})}^{\prime }(x)$ is increasing, ${(H_{\alpha }^{+})}^{\prime }(x)$ is decreasing as functions of α, and

$\left[{(H_{\alpha =1}^{-})}^{\prime }(x)\le {(H_{\alpha =1}^{+})}^{\prime }(x)\right]$, or

2. 

${(H_{\alpha }^{+})}^{\prime }(x)$ is increasing, ${(H_{\alpha }^{-})}^{\prime }(x)$ is decreasing as functions of α, and

$$[{(H_{\alpha =1}^{+})}^{\prime }(x)\le {(H_{\alpha =1}^{-})}^{\prime }(x)]$$

Notation1: ${(H_{\alpha }^{-})}^{\prime }(x)=\frac{d{H}_{\alpha }^{-}(x)}{dx},{(H_{\alpha }^{+})}^{\prime }(x)=\frac{d{H}_{\alpha }^{+}(x)}{dx}$. In both of the above cases, the ${\tilde{H}}_{\alpha }^{\prime }(x)$ derivative is a fuzzy number.

Notation2: The first case concerns the Hukuhara differentiability.

Definition 6.

gH-differentiable at x₀. Let $\tilde{H}:\left[a,b\right]\to$ R_F and $x_0\in \left[a,b\right]$ with $H_{\alpha }^{-}(x)$ and $H_{\alpha }^{+}(x),$ and both differentiable at x₀. We say that [29]:

• $\tilde{H}$is (i)-gH-differentiable at x₀ if:

  $$(\mathrm{i})[{\tilde{H}}_{gH}^{\prime }(x_0){]}_{\alpha }=[{(H_{\alpha }^{-})}^{\prime }(x_0),(H_{\alpha }^{+}{)}^{\prime }(x_0)],\forall \alpha \in [0,1]$$

  (51)
• $\tilde{H}$is (ii)-gH-differentiable at x₀ if:

  $$(\mathrm{i})[{\tilde{H}}_{gH}^{\prime }(x_0){]}_{\alpha }=[{(H_{\alpha }^{+})}^{\prime }(x_0),(H_{\alpha }^{-}{)}^{\prime }(x_0)],\forall \alpha \in [0,1]$$

  (52)

Definition 7.

g-differentiability. Let$\tilde{H}:\left[a,b\right]\to$R_F be such that $[\tilde{H}(x){]}_{\alpha }=[H_{\alpha }^{-}(x),H_{\alpha }^{+}(x)]$. If $H_{\alpha }^{-}(x)$ and $H_{\alpha }^{+}(x)$ are differentiable real-valued functions with respect to x, and uniformly for $\alpha \in \left[0,1\right]$, then $\tilde{H}(x)$ is g-differentiable and we have [29]:

$${[{\tilde{H}}_g^{\prime }(x)]}_{\alpha }=\left[\underset{\beta \ge \alpha }{inf}min\{{(H_{\alpha }^{-})}^{\prime }(x),{(H_{\alpha }^{+})}^{\prime }(x)\},\underset{\beta \ge \alpha }{sup}max\{{(H_{\alpha }^{-})}^{\prime }(x),{(H_{\alpha }^{+})}^{\prime }(x)\}\right]$$

(53)

Definition 8.

The gH-differentiability implies g-differentiability, but the inverse is not true.

Definition 9.

[gH-p] differentiability. A fuzzy-valued function $\tilde{H}$ of two variables is a rule that assigns to each ordered pair of real numbers (x, t), in a set D, a unique fuzzy number denoted by $\tilde{H}(x,t)$. Let $\tilde{H}(x,t)$: D → R_Ƒ, (x₀, t₀) $\in$ D and $H_{\alpha }^{-}(x,t)$, $H_{\alpha }^{+}(x,t)$ and are real valued functions and partial differentiable w.r.t. x. We say that [36,39,40]:

• $\tilde{H}$is [(i)-p]-differentiable w.r.t. x at (x₀, t₀) if:

  $$\frac{\partial {\tilde{H}}_{\alpha }(x_0,t_0)}{\partial x_{i.gH}}=[\frac{\partial H_{\alpha }^{-}(x_0,t_0)}{\partial x},\frac{\partial H_{\alpha }^{+}(x_0,t_0)}{\partial x}]$$

  (54)
• $\tilde{H}$is [(ii)-p]-differentiable w.r.t. x at (x₀, t₀) if:

  $$\frac{\partial {\tilde{H}}_{\alpha }(x_0,t_0)}{\partial x_{i.gH}}=[\frac{\partial H_{\alpha }^{+}(x_0,t_0)}{\partial x},\frac{\partial H_{\alpha }^{-}(x_0,t_0)}{\partial x}]$$

  (55)

Notation. The same is valid for $\frac{\partial {\tilde{H}}_{\alpha }(x_0,t_0)}{\partial t}$.

Definition 10.

Let $\tilde{H}(x,t)$: D → R_Ƒ, and $\frac{\partial {\tilde{H}}_{\alpha }(x_0,t_0)}{\partial x_{i.gH}}$ be [gH-p]-differentiable at (x₀, t₀) $\in$ D with respect to x. We say that [35,39]:

• $\frac{\partial {\tilde{H}}_{\alpha }(x_0,t_0)}{\partial x_{i.gH}}$is [(i)-p]-differentiable w.r.t.x if:

  $$\frac{{\partial }^2{\tilde{H}}_{\alpha }(x_0,t_0)}{\partial {x^2}_{i.gH}}=\{\begin{array}{c}[\frac{{\partial }^2{H}_{\alpha }^{-}(x_0,t_0)}{\partial x^2},\frac{{\partial }^2{H}_{\alpha }^{+}(x_0,t_0)}{\partial x^2}]if\tilde{H}(x,t)is[(i)-p]differentiable\hfill \\ [\frac{{\partial }^2{H}_{\alpha }^{+}(x_0,t_0)}{\partial x^2},\frac{{\partial }^2{H}_{\alpha }^{-}(x_0,t_0)}{\partial x^2}]if\tilde{H}(x,t)is[(ii)-p]differentiable\hfill \end{array}$$

  (56)
• $\frac{\partial {\tilde{H}}_{\alpha }(x_0,t_0)}{\partial x_{i.gH}}$is [(ii)-p]-differentiable w.r.t.x if:

  $$\frac{{\partial }^2{\tilde{H}}_{\alpha }(x_0,t_0)}{\partial {x^2}_{i.gH}}=\{\begin{array}{c}[\frac{{\partial }^2{H}_{\alpha }^{+}(x_0,t_0)}{\partial x^2},\frac{{\partial }^2{H}_{\alpha }^{-}(x_0,t_0)}{\partial x^2}]if\tilde{H}(x,t)is[(i)-p]differentiable\hfill \\ [\frac{{\partial }^2{H}_{\alpha }^{-}(x_0,t_0)}{\partial x^2},\frac{{\partial }^2{H}_{\alpha }^{+}(x_0,t_0)}{\partial x^2}]if\tilde{H}(x,t)is[(ii)-p]differentiable\hfill \end{array}$$

  (57)

4. The Proposed Solution to the Fuzzy Model

4.1. Corresponding System

We can find solutions to the fuzzy problem (41) and the boundary and initial conditions (42) and (43), by utilizing the theories of [34,36], and translating the above fuzzy problem to a system of second order of crisp boundary value problems hereafter, called corresponding system for the fuzzy problem. Therefore, four crisp boundary value problems (BVPs) systems are possible for the fuzzy problem as follows:

System (1,1):

$$\begin{gathered} \frac{\partial h_{\alpha }^{-}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{-}}{\partial {\xi }^2}=0 \\ \frac{\partial h_{\alpha }^{+}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{+}}{\partial {\xi }^2}=0 \end{gathered}$$

System (1,2):

$$\begin{gathered} \frac{\partial h_{\alpha }^{-}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{+}}{\partial {\xi }^2}=0 \\ \frac{\partial h_{\alpha }^{+}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{-}}{\partial {\xi }^2}=0 \end{gathered}$$

System (2,1):

$$\begin{gathered} \frac{\partial h_{\alpha }^{+}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{-}}{\partial {\xi }^2}=0 \\ \frac{\partial h_{\alpha }^{-}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{+}}{\partial {\xi }^2}=0 \end{gathered}$$

System (2,2):

$$\begin{gathered} \frac{\partial h_{\alpha }^{+}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{+}}{\partial {\xi }^2}=0 \\ \frac{\partial h_{\alpha }^{-}}{\partial t}-\frac{{\partial }^2{h}_{\alpha }^{-}}{\partial {\xi }^2}=0 \end{gathered}$$

We will present here only the solution of the (1,1) system, which also describes the physical problem.

First case

$$\frac{\partial h_{\alpha }^{-}}{\partial t}-{\alpha }_1\frac{{\partial }^2{h}_{\alpha }^{-}}{\partial {\xi }^2}=0$$

(58)

Boundary and initial flow condition:

$$\underset{x=0}{h^{-}{(x,t)}_{\alpha }}=d(1-\mathrm{c}(1-\alpha )),\underset{x=L}{ h^{-}(\xi ,\tau )}=d(1-c(1-\alpha )),t\ge 0,$$

(59)

$$\underset{t=0}{h^{-}{(x,t)}_{\alpha }}=(y_0+d)(1-c(1-\alpha ))=E^{-}$$

(60)

Non-dimensional variables

The non-dimensional variables are introduced in Equation (58):

$$H^{-}=\frac{h^{-}}{d},\xi =\frac{\pi x}{L},\tau =\frac{{\pi }^2{\alpha }_{1}t}{L^2},$$

$$\frac{\partial H^{-}}{\partial \tau }=\frac{{\partial }^2{H}^{-}}{\partial {\xi }^2}$$

(61)

$$\xi =0,H^{-}(0,\tau )=1-c(1-\alpha ),\xi =\pi ,H^{-}(1,\tau )=1-c(1-\alpha )$$

$$\tau =0,H^{-}(\xi ,0)=\frac{E^{-}}{d}.$$

(62)

Now, introduce the new:

$$y^{-}=H^{-}(\xi ,\tau )-1_{\ell }^{-}$$

Equation (61) becomes,

$$\frac{\partial y^{-}}{\partial \tau }=\frac{{\partial }^2{y}^{-}}{\partial {\xi }^2}$$

(63)

with the following boundary and initial flow conditions:

$$\xi =0,y^{-}(0,\tau )=0^{-},\xi =\pi ,y^{-}(1,\tau )=0^{-},\tau =0,y^{-}(\xi ,0)=\frac{E^{-}}{d}-1_{\ell }^{-}={\omega }_{\ell }^{-}$$

(64)

Second case

$$\frac{\partial h_{\alpha }^{+}}{\partial t}-{\alpha }_1\frac{{\partial }^2{h}_{\alpha }^{+}}{\partial {\xi }^2}=0$$

(65)

Boundary and initial flow condition:

$$\underset{x=0}{h^{+}{(x,t)}_{\alpha }}=d(1+\mathrm{c}(1-\alpha )),\underset{x=L}{h^{+}(\xi ,\tau )}=d(1+c(1-\alpha )),t\ge 0,$$

(66)

$$\underset{t=0}{h^{+}{(x,t)}_{\alpha }}=(y_0+d)(1+c(1-\alpha ))=E^{+}$$

(67)

Non-dimensional variables

The non-dimensional variables are introduced in Equation (58):

$$H^{+}=\frac{h^{+}}{d},\xi =\frac{\pi x}{L},\tau =\frac{{\pi }^2{\alpha }_{1}t}{L^2},$$

$$\frac{\partial H^{+}}{\partial \tau }=\frac{{\partial }^2+}{\partial {\xi }^2}$$

(68)

$$\xi =0,H^{+}(0,\tau )=1c(1-\alpha ),\xi =\pi ,H^{+}(1,\tau )=1+c(1-\alpha )$$

$$\tau =0,H^{+}(\xi ,0)=\frac{E^{+}}{d}$$

(69)

Now, introduce the new:

$$y^{+}=H^{+}(\xi ,\tau )-1_{\ell }^{+}$$

Equation (68) becomes,

$$\frac{\partial y^{+}}{\partial \tau }=\frac{{\partial }^2{y}^{+}}{\partial {\xi }^2}$$

(70)

with the following boundary and initial flow conditions:

$$\xi =0,y^{+}(0,\tau )=0^{+},\xi =\pi ,y^{+}(1,\tau )=0^{+},\tau =0,y^{+}(\xi ,0)=\frac{E^{+}}{d}-1_{\ell }^{+}={\omega }_{\ell }^{+}$$

(71)

Based on the above, we can finally construct the following expressions:

• First case

  $$\frac{\partial y^{-}}{\partial \tau }=\frac{{\partial }^2{y}^{-}}{\partial {\xi }^2}$$

  (72)

  $$\xi =0,y^{-}(0,\tau )=0^{-},\xi =\pi ,y^{-}(\pi ,\tau )=0^{-},\tau =0,y^{-}(\xi ,0)=\frac{E^{-}}{d}-1_{\ell }^{-}={\omega }_1^{-}$$

  (73)
• Second case

  $$\frac{\partial y^{+}}{\partial \tau }=\frac{{\partial }^2{y}^{+}}{\partial {\xi }^2}$$

  (74)

  $$\xi =0,y^{+}(0,\tau )=0^{+},\xi =\pi ,y^{+}(\pi ,\tau )=0^{+},\tau =0,y^{+}(\xi ,0)=\frac{E^{+}}{d}-1_{\ell }^{+}={\omega }_1^{+}$$

  (75)

4.2. The Adomian Solution

4.2.1. First Case

For the first case we have the following:

$$\frac{\partial y^{-}}{\partial \tau }-\frac{{\partial }^2{y}^{-}}{\partial {\xi }^2}=0,$$

(76)

Boundary and initial flow condition:

$$\underset{\xi =0}{y^{-}(\xi ,\tau )}=0,\tau \ge 0,\underset{\xi =\pi }{y^{-}(\xi ,\tau )}=0\tau \ge 0,\tau =0,y^{-}(\xi ,0)=\frac{E^{-}}{d}-1_{\ell }^{-}$$

(77)

The Adomian solution is:

$$y^{-}(\xi ,\tau )={{\displaystyle \sum }}_{n=1}^{\infty }{B}^{-}{}_{n}sin(n\xi )e^{-n^2\tau },$$

(78)

where

$$y^{-}(\xi ,0)=\frac{{{\rm E}}^{-}}{d}-1_{\ell }^{-}={\displaystyle \sum }_{n=1}^{\infty }{B}^{-}{}_{n}sin(n\xi )$$

(79)

$$B^{-}{}_n=\{\frac{2{\omega }_1^{-}}{n\pi }[1-(-1{)}^n]\},{\omega }_1^{-}(\alpha )=\frac{E^{-}}{d}-1_{\ell }^{-}$$

(80)

$$H_{\alpha }^{-}(\xi ,\tau )=y^{-}(\xi ,\tau )+1_{\ell }^{-}$$

(81)

$$h_{\alpha }^{-}(\xi ,\tau )=d·H_{\alpha }^{-}(\xi ,\tau )=d\left\{y^{-}(\xi ,\tau )+1_{\ell }^{-}\right\}$$

(82)

Boundary conditions:

$$\underset{x=0}{h_{\alpha }^{-}(x,t)}=d\underset{\xi =0}{H_{\alpha }^{-}(\xi ,\tau )}=d\{\underset{\xi =0}{y(\xi ,\tau )}+1_{\ell }^{-}\}=d·1_{\ell }^{-}$$

(83)

$$\underset{\xi =L}{h_{\alpha }^{-}(x,t)}=d\underset{\xi =\pi }{H_{\alpha }^{-}(\xi ,\tau )}=d\{\underset{\xi =\pi }{y(\xi ,\tau )}+1_{\ell }^{-}\}=d·1_{\ell }^{-}$$

(84)

Initial flow condition:

$$\underset{t=0}{{[h^{-}(x,t)]}_{\alpha }}=d(\underset{\tau =0}{y(\xi ,\tau )}+1_{\ell }^{-})=E^{-}$$

(85)

Therefore, the Adomian solution takes the following form:

$$h_{\alpha }^{-}(x,t)=d\{{{\displaystyle \sum }}_{n=1}^{\infty }{B}_n^{-}sin(n\xi )e^{-n^2\tau }+1_{\ell }^{-}\},\xi =\frac{\pi x}{L},\tau =\frac{{\pi }^2{\alpha }_{1}t}{L^2}$$

(86)

and is the first fuzzy solution of the problem.

4.2.2. Second Case

For the second case initially, we set as the following:

$$y^{+}(\xi ,\tau )=H_{\alpha }^{+}(\xi ,\tau )-1_{\ell }^{+}$$

(87)

and the following equation arises:

$$\frac{\partial y^{+}}{\partial \tau }-\frac{{\partial }^2{y}^{+}}{\partial {\xi }^2}=0,$$

(88)

Boundary and initial flow conditions:

$$\underset{\xi =0}{y^{+}(\xi ,\tau )}=0,\tau \ge 0,\underset{\xi =\pi }{y^{+}(\xi ,\tau )}=0\tau \ge 0,\tau =0,y^{+}(\xi ,0)=\frac{E^{+}}{d}-1_{\ell }^{+}$$

(89)

The Adomian solution is:

$$y^{+}(\xi ,\tau )={{\displaystyle \sum }}_{n=1}^{\infty }{B}^{+}{}_{n}sin(n\xi )e^{-n^2\tau },$$

(90)

where

$$y^{+}(\xi ,0)=\frac{{{\rm E}}^{+}}{d}-1_{\ell }^{+}={\displaystyle \sum }_{n=1}^{\infty }{B}^{+}{}_{n}sin(n\xi )$$

(91)

$$B^{+}{}_n=\{\frac{2{\omega }_1^{+}}{n\pi }[1-(-1{)}^n]\}=\{{ }_{\frac{4{\omega }_1^{+}}{n\pi }n=2k+1}^{0n=2k},{\omega }_1^{+}(\alpha )=\frac{E^{+}}{d}-1_{\ell }^{+}$$

(92)

$$H_{\alpha }^{+}(\xi ,\tau )=y^{+}(\xi ,\tau )+1_{\ell }^{+}$$

(93)

$$h_{\alpha }^{+}(\xi ,\tau )=d·H_{\alpha }^{+}(\xi ,\tau )=d(y^{+}(\xi ,\tau )+1_{\ell }^{+})$$

(94)

Boundary conditions:

$$\underset{x=0}{h_{\alpha }^{+}(x,t)}=d·\underset{\xi =0}{H_{\alpha }^{+}(\xi ,\tau )}=d(\underset{\xi =0}{y^{+}(\xi ,\tau )}+1_{\ell }^{+})=d·1_{\hslash }^{+}$$

(95)

$$\underset{x=L}{h_{\alpha }^{+}(x,t)}=d·\underset{\xi =\pi }{H_{\alpha }^{+}(\xi ,\tau )}=d(\underset{\xi =\pi }{y^{+}(\xi ,\tau )}+1_{\ell }^{+})=d·1_{\ell }^{+}$$

(96)

Initial flow condition:

$$\underset{t=0}{{[h^{+}(x,t)]}_{\alpha }}=d\{\underset{\tau =0}{H+ (\xi ,\tau )}+1_{\ell }^{-}-1_{\ell }^{-}\}=E^{+}$$

(97)

Therefore, the Adomian solution takes the following form:

$$h_{\alpha }^{+}(x,t)=d\{{{\displaystyle \sum }}_{n=1}^{\infty }{B}_n^{+}sin(n\xi )e^{-n^2\tau }+1_{\ell }^{+}\},\xi =\frac{\pi x}{L},\tau =\frac{{\pi }^2{\alpha }_{1}t}{L^2}$$

(98)

and is the second fuzzy solution of the problem.

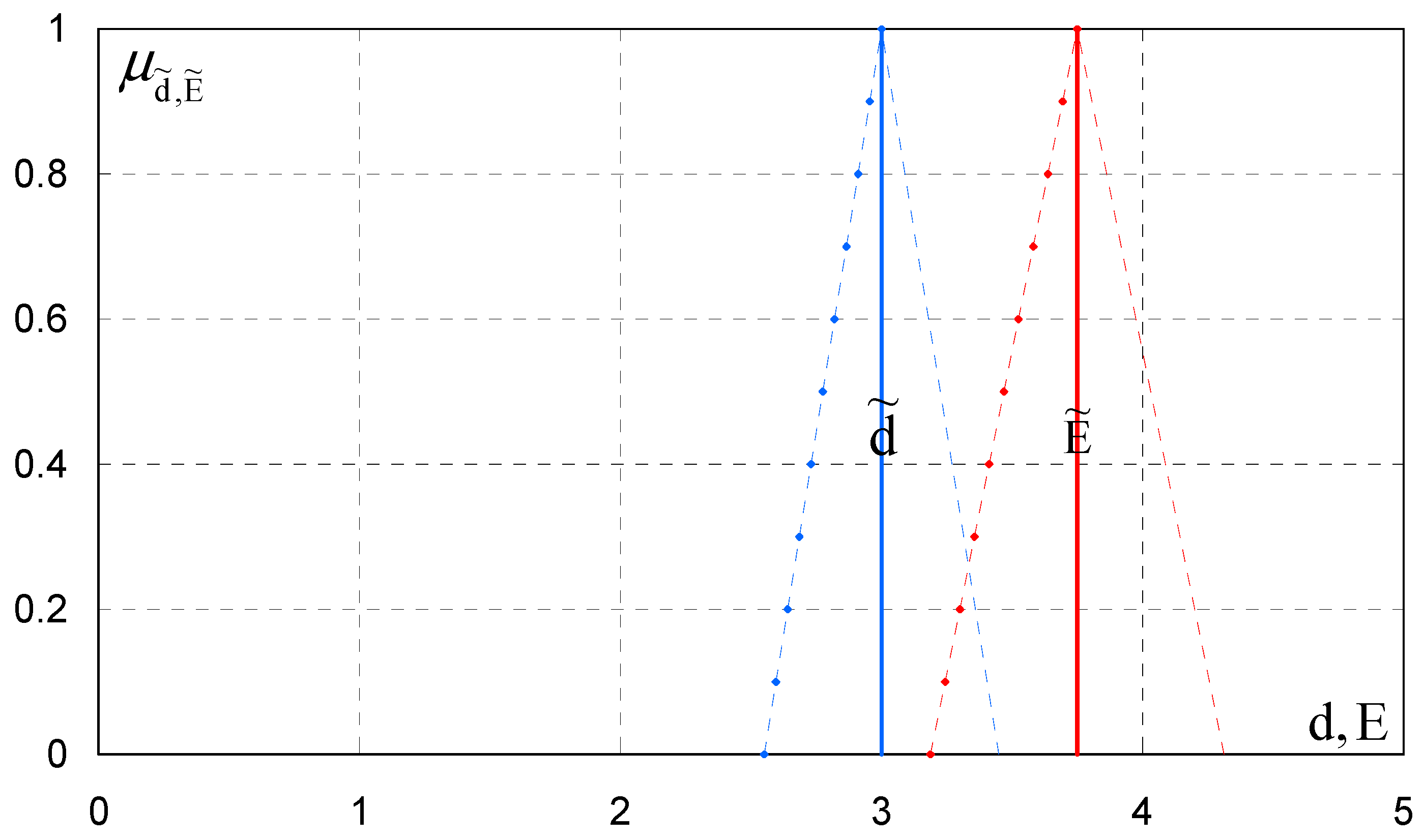
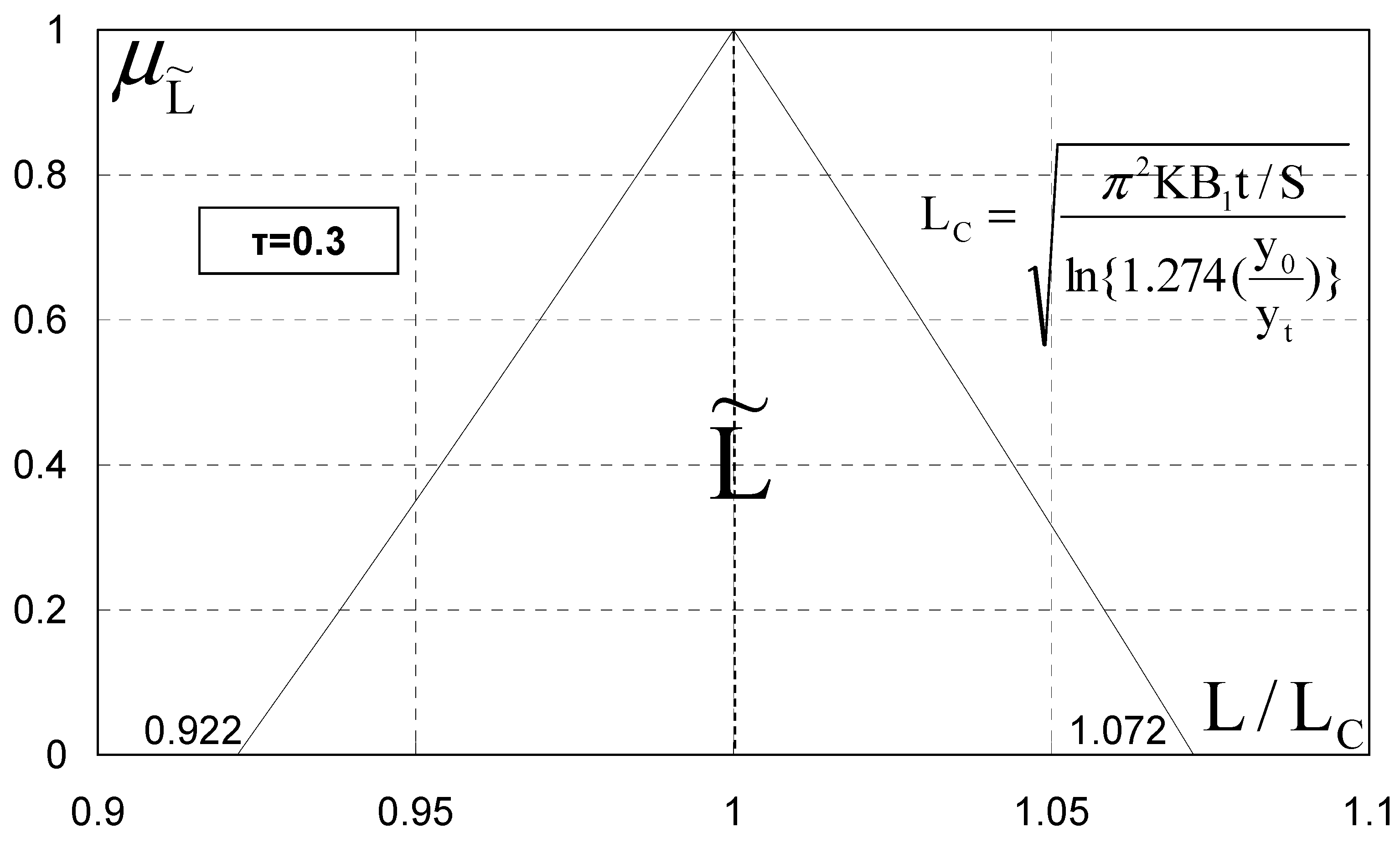
4.3. Fuzzy Drain Spacing

The ratio $y_0/y_t$ is equal with the ratio $y_0^{\pm }/y_t^{\pm }$. Thus, the length L is a function of α-cut as follows:

Assume the following:

$$B_1=\frac{{\overline{y}}_0}{2}+d,$$

(99)

For the fuzzy case:

$$[{\tilde{B}}_2{]}_{\alpha }=[\frac{{\tilde{y}}_0}{2}+\tilde{d}{]}_{\alpha }=[B_2^{-},B_2^{+}]=B_1[1_{\ell }^{-},1_{\ell }^{+}]$$

(100)

Based on the above equation, Equation (39) formed as follows:

$$\tilde{L}=\sqrt{\frac{{\pi }^2(Kt/S){\tilde{B}}_2}{ln\{1.274(\frac{{\overline{y}}_0}{y_t})\}}},$$

(101)

or

$$[\tilde{L}{]}_{\alpha }=[L_{\alpha }^{-},L_{\alpha }^{+}],$$

(102)

where

$$L_{\alpha }^{-}=\sqrt{\frac{{\pi }^2(Kt/S)B_{2\alpha }^{-}}{ln\{1.274(\frac{y_0}{y_t})\}}}=\sqrt{\frac{{\pi }^2(Kt/S)B_1}{ln\{1.274(\frac{y_0}{y_t)})\}}}(\sqrt{1_{\ell }^{-}})=L_C\sqrt{1_{\ell }^{-}}$$

(103)

and

$$L_{\alpha }^{+}=\sqrt{\frac{\pi 2_{ }(Kt/S)B_{\alpha }^{+}}{ln\{1.274(\frac{y_0}{y_t})\}}}=\sqrt{\frac{{\pi }^2(\frac{Kt}{S})B_1}{ln\{1.274(\frac{y_0}{y_t})\}}}(\sqrt{1_{\ell }^{+}})=L_C\sqrt{1_{\ell }^{+}}$$

(104)

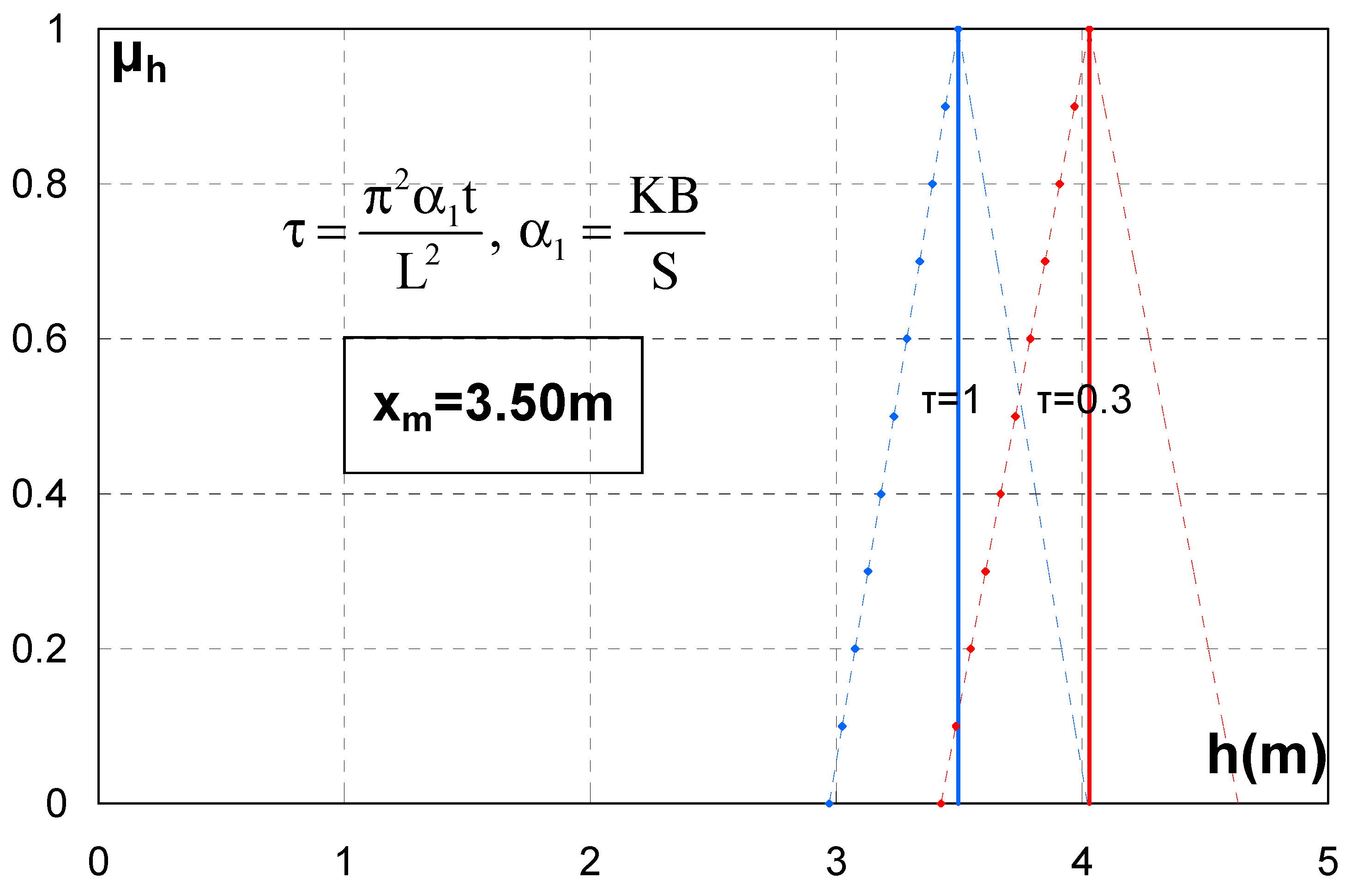
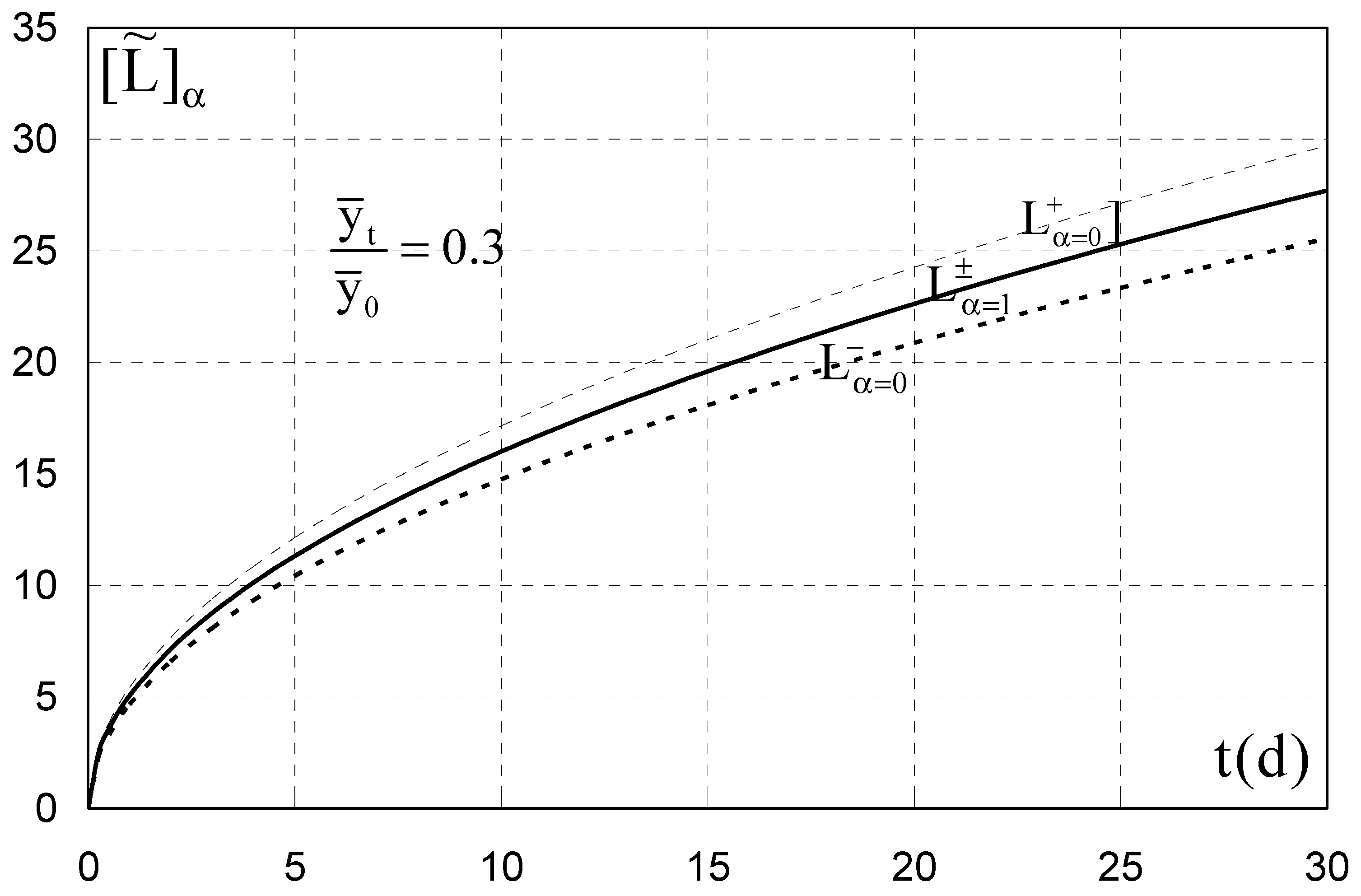
5. Results—Application

For the case of Figure 1, the following are valid: Κ = 0.2 m/d, S = 0.2, d = 3 m, E = 4.5 m, and α₁ = KB/S = 3.75 m²/d. An uncertainty of 15% is introduced to the boundary and initial flow conditions. Based on the above, the values are calculated and plotted on Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Specifically, in Figure 3, the fuzzy boundary and initial flow conditions are presented while Figure 4 presents the drain water table profiles for the non-dimensional times of τ = 0.3 and τ = 1.

Figure 5 provides the water table membership functions for the non-dimensional times of τ = 0.3 and τ = 1 at the position x = 3.5 m. From this figure, the results indicate that at the position x = 3.5 m and for τ = 1, for the classical case, the h drain value is equal to 3.49 m. On the other hand, based on fuzzy logic and also on the possibility theory, for α = 0.05, the above value is in the interval [2.99, 3.99] with a 95% degree of confidence.

Similarly, Figure 6 shows the membership function of the water table for the non-dimensional times of τ = 0.3 and τ = 1 at the position x = 7 m. From this figure, the results indicate that at the position x = 7 m and for τ = 1, for the classical case, the h drain value is equal to 3.7 m. On the other hand, based on fuzzy logic and also on the possibility theory, for α = 0.05, the above value is in the interval [3.17, 4.23] with a 95% degree of confidence.

Figure 7 presents the drain spacing membership functions for τ = 0.3. Finally, Figure 8 shows the variation of the drain spacing for the above values (K, B, S, etc.) with respect to time, in days. From Figure 7 and Figure 8 and based on the above values, for the non-dimensional time τ = 0.3(t = 1.83d), results indicate that in classical logic the drain spacing value is Lc = 15 m. However, based on the fuzzy logic and also on the possibility theory for α = 0.05, the value of drain spacing is in the interval L = [13.89, 16.03] with a 95% degree of confidence.

6. Discussion and Future Research

Well-drained agricultural lands have longer periods with good soil health, and this could lead to a more efficient production as well as economic benefits. To find the optimal drain spacing is very crucial in order to design a drainage system, and it is still a tedious task. Farmers, landowners, agri-consultants and contractors are some cases that are directly interested in the accurate drain spacing.

Based on our expertise in these fields we believe that the most crucial uncertainties of this drainage problem appear on the boundary and initial flow conditions; in addition, previous works have dealt with these uncertainties in groundwater flow problems [41,42,43,44]. These uncertainties could have bad consequences for the soils and the plant growth if they are not included in the calculations. In this context, the innovative findings of this research regarding the drain spacing calculation, could strongly support the general land reclamation problem and therefore international and European directives such as the Common Agricultural Policy (CAP) and the Sustainable Development Goals (SDGs).

We must also mention that drainage no longer plays the significant role in the food production process that it played in the previous years. However, it will continue to play a major part in maintaining the present levels of food production. This is valid especially of rainfed lands, much of whose productivity would diminish substantially without drainage, and particularly of irrigated land. Without drainage, a large part of the irrigated land in the arid and sub-arid zones would not be sustainable and would be doomed to degrade into a waterlogged and/or salinized wasteland. In addition, in the same context, our approach aims to prevent the inflow of water, due to the increase in the phreatic level of the aquifer, towards the aeration zone. The use of our approach in the future, for a drainage network design and construction, requires the knowledge of the intensity of the artificial rain coming from the irrigation, in order to accurately calculate the required remaining time of the useful water in the aeration zone needed by the root substrate for the plants to grow.

Our proposed solution could not be calibrated and validated at this phase, mainly due to the lack of in situ measurements of the various soil and hydraulic parameters. Our approach at the moment is in a theoretical framework but without affecting the accuracy and reliability of the solution, as this approach is based mainly on the well-known and tested Glover-Dumm equation by adding the uncertainty part. An extended version of this work could be undoubtably, and its validation with in-situ measurements under controlled conditions and field work, as well as its practical application in the field with possible comparisons with other fuzzy solutions of drain spacing, will probably be developed in the future.

Furthermore, it is crucial to highlight that the hydraulic conductivity and soil texture are key factors in determining the optimal drain spacing. Hydraulic conductivity is a soil parameter which demands in situ measurements such as the auger method or soil sample analysis in the laboratory; in addition, it is a parameter that presents great variability even at parcel levels, creating difficult conditions for its determination and costly laboratory and in situ analyses. However, its importance in the drain spacing equations is more than critical and future research could focus on the inclusion of the uncertainties contained in this parameter. In addition, and in this context, innovative low cost in situ solutions (such as a portable spectrometer) [45] could be used to measure key soil parameters and support the drain spacing problem with valuable input data.

7. Conclusions

The ADM theory allows for finding an approximate solution of the differential equations with a satisfactory accuracy and, in some cases, as in the present work, for the linearized Boussinesq equation, that is identical to the accurate analytical solution.

Based on Figure 4, Figure 5 and Figure 6, the results indicate that the absolute fuzzy value decreases when the time increases, while the relevant value remains the same. On the contrary, from Figure 8, which refers on the drain spacing, results indicate that the absolute fuzzy value increases when the time increases, while the relevant value again remains the same.

The Khastan and Nieto (2010) [36] and Bede and Stefanini theory (2013) [34] with the generalized Hukuhara (g-H) derivative, as well as its extension to the Allahviranloo et al. (2015) [35] partial differential equations, allows researchers to solve practical problems that are useful in engineering. It is now possible for engineers to take the fuzziness of the various sizes involved into consideration and to solve the fuzzy problems.

The importance of the possibility theory is very crucial because it allows the researchers to find, with a small risk, the interval of variation of the unknown variable value with a degree of confidence greater than 95%.

In our analysis, the climatic conditions were not actively considered as they are not strongly affecting the approach to construct the final proposed fuzzy analytical solution, which was the main goal of this work. All efforts focused on the scientific analysis and evaluation of the construction of the analytical solution by using the innovative Adomian decomposition method (see Appendix A). A general note is that this fuzzy approach is based on the Glover-Dumm equation which, until today, does not have any serious constraint regarding its implementation in different climatic zones. Thus, our approach could be implemented in all types of climatic zones around the globe.

Finally, it should be mentioned that the inclusion of the uncertainties in the hydraulic conductivity parameter combined with the boundary and initial flow condition uncertainties, are in the authors’ future plans, where the achievement could create a promising fuzzy melioration methodology related to the drain spacing problem.