Impedance Pumping and Resonance in a Multi-Vessel System
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Physical Model
2.2. The Mathematical Model
2.3. The Actuation Mechanism Model
2.4. Computational Methods
3. Results
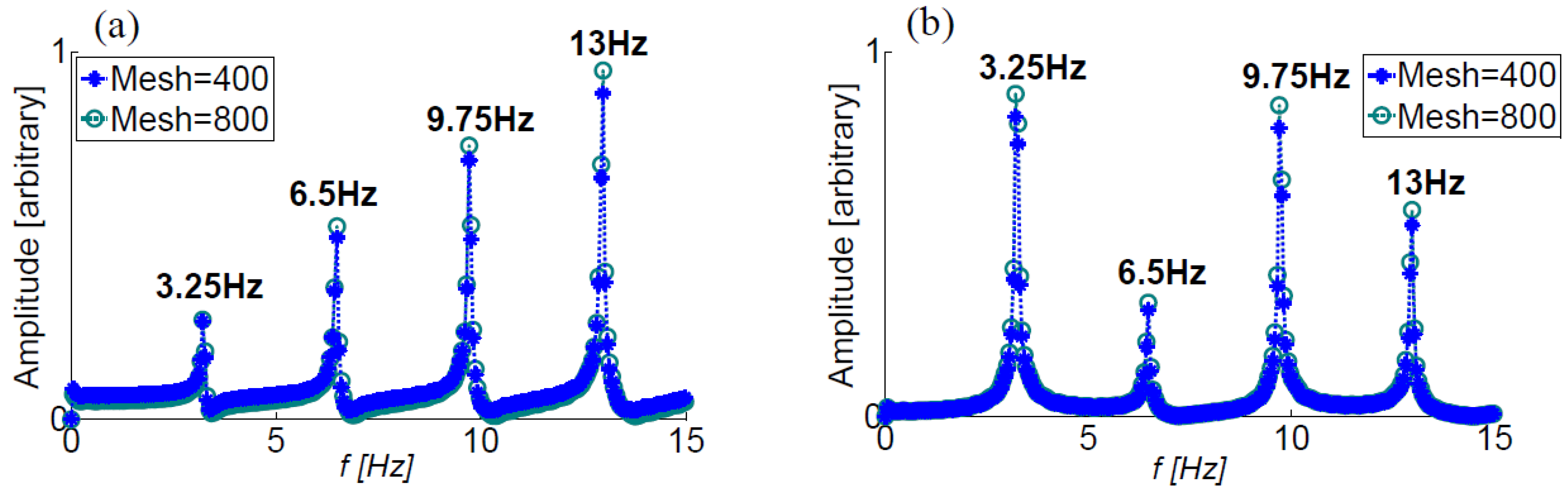
3.1. Natural Frequencies of a Multi-Vessel Compliant System
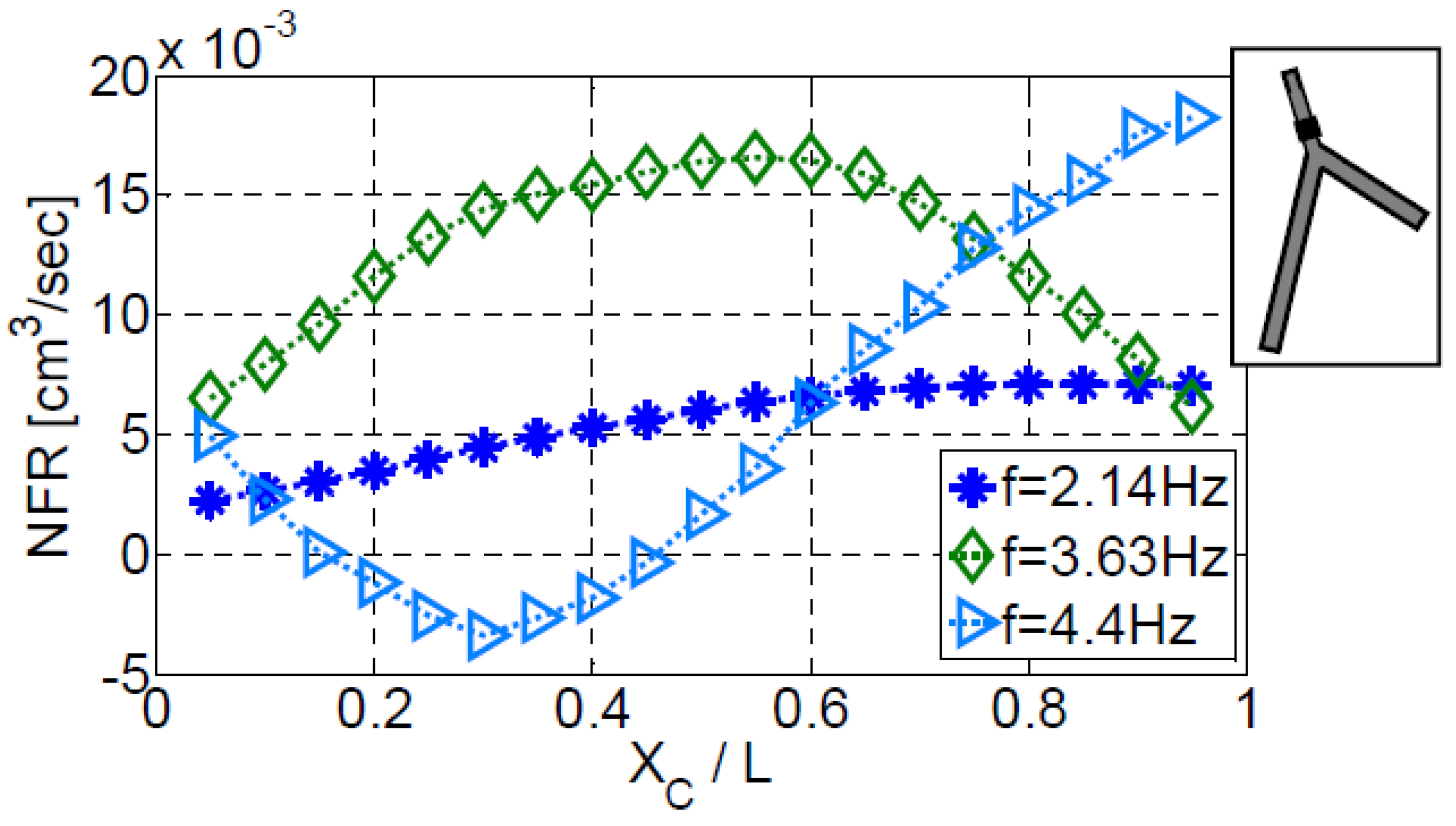
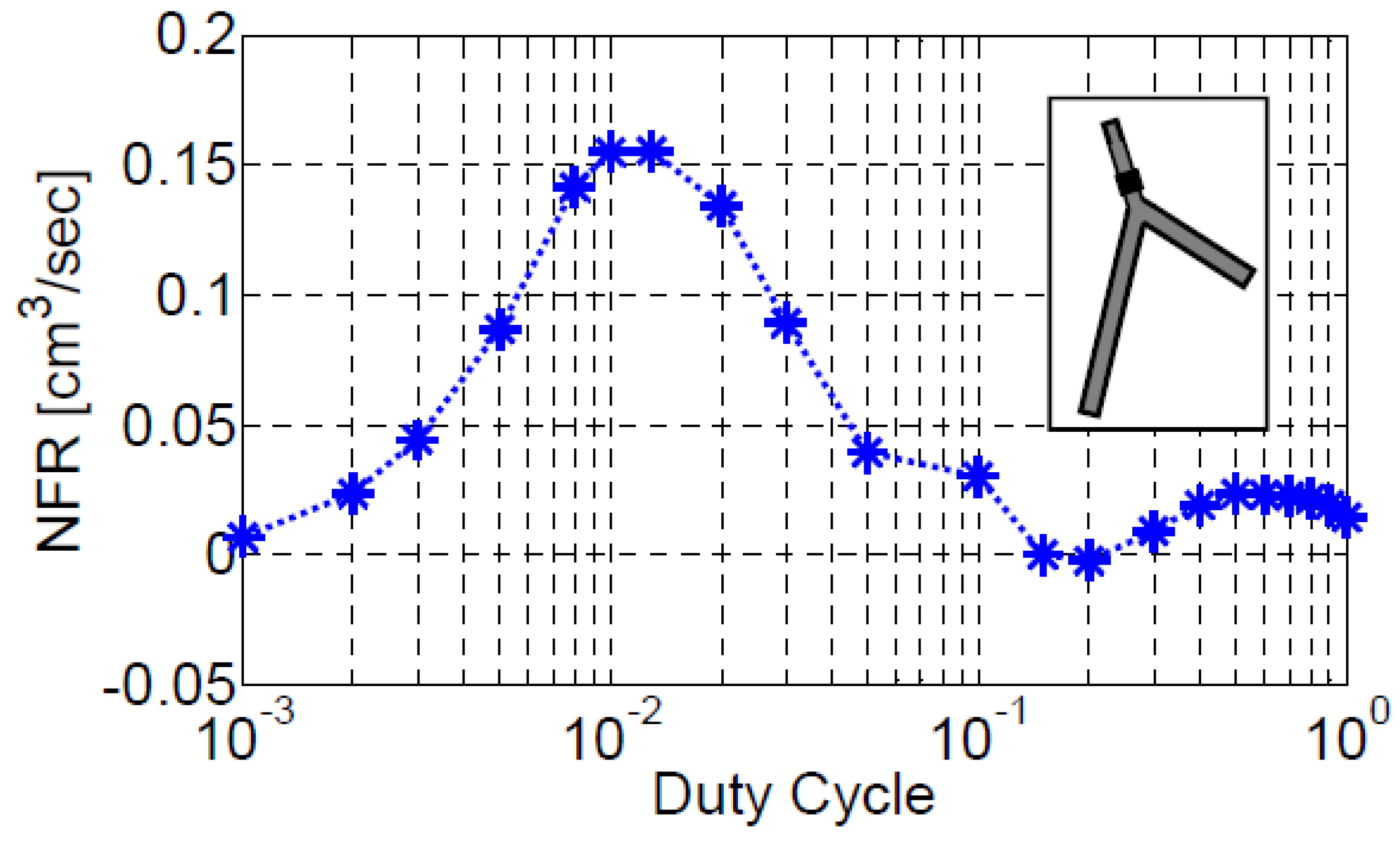
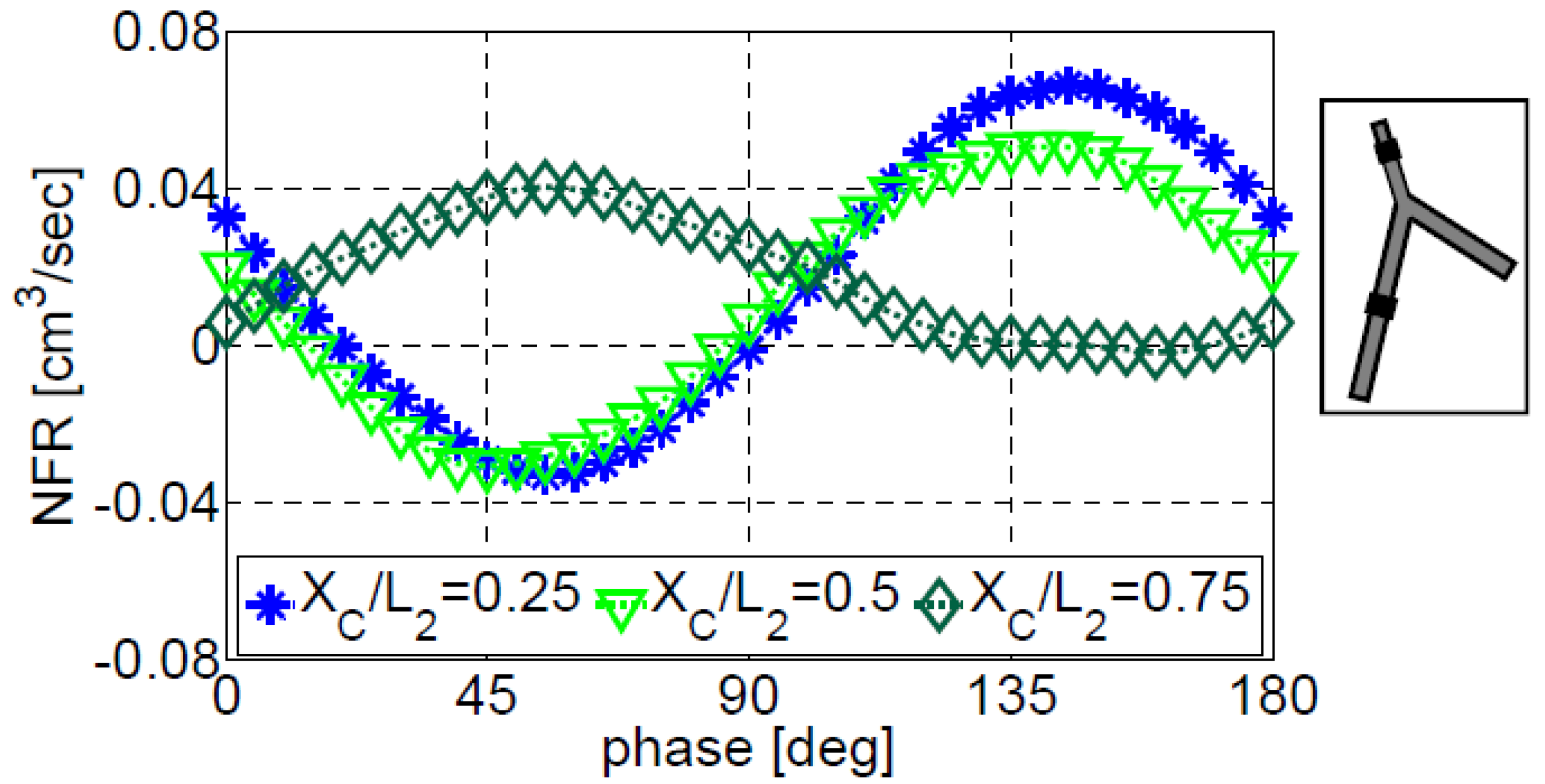
3.2. Impedance Pumping in Multi-Vessels Systems
3.2.1. Three-Vessels Model
3.2.2. Five-Vessels Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hickerson, A.; Rinderknecht, D.; Gharib, M. Experimental study of the behavior of a valveless impedance pump. Exp. Fluids 2005, 38, 534–540. [Google Scholar] [CrossRef]
- Manopoulos, C.; Mathioulakis, D.S.; Tsangaris, S.G. One-dimensional model of valveless pumping in a closed loop and a numerical solution. Phys. Fluids 2006, 18, 017106. [Google Scholar] [CrossRef]
- Rinderknecht, D.; Hickerson, A.I.; Gharib, M. A valveless micro impedance pump driven by electromagnetic actuation. J. Micromech. Microeng. 2005, 15, 861. [Google Scholar] [CrossRef]
- Moser, M.; Huang, J.W.; Schwarz, G.S.; Kenner, T.; Noordergraaf, A. Impedance Defined Flow—Generalization of William Harvey’s Concept of the Circulation—370 years later. Int. J. Cardiovasc. Med. Sci. 1998, 1, 205–211. [Google Scholar]
- Avrahami, I.; Gharib, M. Computational studies of resonance wave pumping in compliant tubes. J. Fluid Mech. 2008, 608, 139–160. [Google Scholar] [CrossRef]
- Pahlevan, N.M.; Gharib, M. In-vitro investigation of a potential wave pumping effect in human aorta. J. Biomech. 2013, 46, 2122–2129. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.Y.; Yeh, S.J.; Leong, K.P.; Kuo, W.S.; Lin, H. Application of a valveless impedance pump in a liquid cooling system. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 783–791. [Google Scholar] [CrossRef]
- Ottesen, J.T. Valveless pumping in a fluid-filled closed elastic tube-system: One-dimensional theory with experimental validation. J. Math. Boil. 2003, 46, 309–332. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.Y.; Chang, H.T. Design and characterization of valveless impedance pumps. J. Mech. 2009, 25, 345–354. [Google Scholar] [CrossRef]
- Jung, E. A Mathematical Model of Valveless Pumping: A Lumped Model with Time-Dependent Compliance, Resistance, and Inertia. Bull. Math. Boil. 2007, 69, 2181–2198. [Google Scholar] [CrossRef] [PubMed]
- Hickerson, A. An Experimental Analysis of the Characteristic Behaviors of an Impedance Pump. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2005. [Google Scholar]
- Loumes, L.; Avrahami, I.; Gharib, M. Resonant pumping in a multilayer impedance pump. Phys. Fluids 2008, 20, 023103. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, M.; Avrahami, I. Net flow rate generation by a multi-pincher impedance pump. Comput. Fluids 2010, 39, 1634–1643. [Google Scholar] [CrossRef]
- Timmermann, S.; Ottesen, J.T. Novel characteristics of valveless pumping. Phys. Fluids 2009, 21, 053601. [Google Scholar] [CrossRef] [Green Version]
- Hickerson, A.I.; Gharib, M. On the resonance of a pliant tube as a mechanism for valveless pumping. J. Fluid Mech. 2006, 555, 141–148. [Google Scholar] [CrossRef]
- Shin, S.J.; Sung, H.J. Three-dimensional simulation of a valveless pump. Int. J. Heat Fluid Flow 2010, 31, 942–951. [Google Scholar] [CrossRef]
- Jung, E.; Peskin, C.S. Two-Dimensional Simulations of Valveless Pumping Using the Immersed Boundary Method. SIAM J. Sci. Comput. 2001, 23, 19–45. [Google Scholar] [CrossRef]
- Shin, S.J.; Chang, C.B.; Sung, H.J. Simulation of a valveless pump with an elastic tube. Int. J. Heat Fluid Flow 2012, 38, 13–23. [Google Scholar] [CrossRef]
- Sheng, C.; Sarwal, S.; Watts, K.; Marble, A. Computational simulation of blood flow in human systemic circulation incorporating an external force field. Med. Boil. Eng. Comput. 1995, 33, 8–17. [Google Scholar] [CrossRef]
- Sherwin, S.J.; Formaggia, L.; Peiró, J.; Franke, V. Computational modelling of 1D blood flow with variable mechanical properties and its application to the simulation of wave propagation in the human arterial system. Int. J. Numer. Methods Fluids 2003, 43, 673–700. [Google Scholar] [CrossRef] [Green Version]
- Kozlovsky, P.; Rosenfeld, M.; Jaffa, A.J.; Elad, D. Dimensionless analysis of valveless pumping in a thick-wall elastic tube: Application to the tubular embryonic heart. J. Biomech. 2015, 48, 1652–1661. [Google Scholar] [CrossRef] [PubMed]
- Olufsen, M.S.; Peskin, C.S.; Kim, W.Y.; Pedersen, E.M.; Nadim, A.; Larsen, J. Numerical Simulation and Experimental Validation of Blood Flow in Arteries with Structured-Tree Outflow Conditions. Ann. Biomed. Eng. 2000, 28, 1281–1299. [Google Scholar] [CrossRef] [PubMed]
- Fullana, J.-M.; Zaleski, S. A branched one-dimensional model of vessel networks. J. Fluid Mech. 2009, 621, 183–204. [Google Scholar] [CrossRef]










| Length | Radius | |
|---|---|---|
| Configuration III-a Identical Lengths | ||
| Configuration III-b Different Lengths | ||
| Configuration V |
| Configuration III-b | ||
| Vessels | Path Length (m) | Theoretical Frequency (Hz) |
| 1 | 0.4 | 6.5 |
| 2 | 0.9 | 2.89 |
| 1 and 2 | 1.3 | 2 |
| 3 | 1.9 | 1.37 |
| 1 and 3 | 2.3 | 1.13 |
| Configuration V | ||
| Vessels | Path Length (m) | Theoretical Frequency (Hz) |
| 5 | 0.3 | 8.67 |
| 1 or 2 or 3 | 0.4 | 6.5 |
| 4 or 2 and 5 | 0.7 | 3.7 |
| 1 and 2 or 1 and 3 | 0.8 | 3.25 |
| 1 and 2 and 5 or 2 and 4 | 1.1 | 2.36 |
| 1 and 2 and 4 | 1.5 | 1.73 |
| Configuration III-b | |
| Calculated Frequency (Hz) | Theoretical Frequency (Hz) |
| 1.19 | 1.13 1.37 |
| 2.14 | 2 2.26 (1.13 × 2) |
| 2.77 | 2.89 2.74 (1.37 × 2) |
| 3.64 | 3.39 (1.13 × 3) 4 (2 × 2) |
| 4.36 | 4 (2 × 2) 4.11 (1.37 × 3) 4.52 (1.13 × 4) |
| 5.55 | 5.48 (1.37 × 4) 5.65 (1.13 × 5) |
| 5.9 | 5.78 (2.89 × 2) 6 (2 × 3) |
| 6.8 | 6.5 (6.5 × 1) 6.85 (1.37 × 5) |
| Configuration V | |
| Calculated Frequency (Hz) | Theoretical Frequency (Hz) |
| 2.37 | 2.36 |
| 3.49 | 3.25 3.7 |
| 4.75 | 4.72 (2.36 × 2) |
| 6.5 | 6.5 6.5 (3.25 × 2) |
| 7.05 | 7.08 (2.36 × 3) |
| 7.92 | 7.4 (3.7 × 2) 7.97 (4.72 + 3.25) 8.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zislin, V.; Rosenfeld, M. Impedance Pumping and Resonance in a Multi-Vessel System. Bioengineering 2018, 5, 63. https://doi.org/10.3390/bioengineering5030063
Zislin V, Rosenfeld M. Impedance Pumping and Resonance in a Multi-Vessel System. Bioengineering. 2018; 5(3):63. https://doi.org/10.3390/bioengineering5030063
Chicago/Turabian StyleZislin, Victor, and Moshe Rosenfeld. 2018. "Impedance Pumping and Resonance in a Multi-Vessel System" Bioengineering 5, no. 3: 63. https://doi.org/10.3390/bioengineering5030063





