Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model for Vibrational Analysis of Single-Walled Carbon Nanotubes

Abstract

In this study, a new anisotropic elastic shell model with a nonlocal strain gradient is developed to investigate the vibrations of simply supported single-walled carbon nanotubes (SWCNTs). The Sanders–Koiter shell theory is used to obtain strain–displacement relationships. Eringen’s nonlocal elasticity and Mindlin’s strain gradient theories are adopted to derive the constitutive equations, where the anisotropic elasticity constants are expressed via Chang’s molecular mechanics model. An analytical method is used to solve the equations of motion and to obtain the natural frequencies of SWCNTs. First, the anisotropic elastic shell model without size effects is validated through comparison with the results of molecular dynamics simulations reported in the literature. Then, the effects of the nonlocal and material parameters on the natural frequencies of SWCNTs with different geometries and wavenumbers are analyzed. From the numerical simulations, it is confirmed that the natural frequencies decrease as the nonlocal parameter increases, while they increase as the material parameter increases. As new results, the reduction in natural frequencies with increasing SWCNT radius and the increase in natural frequencies with increasing wavenumber are both amplified as the material parameter increases, while they are both attenuated as the nonlocal parameter increases.

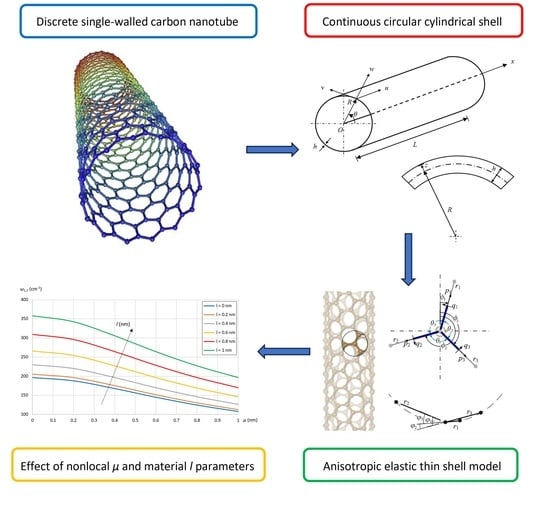
1. Introduction

It is well known in the scientific community that the use of classical continuum mechanics models in studying the dynamics of carbon nanotubes (CNTs) can lead to inaccurate results. This is due to CNTs’ discrete structure and small size. Therefore, to accurately study the vibrations and stability of carbon nanotubes, non-classical continuum mechanics models based on anisotropic and size-dependent theories must be adopted.

To this end, researchers have developed various anisotropic elastic shell theories. A very effective theory is the one proposed by Chang [1,2], in which the prediction of the chirality and size-dependent elasticity properties of single-walled carbon nanotubes was achieved via a molecular mechanics model. The most important result obtained by Chang is that for CNTs, the classical relationship of the isotropic elasticity theory of continuum mechanics between the Young’s modulus and shear modulus no longer holds, and, therefore, a more refined relationship has been proposed to account for the effects of the tubes’ diameter and chiral angle.

Starting from this theory, Ghavanloo and Fazelzadeh [3] proposed an anisotropic elastic shell model, including the chirality effect, to study the vibrational characteristics of SWCNTs. Considering Flügge’s shell theory, they investigated the effects of the chirality and tube diameter on the natural frequencies of SWCNTs, together with the influence of external loads. Using the anisotropic elastic shell model [3], the authors of the present work carried out in Ref. [4] a comparison between different shell theories for the vibrational analysis of SWCNTs, in particular, Donnell’s, Sanders’s, and Flügge’s shell theories. Taking the molecular dynamics results available in the literature as a reference, they obtained that Flügge’s shell theory is not only the most accurate but also the most expensive from a computational point of view; on the other hand, they found that Donnell’s shell theory is not accurate, while Sanders’s shell theory is very accurate in modeling the vibrations of SWCNTs for all geometries and wavenumbers.

In addition to anisotropic models, several size-dependent theories have been introduced in the literature, the first of which is the nonlocal elasticity theory developed by Eringen [5,6]. In Eringen’s nonlocal differential constitutive relations, the stress tensor at the reference point of a body is written as a function of the strain tensor not only at that point but also at all the other points of the body. For this purpose, a nonlocal parameter is inserted into Eringen’s nonlocal elasticity equations, in the form of a small-length-scale constant appropriate to each material, for which the value must be obtained through comparisons with the results of molecular dynamics simulations.

Starting from Eringen’s nonlocal theory and considering the anisotropic model [3], Fazelzadeh and Ghavanloo [7] proposed a nonlocal anisotropic elastic shell model to study the linear vibrations of CNTs with arbitrary chiralities. They studied the effects of the nonlocal parameter on the natural frequencies of zigzag, armchair, and chiral SWCNTs with different geometries and wavenumbers.

Another important size-dependent theory is the strain gradient theory developed by Mindlin [8,9], which represents an extension of the classical theory of elasticity by considering additional higher-order strain gradient terms other than the stress tensor. Specifically, Mindlin’s strain gradient theory assumes that materials cannot simply be modeled as sets of points but must be considered as atoms with higher-order deformation mechanisms at small scales (micro/nano).

For size-dependent structures, constitutive equations that consider both the nonlocal elasticity and strain gradient were first proposed by Aifantis et al. [10,11,12] to capture the dynamic behaviors of CNTs in the frameworks of shear-nondeformable Euler–Bernoulli and shear-deformable Timoshenko beam theories.

Later, Lim [13] developed a refined nonlocal strain gradient theory, in which two different small-length-scale parameters, i.e., nonlocal and strain gradient parameters, are adopted to account for the size-dependent characteristics of CNTs. Dispersion relations with different values of nonlocal and material parameters are analyzed.

The nonlocal strain gradient theory developed by Lim [13] was adopted to study the linear dynamics of beams in the framework of an isotropic elastic beam model in Refs. [14,15,16,17]. The effects of the nonlocal and material parameters on the vibrations and stability of beams were analyzed, where the nonlocal parameter was introduced to consider the influence of the nonlocal elasticity, and the material parameter was introduced to consider the significance of the strain gradient. It was found that when the material parameter is lower than the nonlocal parameter, the beam has stiffness-softening effects on the critical buckling load and natural frequencies, while, in the opposite case, the beam has stiffness-hardening effects on the critical buckling load and natural frequencies. Some interesting reviews of size-dependent continuum mechanics models for the analysis of the linear vibrations of nanostructures can be found in Refs. [18,19,20].

Mehralian et al. [21] developed an isotropic elastic shell model with a nonlocal strain gradient to study the effects of the nonlocal and material parameters on the linear vibrations of SWCNTs. The model reported in Ref. [21] is similar to that of the present work. However, there is a relevant difference, namely, the use of an isotropic (rather than an anisotropic) model, and it was proved that adopting an isotropic model to simulate SWCNT vibrations is inaccurate owing to the intrinsic anisotropic characteristics of the nanostructures [22,23].

The adoption of classical theories of continuum mechanics to model the dynamic behaviors of nanostructures requires the careful choice of equivalent parameters. Specifically, in the case of SWCNTs, their effective discrete structures can be modeled by continuous cylindrical shells if equivalent parameters, namely, the Young’s modulus, Poisson’s ratio, and thickness, are appropriately selected. To this end, Yakobson et al. [24] obtained equivalent parameter values by comparing them with the strain energy values of discrete SWCNTs derived through molecular dynamics simulations. Interesting results for molecular dynamics simulations for SWCNT vibrational analysis can be found in Refs. [25,26,27,28,29].

Readers interested in learning more about shell theories are invited to refer to the fundamental books [30,31,32,33,34,35]. In particular, Leissa [30] studied the linear vibrations of cylindrical shells for different geometries, boundary conditions, and wavenumbers. Furthermore, readers interested in nonlinear vibrations and energy exchanges in CNTs are invited to refer to related papers [36,37,38,39,40,41,42,43,44], where the effects of resonance interactions between different vibrational modes are also studied, e.g., radial breathing and circumferential flexural modes, together with the influences of anisotropy and nonlocality. Finally, static models of CNTs, which consider the effects of nonlocal elasticity along with pull-in buckling issues, can be found in Refs. [45,46].

The main aim of the present work is to develop an advanced elastic shell model for the vibrational analysis of SWCNTs that is capable for simultaneously considering all three previously reported fundamental effects inherent to nanostructures, namely, the anisotropy, nonlocal elasticity, and strain gradient. This, in the authors’ opinion, is very important because a hybrid model that is both anisotropic and size-dependent can lead to more realistic and, therefore, accurate results.

Specifically, in this paper, the Sanders–Koiter shell theory is adopted to obtain the strain–displacement relationships; Eringen’s nonlocal elasticity and Mindlin’s strain gradient theories are used to obtain the constitutive equations, and the anisotropic elasticity constants are expressed using Chang’s molecular mechanics model. The dynamic equations of motion are solved analytically, and the natural frequencies of SWCNTs under simply supported boundary conditions are obtained.

The present model is first validated in the anisotropic form (i.e., without size-dependent effects) through comparisons with molecular dynamics simulation results from the literature. Then, a parametric analysis is performed on the developed comprehensive model to investigate the influences of the size-dependent effects (i.e., nonlocal and material parameters) on the natural frequencies of SWCNTs with different geometries and wavenumbers.

2. Sanders–Koiter Shell Theory for SWCNTs

In the present paper, the actual discrete SWCNT is modeled by an equivalent continuous cylindrical shell, see Figure 1a,b, with radius $R$, length $L$, and thickness $h$. A cylindrical coordinate system $(O,x,\theta ,z)$ is used, where the origin ($O$) of the reference system is located at the center of one end of the shell. Three displacements are measured: longitudinal $u(x,\theta ,t)$, circumferential $v(x,\theta ,t)$, and radial $w(x,\theta ,t)$, where the positive radial displacement ($w$) is assumed to be toward the outside; $(x,\theta )$ are the longitudinal and circumferential coordinates of an arbitrary point on the middle surface of the shell, respectively; $z$ is the radial coordinate along the thickness ($h$) of the shell; and $t$ is the time.

In this paper, the Sanders–Koiter linear shell theory is used to model SWCNT dynamics. The linear relationships between strains and displacements in the Sanders–Koiter theory are based on “Kirchhoff–Love assumptions”, see Ref. [30] for details.

The consequences of these geometric assumptions are that in the presence of a thin cylindrical shell, the transverse shear strains can be neglected $({\gamma }_{xz}={\gamma }_{\theta z}=0)$ in the expressions of the constitutive equations, and the rotational inertia of the shell can be neglected in the expression of the kinetic energy. Considering the previous assumptions, in the Sanders–Koiter linear shell theory, the middle surface strains $({\epsilon }_{x,0},{\epsilon }_{\theta ,0},{\gamma }_{x\theta ,0})$ of the cylindrical shell are written as functions of the displacements $(u,v,w)$ in the following form [30]:

$${\epsilon }_{x,0}=\frac{\partial u}{\partial x} {\epsilon }_{\theta ,0}=\frac{1}{R}\frac{\partial v}{\partial \theta }+\frac{w}{R} {\gamma }_{x\theta ,0}=\frac{1}{R}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial x}$$

(1)

Again, considering the previous assumptions, in the Sanders–Koiter linear shell theory, the middle surface changes in the curvature and torsion $(k_x,k_{\theta },k_{x\theta })$ of the cylindrical shell are expressed as follows [30]:

$$k_x=-\frac{{\partial }^{2}w}{\partial x^2} k_{\theta }=\frac{1}{R^2}\frac{\partial v}{\partial \theta }-\frac{1}{R^2}\frac{{\partial }^{2}w}{\partial {\theta }^2} { k}_{x\theta }=-\frac{2}{R}\frac{{\partial }^{2}w}{\partial x\partial \theta }+\frac{1}{2R}\left(3\frac{\partial v}{\partial x}-\frac{1}{R}\frac{\partial u}{\partial \theta }\right)$$

(2)

According to the Sanders–Koiter shell theory, the strain components $({\epsilon }_x,{\epsilon }_{\theta },{\gamma }_{x\theta })$ at an arbitrary point on the surface of the cylindrical shell are related to the middle surface strains and changes in curvature and torsion via the radial coordinate ($z$) by means of the following relationships [30]:

$${\epsilon }_x={\epsilon }_{x,0}+z{k}_x {\epsilon }_{\theta }={\epsilon }_{\theta ,0}+z{k}_{\theta } {\gamma }_{x\theta }={\gamma }_{x\theta ,0}+z{k}_{x\theta }$$

(3)

The adoption of the Sanders–Koiter shell theory to model SWCNT dynamics in the present work is justified based on the results obtained by the same authors in a previous paper, see Ref. [4]. In that paper, shell theories for the vibrational analysis of SWCNTs based on an anisotropic elastic shell model were compared, specifically for Donnell’s, Sanders’s, and Flugge’s shell theories, where the molecular dynamics simulation results available in the literature were considered as references to verify the accuracy of the three different shell theories. Flügge’s shell theory was found to be the most accurate and, in fact, this theory was adopted in several papers studying the linear vibrations of SWCNTs based on anisotropic elastic shell models, see Refs. [3,7]. On the other hand, it was shown that the additional terms present in the expressions of the force and moment resultants, which give Flügge’s shell theory greater accuracy than those of Sanders’s and Donnell’s shell theories, involve a very large computational effort in the numerical simulations of the dynamic behaviors of SWCNTs. Furthermore, based on the parametric analyses that were performed, it was found that Donnell’s shell theory is not accurate for several geometries and wavenumbers, while Sanders’s shell theory is very accurate for all the geometries and wavenumbers. This is why in the present paper, Sanders’s shell theory is adopted instead of the more accurate, but also more complex, Flügge shell theory for modeling the vibrations of SWCNTs.

Within the Sanders–Koiter linear shell theory, in the next section, a new advanced model of an anisotropic elastic shell will be proposed, considering both the nonlocal elasticity and the strain gradient, i.e., two relevant small-length-scale effects that characterize the dynamic behaviors of SWCNTs.

3. Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model

According to the nonlocal strain gradient theory developed by Li et al. [15], the general constitutive equation for size-dependent structures is expressed as follows:

$$\left(1-{\mu }^2{\nabla }^2\right)\mathit{t}=\mathbf{C}:\mathit{\epsilon }-l^2\nabla \mathbf{C}:\nabla \mathit{\epsilon }$$

(4)

where $\mathit{t}$ is the stress tensor; $\mathbf{C}$ is the fourth-order elasticity tensor; $\mathit{\epsilon }$ is the strain tensor; $\nabla \mathbf{C}$ is the elasticity gradient tensor; $\nabla \mathit{\epsilon }$ is the strain gradient tensor; ${\nabla }^2$ is the Laplace operator; $\mu$ is the nonlocal parameter, which is introduced to study the effect of the nonlocal elasticity; and $l$ is the material parameter, which is introduced to investigate the effect of the strain gradient.

For shell-type structures, the size-dependent behavior must be considered along the longitudinal, circumferential, and radial directions. Therefore, starting from the general form of Equation (4), the constitutive equation of the anisotropic elastic shell theory with a nonlocal strain gradient is given by:

$$\left(1-{\mu }^2{\nabla }^2\right)\mathit{t}=\frac{1}{h}\left(1-l^2{\nabla }^2\right)\mathbf{Y}\mathit{\epsilon }$$

(5)

where $\mathit{t}$ and $\mathit{\epsilon }$ are the stress and strain vectors, respectively, which, for an elastic shell-type structure under the planar stress hypothesis, are, respectively, expressed as follows:

$$\mathit{t}={\left[{\sigma }_x,{\sigma }_{\theta },{\tau }_{x\theta }\right]}^{\mathrm{T}} \mathit{\epsilon }={\left[{\epsilon }_x,{\epsilon }_{\theta },{\gamma }_{x\theta }\right]}^{\mathrm{T}}$$

(6)

where $h$ is the shell thickness, $\mathbf{Y}$ is the corresponding anisotropic elasticity matrix, and

$${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{1}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}$$

(7)

is the Laplace operator represented in the polar coordinate system.

The constitutive Equation (5) can be projected in the $(x,\theta )$ plane in the following form:

$$\left(1-{\mu }^2{\nabla }^2\right){\sigma }_x=\frac{1}{h}\left(1-l^2{\nabla }^2\right)\left(Y_{11}{\epsilon }_x+Y_{12}{\epsilon }_{\theta }+Y_{13}{\gamma }_{x\theta }\right)$$

$$\left(1-{\mu }^2{\nabla }^2\right){\sigma }_{\theta }=\frac{1}{h}\left(1-l^2{\nabla }^2\right)\left(Y_{21}{\epsilon }_x+Y_{22}{\epsilon }_{\theta }+Y_{23}{\gamma }_{x\theta }\right)$$

(8)

$$\left(1-{\mu }^2{\nabla }^2\right){\tau }_{x\theta }=\frac{1}{h}\left(1-l^2{\nabla }^2\right)\left(Y_{31}{\epsilon }_x+Y_{32}{\epsilon }_{\theta }+Y_{33}{\gamma }_{x\theta }\right)$$

The surface elasticity constants, $Y_{ij}$ (8), as elements of the anisotropic elasticity matrix, $\mathbf{Y}$, are given by [1]

$$Y_{ij}=\frac{2}{3\sqrt{3}}\left(K_{\rho }{G}_{li}{G}_{lj}+\frac{{2K}_{\theta }}{a^2}{H}_{li}{H}_{lj}\right) i,j,l=\mathrm{1,2},3 \left(\mathrm{s}\mathrm{u}\mathrm{m} \mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r} l\right)$$

(9)

where $a$ is the carbon–carbon bond length, and $(K_{\rho },K_{\theta })$ are force constants associated with the stretching and angular distortion of the carbon–carbon bond, respectively, see Ref. [1] for details.

The corresponding matrices, $\mathbf{G}$ and $\mathbf{H}$, can be, respectively, calculated as follows [3]:

$$\mathbf{G}={\mathbf{B}}^{-1}\left(\mathbf{I}-\mathbf{D}\mathbf{F}\right), \mathbf{H}=\mathbf{Q}\mathbf{F}$$

(10)

where $\mathbf{I}$ is the identity matrix, matrix $\mathbf{F}$ is given by [3]

$$\mathbf{F}={\left[\mathbf{U}{\mathbf{B}}^{-1}\mathbf{D}-\left(\frac{2K_{\theta }}{K_{\rho }{a}^2}\mathbf{V}\mathbf{A}+\mathbf{W}\right)\right]}^{-1}\mathbf{U}{\mathbf{B}}^{-1}$$

(11)

and matrices $\left(\mathbf{A},\mathbf{B},\mathbf{D},\mathbf{U},\mathbf{V},\mathbf{W}, \mathrm{a}\mathrm{n}\mathrm{d} \mathbf{Q}\right)$ are, respectively, given by [2]

$$\mathbf{A}=\left\{A_{ij}\right\}=\left\{-\cos {\omega }_{ik}\cos {\omega }_{jk}\right\} i,j,k=\mathrm{1,2},3 \left(\mathrm{s}\mathrm{u}\mathrm{m} \mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r} k\right)$$

(12)

$$\mathbf{B}=\frac{1}{3\sqrt{n^2+nm+m^2}}\left(\begin{array}{ccc}(2n+m)\cos {\varphi }_1& -(n-m)\cos {\varphi }_2& -(n+2m)\cos {\varphi }_3\\ \sqrt{3} m\sin {\varphi }_1& -\sqrt{3}(n+m)\sin {\varphi }_2& \sqrt{3} n\sin {\varphi }_3\\ (2n+m)\sin {\varphi }_1& -(n-m)\sin {\varphi }_2& -(n+2m)\sin {\varphi }_3\end{array}\right)$$

(13)

$$\mathbf{D}=\frac{1}{3\sqrt{n^2+nm+m^2}}\left(\begin{array}{ccc}-(2n+m)\sin {\varphi }_1& (n-m)\sin {\varphi }_2& (n+2m)\sin {\varphi }_3\\ \sqrt{3} m\cos {\varphi }_1& -\sqrt{3}(n+m)\cos {\varphi }_2& \sqrt{3} n\cos {\varphi }_3\\ (2n+m)\cos {\varphi }_1& -(n-m)\cos {\varphi }_2& -(n+2m)\cos {\varphi }_3\end{array}\right)$$

(14)

$$\mathbf{U}=\left(\begin{array}{ccc}\sin {\varphi }_1& \sin {\varphi }_2& \sin {\varphi }_3\\ \cos {\varphi }_1& \cos {\varphi }_2& \cos {\varphi }_3\\ m\cos {\varphi }_1& -(n+m)\cos {\varphi }_2& n\cos {\varphi }_3\end{array}\right)$$

(15)

$$\mathbf{V}=\left(\begin{array}{ccc}-\cos {\varphi }_1& -\cos {\varphi }_2& -\cos {\varphi }_3\\ \sin {\varphi }_1& \sin {\varphi }_2& \sin {\varphi }_3\\ 0& 0& 0\end{array}\right)$$

(16)

$$\mathbf{W}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ -m\sin {\varphi }_1& (n+m)\sin {\varphi }_2& -n\sin {\varphi }_3\end{array}\right)$$

(17)

$$\mathbf{Q}=\left\{Q_{ij}\right\}=\left\{-\cos {\omega }_{ji}\right\} i,j=\mathrm{1,2},3$$

(18)

where [2]

$$\cos {\omega }_{ij}=\left\{\begin{array}{c}(\cos {\varphi }_i\sin {\varphi }_k\cos {\phi }_j-\sin {\varphi }_i\cos {\varphi }_k)/\sin {\theta }_j\\ 0\end{array}\right. \begin{array}{c}i\ne j\ne k\\ i=j\end{array}$$

(19)

and $(n,m)$ are the chirality indices of the SWCNT, which define its radius via the following relation [1]:

$$R=\frac{\sqrt{3} a}{2\pi } \sqrt{n^2+nm+m^2}$$

(20)

The structural parameters of the SWCNT, i.e., chiral angles $({\varphi }_1,{\varphi }_2,{\varphi }_3)$, torsion angles $({\phi }_1,{\phi }_2,{\phi }_3)$, and bond angles $({\theta }_{1,i},{\theta }_{2,i},{\theta }_{3,i})$, can be, respectively, calculated by means of the following equations [1]:

$${\varphi }_1=\arccos \frac{2n+m}{2\sqrt{n^2+nm+m^2}} {\varphi }_2=\frac{4\pi }{3}+{\varphi }_1 {\varphi }_3=\frac{2\pi }{3}+{\varphi }_1$$

(21)

$$\begin{gathered} {\phi }_1=\frac{\pi }{\sqrt{n^2+nm+m^2}}\cos {\varphi }_1 {\phi }_2=\frac{\pi }{\sqrt{n^2+nm+m^2}}\cos \left(\frac{\pi }{3}+{\varphi }_1\right) \\ {\phi }_3=\frac{\pi }{\sqrt{n^2+nm+m^2}}\cos \left(\frac{\pi }{3}-{\varphi }_1\right) \end{gathered}$$

(22)

$$\cos {\theta }_i=\sin {\varphi }_j\sin {\varphi }_k\cos {\phi }_i+\cos {\varphi }_j\cos {\varphi }_k i,j,k=\mathrm{1,2},3 i\ne j\ne k$$

(23)

4. Force and Moment Resultants

In the present anisotropic elastic shell model with the nonlocal strain gradient, the force $(N_x,N_{\theta },N_{x\theta })$ and moment $(M_x,M_{\theta },M_{x\theta })$ resultants per unit of length are found by integrating the stress components of the constitutive Equation (8) and considering the thin-shell hypothesis $\left(z/R\ll 1\right)$ of the Sanders–Koiter shell theory as follows:

$$\begin{gathered} \left(1-{\mu }^2{\nabla }^2\right)N_x=\left(1-l^2{\nabla }^2\right)·\left[Y_{11}\frac{\partial u}{\partial x}+\right. \\ \left.+\frac{Y_{12}}{R}\left(\frac{\partial v}{\partial \theta }+w\right)+Y_{13}\left(\frac{\partial v}{\partial x}+\frac{1}{R}\frac{\partial u}{\partial \theta }\right)\right] \end{gathered}$$

(24)

$$\begin{gathered} \left(1-{\mu }^2{\nabla }^2\right)N_{\theta }=\left(1-l^2{\nabla }^2\right)·\left[Y_{21}\frac{\partial u}{\partial x}+\right. \\ \left.+\frac{Y_{22}}{R}\left(\frac{\partial v}{\partial \theta }+w\right)+Y_{23}\left(\frac{\partial v}{\partial x}+\frac{1}{R}\frac{\partial u}{\partial \theta }\right)\right] \end{gathered}$$

(25)

$$\begin{gathered} \left(1-{\mu }^2{\nabla }^2\right)N_{x\theta }=\left(1-l^2{\nabla }^2\right)·\left[Y_{31}\frac{\partial u}{\partial x}+\right. \\ \left.+\frac{Y_{32}}{R}\left(\frac{\partial v}{\partial \theta }+w\right)+Y_{33}\left(\frac{\partial v}{\partial x}+\frac{1}{R}\frac{\partial u}{\partial \theta }\right)\right] \end{gathered}$$

(26)

$$\begin{gathered} \left(1-{\mu }^2{\nabla }^2\right)M_x=\left(1-l^2{\nabla }^2\right)·\left[-X_{11}\frac{{\partial }^{2}w}{{\partial x}^2}+\frac{X_{12}}{R^2}\right.· \\ \left.·\left(\frac{\partial v}{\partial \theta }-\frac{{\partial }^{2}w}{{\partial \theta }^2}\right)+X_{13}\left(-\frac{2}{R}\frac{{\partial }^{2}w}{\partial x\partial \theta }-\frac{1}{2R^2}\frac{\partial u}{\partial \theta }+\frac{3}{2R}\frac{\partial v}{\partial x}\right)\right] \end{gathered}$$

(27)

$$\begin{gathered} \left(1-{\mu }^2{\nabla }^2\right)M_{\theta }=\left(1-l^2{\nabla }^2\right)·\left[-X_{21}\frac{{\partial }^{2}w}{{\partial x}^2}+\frac{X_{22}}{R^2}·\right. \\ ·\left.\left(\frac{\partial v}{\partial \theta }-\frac{{\partial }^{2}w}{{\partial \theta }^2}\right)+X_{23}\left(-\frac{2}{R}\frac{{\partial }^{2}w}{\partial x\partial \theta }-\frac{1}{2R^2}\frac{\partial u}{\partial \theta }+\frac{3}{2R}\frac{\partial v}{\partial x}\right)\right] \end{gathered}$$

(28)

$$\begin{gathered} \left(1-{\mu }^2{\nabla }^2\right)M_{x\theta }=\left(1-l^2{\nabla }^2\right)·\left[-X_{31}\frac{{\partial }^{2}w}{{\partial x}^2}+\frac{X_{32}}{R^2}·\right. \\ ·\left(\frac{\partial v}{\partial \theta }-\frac{{\partial }^{2}w}{{\partial \theta }^2}\right)\left.+X_{33}\left(-\frac{2}{R}\frac{{\partial }^{2}w}{\partial x\partial \theta }-\frac{1}{2R^2}\frac{\partial u}{\partial \theta }+\frac{3}{2R}\frac{\partial v}{\partial x}\right)\right] \end{gathered}$$

(29)

where the elements of the bending stiffness matrix ($\mathbf{X}$) can be defined as follows [3]:

$$X_{ij}=\frac{Y_{ij}{h}^2}{12} i,j=\mathrm{1,2},3$$

(30)

It should be emphasized that the force $(N_x,N_{\theta },N_{x\theta })$ and moment $(M_x,M_{\theta },M_{x\theta })$ resultants per unit of length written considering the Sanders–Koiter shell theory are different from those of the Flügge shell theory because in the latter theory, the ratio $z/R$ is not neglected, i.e., the thin-shell hypothesis is not taken into account, see Ref. [30] for details.

5. Equations of Motion

The classical dynamic equilibrium equations in terms of force and moment resultants are expressed as follows, where external forces and moments are neglected [3]:

$$\frac{\partial N_x}{\partial x}+\frac{1}{R}\frac{\partial N_{x\theta }}{\partial \theta }-\frac{1}{2R^2}\frac{\partial M_{x\theta }}{\partial \theta }-\rho h\frac{{\partial }^{2}u}{{\partial t}^2}=0$$

(31)

$$\frac{1}{R}\frac{\partial N_{\theta }}{\partial \theta }+\frac{\partial N_{x\theta }}{\partial x}+\frac{3}{2R}\frac{\partial M_{x\theta }}{\partial x}+\frac{1}{R^2}\frac{\partial M_{\theta }}{\partial \theta }-\rho h\frac{{\partial }^{2}v}{{\partial t}^2}=0$$

(32)

$$\frac{{\partial }^2{M}_x}{{\partial x}^2}+\frac{2}{R}\frac{{\partial }^2{M}_{x\theta }}{\partial x\partial \theta }+\frac{1}{R^2}\frac{{\partial }^2{M}_{\theta }}{{\partial \theta }^2}-\frac{N_{\theta }}{R}-\rho h\frac{{\partial }^{2}w}{{\partial t}^2}=0$$

(33)

where $\rho h$ is the mass density per unit of area (i.e., surface density) of the SWCNT.

By applying the nonlocal elasticity operator $(1-{\mu }^2{\nabla }^2)$ to the dynamic equilibrium Equations (31)–(33) and then substituting Equations (24)–(29) into the modified forms of Equations (31)–(33), we obtain

$$\begin{gathered} \left(1-l^2{\nabla }^2\right)\left\{\left[Y_{11}\frac{{\partial }^2}{{\partial x}^2}+\frac{2Y_{13}}{R}\frac{{\partial }^2}{\partial x\partial \theta }+\left(\frac{Y_{33}}{R^2}+\frac{X_{33}}{{4R}^4}\right)\frac{{\partial }^2}{{\partial \theta }^2}\right]u\right. \\ +\left[Y_{13}\frac{{\partial }^2}{{\partial x}^2}+\left(\frac{Y_{12}+Y_{33}}{R}-\frac{{3X}_{33}}{4R^3}\right)\frac{{\partial }^2}{\partial x\partial \theta }+\left(\frac{Y_{23}}{R^2}-\frac{X_{23}}{{2R}^4}\right)\frac{{\partial }^2}{{\partial \theta }^2}\right]v \\ \left.+\left[\frac{Y_{12}}{R}\frac{\partial }{\partial x}+\frac{Y_{23}}{R^2}\frac{\partial }{\partial \theta }+\frac{X_{13}}{{2R}^2}\frac{{\partial }^3}{{\partial x}^2\partial \theta }+\frac{X_{33}}{R^3}\frac{{\partial }^3}{\partial x{\partial \theta }^2}+\frac{X_{23}}{{2R}^4}\frac{{\partial }^3}{{\partial \theta }^3}\right]w\right\} \\ =\rho h\left(\frac{{\partial }^{2}u}{{\partial t}^2}-{\mu }^2\frac{{\partial }^{4}u}{{\partial x}^2{\partial t}^2}-{\mu }^2\frac{1}{R^2}\frac{{\partial }^{4}u}{{\partial \theta }^2{\partial t}^2}\right) \end{gathered}$$

(34)

$$\begin{gathered} \left(1-l^2{\nabla }^2\right)\left\{\left[Y_{13}\frac{{\partial }^2}{{\partial x}^2}+\left(\frac{Y_{12}+Y_{33}}{R}-\frac{{3X}_{33}}{{4R}^3}\right)\frac{{\partial }^2}{\partial x\partial \theta }+\left(\frac{Y_{23}}{R^2}-\frac{X_{23}}{{2R}^4}\right)\frac{{\partial }^2}{{\partial \theta }^2}\right]u\right. \\ +\left[\left(Y_{33}+\frac{{9X}_{33}}{{4R}^2}\right)\frac{{\partial }^2}{{\partial x}^2}+\left(\frac{{2Y}_{23}}{R}+\frac{{3X}_{23}}{R^3}\right)\frac{{\partial }^2}{\partial x\partial \theta }+\left(\frac{Y_{22}}{R^2}+\frac{X_{22}}{R^4}\right)\frac{{\partial }^2}{{\partial \theta }^2}\right]v \\ +\left[\frac{Y_{23}}{R}\frac{\partial }{\partial x}+\frac{Y_{22}}{R^2}\frac{\partial }{\partial \theta }-\frac{{3X}_{13}}{2R}\frac{{\partial }^3}{{\partial x}^3}-\left(\frac{X_{12}+{3X}_{33}}{R^2}\right)\frac{{\partial }^3}{{\partial x}^2\partial \theta }-\frac{{7X}_{23}}{2R^3}\frac{{\partial }^3}{\partial x{\partial \theta }^2}\right. \\ \left.\left.-\frac{X_{22}}{R^4}\frac{{\partial }^3}{{\partial \theta }^3}\right]w\right\}=\rho h\left(\frac{{\partial }^{2}v}{{\partial t}^2}-{\mu }^2\frac{{\partial }^{4}v}{{\partial x}^2{\partial t}^2}-{\mu }^2\frac{1}{R^2}\frac{{\partial }^{4}v}{{\partial \theta }^2{\partial t}^2}\right) \end{gathered}$$

(35)

$$\begin{gathered} \left(1-l^2{\nabla }^2\right)\left\{\left[-\frac{Y_{12}}{R}\frac{\partial }{\partial x}-\frac{Y_{23}}{R^2}\frac{\partial }{\partial \theta }-\frac{X_{13}}{{2R}^2}\frac{{\partial }^3}{{\partial x}^2\partial \theta }-\frac{X_{33}}{R^3}\frac{{\partial }^3}{\partial x\partial {\theta }^2}-\frac{X_{23}}{2R^4}\frac{{\partial }^3}{{\partial \theta }^3}\right]u\right. \\ +\left[-\frac{Y_{23}}{R}\frac{\partial }{\partial x}-\frac{Y_{22}}{R^2}\frac{\partial }{\partial \theta }+\frac{{3X}_{13}}{2R}\frac{{\partial }^3}{{\partial x}^3}+\left(\frac{X_{12}+{3X}_{33}}{R^2}\right)\frac{{\partial }^3}{{\partial x}^2\partial \theta }+\frac{7X_{23}}{2R^3}\frac{{\partial }^3}{\partial x{\partial \theta }^2}\right. \\ \left.+\frac{X_{22}}{R^4}\frac{{\partial }^3}{{\partial \theta }^3}\right]v+\left[-\frac{Y_{22}}{R^2}-X_{11}\frac{{\partial }^4}{{\partial x}^4}-\frac{{4X}_{13}}{R}\frac{{\partial }^4}{{\partial x}^3\partial \theta }-\left(\frac{{{2X}_{12}+4X}_{33}}{R^2}\right)\frac{{\partial }^4}{\partial x^2{\partial \theta }^2}\right. \\ \left.\left.-\frac{{4X}_{23}}{R^3}\frac{{\partial }^4}{\partial x{\partial \theta }^3}-\frac{X_{22}}{R^4}\frac{{\partial }^4}{{\partial \theta }^4}\right]w\right\}=\rho h\left(\frac{{\partial }^{2}w}{{\partial t}^2}-{\mu }^2\frac{{\partial }^{4}w}{{\partial x}^2{\partial t}^2}-{\mu }^2\frac{1}{R^2}\frac{{\partial }^{4}w}{{\partial \theta }^2{\partial t}^2}\right) \end{gathered}$$

(36)

which represent the equations of motion for an arbitrary chiral SWCNT in terms of the longitudinal ($u$), circumferential ($v$), and radial ($w$) displacements of the middle surface of the SWCNT.

From the equations of motion (34)–(36), it can be observed that the strain gradient operator $(1-l^2{\nabla }^2)$ is applied to strains and changes in curvature and torsion, while the nonlocal elasticity operator $(1-{\mu }^2{\nabla }^2)$ is applied to accelerations.

6. Solution Method

In this paper, simply supported boundary conditions are considered. These specific boundary conditions impose the geometrical conditions $v=w=0$ on the displacements and the natural conditions $N_x=M_x=0$ on the forces and moments at both edges $x=(0, L)$ of the SWCNT.

A displacement field that satisfies the previous boundary conditions can be written by means of the following expansions:

$$\begin{gathered} u(x,\theta ,t)=\overline{U}\cos \left(\frac{q\pi x}{L}\right)\cos \left(s\theta \right)\cos \left(\omega t\right) \\ v(x,\theta ,t)=\overline{V}\sin \left(\frac{q\pi x}{L}\right)\sin \left(s\theta \right)\cos \left(\omega t\right) \\ w(x,\theta ,t)=\overline{W}\sin \left(\frac{q\pi x}{L}\right)\cos \left(s\theta \right)\cos \left(\omega t\right) \end{gathered}$$

(37)

where $\left(\overline{U},\overline{V},\overline{W}\right)$ are the displacement amplitudes along the longitudinal ($u$), circumferential ($v$), and radial ($w$) directions, respectively; $q$ is the number of longitudinal half-waves; $s$ is the number of circumferential waves; and $L$ is the length and $\omega$ is the natural frequency of the SWCNT.

Substituting expansions (37) into Equations (34)–(36), a set of algebraic equations for the displacement amplitudes $\left(\overline{U},\overline{V},\overline{W}\right)$ is obtained, which can be rewritten in the following matrix form [7]:

$$\mathbf{E}{(q,s,\omega )}_{3\times 3}\left[\begin{array}{c}\overline{U}\\ \overline{V}\\ \overline{W}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$$

(38)

where $\mathbf{E}$ is a non-symmetric matrix, for which the elements are reported in Appendix A.

For a non-trivial solution, i.e., different from $\left(\overline{U}=\overline{V}=\overline{W}=0\right)$, the determinant of matrix $\mathbf{E}$ (38) must be equal to zero:

$$\det {\mathbf{E}(q,s,\omega )}_{3\times 3}=0$$

(39)

Solving Equation (39), we obtain a third-degree algebraic equation in ${\omega }^2$; this last equation provides three different eigenfrequencies for each number of waves $(q,s)$ that give three different vibrational modes (i.e., longitudinal, torsional, and radial modes). Because the highest natural frequency corresponds to the radial vibrational mode, in the numerical results, only the radial natural frequencies will be calculated.

7. Numerical Results

In this paper, the effects of the nonlocal and material parameters on the natural frequencies of SWCNTs are considered. The Sanders–Koiter shell theory is used to obtain strain–displacement relationships. An anisotropic elastic shell model is adopted to consider the intrinsic chirality effects of CNTs. Simply supported boundary conditions are imposed. Vibrational modes with different numbers of waves along the longitudinal and circumferential directions are analyzed. SWCNTs with different chiralities and geometries are studied.

Table 1. Mechanical parameters of the anisotropic elastic shell model [1,2,24].

Carbon–carbon bond length, a (nm)	0.142
Carbon–carbon bond elongation, Kρ (nN/nm)	742
Carbon–carbon bond angle variance, Kθ (nN·nm)	1.42
Equivalent thickness, h (nm)	0.0665
Equivalent mass density, ρ (kg/m3)	11,700
SWCNT radius, R (nm)	1.34

shows the values of the carbon–carbon bond parameters $(a,k_{\rho },k_{\theta })$ and equivalent parameters $(h,\rho )$ retrieved from the pertinent literature. In particular, parameters $k_{\rho }$ and $k_{\theta }$, which are force constants related to the variances in the carbon–carbon bond length ($a$) and angle ($\theta$), respectively, are considered to obtain the surface elasticity constants ($Y_{ij}$) (9) of the SWCNT, using the molecular mechanics model developed by Chang [1,2].

Furthermore, to study the dynamics of a discrete SWCNT by considering a continuous cylindrical shell, an equivalent thickness ($h$) obtained from molecular dynamics simulations and an equivalent mass density ($\rho$) resulting from graphite’s surface density are used, see Ref. [24] for details.

Finally, in the parametric analyses, an SWCNT with radius R = 1.34 nm (i.e., thickness ratio R/h = 20) will be considered. This specific value of the thickness ratio was chosen because it respects the hypothesis underlying the thin-shell theories (in this paper, the Sanders–Koiter shell theory), which is R/h > 10, see Ref. [30] for the details.

It should be underlined that in the numerical results, the natural frequencies of the SWCNTs are expressed in the unit of cm⁻¹, where 1 Hz = 2.998 × 10¹⁰ cm⁻¹.

7.1. Validation of the Anisotropic Elastic Shell Model

The first step in the present work is the validation of the anisotropic elasticity model based on the Sanders–Koiter shell theory, which will be subsequently adopted to analyze the effects of the nonlocal and material parameters on the natural frequencies of SWCNTs.

This validation is carried out by comparing the results of the present anisotropic elastic shell model with those of molecular dynamics simulations available in literature [25]. The natural frequencies of the radial breathing mode (i.e., the nondeformed vibrational mode with no longitudinal and circumferential waves, which is characteristic of CNTs with free–free boundary conditions) for SWCNTs with different chirality indices are considered.

From the comparisons, it can be noted that the percentage difference is relatively low (maximum value ≈ 2.7%; average value ≈ 1.6%) for all the chirality indices that were considered, see

Table 2. Natural frequencies of the radial breathing mode (q = 0; s = 0) of the SWCNT in Table 1 with aspect ratio L/R = 10. Comparisons between anisotropic elasticity model (Sanders’s shell theory) and molecular dynamics simulations.

Natural Frequency, ωRBM (cm−1)			Difference (%)
Chirality Indices (n, m)	Anisotropic Elasticity Model (Sanders’s Shell Theory)	Molecular Dynamics Simulation [25]
(10, 0)	294.310	290.810	1.20
(6, 6)	284.460	278.450	2.16
(12, 0)	245.868	242.576	1.36
(7, 7)	244.074	239.020	2.11
(8, 8)	213.709	209.323	2.10
(14, 0)	211.067	207.980	1.48
(16, 0)	184.870	181.960	1.60
(10, 10)	171.104	167.644	2.06
(18, 0)	164.443	161.773	1.65
(20, 0)	148.073	145.577	1.71
(12, 12)	142.650	139.778	2.05
(25, 0)	118.551	116.439	1.81
(15, 15)	114.161	111.878	2.04
(30, 0)	98.835	97.013	1.88
(18, 18)	95.153	93.253	2.04
(33, 0)	89.865	87.507	2.69
(20, 20)	85.645	83.935	2.04

, and, therefore, the present anisotropic elastic shell model is proven to be accurate.

On the other hand, it should be emphasized that the development and implementation of the anisotropic elastic shell model present a high degree of analytical complexity and considerable computational effort. Therefore, it is useful to check whether the corresponding isotropic elastic shell model, which has a low degree of analytical complexity and less computational effort, can provide similar results.

From the comparison of the results for the isotropic elastic shell model and molecular dynamics simulations [25], it can be observed that the percentage difference is higher for the anisotropic elastic shell model (maximum value ≈ 3.6%; average value ≈ 2.9%) for all the chirality indices that were considered, see

Table 3. Natural frequencies of the radial breathing mode (q = 0; s = 0) of the SWCNT in Table 1 with aspect ratio L/R = 10. Comparison between isotropic elasticity model (Sanders’s shell theory) and molecular dynamics simulations.

Natural Frequency, ωRBM (cm−1)			Difference (%)
Chirality Indices (n, m)	Isotropic Elasticity Model (Sanders’s Shell Theory)	Molecular Dynamics Simulation [25]
(10, 0)	299.083	290.810	2.84
(6, 6)	288.075	278.450	3.46
(12, 0)	249.447	242.576	2.83
(7, 7)	246.812	239.020	3.26
(8, 8)	215.923	209.323	3.15
(14, 0)	213.955	207.980	2.87
(16, 0)	187.002	181.960	2.77
(10, 10)	172.925	167.644	3.15
(18, 0)	166.287	161.773	2.79
(20, 0)	149.741	145.577	2.86
(12, 12)	144.037	139.778	3.05
(25, 0)	119.753	116.439	2.85
(15, 15)	115.183	111.878	2.95
(30, 0)	99.772	97.013	2.84
(18, 18)	96.003	93.253	2.95
(33, 0)	90.665	87.507	3.61
(20, 20)	86.396	83.935	2.93

.

Because the anisotropic elastic shell model has proven to be significantly more accurate than the corresponding isotropic one, it will be adopted in the following parametric analyses. Readers interested in learning more about molecular dynamics simulations and the related processes can find a detailed explanation in Ref. [36].

7.2. Effects of Nonlocal and Material Parameters

In this section, the effects of the nonlocal and material parameters on the natural frequencies of the simply supported SWCNT in Table 1 are studied. Different chiralities and geometries of the SWCNT are analyzed. Vibrational modes with different wavenumbers along the longitudinal and circumferential directions are investigated.

The first goal is to analyze the effects of the nonlocal and material parameters on the natural frequencies of the simply supported SWCNT in Table 1 for a generic chirality, geometry, and wavenumber. This first analysis is carried out to study the deviation in the model with size effects compared to the one without size effects.

In Figure 2, the natural frequencies of the vibrational mode (q = 1; s = 2) with one longitudinal half-wave and two circumferential waves are presented. The chirality indices (n = 34; m = 0) (i.e., zigzag SWCNT) are considered. The thickness ratio R/h = 20 and aspect ratio L/R = 10 are adopted. It is observed that for a fixed value of the material parameter ($l$), the natural frequencies decrease as the nonlocal parameter ($\mu$) increases. In contrast, for a fixed value of the nonlocal parameter ($\mu$), the natural frequencies increase as the material parameter ($l$) increases. There are, therefore, opposite effects between the two small-length-scale parameters on the natural frequencies. This first analysis confirms the results obtained in previous papers, see, for example, Ref. [21], thus providing a validation of the model developed in this work.

The second goal is to study the effects of the nonlocal and material parameters on the natural frequencies of the simply supported SWCNT in Table 1 for different chiralities. This second analysis is carried out to understand if there is a relationship between the size effects and chirality of the SWCNT.

In Figure 3, the natural frequencies of the same vibrational mode (q = 1; s = 2) as in Figure 2 are shown. A SWCNT with the same geometry but with different chirality indices (n = 20; m = 20) (i.e., an armchair SWCNT) is considered. From Figure 3, it can be observed that the effects of the nonlocal ($\mu$) and material ($l$) parameters on the natural frequencies of the vibrational mode (q = 1; s = 2) are the same as those in Figure 2. It can, therefore, be deduced that the effects of the two small-length-scale parameters on the natural frequencies are independent of the chirality of the SWCNT. Starting from this result, the chirality indices (n = 34; m = 0) (i.e., zigzag SWCNT) will be considered in the following simulations.

The third goal is to analyze the effects of the nonlocal and material parameters on the natural frequencies of the simply supported SWCNT in Table 1 for different geometries.

Figure 4 shows the natural frequencies of the same vibrational mode (q = 1; s = 2) as in Figure 2. A SWCNT with the same aspect ratio (L/R = 10) but different thickness ratios (R/h) is analyzed. Without considering the size effects, it is observed that a reduction in the natural frequencies occurs as the value of the thickness ratio increases within the entire interval 20 < R/h < 100. On the one hand, for relatively low thickness ratios (20 < R/h < 50), this reduction is amplified as the value of the material parameter (l) increases, while it is attenuated as the value of the nonlocal parameter (μ) increases. On the other hand, for relatively high thickness ratios (R/h > 80), the reduction is very small, and the natural frequencies are similar for all the values of the nonlocal and material parameters. It can, therefore, be deduced that the effects of the two small-length-scale parameters on the natural frequencies of the SWCNT are strongly dependent on the radius at relatively low thickness ratios, while they are independent at relatively high thickness ratios (i.e., when the equivalent cylindrical shell is very thin).

Figure 5 shows the natural frequencies of the same vibrational mode (q = 1; s = 2) as in Figure 2. A SWCNT with the same thickness ratio (R/h = 20) but different aspect ratios (L/R) is considered. From Figure 5, it can be observed that for each value of the nonlocal ($\mu$) and material ($l$) parameters, the natural frequencies are constant as the value of the aspect ratio (L/R) increases. It can, therefore, be deduced that the effects of the two small-length-scale parameters on the natural frequencies are independent of the length of the SWCNT. It is important to underline that this last result is valid for an SWCNT as a very long tube, with an aspect ratio (L/R) usually between 20 and 100. On the contrary, for a generic cylindrical shell as a tube of medium length, the effects of the small-length-scale parameters on the natural frequencies may become dependent on the length of the shell, see Ref. [30] for details.

The last goal is to investigate the effects of the nonlocal and material parameters on the natural frequencies of the simply supported SWCNT in Table 1 for vibrational modes with different wavenumbers.

First, the number of longitudinal half-waves is evaluated.

In Figure 6, the natural frequencies of the axisymmetric modes (s = 0) of the SWCNT in Table 1 for thickness ratio R/h = 20 and aspect ratio L/R = 10 are considered. The effects of the nonlocal (μ) and material (l) parameters for different numbers of longitudinal half-waves (q) are investigated. We first see that the natural frequency of the nondeformed mode (q = 0; s = 0) is independent of the two small-length-scale parameters (i.e., it is constant). Without considering the size effects, an almost-constant value of the natural frequencies is observed as the number of longitudinal half-waves increases in the interval q = (0–3), and a subsequent increase is observed by further increasing the number of longitudinal half-waves. On the one hand, by increasing the value of the nonlocal parameter (μ), a small decrease in the natural frequencies is found as the number of longitudinal half-waves increases in the interval q = (0–3), and a subsequent small increase is found by further increasing the number of longitudinal half-waves, where for μ = 1 nm, the value of the natural frequency at q = 5 is very similar to that at q = 0. On the other hand, by increasing the value of the material parameter ($l$), a small increase in the natural frequencies is observed as the number of longitudinal half-waves increases in the interval q = (0–3), and a subsequent strong increase is observed by further increasing the number of longitudinal half-waves.

In Figure 7, the natural frequencies of the beam-like modes (s = 1) of the SWCNT in Table 1 for thickness ratio R/h = 20 and aspect ratio L/R = 10 are considered. The effects of the nonlocal (μ) and material (l) parameters for different numbers of longitudinal half-waves (q) are investigated. Without considering the size effects, a small increase in the natural frequencies is observed as the number of longitudinal half-waves increases in the interval q = (0–5). On the one hand, by increasing the value of the nonlocal parameter (μ), a very small decrease in the natural frequencies is observed as the number of longitudinal half-waves increases in the interval q = (0–3), and a subsequent very small increase is observed by further increasing the number of longitudinal half-waves, where for μ = 1 nm, the value of the natural frequency at q = 5 is very similar to that at q = 0. On the other hand, by increasing the value of the material parameter ($l$), an increase in the natural frequencies is obtained as the number of longitudinal half-waves increases in the interval q = (0–5). However, this latter increase due to the material parameter is lower in amplitude than the corresponding one obtained in Figure 6 for the axisymmetric modes (s = 0) in the interval q = (3–5).

In Figure 8, the natural frequencies of the shell-like modes (s = 2) of the SWCNT in Table 1 for thickness ratio R/h = 20 and aspect ratio L/R = 10 are considered. The effects of the nonlocal (μ) and material (l) parameters for different numbers of longitudinal half-waves (q) are investigated. Without considering the size effects, a very small increase in the natural frequencies is observed as the number of longitudinal half-waves increases in the interval q = (0–5). On the one hand, by increasing the value of the nonlocal parameter (μ), an almost-constant behavior in the natural frequencies is found as the number of longitudinal half-waves increases in the interval q = (0–5). On the other hand, by increasing the value of the material parameter ($l$), an increase in the natural frequencies is obtained as the number of longitudinal half-waves increases in the interval q = (0–5). Again, this latter increase due to the material parameter is lower in amplitude than the corresponding one obtained in Figure 7 for the beam-like modes (s = 1) in the interval q = (0–5).

Therefore, comparing Figure 6, Figure 7 and Figure 8, an increase in the natural frequencies is observed as the number of longitudinal half-waves increases. This increase is amplified as the material parameter increases, while it is attenuated as the nonlocal parameter increases. Furthermore, the increase in the natural frequencies due to the material parameter is attenuated as the number of circumferential waves increases.

Then, the number of circumferential waves is considered.

In Figure 9, the natural frequencies of the vibrational modes for q = 0 longitudinal half-waves of the SWCNT in Table 1 for thickness ratio R/h = 20 and aspect ratio L/R = 10 are considered. The effects of the nonlocal (μ) and material (l) parameters for different numbers of circumferential waves (s) are evaluated. It is confirmed that the natural frequency of the nondeformed mode (q = 0; s = 0) is independent of the two small-length-scale parameters (i.e., it is constant). Without considering the size effects, an increase in the natural frequencies is observed as the number of circumferential waves increases in the interval s = (0–5). On the one hand, by increasing the value of the nonlocal parameter (μ), a small increase in the natural frequencies is found as the number of longitudinal half-waves increases in the interval s = (0–5). On the other hand, by increasing the value of the material parameter ($l$), a strong increase in the natural frequencies is observed as the number of circumferential waves increases in the interval s = (0–5).

In Figure 10 and Figure 11, the natural frequencies of the vibrational modes for, respectively, q = 1 and q = 2 longitudinal half-waves of the SWCNT in Table 1 for thickness ratio R/h = 20 and aspect ratio L/R = 10 are considered. The effects of the nonlocal (μ) and material (l) parameters for different numbers of circumferential waves (s) are evaluated. From these figures, for the natural frequencies, a behavior very similar to that in Figure 9 is obtained; i.e., by increasing the value of the nonlocal parameter (μ), the natural frequencies increase slightly as the number of circumferential waves increases, while, by increasing the value of the material parameter (l), they increase strongly as the number of circumferential waves increases.

Therefore, comparing Figure 9, Figure 10 and Figure 11, an increase in the natural frequencies is observed as the number of circumferential waves increases. This increase is amplified as the material parameter increases, while it is attenuated as the nonlocal parameter increases. Furthermore, this behavior is independent of the number of longitudinal half-waves.

8. Conclusions

The main novelty of this paper is the development of an anisotropic elastic shell model with a nonlocal strain gradient to analyze the linear vibrations of SWCNTs. Based on Eringen’s nonlocal elasticity theory, Mindlin’s strain gradient theory, and Chang’s molecular mechanics model, the combined effect of the nonlocal and material parameters on the natural frequencies of simply supported SWCNTs with different chiralities, geometries, and wavenumbers is investigated.

From the numerical simulations, it is confirmed that for a generic vibrational mode, the natural frequencies decrease as the nonlocal parameter increases, while they increase as the material parameter increases. As new results, the reduction in the natural frequencies with increasing SWCNT radius and the increase in the natural frequencies with increasing wavenumber are both amplified as the material parameter increases, while they are both attenuated as the nonlocal parameter increases. Finally, it is found that the effects of nonlocal and material parameters on the natural frequencies are independent of the SWCNT chirality and length.

The model proposed in this paper has two important limitations. First, because the effects of the nonlocal and material parameters on the natural frequencies of the SWCNT were found to be strongly radius-dependent at relatively low thickness ratios, it would be interesting to study the linear vibrations of relatively thick SWCNTs, and toward this aim, a first-order shear-deformation shell theory should be used instead of a thin-shell theory (e.g., the Sanders–Koiter shell theory in this paper). The second important limitation of this paper, as in most of the works available in the literature, is that only the effects of the nonlocal and material parameters were analyzed and not those of the surface parameter, which is a very relevant small-length-scale parameter because it can strongly influence the stress and strain characteristics of the SWCNT.

Therefore, to fill these two gaps, the authors of this work are planning to write a new paper on the combined effects of the nonlocal elasticity, strain gradient, and surface stress on the linear vibrations of SWCNTs in the framework of the first-order shear-deformation shell theory.