Multi-Quanta Spin-Locking Nuclear Magnetic Resonance Relaxation Measurements: An Analysis of the Long-Time Dynamical Properties of Ions and Water Molecules Confined within Dense Clay Sediments
Abstract
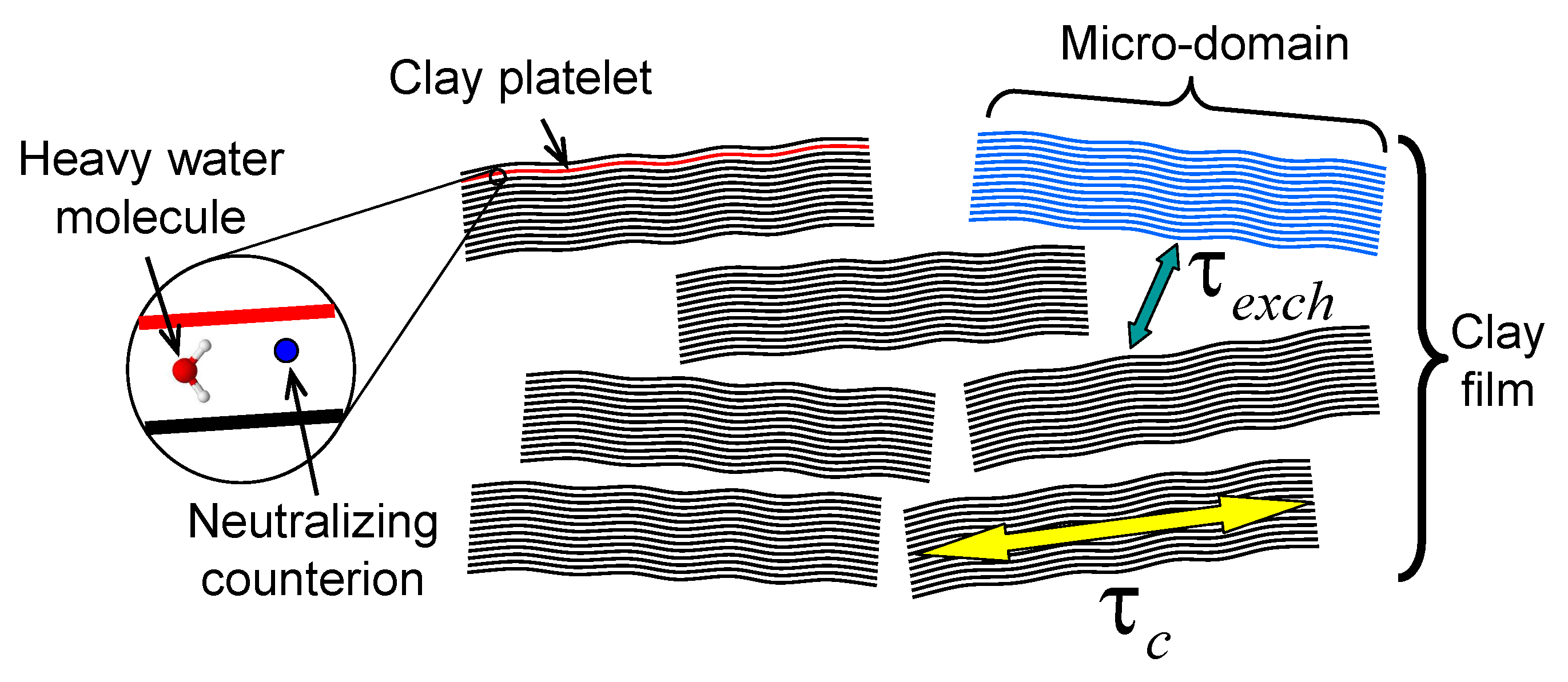
:1. Introduction
2. Sample Preparation and Experimental Setup
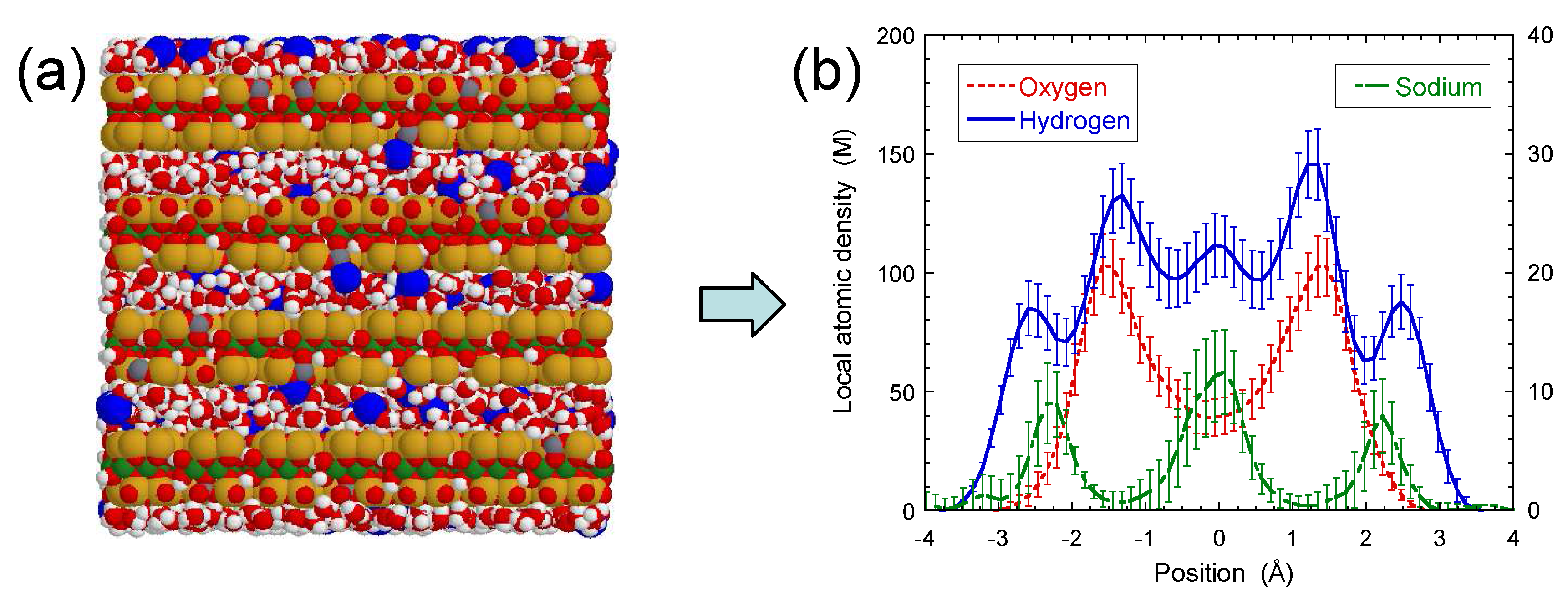
3. Results and Discussion
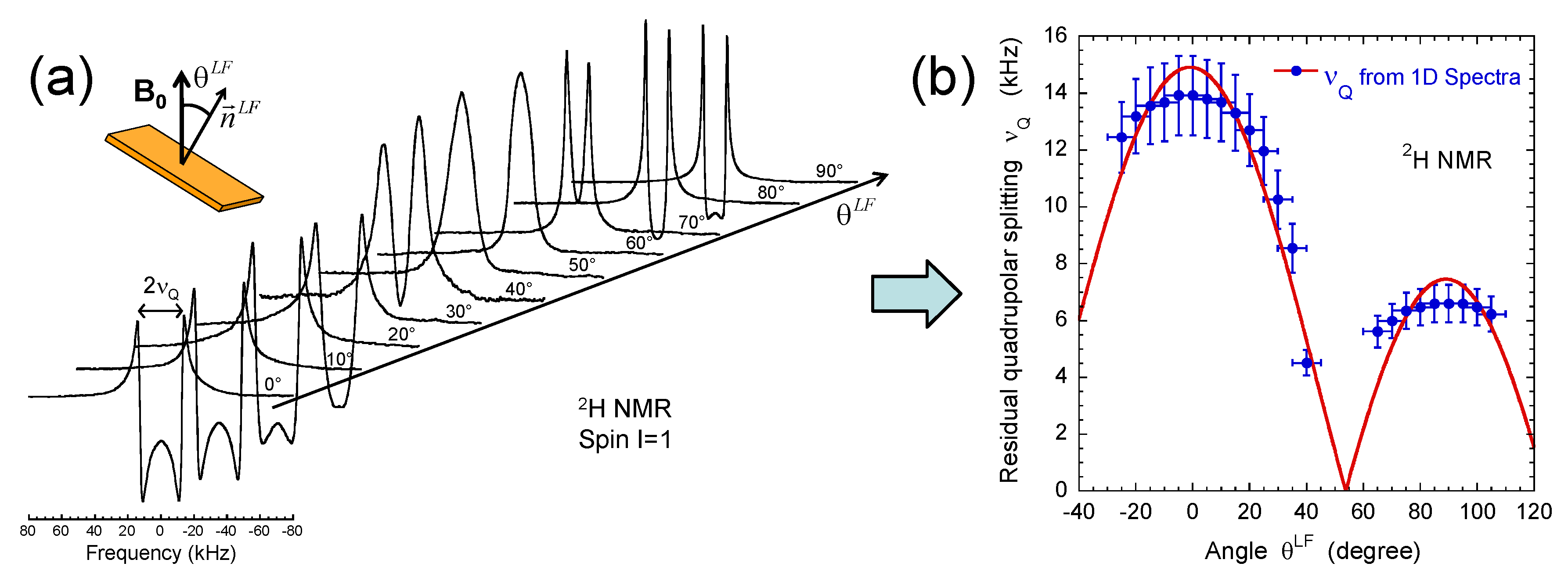
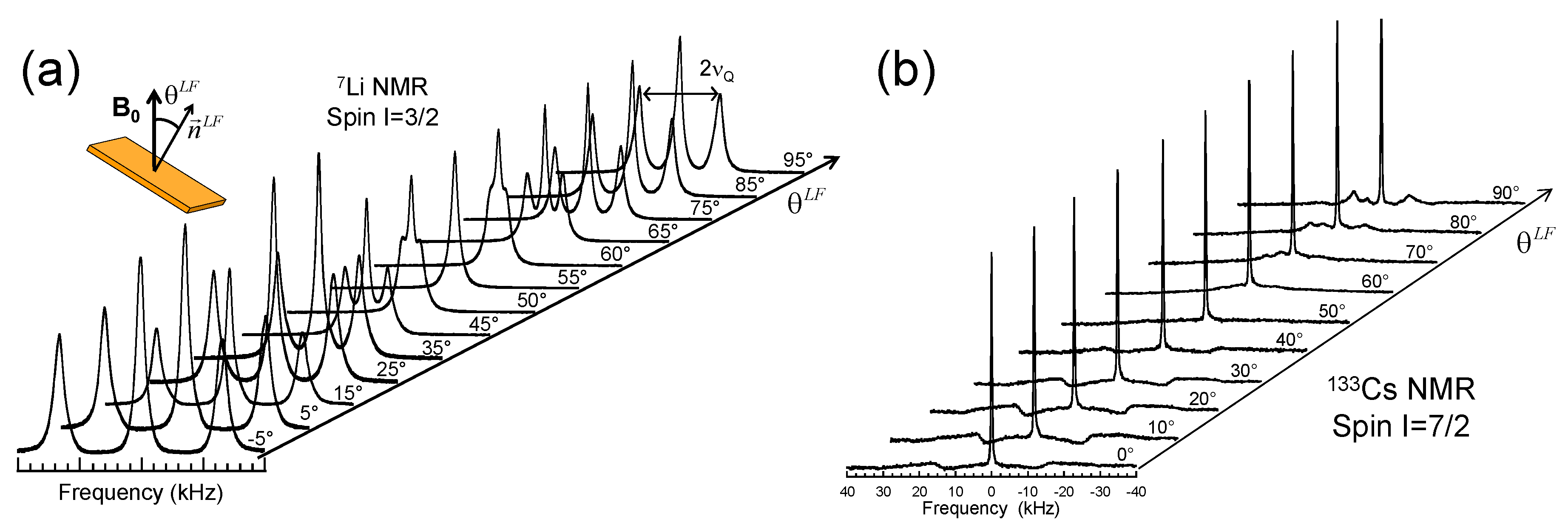
3.1. NMR Spectra
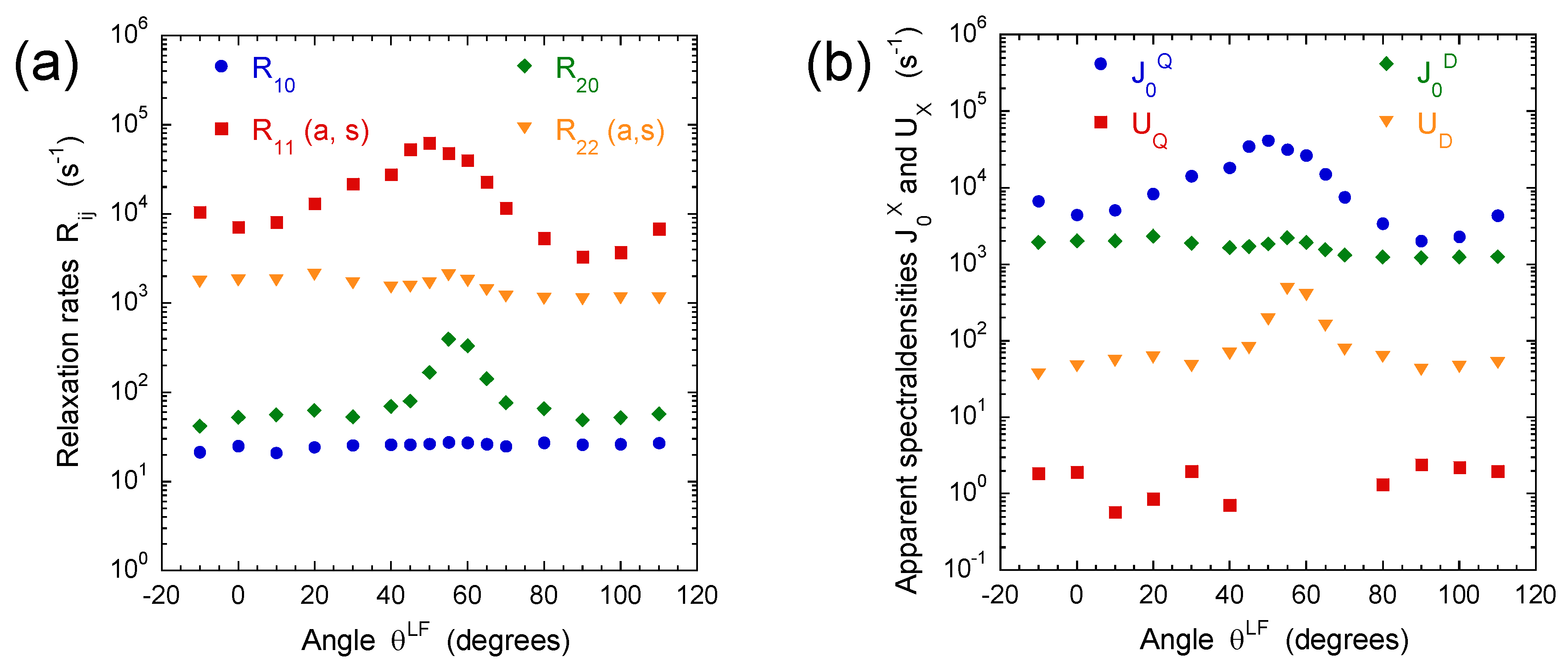
3.2. Multi-Quanta NMR Relaxation Rates
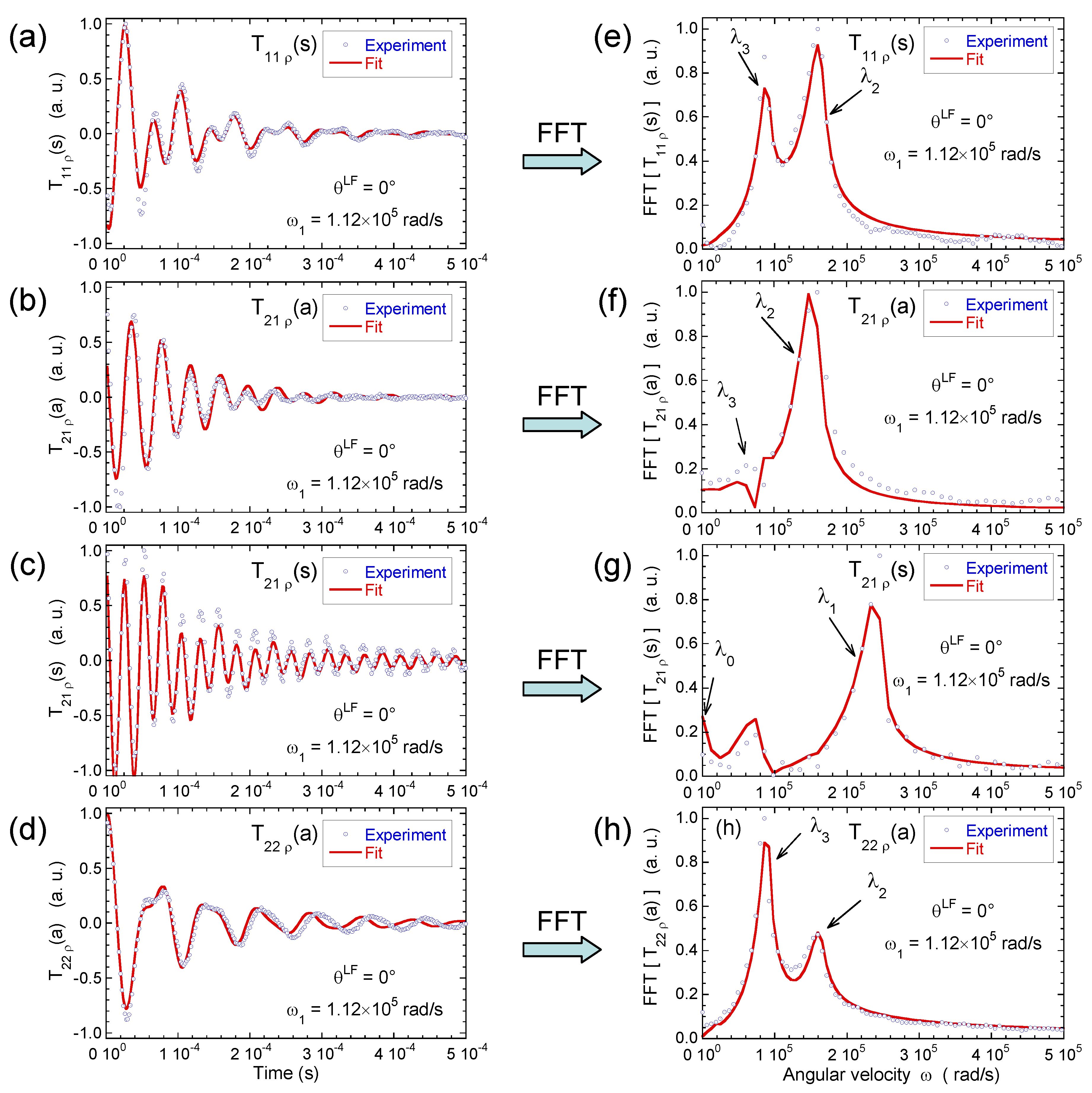
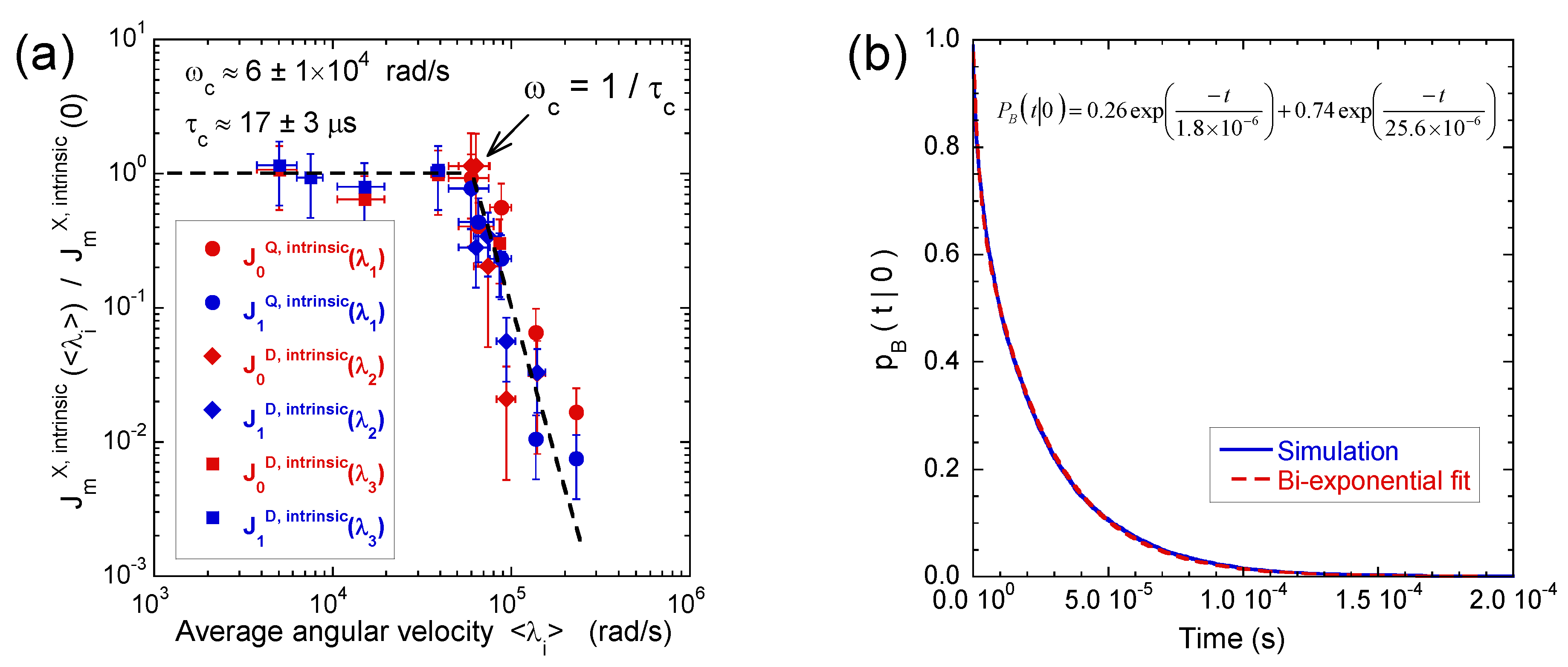
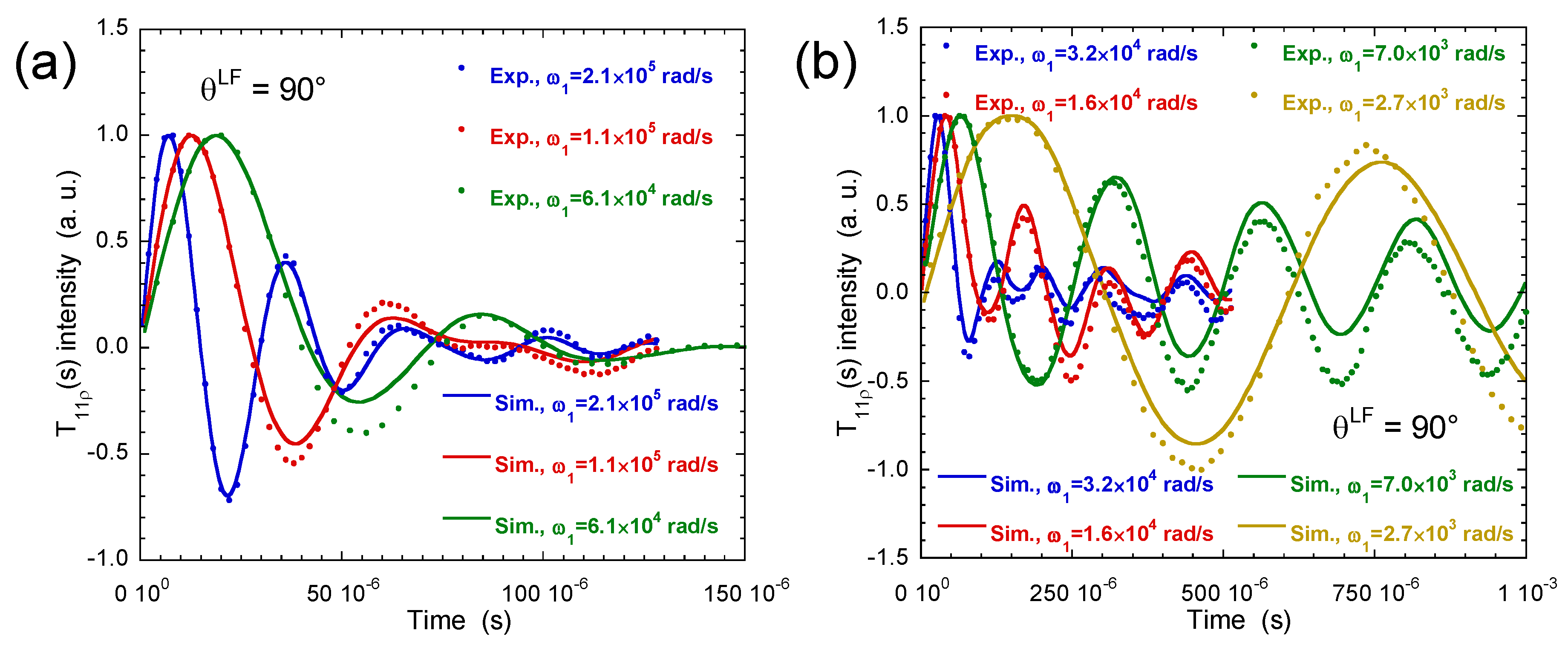
3.3. Multi-Quanta Spin-Locking NMR Relaxometry
3.4. Two-Time Stimulated Echo Attenuation
4. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| EFG | Electric Field Gradient |
| GCMC | Grand Canonical Monte Carlo |
| INS | Inelastic Neutron Scattering |
| NMR | Nuclear Magnetic Resonance |
| QENS | Quasi-Elastic Neutron Scattering |
| TEM | Transmission Electron Microscopy |
Appendix A. Quadrupolar and Heteronuclear Dipolar Hamiltonian
| Isotope | Spin I | Q (10 cm) | 1 + | R in Water (s) |
|---|---|---|---|---|
| Li | 3/2 | 0.042 | 0.74 | 0.03 |
| Na | 3/2 | 0.11 | 5.1 | 16.2 |
| K | 3/2 | 0.09 | 18.3 | 24 |
| Rb | 5/2 | 0.31 | 48.2 | 420 |
| Cs | 7/2 | 0.004 | 111 | 0.08 |
Appendix B. NMR Relaxation Theory
Appendix C. Matrix Representation of the Irreducible Tensor Operators
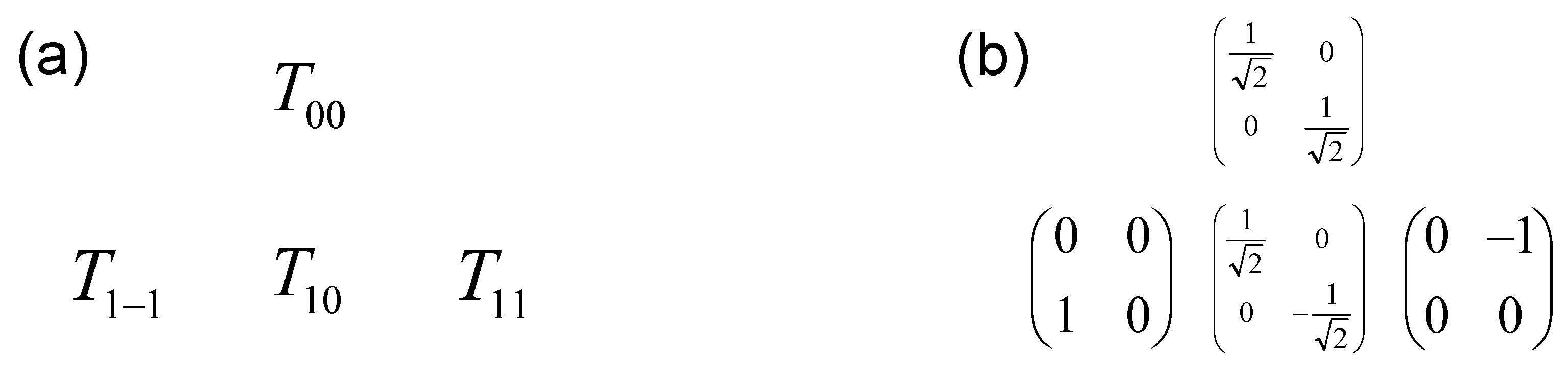
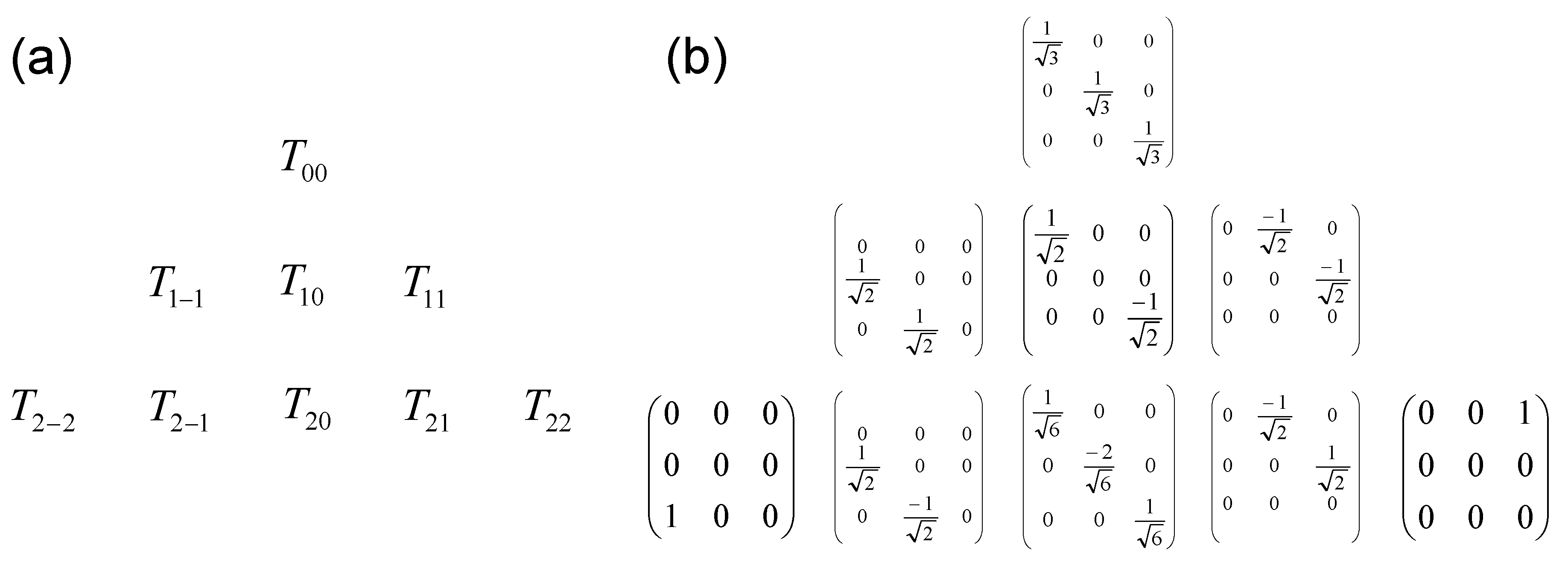
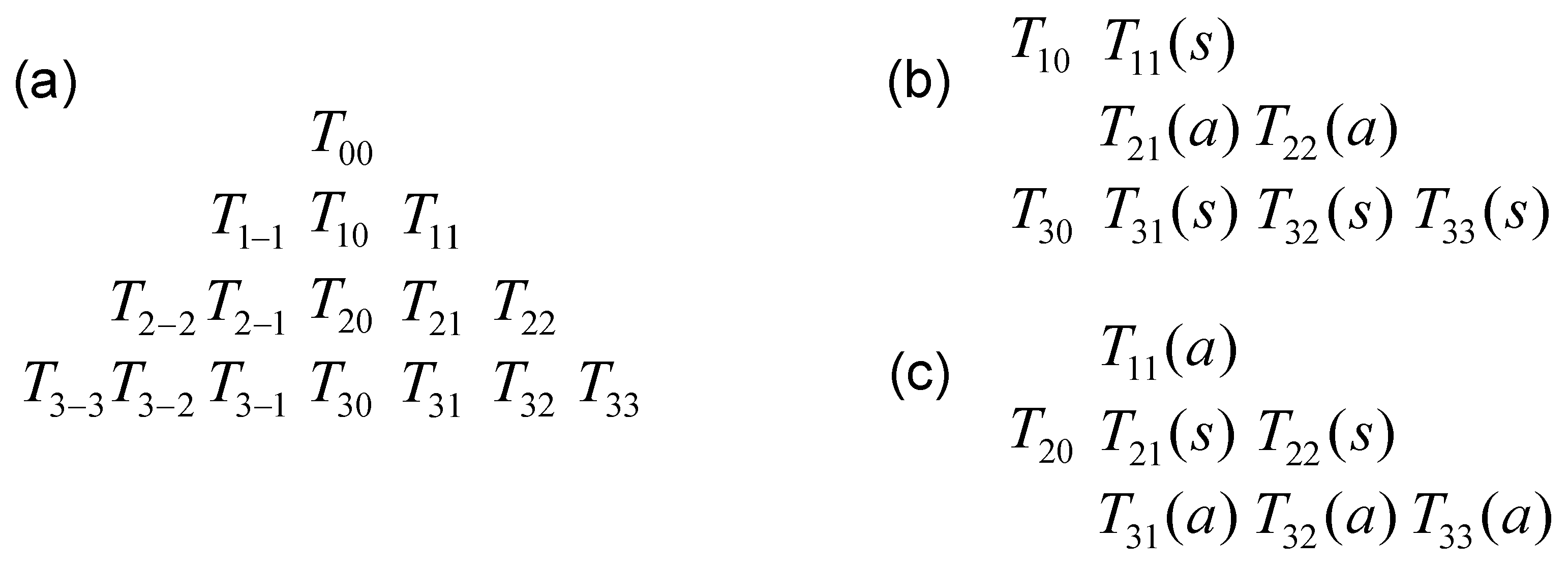
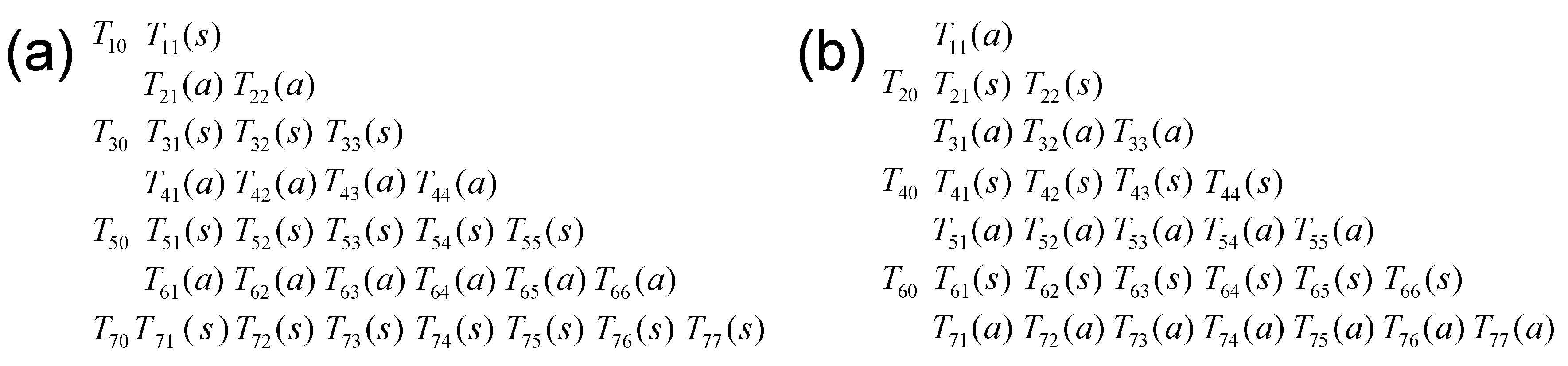
Appendix D. Application to the Relaxation of Quadrupolar Nuclei
References
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Henderson, D. Fundamentals of Inhomogeneous Fluids; M. Dekker: New York, NY, USA, 1992. [Google Scholar]
- Jobbagy, M.; Iyi, N. Interplay of charge density and relative humidity on the structure of nitrate layered double hydroxides. J. Phys. Chem. C 2010, 114, 18153–18158. [Google Scholar] [CrossRef]
- Lee, S.S.; Fenter, P.; Park, C.; Sturchio, N.C.; Nagy, K.L. Hydrated cation speciation at the Muscovite (001)-water interface. Langmuir 2010, 26, 16647–16651. [Google Scholar] [CrossRef] [PubMed]
- Boily, J.F. Water structure and hydrogen bonding at Goethite/water interfaces: Implications for proton affinities. J. Phys. Chem. C 2012, 116, 4714–4724. [Google Scholar] [CrossRef]
- Ho, T.A.; Argyris, D.; Cole, D.R.; Striolo, A. Aqueous NaCl and CsCl solutions confined in crystalline slit-shaped silica nanopores of varying degree of protonation. Langmuir 2012, 28, 1256–1266. [Google Scholar] [CrossRef] [PubMed]
- Malani, A.; Ayappa, K.G. Relaxation and jump dynamics of water at the mica interface. J. Chem. Phys. 2012, 136, 194701. [Google Scholar] [CrossRef] [PubMed]
- Buyukdagli, S.; Blossey, R. Dipolar correlations in structured solvents under nanoconfinement. J. Chem. Phys. 2014, 140, 234903. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Fujimoto, K.; Dai, W.; Hunger, M. Molecular mechanism of heavily adhesive Cs: Why radioactive Cs is not decontaminated from soil. J. Phys. Chem. C 2013, 117, 14075–14080. [Google Scholar] [CrossRef]
- Jiménez-Ruiz, M.; Ferrage, E.; Delville, A.; Michot, L.J. Anisotropy on the collective dynamics of water confined in swelling clay minerals. J. Phys. Chem. A 2012, 116, 2379–2387. [Google Scholar] [CrossRef] [PubMed]
- Michot, L.J.; Ferrage, E.; Delville, A.; Jiménez-Ruiz, M. Influence of layer charge, hydration state and cation nature on the collective dynamics of interlayer water in synthetic swelling clay minerals. Appl. Clay Sci. 2016, 119, 375–384. [Google Scholar] [CrossRef]
- Jiménez-Ruiz, M.; Ferrage, E.; Blanchard, M.; Fernandez-Castanon, J.; Delville, A.; Johnson, M.R.; Michot, L.J. Combination of inelastic neutron scattering experiments and ab Initio quantum calculations for the study of the hydration properties of oriented Saponites. J. Phys. Chem. C 2017, 121, 5029–5040. [Google Scholar] [CrossRef]
- Michot, L.J.; Delville, A.; Humbert, B.; Plazanet, M.; Levitz, P. Diffusion of water in a synthetic clay with tetrahedral charges by combined neutron time-of-flight measurements and molecular dynamics simulations. J. Phys. Chem. C 2007, 111, 9818–9831. [Google Scholar] [CrossRef]
- Michot, L.J.; Ferrage, E.; Jiménez-Ruiz, M.; Boehm, M.; Delville, A. Anisotropic features of water and ion dynamics in synthetic Na- and Ca-smectites with tetrahedral layer charge. A combined Quasi-Elastic Neutron-Scattering and Molecular Dynamics simulations study. J. Phys. Chem. C 2012, 116, 16619–16633. [Google Scholar] [CrossRef]
- Callaghan, P.T. Principles of Nuclear Magnetic Resonance Microscopy; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Delville, A.; Porion, P.; Faugère, A.M. Ion diffusion within charged porous network as probed by nuclear quadrupolar relaxation. J. Phys. Chem. B 2000, 104, 1546–1551. [Google Scholar] [CrossRef]
- Bryar, T.R.; Daughney, C.J.; Knight, R.J. Paramagnetic effects of iron(III) species on nuclear magnetic relaxation of fluid protons in porous media. J. Magn. Reson. 2000, 142, 74–85. [Google Scholar] [CrossRef] [PubMed]
- Porion, P.; Michot, L.J.; Faugère, A.M.; Delville, A. Structural and dynamical properties of the water molecules confined in dense clay sediments: A study combining 2H NMR spectroscopy and multiscale numerical modeling. J. Phys. Chem. C 2007, 111, 5441–5453. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, R.; Lv, W.; Liu, Q.; Wang, X.; Sun, P.; Winter, H.H.; Xue, G. Critical effect of segmental dynamics in polybutadiene/clay nanocomposites characterized by solid state 1H NMR spectroscopy. J. Phys. Chem. C 2014, 118, 5606–5614. [Google Scholar] [CrossRef]
- Bortolotti, V.; Brizi, L.; Brown, R.J.S.; Fantazzini, P.; Mariani, M. Nano and sub-nano multiscale porosity formation and other features revealed by 1H NMR relaxometry during cement hydration. Langmuir 2014, 30, 10871–10877. [Google Scholar] [CrossRef] [PubMed]
- Halle, B. Spin dynamics of exchanging quadrupolar nuclei in locally anisotropic systems. Prog. Nucl. Magn. Reson. Spectrosc. 1996, 28, 137–159. [Google Scholar] [CrossRef]
- Woessner, D.E. Nuclear transfer effects in Nuclear Magnetic Resonance pulse experiments. J. Chem. Phys. 1961, 35, 41–48. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Kimmich, R. NMR: Tomography, Diffusometry, Relaxometry; Springer: Berlin, Germany, 1997. [Google Scholar]
- Delville, A.; Stöver, H.D.H.; Detellier, C. Crown-ether cation decomplexation mechanics. 23Na NMR studies of the sodium cation complexes with dibenzo-24-crown-8 and dibenzo-18-crown-6 in nitromethane and acetonitrile. J. Am. Chem. Soc. 1987, 109, 7293–7301. [Google Scholar] [CrossRef]
- Delville, A.; Detellier, C.; Laszlo, P. Determination of the correlation time for a slowly reorienting spin-3/2 nucleus: Binding of Na+ with the 5’-GMP supramolecular assembly. J. Magn. Reson. 1979, 34, 301–315. [Google Scholar]
- Delville, A.; Grandjean, J.; Laszlo, P.; Gerday, C.; Grabarek, Z.; Drabikowski, W. Sodium-23 nuclear magnetic resonance as an indicator of sodium binding to Troponin C and tryptic fragments, in relation to calcium content and attendant conformational changes. Eur. J. Biochem. 1980, 105, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Delville, A.; Laszlo, P.; Schyns, R. Displacement of sodium ions by surfactant ions from DNA: A 23Na NMR investigation. Biophys. Chem. 1986, 24, 121–133. [Google Scholar] [CrossRef]
- Liu, G.; Li, Y.; Jonas, J. Confined geometry effects on reorientational dynamics of molecular liquids in porous silica glasses. J. Chem. Phys. 1991, 95, 6892–6901. [Google Scholar] [CrossRef]
- Korb, J.P.; Whaley-Hodges, M.; Bryant, R.G. Translational diffusion of liquids at surfaces of microporous materials: Theoretical analysis of field-cycling magnetic relaxation measurements. Phys. Rev. E 1997, 56, 1934–1945. [Google Scholar] [CrossRef]
- Levitz, P.E. Confined dynamics, forms and transitions in colloidal systems: From clay to DNA. Magn. Reson. Imaging 2005, 23, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Korb, J.P. Nuclear magnetic relaxation of liquids in porous media. New J. Phys. 2011, 13, 035016. [Google Scholar] [CrossRef]
- Delville, A.; Letellier, M. Structure and dynamics of simple liquids in heterogeneous condition: An NMR study of the clay water interface. Langmuir 1995, 11, 1361–1367. [Google Scholar] [CrossRef]
- Avogadro, A.; Villa, M. Nuclear magnetic resonance in a two-dimensional system. J. Chem. Phys. 1977, 66, 2359–2367. [Google Scholar] [CrossRef]
- Korb, J.P.; Ahadi, M.; McConnell, H.M. Paramagnetically enhanced nuclear relaxation in lamellar phases. J. Phys. Chem. 1987, 91, 1255–1259. [Google Scholar] [CrossRef]
- Korb, J.P.; Delville, A.; Xu, S.; Demeulenaere, G.; Costa, P.; Jonas, J. Relative Role of Surface Interactions and Topological Effects in Nuclear-Magnetic-Resonance of Confined Liquids. J. Chem. Phys. 1994, 101, 7074–7081. [Google Scholar] [CrossRef]
- Pasquier, V.; Levitz, P.; Delville, A. 129Xe NMR as a probe of gas diffusion and relaxation in disordered porous media: An application to Vycor. J. Phys. Chem. 1996, 100, 10249–10256. [Google Scholar] [CrossRef]
- Korb, J.P.; Malier, L.; Cros, F.; Xu, S.; Jonas, J. Surface dynamics of liquids in nanopores. Phys. Rev. Lett. 1996, 77, 2312–2315. [Google Scholar] [CrossRef] [PubMed]
- Faux, D.A.; McDonald, P.J.; Howlett, N.C. Nuclear-magnetic-resonance relaxation due to the translational diffusion of fluid confined to quasi-two-dimensional pores. Phys. Rev. E 2017, 95, 033116. [Google Scholar] [CrossRef] [PubMed]
- Porion, P.; Michot, L.J.; Faugère, A.M.; Delville, A. Influence of confinement on the long-range mobility of water molecules within clay aggregates: A 2H NMR analysis using spin-locking relaxation rates. J. Phys. Chem. C 2007, 111, 13117–13128. [Google Scholar] [CrossRef]
- Trausch, G.; Canet, D.; Cadène, A.; Turq, P. Separation of components of a 1H NMR composite signal by nutation experiments under low amplitude radio-frequency fields. Application to the water signal in clays. Chem. Phys. Lett. 2006, 433, 228–233. [Google Scholar] [CrossRef]
- Fleury, M.; Canet, D. Water orientation in smectites using NMR nutation experiments. J. Phys. Chem. C 2014, 118, 4733–4740. [Google Scholar] [CrossRef]
- Volgmann, K.; Epp, V.; Langer, J.; Stanje, B.; Heine, J.; Nakhal, S.; Lerch, M.; Wilkening, M.; Heitjans, P. Solid-state NMR to study translational Li ion dynamics in solids with low-dimensional diffusion pathways. Z. Phys. Chem. 2017, 231, 1215–1241. [Google Scholar] [CrossRef]
- Godefroy, S.; Fleury, M.; Deflandre, F.; Korb, J.P. Temperature effect on NMR surface relaxation in rocks for well logging applications. J. Phys. Chem. B 2002, 106, 11183–11190. [Google Scholar] [CrossRef]
- Leon, N.; Korb, J.P.; Bonalde, I.; Levitz, P. Universal nuclear spin relaxation and long-range order in nematics strongly confined in mass fractal silica gels. Phys. Rev. Lett. 2004, 92, 195504. [Google Scholar] [CrossRef] [PubMed]
- Kruk, D.; Meier, R.; Rössler, E.A. Nuclear magnetic resonance relaxometry as a method of measuring translational diffusion coefficients in liquids. Phys. Rev. E 2012, 85, 020201(R). [Google Scholar] [CrossRef] [PubMed]
- Muncaci, S.; Mattea, C.; Stapf, S.; Ardelean, I. Frequency-dependent NMR relaxation of liquids confined inside porous media containing an increased amount of magnetic impurities. Magn. Reson. Chem. 2013, 51, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Kimmich, R.; Fatkullin, N. Self-diffusion studies by intra- and inter-molecular spin-lattice relaxometry using field-cycling: Liquids, plastic crystals, porous media, and polymer segments. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 101, 18–50. [Google Scholar] [CrossRef] [PubMed]
- Harris, R.K.; Mann, B.E. NMR and the Periodic Table; Academic Press: London, UK, 1978. [Google Scholar]
- Porion, P.; Delville, A. Multinuclear NMR study of the structure and micro-dynamics of counterions and water molecules within clay colloids. Curr. Opin. Colloid Interface Sci. 2009, 14, 216–222. [Google Scholar] [CrossRef]
- Porion, P.; Michot, L.J.; Warmont, F.; Faugère, A.M.; Delville, A. Long-time dynamics of confined water molecules probed by 2H NMR multiquanta relaxometry: An application to dense clay sediments. J. Phys. Chem. C 2012, 116, 17682–17697. [Google Scholar] [CrossRef]
- Porion, P.; Faugère, A.M.; Delville, A. Multiscale water dynamics within dense clay sediments probed by 2H multiquanta NMR relaxometry and two-time stimulated echo NMR spectroscopy. J. Phys. Chem. C 2013, 117, 26119–26134. [Google Scholar] [CrossRef]
- Porion, P.; Faugère, A.M.; Delville, A. Structural and dynamical properties of water molecules confined within clay sediments probed by deuterium NMR spectroscopy, multiquanta relaxometry, and two-time stimulated echo attenuation. J. Phys. Chem. C 2014, 118, 20429–20444. [Google Scholar] [CrossRef]
- Porion, P.; Faugère, A.M.; Delville, A. Long-time scale ionic dynamics in dense clay sediments measured by the frequency variation of the 7Li multiple-quantum NMR relaxation rates in relation with a multiscale modeling. J. Phys. Chem. C 2009, 113, 10580–10597. [Google Scholar] [CrossRef]
- Porion, P.; Warmont, F.; Faugère, A.M.; Rollet, A.L.; Dubois, E.; Marry, V.; Michot, L.J.; Delville, A. 133Cs Nuclear Magnetic Resonance relaxometry as a probe of the mobility of cesium cations confined within dense clay sediments. J. Phys. Chem. C 2015, 119, 15360–15372. [Google Scholar] [CrossRef]
- Rinnert, E.; Carteret, C.; Humbert, B.; Fragneto-Cusani, G.; Ramsay, J.D.F.; Delville, A.; Robert, J.L.; Bihannic, I.; Pelletier, M.; Michot, L.J. Hydration of a synthetic clay with tetrahedral charges: A multidisciplinary experimental and numerical study. J. Phys. Chem. B 2005, 109, 23745–23759. [Google Scholar] [CrossRef] [PubMed]
- Ferrage, E.; Sakharov, B.A.; Michot, L.J.; Delville, A.; Bauer, A.; Lanson, B.; Grangeon, S.; Frapper, G.; Jiménez-Ruiz, M.; Cuello, G.J. Hydration properties and interlayer organization of water and ions in synthetic Na-smectite with tetrahedral layer charge. Part 2. Toward a precise coupling between molecular simulations and diffraction data. J. Phys. Chem. C 2011, 115, 1867–1881. [Google Scholar] [CrossRef]
- Dazas, B.; Lanson, B.; Delville, A.; Robert, J.L.; Komarneni, S.; Michot, L.J.; Ferrage, E. Influence of tetrahedral layer charge on the organization of interlayer water and ions in synthetic Na-saturated smectites. J. Phys. Chem. C 2015, 119, 4158–4172. [Google Scholar] [CrossRef]
- Böhmer, R.; Qi, F. Spin relaxation and ultra-slow Li motion in an aluminosilicate glass ceramic. Solid State Nucl. Magn. Reson. 2007, 31, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Porion, P.; Faugère, A.M.; Delville, A. Long-distance water exchange within dense clay sediments probed by two-time 2H stimulated echo NMR spectroscopy. J. Phys. Chem. C 2013, 117, 9920–9931. [Google Scholar] [CrossRef]
- Michot, L.J.; Bihannic, I.; Porsch, K.; Maddi, S.; Baravian, C.; Mougel, J.; Levitz, P. Phase diagrams of Wyoming Na-Montmorillonite clay. Influence of particle anisotropy. Langmuir 2004, 20, 10829–10837. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, D.T.; Hunt, M.J.; Mackay, A.L. Deuteron interactions in pure quadrupole-resonance. J. Magn. Reson. 1975, 20, 505–514. [Google Scholar] [CrossRef]
- Mehring, M. Principles of High Resolution NMR in Solids, 2nd ed.; Springer: Berlin, Germany, 1983. [Google Scholar]
- Porion, P.; Faugère, A.M.; Delville, A. 7Li NMR spectroscopy and multiquantum relaxation as a probe of the microstructure and dynamics of confined Li+ cations: An application to dense clay sediments. J. Phys. Chem. C 2008, 112, 9808–9821. [Google Scholar] [CrossRef]
- Porion, P.; Faugère, A.M.; Lécolier, E.; Gherardi, B.; Delville, A. 23Na Nuclear quadripolar relaxation as a probe of the microstructure and dynamics of aqueous clay dispersions: An application to Laponite gels. J. Phys. Chem. B 1998, 102, 3477–3485. [Google Scholar] [CrossRef]
- Bowden, G.J.; Hutchison, W.D. Tensor operator formalism for multiple-quantum NMR. 1. Spin-1 nuclei. J. Magn. Reson. 1986, 67, 403–414. [Google Scholar] [CrossRef]
- Bowden, G.J.; Hutchison, W.D.; Khachan, J. Tensor operator formalism for multiple-quantum NMR. 2. Spins-3/2, spin-2, and spin-5/2 and general I. J. Magn. Reson. 1986, 67, 415–437. [Google Scholar]
- Müller, N.; Bodenhausen, G.; Ernst, R.R. Relaxation-induced violations of coherence transfer selection rules in Nuclear Magnetic Resonance. J. Magn. Reson. 1987, 75, 297–334. [Google Scholar] [CrossRef]
- Ngouana, W.B.F.; Kalinichev, A.G. Structural arrangements of isomorphic substitutions in smectites: Molecular simulation of the swelling properties, interlayer structure, and dynamics of hydrated Cs-Montmorillonite revisited with new clay models. J. Phys. Chem. C 2014, 118, 12758–12773. [Google Scholar]
- Marry, V.; Turq, P.; Cartailler, T.; Levesque, D. Microscopic simulation of structure and dynamics of water and counterions in a monohydrated Montmorillonite. J. Chem. Phys. 2002, 117, 3454–3463. [Google Scholar] [CrossRef]
- Kosakowski, G.; Churakov, S.V.; Thoenen, T. Diffusion of Na and Cs in Montmorillonite. Clays Clay Miner. 2008, 56, 190–206. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Wang, R.; Zhou, H. Effects of layer-charge distribution on the thermodynamic and microscopic properties of Cs-smectite. Geochim. Cosmochim. Acta 2008, 72, 1837–1847. [Google Scholar] [CrossRef]
- Bourg, I.C.; Sposito, G. Connecting the molecular scale to the continuum scale for diffusion processes in smectite-rich porous media. Environ. Sci. Technol. 2010, 44, 2085–2091. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Zaoui, A. How water and counterions diffuse into the hydrated Montmorillonite. Solid State Ion. 2011, 203, 80–85. [Google Scholar]
- Cuperlovic, M.; Meresi, G.H.; Palke, W.E.; Gerig, J.T. Spin relaxation and chemical exchange in NMR simulations. J. Magn. Reson. 2000, 142, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Hertz, H.G. Magnetic relaxation by quadrupole interaction of ionic nuclei in electrolyte solutions. Part I: Limiting values for infinite dilution. Ber. Bunsenges. Phys. Chem. 1973, 77, 531–540. [Google Scholar] [CrossRef]
- Redfield, A.G. On the theory of relaxation processes. IBM J. Res. Dev. 1957, 1, 19–31. [Google Scholar]
- Van der Maarel, J.R.C. The relaxation dynamics of spin I=1 nuclei with a static quadrupolar coupling and a radio-frequency field. J. Chem. Phys. 1993, 99, 5646–5653. [Google Scholar] [CrossRef]
- Van der Maarel, J.R.C. Thermal relaxation and coherence dynamics of spin 3/2. I. Static and fluctuating quadrupolar interactions in the multipole basis. Concepts Magn. Reson. Part A 2003, 19A, 97–116. [Google Scholar] [CrossRef]
- Van der Maarel, J.R.C. Thermal relaxation and coherence dynamics of spin 3/2. II. Strong radio-frequency field. Concepts Magn. Reson. Part A 2003, 19A, 117–133. [Google Scholar] [CrossRef]
- Kimmich, R.; Anoardo, E. Field-cycling NMR relaxometry. Prog. Nucl. Magn. Reson. Spectrosc. 2004, 44, 257–320. [Google Scholar] [CrossRef]
- Barbara, T.M.; Vold, R.R.; Vold, R.L. A determination of individual spectral densities in a smectic liquid-crystal from angle dependent nuclear spin relaxation measurements. J. Chem. Phys. 1983, 79, 6338–6340. [Google Scholar] [CrossRef]
- Porion, P.; Al-Mukhtar, M.; Meyer, S.; Faugère, A.M.; Van der Maarel, J.R.C.; Delville, A. Nematic ordering of suspensions of charged anisotropic colloids detected by 23Na Nuclear Quadrupolar Spectroscopy. J. Phys. Chem. B 2001, 105, 10505–10514. [Google Scholar] [CrossRef]



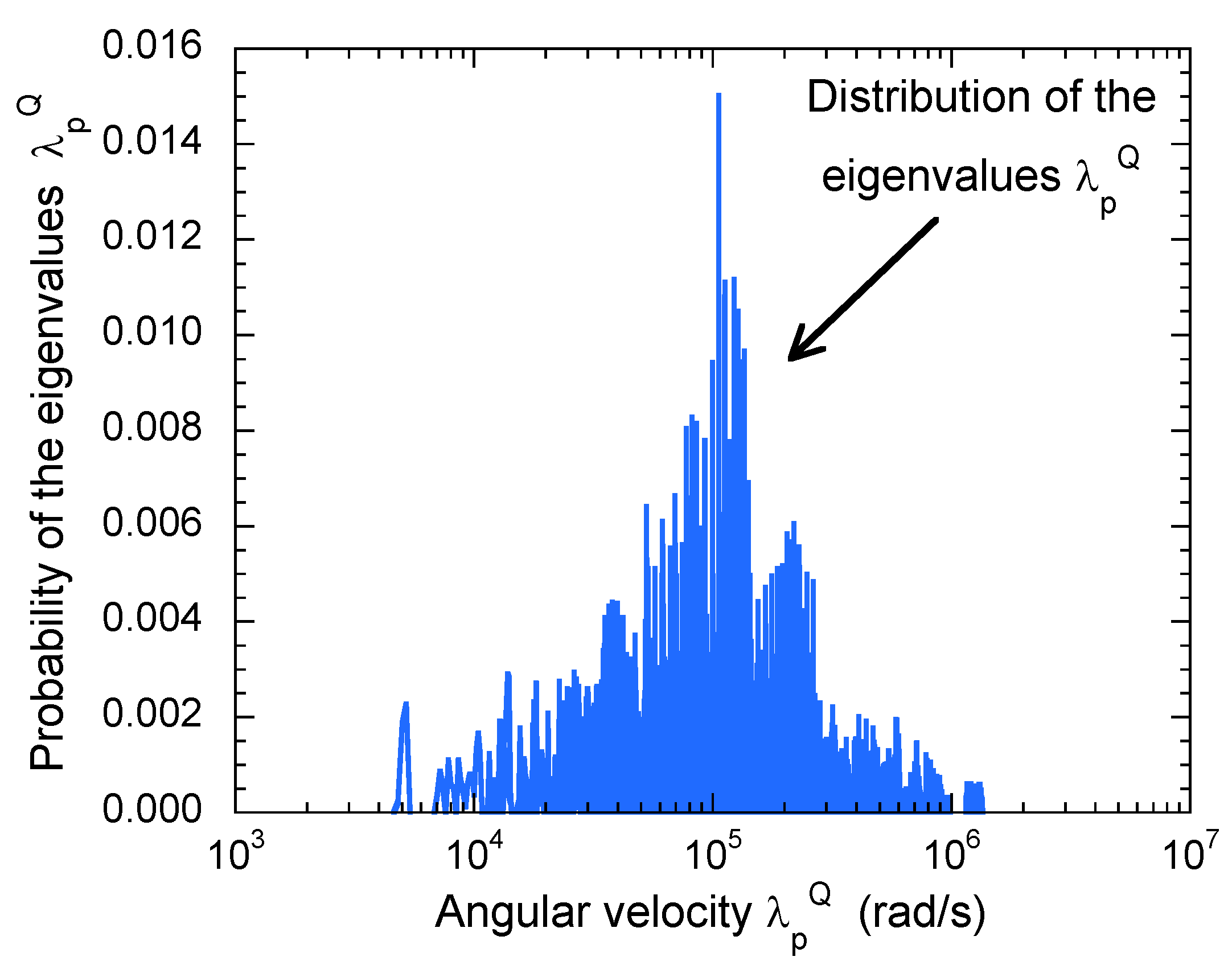
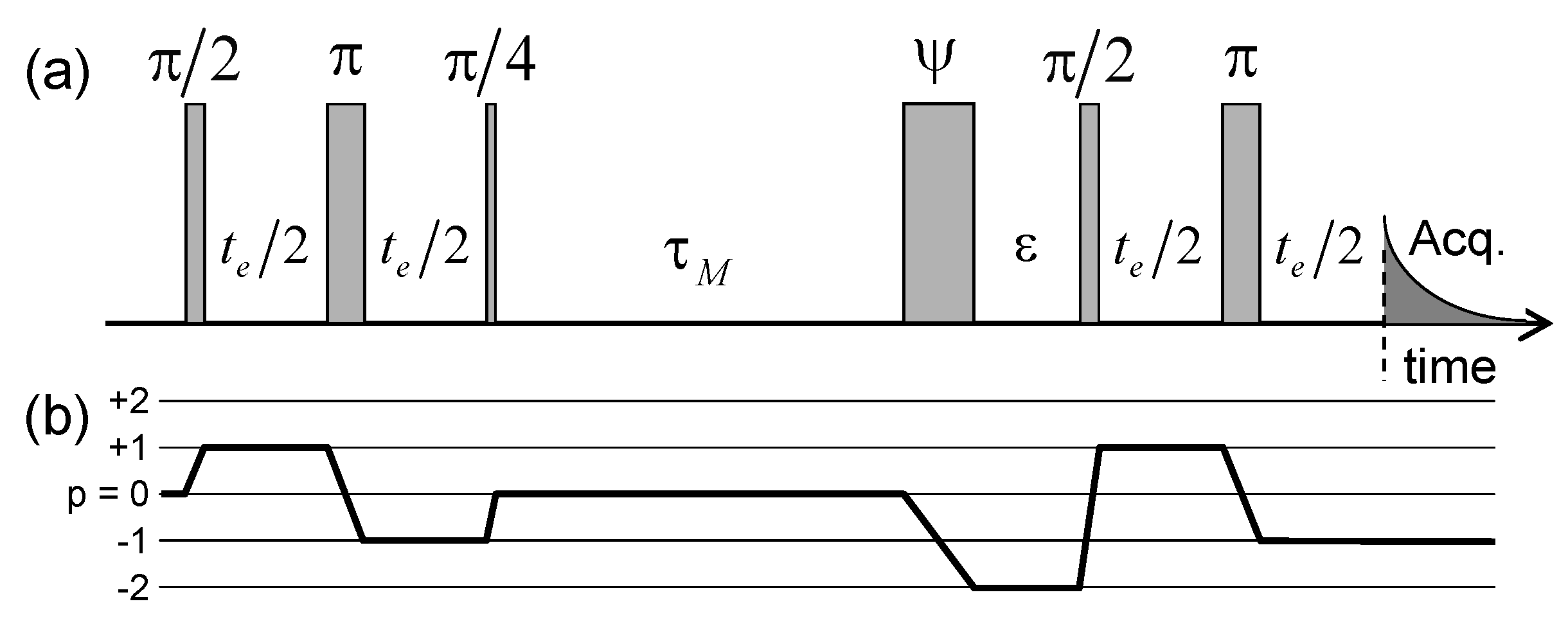

| (10 rad/s) | (10 rad/s) | (10 rad/s) | (10 rad/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.122 | 2.46 | 2.28 | 2.22 | 1.60 | 1.36 | 1.23 | 0.86 | 0.86 | 0.86 | |||
| 0.561 | 1.48 | 1.29 | 1.36 | 1.11 | 0.86 | 0.86 | 0.37 | 0.37 | 0.43 | |||
| 0.280 | 1.05 | 0.80 | 0.80 | 0.92 | 0.68 | 0.62 | 0.18 | 0.18 | 0.09 | |||
| 0.140 | 0.86 | 0.55 | 0.55 | 0.80 | 0.62 | 0.49 | 0.06 | 0.06 | 0.09 | |||
| 0.070 | 0.80 | 0.55 | 0.43 | 0.80 | 0.55 | 0.43 | 0.06 | 0.06 | 0.03 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porion, P.; Delville, A. Multi-Quanta Spin-Locking Nuclear Magnetic Resonance Relaxation Measurements: An Analysis of the Long-Time Dynamical Properties of Ions and Water Molecules Confined within Dense Clay Sediments. Magnetochemistry 2017, 3, 35. https://doi.org/10.3390/magnetochemistry3040035
Porion P, Delville A. Multi-Quanta Spin-Locking Nuclear Magnetic Resonance Relaxation Measurements: An Analysis of the Long-Time Dynamical Properties of Ions and Water Molecules Confined within Dense Clay Sediments. Magnetochemistry. 2017; 3(4):35. https://doi.org/10.3390/magnetochemistry3040035
Chicago/Turabian StylePorion, Patrice, and Alfred Delville. 2017. "Multi-Quanta Spin-Locking Nuclear Magnetic Resonance Relaxation Measurements: An Analysis of the Long-Time Dynamical Properties of Ions and Water Molecules Confined within Dense Clay Sediments" Magnetochemistry 3, no. 4: 35. https://doi.org/10.3390/magnetochemistry3040035




