Statistical Modeling Procedures for Rapid Battery Pack Characterization

Abstract

As lithium-ion battery (LIB) cells degrade over time and usage, it is crucial to understand their remaining capacity, also known as State of Health (SoH), and inconsistencies between cells in a pack, also known as cell-to-cell variation (CtCV), to appropriately operate and maintain LIB packs. This study outlines efforts to model pack SoH and SoH CtCV of nickel-cobalt-aluminum (NCA) and lithium-iron-phosphate (LFP) battery packs consisting of four cells in series using pack-level voltage data. Using small training data sets and rapid testing procedures, partial least squares regression (PLS) models were built and achieved a mean absolute error of 0.38% and 1.43% pack SoH for the NCA and LFP packs, respectively. PLS models were also built that correctly categorized the packs as having low, medium, and high-ranked SoH CtCV 72.5% and 65% of the time for the NCA and LFP packs, respectively. This study further investigates the relationships between pack SoH, SoH CtCV, and the voltage response of the NCA and LFP packs. The slope of the discharge voltage response of the NCA packs was shown to have a strong correlation with pack dynamics and pack SoH, and the lowest SoH cell within the NCA packs was shown to dominate the dynamic response of the entire pack.

1. Introduction

Lithium-ion batteries (LIBs) have become an increasingly integral technology world-wide due to their vast array of applications. Many products ranging from the size of a cell phone to electric vehicles (EVs) and even utility-scale energy storage increasingly rely on LIB technology for their ability to store and provide energy and power [1,2]. Over time and usage, the health of LIBs degrade due to a variety of mechanisms [3,4,5,6]. Battery state of health (SoH) is a critical parameter that must be assessed throughout the life of a LIB to ensure their safe and proper usage.

Accurate assessment of LIB SoH can be challenging based on the limits imposed by their end use. Depending on the application, methods for SoH assessment may be constrained in terms of the timeliness required for SoH estimates, access to data or equipment, and computational resources available. The methods most commonly cited in the LIB SoH estimation literature may be loosely classified into four broad categories, including electrochemical models, empirical models, incremental capacity analysis (ICA)-based models, and data-driven models [7]. Electrochemical models can provide highly accurate SoH estimations; however, these models generally require significant computation and a large number of parameter assumptions and optimization [7,8,9]. Empirical methods can achieve reasonable SoH estimation accuracy with low computational effort, though producing the requisite amount of empirical data for these methods to function effectively may require an exorbitant amount of time and effort [7]. ICA methods allow for accurate SoH evaluations that provide information about specific internal cell degradation mechanisms, but long testing times are required and results are highly sensitive to measurement noise [10,11,12]. Some of the most precise SoH models are data-driven, which include highly robust data processing procedures like artificial neural networks or support vector machines [8,13,14]. However, these high fidelity models generally involve significant computational resources relative to other modeling methods and often require historical battery use data sets [8,10,15].

Though the LIB SoH modeling literature is quite robust, the significant majority of published research focuses on modeling at the cell, and notably not pack level [7,9,10,11,13,16]. Commonly, LIBs are required to be connected in series and/or parallel packs in order to serve the proper energy and power requirements of their end use. This limits the real-world applicability of cell-level studies, as issues with highly computational and burdensome SoH estimation methods and errors at the cell level compound significantly at the pack level. Nevertheless, many articles currently published looking at pack-level SoH estimations require measurements and modeling at the cell level that are then aggregated into one overall pack model [17,18,19,20,21,22]. Of the few published models relying on pack-level data, many require massive amounts of historical pack usage data and utilize powerful computing methods that may not be available for all battery modeling applications [23,24,25,26]. More studies are needed to contribute to the LIB modeling literature that provide accurate SoH estimations via the use of pack-level data and computationally efficient methods.

Another major difficulty in quantifying the SoH of a battery pack is that all cells within a pack may not degrade equally or in the same way over time. The variations of cell parameters within a pack, such as SoH, state of charge (SoC), or internal resistance, is often referred to as cell-to-cell variation (CtCV) [17,18]. CtCV in a pack that primarily occurs due to manufacturing inconsistencies of the cells or inconsistency in usage conditions, such as SoC range of operation or thermal distributions within a pack [17,18,27,28,29,30,31]. CtCV may cause electrical and/or thermal stresses on the LIB packs, which can adversely affect their safety and efficiency [32,33]. To alleviate these issues, an EV’s or energy storage system’s (ESS) battery management system (BMS) may perform cell balancing to address SoC imbalances within a pack [34,35,36]. This cell balancing does little to address other causes of CtCV; however, there is almost certainly a divergence of cell parameters over time.

In light of the safety and efficiency issues that arise from CtCV, the detection and modeling of pack inhomogeneities is also of great interest being studied in the LIB literature. Apart from assessing individual cell parameters such as cell SoH or internal resistance, several studies employed ICA methods to detect variation among cells in a pack [37,38]. These methods may be effective to detect CtCV but still share the same deficiencies in timeliness and measurement sensitivity, as described previously. Other studies implemented electrochemical impedance spectroscopy (EIS) to detect CtCV [38,39], but this incurs high costs associated with testing equipment and often requires long testing procedures [10,12,40]. Further exploration into methods that can successfully detect CtCV would provide great value to the LIB modeling literature.

This paper details efforts taken to respond to the dearth of battery pack SoH models that solely utilize the pack-level data, and in addition, provides insight into the assessment of CtCV. The models built for this study do not require historical battery pack usage data and use relatively small data sets, quick testing procedures, and computationally inexpensive modeling methods. The following sections detail models built using empirical statistical methods that rely on the pack-level voltage measurements of series packs to estimate pack SoH and SoH CtCV.

2. Materials and Methods

2.1. Experimental Setup

LIB packs consisting of four cells in series were formed and tested for this study. Battery voltages were measured, and current pulses were applied to the experimental battery packs using an Arbin Instruments BT-2043 Battery Test System. Series packs consisting of four cells were chosen due to the voltage limits of the Arbin system.

Capacity tests were performed to characterize the initial SoH of 2.5 Ah NCA and 1.5 Ah LFP 18,650 cylindrical cells. For the purposes of this paper, the SoH of a battery cell and battery pack is defined in terms of capacity fade by Equations (1) and (2), respectively:

$$Cell SoH (\%)=\frac{Q}{Q_r}\times 100\%$$

(1)

$$Pack SoH \left(\%\right)=\frac{\sum _{i=1}^n\left(Q_i\right)}{\sum _{i=1}^n\left({Q_r}_i\right)}$$

(2)

where Q is defined as the at-present Ah capacity, Q_r is the nominal or rated capacity of a cell in Ah, and n is the number of cells in a pack. In practice, most of the BMSs in EVs and ESSs utilize passive cell balancing techniques that limit pack capacity to that of the weakest cells within a pack [19,20,36,41,42]. Therefore, pack SoH is often defined solely in terms of the most degraded cells within a pack, limiting information gathered regarding the health of other battery cells. Thus, modeling pack SoH in terms of all the cells within a pack, such as in Equation (2), is useful to fully understand the overall health of a pack.

For each cell chemistry, several cells were cycled to degrade their capacities to four SoH setpoints. Four cells were cycled to approximately 80%, 85%, and 90%, and five were cycled to approximately 95% SoH for each chemistry, totaling 17 experimental cells per chemistry. 80% was chosen as the minimum cell SoH used due to the fact that EV battery packs are often retired once they degrade to 80% SoH [7,12,25,43], and an EV’s pack SoH is often defined by its lowest capacity cells [19,20]. Experimental cells were assembled to form packs that ranged from a pack SoH of 80% (four cells at 80% SoH) to 95% (four cells at 95% SoH) in increments of 1.25% SoH. For each pack SoH setpoint, except for 80% and 95%, there were a multitude of cell SoH combinations that could be used to form a pack. For instance, a pack with four cells at 85% SoH would have the same pack SoH as a pack with two cells at 90% and two cells at 80% SoH. The number of cells degraded to each setpoint was chosen to allow redundancy to improve the robustness of models and provide the ability to produce various SoH CtCV at each pack SoH setpoint.

In pursuit of increasing the accuracy of the models, the goal was to administer testing procedures that would elicit substantially different pack voltage responses to current pulses among different pack SoH and SoH CtCV. All cells were charged to 5% SoC before testing due to the results published by [44] that showed a larger divergence of differently aged cells’ SoC-OCV curves for LFP cells at low SoC ranges. A study performed by Nikolian et al. [45] also showed a high battery parameter divergence at low SoCs for NMC cells, which have been shown to exhibit similar voltage behavior to NCA batteries [46]. A 5% SoC also corresponds to a steeper portion of SoC-OCV curves for both chemistries [47], which would provoke more substantial pack voltage responses to applied current.

Figure 1 shows the test profile of current pulses applied to the experimental packs. It should be noted that the total Ah charged during the 10 s 2C pulse were equivalent to the Ah removed during the 80 s 0.25C discharge pulse. This ensured a 5% SoC was maintained among the cells. The choice of pulse profile was due to the safety constraints of the batteries as well as the desire to produce enough of a divergence in the voltage response of the different pack types in a short amount of time. Figure 2 shows the 3D printed test fixture that was used to quickly form and test the experimental battery packs.

2.2. Modeling

2.2.1. Data Setup and Processing

There were a total of 140 pulse tests conducted on a variety of packs with different pack SoH and SoH CtCV for each of the NCA and LFP chemistries. The 140 tests were split into 100 tests for training the models and 40 tests for validation (“testing data set”). The 100:40 ratio of training to testing data is based on observations in empirical studies which have shown that accurate models can be optimally trained with a reduced risk of over-fitting when the data is split in a ratio of 70–80% for training and 20–30% for testing [48].

The voltage data for each of the 140 tests was recorded and then the respective at-rest pack voltage was subtracted from all data points within the test. This made the voltage response used to train and test the models the change in voltage from rest, and not the absolute voltage of the packs. All modeling was performed using RStudio software [49] version 2022.07.1.

Much of the post-processing of the experimental results explored the relationships between various battery parameters and pack voltage response. These relationships were primarily identified by calculating the Pearson correlation coefficient [50] (ρ) and partial correlations [51] between variables. For reference, ρ is a statistical measure of the strength of a linear relationship between two variables. The maximum ρ value of 1 indicates a perfect positive linear relationship between two variables. Inversely, the minimum ρ value of −1 indicates a perfectly negative linear correlation. Considerations for what is considered a strong, moderate, or weak correlation is somewhat subjective and application-based, but the closer ρ is to 1 or −1, the stronger the linear relationship is between two variables. For more information regarding the Pearson correlation coefficient, see [50]. A partial correlation similarly describes the relationship between two variables, but also controls for the influence of a third confounding variable. Partial correlations are necessary to remove the influence of a confounding variable on the two variables whose direct relationships are being examined. For more information on partial correlations, see [51].

2.2.2. Model Selection and Parameters

Amongst the various SoH modeling methods used in the literature, this study leveraged empirical models based on pulse tests. Pulse tests are a common testing procedure that have been shown to produce sufficient data in a short timespan to allow various empirical and data-driven models to accurately estimate SoH [11,52,53,54,55]. Relative to data-driven models, which generally require a large amount of data and computational resources [13], empirical models are more suitable for smaller data sets and there are certain modeling techniques which can be implemented swiftly and easily.

There are a number of different types of empirical models, ranging from simple ones, such as linear regression, to more complicated ones, such as general additive models. For this study, a partial least squares (PLS) regression model framework was selected. In short, PLS regression is a modeling technique that is used to transform collinear variables (e.g., voltage response measurements) into uncorrelated components (i.e., “latent variables”) that are maximally correlated with a regression response variable (e.g., pack SoH). The PLS algorithm estimates regression coefficients for these components in an equation that predicts the response variable. For more information on PLS, see [56].

The “variables” of the model consisted of the voltage response measurements for each pack at each second of the 170 s test. The two main factors that favored the use of PLS models were the fact that there are more variables (170) than the number of observations (100) and there is a large degree of collinearity between the voltage responses at different times in the test [56].

Beyond pack SoH, additional modeling of the SoH CtCV of the packs was performed. As a measure of SoH CtCV, the standard deviation of cell SoH within a pack was modeled using the same variables as the pack SoH model. The pack standard deviation as well as PLS regression equations for pack SoH and pack standard deviation were as follows:

$${\sigma }_{pack}(\%)=\sqrt{\frac{\sum _{i=1}^n{\left(x_i-\mu \right)}^2}{n}}$$

(3)

$$Pack SoH={\beta }_0+{\beta }_1{V}_1+{\beta }_2{V}_2,\dots {{\beta }_{169}V}_{169},+{\beta }_{MinCell}\cdot MinCell$$

(4)

$${\sigma }_{pack}={\beta }_0+{\beta }_1{V}_1+{\beta }_2{V}_2,\dots {{\beta }_{169}V}_{169},+{\beta }_{MinCell}\cdot MinCell$$

(5)

where ${\sigma }_{pack}$ is defined as the pack standard deviation, n is the number of cells in the pack (i.e., 4), $x_i$ is an individual cell SoH, $\mu$ is the average cell SoH within a pack, V is the voltage response at a given second denoted in the subscript, and “MinCell” is the minimum cell SoH within a pack. The $\beta$ variables are coefficient values solved for via PLS regression, which is then applied to the new data (i.e., testing data set) to produce predictions of ${\sigma }_{pack}$ or pack SoH.

Models predicting pack SoH and ${\sigma }_{pack}$ for both chemistries were designed both with and without the inclusion of the MinCell variable. This was for several reasons. Firstly, in efforts to produce a model as simple as possible, the efficacy of solely using pack terminal voltage data (i.e., not including MinCell) was explored. Secondly, comparing models with and without MinCell would quantify the significance of including the impactful cell that often defines the overall pack energy and power capabilities.

2.2.3. Model Validation

The number of PLS latent variables selected in all final models were determined based on the minimum root mean squared error (RMSE) found using leave-one-out cross-validation [57] (LOOCV) on models containing 0 through 20 components. The final accuracy of the models was determined by applying the model trained on the training data set onto the testing data set and reporting the mean absolute error (MAE), RMSE, and maximum absolute error (MaxAE). Additionally, for increased interpretability, the standard deviations of the packs were categorized into low, medium, and high (L/M/H) standard deviation packs.

L/M/H categorization was performed by dividing the training set packs’ standard deviations into terciles. Packs with standard deviations in the lower third of all the training pack standard deviations were defined as having a “low” standard deviation and so on for the “medium” and “high” standard deviation packs. The accuracy of the standard deviation models was also reported as a function of how often the models’ predictions on the testing data sets correctly corresponded to their L/M/H ranking. The models did not directly predict a pack’s L/M/H classification, however. For example, if the lowest tercile of the training data set was from 1% to 3%, and the model predicted a testing pack’s standard deviation as 4% (corresponding to a medium ranking) when the testing pack’s actual standard deviation was 2% (corresponding to a low ranking), the prediction would be considered incorrect. If 30 out of 40 packs in the testing data set were correctly categorized in the proper L/M/H rankings, the model would be reported to have an accuracy of 75%.

The overall model building and validation procedures used for this study are summarized in Figure 3. The initial data collection step shown in the figure was performed twice, once for the NCA packs and once for the LFP packs, totaling an overall 280 experimental tests used for this study. Then, for each chemistry, the remaining model building and validation steps were performed four times. Two pack SoH models were built and validated that either included or excluded the MinCell variable, and two SoH CtCV models were built with and without the MinCell variable.

3. Results and Discussion

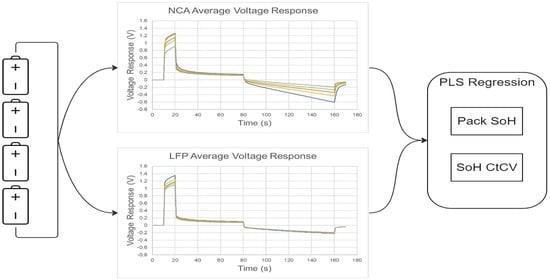
3.1. Voltage Response vs. Pack SoH

The average voltage response of packs with various pack SoH setpoints is illustrated in Figure 4 and Figure 5. Both the NCA and LFP chemistries show significant deviations in voltage response across the various pack SoH setpoints during the test profile. The voltage response of the packs can be attributed generally into three categories: a change in OCV due to a change in SoC, an immediate voltage jump from a change in the applied current due to ohmic resistance, and the dynamic voltage response of the cells, which is often modeled as resistor–capacitor pairs in battery equivalent circuit models [58]. The extent to which these mechanisms play a role in the voltage response of NCA and LFP batteries varies and is exhibited in the differences between Figure 4 and Figure 5.

There are several similarities, however, shown among the voltage responses of the different chemistries. Firstly, a close examination of Figure 4 and Figure 5 shows the NCA and LFP packs having a very small amount of voltage deviation after an extended rest period (near 80 s into the test). This would allude to the voltage changes between packs in OCV due to the SoC change being minimal for both chemistries. Next, Figure 4 and Figure 5 show a variation between pack SoH setpoints in immediate voltage changes as the current is applied or removed during seconds 10, 20, 80, and 160. This exemplifies the inverse relationship between ohmic resistance and SoH for NCA and LFP batteries, which is supported by the literature [59,60]. Calculation of the ohmic resistance of the packs provided further evidence of the relationships illustrated between SoH and ohmic resistance, with statistically significant (95% confidence level) [50] ρ values of −0.54 and −0.68 for the NCA and LFP packs, respectively.

The most glaring differences between the chemistries occurs during the extended low-current discharge from seconds 80 to 160. The NCA packs show a wide deviation in voltage response during this time, while the LFP packs show minimal differences amongst the different pack SoH setpoints. This is explained via the calculated correlation coefficient values for pack SoH and a pack’s time constant (a proxy for pack dynamics), ${\tau }_{pack}$. Time constant values at the pack and cell level were determined by applying 10 s 2C charge pulses and calculating the amount of time it took for the voltages to degrade (following instantaneous voltage drops from the change in the current) approximately 63% towards their at-rest values. The ρ value describing the relationship between pack SoH and ${\tau }_{pack}$ was 0.91 for the NCA packs, while this relationship was statistically insignificant for the LFP packs. Additional analysis showed that the absolute slope of the voltage response from seconds 85 to 160 for the NCA packs has a very strong correlation to ${\tau }_{pack}$, with a ρ value of −0.90. In contrast, this relationship showed very weak for the LFP packs with a corresponding ρ value of 0.28. In summary, the slope of the pack voltage response closely represents the pack dynamics.

3.2. Pack SoH Model Results

The accuracy of the NCA and LFP SoH models’ predictions for the testing data sets are reported in

Table 1. Pack SoH model results for NCA and LFP packs. Mean Absolute Error (MAE), Root mean squared error (RMSE), and Maximum Absolute Error (MaxAE) are reported. The accuracy of models both including and excluding the “MinCell” variable are reported for both chemistries.

Pack SoH Model	MAE (% SoH)	RMSE (% SoH)	MaxAE (% SoH)
NCA (MinCell Included)	0.38	0.47	1.09
LFP (MinCell Included)	1.43	1.92	6.58
NCA (MinCell Excluded)	0.41	0.51	1.12
LFP (MinCell Excluded)	8.50	10.99	26.67

. Results show that the NCA pack SoH model is substantially more accurate when compared to the LFP model. This appears reasonable, considering the NCA packs had a much more diverse voltage response amongst different pack SoH compared to the LFP packs. With a stronger association between pack SoH and pack voltage response, the model was able to leverage these relationships to produce higher accuracy estimates.

Including MinCell in the pack SoH models drastically improved the accuracy for the LFP packs and only marginally improved the NCA pack SoH model. For the LFP packs, including MinCell was required to meet reasonable accuracy. Even so, the ability to produce an accurate model using the data from both the pack voltage terminals and the weakest cell in the pack is substantially less burdensome than modeling the SoH of all the individual cells in the pack. In practical applications, the pack performance-limiting cell(s) can be easily identified based on the weakest cells reaching the upper and lower cutoff voltages first during cycling. The added computational resources required for the SoH estimation of the weakest cells may be reasonable to accommodate for a BMS, especially considering the simplicity of the PLS estimation procedure. The NCA pack SoH model that solely relied on the pack-level voltage data was extremely accurate. Results indicate that these modeling procedures may work especially well for cell chemistries in which dynamic behavior is strongly affected by cell aging (e.g., NMC [61]) and may not require any information at the cell level.

The under 3 min testing time makes these SoH estimation procedures immensely advantageous over other testing methods, such as EIS or ICA. The ease of data collection and lack of reliance on historical battery usage data provides additional advantages over pack-level SoH models found in the literature and various data-driven methods. While the size of the experimental packs pale in comparison to that of an ESS or EV pack, the results and methodology outlined in this study provide a roadmap for further experimentation. Moreover, given the modularity of large battery packs that are a combination of smaller battery strings and modules, these techniques may offer a critical simplification to estimate SoH at resolutions above the cell level.

3.3. Voltage Response vs. SoH CtCV

The average voltage response of packs with the same SoH setpoints, but different standard deviation rankings (i.e., L/M/H), was investigated and exemplified in Figure 6 and Figure 7.

While the relative magnitude of the voltage response was seemingly random between L/M/H packs for both chemistries across multiple pack SoH setpoints (as demonstrated between Figure 6 and Figure 7), one parameter consistently behaved in accordance with pack ranking for the NCA packs. For the NCA packs, regardless of which pack ranking had experienced the largest average voltage response during the 10 s charging pulse, the absolute slope of the pack voltage response during the discharge pulse was always in rank order. Specifically, the smallest magnitude voltage response slope corresponded to the “Low” standard deviation ranked packs (i.e., the most homogenous packs), the next highest were the “Medium” packs, and the steepest slopes corresponded to the “High” standard deviation packs. This relationship was always true during the discharge pulses across all pack SoH setpoints where each L/M/H ranking was represented. This relationship did not extend to the LFP packs, most likely due to the aforementioned weak relationship between the discharge slope and LFP pack dynamics.

In order to further investigate the relationships between the pack voltage response and pack standard deviation (i.e., SoH CtCV), it was necessary to isolate and parse out the relationships between the pack voltage response and the pack SoH established in Section 3.1. To that end, partial correlations were calculated between various pack parameters, controlling for the parameters’ relationships to pack SoH. Key findings of this analysis are demonstrated in

Table 2. Partial correlation coefficient values for NCA and LFP packs, controlling for pack SoH interactions. (NSS = Not statistically significant at 95% confidence level).

Partial Correlations	NCA	LFP
$\rho$ (${\tau }_{pack}$, ${\tau }_{MinCell}$)	0.68	0.26
$\rho$(${\tau }_{pack}$, $\tau$ of 2nd lowest SoH cell in pack)	NSS	0.21
$\rho$(${\tau }_{pack}$, $\tau$ of 3rd lowest SoH cell in pack)	−0.32	0.31
$\rho$(${\tau }_{pack}$, $\tau$ of highest SoH cell in pack)	−0.50	NSS
$\rho$(${\sigma }_{pack}$, ${\tau }_{MinCell}$)	−0.65	NSS
$\rho$(${\sigma }_{pack}$, ${\tau }_{pack}$)	−0.70	NSS
$\rho$(${\sigma }_{pack}$, Pack ohmic resistance)	0.02	NSS
$\rho$(|Discharge slope|, ${\sigma }_{pack}$)	0.24	−0.23
$\rho$(|Discharge slope|,${\tau }_{pack}$)	−0.41	0.25
$\rho$(|Discharge slope|,${\tau }_{MinCell}$)	−0.56	0.20
$\rho$(|Discharge slope|, Pack ohmic resistance)	NSS	NSS

.

Results showed that for the NCA packs, the lowest SoH cell (i.e., MinCell) dominated the overall pack’s dynamics, with a partial correlation $\rho$ value describing the relationship between ${\tau }_{pack}$ and ${\tau }_{MinCell}$ of 0.68. This correlation was much stronger compared to ${\tau }_{pack}$ and any other cell’s time constant. This therefore may explain the moderately strong relationship found between ${\sigma }_{pack}$ and ${\tau }_{MinCell}$, which had a partial $\rho$ value of −0.65 for the NCA packs. Considering packs with a higher standard deviation will inherently have a lower minimum cell SoH compared to homogenous packs of the same total SoH, the dynamics of the packs will be different due to the substantial influence of the minimum SoH cell. Therefore, the time constant of a pack can offer insight into the SoH CtCV of the pack relative to other packs of the same total SoH. Future studies should explore further leveraging these intra-pack relationships for accurate CtCV detection models.

Regarding the voltage response slope and the standard deviation relationship observed, the partial $\rho$ value showed a weak relationship between the two variables with a value of only 0.24 for the NCA packs. Given the moderately strong $\rho$ value for the NCA packs’ absolute discharge slope and ${\tau }_{MinCell}$ (controlling for pack SoH) of −0.56, it would appear that while ${\tau }_{MinCell}$ correlates with ${\sigma }_{pack}$ and discharge slope individually, ${\sigma }_{pack}$ and the discharge slope are relatively independent of one another directly. All of the relationships described in this section were weak or statistically insignificant for the LFP packs, most likely due to the weak relationship between cell dynamics and the SoH described in Section 3.1.

3.4. Standard Deviation Model Results

Table 3. Pack SoH model results for NCA and LFP packs. Mean Absolute Error (MAE), Root mean squared error (RMSE), and Maximum Absolute Error (MaxAE) are reported. The accuracy of models both including and excluding the “MinCell” variable are reported for both chemistries. Categorization Accuracy refers to the percentage the model correctly estimated if a pack was in the Low, Medium, or High standard deviation ranking.

${\mathit{\sigma }}_{\mathit{p}\mathit{a}\mathit{c}\mathit{k}}$ Model	MAE (% SoH)	RMSE (% SoH)	MaxAE (% SoH)	Categorization Accuracy (%)
NCA (MinCell Included)	0.69	0.84	1.83	72.50
LFP (MinCell Included)	0.77	1.02	2.35	65.00
NCA (MinCell Excluded)	1.43	1.70	4.74	43.59
LFP (MinCell Excluded)	12.62	15.14	31.18	20.00

details the accuracy of the pack standard deviation models for both chemistries. Without the inclusion of MinCell, both models performed extremely poorly in properly categorizing the pack standard deviation. The inclusion of the minimum SoH cell increased the accuracy of both substantially. This is likely due to the fact that the training data for the standard deviation models was the same as the SoH models. If the information present in the data alluded to the overall pack SoH, then the inclusion of the SoH of one of four cells, and specifically the minimum SoH cell, provided enough data to produce a modestly accurate categorization. The NCA model was more accurate, perhaps primarily due to the higher accuracy of NCA pack SoH estimation, though the relationship between the dynamic voltage response and ${\sigma }_{pack}$ being stronger in the NCA packs than the LFP packs may have played a role as well. For both MinCell-inclusive models, no “High” standard deviation packs were predicted as “Low” and vice versa, but packs were often misclassified as having a “Medium” standard deviation. Results indicate that pack-level voltage data and the minimum SoH cell in a pack can provide a basic understanding of SoH CtCV. Experimentation on larger packs will need to be undertaken to establish the limits of this premise.

Further study of the relationship between the pack voltage response and pack SoH and SoH CtCV will be required to produce more accurate testing and modeling procedures. Each model’s estimation error may be reduced with further optimization of the pulse test profile, either via the systematic empirical testing of packs with different pulse profiles or the theoretical modeling of pack voltage responses that are fed into the PLS algorithm for pulse profile selection.

Provided the proper testing equipment is available, future work should apply these testing and modeling procedures on larger packs. It is reasonable to assume that placing more cells in series would increase model prediction errors due to the added complexity of a larger pack’s voltage response. Exploring the extent to which model accuracy remains reasonable on larger packs would provide valuable insight regarding the practical limitations of these methods in estimating pack SoH and detecting SoH CtCV.

4. Conclusions

The differences in voltage response between the NCA and LFP packs were most acutely exhibited in their dynamic voltage behavior during the extended low-current discharge. The highly dynamic behavior of the NCA packs allowed for an accurate SoH model that solely relied on the pack terminal voltage data, which produced an MAE of 0.41% SoH. The pack SoH model for the less dynamic LFP packs required the inclusion of information of a pack’s minimum SoH cell (i.e., “MinCell”) to achieve a reasonable predictive accuracy of 1.43% MAE. Results indicate the methods used in this study may be best suited for LIB chemistries for which dynamic voltage behavior is strongly influenced by SoH.

For both chemistries, the SoH CtCV models were excessively inaccurate without the inclusion of the MinCell variable as a model input. The addition of the MinCell variable produced a marginally accurate model that correctly categorized SoH CtCV 72.5% and 65% of the time for the NCA and LFP packs, respectively. Voltage data analysis showed that for the NCA packs, the minimum SoH cell within the pack dominated the overall dynamic response of the pack. This information may be leveraged for future CtCV detection techniques. No notable relationships between the LFP packs’ voltage responses and cell dynamics were observed.

The outcomes of this study provide a methodology and results for the rapid and accurate modeling of LIB pack SoH and SoH CtCV. The short length of the testing procedures, small training data set, primary usage of pack-level data, and computationally efficient modeling methods pose major advantages over other modeling practices widely used in the literature.