A Coupled Nonlinear Viscoelastic–Viscoplastic Thermomechanical Model for Polymeric Lithium-Ion Battery Separators
Abstract
:1. Introduction
2. Theoretical Background
2.1. Viscoelasticity
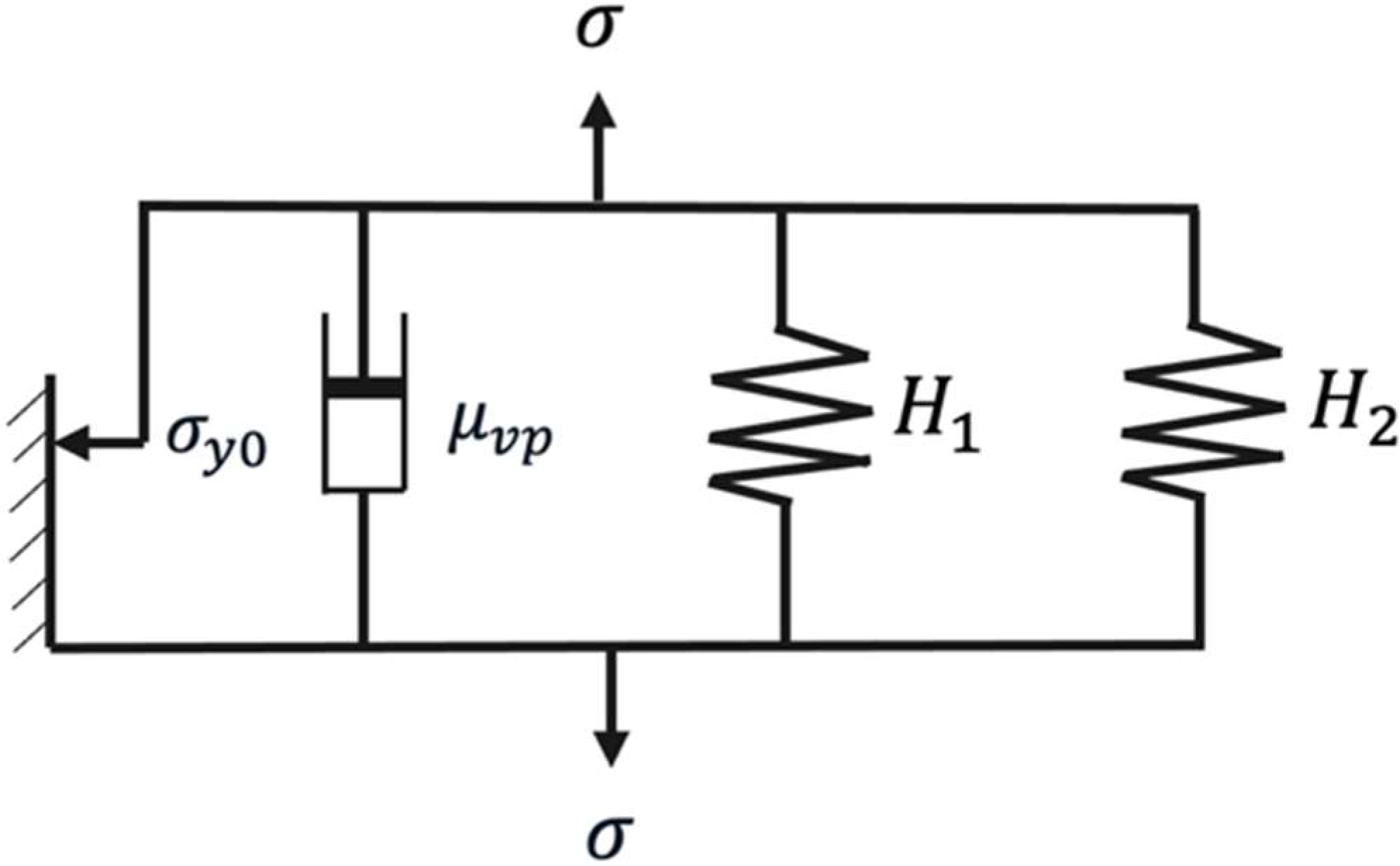
2.2. Viscoplasticity
3. Experimental Procedure
4. Model Parameter Identification
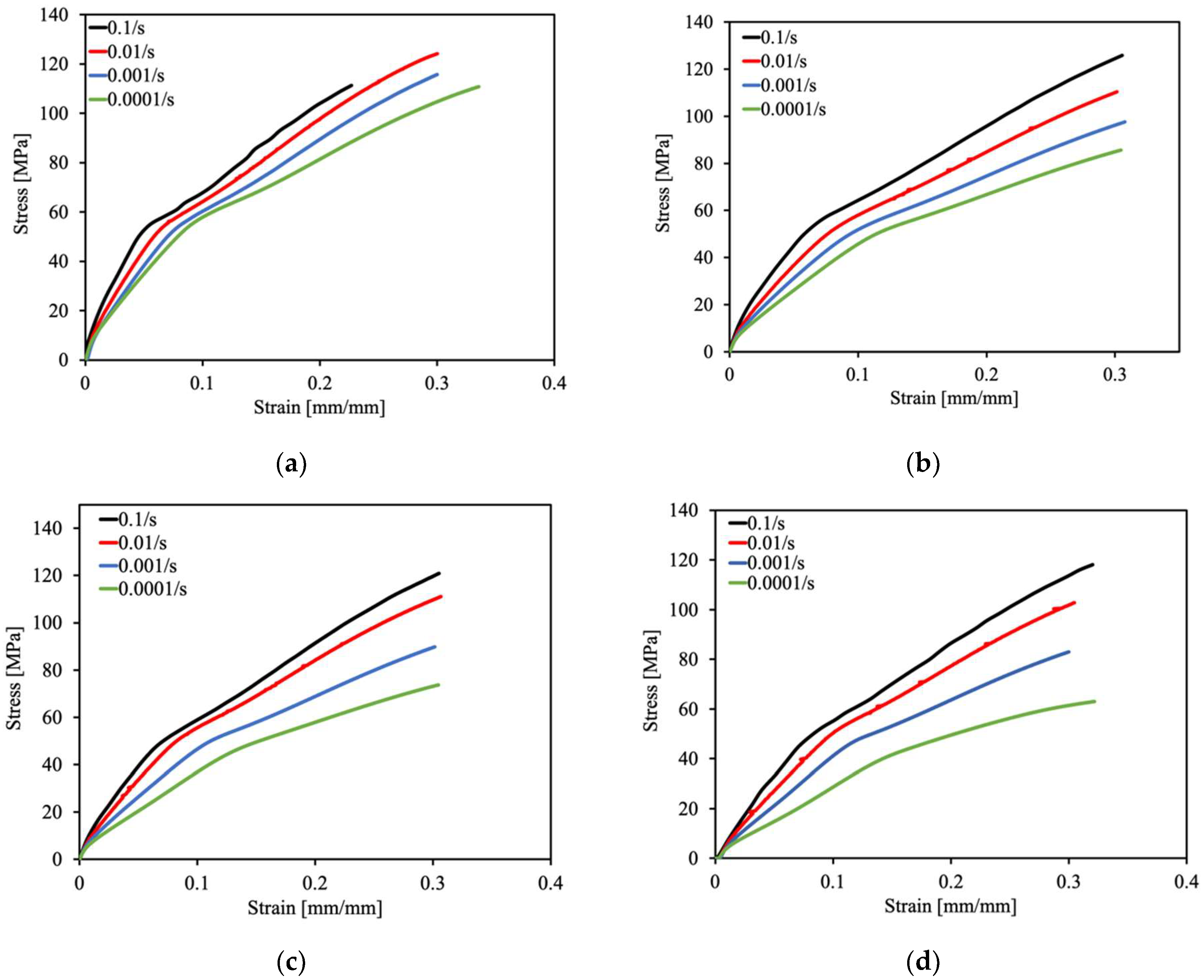
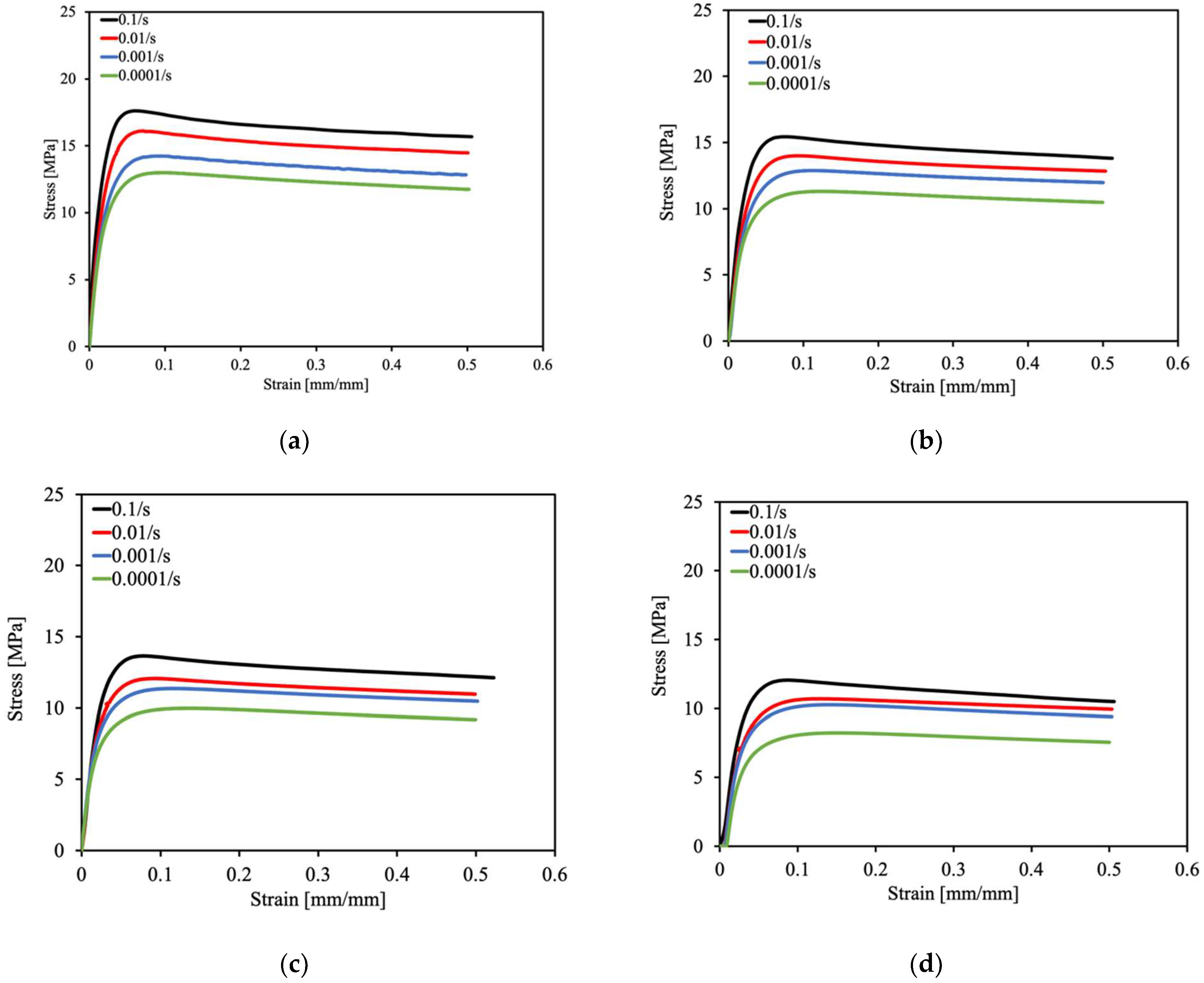
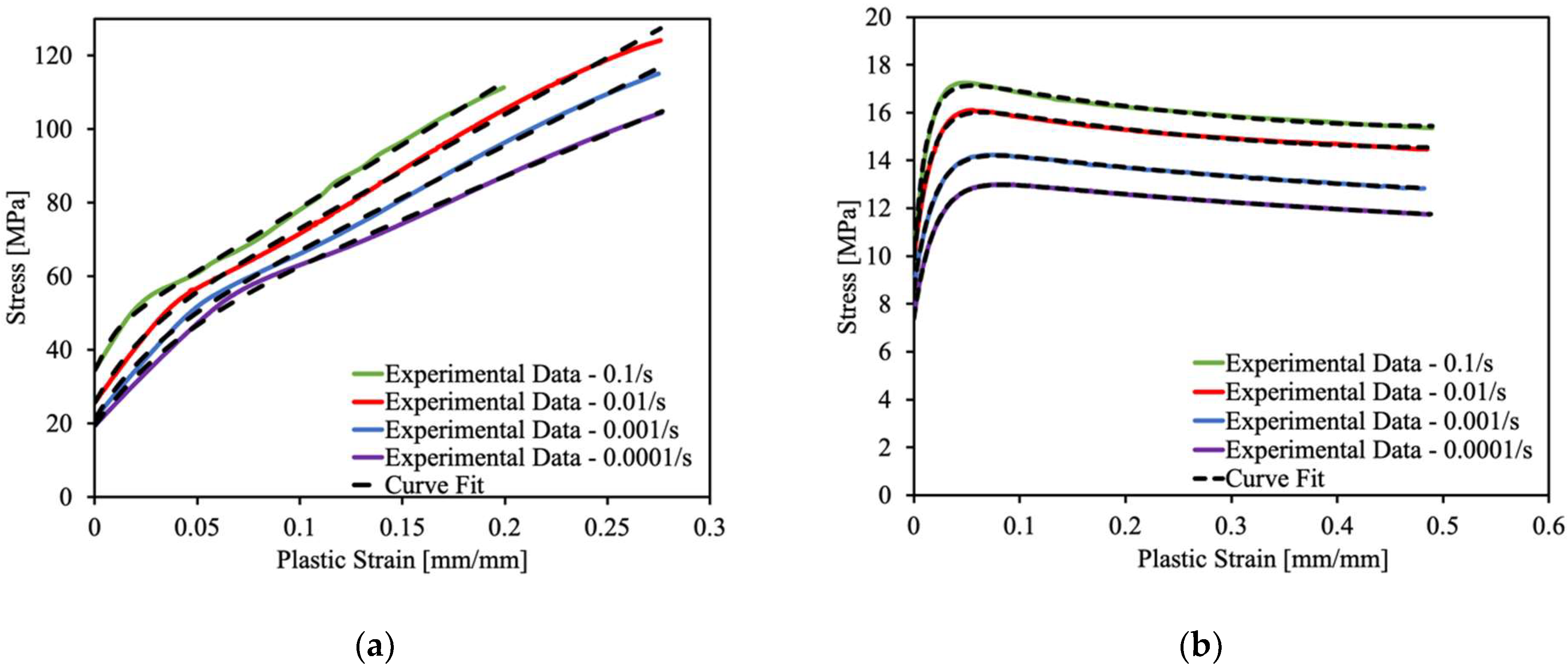
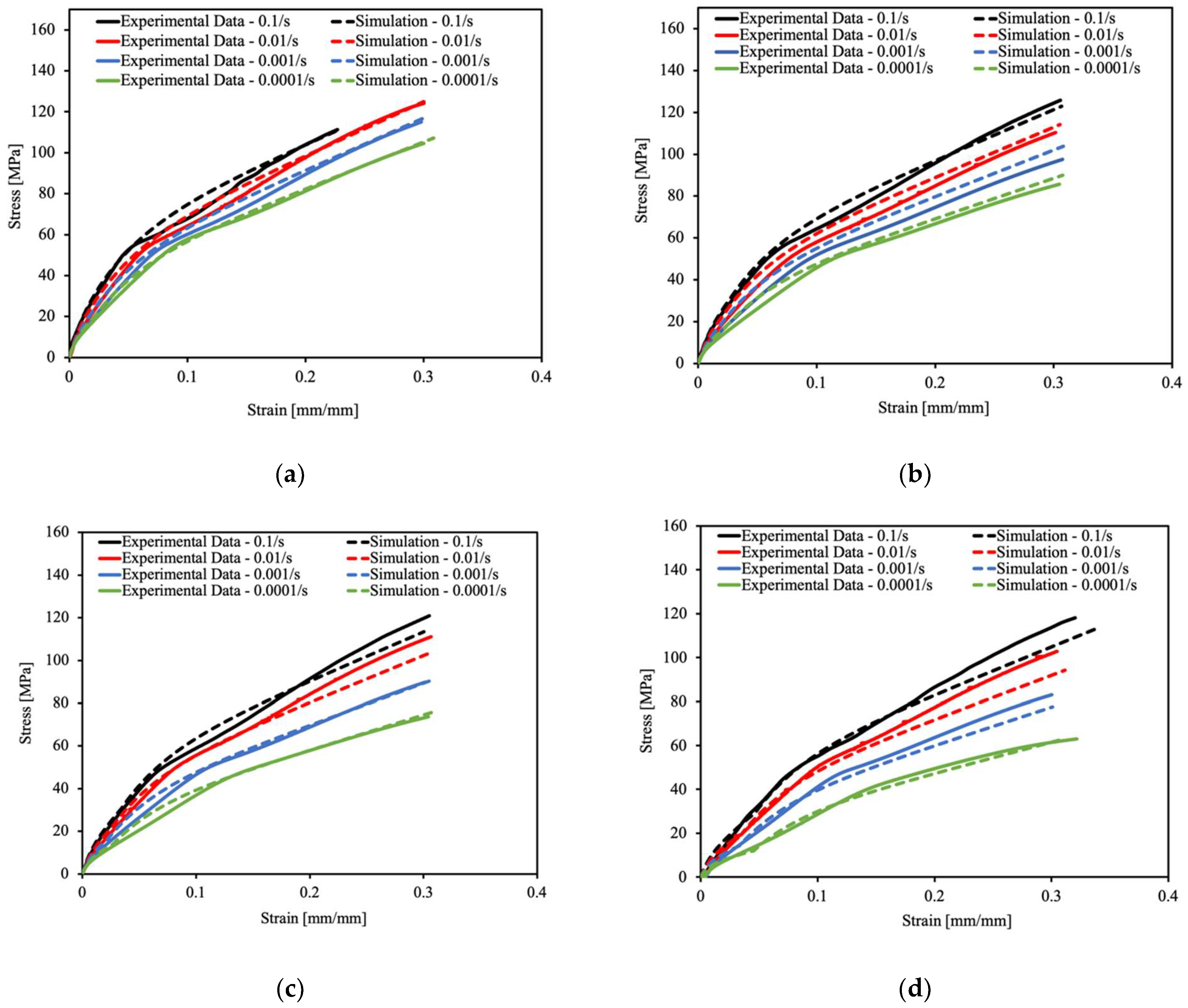
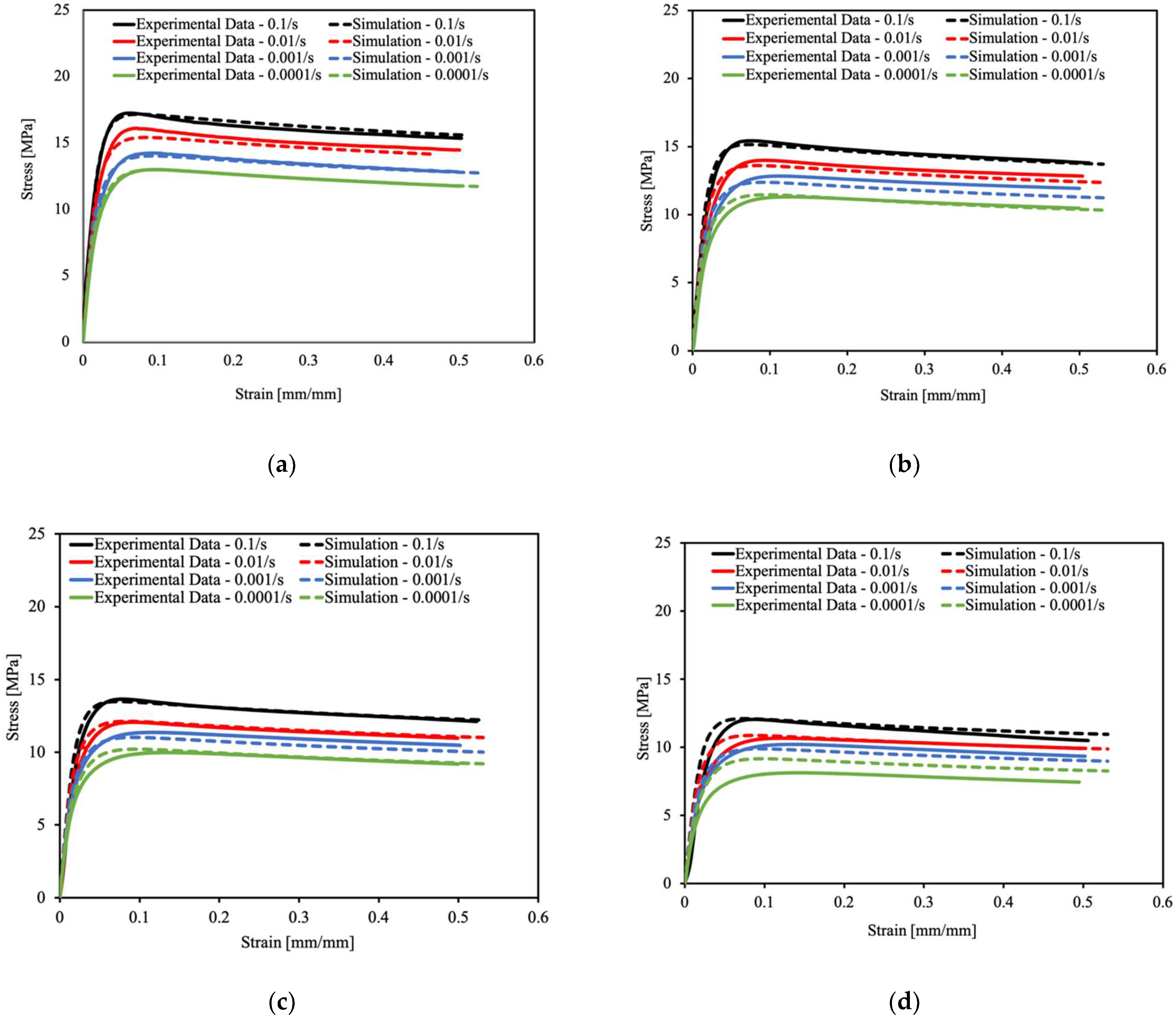
4.1. Strain-Rate-Dependent Model Parameters at the Reference Temperature
4.2. Temperature Dependence and Parameter Identification
5. Results and Discussions
5.1. Model Implementation
5.2. Biaxial Punch Simulations
5.3. Uniaxial Tensile Tests
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, B.; Jia, Y.; Yuan, C.; Wang, L.; Gao, X.; Yin, S.; Xu, J. Safety issues and mechanisms of lithium-ion battery cell upon mechanical abusive loading: A review. Energy Storage Mater. 2020, 24, 85–112. [Google Scholar] [CrossRef]
- Deng, J.; Bae, C.; Denlinger, A.; Miller, T. Progress in battery safety modeling. Prog. Energy 2022, 4, 043001. [Google Scholar] [CrossRef]
- Liu, B.; Duan, X.; Yuan, C.; Wang, L.; Li, J.; Finegan, D.P.; Feng, B.; Xu, J. Quantifying and modeling of stress-driven short-circuits in lithium-ion batteries in electrified vehicles. J. Mater. Chem. A 2021, 9, 7102–7113. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium-ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Yan, S.; Deng, J.; Bae, C.; He, Y.; Asta, A.; Xiao, X. In-plane orthotropic property characterization of a polymeric battery separator. Polym. Test. 2018, 72, 46–54. [Google Scholar] [CrossRef]
- Avdeev, I.; Martinsen, M.; Francis, A. Rate-and temperature-dependent material behavior of a multilayer polymer battery separator. J. Mater. Eng. Perform. 2014, 23, 315–325. [Google Scholar] [CrossRef]
- Xu, J.; Wang, L.; Guan, J.; Yin, S. Coupled effect of strain rate and solvent on dynamic mechanical behaviors of separators in lithium-ion batteries. Mater. Des. 2016, 95, 319–328. [Google Scholar] [CrossRef]
- Zhu, J.; Wierzbicki, T.; Li, W. A review of safety-focused mechanical modeling of commercial lithium-ion batteries. J. Power Sources 2018, 378, 153–168. [Google Scholar] [CrossRef]
- Zhang, X.; Sahraei, E.; Wang, K. Li-ion battery separators, mechanical integrity and failure mechanisms leading to soft and hard internal shorts. Sci. Rep. 2016, 6, 32578. [Google Scholar] [CrossRef]
- Cannarella, J.; Liu, X.; Leng, C.Z.; Sinko, P.D.; Gor, G.Y.; Arnold, C.B. Mechanical properties of a battery separator under compression and tension. J. Electrochem. Soc. 2014, 161, F3117. [Google Scholar] [CrossRef]
- Sheidaei, A.; Xiao, X.; Huang, X.; Hitt, J. Mechanical behavior of a battery separator in electrolyte solutions. J. Power Sources 2011, 196, 8728–8734. [Google Scholar] [CrossRef]
- Yan, S.; Deng, J.; Bae, C.; Xiao, X. Thermal expansion/shrinkage measurement of battery separators using a dynamic mechanical analyzer. Polym. Test. 2018, 71, 65–71. [Google Scholar] [CrossRef]
- Love, C.T. Thermomechanical analysis and durability of commercial micro-porous polymer Li-ion battery separators. J. Power Sources 2011, 196, 2905–2912. [Google Scholar] [CrossRef]
- Chen, J.; Hu, H.; Li, S.; He, Y. Evolution of mechanical properties of polypropylene separator in liquid electrolytes for lithium-ion batteries. J. Appl. Polym. Sci. 2018, 135, 46441. [Google Scholar] [CrossRef]
- Gor, Y.; Cannarella, J.; Leng, C.Z.; Vishnyakov, A.; Arnold, C.B. Swelling and softening of lithium-ion battery separators in electrolyte solvents. J. Power Sources 2015, 294, 167–172. [Google Scholar] [CrossRef]
- Yan, S.; Xiao, X.; Huang, X.; Li, X.; Qi, Y. Unveiling the environment-dependent mechanical properties of porous polypropylene separators. Polymer 2014, 55, 6282–6292. [Google Scholar] [CrossRef]
- Yan, S.; Deng, J.; Bae, C.; Kalnaus, S.; Xiao, X. Orthotropic viscoelastic modeling of polymeric battery separator. J. Electrochem. Soc. 2020, 167, 090530. [Google Scholar] [CrossRef]
- Ihuaenyi, R.C.; Yan, S.; Deng, J.; Bae, C.; Sakib, I.; Xiao, X. Orthotropic thermo-viscoelastic model for polymeric battery separators with electrolyte effect. J. Electrochem. Soc. 2021, 168, 090536. [Google Scholar] [CrossRef]
- Ihuaenyi, R.C.; Deng, J.; Bae, C.; Xiao, X. An orthotropic nonlinear thermoviscoelastic model for polymeric battery separators. J. Electrochem. Soc. 2023, 170, 010520. [Google Scholar] [CrossRef]
- Zhao, G.; Xi, H.; Yang, J. Transversely Isotropic Constitutive Model of the Polypropylene Separator Based on Rich–Hill Elastoplastic Constitutive Theory. J. Electrochem. Energy Convers. Storage 2021, 18, 020911. [Google Scholar] [CrossRef]
- Zhang, X.; Sahraei, E.; Wang, K. Deformation and failure characteristics of four types of lithium-ion battery separators. J. Power Sources 2016, 327, 693–701. [Google Scholar] [CrossRef]
- Xie, W.; Wu, L.; Liu, W.; Dang, Y.; Tang, A.; Luo, Y. Modelling electrolyte-immersed tensile property of polypropylene separator for lithium-ion battery. Mech. Mater. 2021, 152, 103667. [Google Scholar] [CrossRef]
- Makki, M.; Ayoub, G.; Lee, C.W. Modeling the anisotropic behavior of highly orthotropic lithium-ion batteries polymer separators. Int. J. Solids Struct. 2023, 264, 112102. [Google Scholar] [CrossRef]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials; Dover Publications, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Schapery, R.A. Nonlinear viscoelastic and viscoplastic constitutive equations based on thermodynamics. Mech. Time-Depend. Mater. 1997, 1, 209–240. [Google Scholar] [CrossRef]
- Schapery, R.A. Nonlinear viscoelastic and viscoplastic constitutive equations with growing damage. Int. J. Fract. 1999, 97, 33–66. [Google Scholar] [CrossRef]
- Lai, J.; Bakker, A. An integral constitutive equation for nonlinear plasto-viscoelastic behavior of high-density polyethylene. Polym. Eng. Sci. 1995, 35, 1339–1347. [Google Scholar] [CrossRef]
- Brusselle-Dupend, N.; Lai, D.; Feaugas, X.; Guigon, M.; Clavel, M. Mechanical behavior of a semicrystalline polymer before necking. Part I: Characterization of uniaxial behavior. Polym. Eng. Sci. 2001, 41, 66–76. [Google Scholar] [CrossRef]
- Brusselle-Dupend, N.; Lai, D.; Feaugas, X.; Guigon, M.; Clavel, M. Mechanical behavior of a semicrystalline polymer before necking. Part II: Modeling of uniaxial behavior. Polym. Eng. Sci. 2003, 43, 501–518. [Google Scholar] [CrossRef]
- Kletschkowski, T.; Schomburg, U.; Bertram, A. An endochronic viscoplastic approach for materials with different behavior in tension and compression. Mech. Time-Depend. Mater. 2004, 8, 119–135. [Google Scholar] [CrossRef]
- Zhang, C.; Moore, I.D. Nonlinear mechanical response of high-density polyethylene. Part I: Experimental investigation and model evaluation. Polym. Eng. Sci. 1997, 37, 404–413. [Google Scholar] [CrossRef]
- Zhang, C.; Moore, I.D. Nonlinear mechanical response of high-density polyethylene. Part II: Uniaxial constitutive modeling. Polym. Eng. Sci. 1997, 37, 414–420. [Google Scholar] [CrossRef]
- Peric, D.; Dettmer, W. A computational model for generalized inelastic materials at finite strains combining elastic, viscoelastic and plastic material behavior. Eng. Comput. 2003, 20, 768–787. [Google Scholar] [CrossRef]
- Wang, W.M.; Sluys, L.J.; Borst, R.R. Viscoplasticity for instabilities due to strain softening and strain-rate softening. Int. J. Numer. Methods Eng. 1997, 40, 3839–3864. [Google Scholar] [CrossRef]
- Ristinmaa, M.; Ottosen, N.S. Consequences of dynamic yield surface in viscoplasticity. Int. J. Solids Struct. 2000, 37, 4601–4622. [Google Scholar] [CrossRef]
- Carosio, A.; Willam, K.; Etse, G. On the consistency of viscoplastic formulations. Int. J. Solids Struct. 2000, 37, 7349–7369. [Google Scholar] [CrossRef]
- Heeres, O.M.; Suiker, A.S.J.; De Borst, R. A comparison between the Perzyna viscoplastic model and the consistency viscoplastic model. Eur. J. Mech. A/Solids 2002, 21, 1–12. [Google Scholar] [CrossRef]
- Zaera, R.; Fernandez-Saez, J. An implicit consistent algorithm for the integration of thermoviscoplastic constitutive equations in adiabatic conditions and finite deformations. Int. J. Solids Struct. 2006, 43, 1594–1612. [Google Scholar] [CrossRef]
- Perzyna, P. Fundamental Problems in Viscoplasticity. Adv. Appl. Mech. 1966, 9, 243–377. [Google Scholar]
- Duvaut, G.; Lions, J.L. Les Inequations en Mecanique et en Physique; Dunod: Paris, France, 1972. [Google Scholar]
- Zienkiewicz, O.C.; Cormeau, I.C. Visco-Plasticity-Plasticity and Creep in Elastic Solids—A unified numerical solution approach. Int. J. Numer. Methods Eng. 1974, 8, 821–845. [Google Scholar] [CrossRef]
- Hughes, T.J.; Taylor, R.L. Unconditionally stable algorithms for quasi-static elasto/visco-plastic finite element analysis. Comput. Struct. 1978, 8, 169–173. [Google Scholar] [CrossRef]
- Cormeau, I. Numerical stability in quasistatic elasto/viscoplasticity. Int. J. Numer. Methods Eng. 1975, 9, 109–127. [Google Scholar] [CrossRef]
- Simo, J.C.; Kennedy, J.G.; Govindjee, S. Non-smooth multisurface plasticity and viscoplasticity. Loading/unloading conditions and numerical algorithms. Int. J. Numer. Methods Eng. 1988, 26, 2161–2185. [Google Scholar] [CrossRef]
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Peric, D. On a class of constitutive equations in viscoplasticity: Formulation and computational issues. Int. J. Numer. Methods Eng. 1993, 36, 1365–1393. [Google Scholar] [CrossRef]
- Ristinmaa, M.; Ottosen, N.S. Viscoplasticity based on an additive split of the conjugated forces. Eur. J. Mech. A/Solids 1998, 17, 207–235. [Google Scholar] [CrossRef]
- Runesson, K.; Ristinmaa, M.; Mahler, L. Comparison of viscoplasticity formats and algorithms. Mech. Cohesive-Frict. Mater. 1999, 4, 75–98. [Google Scholar] [CrossRef]
- Caggiano, A.; Martinelli, E.; Schicchi, D.S.; Etse, G. A modified Duvaut-Lions zero-thickness interface model for simulating the rate-dependent bond behavior of FRP-concrete joints. Compos. Part B Eng. 2018, 149, 260–267. [Google Scholar] [CrossRef]
- Ibrahimbegovic, A.; Chorfi, L. Viscoplasticity model at finite deformations with combined isotropic and kinematic hardening. Comput. Struct. 2000, 77, 509–525. [Google Scholar] [CrossRef]
- Nedjar, B. Frameworks for finite strain viscoelastic-plasticity based on multiplicative decompositions. Part I: Continuum formulations. Comput. Methods Appl. Mech. Eng. 2002, 191, 1541–1562. [Google Scholar] [CrossRef]
- Shutov, V.; Kreißig, R. Finite strain viscoplasticity with nonlinear kinematic hardening: Phenomenological modeling and time integration. Comput. Methods Appl. Mech. Eng. 2008, 197, 2015–2029. [Google Scholar] [CrossRef]
- Kowalczyk-Gajewska, K.; Pieczyska, E.A.; Golasinski, K.; Maj, M.; Kuramoto, S.; Furutab, T. A finite strain elastic-viscoplastic model of Gum Metal. Int. J. Plast. 2019, 119, 85–101. [Google Scholar] [CrossRef]
- G’sell, C.; Jonas, J.J. Determination of the plastic behaviour of solid polymers at constant true strain rate. J. Mater. Sci. 1979, 14, 583–591. [Google Scholar] [CrossRef]
- Morin, D.; Haugou, G.; Lauro, F.; Bennani, B.; Bourel, B. Elasto-viscoplasticity behaviour of a structural adhesive under compression loadings at low, moderate and high strain rates. J. Dyn. Behav. Mater. 2015, 1, 124–135. [Google Scholar] [CrossRef]
- Múgica, J.I.; Aretxabaleta, L.; Ulacia, I.; Aurrekoetxea, J. Rate-dependent phenomenological model for self-reinforced polymers. Compos. Part A Appl. Sci. Manuf. 2016, 84, 96–102. [Google Scholar] [CrossRef]
- Schoßig, M.; Bierögel, C.; Grellmann, W.; Mecklenburg, T. Mechanical behavior of glass-fiber reinforced thermoplastic materials under high strain rates. Polym. Test. 2008, 27, 893–900. [Google Scholar] [CrossRef]
- Torres, J.P.; Frontini, P.M.; Aretxabaleta, L. Experimental characterization and computational simulations of the low-velocity impact behaviour of polypropylene. Polym. Int. 2013, 62, 1553–1559. [Google Scholar] [CrossRef]
- Johnson, R.; Cook, W.H. A constitutive model and data for materials subjected to large strains, high strain rates, high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Chen, F.; Ou, H.; Lu, B.; Long, H. A constitutive model of polyether-ether-ketone (PEEK). J. Mech. Behav. Biomed. Mater. 2016, 53, 427–433. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Rusinek, A.; Jankowiak, T.; Arias, A. Mechanical impact behavior of polyether–ether–ketone (PEEK). Compos. Struct. 2015, 124, 88–99. [Google Scholar] [CrossRef]
- Nasraoui, M.; Forquin, P.; Siad, L.; Rusinek, A. Influence of strain rate, temperature and adiabatic heating on the mechanical behaviour of poly-methyl-methacrylate: Experimental and modelling analyses. Mater. Des. 2012, 37, 500–509. [Google Scholar] [CrossRef]
- Duan, Y.; Saigal, A.; Greif, R.; Zimmerman, M.A. A uniform phenomenological constitutive model for glassy and semicrystalline polymers. Polym. Eng. Sci. 2001, 41, 1322–1328. [Google Scholar] [CrossRef]
- Zhu, H.; Ou, H.; Popov, A. A new phenomenological constitutive model for thermoplastics. Mech. Mater. 2021, 157, 103817. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Ward, I.M.; Sweeney, J. An Introduction to the Mechanical Properties of Solid Polymers; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity. An Introduction; Springer: New York, NY, USA, 2008; pp. 99–157. [Google Scholar]
- Wineman, A.S.; Rajagopal, K.R. Mechanical Response of Polymers: An Introduction; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Christensen, R.M. Theory of Viscoelasticity: An Introduction, 2nd ed.; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Schapery, R.A. On the characterization of nonlinear viscoelastic materials. Polym. Eng. Sci. 1969, 9, 295–310. [Google Scholar] [CrossRef]
- Daniel, I.M.; Ishai, O. Engineering Mechanics of Composite Materials; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Kalnaus, S.; Kumar, A.; Wang, Y.; Li, J.; Simunovic, S.; Turner, J.A.; Gorney, P. Strain distribution and failure mode of polymer separators for Li-ion batteries under biaxial loading. J. Power Sources 2018, 378, 139–145. [Google Scholar] [CrossRef]



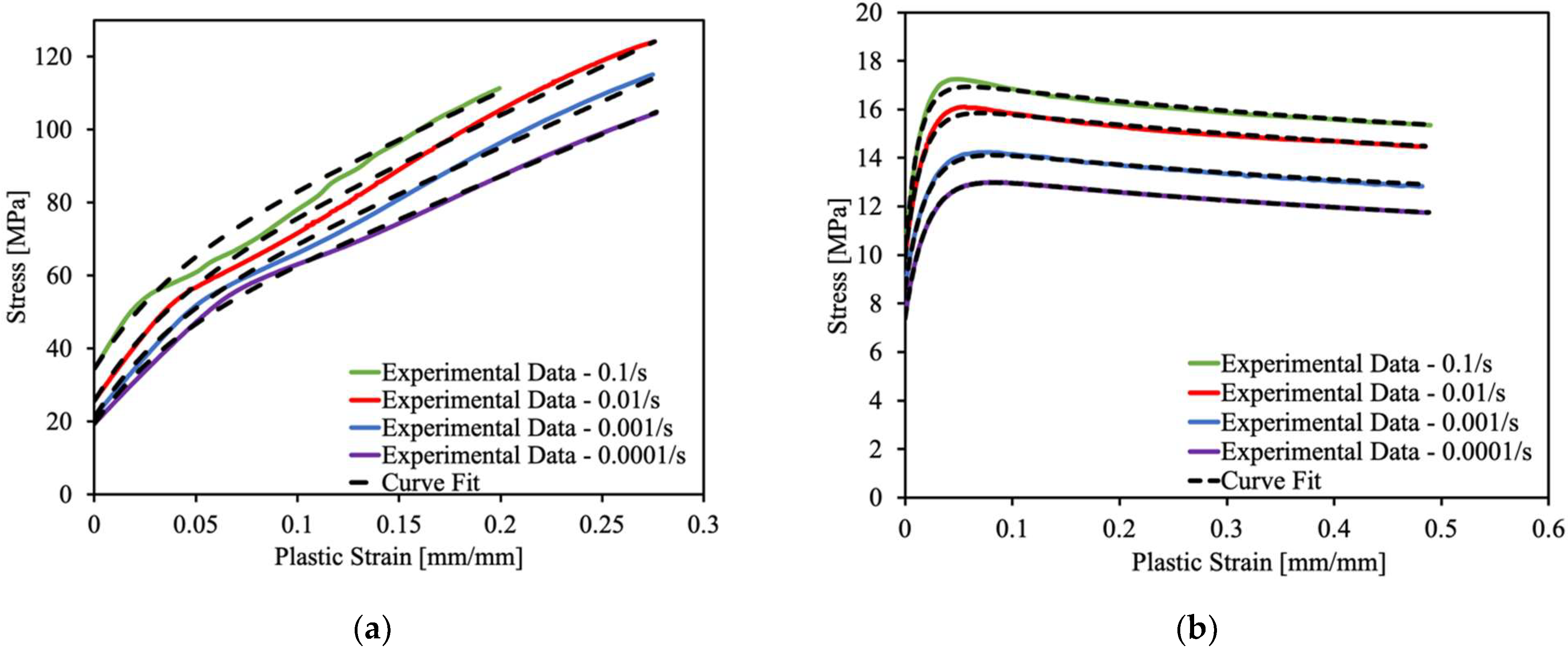
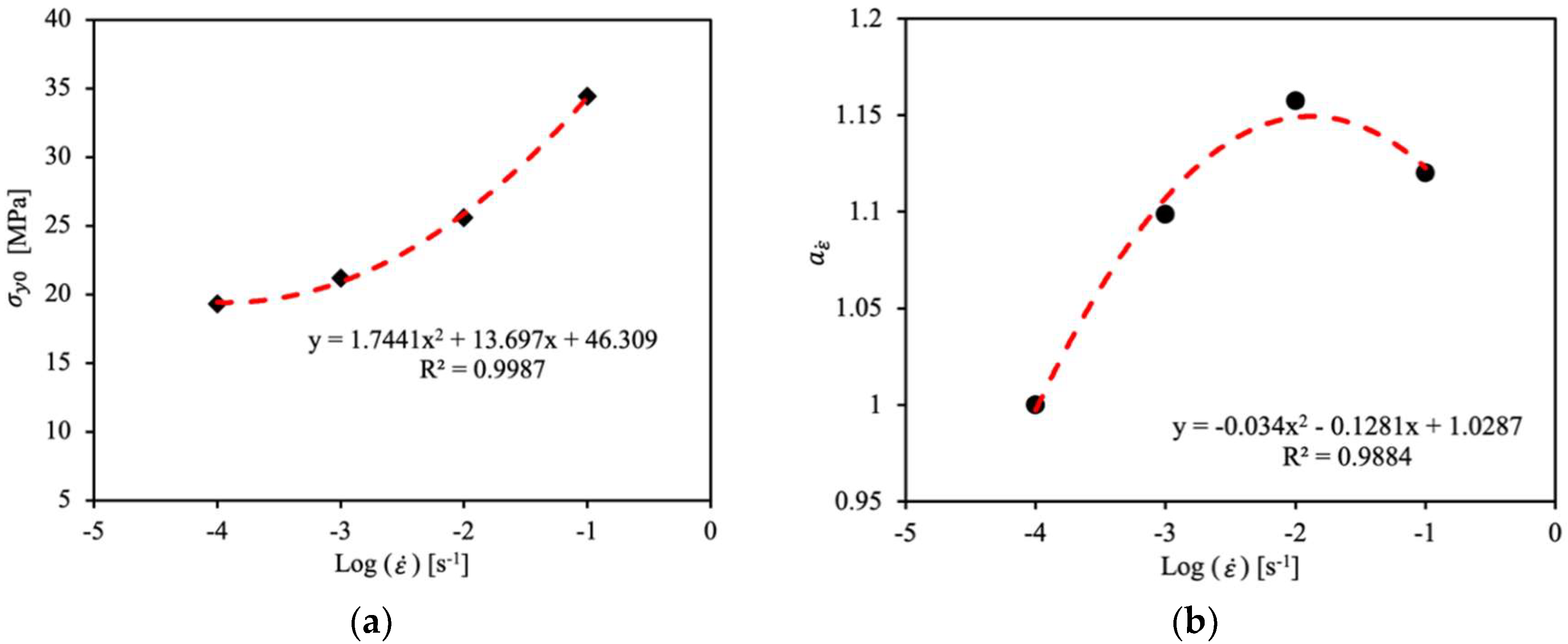
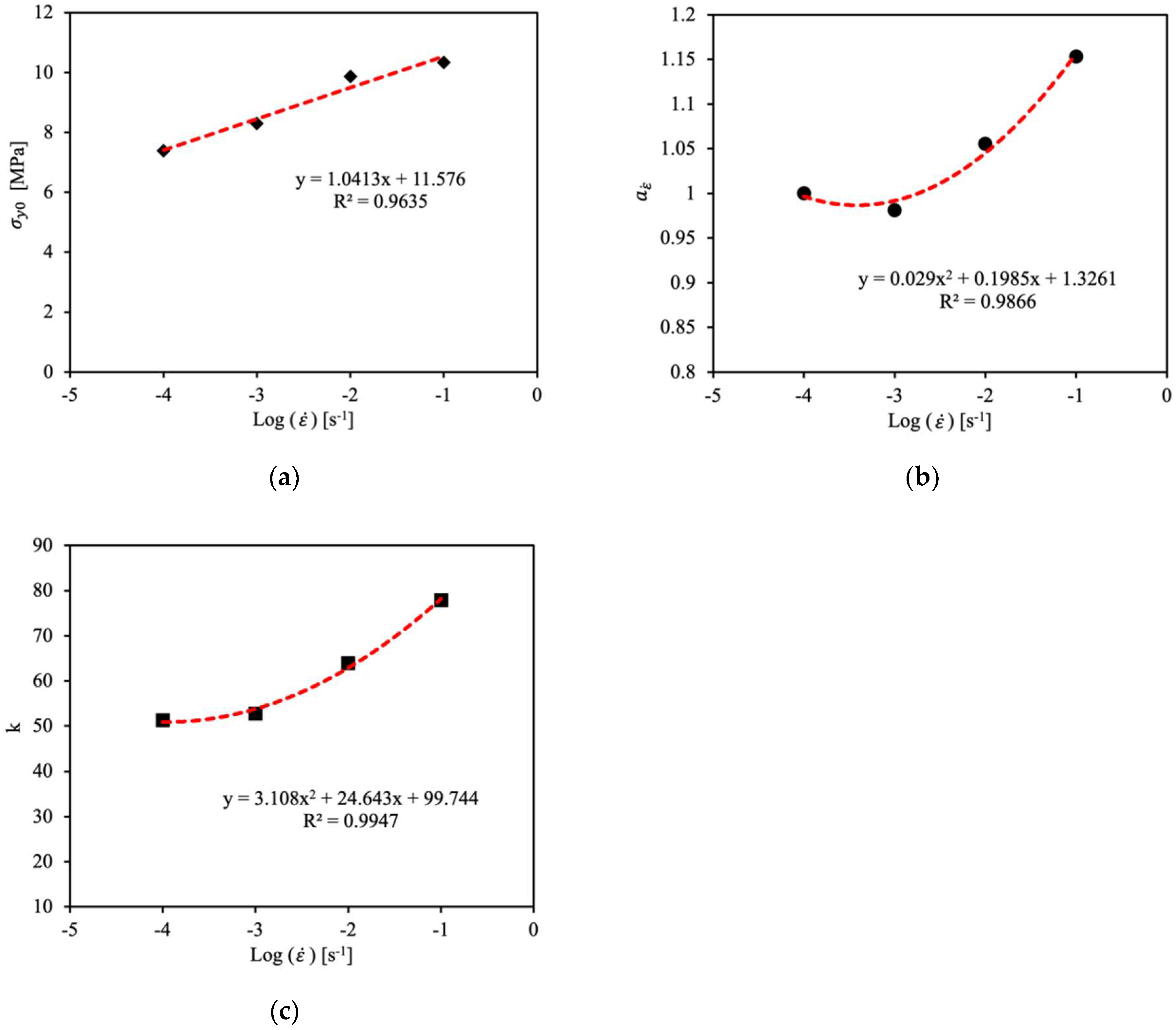

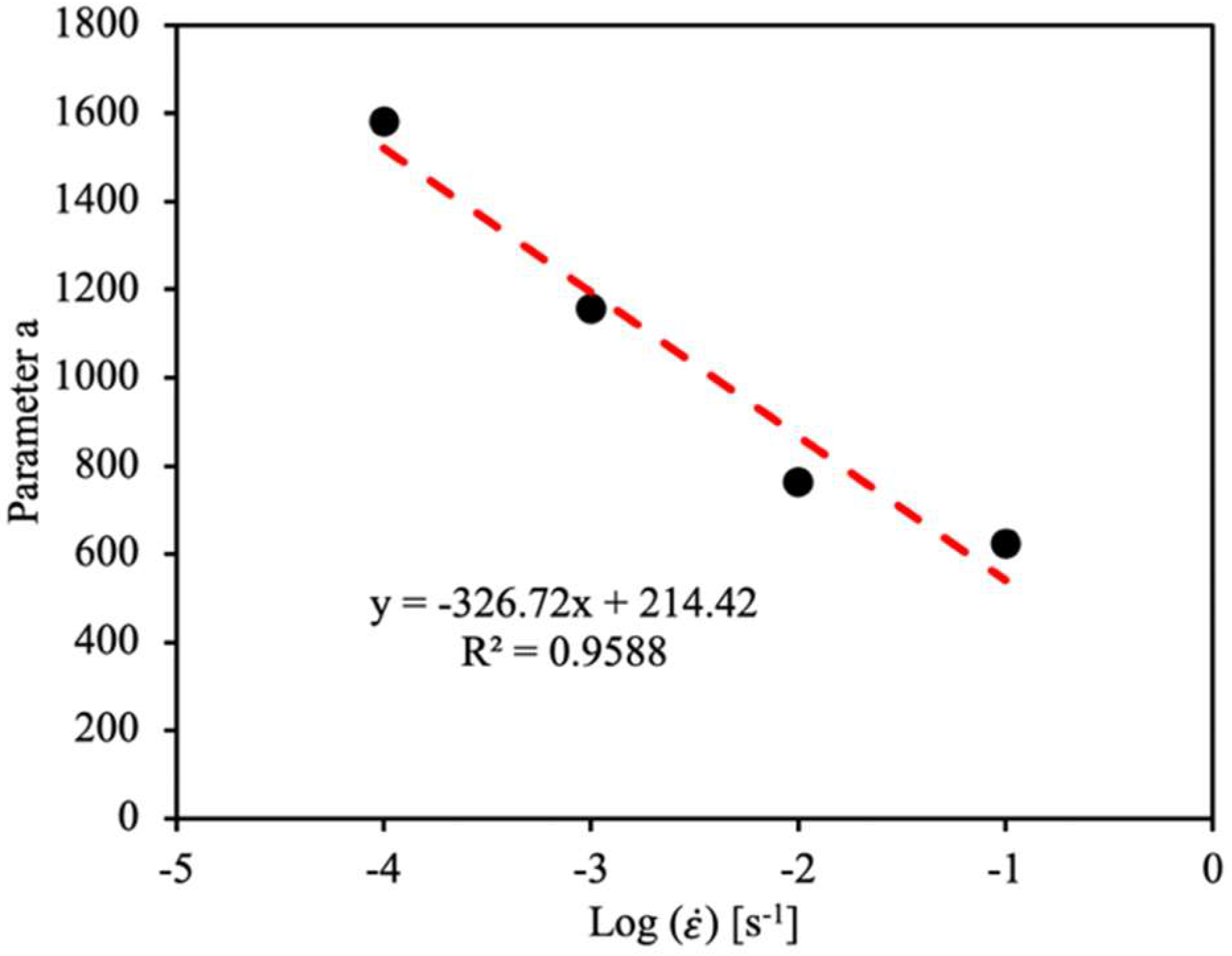

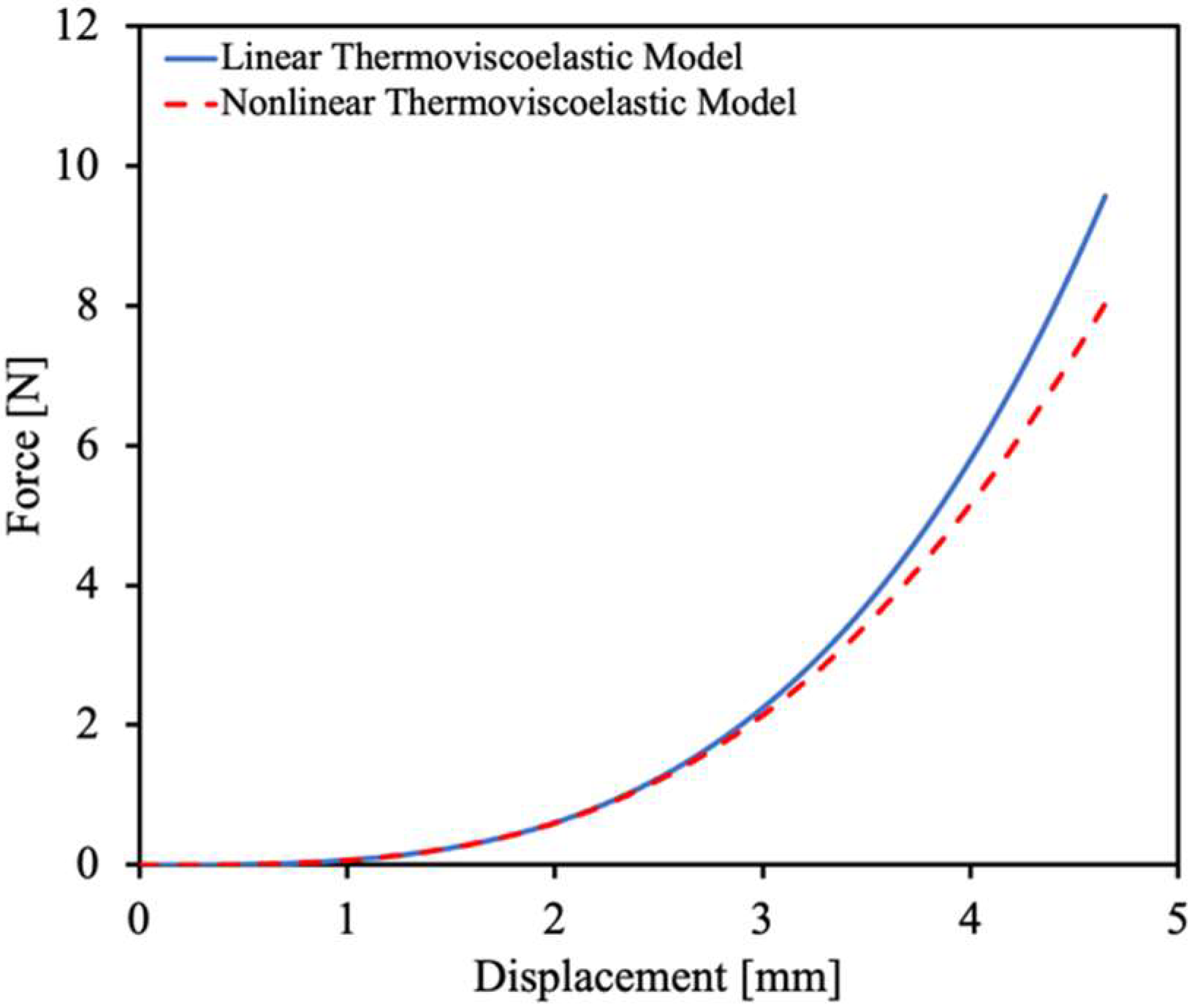
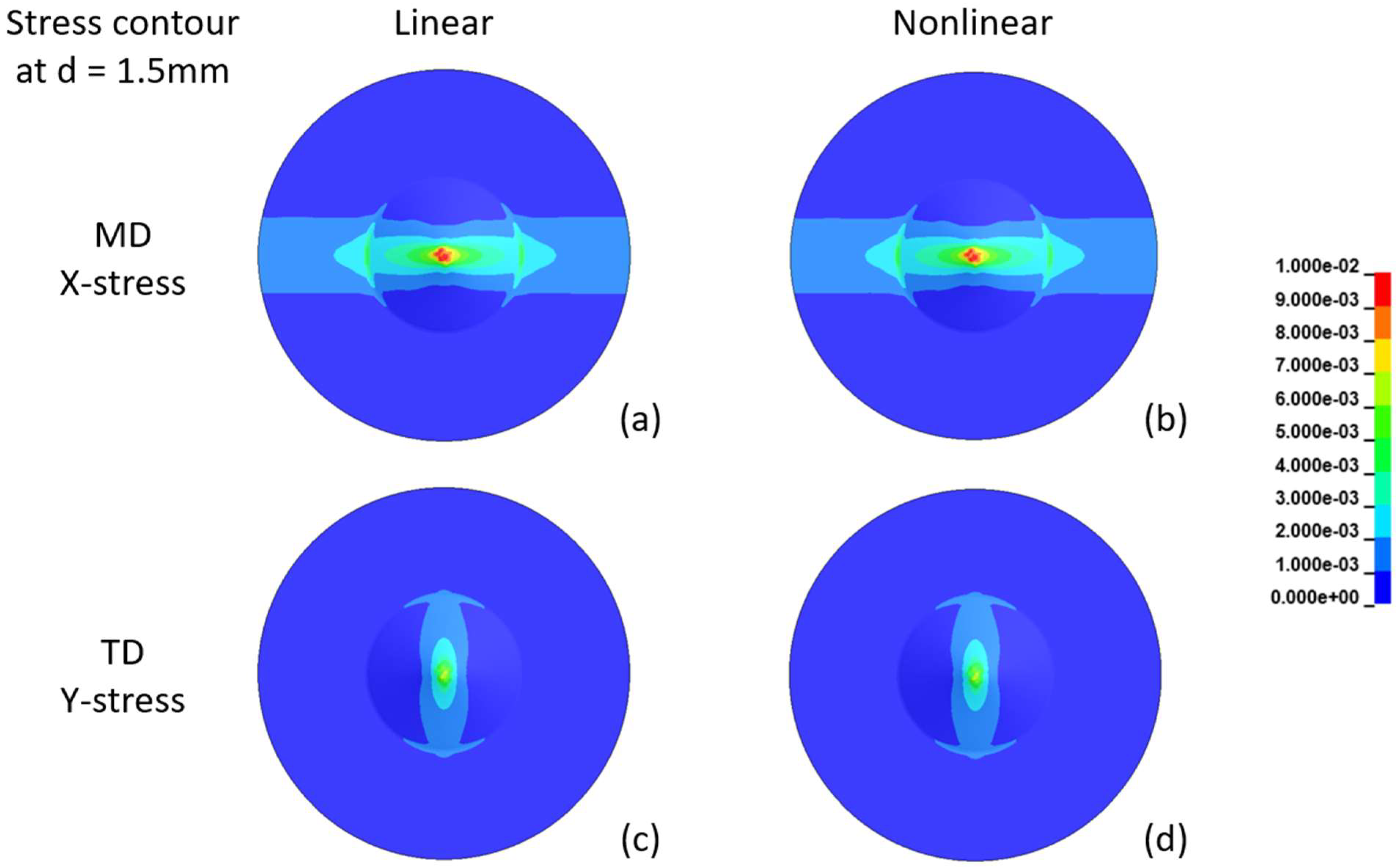
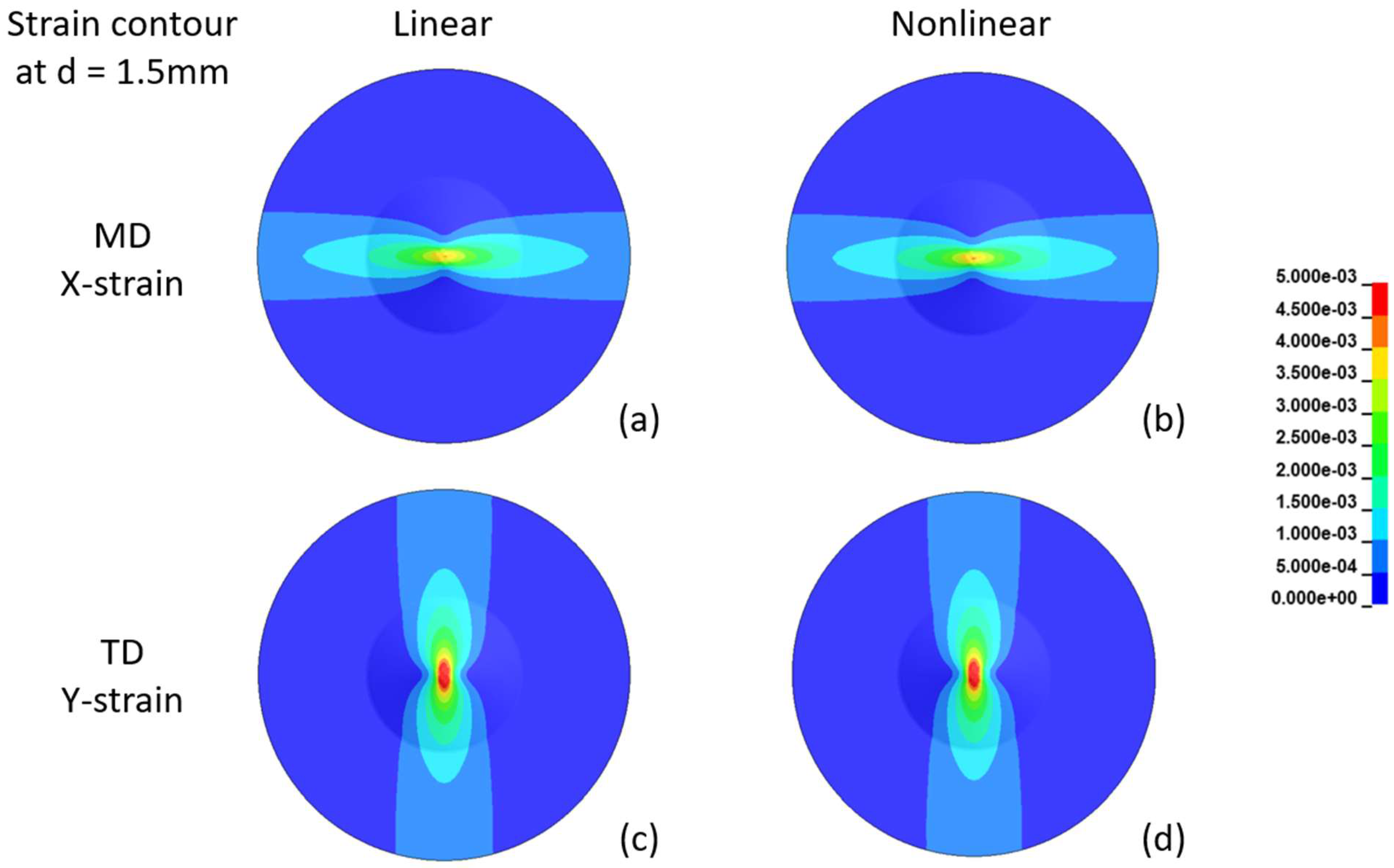
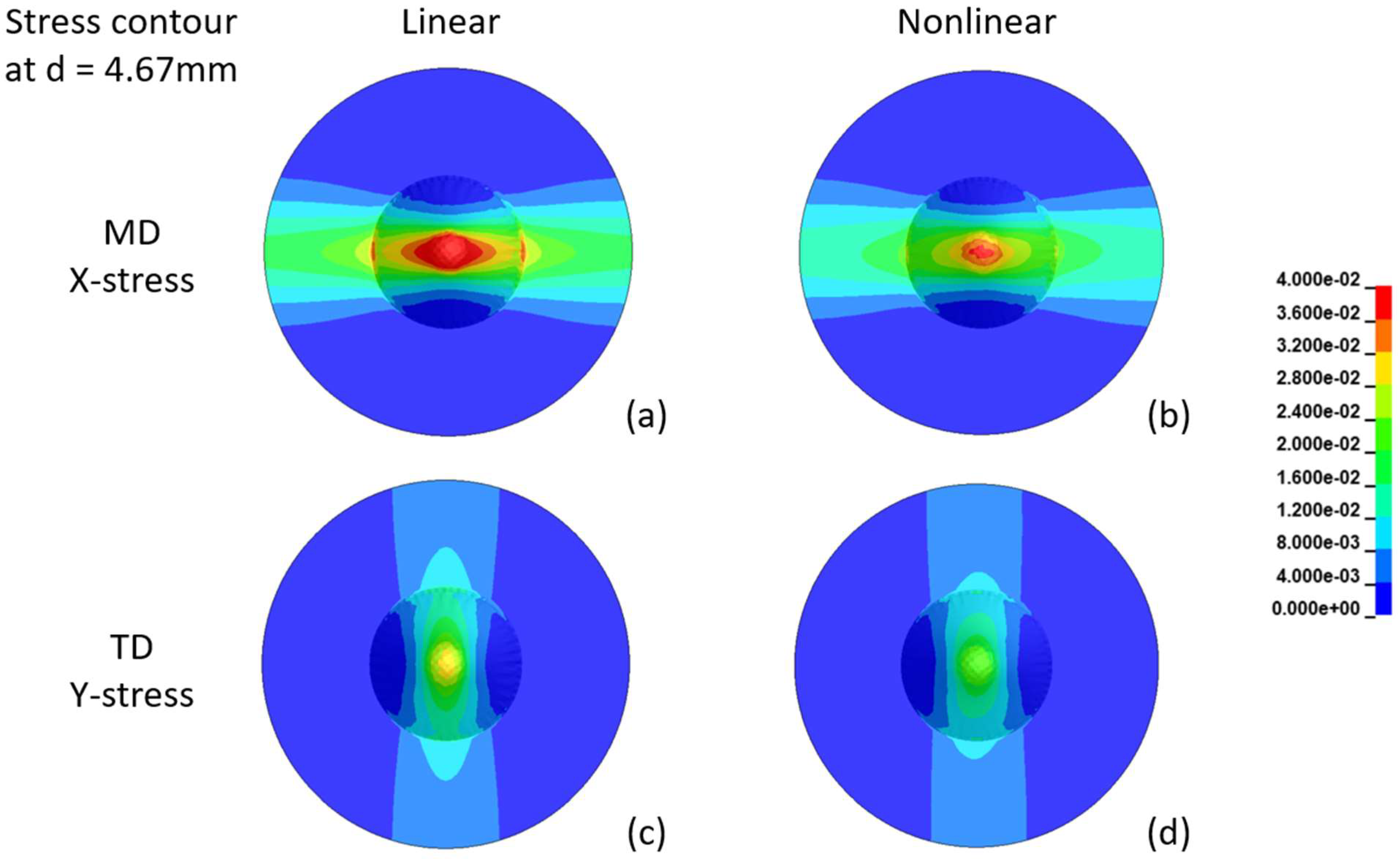
| 0.0001 | 19.33 | 22.19 | 25.21 | 0 | 228.77 | 1 |
| 0.001 | 21.20 | 18.11 | 34.44 | 0 | 281.24 | 1 |
| 0.01 | 25.61 | 16.84 | 41.29 | 0 | 307.71 | 1 |
| 0.1 | 34.45 | 9.70 | 115.36 | 0 | 343.93 | 1 |
| 0.0001 | 7.39 | 6.06 | 51.25 | −4.79 | 2.76 | 2 |
| 0.001 | 8.61 | 6.13 | 52.74 | −5.98 | 4.24 | 2 |
| 0.01 | 9.83 | 6.74 | 63.94 | −8.06 | 7.85 | 2 |
| 0.1 | 10.33 | 7.35 | 77.86 | −8.74 | 8.49 | 2 |
| 0.0001 | 19.33 | 22.19 | 25.21 | 0 | 228.77 | 1 | 1 |
| 0.001 | 21.20 | 22.19 | 25.21 | 0 | 228.77 | 1 | 1.09 |
| 0.01 | 25.61 | 22.19 | 25.21 | 0 | 228.77 | 1 | 1.16 |
| 0.1 | 34.45 | 22.19 | 25.21 | 0 | 228.77 | 1 | 1.12 |
| 0.0001 | 7.39 | 6.06 | 51.25 | −4.79 | 2.76 | 2 | 1 |
| 0.001 | 8.61 | 6.06 | 52.74 | −4.79 | 2.76 | 2 | 0.98 |
| 0.01 | 9.83 | 6.06 | 63.94 | −4.79 | 2.76 | 2 | 1.06 |
| 0.1 | 10.33 | 6.06 | 77.86 | −4.79 | 2.76 | 2 | 1.16 |
| TD Average | |||||
|---|---|---|---|---|---|
| 0.0001 | 1581.70 | 1298.60 | 1293.60 | 1305.6 | 1299.27 |
| 0.001 | 1156.40 | 918.87 | 910.48 | 908.12 | 912.49 |
| 0.01 | 763.02 | 1144.5 | 1144.50 | 1154.30 | 1149.47 |
| 0.1 | 632.76 | 965.24 | 1063.4 | 1095.4 | 1041.35 |
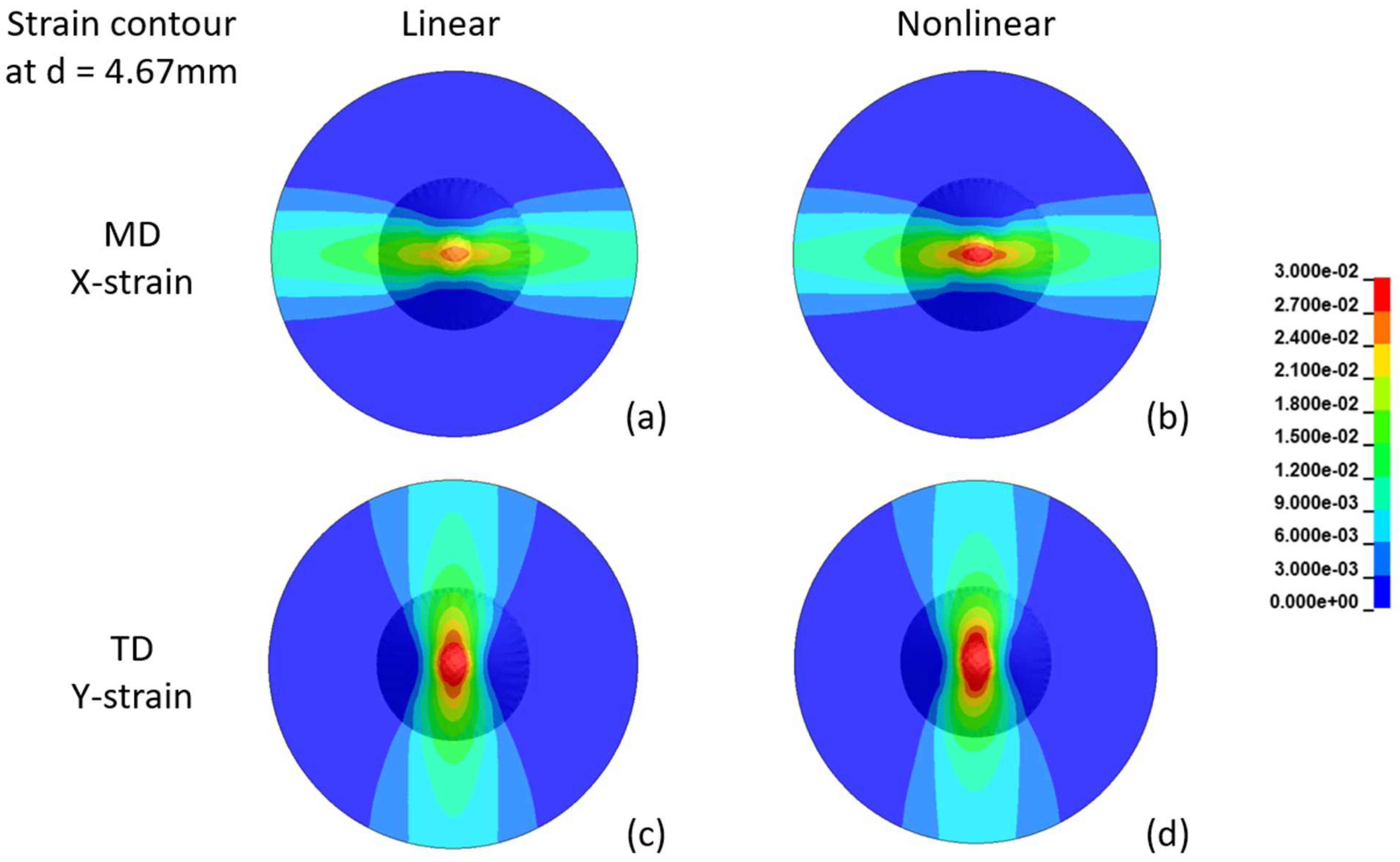
| d = 1.5 mm | d = 4.67 mm | |||||
|---|---|---|---|---|---|---|
| Maximum Stress (MPa) | Linear Model | Nonlinear Model | Nonlinear/ Linear Ratio | Linear Model | Nonlinear Model | Nonlinear/ Linear Ratio |
| MD | 13.32 | 12.74 | 0.96 | 51.95 | 38.99 | 0.75 |
| TD | 8.35 | 7.96 | 0.95 | 31.79 | 24.14 | 0.76 |
| TD/MD Ratio | 0.63 | 0.62 | 0.61 | 0.62 | ||
| Maximum Strain (%) | ||||||
| MD | 0.43 | 0.44 | 1.02 | 2.63 | 2.98 | 1.14 |
| TD | 0.70 | 0.71 | 1.02 | 3.44 | 3.73 | 1.08 |
| TD/MD Ratio | 1.62 | 1.62 | 1.31 | 1.25 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ihuaenyi, R.C.; Deng, J.; Bae, C.; Xiao, X. A Coupled Nonlinear Viscoelastic–Viscoplastic Thermomechanical Model for Polymeric Lithium-Ion Battery Separators. Batteries 2023, 9, 475. https://doi.org/10.3390/batteries9090475
Ihuaenyi RC, Deng J, Bae C, Xiao X. A Coupled Nonlinear Viscoelastic–Viscoplastic Thermomechanical Model for Polymeric Lithium-Ion Battery Separators. Batteries. 2023; 9(9):475. https://doi.org/10.3390/batteries9090475
Chicago/Turabian StyleIhuaenyi, Royal Chibuzor, Jie Deng, Chulheung Bae, and Xinran Xiao. 2023. "A Coupled Nonlinear Viscoelastic–Viscoplastic Thermomechanical Model for Polymeric Lithium-Ion Battery Separators" Batteries 9, no. 9: 475. https://doi.org/10.3390/batteries9090475





