Autoencoder-Based Unsupervised Surface Defect Detection Using Two-Stage Training
Abstract
1. Introduction
- Partial defect reconstruction: Sometimes, the trained model might also reconstruct the defective region, thereby diminishing its ability to distinguish between defective and non-defective regions.
- Noise-free normal background: Even if defects are identified, the reconstructed normal background often contains noise, making it harder to isolate the defects accurately.
- We propose a two-stage training strategy involving normal training samples and training samples with artificial defects.
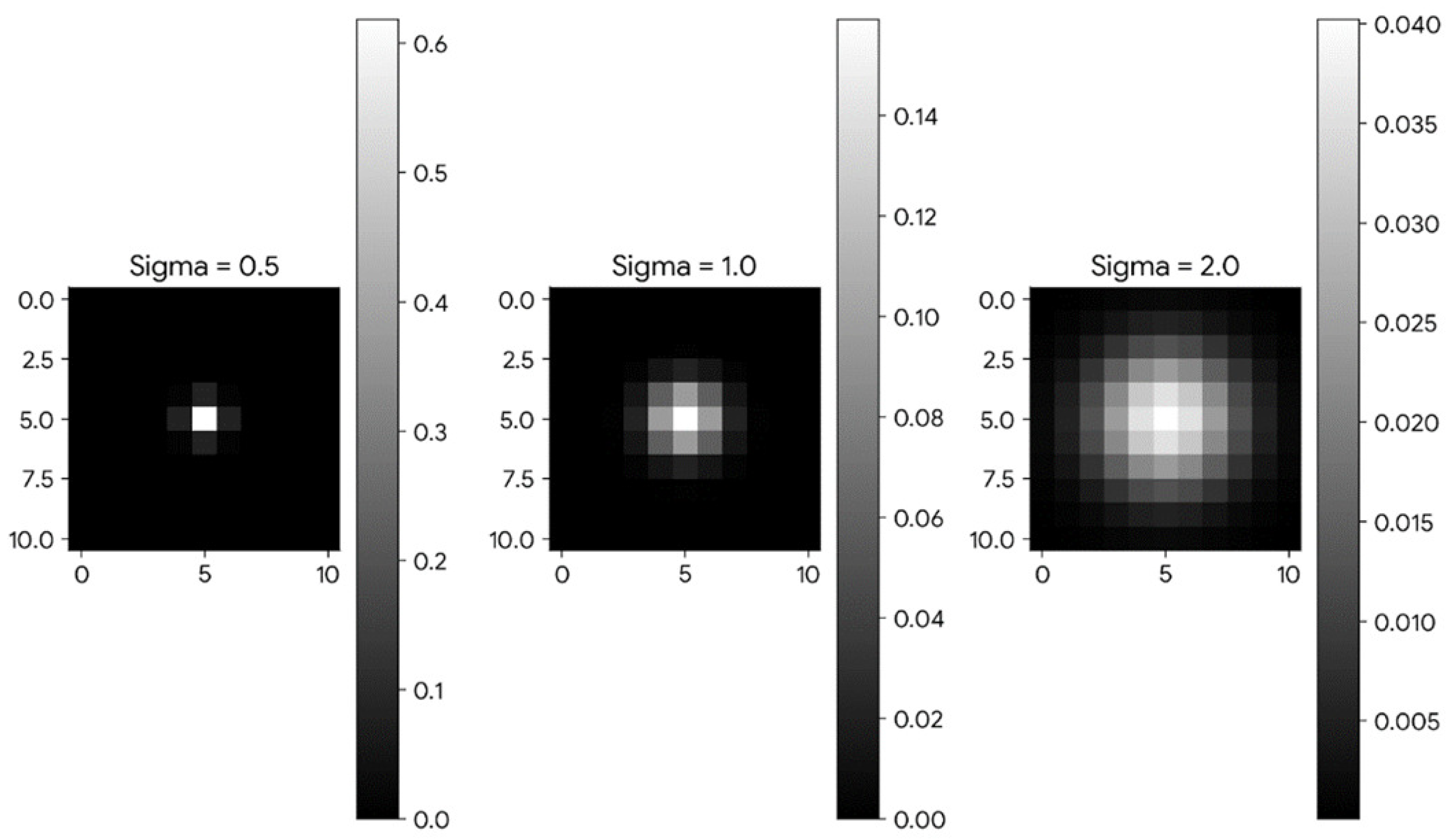
- The AW-SSIM loss function is proposed, removing the independence between the three sub-functions of the SSIM and dynamically adjusting the standard deviation () for the Gaussian window.
- We propose an artificial defect generation algorithm (ADGA), a novel algorithm specifically designed to create artificial defects that closely resemble various real-world defects.
- To improve the quality of normal background reconstruction and defect identification, we propose a combined SSIM and LPIPS loss function for the second stage of training.
2. Related Works
3. Methodology
3.1. Overall Network Architecture
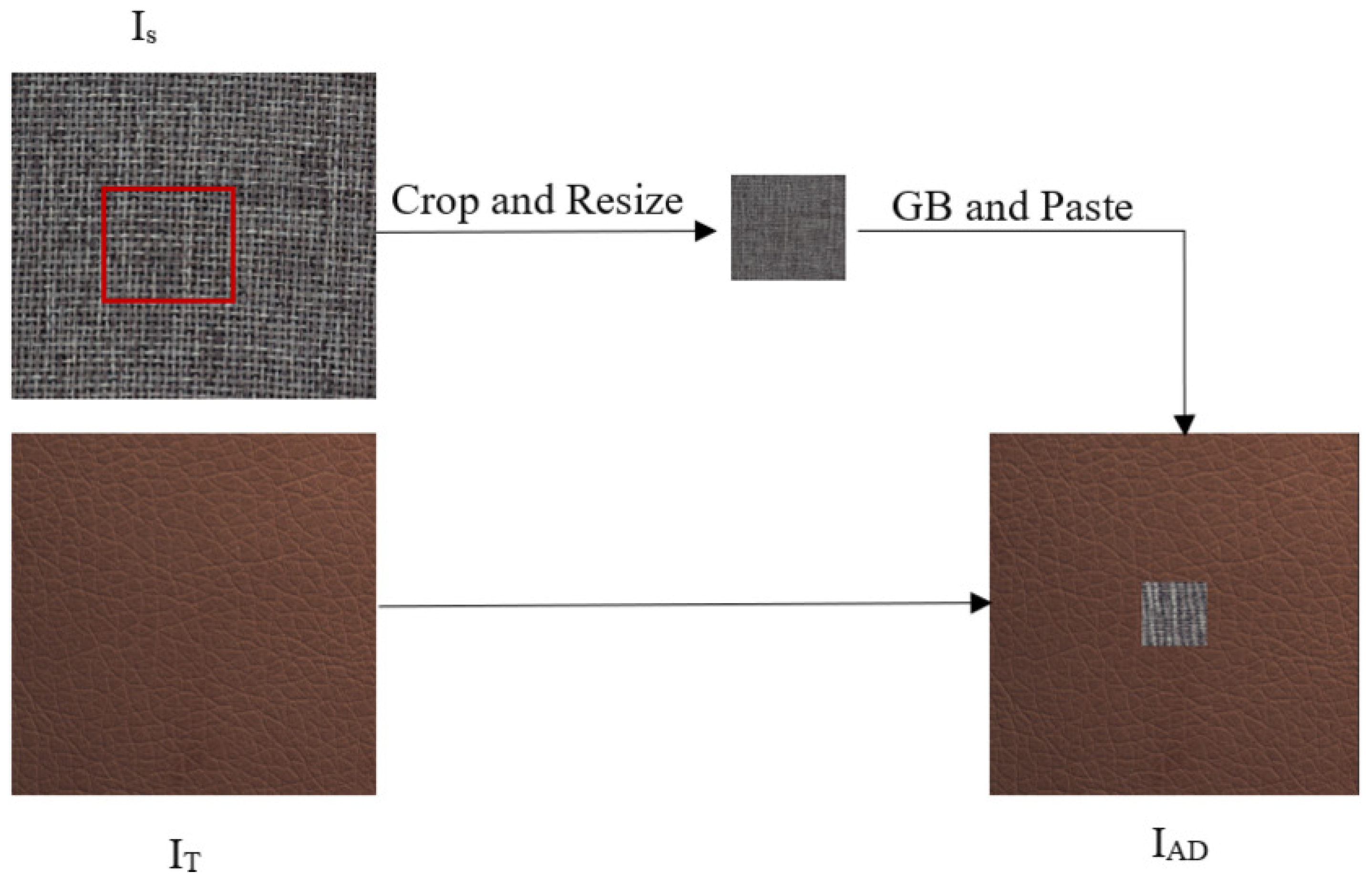
3.2. Artificial Defect Generation Algorithm (ADGA)
3.3. SSIM Loss Function Improvement
3.4. Combined AW-SSIM and LPIPS Loss for Stage Two of Training
4. Experimentation
4.1. Overall Performance Comparison
4.2. Ablation Study
4.2.1. The Influence of AW-SSIM
4.2.2. The Influence of the Combined LPIPS and AW-SSIM Loss
4.2.3. Influence of Two-Stage Training
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, K.; Yan, Y.; Li, P.; Jing, J.; Liu, X.; Wang, Z. Fabric defect detection using salience metric for color dissimilarity and positional aggregation. IEEE Access 2018, 6, 38137–38149. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J.; Tian, Y.; Chen, H.; Sun, H.; Liu, K. A simple guidance template-based defect detection method for strip steel surfaces. IEEE Trans. Ind. Inform. 2019, 15, 2798–2809. [Google Scholar] [CrossRef]
- Ruz, G.A.; Estévez, P.A.; Ramírez, P.A. Automated visual inspection system for wood defect classification using computational intelligence techniques. Int. J. Syst. Sci. 2009, 40, 163–172. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhou, M.; Slabaugh, G.G.; Zhai, J.; Fang, T. Automatic detection of bridge deck condition from ground penetrating radar images. IEEE Trans. Autom. Sci. Eng. 2011, 8, 633–640. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, Y.; Zhao, F.; Zhang, E.; Wu, Z.; Shao, L. Surface defect detection methods for industrial products: A review. Appl. Sci. 2021, 11, 7657. [Google Scholar] [CrossRef]
- Tang, L.B.; Kong, J.; Wu, S. Review of surface defect detection based on machine vision. J. Image Graph. 2017, 22, 1640–1663. [Google Scholar]
- Song, W.; Chen, T.; Gu, Z.; Gai, W.; Huang, W.; Wang, B. Wood materials defects detection using image block percentile color histogram and eigenvector texture feature. In Proceedings of the First International Conference on Information Sciences, Machinery, Materials and Energy, Beijing, China, 24–26 April 2015; pp. 779–783. [Google Scholar] [CrossRef]
- Wang, F.L.; Zuo, B. Detection of surface cutting defect on magnet using Fourier image reconstruction. J. Cent. South Univ. 2016, 23, 1123–1131. [Google Scholar] [CrossRef]
- Tsai, D.-M.; Huang, C.-K. Defect detection in electronic surfaces using template-based Fourier image reconstruction. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 163–172. [Google Scholar] [CrossRef]
- Ren, R.; Hung, T.; Tan, K.C. A generic deep-learning-based approach for automated surface inspection. IEEE Trans. Cybern. 2018, 48, 929–940. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Song, K.; He, Y.; Xu, J.; Yan, Y.; Meng, Q. PGA-Net: Pyramid feature fusion and global context attention network for automated surface defect detection. IEEE Trans. Ind. Inform. 2020, 16, 7448–7458. [Google Scholar] [CrossRef]
- Tabernik, D.; Skvarč, J.; Šela, S.; Skočaj, D. Segmentation-based deep-learning approach for surface-defect detection. J. Intell. Manuf. 2020, 31, 759–776. [Google Scholar] [CrossRef]
- Du, B.; Wan, F.; Lei, G.; Xu, L.; Xu, C.; Xiong, Y. YOLO-MBBi: PCB surface defect detection method based on enhanced YOLOv5. Electronics 2023, 12, 2821. [Google Scholar] [CrossRef]
- Tang, J.; Liu, S.; Zhao, D.; Tang, L.; Zou, W.; Zheng, B. PCB-YOLO: An improved detection algorithm of PCB surface defects based on YOLOv5. Sustainability 2023, 15, 5963. [Google Scholar] [CrossRef]
- Santoso, A.D.; Cahyono, F.B.; Prahasta, B.; Sutrisno, I.; Khumaidi, A. Development of pcb defect detection system using image processing with yolo cnn method. Int. J. Artif. Intell. Res. 2022, 6, 2579–7298. [Google Scholar]
- Cheng, X.; Yu, J. RetinaNet with difference channel attention and adaptively spatial feature fusion for steel surface defect detection. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot Multibox Detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14. Springer International Publishing: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Perera, P.; Nallapati, R.; Xiang, B. OCGAN: One-Class Novelty Detection Using GANs with Constrained Latent Representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 2893–2901. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery. In Proceedings of the 25th International Conference on Information Processing in Medical Imaging (IPMI), Boone, NC, USA, 25–30 June 2017; Springer International Publishing: Cham, Switzerland, 2017; pp. 146–157. [Google Scholar]
- Bergmann, P.; Löwe, S.; Fauser, M.; Sattlegger, D.; Steger, C. Improving Unsupervised Defect Segmentation by Applying Structural Similarity to Autoencoders. arXiv 2018, arXiv:1807.02011. [Google Scholar]
- Lu, Y. The Level Weighted Structural Similarity Loss: A Step Away from MSE. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 9989–9990. [Google Scholar] [CrossRef]
- Bionda, A.; Frittoli, L.; Boracchi, G. Deep Autoencoders for Anomaly Detection in Textured Images using CW-SSIM. In Proceedings of the International Conference on Image Analysis and Processing, Lecce, Italy, 23–27 May 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 669–680. [Google Scholar]
- Chamberland, O.; Reckzin, M.; Hashim, H.A. An Autoencoder with Convolutional Neural Network for Surface Defect Detection on Cast Components. J. Fail. Anal. Prev. 2023, 23, 1633–1644. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Zhou, Q.; Song, K.; Yin, Z. An Anomaly Feature-Editing-Based Adversarial Network for Texture Defect Visual Inspection. IEEE Trans. Ind. Inform. 2021, 17, 2220–2230. [Google Scholar] [CrossRef]
- Li, C.-L.; Sohn, K.; Yoon, J.; Pfister, T. CutPaste: Self-Supervised Learning for Anomaly Detection and Localization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 9659–9669. [Google Scholar]
- Luo, W.; Niu, T.; Tang, L.; Yu, W.; Li, B. Clear Memory-Augmented Auto-Encoder for Surface Defect Detection. arXiv 2022, arXiv:2208.03879. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Langs, G.; Schmidt-Erfurth, U. f-AnoGAN: Fast Unsupervised Anomaly Detection with Generative Adversarial Networks. Med. Image Anal. 2019, 54, 30–44. [Google Scholar] [CrossRef] [PubMed]
- Pidhorskyi, S.; Almohsen, R.; Doretto, G. Generative Probabilistic Novelty Detection with Adversarial Autoencoders. In Proceedings of the Advances in Neural Information Processing Systems 31 (NIPS), Palais des Congrès de Montréal, Montréal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Masci, J.; Meier, U.; Cireşan, D.; Schmidhuber, J. Stacked Convolutional Auto-Encoders for Hierarchical Feature Extraction. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6791, pp. 52–59. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial Autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Schneider, S.; Antensteiner, D.; Soukup, D.; Scheutz, M. Autoencoders - A Comparative Analysis in the Realm of Anomaly Detection. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 1985–1991. [Google Scholar]
- Yang, H.; Chen, Y.; Song, K.; Yin, Z. Multiscale Feature-Clustering-Based Fully Convolutional Autoencoder for Fast Accurate Visual Inspection of Texture Surface Defects. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1450–1467. [Google Scholar] [CrossRef]
- Hu, C.; Yao, J.; Wu, W.; Qiu, W.; Zhu, L. A Lightweight Reconstruction Network for Surface Defect Inspection. arXiv 2022, arXiv:2212.12878. [Google Scholar]
- Gong, D.; Liu, L.; Le, V.; Saha, B.; Mansour, M.R.; Venkatesh, S.; van den Hengel, A. Memorizing Normality to Detect Anomaly: Memory-Augmented Deep Autoencoder for Unsupervised Anomaly Detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1705–1714. [Google Scholar]
- Tan, D.S.; Chen, Y.-C.; Chen, T.P.-C.; Chen, W.-C. TrustMAE: A Noise-Resilient Defect Classification Framework using Memory-Augmented Auto-Encoders with Trust Regions. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 276–285. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. Ganomaly: Semi-supervised anomaly detection via adversarial training. In Proceedings of the Computer Vision–ACCV 2018: 14th Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; pp. 622–637. [Google Scholar]
- Akçay, S.; Atapour-Abarghouei, A.; Breckon, T.P. Skip-GANomaly: Skip Connected and Adversarially Trained Encoder-Decoder Anomaly Detection. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Xiao, Q.; Shao, S.; Wang, J. Memory-augmented adversarial autoencoders for multivariate time-series anomaly detection with deep reconstruction and prediction. arXiv 2021, arXiv:2110.08306. [Google Scholar]
- Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD—A Comprehensive Real-World Dataset for Unsupervised Anomaly Detection. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9584–9592. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Dehaene, D.; Frigo, O.; Combrexelle, S.; Eline, P. Iterative energy-based projection on a normal data manifold for anomaly localization. arXiv 2020, arXiv:2002.03734. [Google Scholar]
- Song, K.; Yang, H.; Yin, Z. Anomaly Composition and Decomposition Network for Accurate Visual Inspection of Texture Defects. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]





| Category | AE-SSIM | AnoGAN | f-AnoGAN | MS-FCAE | MemAE | TrustMAE | VAE | ACDN | AFEAN | CMA-AE | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tile | 59.00 | 50.00 | 72.00 | 53.20 | 70.76 | 82.48 | 65.40 | 93.60 | 85.70 | 98.82 | 96.56 |
| Wood | 73.00 | 62.00 | 74.00 | 81.20 | 85.44 | 92.62 | 83.80 | 92.90 | 92.20 | 96.96 | 97.10 |
| Leather | 78.00 | 64.00 | 83.00 | 91.70 | 92.91 | 98.05 | 92.50 | 98.40 | 96.10 | 99.13 | 98.76 |
| Carpet | 87.00 | 54.00 | 66.00 | 78.20 | 81.16 | 98.53 | 73.50 | 91.10 | 91.40 | 91.25 | 99.20 |
| Hazelnut | 96.60 | 87.00 | 63.15 | 78.50 | 81.16 | 97.15 | 98.80 | 94.10 | 92.80 | 97.10 | 98.89 |
| Pill | 89.50 | 93.25 | 64.07 | 80.60 | 77.88 | 89.90 | 93.50 | 92.80 | 89.60 | 92.65 | 95.64 |
| average | 80.51 | 68.38 | 70.37 | 77.23 | 81.55 | 93.12 | 84.50 | 93.81 | 91.3 | 95.98 | 97.69 |
| Training | One-Stage Training | Two-Stage Training | ||
|---|---|---|---|---|
| Loss | SSIM + L1 | LPIPS + SSIM | AW-SSIM | AW-SSIM + LPIPS |
| AuROC | 86.7 | 90.86 | 95.60 | 98.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Getachew Shiferaw, T.; Yao, L. Autoencoder-Based Unsupervised Surface Defect Detection Using Two-Stage Training. J. Imaging 2024, 10, 111. https://doi.org/10.3390/jimaging10050111
Getachew Shiferaw T, Yao L. Autoencoder-Based Unsupervised Surface Defect Detection Using Two-Stage Training. Journal of Imaging. 2024; 10(5):111. https://doi.org/10.3390/jimaging10050111
Chicago/Turabian StyleGetachew Shiferaw, Tesfaye, and Li Yao. 2024. "Autoencoder-Based Unsupervised Surface Defect Detection Using Two-Stage Training" Journal of Imaging 10, no. 5: 111. https://doi.org/10.3390/jimaging10050111
APA StyleGetachew Shiferaw, T., & Yao, L. (2024). Autoencoder-Based Unsupervised Surface Defect Detection Using Two-Stage Training. Journal of Imaging, 10(5), 111. https://doi.org/10.3390/jimaging10050111






