An Evaluation of the Design Parameters of a Variable Bearing Profile Considering Journal Perturbation in Rotor–Bearing Systems
Abstract
:1. Introduction
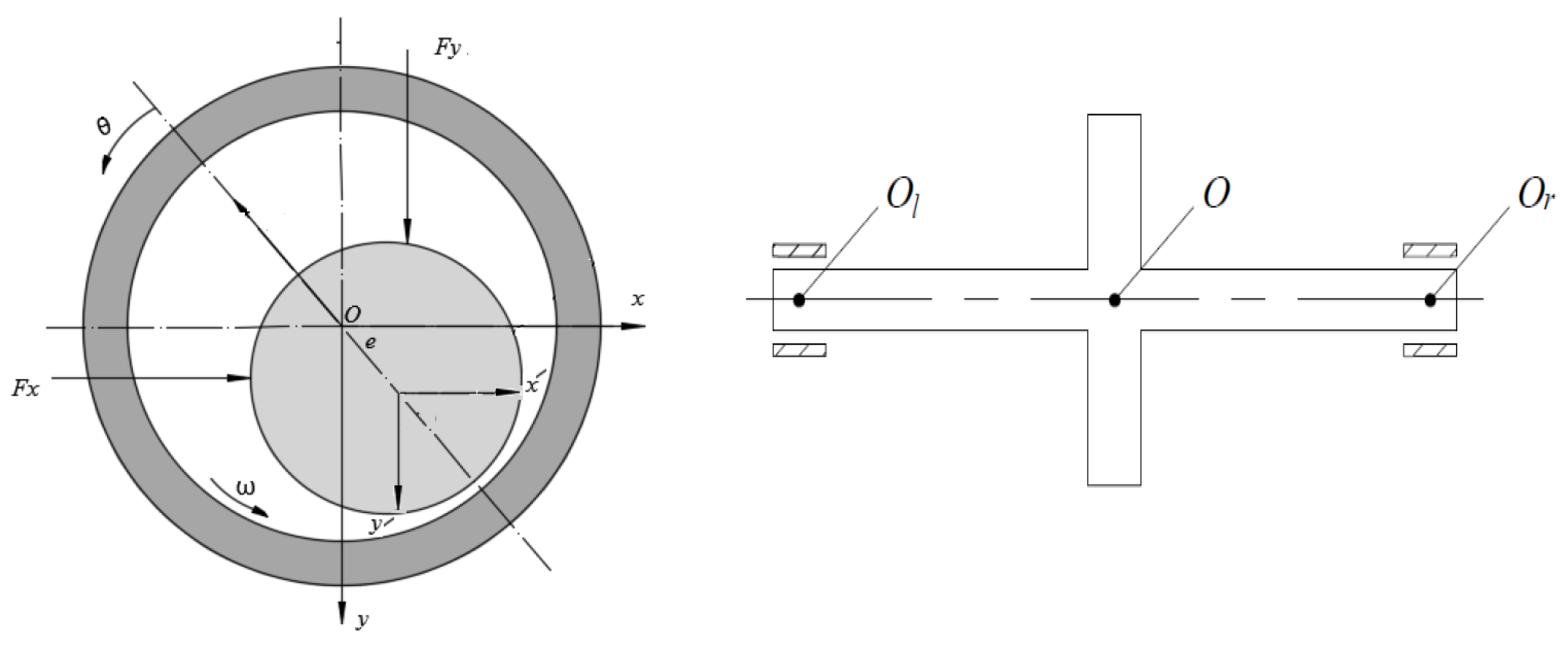
2. Equations Related to the Hydrodynamic Lubrication Regime
- ▪
- The pressure value: at position
- ▪
- The pressure gradient and the pressure value: at position .
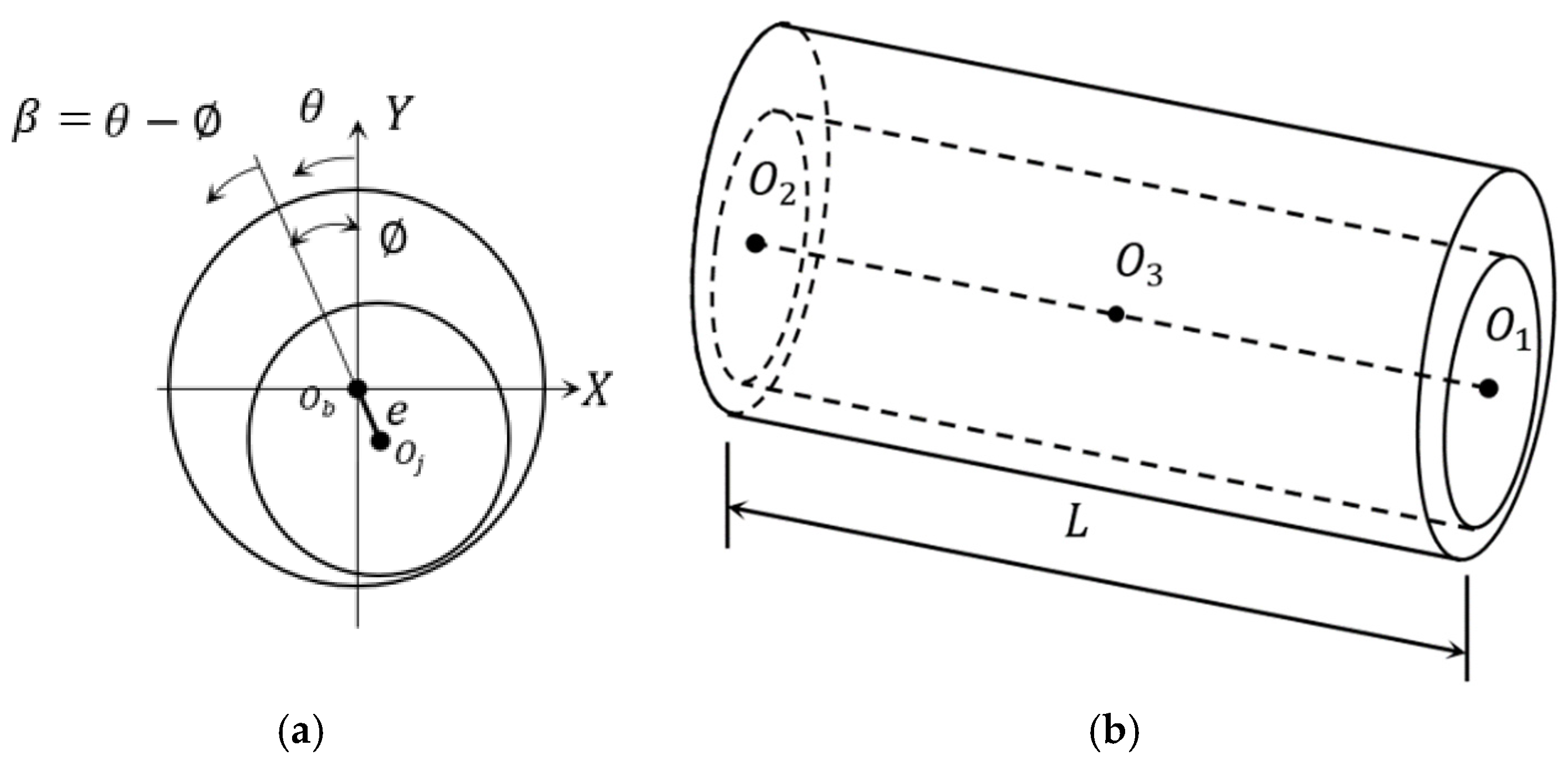
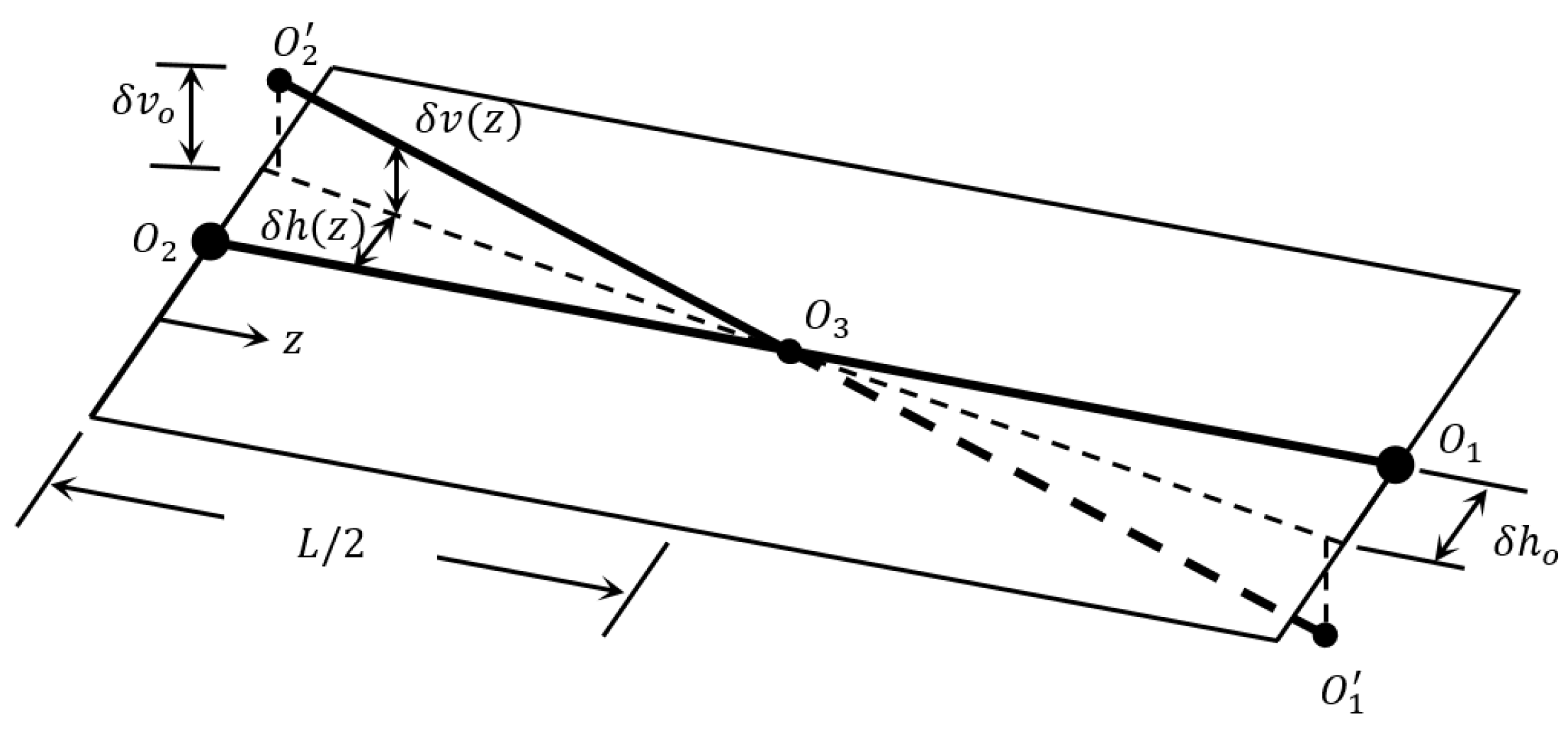
3. Three-Dimensional Misalignment Model
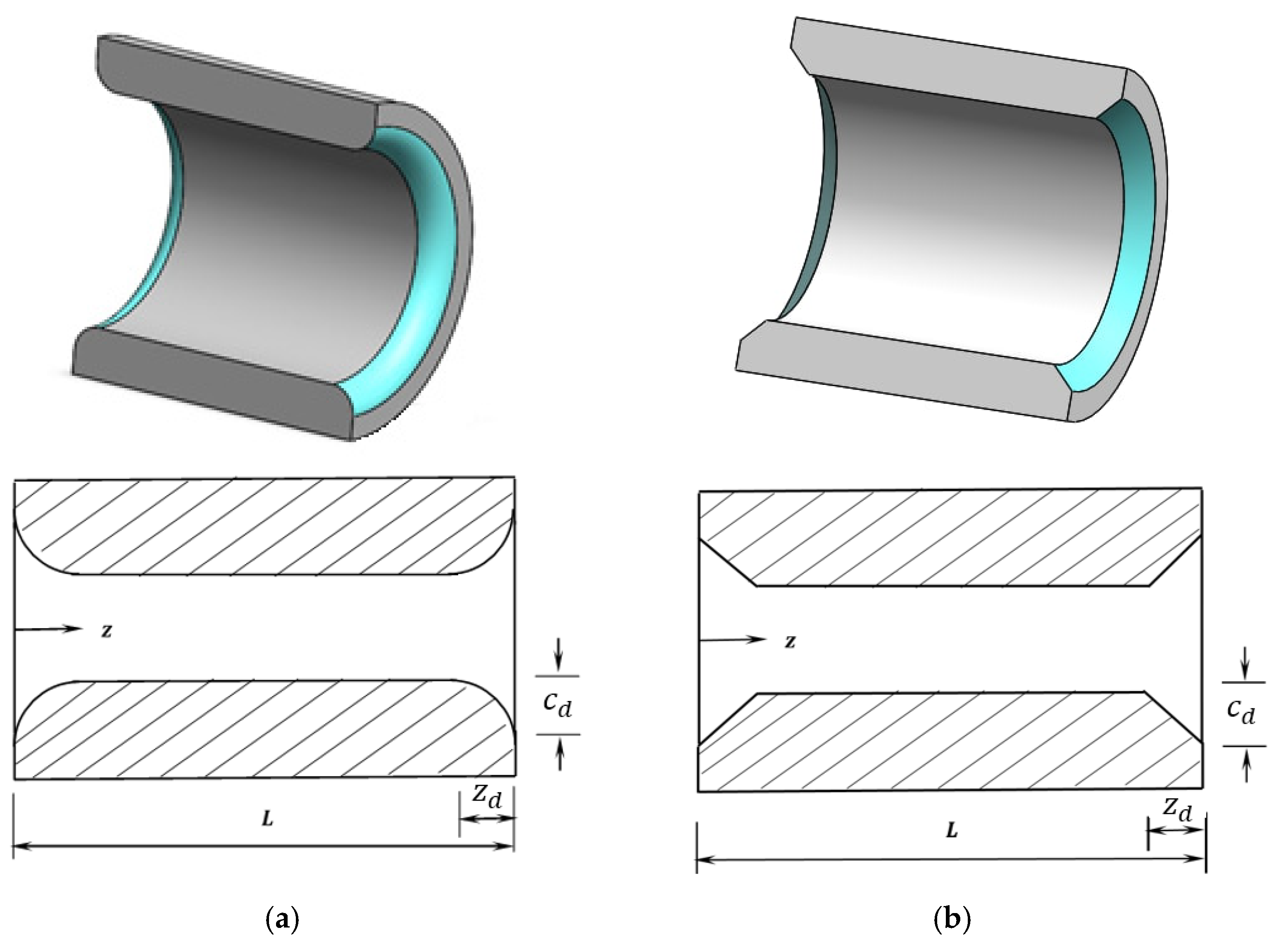
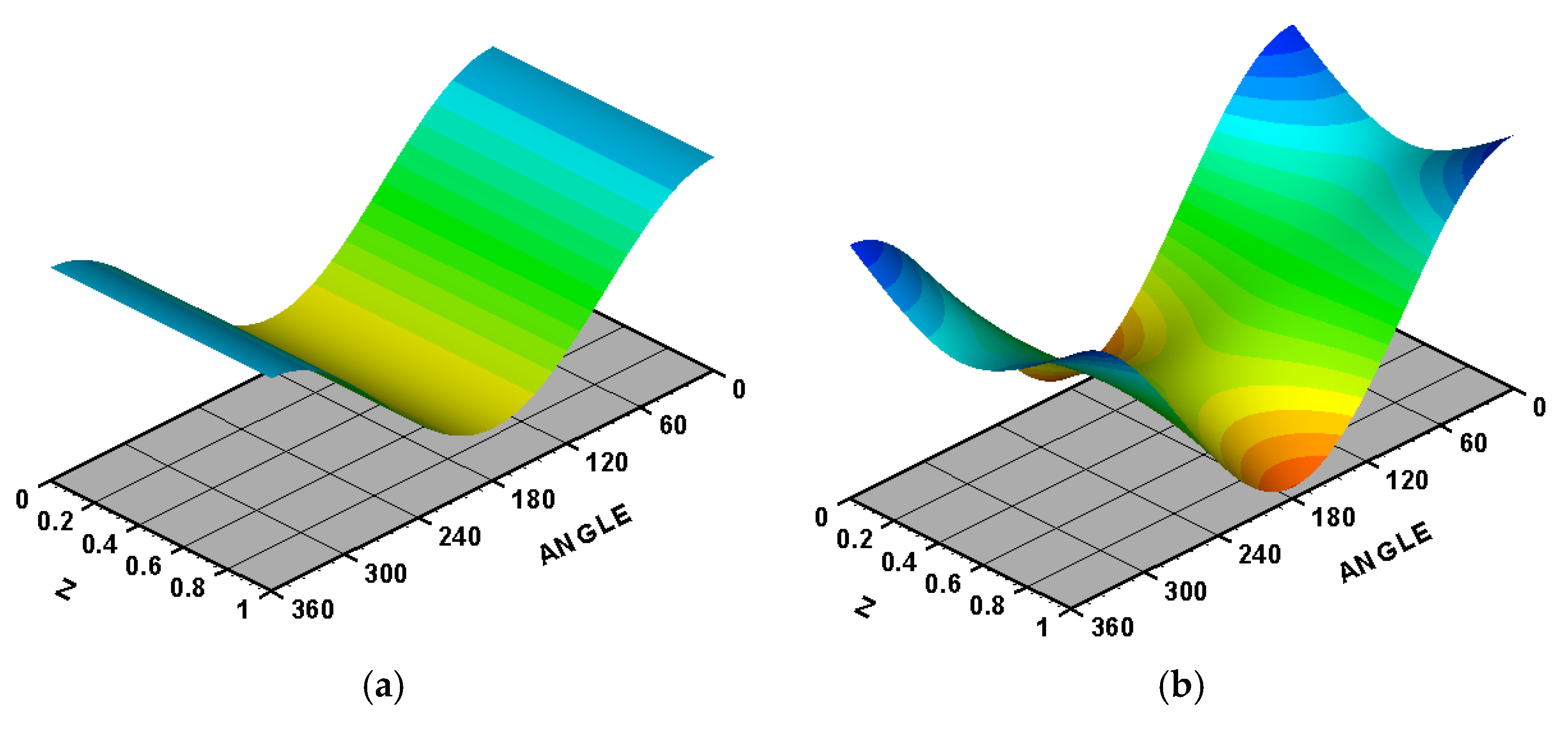
4. Design of the Bearing Profile
- ▪
- Curved type:
- ▪
- Linear type:
5. Dynamic Characteristics of the Rotor–Bearing System
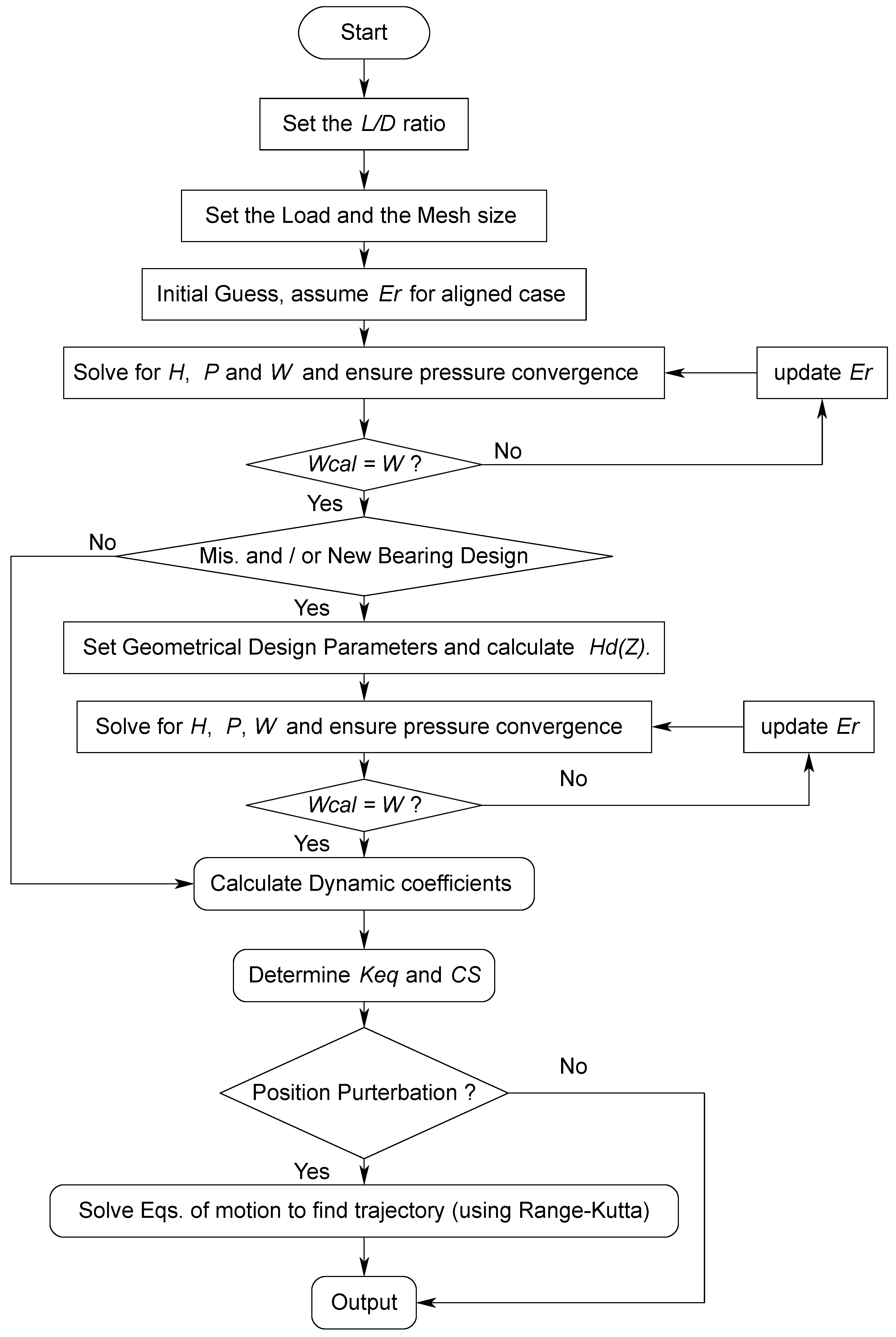
6. Numerical Solution
7. Results and Discussions
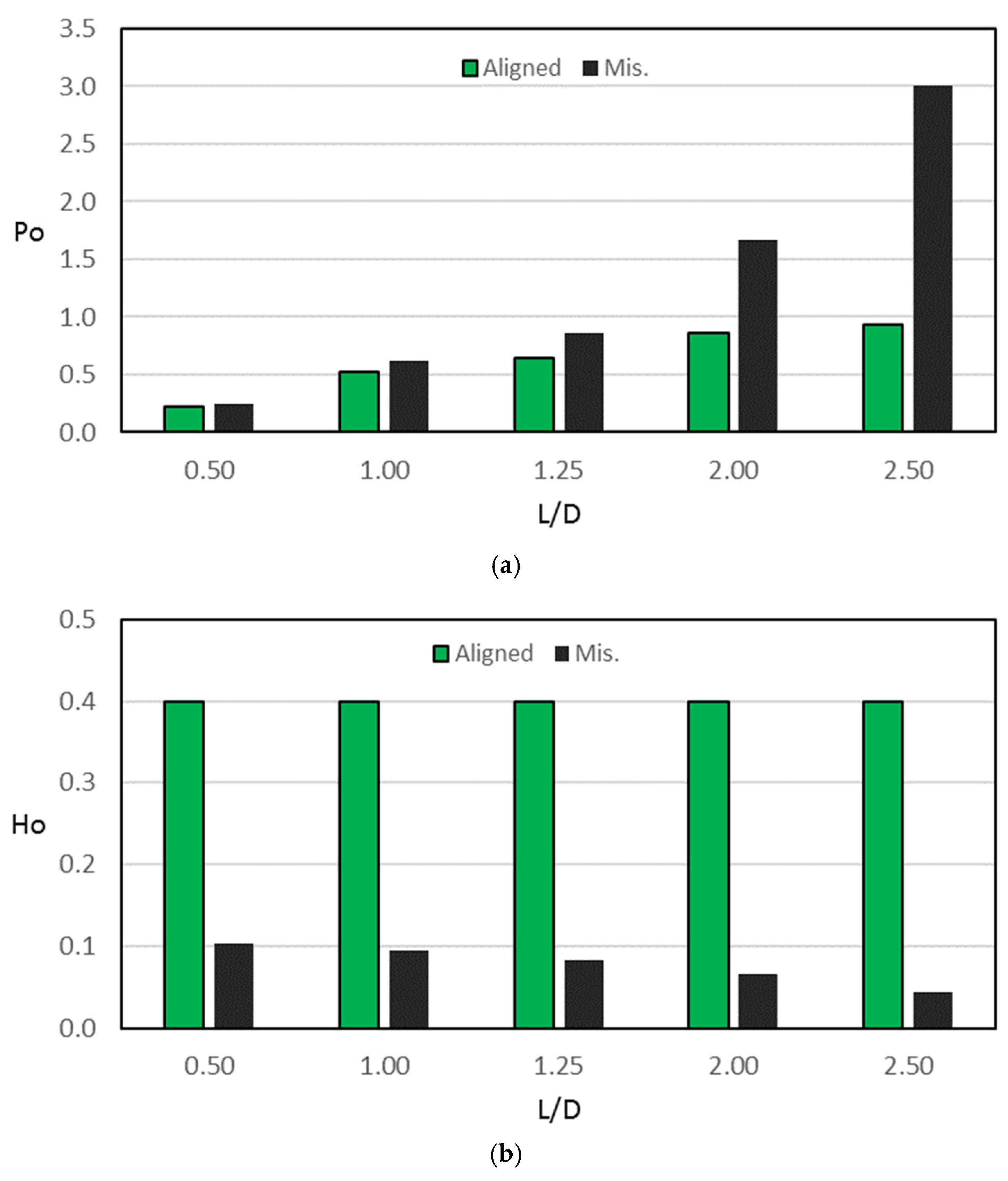
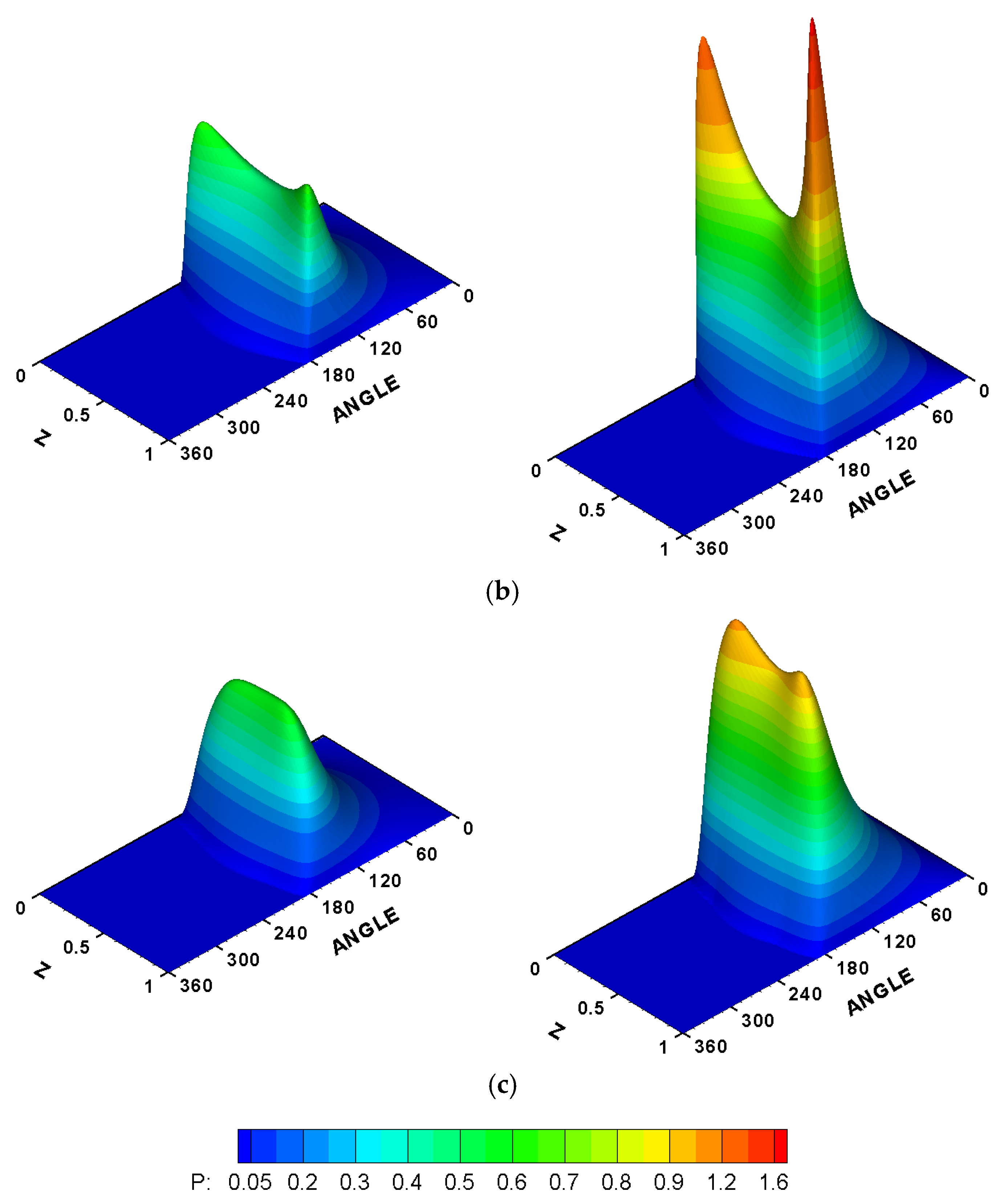
7.1. Effect of Mesh Density and Validation of the Current Model
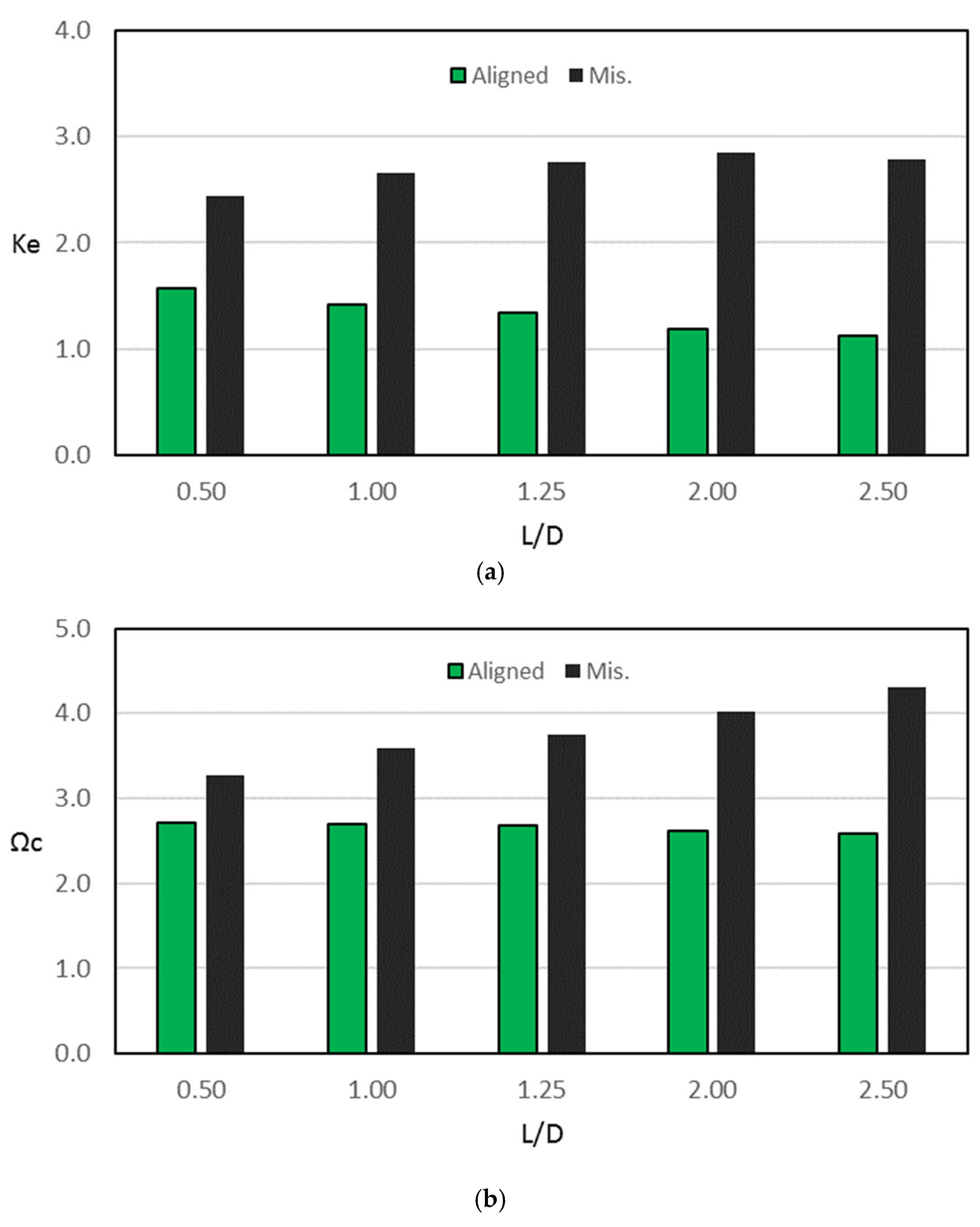
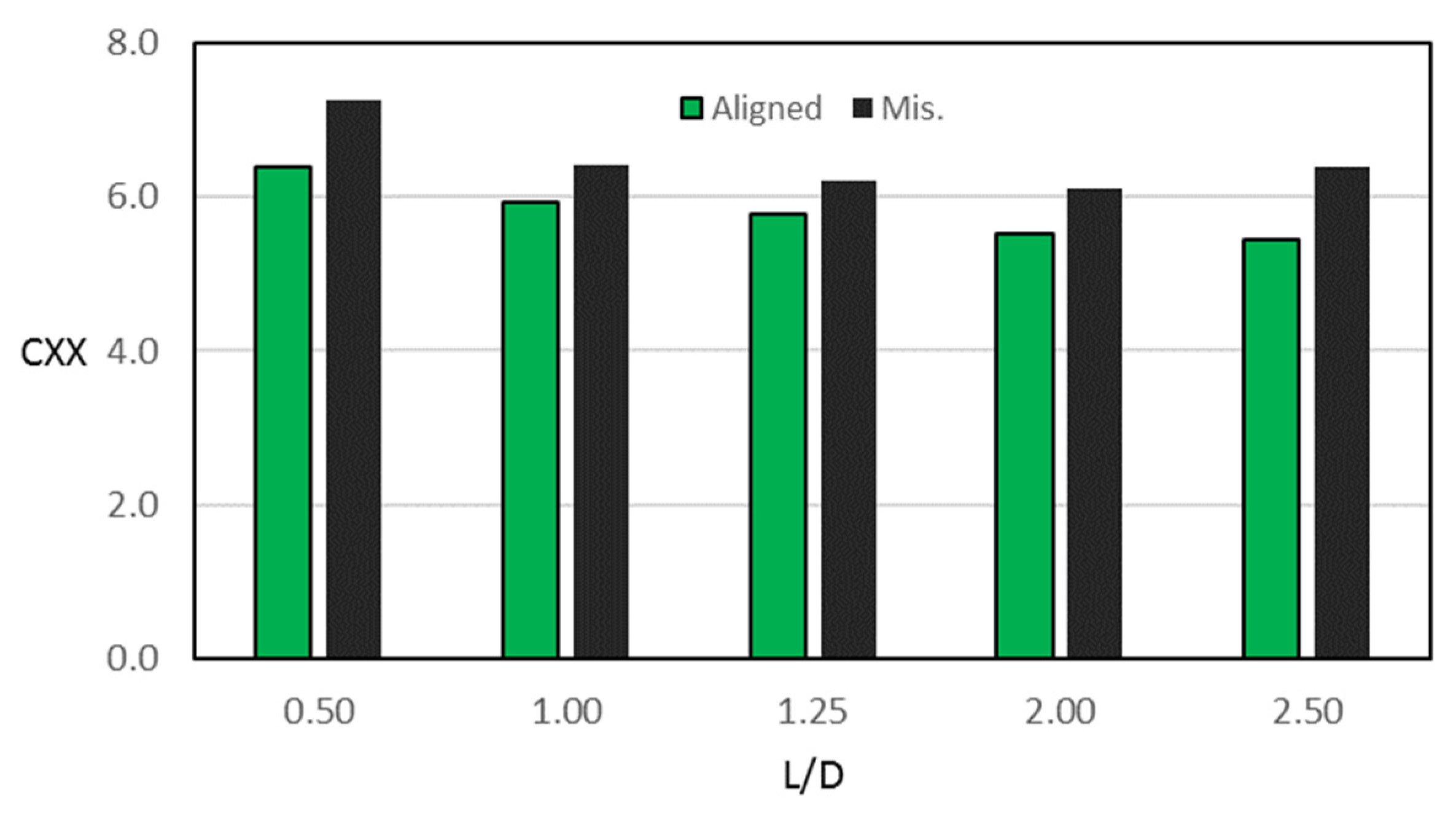
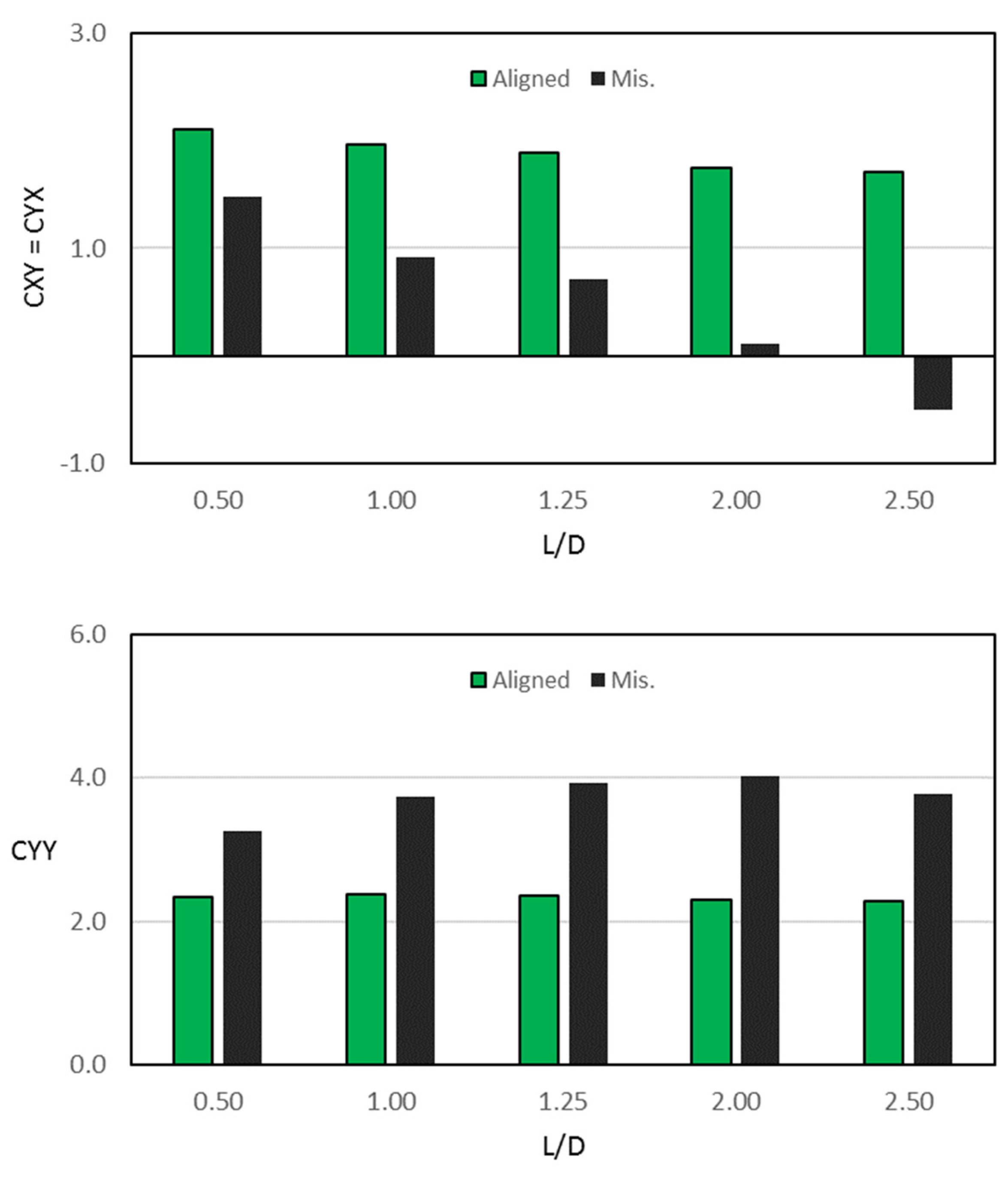
7.2. Effect of the 3D Misalignment on the Characteristics of the System
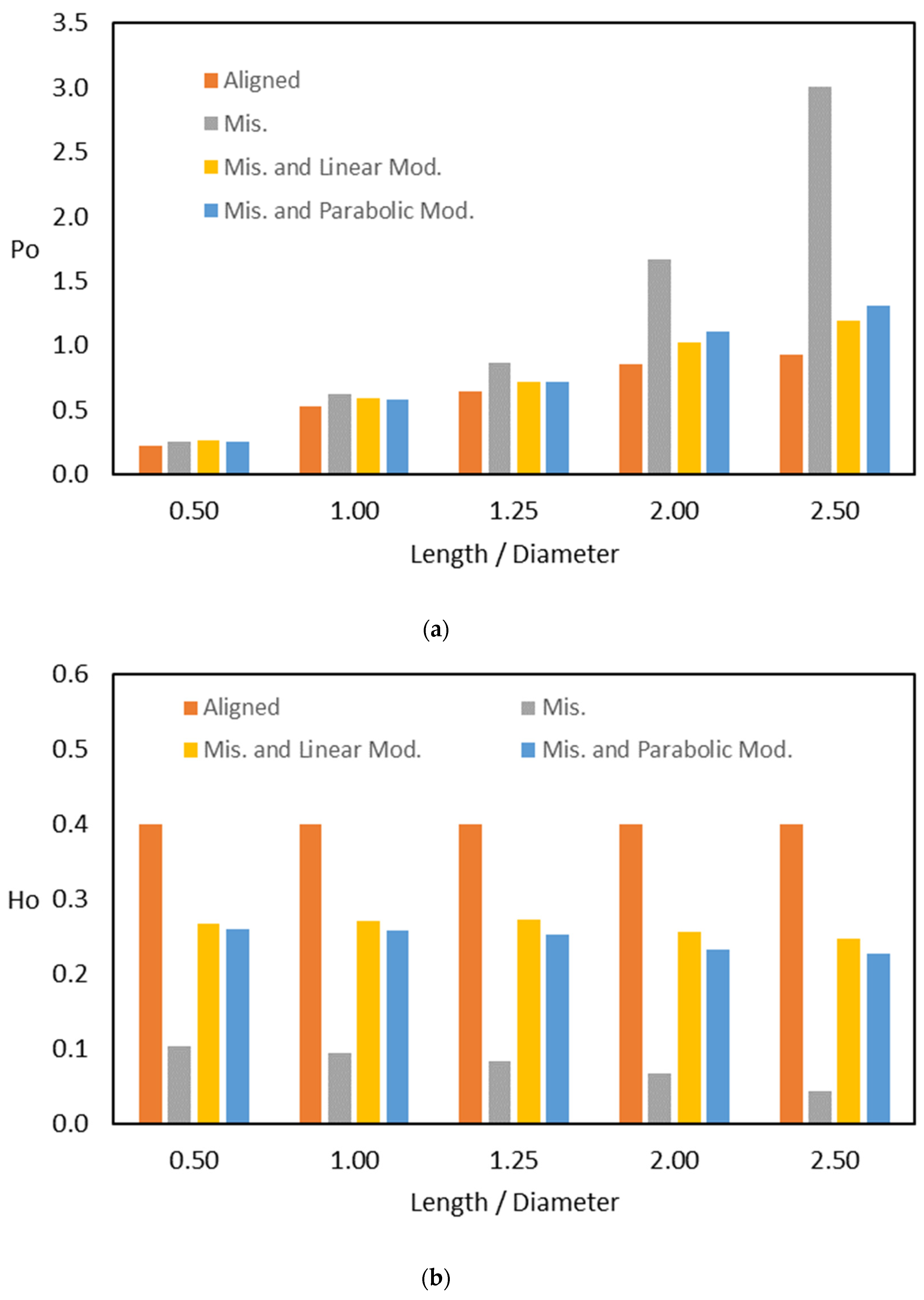
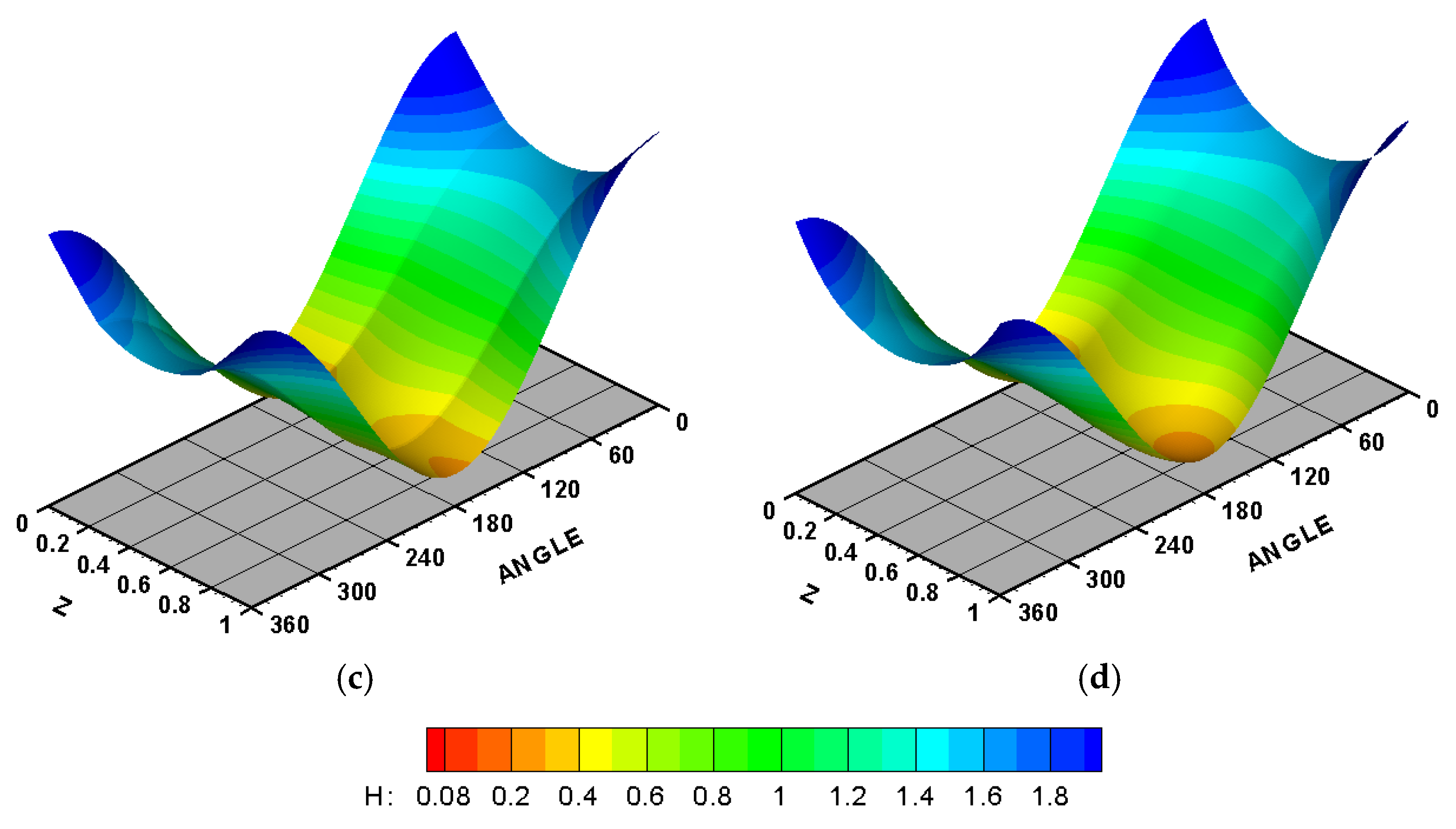
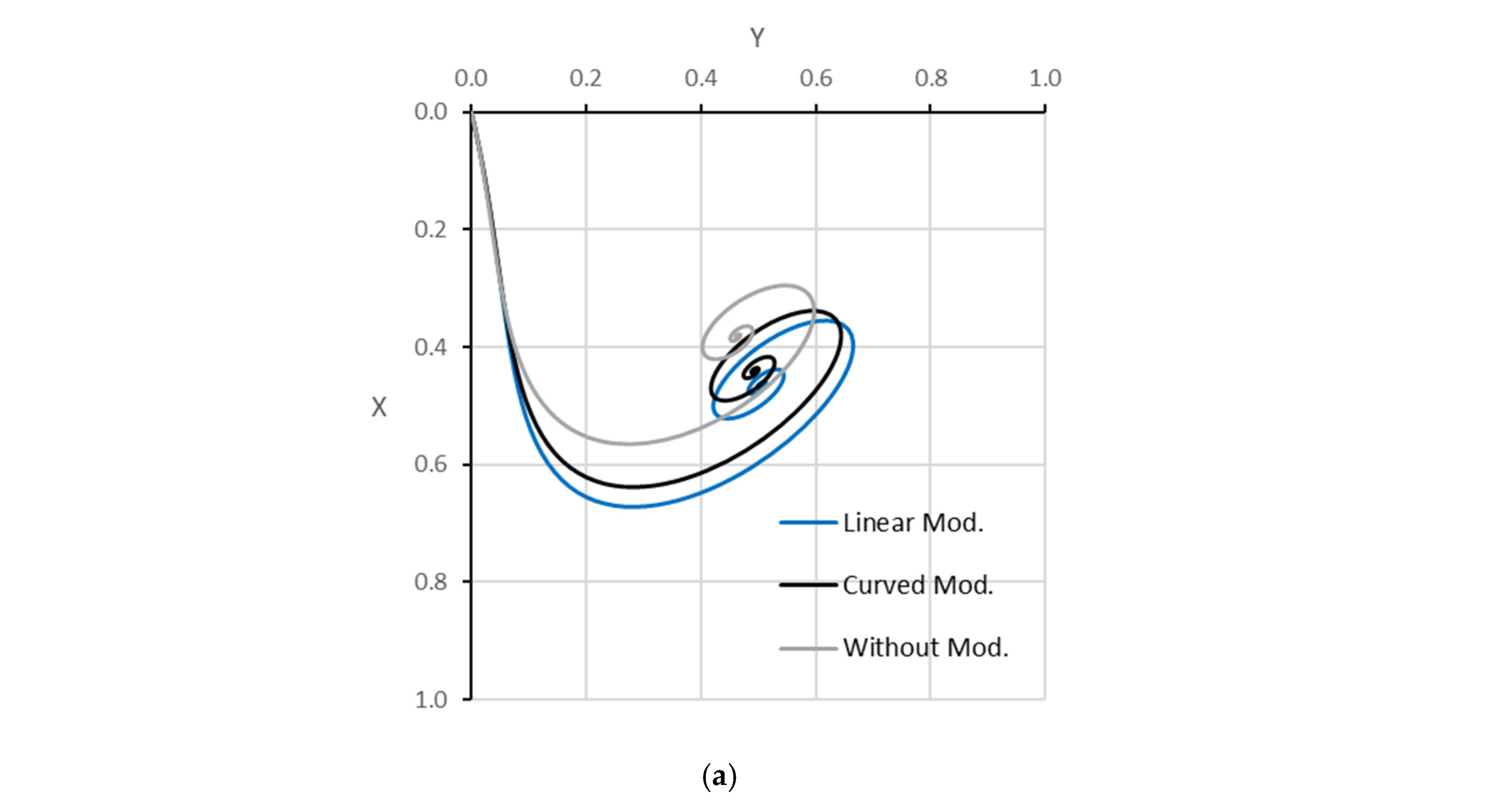
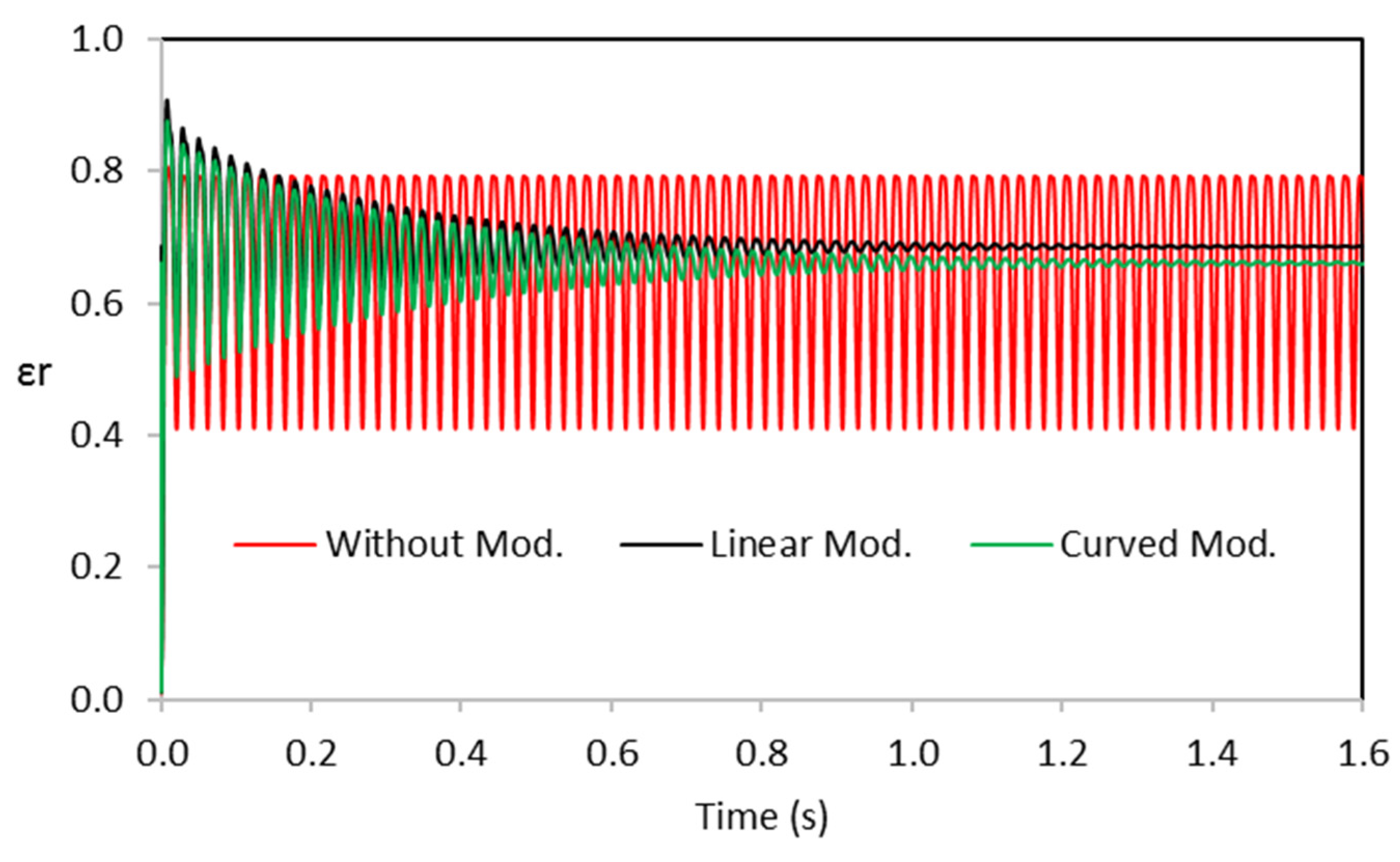
7.3. Modification Effect on the Characteristics of Misaligned Journal Bearing
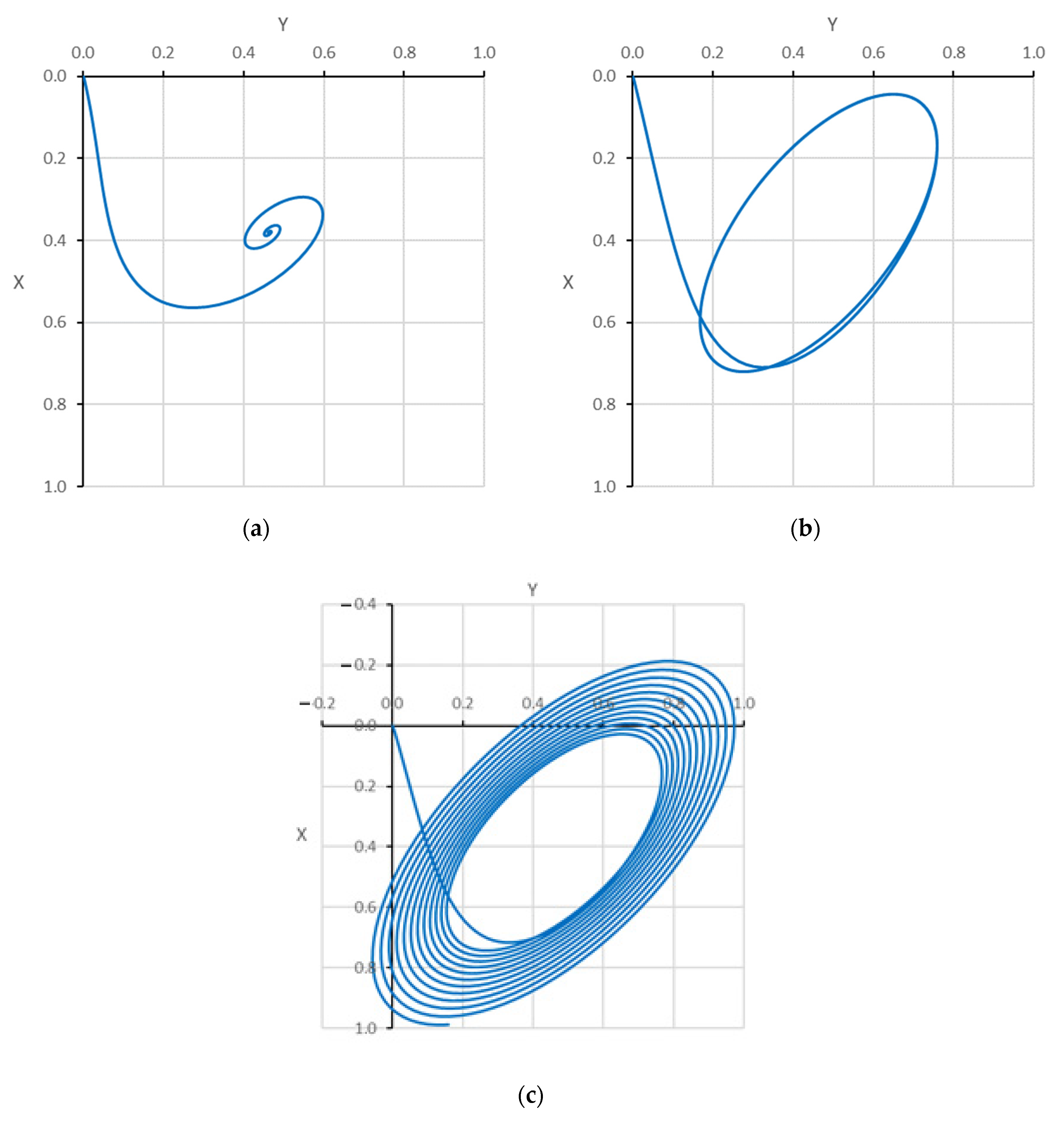
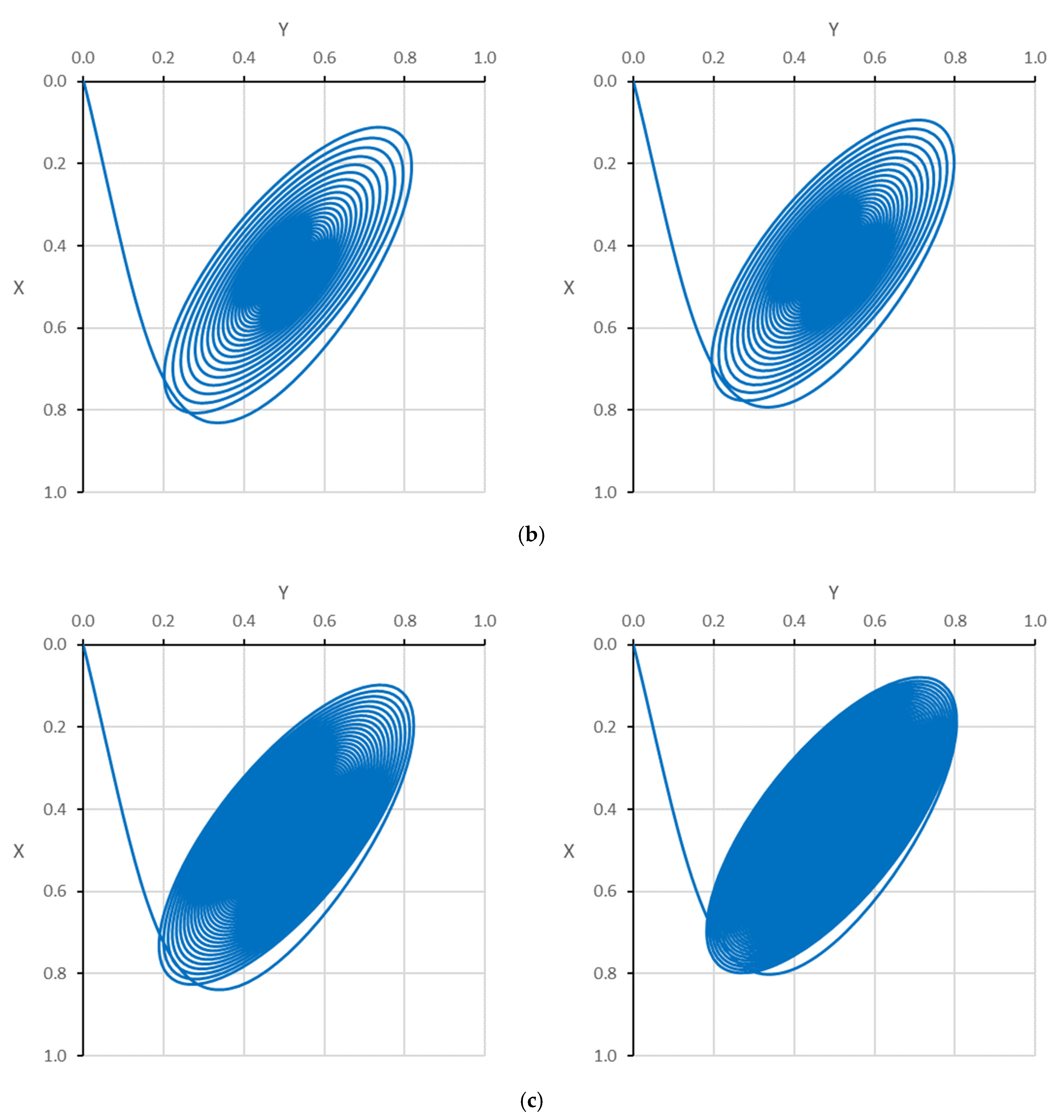
7.4. Effect of Modification on the Journal Trajectory
8. Conclusions and Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, X.; Wu, W.; Yuan, S. Mixed-lubrication analysis of misaligned journal bearing considering turbulence and cavitation. AIP Adv. 2022, 12, 015213. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M. On the characteristics of misaligned journal bearings. Lubricants 2015, 3, 27–53. [Google Scholar] [CrossRef]
- Guo, J.; Xiang, G.; Wang, J.; Song, Y.; Cai, J.; Dai, H. On the dynamic wear behavior of misaligned journal bearing with profile modification under mixed lubrication. Surf. Topogr. Metrol. Prop. 2022, 10, 025026. [Google Scholar] [CrossRef]
- Dufrane, K.; Kannel, J.; McCloskey, T. Wear of steam turbine journal bearings at low operating speeds. J. Tribol. 1983, 105, 313–317. [Google Scholar] [CrossRef]
- Jang, J.; Khonsari, M.M. On the wear of dynamically loaded engine bearings with provision for misalignment and surface roughness. Tribol. Int. 2020, 141, 105919. [Google Scholar] [CrossRef]
- Ebrat, O.; Mourelatos, Z.P.; Vlahopoulos, N.; Vaidyanathan, K. Calculation of journal bearing dynamic characteristics including journal misalignment and bearing structural deformation©. Tribol. Trans. 2004, 47, 94–102. [Google Scholar] [CrossRef]
- Sun, J.; Gui, C.L. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation. Tribol. Int. 2004, 37, 841–848. [Google Scholar] [CrossRef]
- Manser, B.; Belaidi, I.; Hamrani, A.; Khelladi, S.; Bakir, F. Performance of hydrodynamic journal bearing under the combined influence of textured surface and journal misalignment: A numerical survey. Comptes Rendus Mécanique 2019, 347, 141–165. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; Wang, J.; Xiao, K.; Li, J. A transient hydrodynamic lubrication comparative analysis for misaligned micro-grooved bearing considering axial reciprocating movement of shaft. Tribol. Int. 2018, 132, 11–23. [Google Scholar] [CrossRef]
- Ma, J.; Fu, C.; Zhang, H.; Chu, F.; Shi, Z.; Gu, F.; Ball, A.D. Modelling non-Gaussian surfaces and misalignment for condition monitoring of journal bearings. Measurement 2021, 174, 108983. [Google Scholar] [CrossRef]
- Jamali, H.U.; Al-Hamood, A. A New Method for the Analysis of Misaligned Journal Bearing. Tribol. Ind. 2018, 40, 213–224. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.G.; Papadopoulos, C.A. A study of friction in worn misaligned journal bearings under severe hydrodynamic lubrication. Tribol. Int. 2008, 41, 461–472. [Google Scholar] [CrossRef]
- Nacy, S.M. Effect of Chamfering on Side-Leakage Flow Rate of Journal Bearings. Wear 1997, 212, 95–102. [Google Scholar] [CrossRef]
- Fillon, M.; Bouyer, J. Thermohydrodynamic Analysis of a Worn Plain Journal Bearing. Tribol. Int. 2004, 37, 129–136. [Google Scholar] [CrossRef]
- Strzelecki, S. Operating Characteristics of Heavy Loaded Cylindrical Journal Bearing with Variable Axial Profile. Mater. Res. 2005, 8, 481–486. [Google Scholar] [CrossRef]
- Chasalevris, A.; Dohnal, F. Enhancing Stability of Industrial Turbines Using Adjustable Partial Arc Bearings. J. Phys. Conf. Ser. 2016, 744, 12152. [Google Scholar] [CrossRef]
- Ren, P.; Zuo, Z.; Huang, W. Effects of axial profile on the main bearing performance of internal combustion engine and its optimization using multiobjective optimization algorithms. J. Mech. Sci. Technol. 2021, 35, 3519–3531. [Google Scholar] [CrossRef]
- Allmaier, H.; Offner, G. Current Challenges and Frontiers for the EHD Simulation of Journal Bearings: A Review; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Atlassi, K.; Nabhani, M.; El Khlifi, M. Ferrofluid squeeze film lubrication: Surface roughness effect. Ind. Lubr. Tribol. 2023, 75, 133–142. [Google Scholar] [CrossRef]
- Chasalevris, A.; Sfyris, D. Evaluation of the Finite Journal Bearing Characteristics, Using the Exact Analytical Solution of the Reynolds Equation. Tribol. Int. 2013, 57, 216–234. [Google Scholar] [CrossRef]
- Hamrock, B.J. Fundamentals of Fluid Film Lubrication; McGraw-Hill Inc.: New York, NY, USA, 1991. [Google Scholar]
- Harnoy, A. Bearing Design in Machinery: Engineering Tribology and Lubrication, 1st ed.; Marcel Dekker Inc.: New York, NY, USA; Basel, Switzerland, 2002. [Google Scholar]
- Feng, H.; Jiang, S.; Ji, A. Investigation of the Static and Dynamic Characteristics of Water-Lubricated Hydrodynamic Journal Bearing Considering Turbulent, Thermo-hydrodynamic and Misaligned Effects. Tribol. Int. 2019, 130, 245–260. [Google Scholar] [CrossRef]
- Nicholas, J.C. Hydrodynamic journal bearings, types, characteristics and applications. In Proceedings of the 20th Annual Meeting, Valencia, Spain, 8–12 July 1996; The Vibration Institute: Willowbrook, IL, USA, 2016; pp. 79–100. [Google Scholar]
- Lund, J.W.; Thomsen, K.K. A Calculation Method and Data for the Dynamic Coefficients of Oil-Lubricated Journal Bearings; ASME: New York, NY, USA, 1978. [Google Scholar]
- Someya, T. Journal Bearing Databook; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Tieu, A.K.; Qiu, Z.L. Stability of Finite Journal Bearings—From Linear and Nonlinear Bearing Forces. Tribol. Trans. 1995, 38, 627–635. [Google Scholar] [CrossRef]
- Shi, Y.; Li, M. Study on nonlinear dynamics of the marine rotor-bearing system under yawing motion. J. Phys. Conf. Ser. 2020, 1676, 012156. [Google Scholar] [CrossRef]
- D’Amato, R.; Amato, G.; Wang, C.; Ruggiero, A. A Novel Tracking Control Strategy with Adaptive Noise Cancellation for Flexible Rotor Trajectories in Lubricated Bearings. IEEE/ASME Trans. Mechatron. 2021, 27, 753–765. [Google Scholar] [CrossRef]
- Atlassi, K.; Nabhani, M.; El Khlifi, M. Rotational viscosity effect on the stability of finite journal bearings lubricated by ferrofluids. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 548. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamzah, A.A.; Abbas, A.F.; Mohammed, M.N.; Aljibori, H.S.S.; Jamali, H.U.; Abdullah, O.I. An Evaluation of the Design Parameters of a Variable Bearing Profile Considering Journal Perturbation in Rotor–Bearing Systems. Designs 2023, 7, 116. https://doi.org/10.3390/designs7050116
Hamzah AA, Abbas AF, Mohammed MN, Aljibori HSS, Jamali HU, Abdullah OI. An Evaluation of the Design Parameters of a Variable Bearing Profile Considering Journal Perturbation in Rotor–Bearing Systems. Designs. 2023; 7(5):116. https://doi.org/10.3390/designs7050116
Chicago/Turabian StyleHamzah, Adawiya Ali, Abbas Fadhil Abbas, M. N. Mohammed, H. S. S. Aljibori, Hazim U. Jamali, and Oday I. Abdullah. 2023. "An Evaluation of the Design Parameters of a Variable Bearing Profile Considering Journal Perturbation in Rotor–Bearing Systems" Designs 7, no. 5: 116. https://doi.org/10.3390/designs7050116






