Investigation of Stability of CO2 Microbubbles—Colloidal Gas Aphrons for Enhanced Oil Recovery Using Definitive Screening Design
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Definitive Screening Design
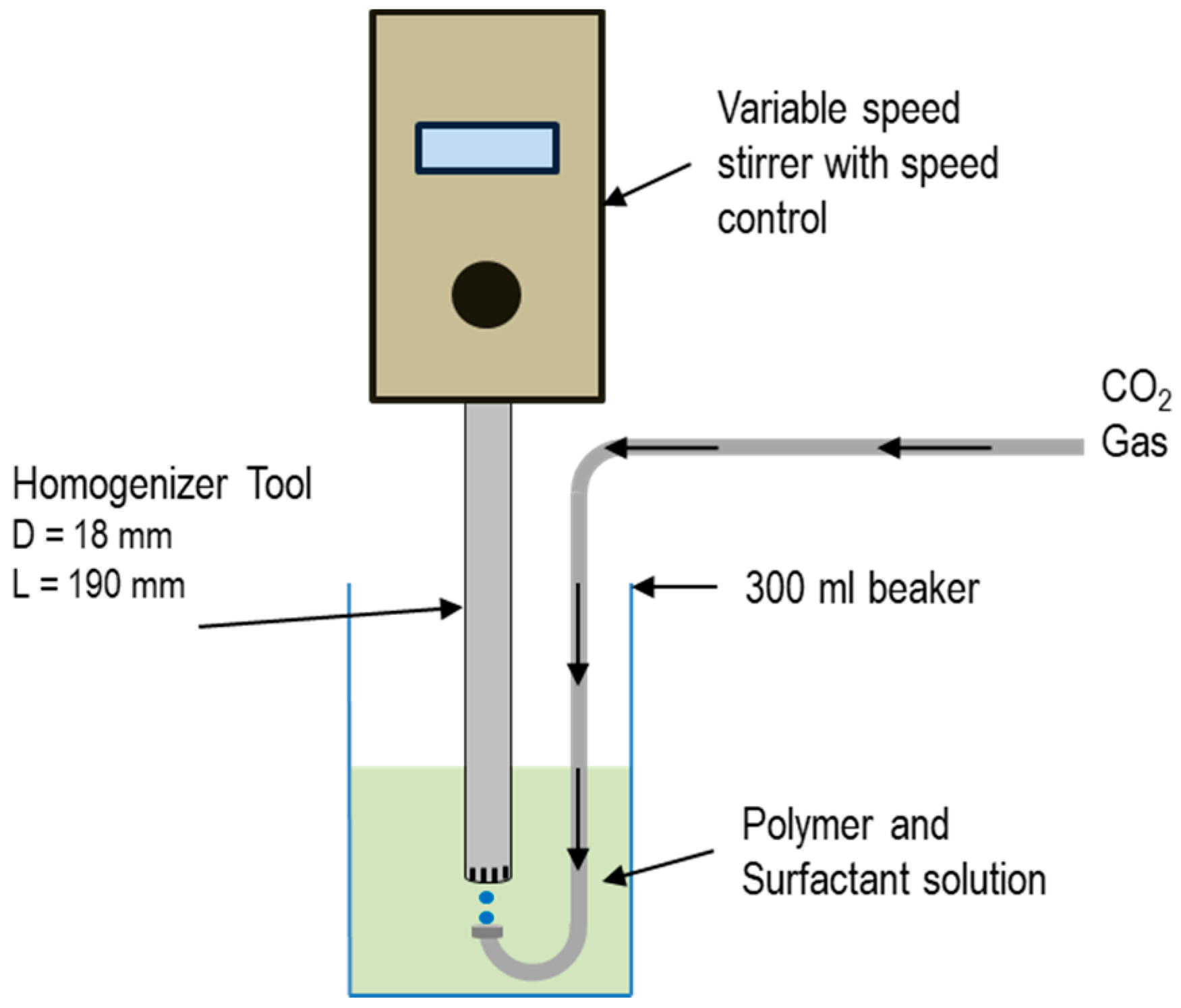
2.3. Preparation of Fluid
2.4. Stability of CO2 Microbubbles
2.5. Visualization of CO2 Microbubbles
3. Results and Discussion
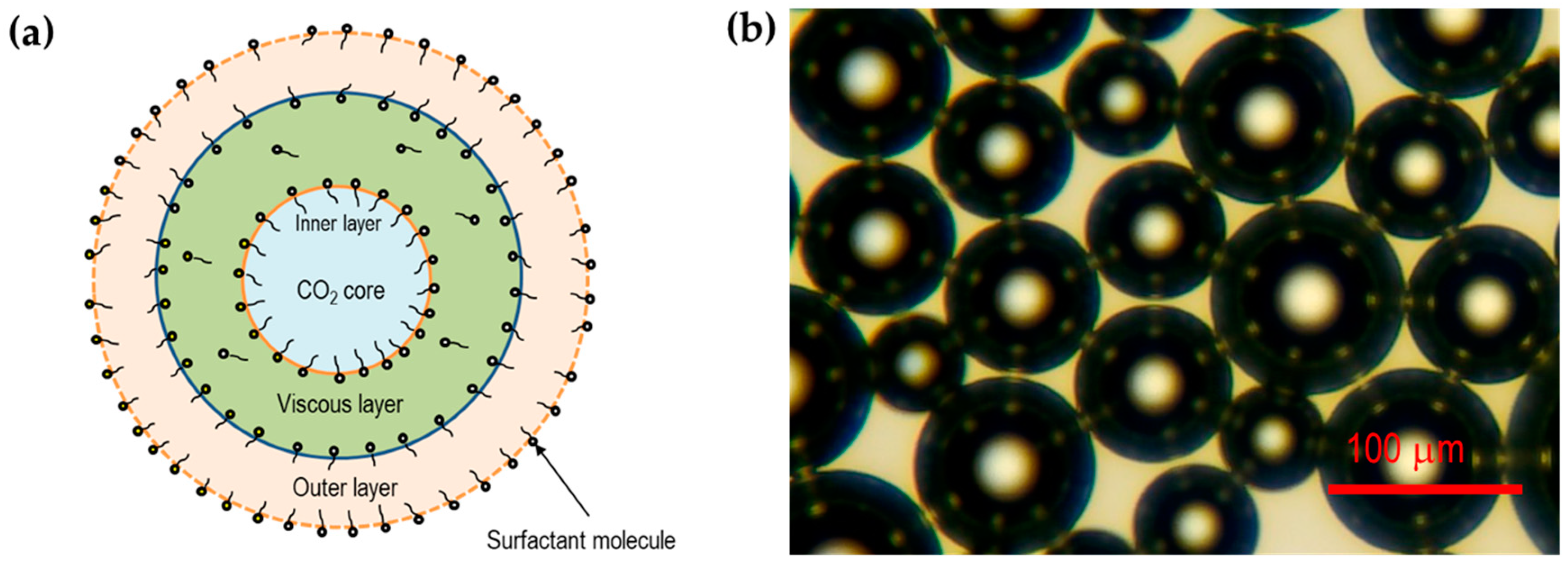
3.1. Characterization of CO2 Microbubbles
3.2. Data obtained from Stability Test
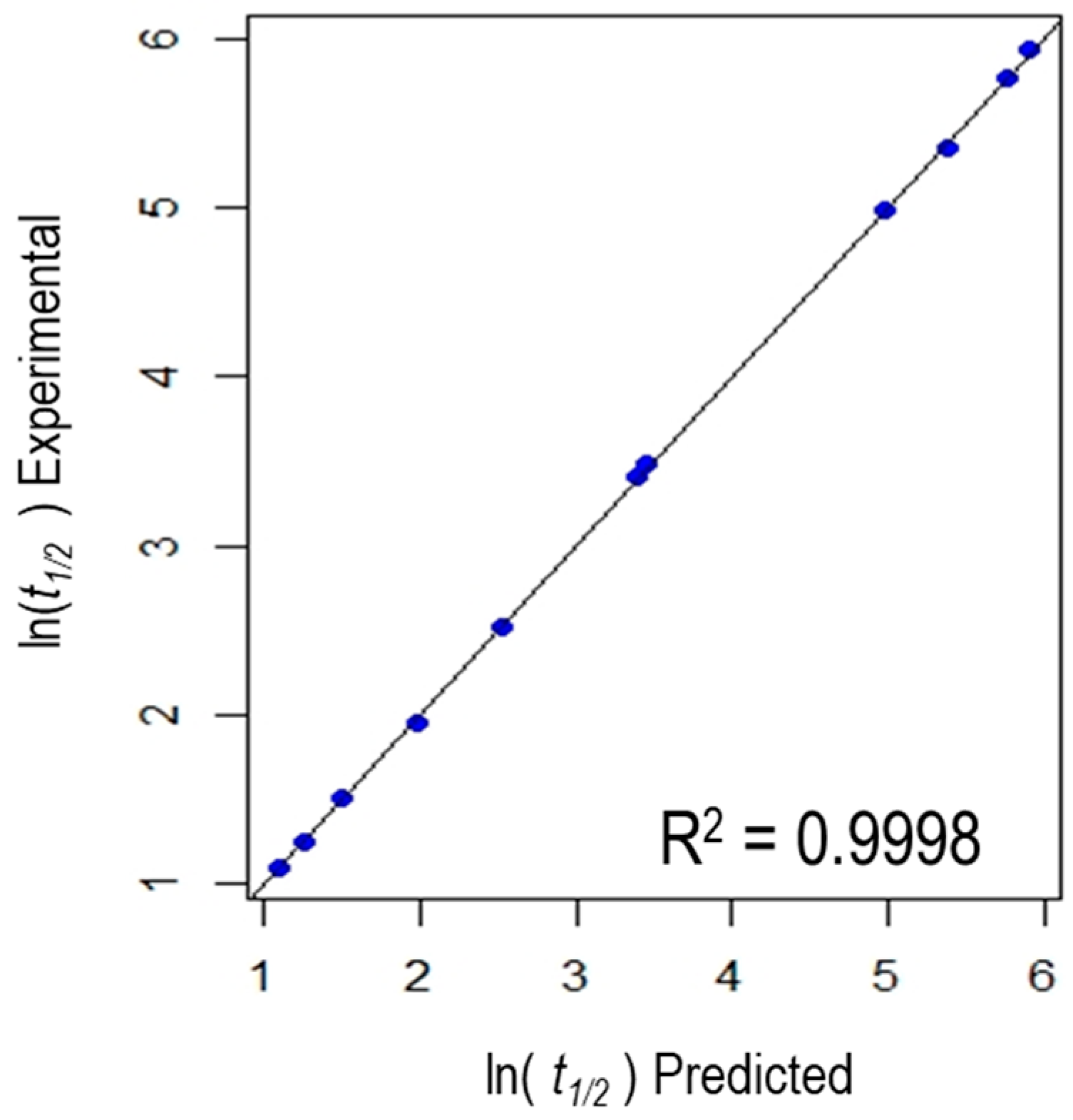
3.3. Statistical Analysis
3.4. Effect of Factors on CO2 Microbubbles Dispersion Stability
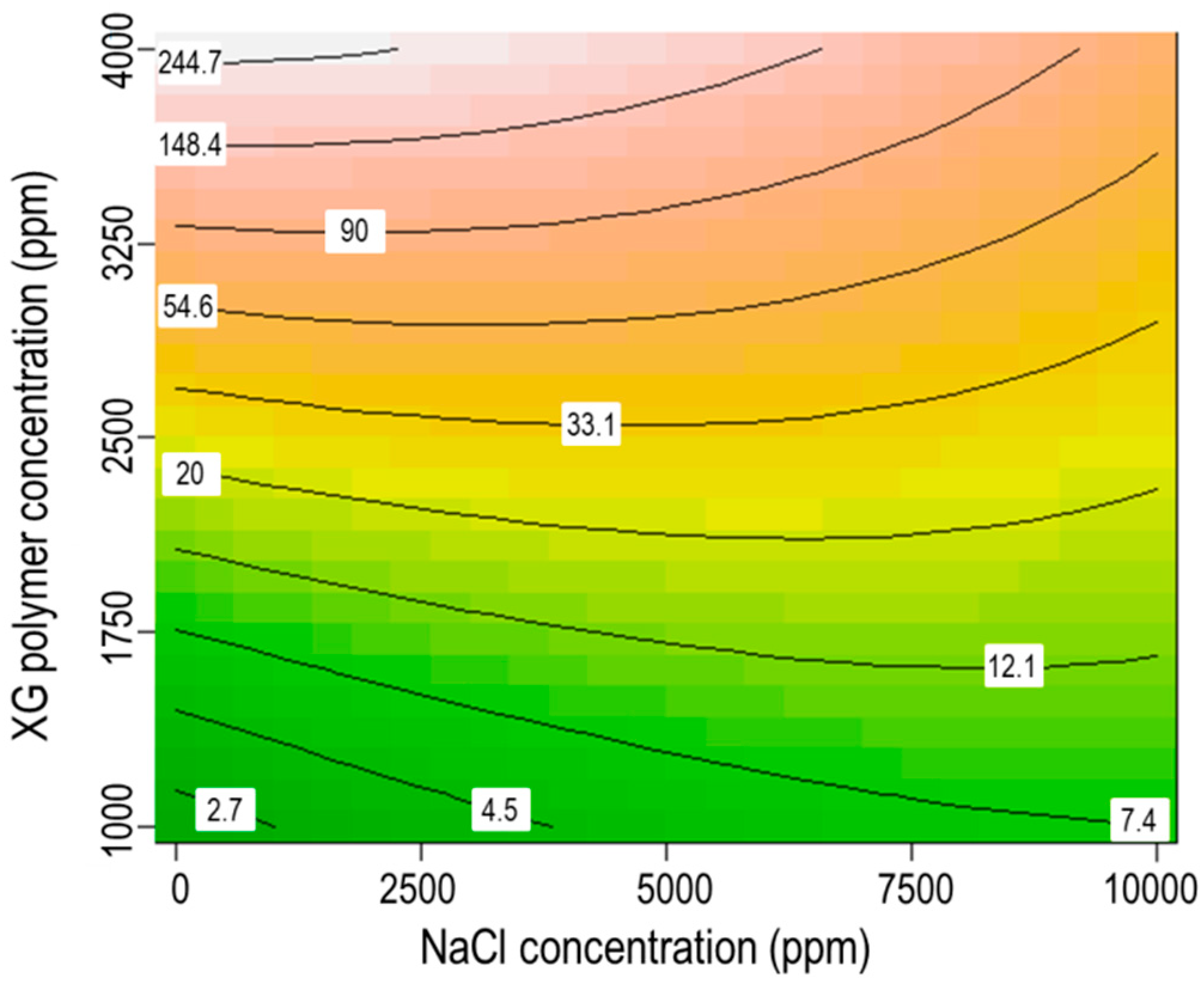
3.5. Interaction between XG Polymer Concentration and Salinity
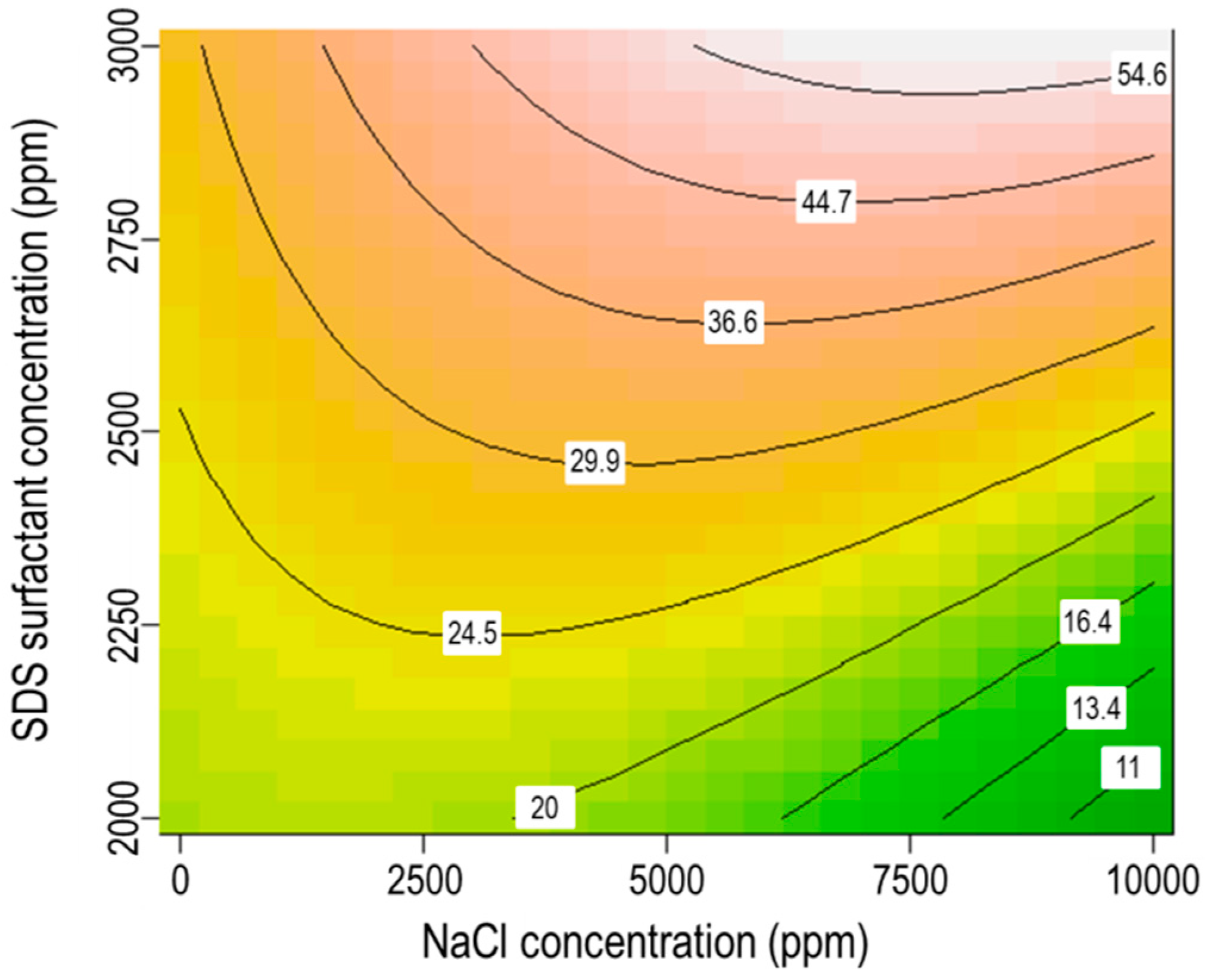
3.6. Interaction between SDS Surfactant Concentration and Salinity
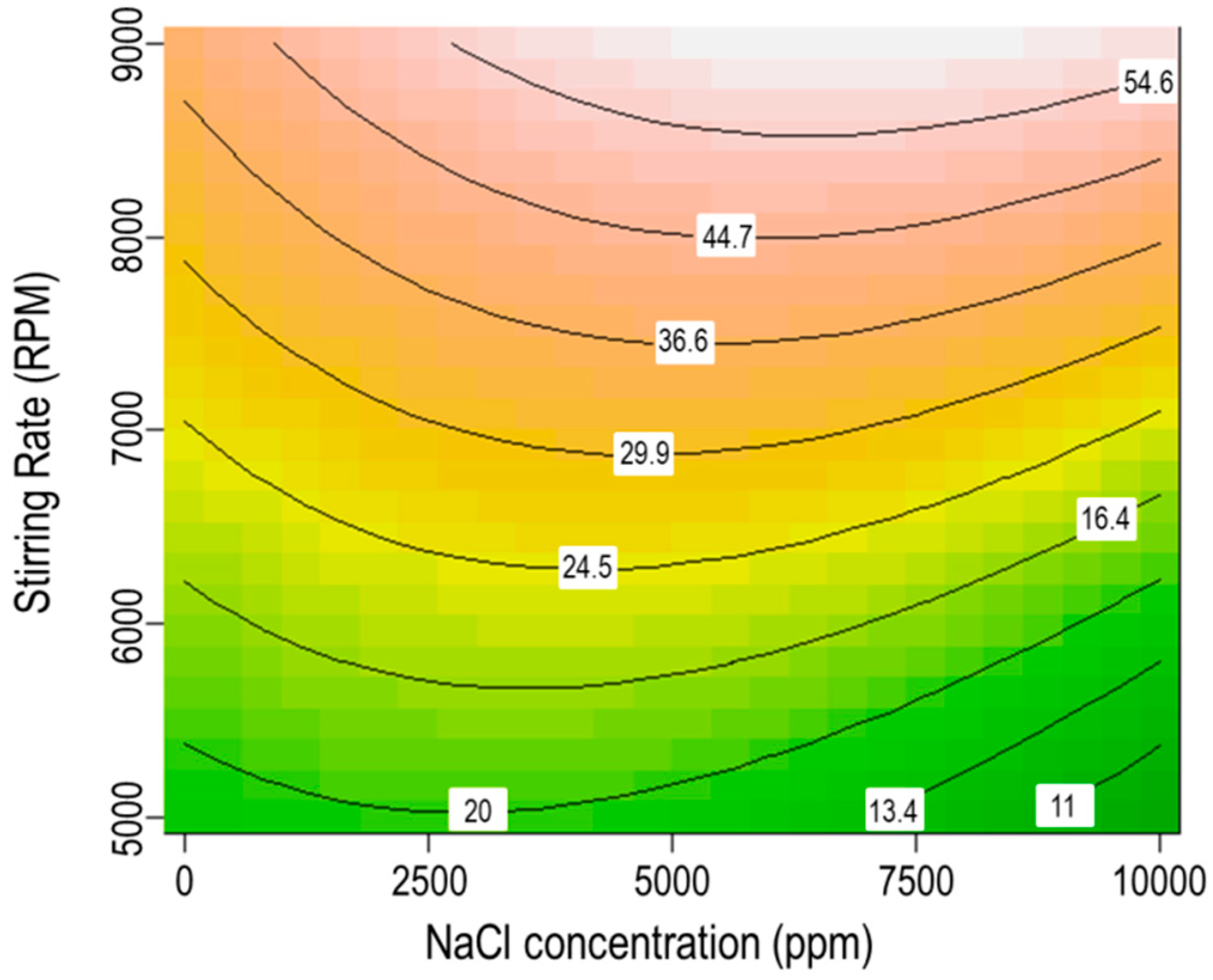
3.7. Interaction between Stirring Rate and Salinity
3.8. Limitation of This Work
4. Conclusions
- XG Polymer concentration is the most significant factor to improve the stability of CO2 microbubbles dispersion.
- CO2 microbubbles stability increases for higher SDS surfactant concentrations and stirring rates but decreases with increasing salinity.
- The interaction of XG polymer concentration and salinity was more considerable than the interactions of SDS surfactant concentration and salinity or stirring rate and salinity on the stability of CO2 microbubbles.
- Increasing NaCl concentration in solution can enhance the function of SDS surfactant and stirring rate to form microbubbles, whereas, it can also reduce the efficiency of polymers in stabilizing microbubbles.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Azzolina, N.A.; Nakles, D.V.; Gorecki, C.D.; Peck, W.D.; Ayash, S.C.; Melzer, L.S.; Chatterjee, S. CO2 storage associated with CO2 enhanced oil recovery: A statistical analysis of historical operations. Int. J. Greenh. Gas Control 2015, 37, 384–397. [Google Scholar] [CrossRef] [Green Version]
- Bachu, S. Identification of oil reservoirs suitable for CO2-EOR and CO2 storage (CCUS) using reserves databases, with application to Alberta, Canada. Int. J. Greenh. Gas Control 2016, 44, 152–165. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Sugai, Y.; Nguele, R.; Sasaki, K. Integrated workflow in 3D geological model construction for evaluation of CO2 storage capacity of a fractured basement reservoir in Cuu Long Basin, Vietnam. Int. J. Greenh. Gas Control 2019, 90, 102826. [Google Scholar] [CrossRef]
- Czarnota, R.; Janiga, D.; Stopa, J.; Wojnarowski, P. Determination of minimum miscibility pressure for CO2 and oil system using acoustically monitored separator. J. CO2 Util. 2017, 17, 32–36. [Google Scholar] [CrossRef]
- Janiga, D.; Czarnota, R.; Kuk, E.; Stopa, J.; Wojnarowski, P. Measurement of Oil-CO2 diffusion coefficient using pulse-echo method for pressure-volume decay approach under reservoir conditions. J. Pet. Sci. Eng. 2020, 185, 106636. [Google Scholar] [CrossRef]
- Rezk, M.G.; Foroozesh, J. Effect of CO2 mass transfer on rate of oil properties changes: Application to CO2-EOR projects. J. Pet. Sci. Eng. 2019, 180, 298–309. [Google Scholar] [CrossRef]
- Lake, L.W. Enhanced Oil Recovery; Prentice Hall: Old Tappan, NJ, USA, 1989; ISBN1 0132816016. ISBN2 9780132816014. [Google Scholar]
- Ghedan, S. Global laboratory experience of CO2-EOR flooding. In Proceedings of the SPE/EAGE Reservoir Characterization & Simulation Conference, Abu Dabi, UAE, 19–21 October 2009; pp. 883–897. [Google Scholar] [CrossRef]
- Dang, C.; Nghiem, L.; Nguyen, N.; Chen, Z.; Nguyen, Q. Evaluation of CO2 Low Salinity Water-Alternating-Gas for enhanced oil recovery. J. Nat. Gas Sci. Eng. 2016, 35, 237–258. [Google Scholar] [CrossRef]
- Telmadarreie, A.; Trivedi, J.J. Evaluating the Performance of CO2 Foam and CO2 Polymer Enhanced Foam for Heavy Oil Recovery: Laboratory Experiments in Unconsolidated and Consolidated Porous Media. In Proceedings of the SPE International Heavy Oil Conference and Exhibition, Kuwait City, Kuwait, 10–12 December 2018. [Google Scholar] [CrossRef]
- Telmadarreie, A.; Trivedi, J. Static and Dynamic Performance of Wet Foam and Polymer-Enhanced Foam in the Presence of Heavy Oil. Colloids Interfaces 2018, 2, 38. [Google Scholar] [CrossRef] [Green Version]
- Sebba, F. Foams and Biliquid Foams-Aphrons; Wiley: Chichester, UK, 1987. [Google Scholar]
- Brookey, T. “Micro-bubbles”: New aphron drill-in fluid technique reduces formation damage in horizontal wells. In Proceedings of the SPE Formation Damage Control Conference, Lafayette, LA, USA, 18–19 February 1998; pp. 645–656. [Google Scholar]
- Ivan, C.D.; Quintana, J.L.; Blake, L.D. Aphron-Base Drilling Fluid: Evolving Technologies for Lost Circulation Control. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–3 October 2001; pp. 553–558. [Google Scholar] [CrossRef]
- White, C.C.; Chesters, A.P.; Ivan, C.D.; Maikranz, S.; Nouris, R. Aphron-based drilling fluid: Novel technology for drilling depleted formations. World Oil 2003, 224, 37–43. [Google Scholar]
- Ramirez, F.; Greaves, R.; Montilva, J. Experience using microbubbles-aphron drilling fluid in mature reservoirs of Lake Maracaibo. In Proceedings of the International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 20–21 February 2002. [Google Scholar]
- Bjorndalen, N.; Kuru, E. Stability of microbubble-based drilling fluids under downhole conditions. J. Can. Pet. Technol. 2008, 47, 40–47. [Google Scholar] [CrossRef]
- Bjorndalen, N.; Kuru, E. Physico-chemical characterization of aphron based drilling fluids. In Proceedings of the Canadian International Petroleum Conference, Calgary, AB, Canada, 7–9 June 2005. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Galedarzadeh, M.; Shadizadeh, S.R. Colloidal gas aphron drilling fluid properties generated by natural surfactants: Experimental investigation. J. Nat. Gas Sci. Eng. 2015, 27, 1109–1117. [Google Scholar] [CrossRef]
- Samuel, S.R. A Laboratory Study of Aqueous Colloidal Gas Aphrons for Enhanced Oil Recovery Applications. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2012. [Google Scholar]
- Khamehchi, E.; Tabibzadeh, S.; Alizadeh, A. Rheological properties of Aphron based drilling fluids. Pet. Explor. Dev. 2016, 43, 1076–1081. [Google Scholar] [CrossRef]
- Alizadeh, A.; Khamehchi, E. Experimental investigation of the oil based Aphron drilling fluid for determining the most stable fluid formulation. J. Pet. Sci. Eng. 2019, 174, 525–532. [Google Scholar] [CrossRef]
- Save, S.V.; Pangarkar, V.G. Characterisation of colloidal gas aphrons. Carbohydr. Polym. 1994, 127, 35–54. [Google Scholar] [CrossRef]
- Jauregi, P.; Gilmour, S.; Varley, J. Characterisation of colloidal gas aphrons for subsequent use for protein recovery. Chem. Eng. J. 1997, 65, 1–11. [Google Scholar] [CrossRef]
- Tabzar, A.; Arabloo, M.; Ghazanfari, M.H. Rheology, stability and filtration characteristics of Colloidal Gas Aphron fluids: Role of surfactant and polymer type. J. Nat. Gas Sci. Eng. 2015, 26, 895–906. [Google Scholar] [CrossRef]
- Hosseini-Kaldozakh, S.; Khamehchi, E.; Dabir, B.; Alizadeh, A.; Mansoori, Z. Experimental Investigation of Water Based Colloidal Gas Aphron Fluid Stability. Colloids Interfaces 2019, 3, 31. [Google Scholar] [CrossRef] [Green Version]
- Alizadeh, A.; Khamehchi, E. Modeling of micro-bubble surfactant multi-layer drilling fluid stability based on single bubble behavior under pressure and temperature in a deviated gas well. J. Nat. Gas Sci. Eng. 2015, 26, 42–50. [Google Scholar] [CrossRef]
- Alizadeh, A.; Khamehchi, E. A model for predicting size distribution and liquid drainage from micro-bubble surfactant multi-layer fluids using population balance. Colloid Polym. Sci. 2015, 293, 3419–3427. [Google Scholar] [CrossRef]
- Alizadeh, A.; Khamehchi, E. Mathematical modeling of the Colloidal Gas Aphron transport through porous medium using the filtration theory. J. Nat. Gas Sci. Eng. 2017, 44, 37–53. [Google Scholar] [CrossRef] [Green Version]
- Bjorndalen, N.; Alvarez, J.; Jossy, E.; Kuru, E. An Experimental Study of the Pore-Blocking Mechanisms of Aphron Drilling Fluids Using Micromodels. In Proceedings of the SPE International Symposium on Oilfield Chemistry, The Woodlands, TX, USA, 20–22 April 2009. [Google Scholar] [CrossRef]
- Shi, S.; Wang, Y.; Li, Z.; Chen, Q.; Zhao, Z. Laboratory investigation of the factors impact on bubble size, pore blocking and enhanced oil recovery with aqueous Colloidal Gas Aphron. J. Pet. Explor. Prod. Technol. 2016, 6, 409–417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akai, T.; Xue, Z.; Yamashita, Y.; Yoshizawa, M. Application of CO2 micro bubble for the innovative CO2-EOR. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 9–12 November 2015. [Google Scholar]
- Natawijaya, M.A.; Sugai, Y.; Anggara, F. CO2 microbubble colloidal gas aphrons for EOR application: The generation using porous filter, diameter size analysis and gas blocking impact on sweep efficiency. J. Pet. Explor. Prod. Technol. 2020, 10, 103–113. [Google Scholar] [CrossRef] [Green Version]
- Telmadarreie, A.; Doda, A.; Trivedi, J.J.; Kuru, E.; Choi, P. CO2 microbubbles—A potential fluid for enhanced oil recovery: Bulk and porous media studies. J. Pet. Sci. Eng. 2016, 138, 160–173. [Google Scholar] [CrossRef]
- Ghosh, M. Laboratory Study on the Generation and Characterisation of CO2 Colloidal Gas Aphrons. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2013. [Google Scholar]
- Jones, B.; Nachtsheim, C.J. A class of three-level designs for definitive screening in the presence of second-order effects. J. Qual. Technol. 2011, 43, 1–15. [Google Scholar] [CrossRef]
- Weese, M.L.; Ramsey, P.J.; Montgomery, D.C. Analysis of definitive screening designs: Screening vs prediction. Appl. Stoch. Model. Bus. Ind. 2018, 34, 244–255. [Google Scholar] [CrossRef]
- Erler, A.; de Mas, N.; Ramsey, P.; Henderson, G. Efficient biological process characterization by definitive-screening designs: The formaldehyde treatment of a therapeutic protein as a case study. Biotechnol. Lett. 2013, 35, 323–329. [Google Scholar] [CrossRef]
- Parmar, R.; Majumder, S.K. Chemical Engineering and Processing: Process Intensification Microbubble generation and microbubble-aided transport process intensification—A state-of-the-art report. Chem. Eng. Process. 2013, 64, 79–97. [Google Scholar] [CrossRef]
- Libbrecht, W.; Deruyck, F.; Poelman, H.; Verberckmoes, A.; Thybaut, J.; De Clercq, J.; Van Der Voort, P. Optimization of soft templated mesoporous carbon synthesis using Definitive Screening Design. Chem. Eng. J. 2015, 259, 126–134. [Google Scholar] [CrossRef]
- Zhao, J.; Li, W.; Qu, H.; Tian, G.; Wei, Y. Application of definitive screening design to quantify the effects of process parameters on key granule characteristics and optimize operating parameters in pulsed-spray fluid-bed granulation. Particuology 2019, 43, 56–65. [Google Scholar] [CrossRef]
- John, A. Package ‘Daewr.’, Version 1.2-2; John Lawson: Provo, UT, USA, 2020. [Google Scholar]
- Feng, W.; Singhal, N.; Swift, S. Drainage mechanism of microbubble dispersion and factors influencing its stability. J. Colloid Interface Sci. 2009, 337, 548–554. [Google Scholar] [CrossRef]
- Pasdar, M.; Kazemzadeh, E.; Kamari, E.; Ghazanfari, M.H.; Soleymani, M. Monitoring the role of polymer and surfactant concentrations on bubble size distribution in colloidal gas aphron based fluids. Colloids Surf. A Phys. Eng. Asp. 2018, 556, 93–98. [Google Scholar] [CrossRef]
- Yan, Y.L.; Qu, C.T.; Zhang, N.S.; Yang, Z.G.; Liu, L. A study on the kinetics of liquid drainage from colloidal gas aphrons (CGAs). Colloids Surf. A Phys. Eng. Asp. 2005, 259, 167–172. [Google Scholar] [CrossRef]
- Arabloo, M.; Pordel Shahri, M. Experimental studies on stability and viscoplastic modeling of colloidal gas aphron (CGA) based drilling fluids. J. Pet. Sci. Eng. 2014, 113, 8–22. [Google Scholar] [CrossRef]
- Wassenius, H.; Nydén, M.; Holmberg, K. Dispersion stability evaluated by experimental design. J. Dispers. Sci. Technol. 2001, 22, 297–309. [Google Scholar] [CrossRef]
- Sahu, U.K.; Mahapatra, S.S.; Patel, R.K. Application of Box–Behnken Design in response surface methodology for adsorptive removal of arsenic from aqueous solution using CeO2/Fe2O3/graphene nanocomposite. Mater. Chem. Phys. 2018, 207, 233–242. [Google Scholar] [CrossRef]
- Dahmoune, F.; Spigno, G.; Moussi, K.; Remini, H.; Cherbal, A.; Madani, K. Pistacia lentiscus leaves as a source of phenolic compounds: Microwave-assisted extraction optimized and compared with ultrasound-assisted and conventional solvent extraction. Ind. Crop. Prod. 2014, 61, 31–40. [Google Scholar] [CrossRef]
- Ekren, B.Y.; Heragu, S.S. Simulation-based regression analysis for the rack configuration of an autonomous vehicle storage and retrieval system. Int. J. Prod. Res. 2010, 48, 6257–6274. [Google Scholar] [CrossRef]
- Sadoun, O.; Rezgui, F.; G’Sell, C. Optimization of valsartan encapsulation in biodegradables polyesters using Box-Behnken design. Mater. Sci. Eng. C 2018, 90, 189–197. [Google Scholar] [CrossRef]
- Keshavarzi, B.; Mahmoudvand, M.; Javadi, A.; Bahramian, A.; Miller, R.; Eckert, K. Salt Effects on Formation and Stability of Colloidal Gas Aphrons Produced by Anionic and Zwitterionic Surfactants in Xanthan Gum Solution. Colloids Interfaces 2020, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Pandey, S.; Bagwe, R.P.; Shah, D.O. Effect of counterions on surface and foaming properties of dodecyl sulfate. J. Colloid Interface Sci. 2003, 267, 160–166. [Google Scholar] [CrossRef]
- Xu, Q.; Nakajima, M.; Ichikawa, S.; Nakamura, N.; Roy, P.; Okadome, H.; Shiina, T. Effects of surfactant and electrolyte concentrations on bubble formation and stabilization. J. Colloid Interface Sci. 2009, 332, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Sadeghialiabadi, H.; Amiri, M.C. A new stability index for characterizing the colloidal gas aphrons dispersion. Colloids Surf. A Phys. Eng. Asp. 2015, 471, 170–177. [Google Scholar] [CrossRef]
- Longe, T.A. Colloidal Gas Aphrons: Generation, Flow Characterization and Application in Soil and Groundwater Decontamination. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1989. [Google Scholar]
- Popov, P.; Growcock, F. R&D validates effectiveness of aphron drilling fluids. Drill. Contract. 2005, 61, 55–58. [Google Scholar]




| Factors Code | Factors Name | Level of Factor | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| A | XG Polymer Concentration (ppm) | 1000 | 2500 | 4000 |
| B | SDS Surfactant Concentration (ppm) | 2000 | 2500 | 3000 |
| C | Salinity (ppm) | 0 | 5000 | 10000 |
| D | Stirring Time (min) | 4 | 7 | 9 |
| E | Stirring Rate (rpm) | 5000 | 7000 | 9000 |
| Exp. | Coded Values | Actual Values | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | XG Polymer Conc. (ppm) | SDS Surfactant Conc. (ppm) | Salinity (ppm) | Stirring Time (min) | Stirring Rate (rpm) | |
| 1 | 0 | 1 | 1 | 1 | 1 | 2500 | 3000 | 10,000 | 10 | 9000 |
| 2 | 0 | −1 | −1 | −1 | −1 | 2500 | 2000 | 0 | 4 | 5000 |
| 3 | 1 | 0 | 1 | 1 | −1 | 4000 | 2500 | 10,000 | 10 | 5000 |
| 4 | −1 | 0 | −1 | −1 | 1 | 1000 | 2500 | 0 | 4 | 9000 |
| 5 | 1 | −1 | 0 | 1 | 1 | 4000 | 2000 | 5000 | 10 | 9000 |
| 6 | −1 | 1 | 0 | −1 | −1 | 1000 | 3000 | 5000 | 4 | 5000 |
| 7 | 1 | −1 | −1 | 0 | 1 | 4000 | 2000 | 0 | 7 | 9000 |
| 8 | −1 | 1 | 1 | 0 | −1 | 1000 | 3000 | 10,000 | 7 | 5000 |
| 9 | 1 | 1 | −1 | −1 | 0 | 4000 | 3000 | 0 | 4 | 7000 |
| 10 | −1 | −1 | 1 | 1 | 0 | 1000 | 2000 | 10,000 | 10 | 7000 |
| 11 | 0 | 0 | 0 | 0 | 0 | 2500 | 2500 | 5000 | 4 | 7000 |
| Experiment | Mean Diameter (μm) | Standard Deviation (μm) |
|---|---|---|
| 1 | 107.4 | 41.8 |
| 2 | 140.1 | 64.5 |
| 3 | 138.8 | 44.2 |
| 4 | 86.6 | 36.5 |
| 5 | 150.1 | 60.0 |
| 6 | 119.6 | 36.8 |
| 7 | 115.1 | 59.6 |
| 8 | 129.3 | 50.7 |
| 9 | 91.6 | 33.9 |
| 10 | 94.3 | 30.7 |
| 11 | 162.7 | 57.3 |
| Exp. | Final Liquid Volume (mL) | t1/2 (min) |
|---|---|---|
| 1 | 42 | 147.0 |
| 2 | 66 | 12.5 |
| 3 | 57 | 30.0 |
| 4 | 83 | 3.5 |
| 5 | 40 | 210.0 |
| 6 | 95 | 4.0 |
| 7 | 45 | 380.0 |
| 8 | 45 | 7.0 |
| 9 | 85 | 318.0 |
| 10 | 85 | 3.0 |
| 11 | 33 | 32.5 |
| Coefficient | Coded Term | Estimate | Standard Error | t-Value | p-Value |
|---|---|---|---|---|---|
| β0 | Intercept | 3.44414 | 0.03146 | 109.473 | 8.34 × 10−5 |
| β1 | A | 1.78542 | 0.02060 | 86.687 | 0.000133 |
| β2 | B | 0.53791 | 0.02060 | 26.117 | 0.001463 |
| β3 | C | −0.01799 | 0.02060 | −0.873 | 0.474559 |
| β5 | E | 0.70282 | 0.02060 | 34.124 | 0.000858 |
| β13 | CA | −0.62486 | 0.02345 | −26.647 | 0.019436 |
| β23 | CB | 0.36633 | 0.02345 | 15.622 | 0.001405 |
| β35 | CE | 0.21995 | 0.02345 | 9.380 | 0.004073 |
| β33 | C2 | −0.27234 | 0.03853 | −7.068 | 0.011176 |
| R2 = 0.9998, Adjusted R2 = 0.9991, F-value = 1462, p-value = 0.0006837 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen Hai Le, N.; Sugai, Y.; Sasaki, K. Investigation of Stability of CO2 Microbubbles—Colloidal Gas Aphrons for Enhanced Oil Recovery Using Definitive Screening Design. Colloids Interfaces 2020, 4, 26. https://doi.org/10.3390/colloids4020026
Nguyen Hai Le N, Sugai Y, Sasaki K. Investigation of Stability of CO2 Microbubbles—Colloidal Gas Aphrons for Enhanced Oil Recovery Using Definitive Screening Design. Colloids and Interfaces. 2020; 4(2):26. https://doi.org/10.3390/colloids4020026
Chicago/Turabian StyleNguyen Hai Le, Nam, Yuichi Sugai, and Kyuro Sasaki. 2020. "Investigation of Stability of CO2 Microbubbles—Colloidal Gas Aphrons for Enhanced Oil Recovery Using Definitive Screening Design" Colloids and Interfaces 4, no. 2: 26. https://doi.org/10.3390/colloids4020026




