Modelling and Control of Longitudinal Vibrations in a Radio Frequency Cavity
Abstract
:1. Introduction
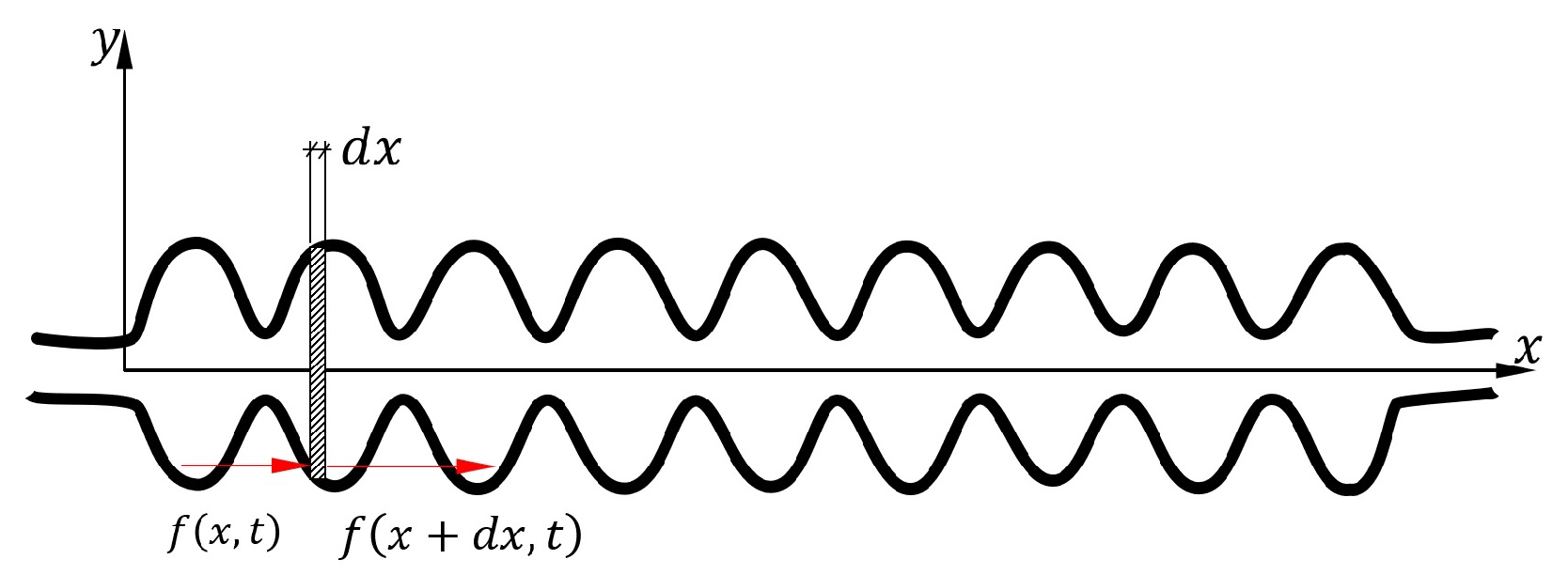
2. Longitudinal Flexural Dynamic Modeling
- (a)
- Free–Free Boundary ConditionThe boundary conditions are assumed to be free–free, i.e., at both ends of the beam, and the force is zero. Thus, the frequency and the mode shape function for this boundary condition can be defined as
- (b)
- Free–Fixed Boundary ConditionAssumes that the beam is fixed at one end and free at the other end. The frequency and mode shape, in this case, have been obtained as
- (c)
- Free-Ends-Fixed Middle Boundary ConditionAssumes that the beam is free at both ends but fixed in the middle. The dynamic is symmetric about the midpoint . For this type of boundary condition, the frequency and mode shapes are determined as
3. Free Vibration Analysis
3.1. Energy Method
3.2. Virtual Work
- (a)
- Free–FreeFor this boundary condition with a uniform cross-section dynamic, the mode shape function can be defined as (13). So, the generalized force function will be
- (b)
- Fixed–FreeFor this boundary condition, the mode shape function is defined in Equation (15), and the input vector is
- (c)
- Ends Free–Middle FixedIn this condition, the output of the system is a displacement function at point x = 0, and it is defined aswhere
3.3. Transfer Function of the System
4. Controller Design
4.1. Controllability
4.2. Lyapunov-Based Controller
4.3. Observability
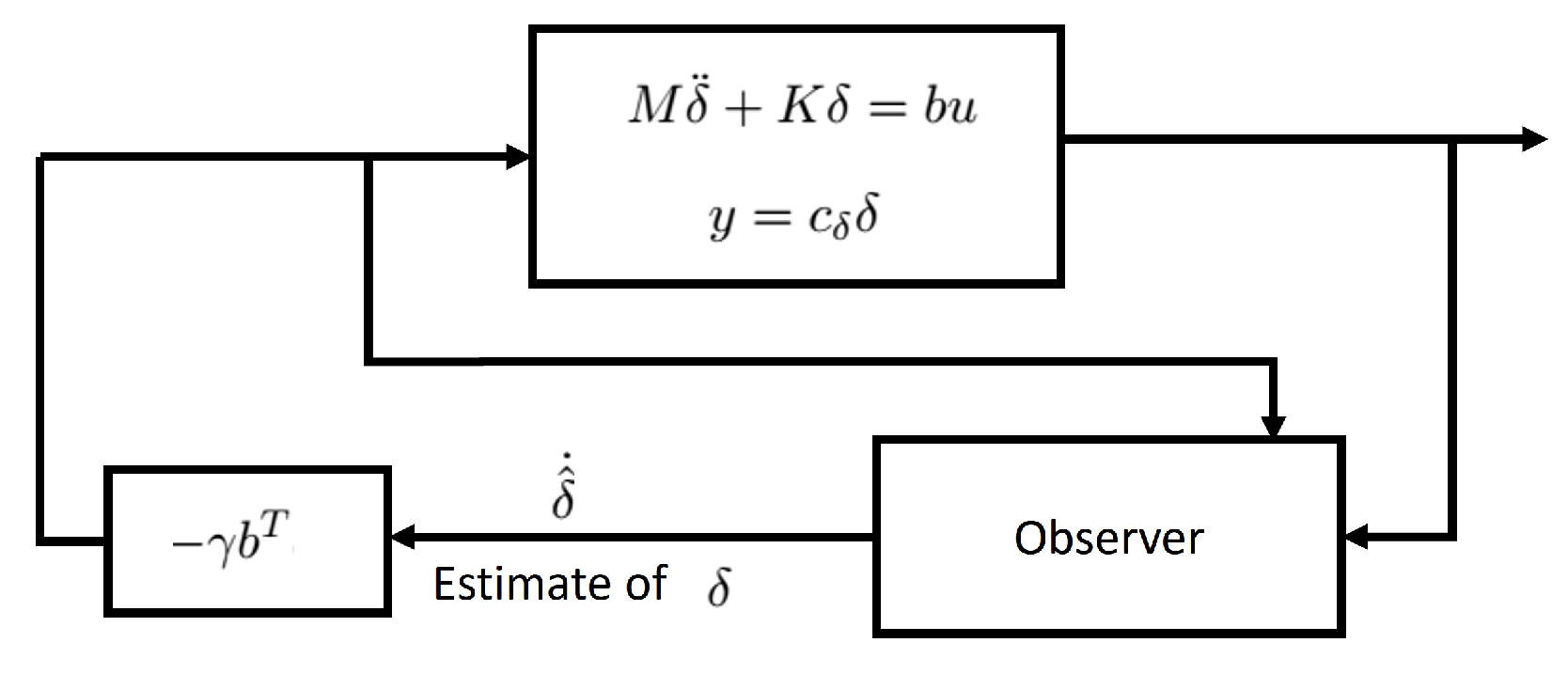
4.4. Observer Design
4.5. Observer-Based Controller Transfer Function
5. Experiment and Simulation Studies
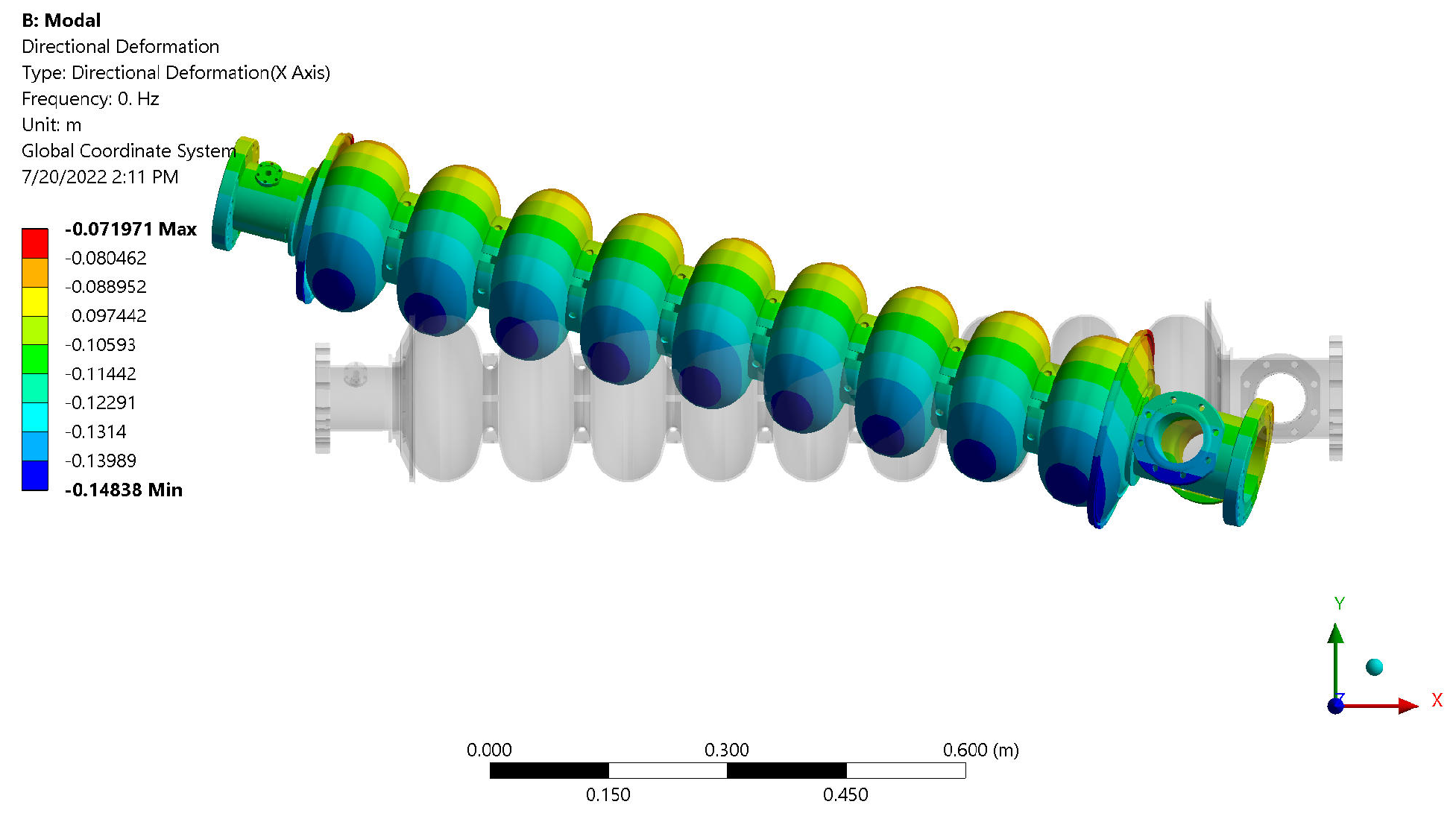
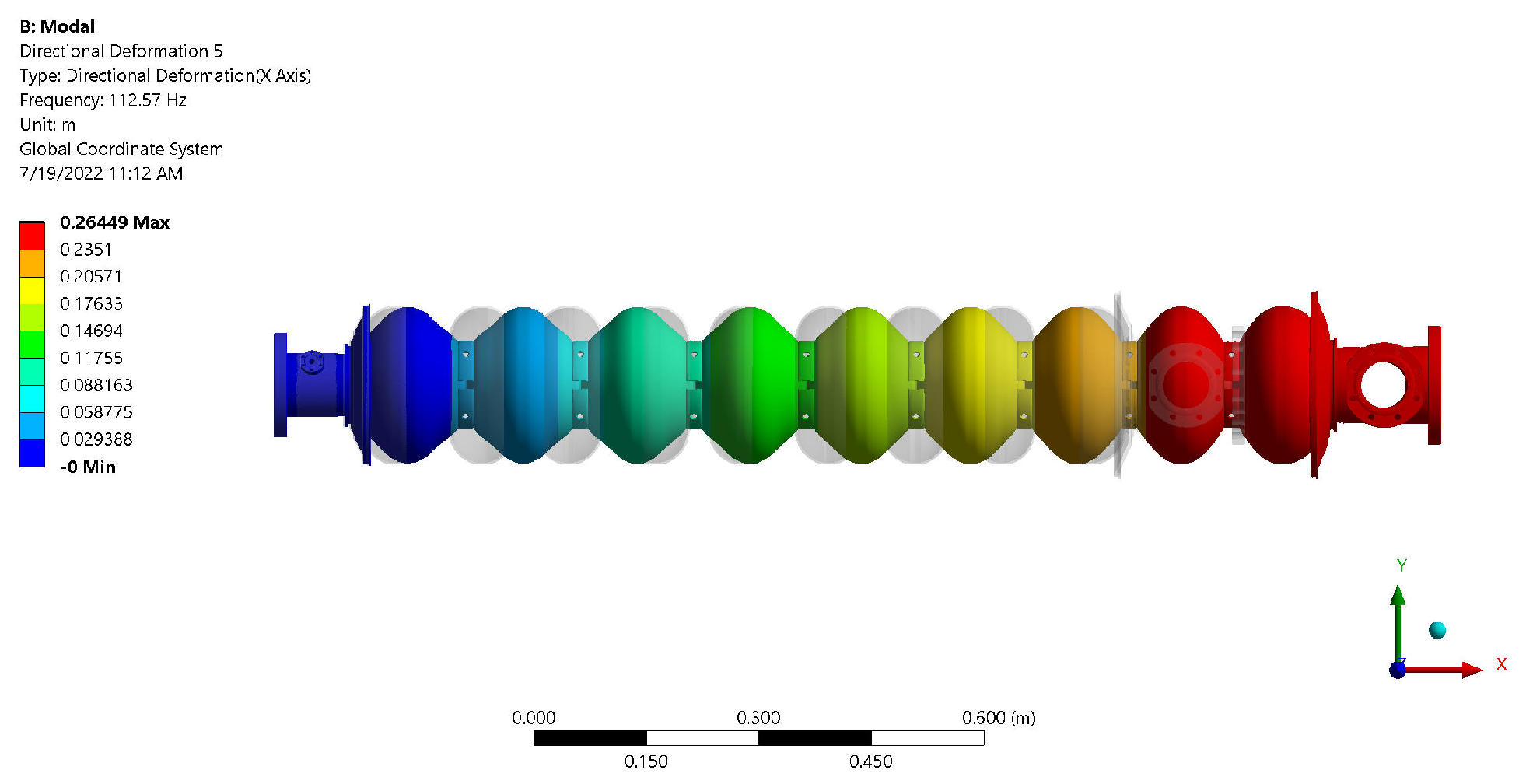
5.1. Model Verification Using ANSYS Mechanical Analysis
5.1.1. Free–Free Ends Model in ANSYS
5.1.2. Midway–Fixed and Both-Ends-Free Models in ANSYS
5.1.3. Fixed–Free Ends Model in ANSYS
5.1.4. Fixed–Fixed Ends Model in ANSYS
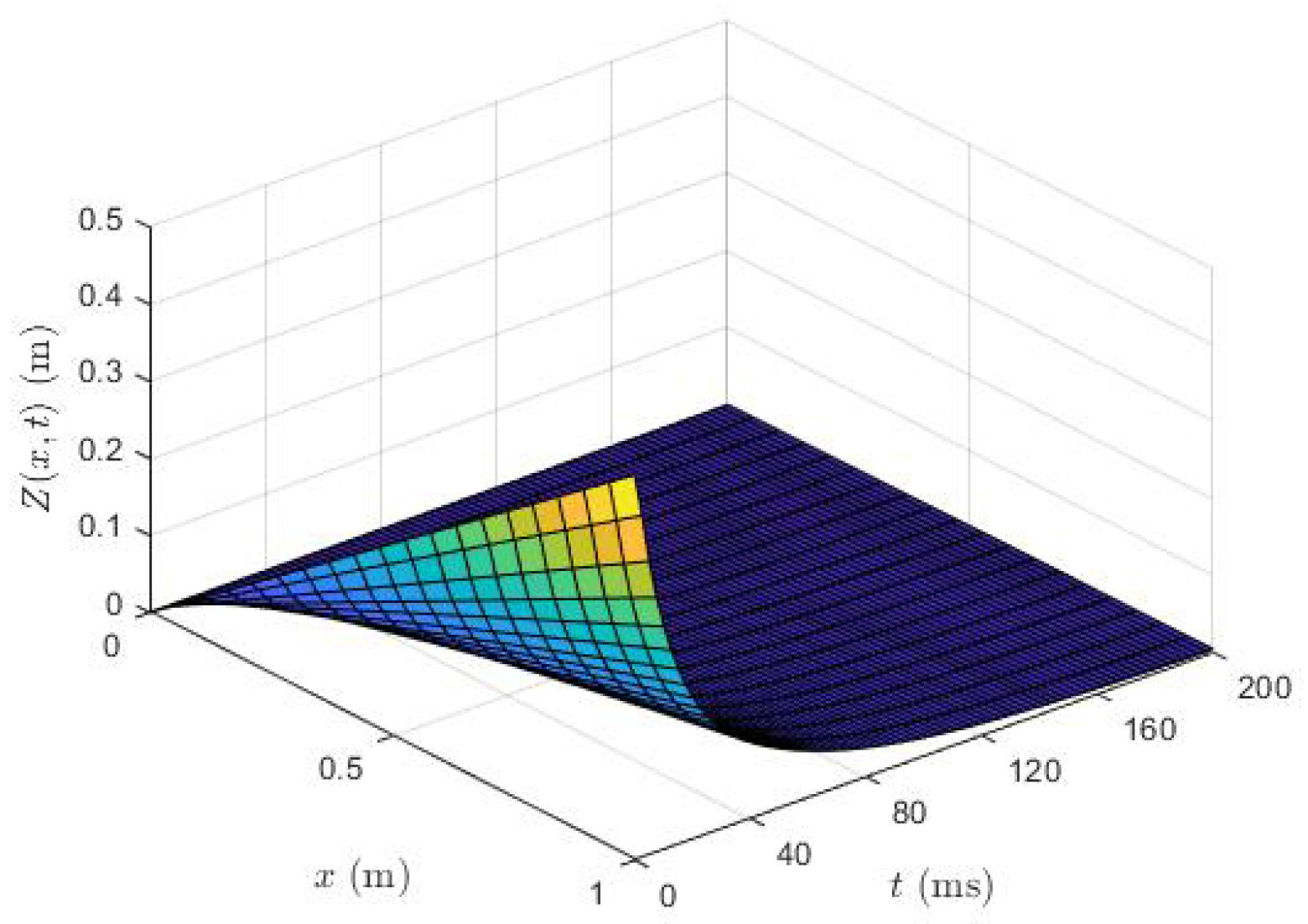
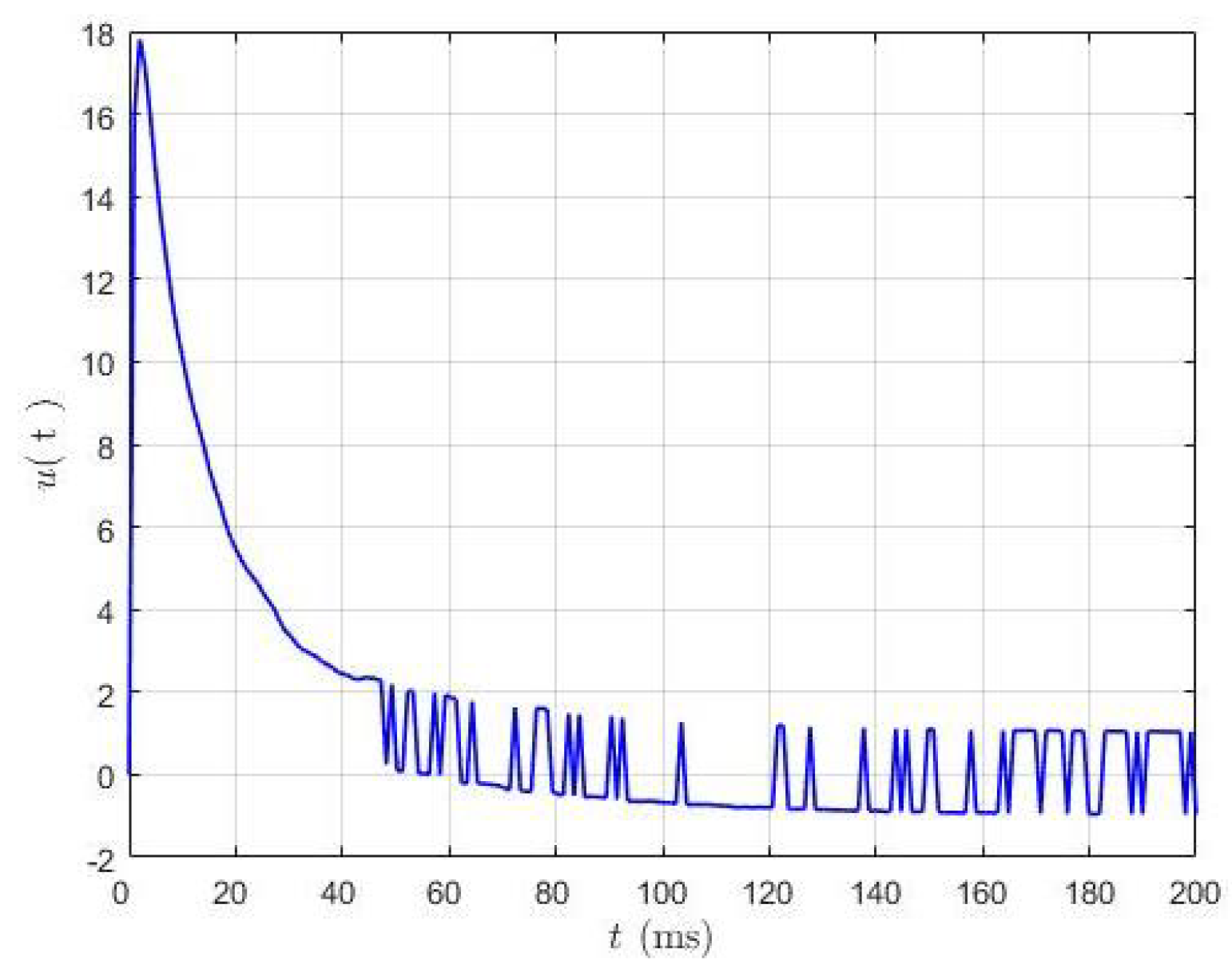
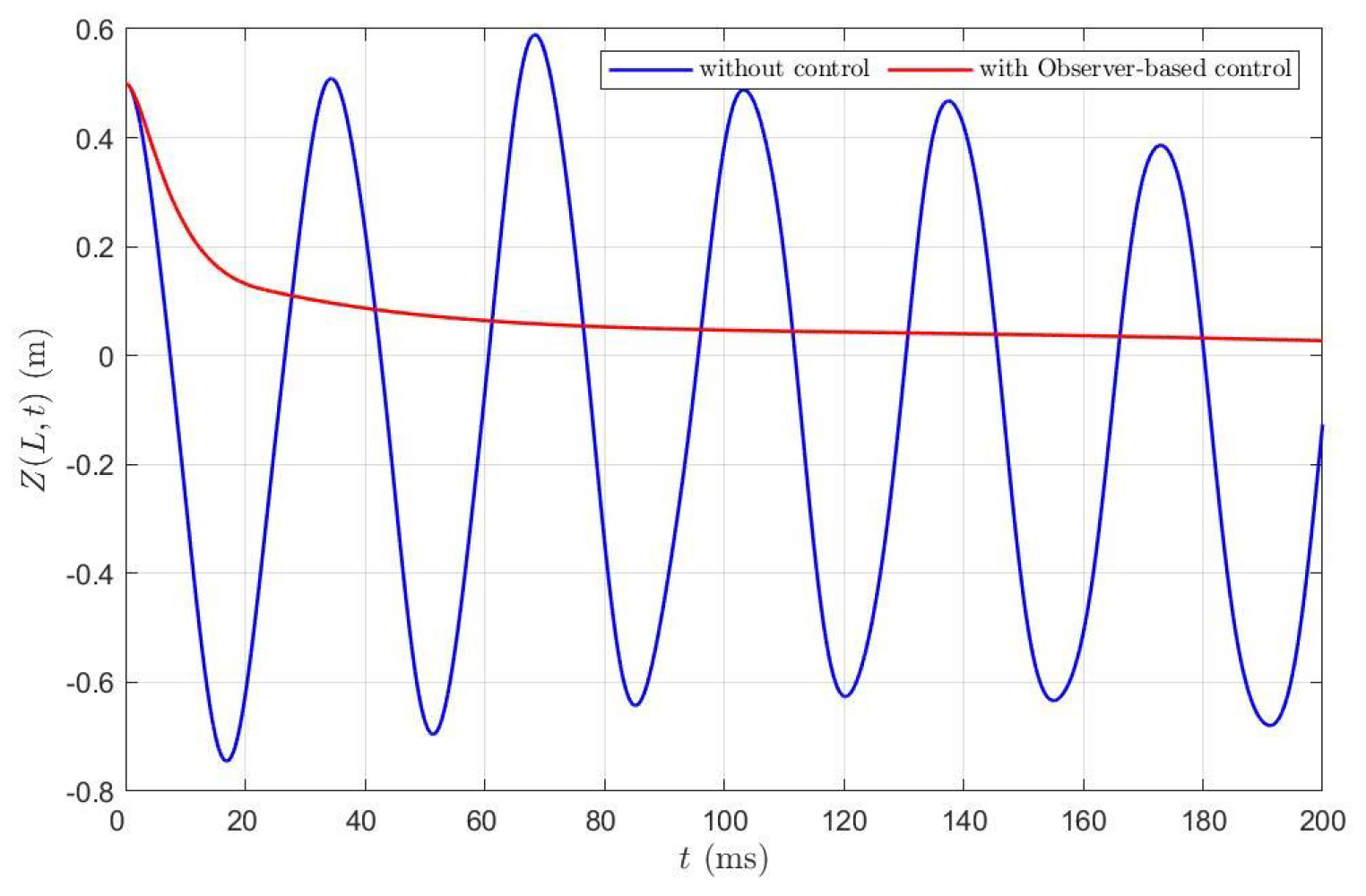
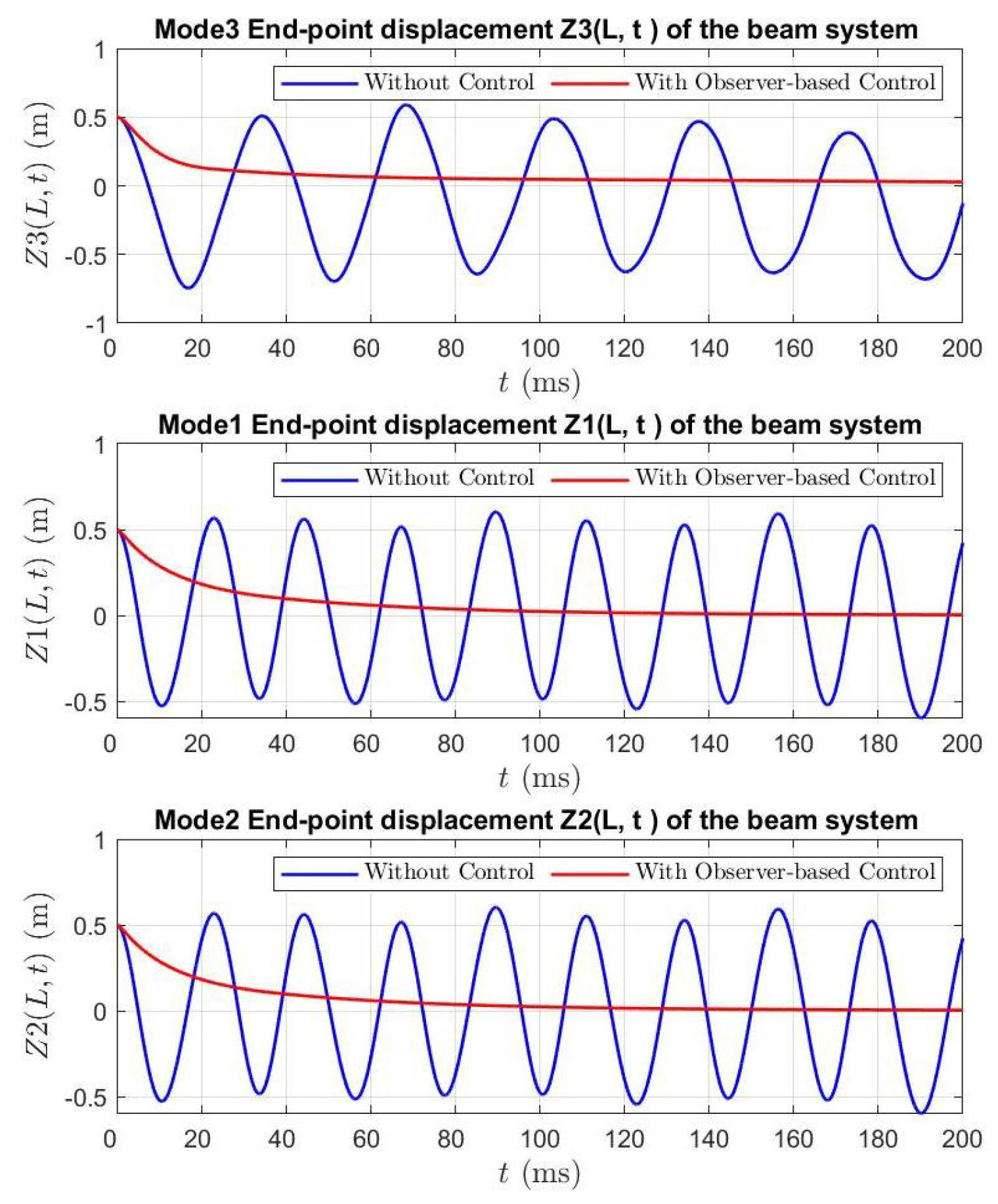
5.2. Active Vibration Control Design in MATLAB
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dilling, J.; Krücken, R.; Merminga, L. ISAC and ARIEL: The TRIUMF Radioactive Beam Facilities and the Scientific Program; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Wangler, T.P. RF Linear Accelerators; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kolb, P.U. The TRIUMF n.ine-c.ell SRF c.avity for ARIEL. Ph.D. Thesis, University of British Columbia, Columbia, UK, 2016. [Google Scholar]
- Arnold, A. Simulation und Messung der Hochfrequenzeigenschaften Einer Supraleitenden Photo-Elektronenquelle. Ph.D. Thesis, Universiät Rostock, Fakultät für Informatik und Elektrotechnik, Rostock, Germany, 2012. [Google Scholar]
- Marziali, A. Microphonics in Superconducting Linear Accelerators and Wavelength Shifting in Free Electron Lasers. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1995. [Google Scholar]
- Schilcher, T. Vector Sum Control of Pulsed Accelerating Fields in Lorentz Force Detuned Superconducting Cavities; Technical Report; DESY: Hamburg, Germany, 1998. [Google Scholar]
- Keikha, M.; Moallem, M.; Zhu, G.; Fong, K. Microphonic Noise Cancellation in Super-Conducting Cavity. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 449–454. [Google Scholar]
- Keikha, M.; Kahnamouei, J.T.; Moallem, M. Radio Frequency Cavity’s Analytical Model and Control Design. Vibration 2023, 6, 319–342. [Google Scholar] [CrossRef]
- Alnuaimi, M.; BuAbdulla, A.; Silva, T.; Altamimi, S.; Lee, D.W.; Al Teneiji, M. Active Vibration Control of Piezoelectric Beam Using the PID Controller. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Virtual, 1–5 November 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85628, p. V07BT07A060. [Google Scholar]
- Shah, U.H.; Hong, K.S. Active vibration control of a flexible rod moving in water: Application to nuclear refueling machines. Automatica 2018, 93, 231–243. [Google Scholar] [CrossRef]
- Pham, P.T.; Nguyen, Q.C.; Hong, K.S. Vibration control of an axially moving beam attached to a translating base. In Proceedings of the 2021 International Symposium of Asian Control Association on Intelligent Robotics and Industrial Automation (IRIA), Goa, India, 20–22 September 2021; pp. 370–375. [Google Scholar]
- Pham, P.T.; Kim, G.H.; Nguyen, Q.C.; Hong, K.S. Control of a non-uniform flexible beam: Identification of first two modes. Int. J. Control Autom. Syst. 2021, 19, 3698–3707. [Google Scholar] [CrossRef]
- Koplow, M.A.; Bhattacharyya, A.; Mann, B.P. Closed form solutions for the dynamic response of Euler–Bernoulli beams with step changes in cross section. J. Sound Vib. 2006, 295, 214–225. [Google Scholar] [CrossRef]
- Kumar, B.; Sujith, R. Exact solutions for the longitudinal vibration of non-uniform rods. J. Sound Vib. 1997, 207, 721–729. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y. The free vibration of a type of tapered beams. Comput. Methods Appl. Mech. Eng. 2000, 188, 203–216. [Google Scholar] [CrossRef]
- Auciello, N.M. On the transverse vibrations of non-uniform beams with axial loads and elastically restrained ends. Int. J. Mech. Sci. 2001, 43, 193–208. [Google Scholar] [CrossRef]
- Eisenberger, M. Exact longitudinal vibration frequencies of a variable cross-section rod. Appl. Acoust. 1991, 34, 123–130. [Google Scholar] [CrossRef]
- Matsuda, H.; Sakiyama, T.; Morita, C.; Kawakami, M. Longitudinal impulsive response analysis of variable cross-section bars. J. Sound Vib. 1995, 181, 541–551. [Google Scholar] [CrossRef]
- Bapat, C.N. Vibration of rods with uniformly tapered sections. J. Sound Vib. 1995, 185, 185–189. [Google Scholar] [CrossRef]
- Lau, J. Vibration frequencies for a non-uniform beam with end mass. J. Sound Vib. 1984, 97, 513–521. [Google Scholar] [CrossRef]
- Abrate, S. Vibration of non-uniform rods and beams. J. Sound Vib. 1995, 185, 703–716. [Google Scholar] [CrossRef]
- Li, Q. Exact solutions for free longitudinal vibrations of non-uniform rods. J. Sound Vib. 2000, 234, 1–19. [Google Scholar] [CrossRef]
- Chen, L.Q.; Ding, H. Steady-state transverse response in coupled planar vibration of axially moving viscoelastic beams. J. Vib. Acoust. 2010, 132, 011009. [Google Scholar] [CrossRef]
- Zhang, Z.; Rustighi, E.; Chen, Y.; Hua, H. Active control of the longitudinal-lateral vibration of a shaft-plate coupled system. J. Vib. Acoust. 2012, 134, 061002. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Free vibration analysis of axially functionally graded tapered Bernoulli–Euler microbeams based on the modified couple stress theory. Compos. Struct. 2013, 98, 314–322. [Google Scholar] [CrossRef]
- Khot, S.; Yelve, N.P.; Tomar, R.; Desai, S.; Vittal, S. Active vibration control of cantilever beam by using PID based output feedback controller. J. Vib. Control 2012, 18, 366–372. [Google Scholar] [CrossRef]
- Parameswaran, A.P.; Gangadharan, K. Parametric modeling and FPGA based real time active vibration control of a piezoelectric laminate cantilever beam at resonance. J. Vib. Control 2015, 21, 2881–2895. [Google Scholar] [CrossRef]
- Sangpet, T.; Kuntanapreeda, S.; Schmidt, R. An adaptive PID-like controller for vibration suppression of piezo-actuated flexible beams. J. Vib. Control 2018, 24, 2656–2670. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H. Adaptive modal vibration control for smart flexible beam with two piezoelectric actuators by multivariable self-tuning control. J. Vib. Control 2020, 26, 490–504. [Google Scholar] [CrossRef]




| Boundary Condition | Frequency (rad/s) | Mode Shape |
|---|---|---|
| Free–Free | ||
| Fixed–Free | ||
| Free–Mid Fixed |
| Mode | Free–Free | Fixed–Free | Free–Mid Fixed | Fixed–Fixed |
|---|---|---|---|---|
| 1 | 0 | 8.64908 | 19.0875 | 82.049 |
| 2 | 0 | 8.81699 | 19.6901 | 85.962 |
| 3 | 0 | 56.8637 | 40.7481 | 200.68 |
| 4 | 47.396 | 59.1113 | 46.3741 | 200.47 |
| 5 | 49.182 | 112.567 | 127.646 | 299.59 |
| 6 | 129.69 | 153.406 | 147.42 | 342.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keikha, M.; Kahnamouei, J.T.; Moallem, M. Modelling and Control of Longitudinal Vibrations in a Radio Frequency Cavity. Vibration 2024, 7, 129-145. https://doi.org/10.3390/vibration7010007
Keikha M, Kahnamouei JT, Moallem M. Modelling and Control of Longitudinal Vibrations in a Radio Frequency Cavity. Vibration. 2024; 7(1):129-145. https://doi.org/10.3390/vibration7010007
Chicago/Turabian StyleKeikha, Mahsa, Jalal Taheri Kahnamouei, and Mehrdad Moallem. 2024. "Modelling and Control of Longitudinal Vibrations in a Radio Frequency Cavity" Vibration 7, no. 1: 129-145. https://doi.org/10.3390/vibration7010007






