The Impact of Misspecified Random Effect Distribution in a Weibull Regression Mixed Model
Abstract
:1. Introduction
2. A Case Study of Lifetime in an Abrasive Process
3. Weibull Regression Mixed Model
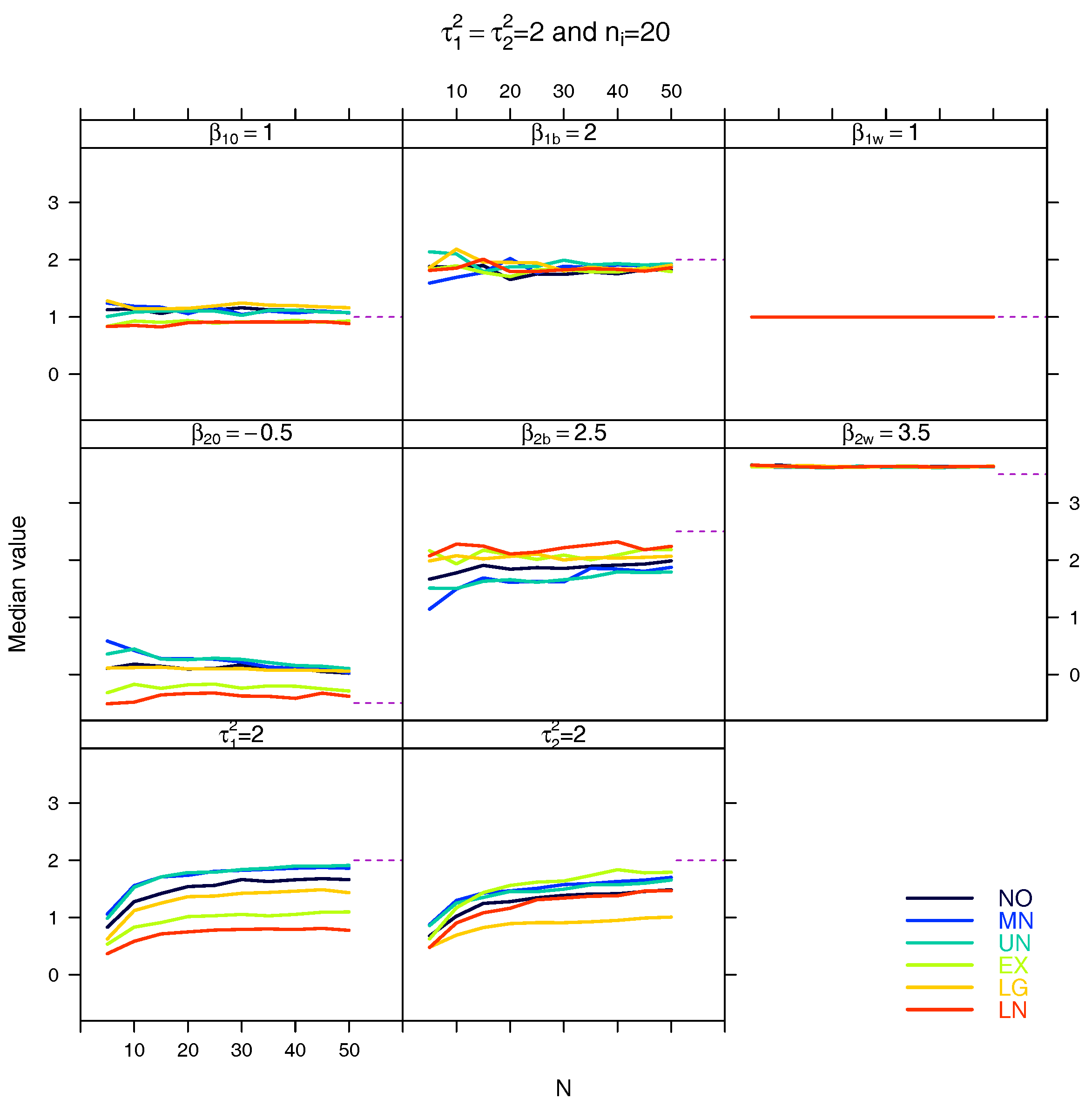
4. Simulation Study
5. Results
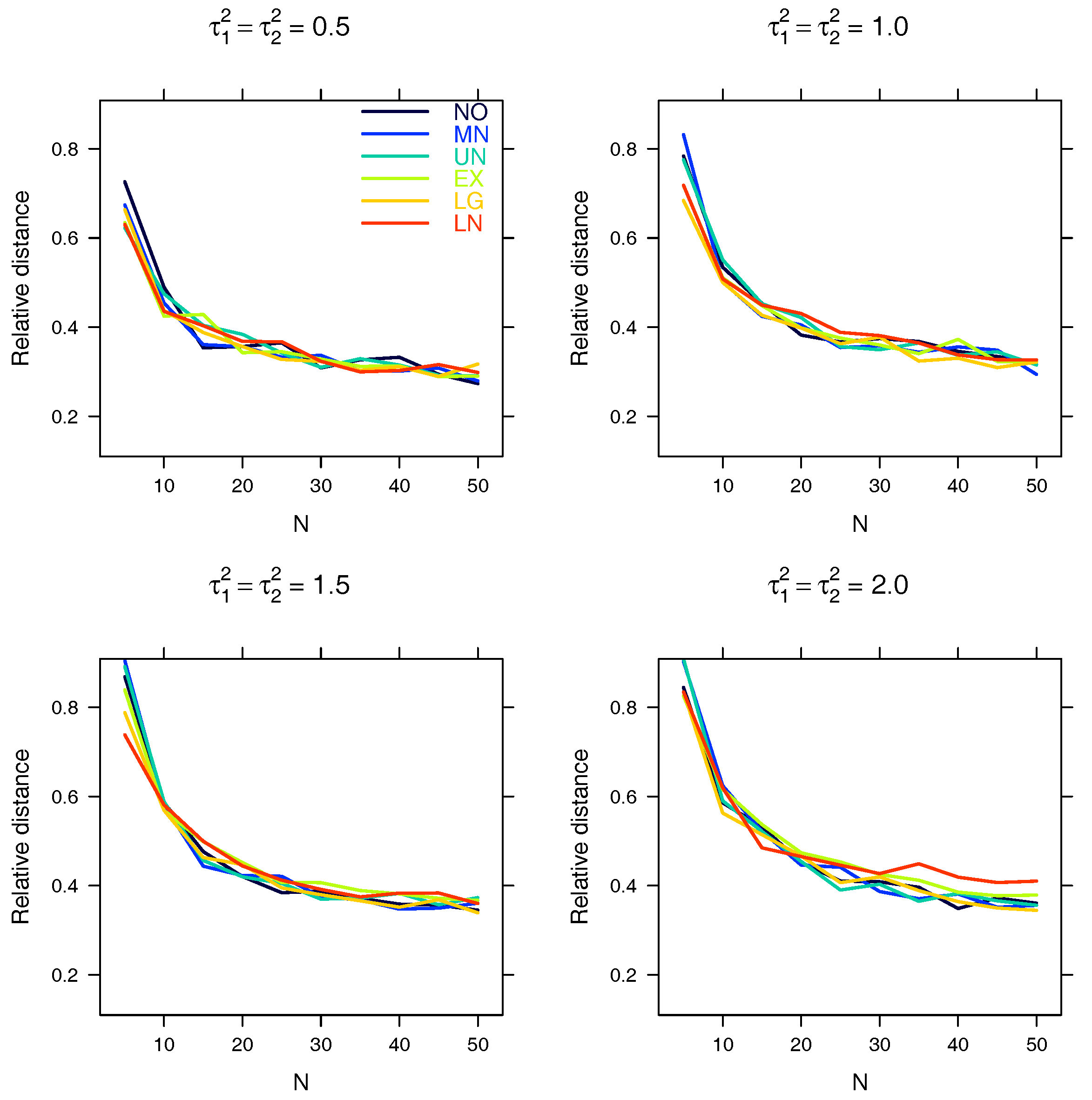
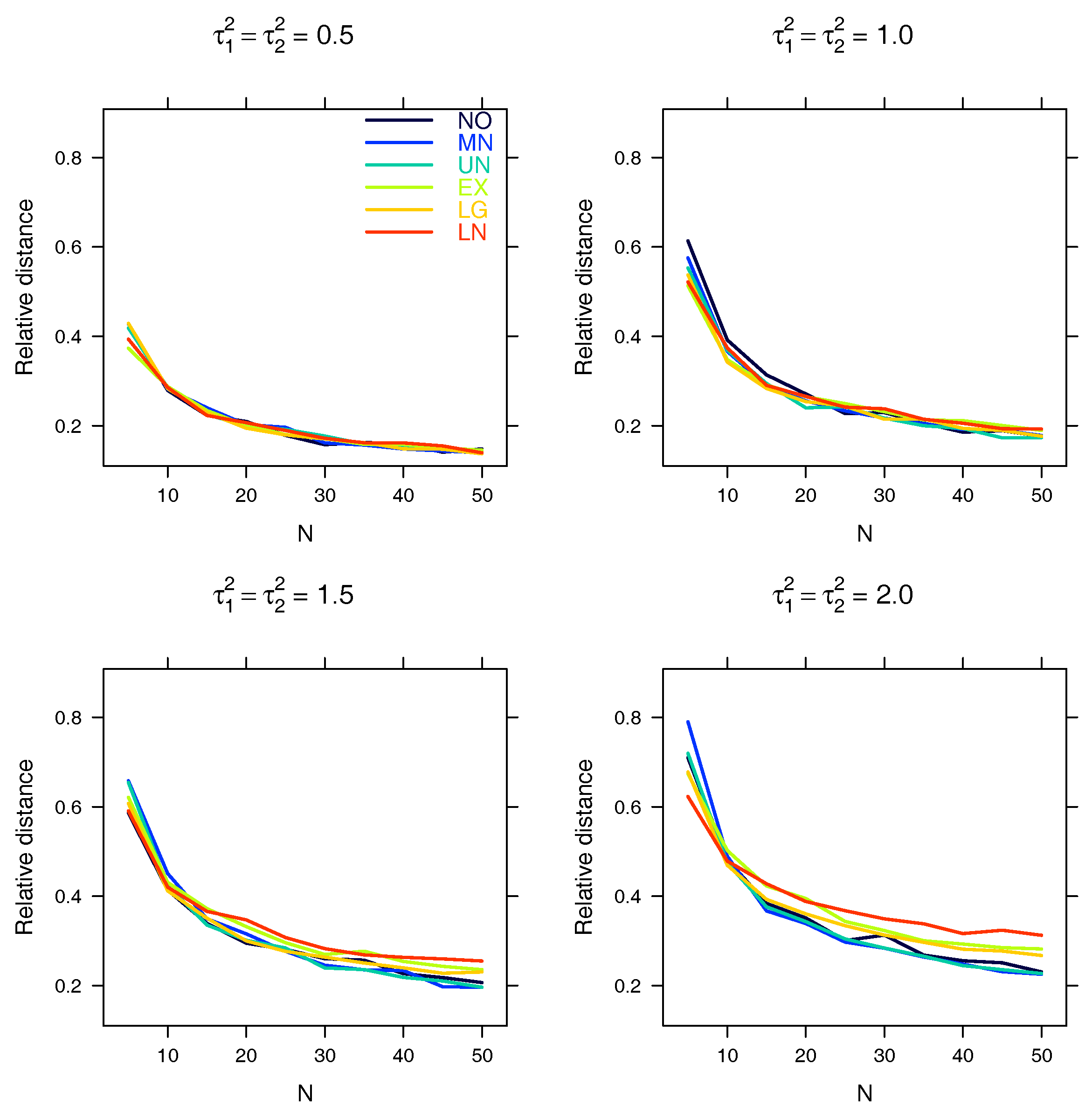
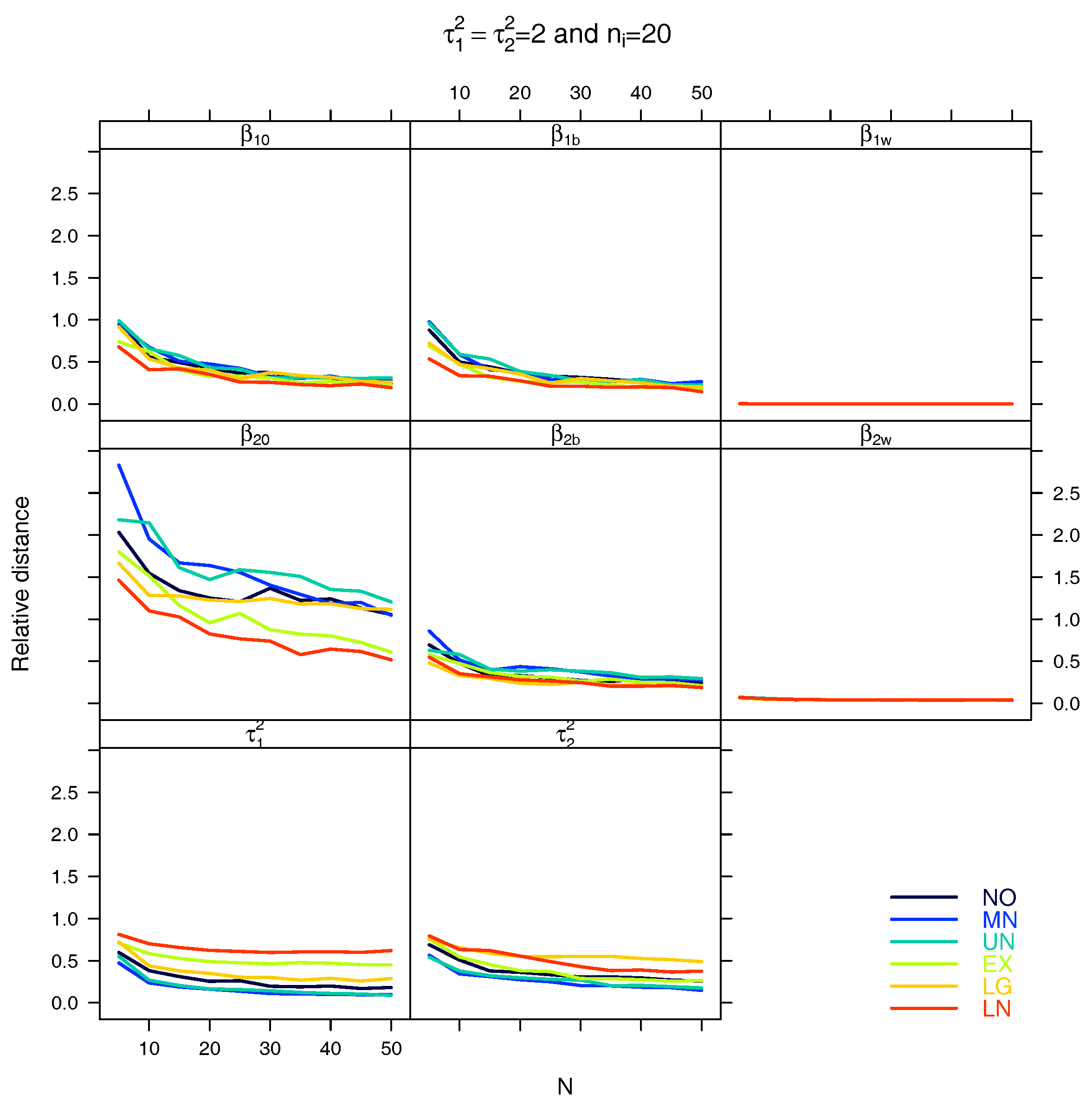
5.1. Relative Distance between the Estimated Parameter Vector and the True Parameter Vector
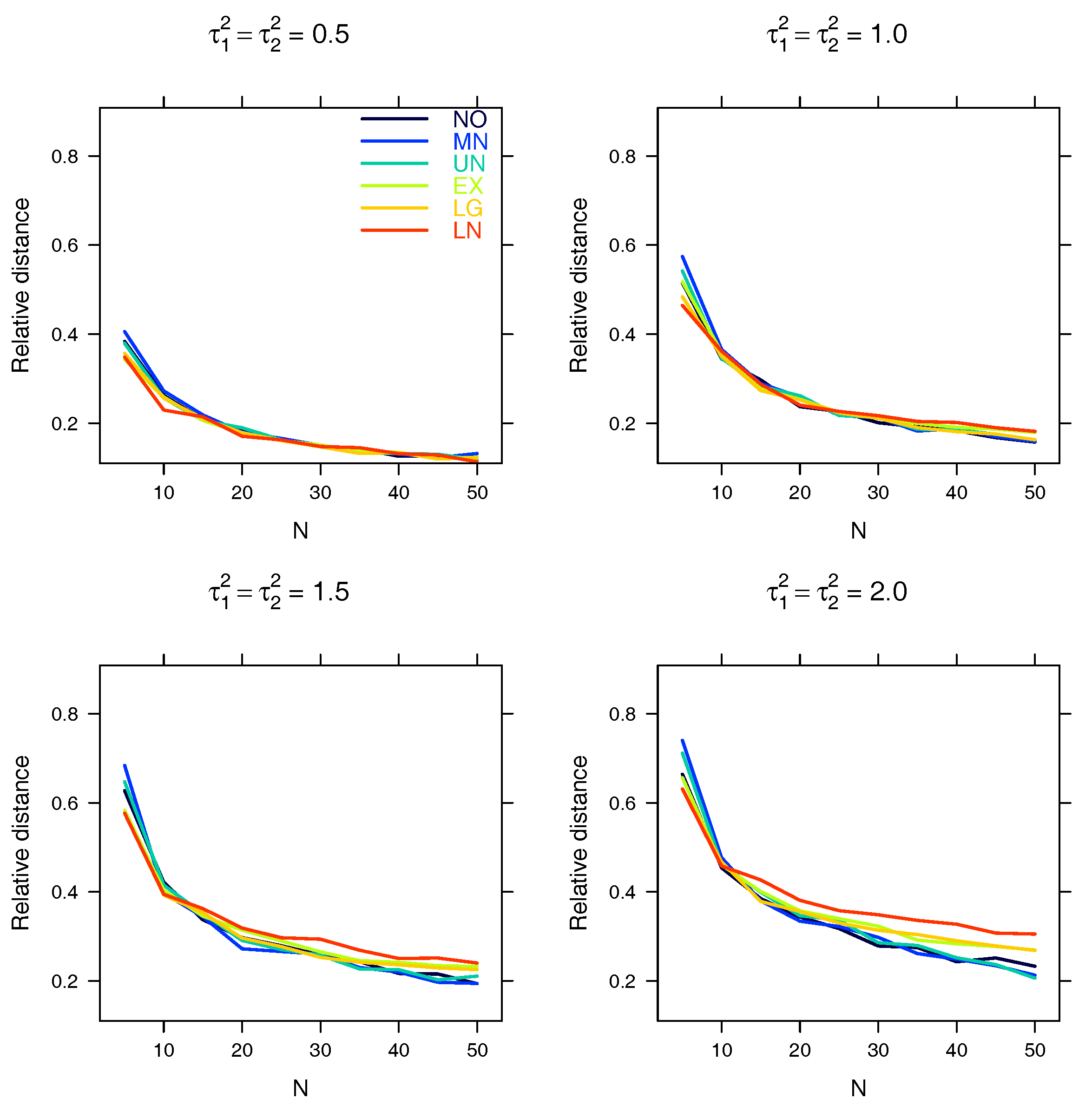
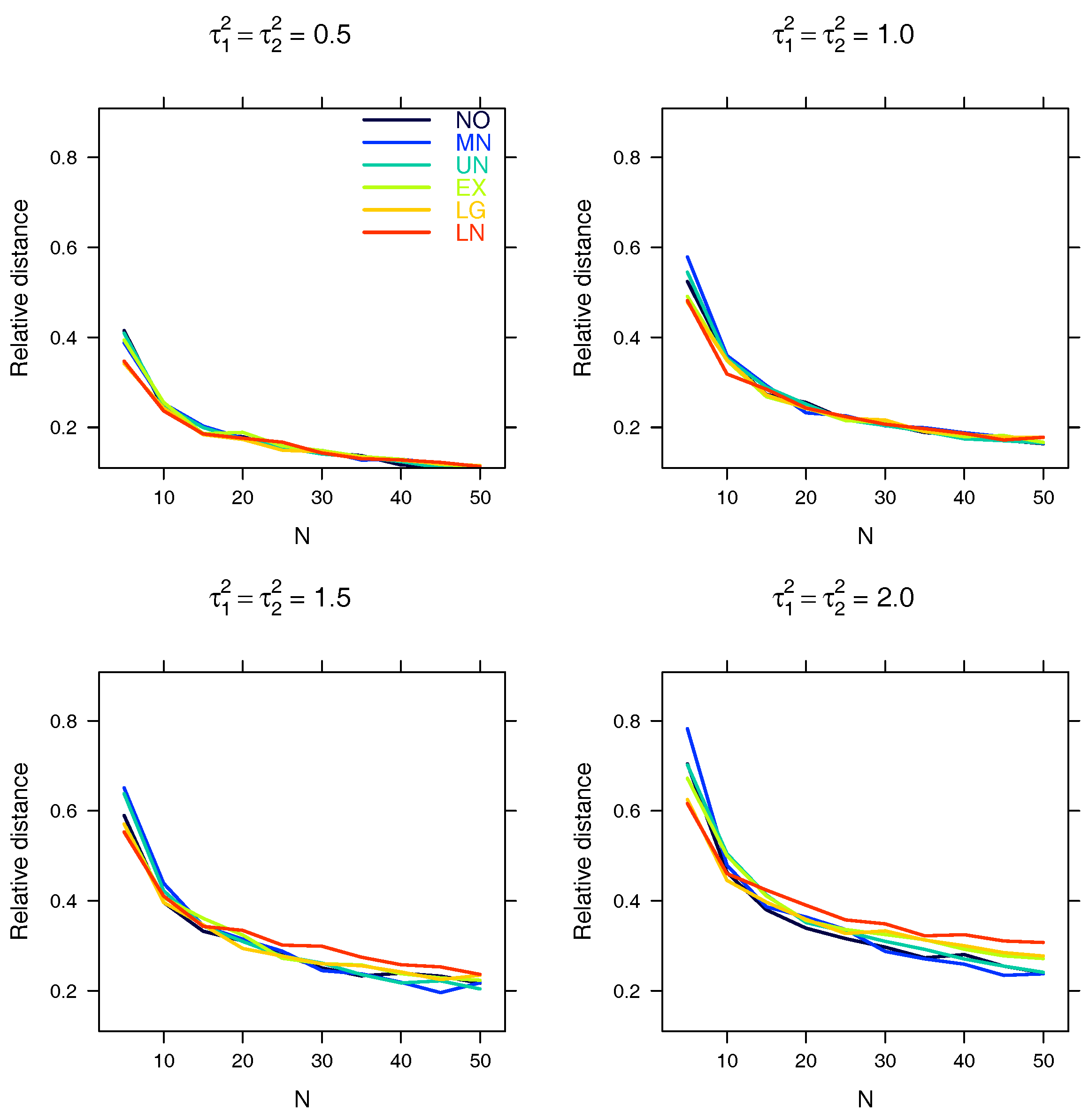
5.2. Relative Distance between the Estimated Parameter and the True Parameter
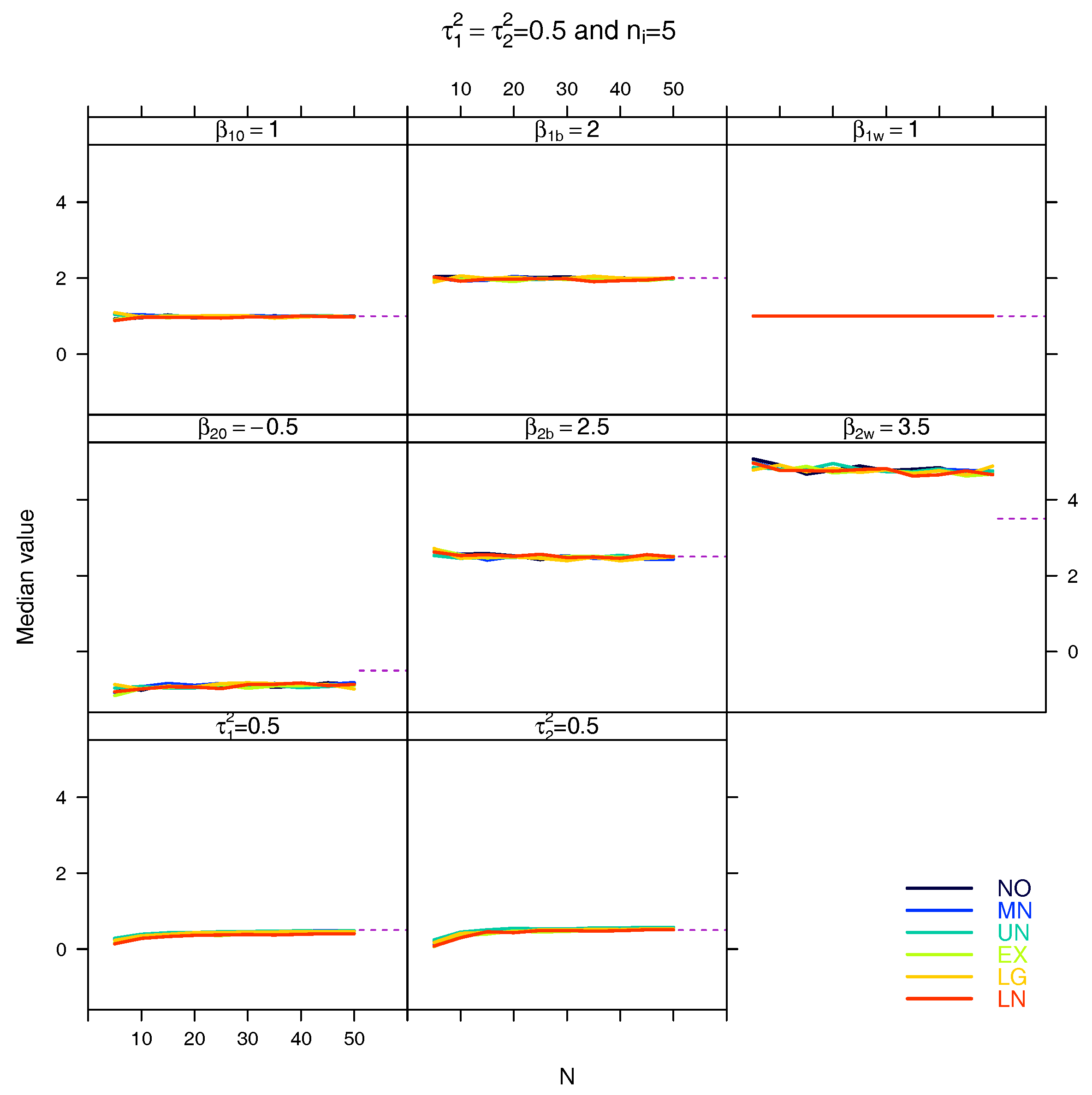
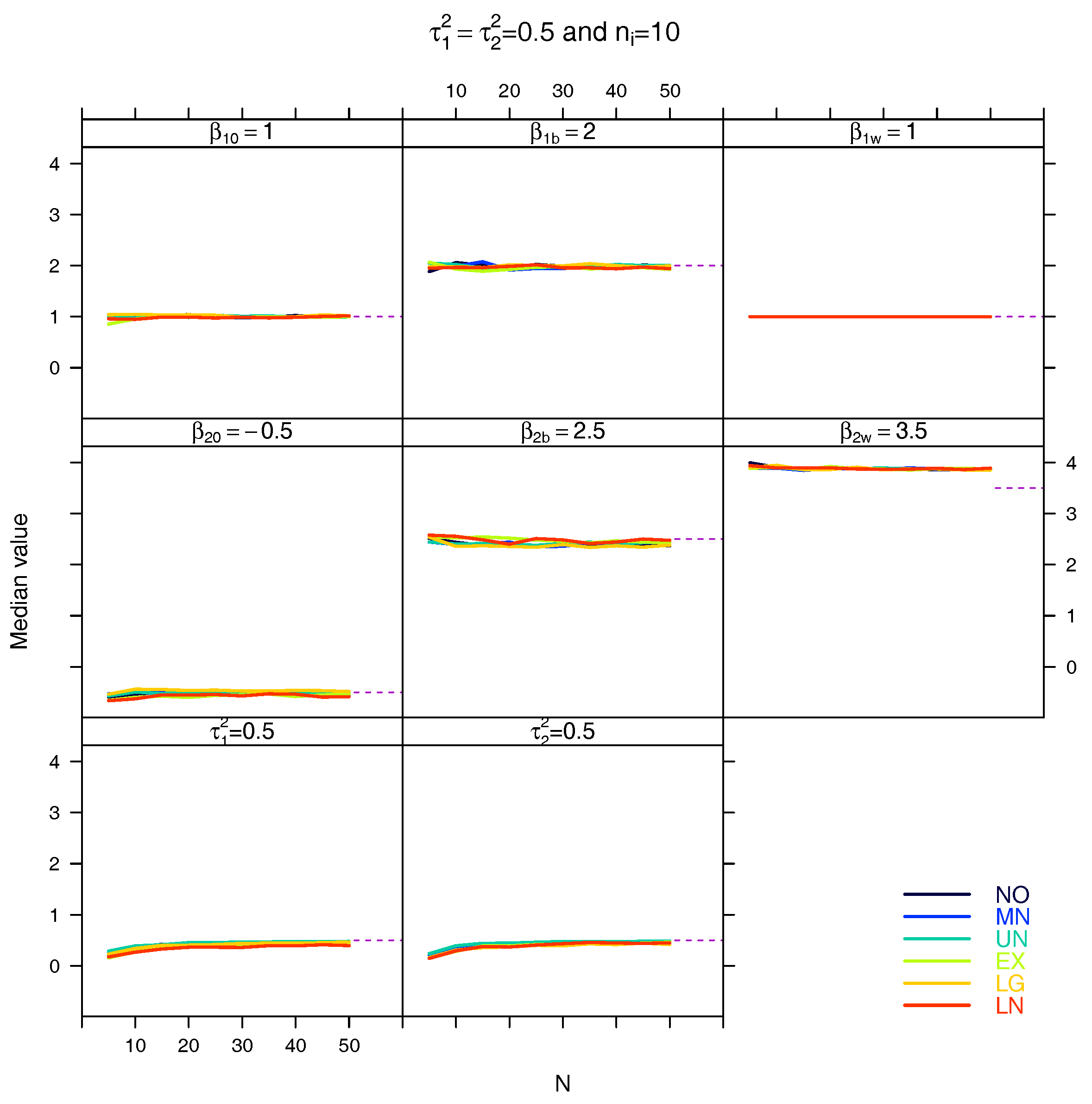
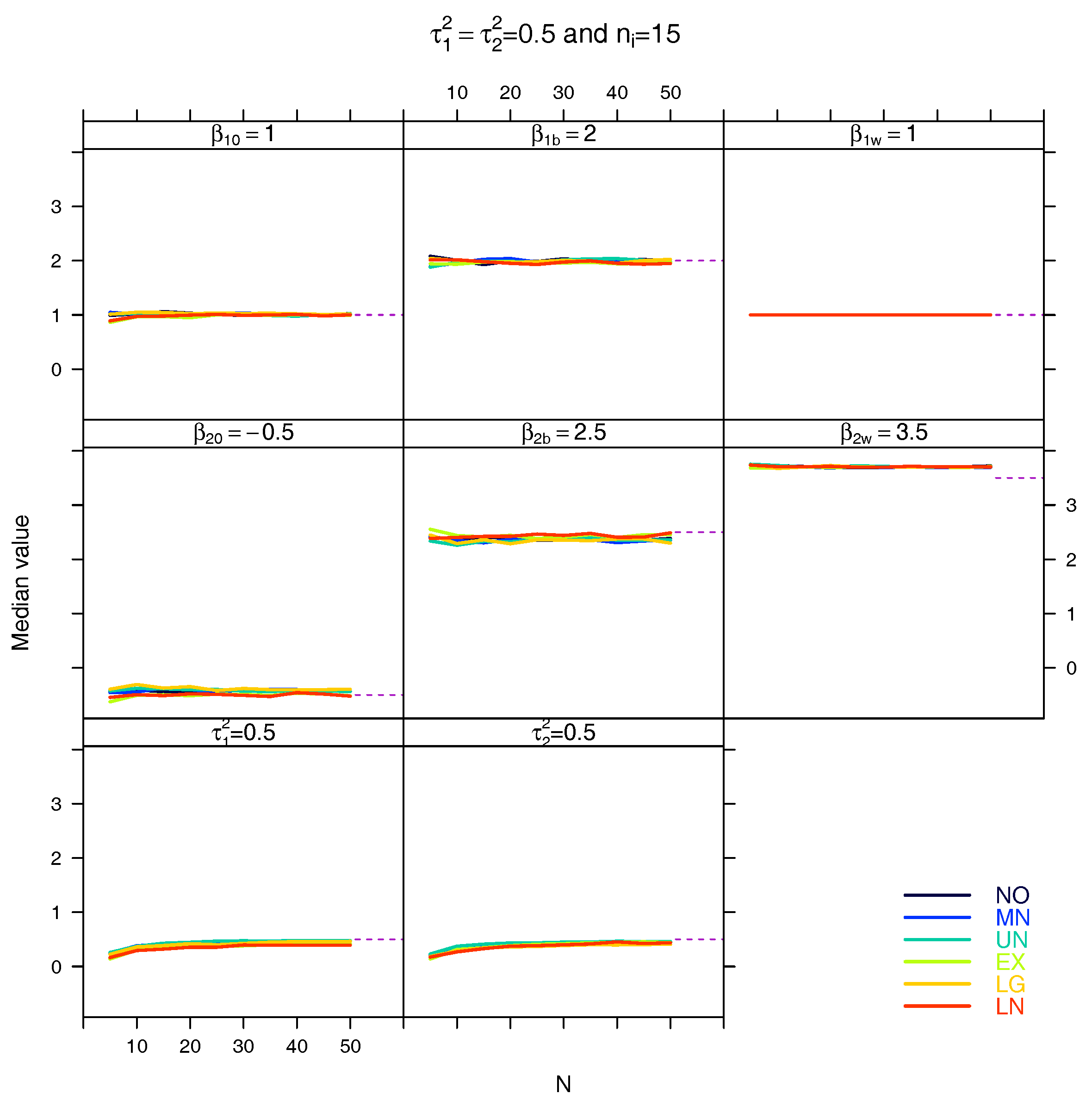
5.3. Median for the Estimated Fixed Parameters
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| GLMM | Generalized linear mixed model |
| LMM | Linear mixed model |
| LRM | Logistic random model |
| Third parameterization of Weibull distribution | |
| GHQ | Gauss–Hermite quadrature |
| Relative distance |
Appendix A
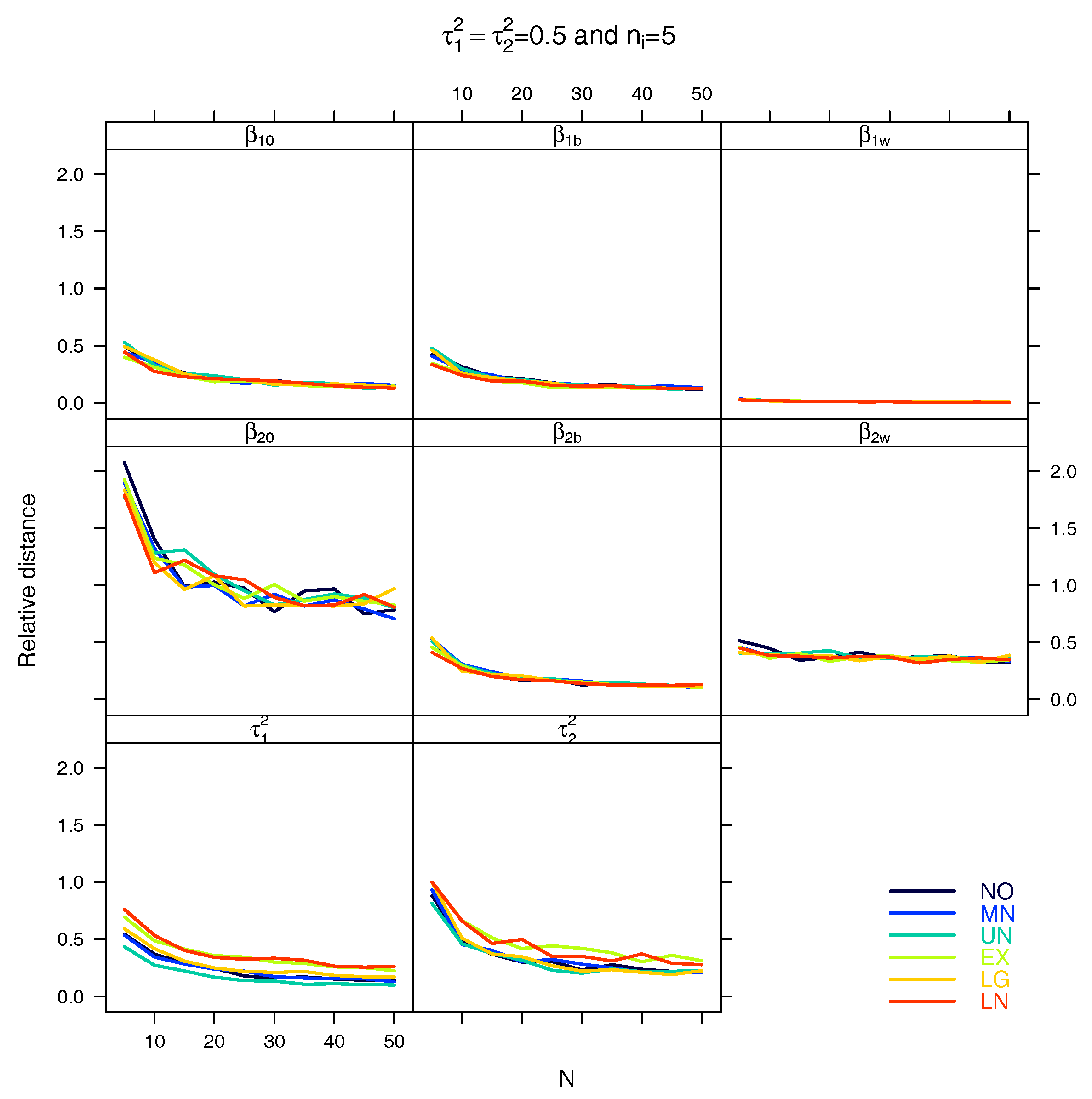
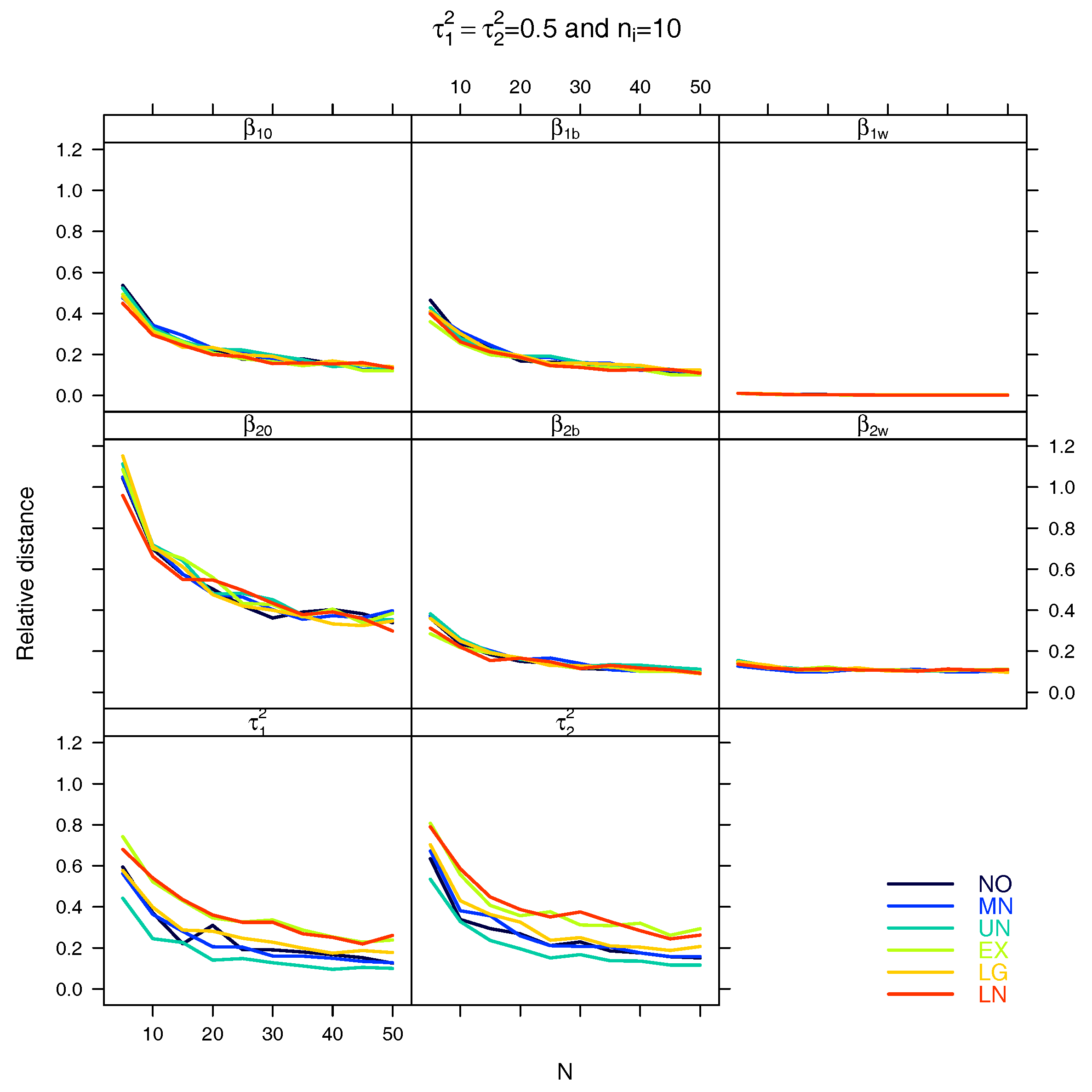

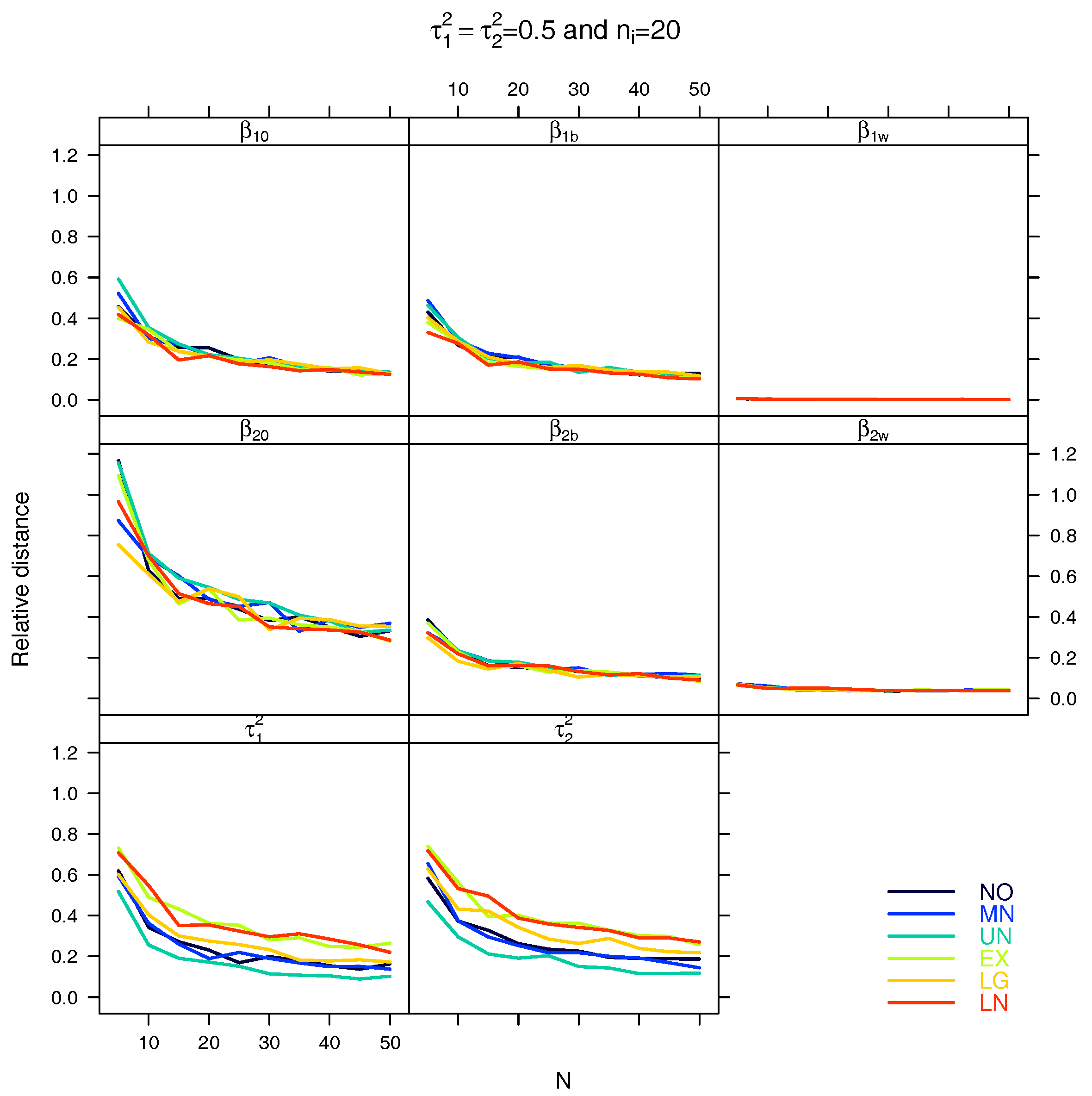
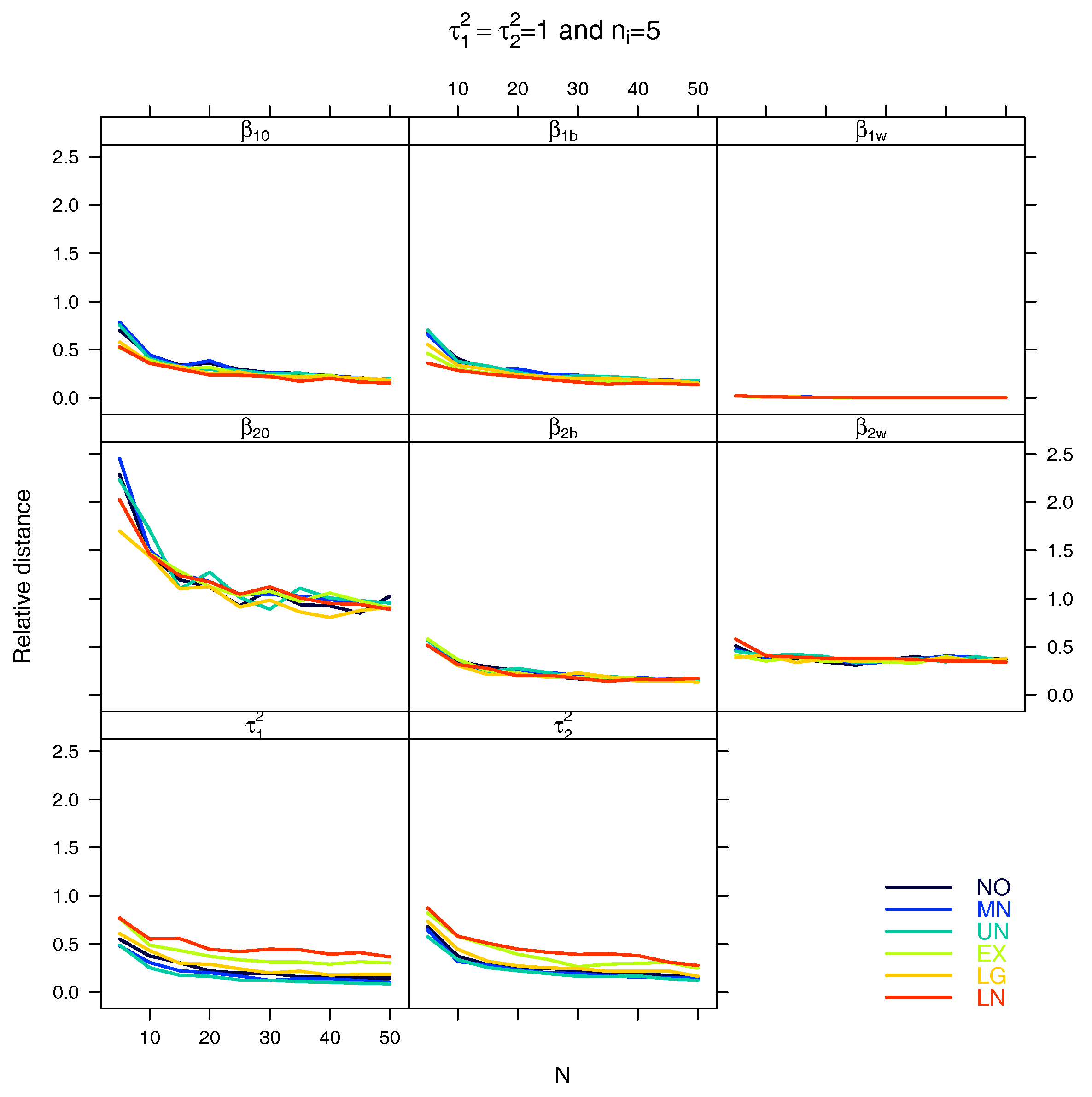
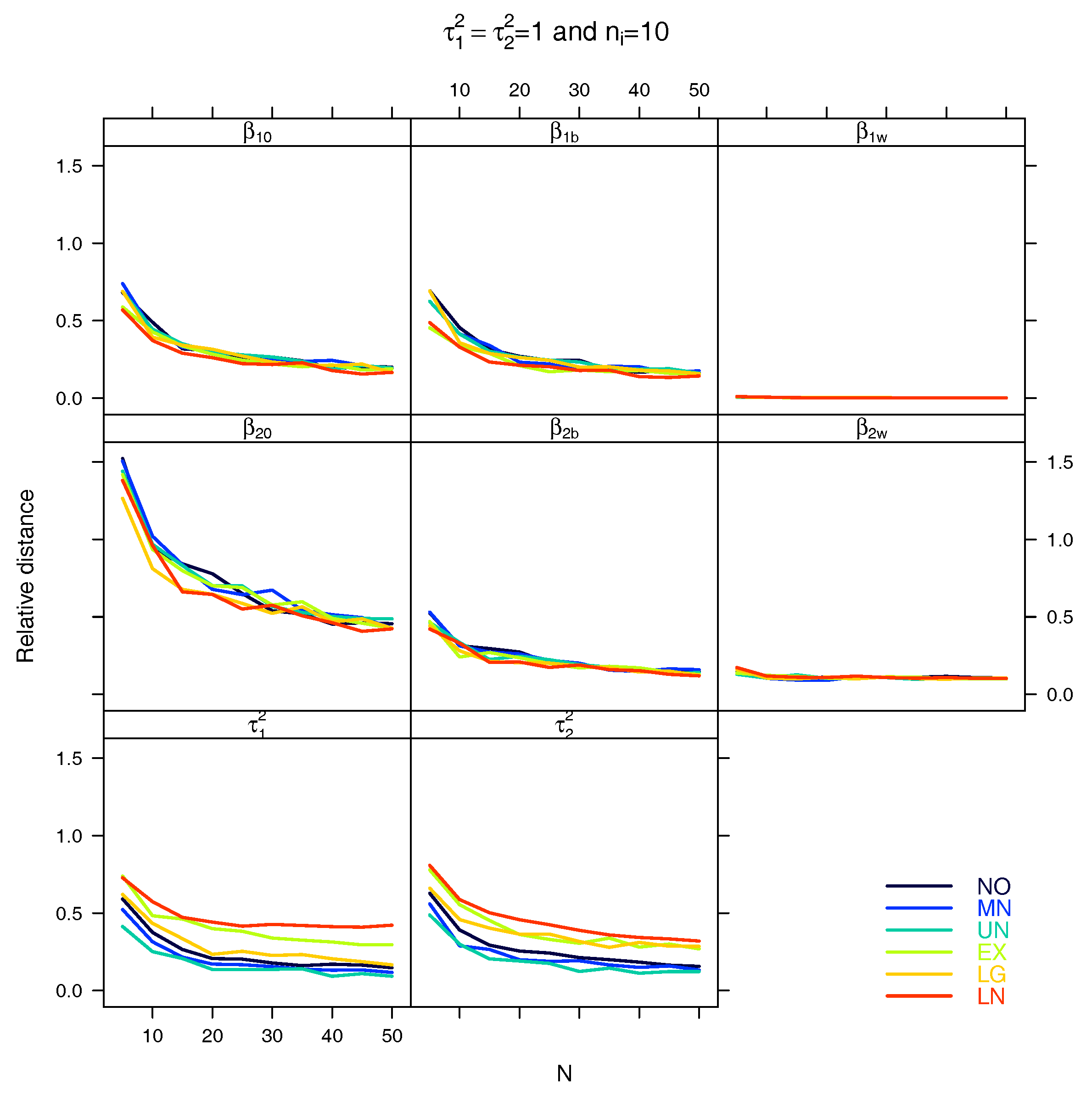

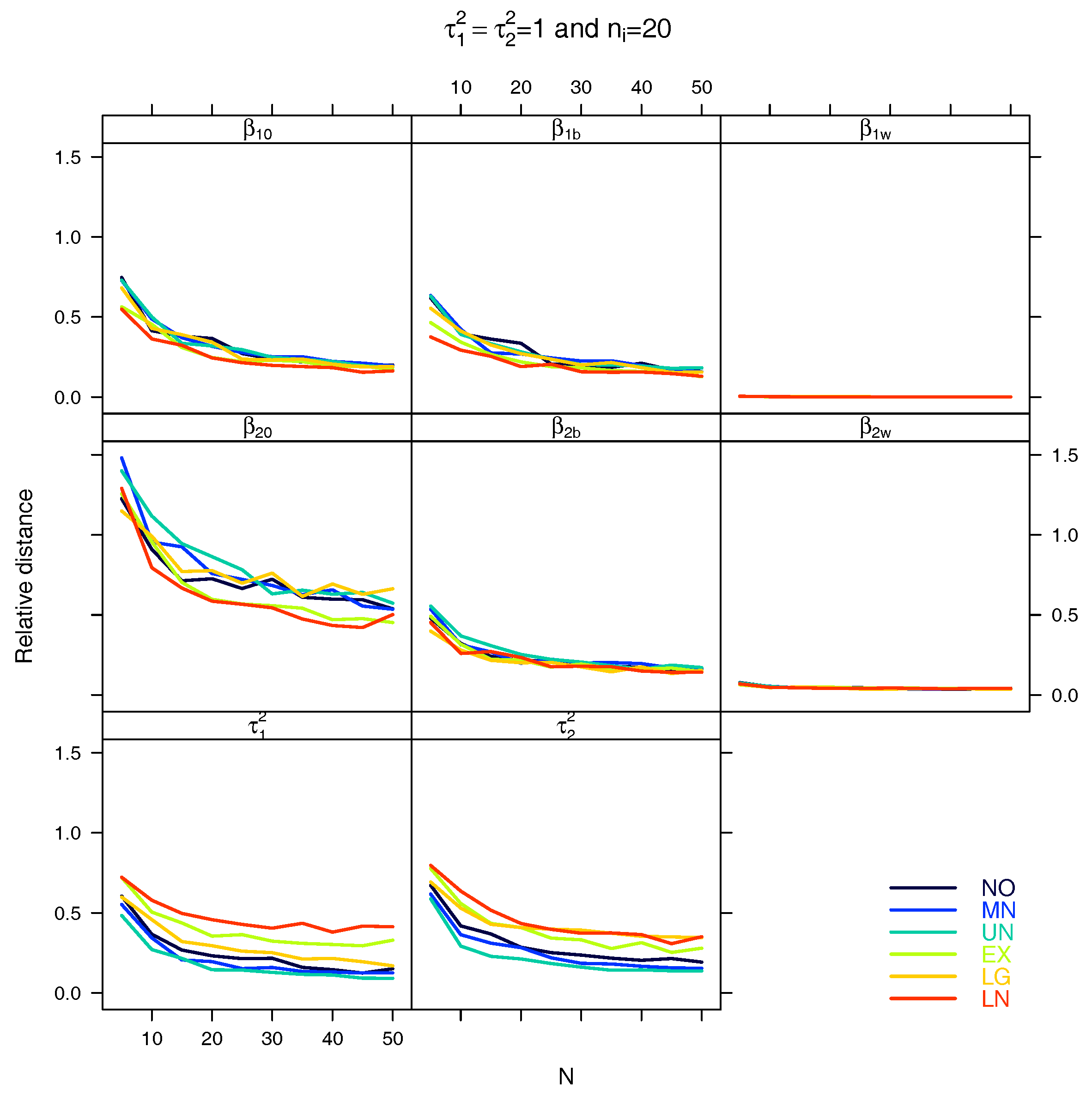
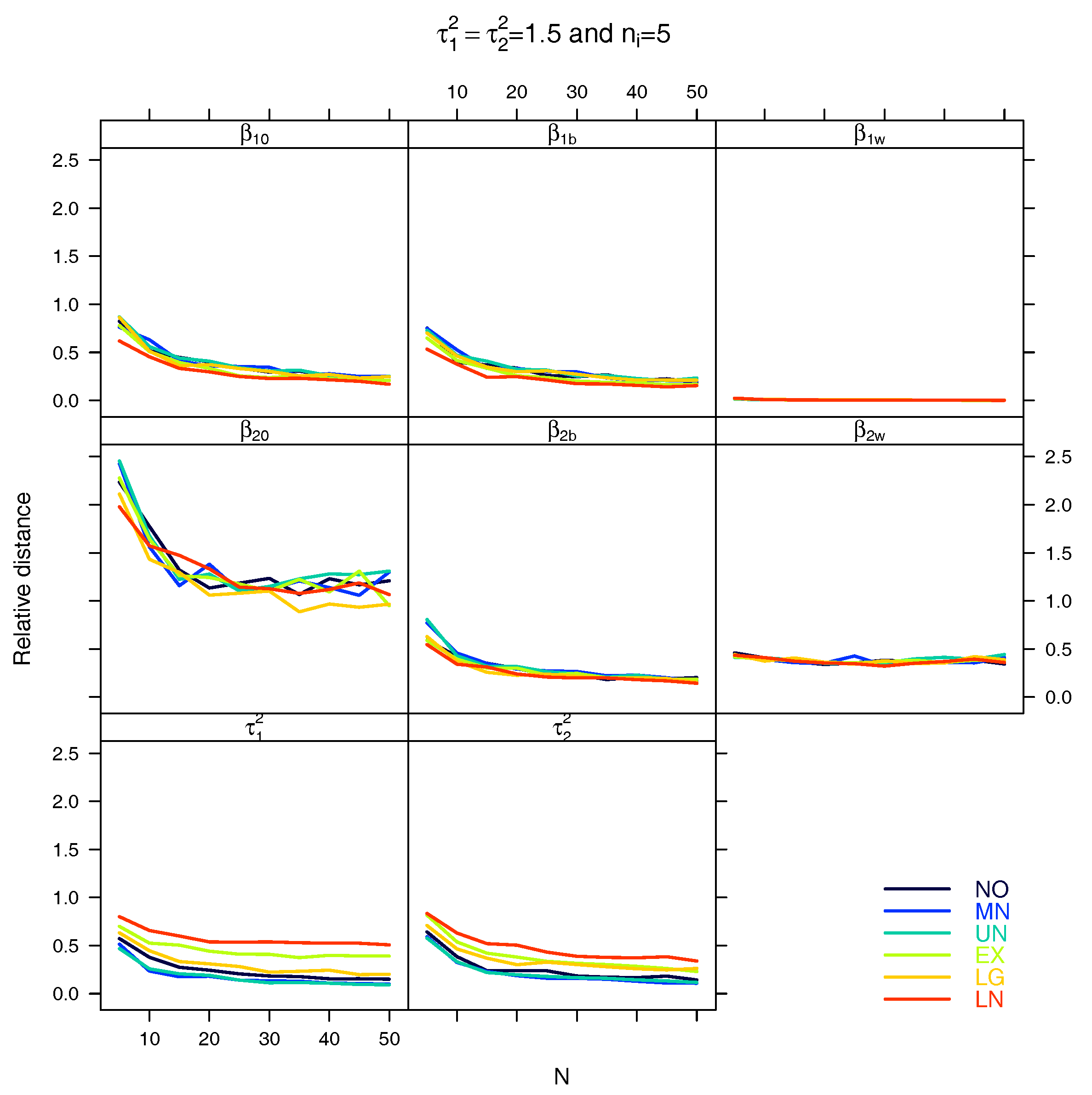
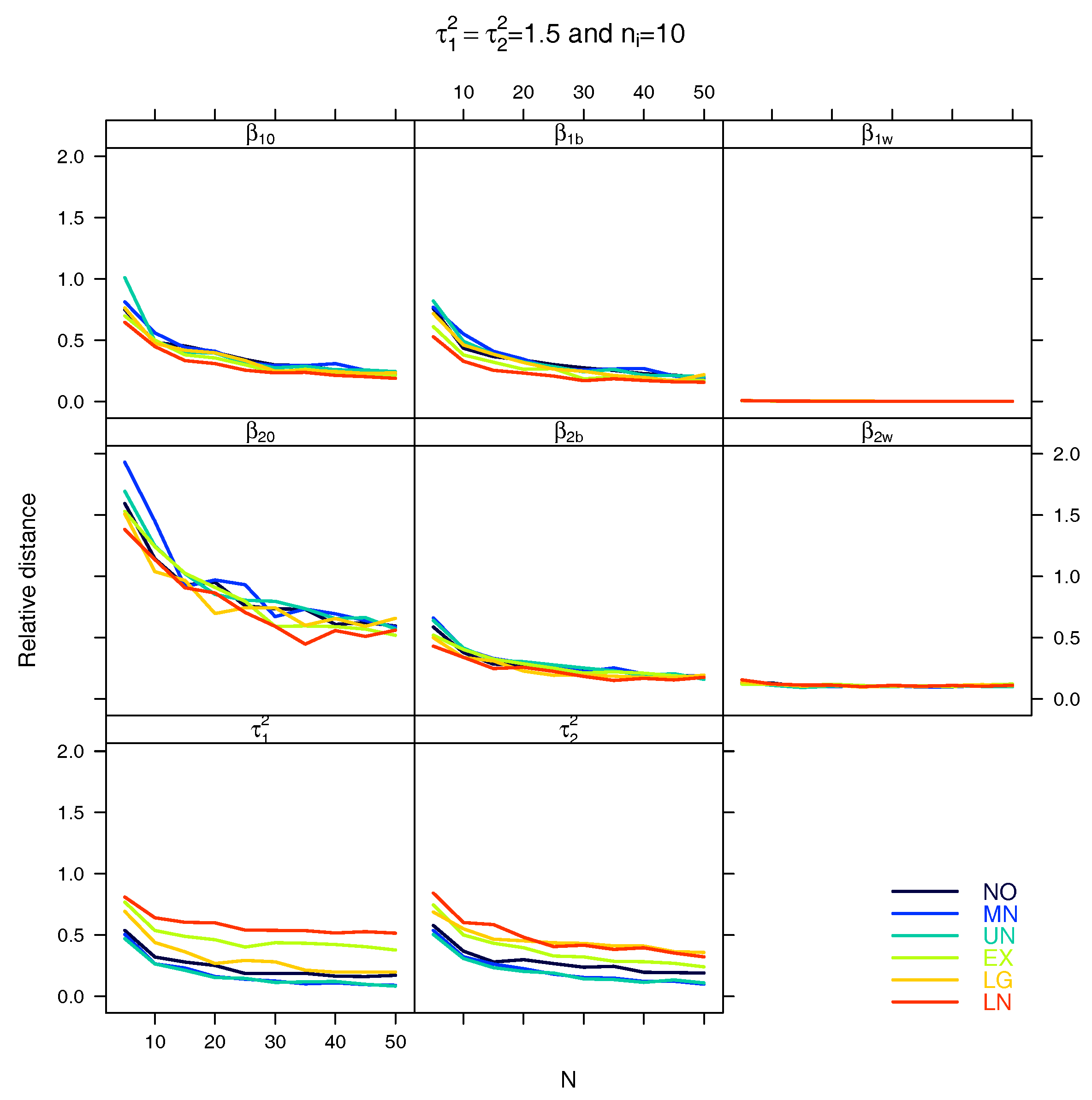
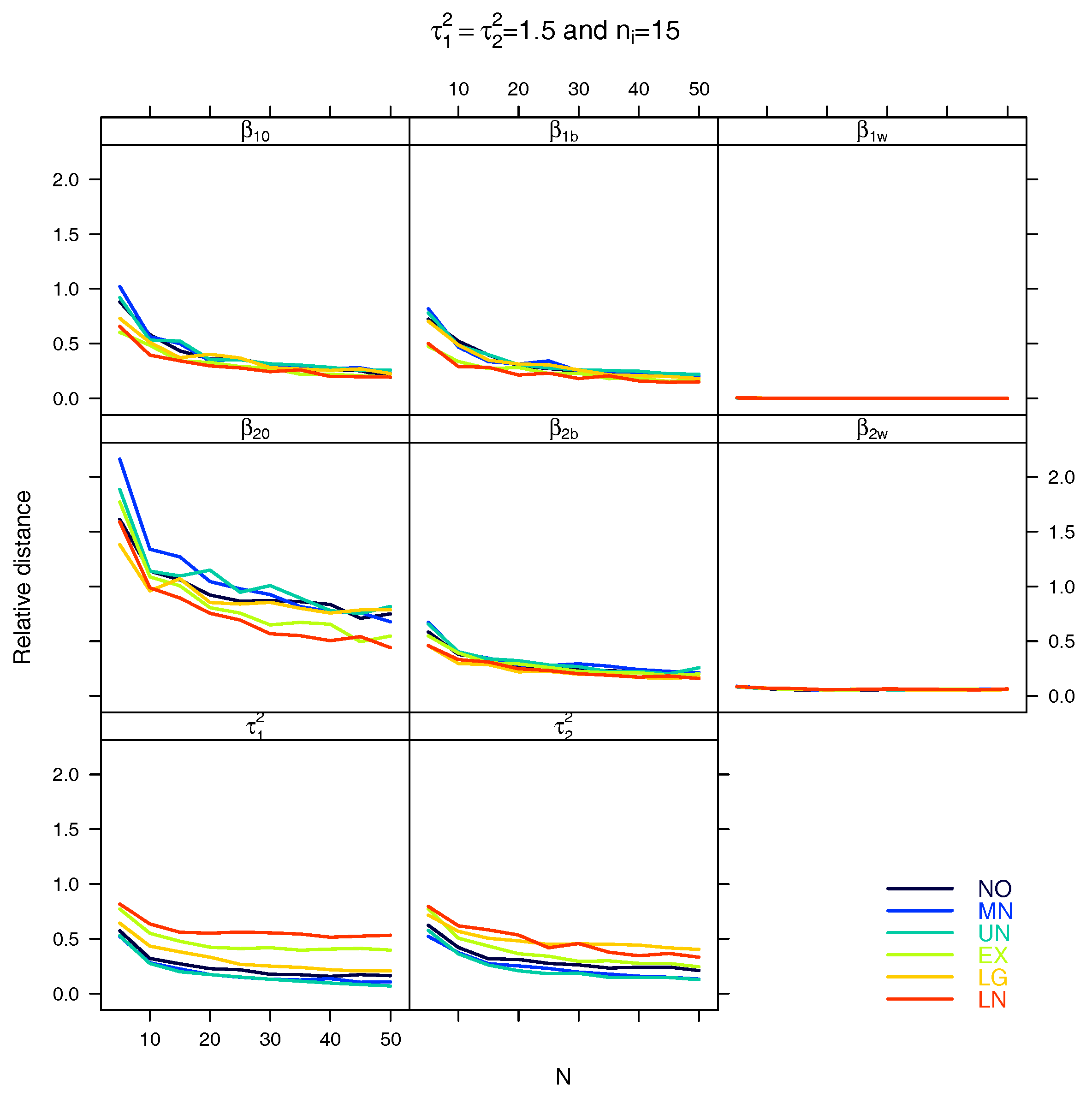
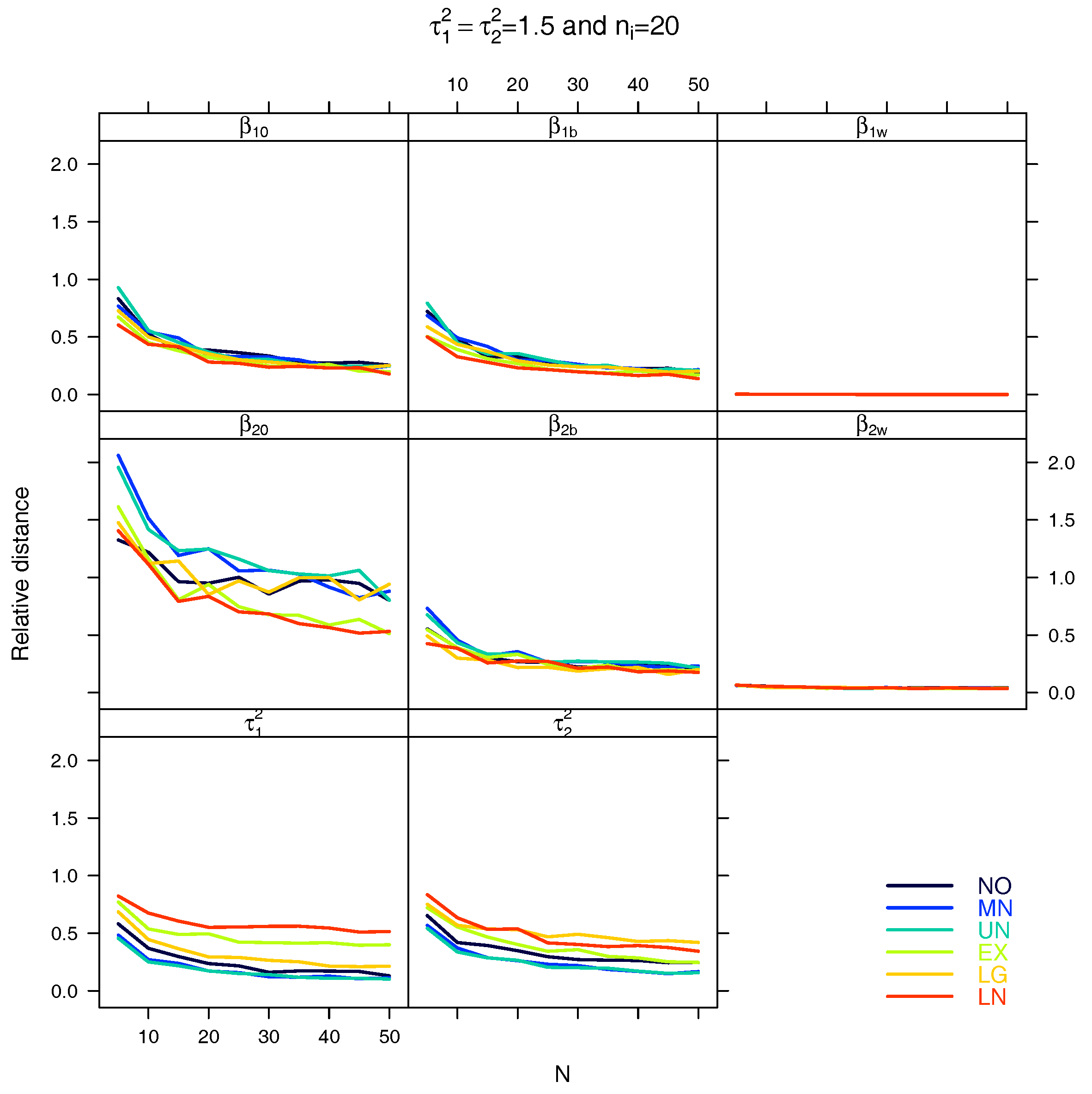
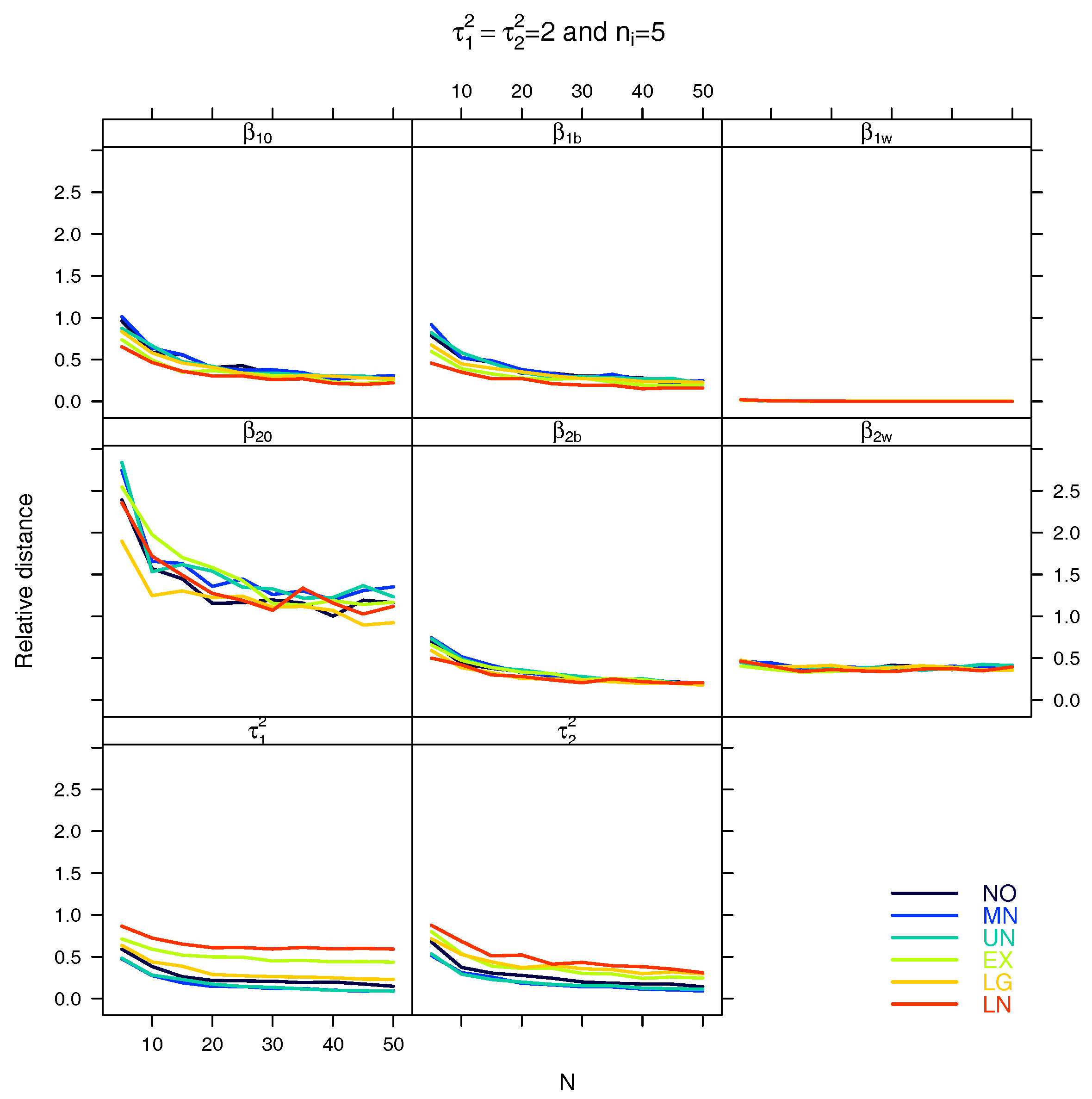

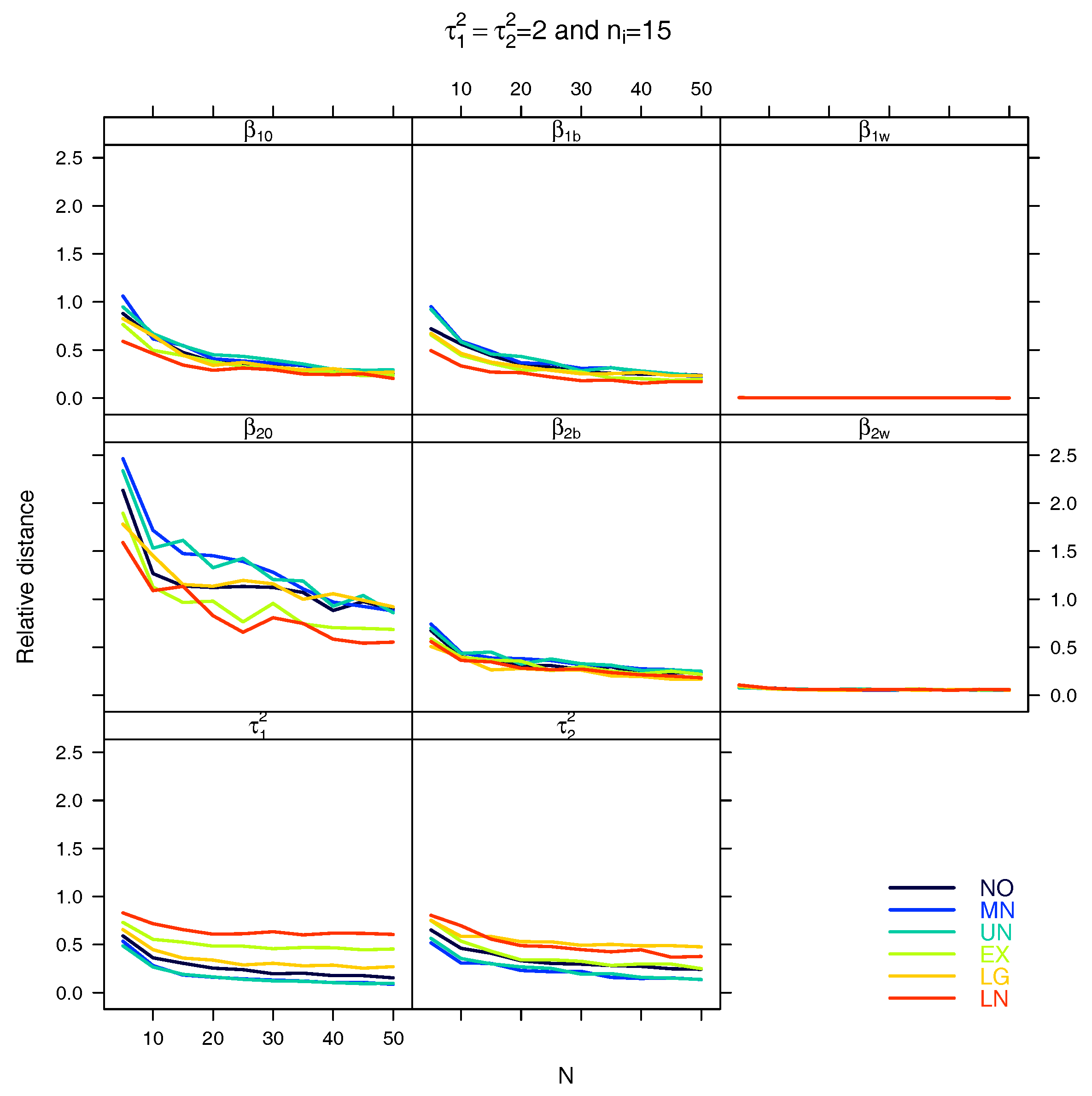


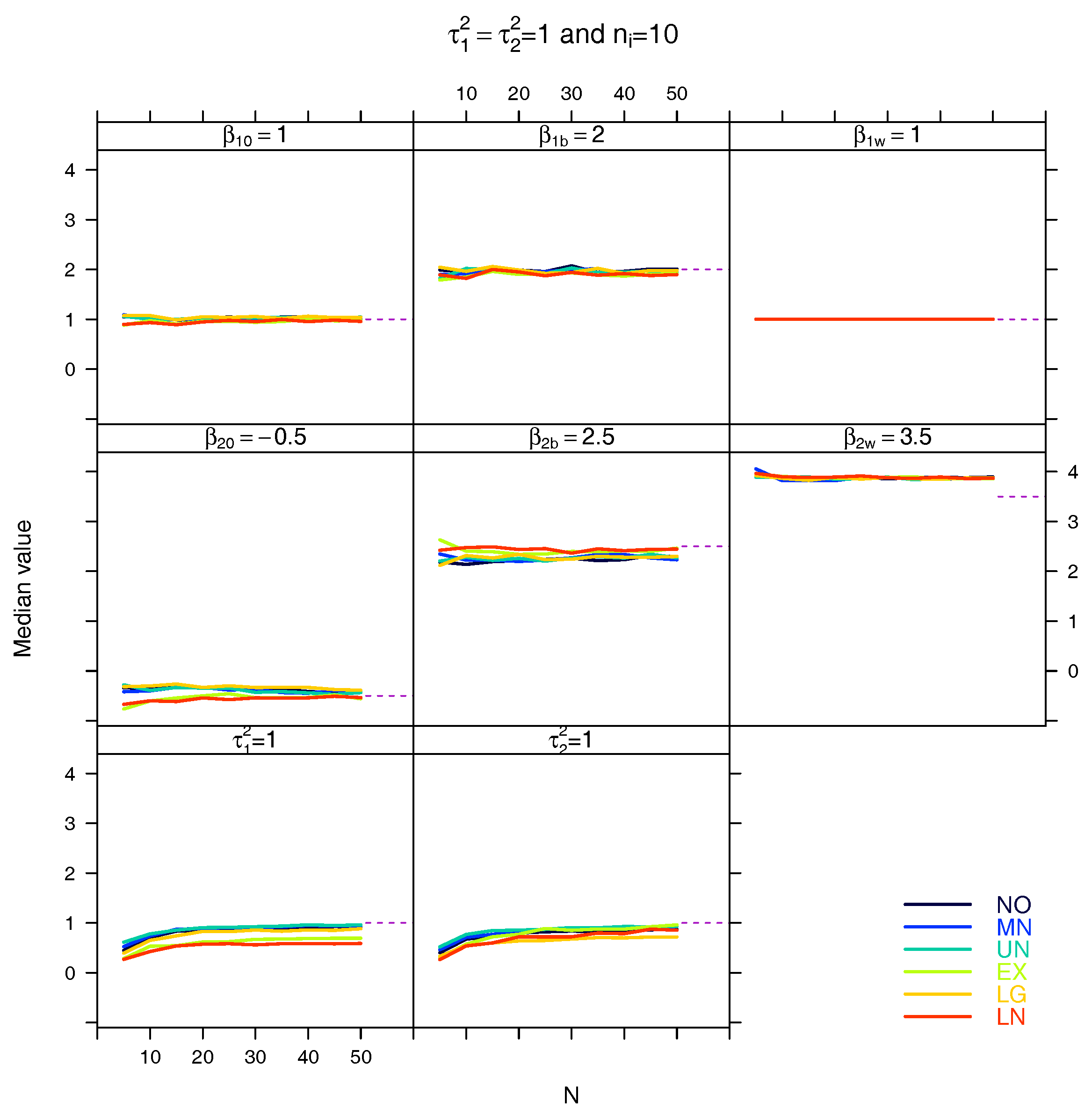

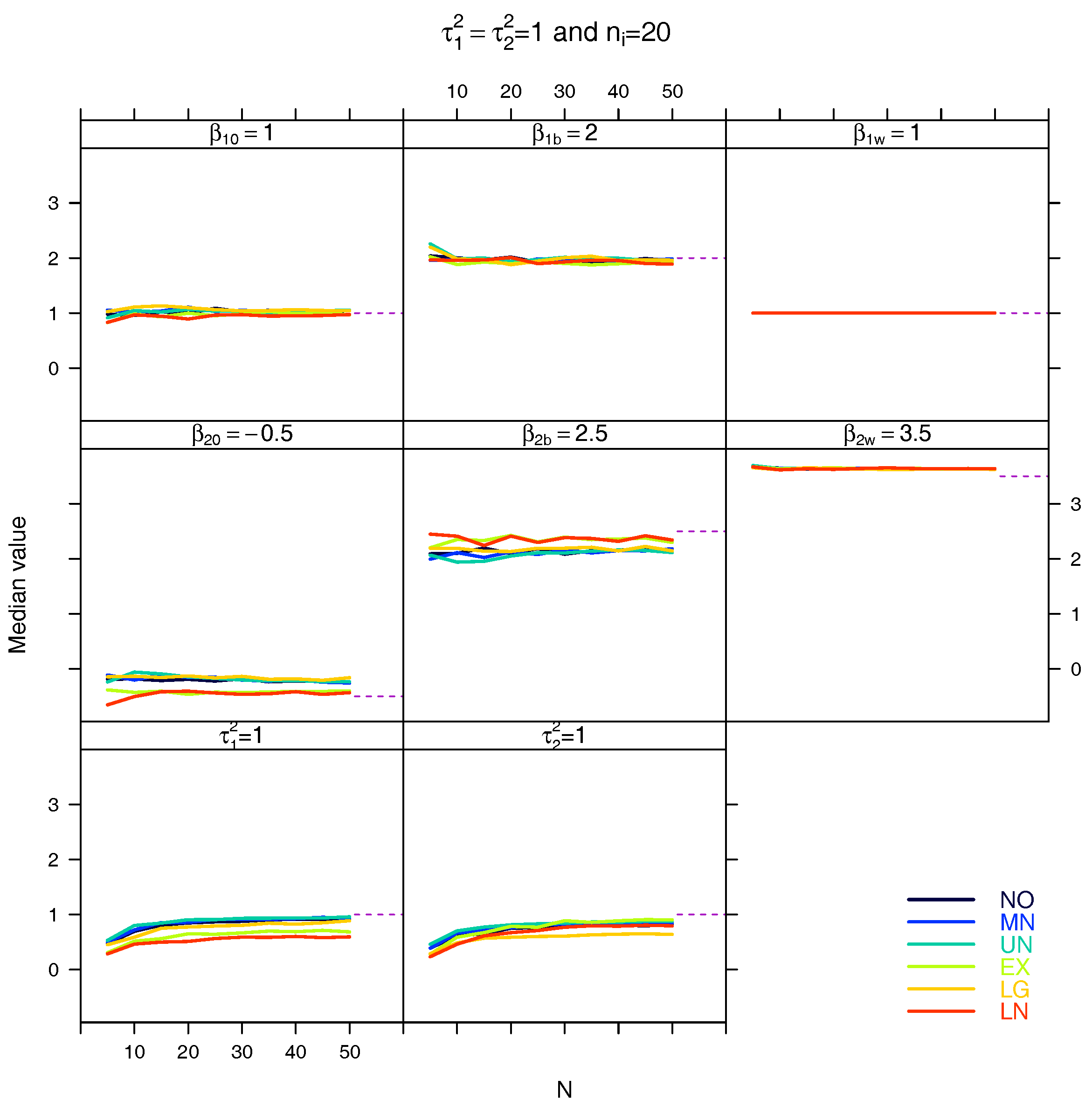
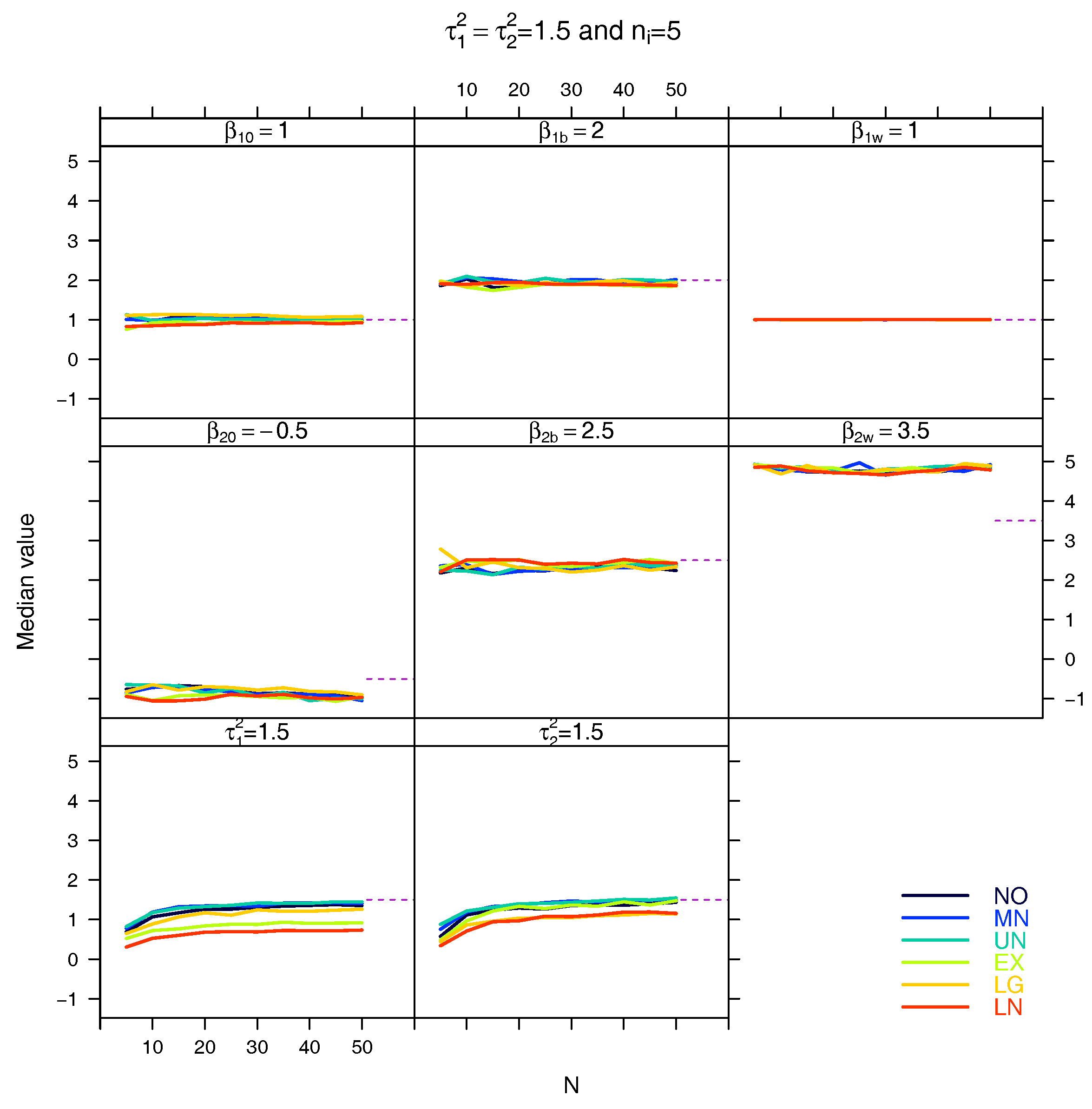
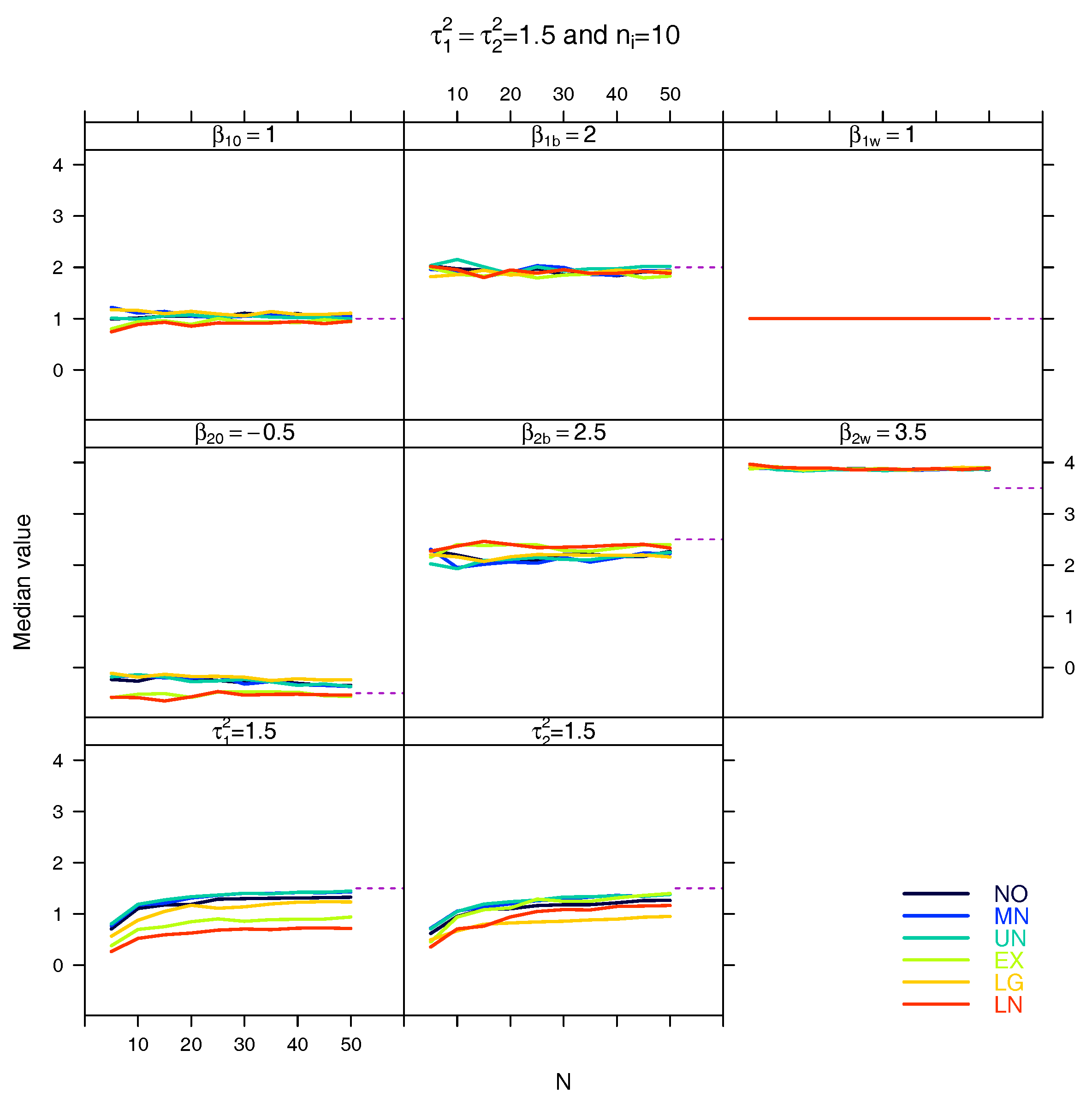
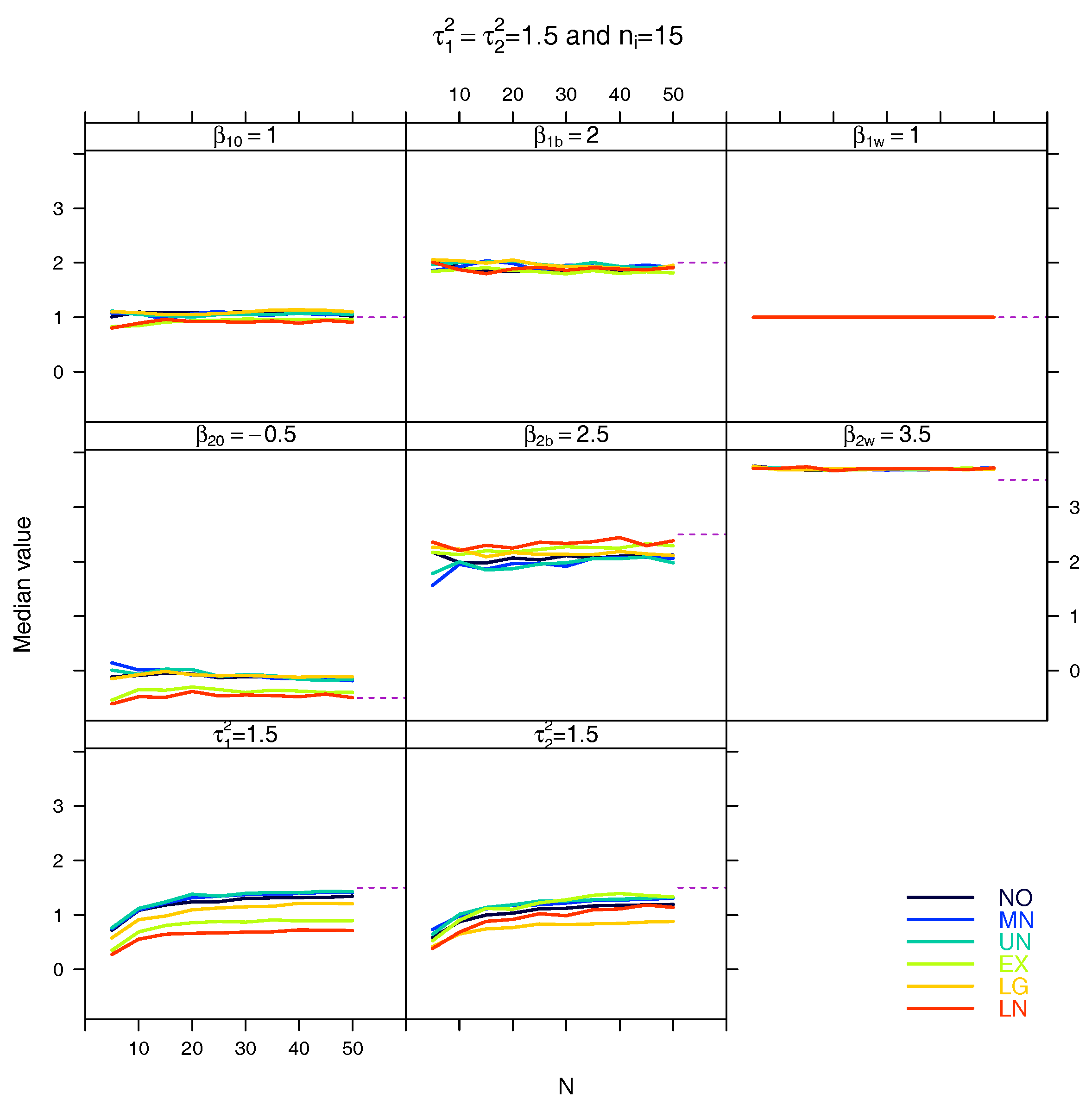
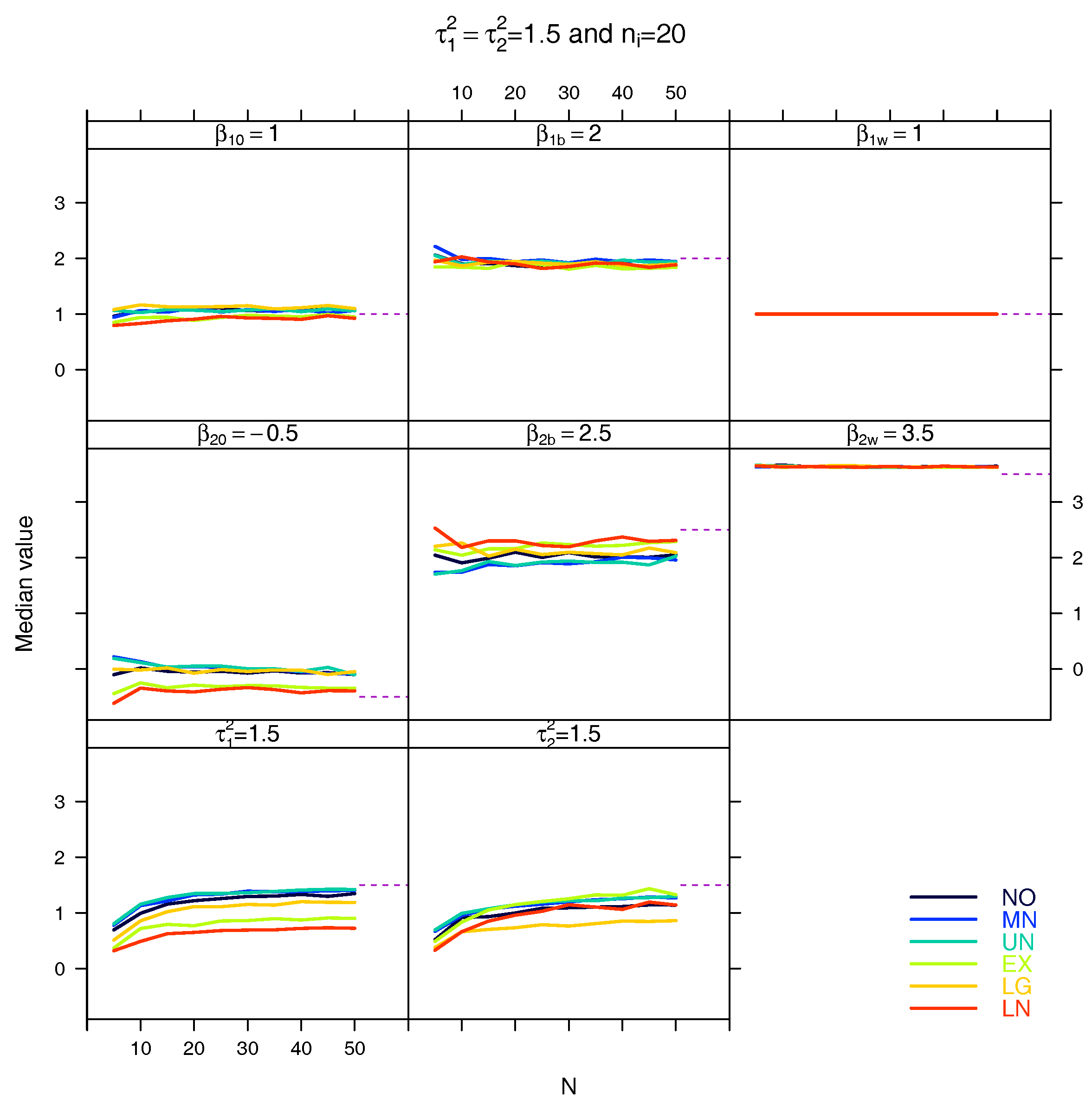

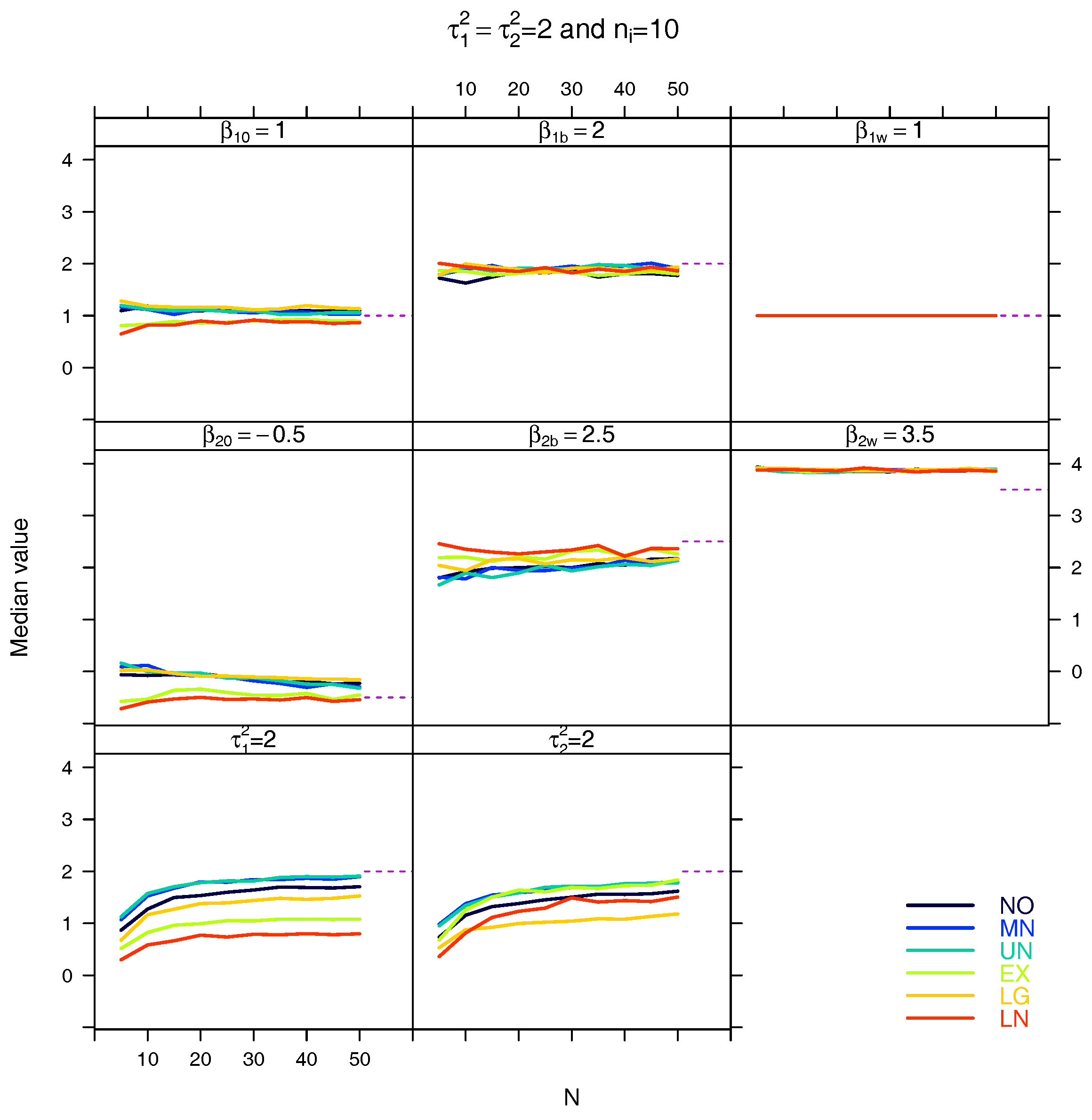
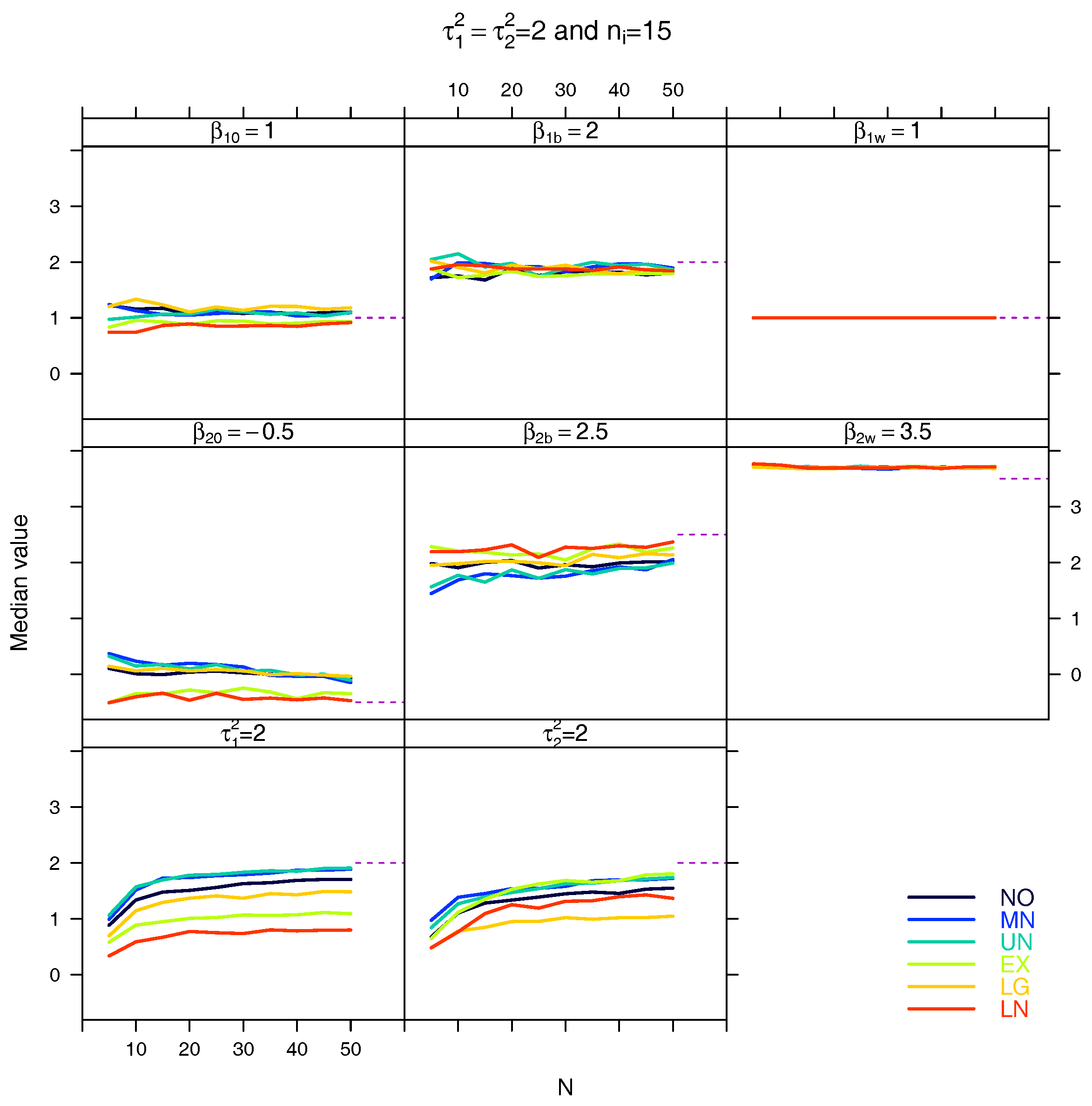
References
- Huang, X. Diagnosis of random-effect model misspecification in generalized linear mixed models for binary response. Biometrics 2009, 65, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Neuhaus, J.M.; McCulloch, C.E. The effect of misspecification of random effects distributions in clustered data settings with outcome-dependent sampling. Can. J. Stat. Revue Can. Stat. 2011, 39, 488–497. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, C.E.; Neuhaus, J.M. Misspecifying the Shape of a Random Effects Distribution: Why Getting It Wrong May Not Matter. Stat. Sci. 2011, 26, 388–402. [Google Scholar] [CrossRef]
- Verbeke, G.; Lesaffre, E. The effect of misspecifiying the random-effects distribution in linear mixed models for longitudinal data. Comput. Stat. Data Anal. 1997, 23, 541–556. [Google Scholar] [CrossRef]
- Neuhaus, J.M.; Hauck, W.W.; Kalbfleisch, J.D. The Effects of Mixture Distribution Misspecification when Fitting Mixed-Effects Logistic Models. Biometrika 1992, 79, 755–762. [Google Scholar] [CrossRef]
- Heagerty, P.J.; Kurland, B.F. Misspecified Maximum Likelihood Estimates and Generalised Linear Mixed Models. Biometrika 2001, 88, 973–985. [Google Scholar] [CrossRef]
- Agresti, A.; Caffo, B.; Ohman-Strickland, P. Examples in which misspecification of a random effects distribution reduces efficiency, and possible remedies. Comput. Stat. Data Anal. 2004, 47, 639–653. [Google Scholar] [CrossRef]
- Litière, S.; Alonso, A.; Molenberghs, G. Type I and Type II Error Under Random-Effects Misspecification in Generalized Linear Mixed Models. Biometrics 2007, 63, 1038–1044. [Google Scholar] [CrossRef] [PubMed]
- Litière, S.; Alonso, A.; Molenberghs, G. The impact of a misspecified random-effects distribution on the estimation and the performance of inferential procedures in generalized linear mixed models. Stat. Med. 2008, 27, 3125–3144. [Google Scholar] [CrossRef] [PubMed]
- Neuhaus, J.M.; McCulloch, C.E.; Boylan, R. A note on Type II error under random effects misspecifications in generalized linear mixed models. Biometrics 2011, 67, 654–660. [Google Scholar] [CrossRef] [PubMed]
- Litière, S.; Alonso, A.; Molenberghs, G. Rejoinder to “A Note on Type II Error Under Random Effects Misspecification in Generalized Linear Mixed Models”. Biometrics 2011, 67, 656–660. [Google Scholar] [CrossRef]
- McCulloch, C.E.; Neuhaus, J.M. Prediction of Random Effects in Linear and Generalized Linear Models under Model Misspecification. Biometrics 2011, 67, 270–279. [Google Scholar] [CrossRef] [PubMed]
- Neuhaus, J.M.; McCulloch, C.E.; Boylan, R. Estimation of covariate effects in generalized linear mixed models with a misspecified distribution of random intercepts and slopes. Stat. Med. 2013, 32, 2419–2429. [Google Scholar] [CrossRef] [PubMed]
- Fleming, R.A. The Weibull model and an ecological application: Describing the dynamics of foliage biomass on Scots pine. Ecol. Model. 2001, 138, 309–319. [Google Scholar] [CrossRef]
- Carroll, K.J. On the use and utility of the Weibull model in the analysis of survival data. Control. Clin. Trials 2003, 24, 682–701. [Google Scholar] [CrossRef]
- Abdel-Ghaly, A.A.; Attia, A.F.; Abdel-Ghani, M.M. The maximum likelihood estimates in step partially accelerated life test for the Weibull parameters in censored data. Commun. Stat. Theory Methods 2002, 31, 551–573. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Lai, C.D. Generalized Weibull Distributions; Springer: Berlin, Germany, 2013. [Google Scholar]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models, 1st ed.; Wiley Series in Probability and Statistics; J. Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Rinne, H. The Weibull Distribution: A Handbook, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Almalki, S.J.; Nadarajah, S. Modifications of the Weibull distribution: A review. Reliab. Eng. Syst. Saf. 2014, 124, 32–55. [Google Scholar] [CrossRef]
- Bagheri, S.F.; Samani, E.B.; Ganjali, M. The generalized modified Weibull power series distribution: Theory and applications. Comput. Stat. Data Anal. 2016, 94, 136–160. [Google Scholar] [CrossRef]
- Domma, F.; Condino, F.; Popović, B. A new generalized weighted Weibull distribution with decreasing, increasing, upside-down bathtub, N-shape and M-shape hazard rate. J. Appl. Stat. 2017, 44, 2978–2993. [Google Scholar] [CrossRef]
- Silva, G.O.; Ortega, E.M.; Cordeiro, G.M. A log-extended Weibull regression model. Comput. Stat. Data Anal. 2009, 53, 4482–4489. [Google Scholar] [CrossRef]
- Vigas, V.P.; Silva, G.O.; Louzada, F. The Poisson-Weibull Regression Model. Chil. J. Stat. 2017, 8, 25–51. [Google Scholar]
- Prataviera, F.; Ortega, E.M.; Cordeiro, G.M.; Pescim, R.R.; Verssani, B.A. A new generalized odd log-logistic flexible Weibull regression model with applications in repairable systems. Reliab. Eng. Syst. Saf. 2018, 176, 13–26. [Google Scholar] [CrossRef]
- Sohn, S.Y.; Yoon, K.B.; Chang, I.S. Random effects model for the reliability management of modules of a fighter aircraft. Reliab. Eng. Syst. Saf. 2006, 91, 433–437. [Google Scholar] [CrossRef]
- Sohn, S.Y.; Chang, I.S.; Moon, T.H. Random effects Weibull regression model for occupational lifetime. Eur. J. Oper. Res. 2007, 179, 124–131. [Google Scholar] [CrossRef]
- Bartolucci, A.A.; Bae, S.; Singh, K.P. Establishing a Bayesian predictive survival model adjusting for random effects. Math. Comput. Simul. 2008, 78, 328–334. [Google Scholar] [CrossRef]
- Lv, S.; Niu, Z.; Cui, Q.; He, Z.; Wang, G. Reliability improvement through designed experiments with random effects. Comput. Ind. Eng. 2017, 112, 231–237. [Google Scholar] [CrossRef]
- Stasinopoulos, M.; Rigby, B. gamlss.dist: Distributions for Generalized Additive Models for Location Scale and Shape. Available online: https://cran.r-project.org/web/packages/gamlss.dist/gamlss.dist.pdf (accessed on 30 May 2018).
- Pinheiro, J.C.; Chao, E.C. Efficient Laplacian and Adaptive Gaussian Quadrature Algorithms for Multilevel Generalized Linear Mixed Models. J. Comput. Graph. Stat. 2006, 15, 58–81. [Google Scholar] [CrossRef]
- Alonso, A.; Litière, S.; Molenberghs, G. A family of tests to detect misspecifications in the random-effects structure of generalized linear mixed models. Comput. Stat. Data Anal. 2008, 52, 4474–4486. [Google Scholar] [CrossRef]
- Alonso, A.; Litière, S.; Molenberghs, G. Testing for misspecification in generalized linear mixed models. Biostatistics 2010, 11, 771–786. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Drikvandi, R.; Verbeke, G.; Molenberghs, G. Diagnosing misspecification of the random-effects distribution in mixed models. Biometrics 2017, 73, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Efendi, A.; Drikvandi, R.; Verbeke, G.; Molenberghs, G. A goodness-of-fit test for the random-effects distribution in mixed models. Stat. Methods Med. Res. 2017, 26, 970–983. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Model for | Estimate | Std. Error | t-Value | p-Value |
| Intercept | 0.96 | 0.0065 | 149.1 | < |
| 1.80 | 0.0094 | 191.3 | < | |
| 0.99 | 0.0077 | 127.8 | < | |
| Model for | Estimate | Std. Error | t-Value | p-Value |
| Intercept | −0.64 | 0.1620 | −3.97 | 0.000125 |
| 2.69 | 0.2454 | 10.97 | < | |
| 3.62 | 0.2078 | 17.45 | < | |
| 486.46 | 560.93 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández, F.; Giampaoli, V. The Impact of Misspecified Random Effect Distribution in a Weibull Regression Mixed Model. Stats 2018, 1, 48-76. https://doi.org/10.3390/stats1010005
Hernández F, Giampaoli V. The Impact of Misspecified Random Effect Distribution in a Weibull Regression Mixed Model. Stats. 2018; 1(1):48-76. https://doi.org/10.3390/stats1010005
Chicago/Turabian StyleHernández, Freddy, and Viviana Giampaoli. 2018. "The Impact of Misspecified Random Effect Distribution in a Weibull Regression Mixed Model" Stats 1, no. 1: 48-76. https://doi.org/10.3390/stats1010005






