Building W Matrices Using Selected Geostatistical Tools: Empirical Examination and Application
Abstract
:1. Introduction
2. Selected Geospatial Tools in Weight Matrix Construction and Examination: Proposal
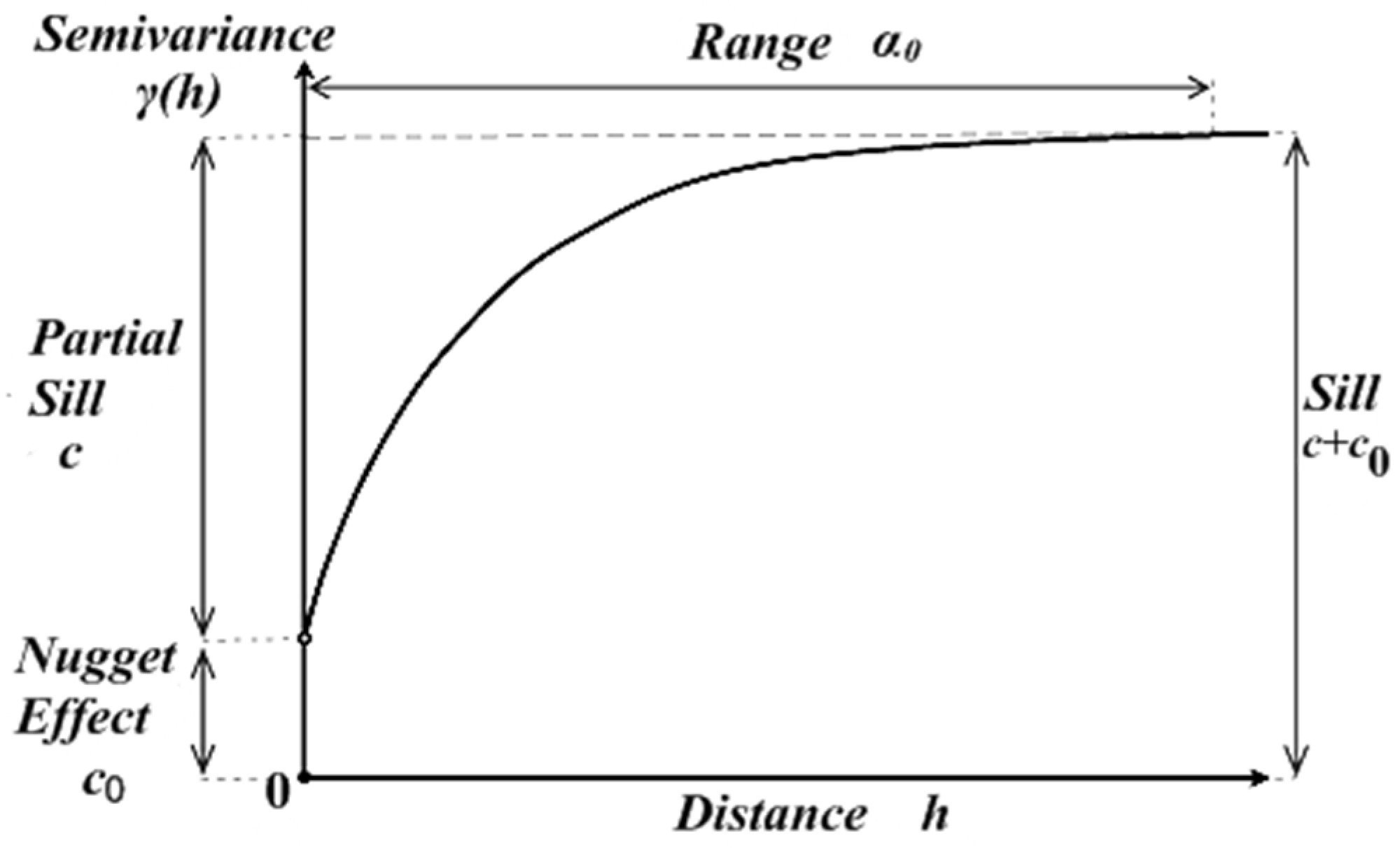
2.1. Semivariograms
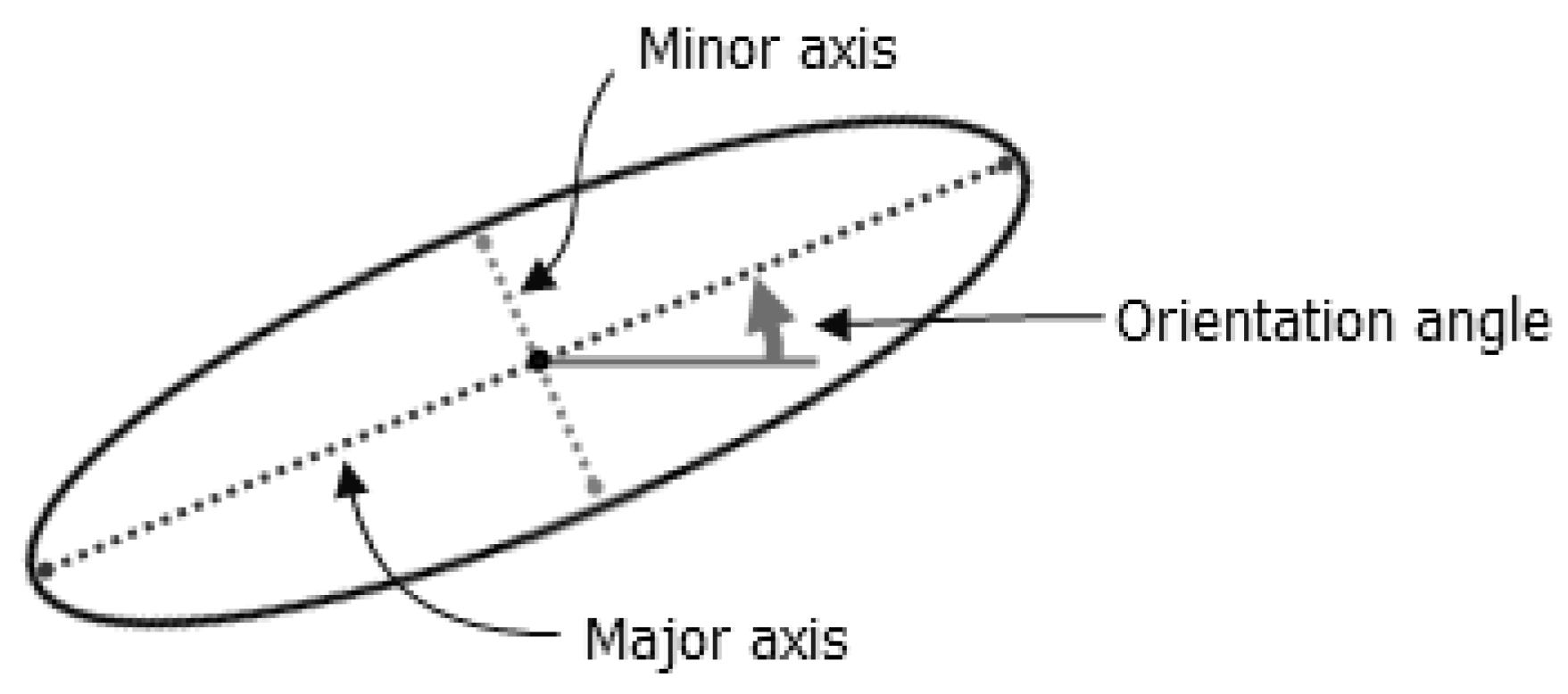
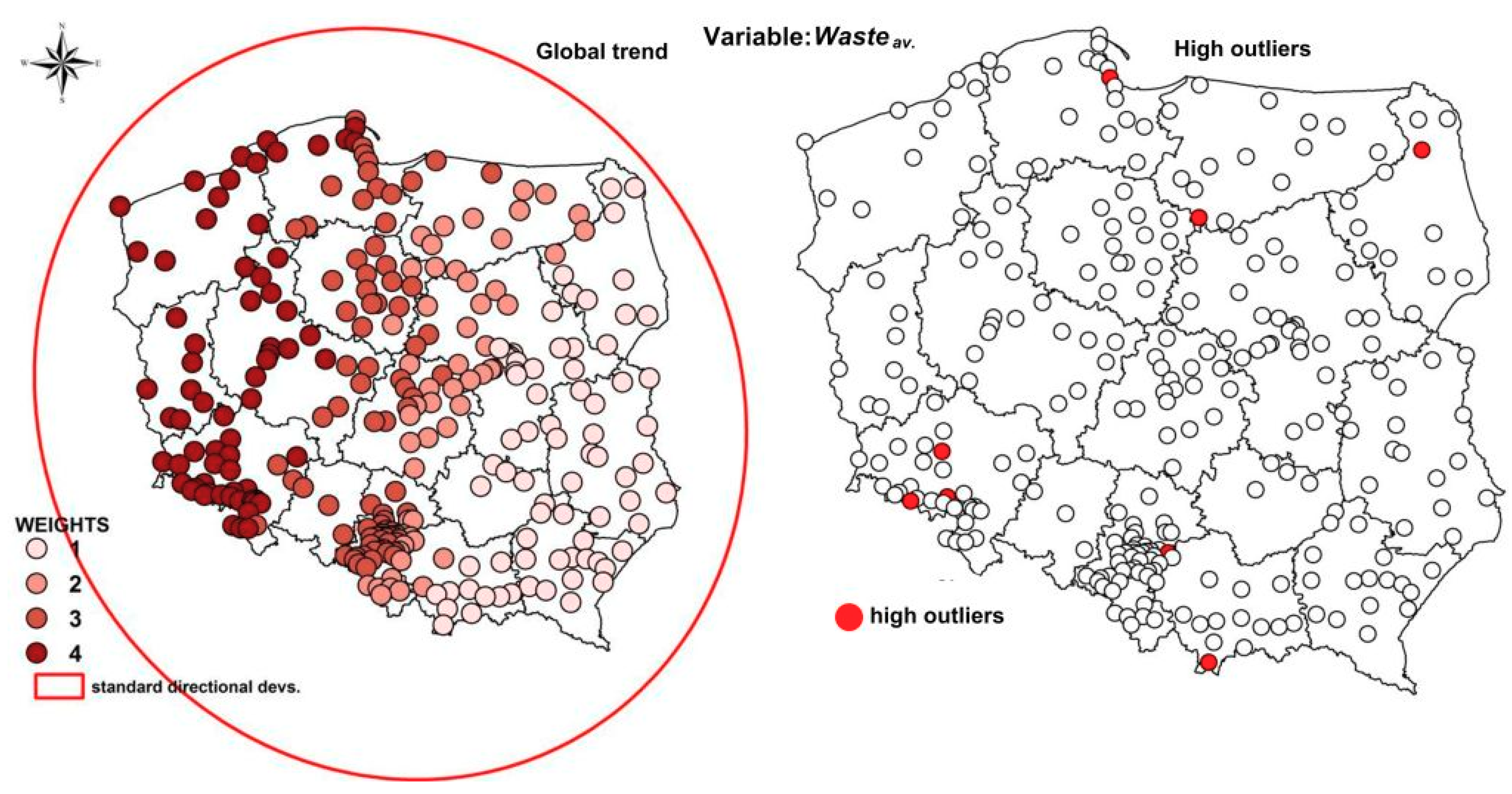
2.2. Standard Deviational Ellipse
2.3. Trend Surface Analysis
2.4. ESDA and Spatial Models
3. Results
3.1. Spatial Weight Matrices
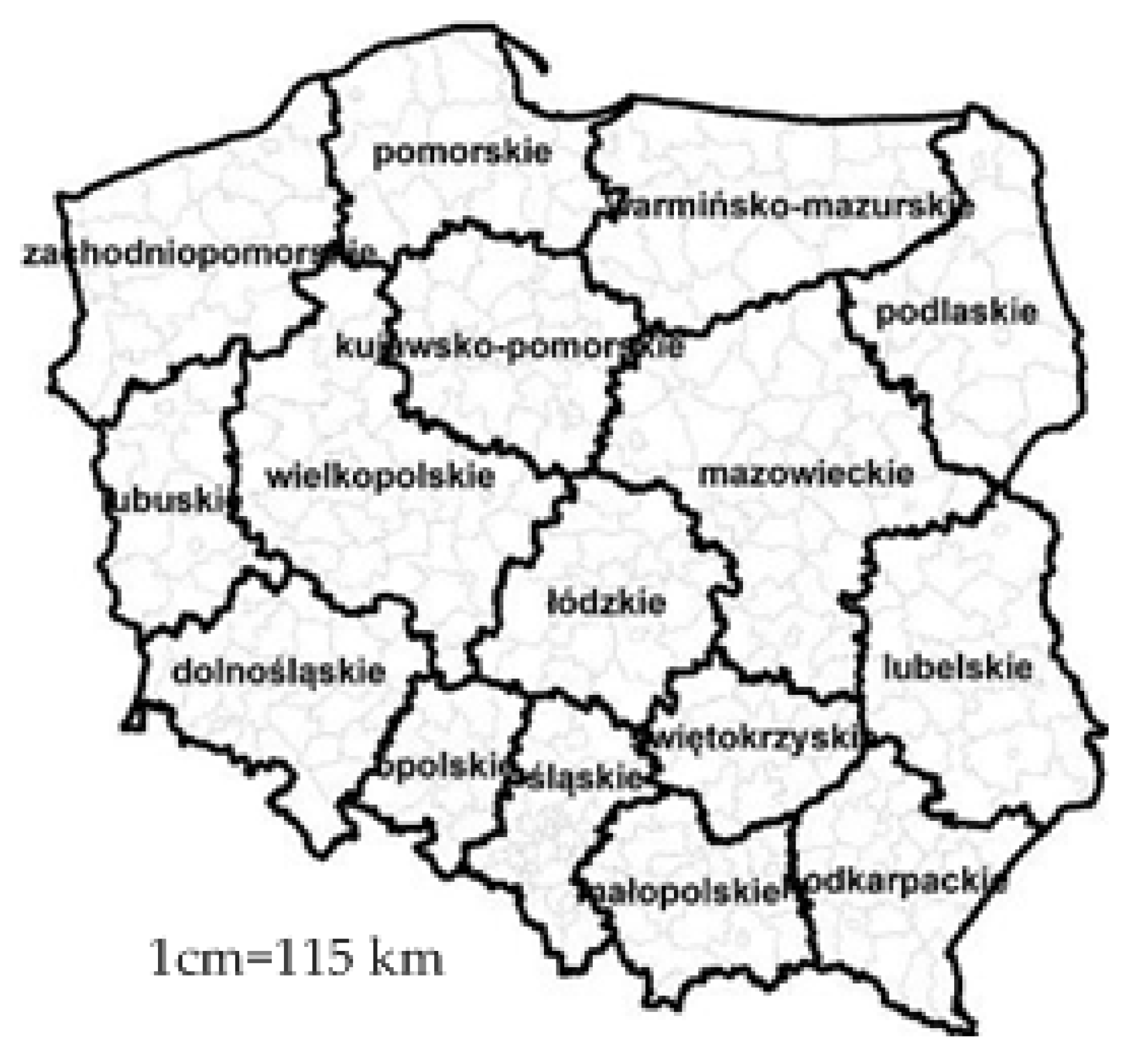
3.1.1. Geographical Distance
3.1.2. Directional Matrix
3.1.3. Random Weight Matrix
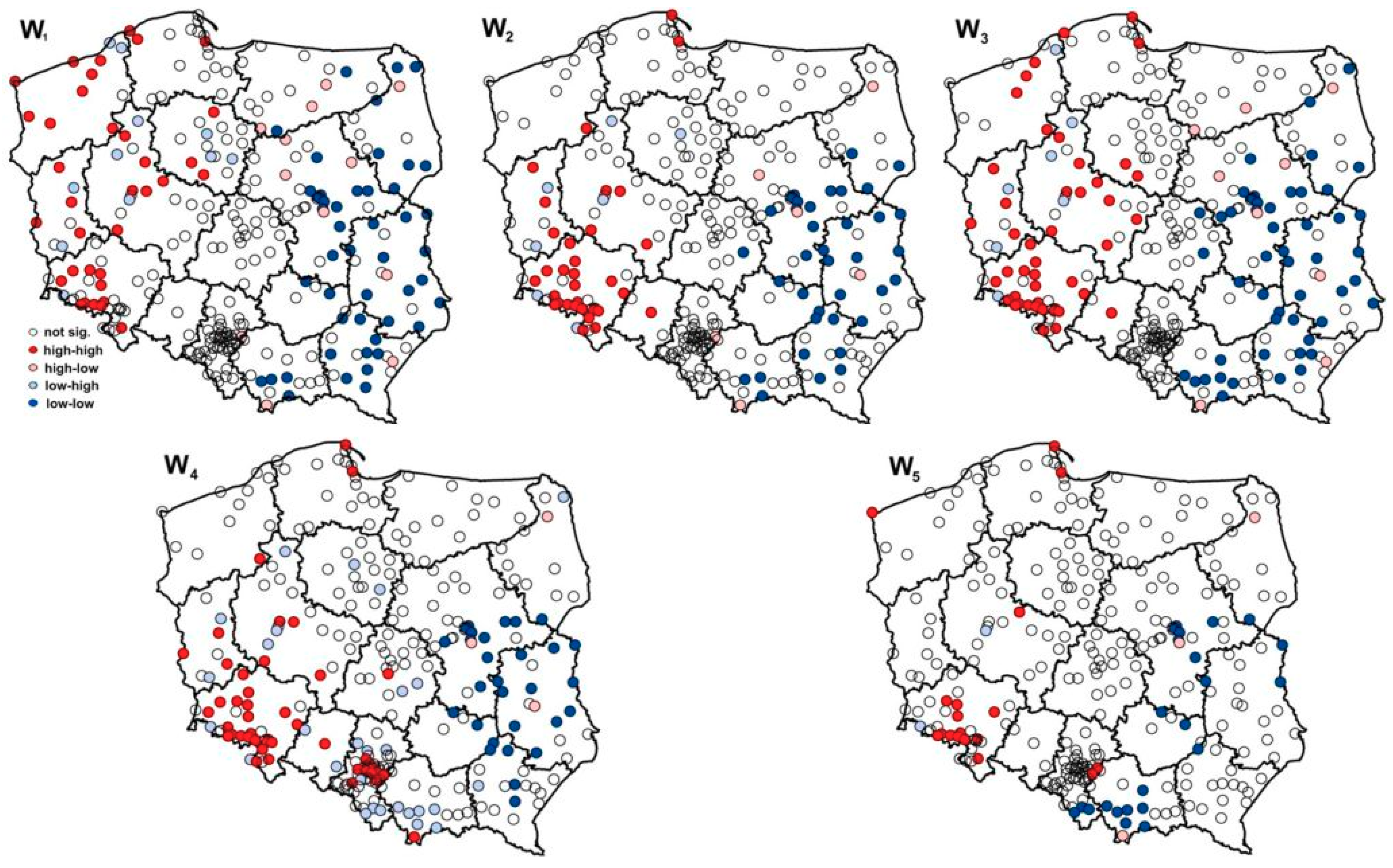
3.2. ESDA
3.3. Spatial Modelling
- Substantive and formal correctness of conclusions; therefore, the designed matrices are correct;
- Consistency and stability of modelling results (i.e., statistically significant similarity of parameter estimates);
- Differences in the values of estimates of parameters reflecting the existing spatial processes;
- Selection of a spatial weight matrix should be dictated by the research objective, and the application of different matrices may alter the conclusions concerning spatial processes.
4. Discussion
- How can a directional matrix be built based on the semivariogram? Is there a possibility of attributing values to weights in the matrix based on this geostatistical measure?
- Is the construction of the matrix for the particular periods of research justified and essential (should one include a matrix designed for each period in the model?), and how can it be done (for example, in spatial panel models)?
- Is the construction of other or specific matrices essential for external variables compared to internal variables in SLX models?
- What are the possibilities to use other geospatial methods (e.g., geographically weighted or autoregressive regression) to investigate the effects of spatial endogenous weighting matrices on the modelling results in terms of the heterogeneous relationships between variables?
5. Conclusions
Funding
Conflicts of Interest
Appendix A
| Statistics | Waste | Revenues | dWaste | dRevenues |
|---|---|---|---|---|
| Mean | 205.9 | 2915.2 | 1.02 | 1.08 |
| Max | 609 | 8506 | 8.1 | 2.7 |
| St. Deviation | 69.1 | 944.6 | 0.30 | 0.11 |
| Coefficient of Variation | 33% | 32% | 30% | 11% |
| Median | 206 | 2748 | 0.99 | 1.07 |
| Min | 6 | 1267 | −0.05 | 0.48 |
| Waste | Revenues | dRevenues | dWaste | Waste | Revenues | dRevenues | dWaste | |
|---|---|---|---|---|---|---|---|---|
| Year | 2005 | 2006 | ||||||
| Mean | 214.6 | 1969.6 | 1.12 | 1.03 | 218.4 | 2223.0 | 1.13 | 1.03 |
| St. Deviation | 70.7 | 473.7 | 0.05 | 0.38 | 69.4 | 606.3 | 0.10 | 0.32 |
| Coefficient of Variation | 33% | 24% | 4.3% | 36.6% | 32% | 27% | 9.3% | 31.1% |
| Max | 440 | 4143 | 1.47 | 4.88 | 464 | 5975 | 1.73 | 4.85 |
| Min | 19 | 1267 | 0.99 | 0.003 | 19 | 1397 | 0.80 | 0.29 |
| Median | 212 | 1808 | 1.12 | 1.004 | 214 | 2033 | 1.12 | 0.98 |
| Year | 2007 | 2008 | ||||||
| Mean | 218.8 | 2497.8 | 1.13 | 1.02 | 208.9 | 2663.2 | 1.08 | 1.02 |
| St. Deviation | 68.4 | 702.2 | 0.14 | 0.24 | 77.5 | 658.7 | 0.10 | 0.22 |
| Coefficient of Variation | 31% | 28% | 12.3% | 23.3% | 37% | 25% | 9.5% | 21.7% |
| Max | 461 | 6703 | 2.68 | 2.84 | 609 | 7212 | 1.61 | 1.98 |
| Min | 18 | 1604 | 0.67 | 0.29 | 1 | 1635 | 0.48 | 0.39 |
| Median | 218 | 2257 | 1.12 | 1.00 | 207 | 2426 | 1.08 | 0.99 |
| Year | 2009 | 2010 | ||||||
| Mean | 210.2 | 2713.9 | 1.02 | 1.03 | 205.9 | 3002.1 | 1.11 | 1.02 |
| St. Deviation | 76.0 | 633.7 | 0.09 | 0.28 | 76.4 | 841.0 | 0.15 | 0.22 |
| Coefficient of Variation | 36% | 23% | 9.2% | 27.5% | 37% | 28% | 13.9% | 21.1% |
| Max | 528 | 6200 | 1.35 | 2.57 | 521 | 8506 | 2.47 | 2.48 |
| Min | 15 | 1763 | 0.73 | 0.19 | 10 | 1971 | 0.69 | 0.49 |
| Median | 213 | 2491 | 1.02 | 1.00 | 204 | 2725 | 1.08 | 1.00 |
| Year | 2011 | 2012 | ||||||
| Mean | 204.0 | 3144.6 | 1.06 | 1.03 | 197.9 | 3232.8 | 1.03 | 1.00 |
| St. Deviation | 69.7 | 845.2 | 0.13 | 0.26 | 65.2 | 894.3 | 0.11 | 0.24 |
| Coefficient of Variation | 34% | 27% | 12.3% | 25.6% | 33% | 28% | 11.0% | 23.6% |
| Max | 580 | 7246 | 1.81 | 2.83 | 423 | 7073 | 1.46 | 2.66 |
| Min | 10 | 1967 | 0.55 | 0.34 | 14 | 1971 | 0.60 | 0.32 |
| Median | 206 | 2865 | 1.04 | 1.00 | 200 | 2915 | 1.03 | 0.99 |
| Year | 2013 | 2014 | ||||||
| Mean | 193.7 | 3361.1 | 1.05 | 1.01 | 194.5 | 3572.4 | 1.07 | 1.03 |
| St. Deviation | 58.0 | 913.1 | 0.08 | 0.22 | 57.0 | 936.3 | 0.08 | 0.32 |
| Coefficient of Variation | 30% | 27% | 8.1% | 21.5% | 29% | 26% | 7.5% | 30.9% |
| Max | 432 | 8305 | 1.31 | 2.29 | 388 | 7204 | 1.61 | 4.62 |
| Min | 36 | 2194 | 0.69 | 0.13 | 14 | 2249 | 0.84 | 0.03 |
| Median | 195 | 2989 | 1.05 | 1.00 | 201 | 3225 | 1.06 | 0.99 |
| Year | 2015 | |||||||
| Mean | 197.4 | 3686.6 | 1.03 | 1.06 | Waste—volume of collected mixed municipal waste in kg per capita, dWaste—dynamics of change of the Waste in the time period from 2005 to 2015, Revenues—revenues of cities in PLN per capita, dRevenues—dynamics of change of the revenues in the time period from 2005 to 2015, n = 279, T = 11, N = 3069 | |||
| St. Deviation | 64.7 | 972.3 | 0.07 | 0.52 | ||||
| Coefficient of Variation | 33% | 26% | 7.2% | 49.4% | ||||
| Max | 597 | 7934 | 1.41 | 8.07 | ||||
| Min | 6 | 2249 | 0.76 | −0.05 | ||||
| Median | 200 | 3288 | 1.03 | 1.00 | ||||
| Tests | Statistics |
|---|---|
| Wilks’ lambda | 0.55 *** |
| Pillai’s trace | 0.47 *** |
| Lawley–Hotelling trace | 0.77 *** |
| Roy’s largest root | 0.72 *** |
| Up to 57 km: close (W1) | Up to 263 km: medium (W2) |
| Number of regions: 279 | Number of regions: 279 |
| Number of nonzero links: 10,470 | Number of nonzero links: 13,892 |
| Percentage nonzero weights: 13.5 | Percentage nonzero weights: 17.9 |
| Average number of links: 38. | Average number of links: 50 |
| 1 least connected region: 27 with 5 links, | 1 least connected region: 27 with 6 links; |
| 1 most connected region: 194 with 69 links; | 1 most connected region: 184 with 87 links |
| Up to 545 km: far (W3) | Directional: (W4) |
| Number of regions: 279 | Number of regions: 279 |
| Number of nonzero links: 37,750 | Number of nonzero links: 14,793 |
| Percentage nonzero weights: 48.5 | Percentage nonzero weights: 29 |
| Average number of links: 135 | Average number of links: 50 |
| 1 least connected region: 27 with 32 links; | 1 least connected region: 27 with 6 links; |
| 1 most connected region: 142 with 215 links | 1 most connected region:184 with 87 links |
| Random: (W5) | |
| Number of regions: 279 Number of nonzero links: 2232 Percentage nonzero weights: 2.867384 Average number of links: 8 Non-symmetric neighbours list | W1, W2, W3—Geographical Distance Matrices W4—Directional Matrix W5—Exogenous (Random) Matrix |
References
- Kooijman, S. Some Remarks on the Statistical Analysis of Grids Especially with Respect to Ecology. Ann. Syst. Res. 1976, 5, 113–132. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Angulo, A.; Burridge, P.; Mur, J. Testing for Breaks in the Weighting Matrix; Documentos de Trabajo, Facultad de Ciencias Económicas y Empresariales, Universidad de Zaragoza: Zaragoza, Spain, 2017; Available online: http://www.dteconz.unizar.es/DT2017-01.pdf (accessed on 17 August 2016).
- LeSage, J.; Pace, R. The Biggest Myth in Spatial Econometrics. Econometrics 2014, 2, 217–249. [Google Scholar] [CrossRef] [Green Version]
- Harris, R.; Moffat, J.; Kravtsova, V. In search of ‘W’. Spat. Econ. Anal. 2011, 6, 249–270. [Google Scholar] [CrossRef]
- Lee, D.T. On k-Nearest Neighbor Voronoi Diagrams in the Plane. IEEE Trans. Comp. 1982, C-31, 478–487. [Google Scholar] [CrossRef]
- Griffith, D.A. Some Guidelines for Specifying the Geographic Weights Matrix. In Practical Handbook of Spatial Statistics; Arlinhaus, S.L., Ed.; CRC: Boca Raton, FL, USA, 1996; pp. 65–82. ISBN 10 0849301327. [Google Scholar]
- Getis, A.; Aldstadt, J. Constructing the Spatial Weights Matrix Using a Local Statistic Spatial. Geogr. Anal. 2004, 36, 90–104. [Google Scholar] [CrossRef]
- Fernández, E.; Mayor, M.; Rodríguez, J. Estimating spatial autoregressive models by GME-GCE techniques. Int. Reg. Sci. Rev. 2009, 32, 148–172. [Google Scholar] [CrossRef]
- Mur, J.; Paelinck, J. Deriving the W-matrix via p-median complete correlation analysis of residuals. Ann. Reg. Sci. 2010, 47, 253–267. [Google Scholar] [CrossRef]
- Stewart, M.; Zhukov, Y. Choosing Your Neighbors: The Sensitivity of Geographical Diffusion in International Relations. 2010. Available online: http://isites.harvard.edu/fs/docs/icb.topic668784.files/Stewart _Zhukov_ISA.pdf (accessed on 24 June 2017).
- Hondroyiannis, G.; Kelejian, H.H.; Tavlas, G.S. Spatial Aspects of Contagion Among Emerging Economies. Spat. Econ. Anal. 2009, 4, 191–211. [Google Scholar] [CrossRef]
- Kelejian, H.; Piras, G. Estimation of spatial models with endogenous weighting matrices, and an application to a demand model for cigarettes. Reg. Sci. Urban Econ. 2014, 46, 140–149. [Google Scholar] [CrossRef]
- Benjanuvatra, S.; Burridge, P. QML Estimation of the Spatial Weight Matrix in the MR-SAR Model; DERS University of York Working Paper; University of York: York, UK, 2015; Available online: http://rri.wvu.edu/wp-content/uploads/2013/07/Fullpaper_3.A.3.pdf (accessed on 17 August 2016).
- Qu, X.; Lee, L. Estimating a spatial autoregressive model with an endogenous spatial weight matrix. J. Econ. 2015, 184, 209–232. [Google Scholar] [CrossRef]
- Getis, A. Spatial weights matrices. Geogr. Anal. 2009, 41, 404–410. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, K. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009; ISBN 9781420064247. [Google Scholar]
- World Bank. Available online: http://siteresources.worldbank.org/INTURBANDEVELOPMENT/Resources/336387-334852610766/Chap2.pdf (accessed on 27 May 2018).
- Tobler, W. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; Wiley Interscience: Hoboken, NJ, USA, 1993. [Google Scholar]
- Matheron, G. Principles of Geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Matheron, G. The Intrinsic Random Functions and Their Applications. Adv. Appl. Probab. 1973, 5, 439–468. [Google Scholar] [CrossRef]
- Waller, L.A.; Gotway, C.A. Applied Spatial Statistics for Public Health Data; Wiley: Hoboken, NJ, USA, 2004; ISBN 978-0-471-38771-8. [Google Scholar]
- Mohebbi, M.; Wolfe, R.; Jolley, D. A Poisson regression approach for modelling spatial autocorrelation between geographically referenced observations. BMC Med. Res. Methodol. 2011, 11, 133. [Google Scholar] [CrossRef] [PubMed]
- Hohn, M.E. Geostatistics and Petroleum Geology; Van Nostrand Reinhold: New York, NY, USA, 1988; p. 10. [Google Scholar]
- Bao, S.D. Soil and Agricultural Chemistry Analysis; China Agricultural Press: Beijing, China, 1999. [Google Scholar]
- SAS/STAT(R) 9.2 User’s Guide, Second Edition. Available online: https://support.sas.com/documentation /cdl/en/statug/63033/HTML/default/viewer.htm#statug_variogram_a0000000386.htm (accessed on 24 May 2018).
- Hanke, R.J.; Fischer, P.M.; Pollyea, R.M. Directional semivariogram analysis to identify and rank controls on the spatial variability of fracture networks. J. Struct. Geol. 2018, 108, 34–51. [Google Scholar] [CrossRef]
- Variograms. Available online: http://geog.uoregon.edu/GeogR/topics/variograms.html (accessed on 22 July 2018).
- How zonal geometry works. Available online: http://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-analyst-toolbox/h-how-zonal-geometry-works.htm (accessed on 13 May 2018).
- Lefever, D.W. Measuring Geographic Concentration by Means of the Standard Deviational Ellipse. Am. J. Sociol. 1926, 32, 88–94. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Shi, B.; Inyang, H.I. GIS-based Quantitative Analysis of Orientation Anisotropy of Contaminant Barrier Particles Using Standard Deviational Ellipse. Soil Sediment Contam. Int. J. 2008, 17, 437–447. [Google Scholar] [CrossRef]
- Wang, B.; Shi, W.; Miao, Z. Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space. PLoS ONE 2015, 10, e118537. [Google Scholar] [CrossRef] [PubMed]
- ArcGIS for Desktop. Available online: http://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-statistics-toolbox/directional-distribution.htm (accessed on 17 August 2018).
- Chojnicki, Z.; Czyż, T. Zastosowania analizy trendu powierzchniowego w geografii. [Trend surface analysis in geography]. Prz. Geogr. 1975, 47, 235–261. [Google Scholar]
- Unwin, J.D. An Introduction to Trend Surface Analysis. Concepts and Techniques in Modern Geography; Geo Books: Norwich, UK, 1978; ISBN 0902246518. [Google Scholar]
- Moran, P.A.P. The interpretation of statistical maps. J. R. Stat. Soc. 1948, 10, 243–251. [Google Scholar]
- Baltagi, B. Econometric Analysis of Panel Data, 4th ed.; John Wiley and Sons: New York, NY, USA, 2008. [Google Scholar]
- Elhorst, J. Spatial Econometrics: From Cross-Sectional Data to Spatial Panels; Springer: New York, NY, USA, 2014. [Google Scholar]
- Mur, J.; López, F.; Angulo, A. Spatial SUR models: Specification, Testing and Selection. 2010. Available online: http://www.agecon.purdue.edu/sea_2010/Sessions/Spatial%20Effects%20in%20SUR%20Models.%20Specification%20and%20Testing.pdf (accessed on 20 July 2018).
- Wysocka, P. Kluczowe czynniki wpływające na ilość odpadów powstających w przestrzeni miejskiej. In Nowe Trendy w Naukach Humanistycznych i Społeczno-Ekonomicznych; Kuczera, M., Ed.; Creativetime: New York, NY, USA, 2014; Available online: http://pwysocka-wastemodeling.home.amu.edu.pl/wp-content/uploads/2014/05/Czynniki_Wysocka_2012.pdf (accessed on 13 March 2018).
- Kłos, L. Environmental Awareness of Polish People—Overview of Research. In Studia i Prace Wydziału Nauk Ekonomicznych i Zarządzania; Kryk, B., Skubiak, B., Eds.; Wydawnictwo Naukowe Uniwersytetu Szczecińskiego: Szczecin, Poland, 2015; Volume 42. [Google Scholar]
- Cheba, K. Methods of forecasting changes in municipal waste production in case of cities. AUL Folia Oecon. 2014, 3, 223–229. [Google Scholar]
- Antczak, E. Economic Development and Transfrontier Shipments of Waste in Poland—Spatio-Temporal Analysis. Comp. Econ. Res. 2014, 17, 6–21. [Google Scholar] [CrossRef]
- Terms Used in Official Statistics. Available online: http://stat.gov.pl/en/metainformations/glossary /terms-used-in-officialstatistics/265,term.html?pdf=1 (accessed on 27 October 2017).
- Eurostat, Municipal Waste Statistic. Available online: http://ec.europa.eu/eurostat/statistics-explained/index.php/Municipal_waste _statistics (accessed on 25 October 2017).
- Eurostat, Database, Environment—Waste Streams. Available online: http://ec.europa.eu/eurostat/data/database (accessed on 25 October 2017).
- Chief Inspectorate for Environmental Protection. Available online: http://www.gios.gov.pl/stansrodowiska/gios/pokaz_artykul/en/front/stanwpolsce/srodowisko_i_zdrowie/odpady (accessed on 25 October 2017).
- Cyranka, M.; Jurczyk, M.; Pająk, T. Municipal Waste-to-Energy plants in Poland—Current projects. E3S Web Conf. 2016, 10, 00070. [Google Scholar] [CrossRef]
- Waste Incineration Plants. Available online: http://spalarnie-odpadow.pl/spalarnie-w-polsce-i-na-swiecie/ (accessed on 25 October 2017).
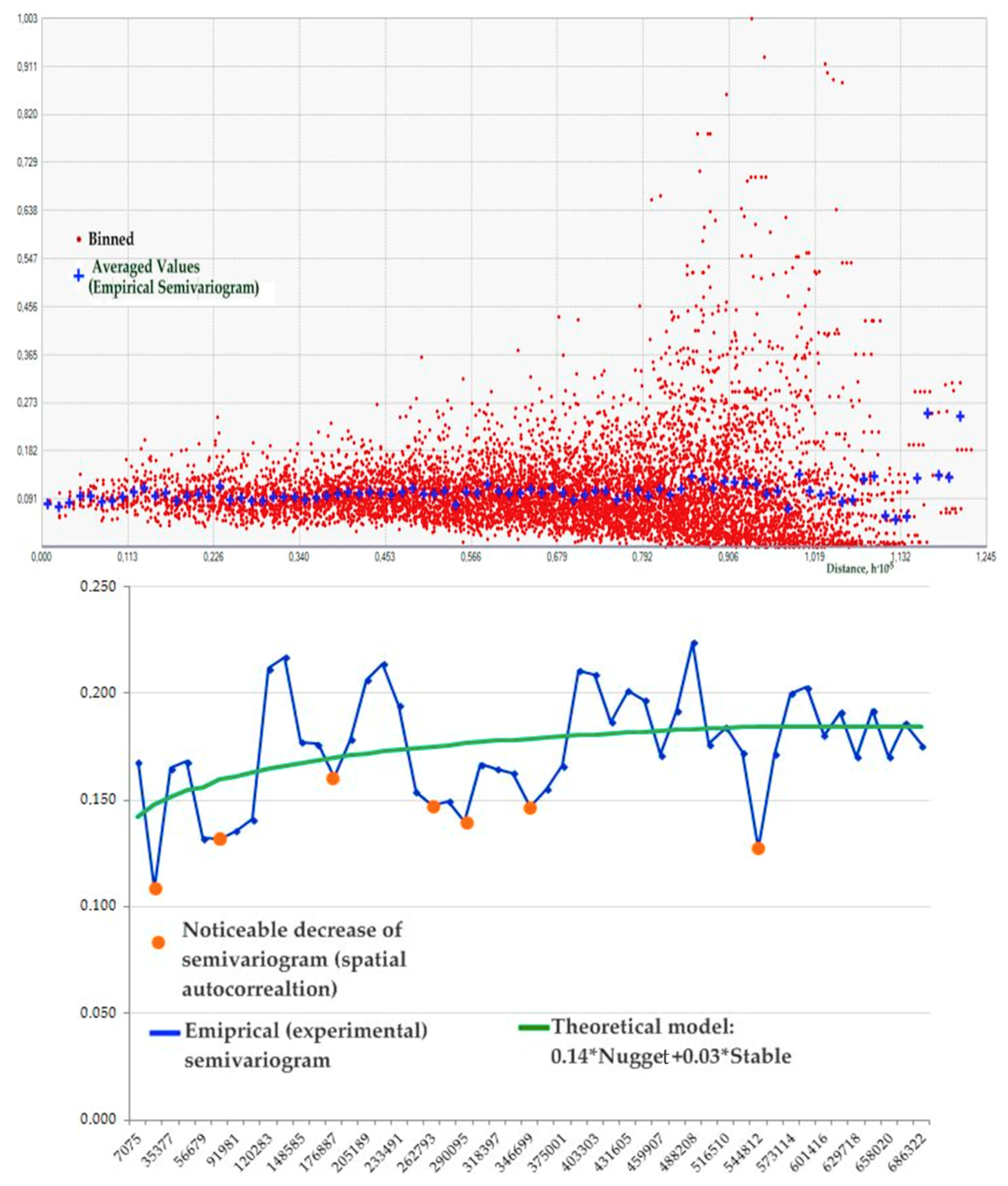
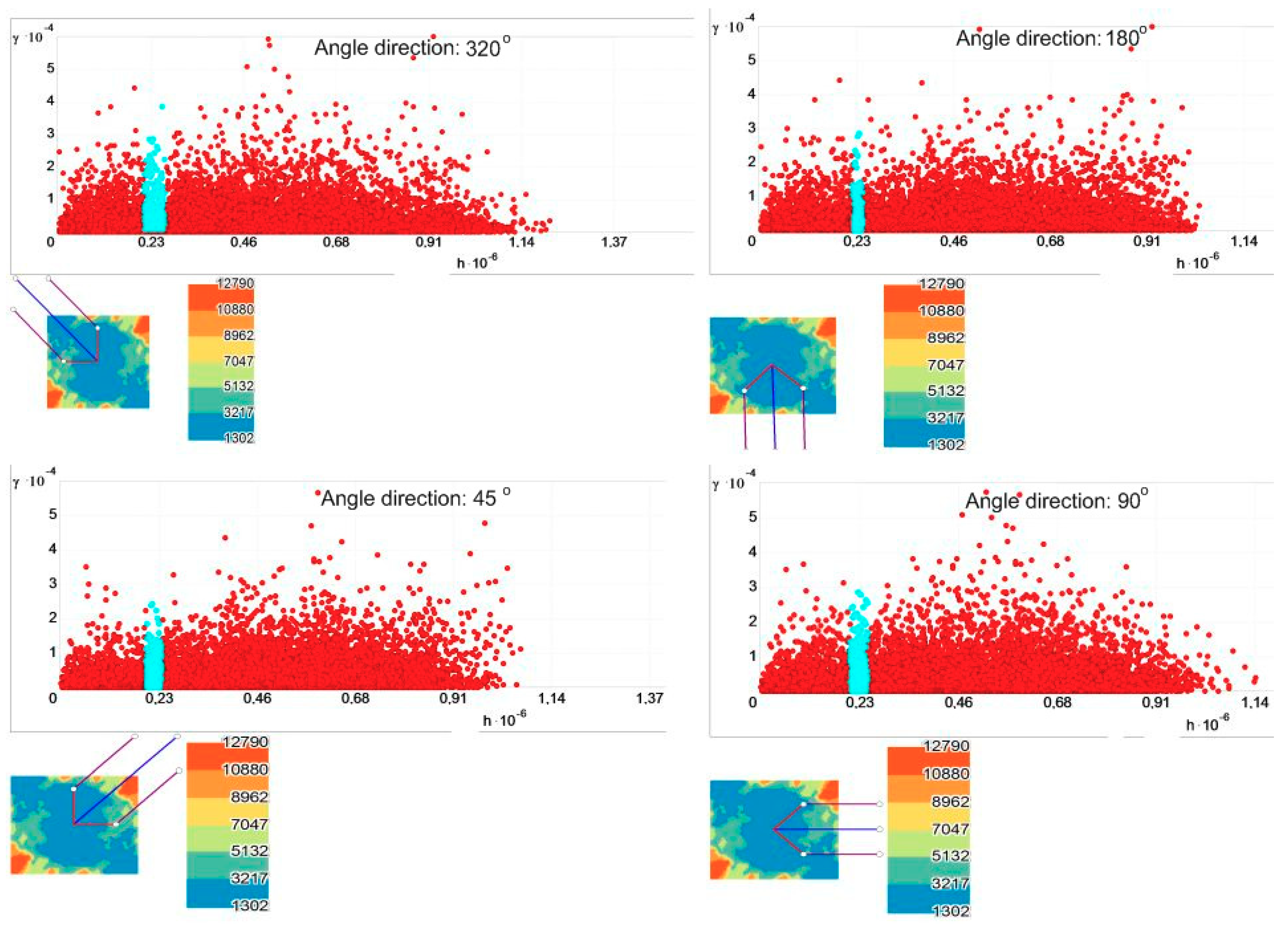

| Class | Distance | Semivariogram | Class | Distance | Semivariogram |
|---|---|---|---|---|---|
| Wasteav | Wasteav | ||||
| 1 | 7075 | 0.168 | 21 | 290,095 | 0.140 |
| 2 | 21,226 | 0.109 | 22 | 304,246 | 0.167 |
| 3 | 35,377 | 0.165 | 23 | 318,397 | 0.165 |
| 4 | 49,528 | 0.168 | 24 | 332,548 | 0.163 |
| 5 | 56,831 | 0.132 | 25 | 346,699 | 0.147 |
| 6 | 77,830 | 0.132 | 26 | 360,850 | 0.155 |
| 7 | 91,981 | 0.136 | 27 | 375,001 | 0.166 |
| 8 | 106,132 | 0.141 | 28 | 389,152 | 0.211 |
| 9 | 120,283 | 0.212 | 29 | 403,303 | 0.209 |
| 10 | 134,434 | 0.217 | 30 | 417,454 | 0.187 |
| 11 | 148,585 | 0.177 | 31 | 431,605 | 0.201 |
| 12 | 162,736 | 0.176 | 32 | 445,756 | 0.197 |
| 13 | 176,887 | 0.161 | 33 | 459,907 | 0.171 |
| 14 | 191,038 | 0.179 | 34 | 474,057 | 0.192 |
| 15 | 205,189 | 0.206 | 35 | 488,208 | 0.224 |
| 16 | 219,340 | 0.214 | 36 | 502,359 | 0.176 |
| 17 | 233,491 | 0.194 | 37 | 516,510 | 0.184 |
| 18 | 247,642 | 0.154 | 38 | 530,661 | 0.173 |
| 19 | 262,793 | 0.148 | 39 | 544,812 | 0.127 |
| 20 | 275,944 | 0.149 | 40 | 558,963 | 0.172 |
| Moran’s I | Wasteav. | Waste2005 | Waste2010 | Waste2015 |
|---|---|---|---|---|
| Up to 57 km: close (W1) | 0.18 *** | 0.09 *** | 0.17 *** | 0.09 *** |
| Up to 263 km: medium (W2) | 0.16 *** | 0.08 *** | 0.15 *** | 0.08 *** |
| Up to 545 km: far (W3) | 0.07 *** | 0.05 *** | 0.08 *** | 0.04 *** |
| Directional: (W4) | 0.15 *** | 0.20 *** | 0.20 *** | 0.10 *** |
| Random: (W5) | 0.19 *** | 0.15 *** | 0.20 *** | 0.15 *** |
| Model | Spatial Weight Matrix | α0 | α1 | λ |
|---|---|---|---|---|
| Up to 57 km: close (W1) | 2.25 *** | 0.58 *** | 0.37 *** | |
| Up to 263 km: medium (W2) | 2.25 *** | 0.58 *** | 0.41 *** | |
| Up to 545 km: far (W3) | 2.25 *** | 0.58 *** | 0.44 *** | |
| Directional: (W4) | 2.25 *** | 0.58 *** | 0.10 *** | |
| Random: (W5) | 2.25 *** | 0.57 *** | 0.19 *** |
| Model | Spatial Weight Matrix | Year | α0 n | α1 n | λnnn |
|---|---|---|---|---|---|
| W1 | 2005 | 2.31 *** | 0.12 ** | 0.14 | |
| W2 | 2.31 *** | 0.14 ** | 0.16 | ||
| W3 | 2.49 *** | 0.20 ** | −0.02 | ||
| W4 | 2.28 *** | 0.15 ** | 0.18 * | ||
| W5 | 2.52 *** | 0.02 ** | 0.16 ** | ||
| W1 | 2006 | 2.31 *** | −0.03 | 0.23 * | |
| W2 | 2.31 *** | −0.04 | 0.19 | ||
| W3 | 2.35 *** | −0.04 | 0.07 | ||
| W4 | 2.28 *** | −0.05 | 0.18 * | ||
| W5 | 2.35 *** | −0.03 | 0.11 * | ||
| W1 | 2007 | 2.31 *** | 0.008 * | 0.20 * | |
| W2 | 2.31 *** | 0.005 * | 0.16 | ||
| W3 | 2.27 *** | 0.04 * | −0.05 | ||
| W4 | 2.28 *** | 0.01 * | 0.17 * | ||
| W5 | 2.27 *** | 0.04 * | 0.05 | ||
| W1 | 2008 | 2.27 *** | 0.09 * | −0.02 | |
| W2 | 2.27 *** | 0.09 * | 0.003 | ||
| W3 | 2.34 *** | 0.06 * | −0.09 | ||
| W4 | 2.26 *** | 0.10 * | 0.17 ** | ||
| W5 | 2.28 *** | 0.05 * | −0.008 | ||
| W1 | 2009 | 2.29 *** | 0.09 * | 0.32 ** | |
| W2 | 2.29 *** | 0.07 * | 0.30 ** | ||
| W3 | 2.29 *** | 0.002 * | 0.47 ** | ||
| W4 | 2.26 *** | 0.11 * | 0.18 * | ||
| W5 | 2.29 *** | 0.01 * | 0.13 * | ||
| W1 | 2010 | 2.28 *** | −0.02 | 0.28 ** | |
| W2 | 2.28 *** | −0.02 | 0.29 ** | ||
| W3 | 2.32 *** | −0.05 | 0.41 ** | ||
| W4 | 2.24 *** | −0.03 | 0.18 * | ||
| W5 | 2.32 *** | −0.04 | 0.16 ** | ||
| W1 | 2011 | 2.28 *** | −0.004 | 0.21 ** | |
| W2 | 2.28 *** | −0.006 | 0.23 * | ||
| W3 | 2.31 *** | −0.03 | 0.37 ** | ||
| W4 | 2.26 *** | −0.01 | 0.17 * | ||
| W5 | 2.32 *** | −0.001 | 0.17 ** | ||
| W1 | 2012 | 2.27 *** | 0.03 * | 0.21 * | |
| W2 | 2.27 *** | 0.03 * | 0.20 * | ||
| W3 | 2.30 *** | 0.03 * | 0.28 ** | ||
| W4 | 2.23 *** | 0.01 * | 0.18 * | ||
| W5 | 2.29 *** | 0.002 * | 0.11 * | ||
| W1 | 2013 | 2.26 *** | 0.03 * | 0.39 *** | |
| W2 | 2.26 *** | 0.02 * | 0.42 ** | ||
| W3 | 2.37 *** | 0.01 * | 0.41 ** | ||
| W4 | 2.23 *** | 0.01 * | 0.20 * | ||
| W5 | 2.38 *** | 0.01 * | 0.30 *** | ||
| W1 | 2014 | 2.26 *** | −0.01 | 0.40 *** | |
| W2 | 2.26 *** | −0.007 | 0.40 *** | ||
| W3 | 2.32 *** | −0.05 | 0.20 ** | ||
| W4 | 2.24 *** | −0.04 | 0.24 * | ||
| W5 | 2.32 *** | −0.06 | 0.25 *** | ||
| W1 | 2015 | 2.26 *** | 0.04 * | 0.31 ** | |
| W2 | 2.26 *** | 0.04 * | 0.32 ** | ||
| W3 | 2.35 *** | 0.01 * | 0.31 ** | ||
| W4 | 2.24 *** | 0.03 * | 0.20 * | ||
| W5 | 2.35 *** | 0.09 * | 0.23 *** |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antczak, E. Building W Matrices Using Selected Geostatistical Tools: Empirical Examination and Application. Stats 2018, 1, 112-133. https://doi.org/10.3390/stats1010009
Antczak E. Building W Matrices Using Selected Geostatistical Tools: Empirical Examination and Application. Stats. 2018; 1(1):112-133. https://doi.org/10.3390/stats1010009
Chicago/Turabian StyleAntczak, Elżbieta. 2018. "Building W Matrices Using Selected Geostatistical Tools: Empirical Examination and Application" Stats 1, no. 1: 112-133. https://doi.org/10.3390/stats1010009





