Combined Optimisation of Traffic Light Control Parameters and Autonomous Vehicle Routes

Gallo, Mariano

doi:10.3390/smartcities7030045

Open AccessArticle

Combined Optimisation of Traffic Light Control Parameters and Autonomous Vehicle Routes

by

Mariano Gallo

Department of Engineering, University of Sannio, 82100 Benevento, Italy

Smart Cities 2024, 7(3), 1060-1088; https://doi.org/10.3390/smartcities7030045

Submission received: 6 March 2024 / Revised: 29 April 2024 / Accepted: 1 May 2024 / Published: 3 May 2024

(This article belongs to the Section Smart Transportation)

Download

Browse Figures

Versions Notes

Highlights

What are the main findings?

The proposed method aims to jointly optimise the signal settings and routes of centrally managed autonomous vehicles.
The proposed approach works on several test networks.

What is the implication of the main finding?

In the future, it will be possible to optimise autonomous vehicle routes and traffic light control parameters jointly.
The effects of the proposed procedure can improve total travel time on the network.

Abstract

:

In the near future, fully autonomous vehicles may revolutionise mobility and contribute to the development of the smart city concept. In this work, we assume that vehicles are not only fully autonomous but also centrally controlled by a single operator, who can also define the traffic light control parameters at intersections. With the aim of optimising the system to achieve a global optimum, the operator can define both the routes of the fleet of vehicles and the traffic light control parameters. This paper proposes a model for the joint optimisation of traffic light control parameters and autonomous vehicle routes to achieve the system optimum. The model, which is solved using a gradient algorithm, is tested on networks of different sizes. The results obtained show the validity of the proposed approach and the advantages of centralised management of vehicles and intersection control parameters.

Keywords:

smart mobility; autonomous vehicles; traffic lights; signal settings; optimisation

1. Introduction

Smart mobility [1,2,3], a fundamental component of the smart city, will receive a strong impulse with the spread of autonomous vehicles [4,5,6,7,8,9]. Advances in automation will lead to fully autonomous driving; the user will lose the role of driver and become a passenger. In urban areas, it is also possible to add centralised management of the vehicle fleet to full driving automation; it is assumed that a control centre plans the routes of all vehicles on the road network to optimise the total travel time to obtain the system optimum. A simulation of this type of approach was proposed in [10].

Centralised control of the entire fleet of vehicles may be even more greatly favoured by the trend towards abandoning the concept of car ownership and moving towards the use of shared vehicles, adopting the perspective of Mobility as a Service (MaaS).

A further step towards smart mobility could be the integration of traffic light control into fleet management. This work assumes that a control centre manages both the routes of the autonomous vehicles and the traffic light control parameters, with the aim of achieving system optimality.

The network-based optimisation of traffic light control parameters in the case of human-driven vehicles is a topic widely covered in the literature. Two possible approaches to the problem can be identified: a local approach and a global approach. The first optimises the signal settings of each intersection considering the traffic flows arriving at the same intersection; in this case, the problem can be formulated as an asymmetric assignment problem. The second, on the other hand, is a real network design problem, in which the decision variables are the signal settings of all intersections, and these are optimised to minimise the total travel time of users. A distinction between the two approaches and some solution methods can be found in [11]. In our case, the global approach must be considered, as the local approach does not make sense if we assume that the traffic consists only of autonomous vehicles. In the case of mixed traffic, between autonomous and human-driven vehicles, the local approach could also be valid.

Simulating a fleet of autonomous vehicles in real use requires a dynamic approach; indeed, the routes followed by the vehicles may be changed in real time depending on traffic conditions. In this work, a static approach is adopted because the aim is to assess the impact of the system on overall network performance. The transition to dynamic is possible, however, and will be the subject of further research developments.

This paper is organised as follows: Section 2 examines the background; the model formulation is reported in Section 3; the solution approach is described in Section 4; numerical results on some test networks are summarised in Section 5; and Section 6 concludes and draws the further research activities.

2. Background

The literature has dealt extensively with the problem of designing traffic light control parameters from different perspectives. A complete review would require a dedicated paper. Here, in the first part, we limit our analysis to reviewing the main contributions focused on the design of a traffic light network, neglecting the extensive literature related to isolated or coordinated intersections. In the second part, we will instead focus our review on autonomous vehicles, a more recent but already widely studied topic.

2.1. Optimisation of Signal Settings on a Network

The problem of designing signal settings in a network consists of calculating the traffic light parameters that optimise the network performance, given a topological configuration that is considered known and invariant, taking into account the traffic flows. This problem, also known in the literature as the signal setting design problem (SSDP) [11], can be seen as a special case of the more general equilibrium network design problem (ENDP), in which the signal settings play the role of decision variables, while the topological characteristics of the transport network (road directions, number and width of lanes, etc.) are assumed to be invariant.

The optimisation problem searches for the vector of parameters and the corresponding vector of traffic flows in equilibrium that minimises an objective function, usually the total travel time on the network. A continuous network design problem is thus formulated [12], in which the role of decision variables is assumed by the signal settings. In this case, the decision variables are usually only the effective green times or the ratios between effective green times and cycle times, and a single objective function is optimised in which both traffic flows (descriptive variables) and signal settings are variables. In this case, the problem of optimising traffic light control parameters is tackled with a global approach, also known as global optimisation of signal settings (GOSS) [11].

In the case of flow-responsive traffic lights, the control parameters are adapted to the flows arriving at the intersections; in this second case, the problem consists of determining a vector of traffic flows in equilibrium that is self-reproducing once a local control policy has been defined. This second problem is also known as the combined assignment and control problem and represents the local approach to solving the problem, also known in the literature as local optimisation of signal settings (LOSS) [11,13].

The general formulation of the problem and the distinction between global and local design approaches can be found in [11,13,14,15,16]. A dynamic approach to solving the problem has been proposed by Abdelfatah and Mahmassani [17].

In the remainder of this analysis, we will only refer to the GOSS problem, as it is the one that will be used in this study, modified to take into account the presence of autonomous vehicles.

The GOSS problem must be formulated as a non-linear constrained optimisation problem. The constraints are as follows: (a) the assignment constraint, which forces traffic flows to be in equilibrium and includes the continuity and non-negativity of flow constraints; (b) technical constraints, which express the physical (and practical) admissibility for the values of the traffic signal parameters, such as lower and upper bounds on the green/cycle ratios. The objective function is usually the total travel time on the network; other objective functions may be used, such as minimising the total delay at intersections, or the total pollution caused by the flows on the network.

This problem has been studied in a static environment in [11,18,19,20,21,22,23,24]. Global optimisation that also considers traffic light coordination parameters as variables has been studied in [25,26,27]. Group-based methods were proposed in [28,29]; joint optimisation of signal settings and road pricing was studied by Smith et al. [30]. A dynamic approach has been proposed in [31], and solution methods based on artificial neural networks have been proposed in [32,33].

Solution algorithms for solving the problem in a static environment are based on feasible direction or projected gradient methods. Projected gradient methods have been proposed in [18,34], while Cascetta et al. [11] proposed and compared some feasible direction algorithms.

Al-Sharman et al. [35] proposed a hierarchical reinforcement learning approach to manage autonomous vehicles at unsignalised intersections.

2.2. Autonomous Vehicles

According to the SAE J3016 standard [36], there are six levels of vehicle automation, from Level 0 ‘no automation’ to Level 5 ‘full automation’. In this paper, we will refer to Level 5, assuming that the vehicles are self-driving; hereafter, we will refer to them as autonomous vehicles (AVs). Indeed, we consider a further, non-standardised level of automation, which we can name ‘Level 6′, which provides not only full automation but also centralised route management of all vehicles on the network. Centralised route selection for fleet vehicles can be based on different strategies; on the one hand, one could tend to minimise the routes for individual users, falling into a situation analogous to a deterministic equilibrium assignment; the other hypothesis, which is the one assumed in this work, is that the operator wants to optimise the total cost of the system by routing vehicles in such a way as to minimise the total travel time for all users.

The literature on autonomous vehicles is very large and cannot be covered in this paper; therefore, we refer to the reviews proposed in [37,38,39,40], limiting our investigation mainly to the more recent works. A sociomobility taxonomy was proposed by Kassens-Noor et al. [41], who reviewed and classified several papers accordingly. Paper [42] reviewed control techniques for autonomous and connected vehicles. A review of driver behaviour models was proposed in [43].

Some of the literature has examined the external impacts of this emerging technology. The potential environmental impacts of autonomous vehicles were studied in [44,45,46]. The benefits of autonomous vehicles for community-based trip sharing were estimated by Hasan et al. [47]; the paper examined the potential benefits of autonomous vehicles in reducing the number of vehicles needed to cover all commuting trips, estimating a reduction in daily vehicle use of 92% and vehicle km travelled of around 30%. Carrese et al. [48] studied the potential impact of autonomous vehicles on the choice of residence in Rome, and Moore et al. [49] the potential effects on home and work relocations. May et al. [50] studied the potential impacts of autonomous cars on urban transport, while Harrison et al. [51] evaluated their influence on the liveability of cities. Finally, Rashidi et al. [52] examined the impact on the value of time (VOT) for autonomous vehicle users.

Tian et al. [53] used a stated choice survey to investigate the propensity of individuals to use autonomous vehicles or shared vehicles; the authors showed that on the one hand, people prefer to keep their vehicle or buy an autonomous vehicle rather than use shared vehicles, but on the other hand, they prefer to use autonomous vehicles rather than traditional shared vehicles.

Wang et al. [54] proposed a cooperative autonomous traffic organisation method for autonomous and connected vehicles; the method aims to define vehicle routes to maximise social and individual benefits (safety, energy consumption, comfort) in a network of unsignalised intersections. Sun et al. [55] studied the energy and mobility impacts of connected autonomous vehicles in mixed platoons; they proposed an eco-driving policy on signalised arterial roads that could also reduce consumption for human-driven vehicles. Zhang et al. [56] proposed an energy saving optimisation and control method for autonomous electric vehicles. Intelligent traffic control based on machine learning has been proposed in [57].

Many papers have focused on mixed traffic, assuming the co-presence of human-driven vehicles (HDVs) and autonomous vehicles (AVs). Rey and Levin [58] proposed a new policy for stochastic network traffic control that considers both AVs and HDVs, assuming that AVs drive in dedicated lanes and have reserved signal phases at intersections. Lazar et al. [59] studied a problem whereby some vehicles are autonomous and share the road with normal cars; the AVs are controlled by a planner, while human drivers react dynamically to traffic conditions. The planner uses an AV control policy that tends to indirectly influence human drivers to minimise congestion. Wang et al. [60] considered the problem of uncertain link capacity in mixed-traffic road networks. Guo et al. [61] proposed a daily route allocation scheme for autonomous vehicles to bring the mixed traffic system to a desired traffic state. Chen et al. [62] proposed a cellular automation model to simulate mixed traffic between AVs and HDVs. Other recent work on mixed traffic can be found in [63,64,65,66,67].

Shared autonomous vehicles have been studied in [68,69], while a laboratory experiment of AVs on roads without lanes has been proposed in [70]. Cooperative movement of multiple autonomous vehicles was studied in [71], while eco-driving for autonomous vehicles was studied in [72,73].

Gallo [10] proposed a model and solution methods for optimising the routes of centrally controlled autonomous vehicles in both exclusive and mixed traffic hypotheses.

Other interesting recent studies have been developed by Talebpour and Mahmassani [74], Tettamanti et al. [75], Stern et al. [76], Miglani and Kumar [77], Liard et al. [78], Kumakoshi et al. [79], Zhao et al. [80], and Ge et al. [81].

2.3. Paper Contribution

This paper contributes to the literature by proposing a model for the network-based design of traffic light control parameters under the assumption that all vehicles are autonomous and that routes are centrally defined by a single operator. The system operator optimises not only the routes of the vehicle fleet but also the traffic light control parameters, with the aim of minimising the total costs to obtain a system optimum.

To the best of our knowledge, the proposed approach is original and has not yet been proposed in the literature. Compared to the models mentioned in the literature (Section 2.1), the main difference lies in the approach used to estimate the traffic flows on the network, which is based on the system optimum, whereas previous work has referred to the user optimum.

3. Model Formulation

In this work, we assume that the traffic manager, who controls both the signal settings and the routes of the autonomous vehicles, has the objective of minimising the total generalised travel cost; notations and terminology are summarised in Appendix A (Table A1 and Table A2). On each link in the network, i, we denote by f_i the traffic flow (veh/h) or the flow rate if we refer to periods of less than one hour, and by c_i the generalised travel cost on the same link. Traffic flows and generalised link costs can be arranged in two vectors, f and c, respectively, with a number of elements equal to the number of links. It is assumed that, as in the case of human-driven vehicles (HDVs), the generalised cost on a link is a function of the traffic flow:

c_i = c_i(f_i) ∀i,

(1)

or, in vectorial form:

c = c(f).

(2)

Transport demand is represented by an origin–destination (OD) matrix, whose d_od cells represent the number of trips originating in zone o and ending in zone d. The d_od elements can be organised into a demand vector, d, which has as many elements as there are OD pairs. Each OD pair is connected in the network by one or more paths; in the following, the generic path connecting the od pair is denoted by k,od. The flow on path k, h_k, can be calculated by the percentage of vehicles using this path, ψ_k,od, to travel between o and d, multiplied by the demand d_od:

h_k = ψ_k,od · d_od.

(3)

Path flows can be arranged in a vector, h, which has as many elements as the number of paths; on the other hand, ψ_k,od can be arranged in a matrix, ψ, that has as many rows as the number of paths and as many columns as the number of OD pairs. Using this notation, we can write the following:

h = ψ d.

(4)

Introducing the link-path incidence matrix, A, which has as many rows as the number of links and as many columns as the number of paths, and whose generic element, a_i,k, is equal to 1 if link i belongs to path k and 0 otherwise, it is possible to calculate the link flows as follows:

f = A h = A ψ d.

(5)

Equation (5) shows the relationship between traffic flows, the supply model, and demand. In equilibrium traffic assignment models, the path choice percentages are usually denoted by P and depend on the path costs and then on the link costs, which depend on the flows; in this case, they are considered as probabilities since they are the result of user choice behaviour. There is a large literature on equilibrium traffic assignment models, for which we refer to Cantarella [82]. In this paper, instead, we consider that the path choice percentages can be decided by the traffic operator, as well as the signal settings; therefore, in Equation (5), there is no direct dependence between the matrix ψ and the generalised link costs, c.

Models for calculating traffic flows on a network under the assumption that vehicles cooperate to minimise total cost, rather than minimising the costs perceived by individual users, are known in the literature as system optimal (SO) assignment models [83] (p. 291). System optimal assignment can be formulated with an optimisation model as follows:

f_SO = Arg _f min c(f)^T f,

(6)

subject to:

f ∈ S_f,

(7)

where Equation (7) summarises all feasibility constraints for decision variables f at nodes.

In our study, the objective is the joint optimisation of autonomous vehicle routes and signal settings; in this case, model (6)–(7) cannot be used and is difficult to adapt. We propose an optimisation model whereby the decision variables are the path choice percentages, ψ, and the signal settings, formally summarised in the vector g. The optimisation model is formulated as follows:

[g^, ψ^] = Arg _g_,_ψ min c^T f,

(8)

subject to:

f = A ψ d,

(9)

c = c(f, g),

(10)

ψ ∈ S_ψ,

(11)

g ∈ S_g,

(12)

where Equation (9) is the constraint that relates link flows, f, to demand, d, supply, A, and path choice percentage, ψ. Equation (10) expresses the relationship between costs, flows, and signal settings; Equations (11) and (12) constrain the decision variables to their feasibility sets. Substituting Equation (9) into Equation (10) and then into Equation (8), the model can be written as follows:

[g^, ψ^] = Arg _g_,ψ min c(A ψ d, g)^T (A ψ d),

(13)

subject to:

ψ ∈ S_ψ,

g ∈ S_g,

where the objective function depends only on the decision variables, including the first two constraints; formally, we can also write the objective function more generally as follows:

w(ψ, g) = c(A ψ d, g)^T (A ψ d),

(14)

formulating the following optimisation model:

[g^, ψ^] = Arg _g_,_ψ min w(ψ, g),

(15)

subject to:

ψ ∈ S_ψ,

g ∈ S_g.

This is a non-linear optimisation model with linear constraints, assuming that the feasibility constraints (11) and (12) are linear, being the limits of route percentages and signal settings (minimum and maximum value of effective greens and cycle times). From a theoretical point of view, the existence of an optimal solution is easy to prove: all solutions satisfying constraints (11) and (12) are feasible and, among them, the optimum is the solution corresponding to the best value of the objective function. Since the constraints are in a closed and continuous interval and the variables are independent of each other (constraints on signal settings, if well designed, can be considered as such), some solutions respect all constraints. Regarding the properties of the objective function, it is, generally, not convex; thus, a feasible direction algorithm can lead to a local optimum (see also Section 5).

The general model can be specialised in several ways by defining the constraints of the problem, in particular variables g and constraint (12), while constraint (11) is implicitly defined by the characteristics of the percentages. We propose to specialise the constraints as follows and to consider as signal settings the effective cycle duration of each intersection, assumed to have two phases, and the effective green/effective cycle ratio of one of the two phases (the complement for one gives the ratio for the other phase). The variables are therefore as follows:

g = {C, μ},

where:

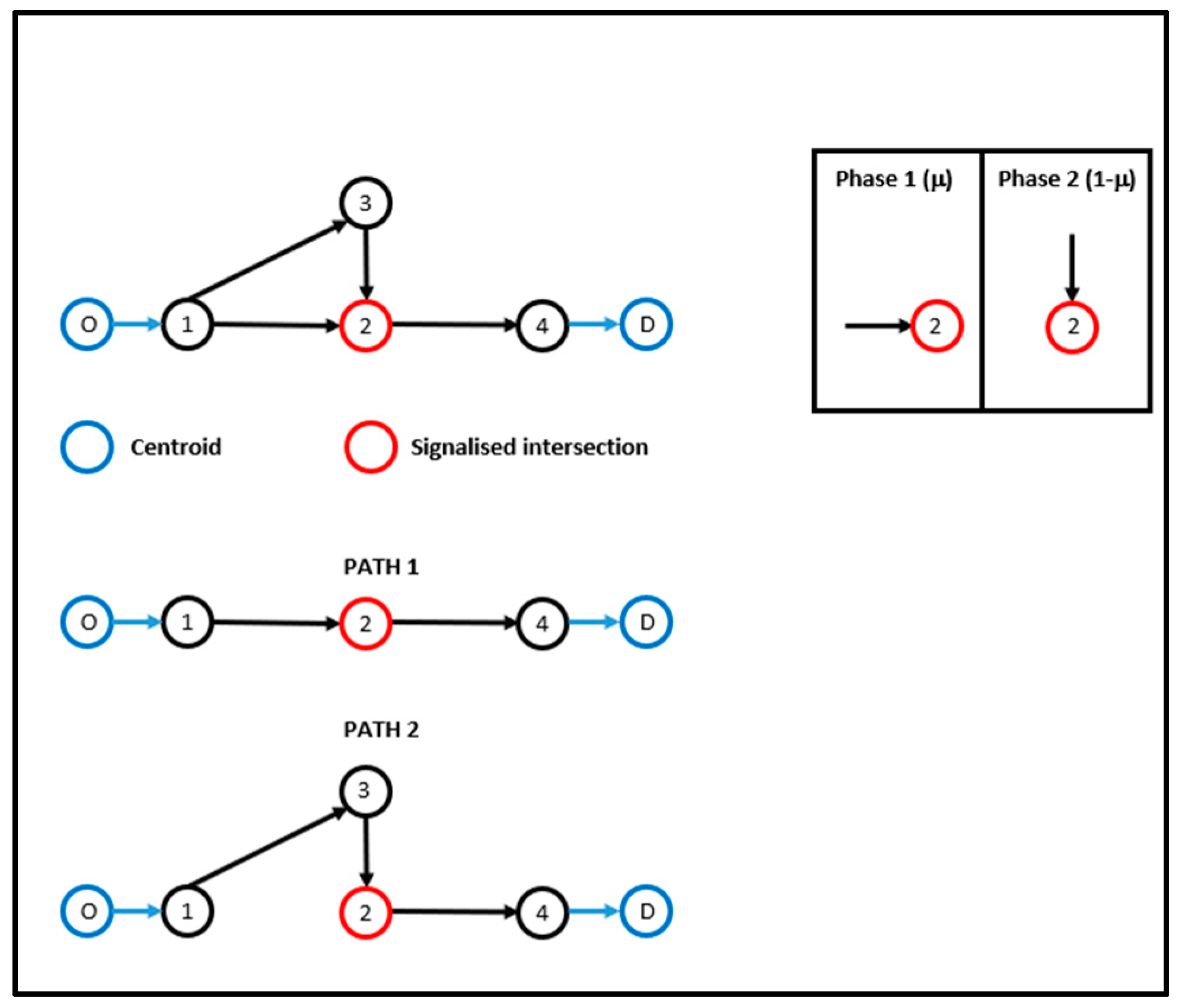
C is the vector of the effective cycle times (s) at each intersection j, C_j;
μ is the vector of the ratios, μ_j, between the effective green time of a phase (conventionally, phase 1) at intersection j, eg_j¹, and the effective cycle time, C_j: μ_j = eg_j¹/ C_j. So, at intersection j, the ratio for phase 1 is μ_j and for phase 2 is 1 − μ_j.

Under these assumptions, the number of g variables is two times the number of signalised intersections. The constraints are then as follows:

0 ≤ ψ_k,od ≤ 1 ∀k, ∀od,

(16)

∑_k_∈_Sod ψ_k_,od =1 ∀od,

(17)

C_min ≤ C_j ≤ C_max ∀j,

(18)

μ_min ≤ μ_j ≤ μ_max ∀j.

(19)

Constraint (16) imposes that the percentage of path choice must be in the closed interval [0,1]. Constraint (17) imposes that, for each od pair, the sum of the path choice percentages must be equal to 1. Constraints (18) and (19) impose limits on the values of the signal settings, e.g., cycle length between 30 and 120 s and ratios between 0.2 and 0.8.

4. Solution Algorithm

Any feasible descent direction algorithm can be used to solve the optimisation problem (15)–(19). Since the objective function is not convex, this algorithm would lead to a local optimum. To overcome this problem, a multi-start approach can be used [84], which uses admissible but distant values of the initial solutions, to explore the solution set.

As a descent algorithm, a projected gradient algorithm is proposed, where the partial derivatives of the objective function are computed numerically. For the multi-start approach, some initial solutions are generated assuming fixed variables ψ_k,od and C_j, operating only on the μ_j ratios, as follows:

Base solution:

ψ_k,od = 1/np_od ∀od,

where np_od is the number of feasible paths connecting the od pair;

C_j = (C_min + C_max)/2 ∀j;

Μ_j = 0.5 ∀j.

Distant solutions:

Ψ_k,od = 1/np_od ∀od;

C_j = (C_min + C_max)/2 ∀j;

(1) μ_j = μ_min ∀j;

(2) μ_j = μ_max ∀j;

(3) μ_j = μ_min ∀j even number and

μ_j = μ_max ∀j odd number;

(4) μ_j = μ_max ∀j even number and

μ_j = μ_min ∀j odd number.

Random solutions:

ψ_k,od = 1/np_od ∀od;

C_j = Random.Between(C_min, C_max) ∀j;

μ_j = Random.Between(μ_min, μ_max) ∀j.

The number of random solutions to be generated can be set according to the complexity of the network and the number of decision variables.

5. Numerical Results

We have tested the proposed approach on three networks. The first is very simple, with only one signalised intersection, and is useful for exploring some features of the problem (for example, the non-convexity of the objective function). The second has only one OD pair but four signalised intersections and was used to test and refine the solution algorithm. Finally, the third is the Sioux Falls network, widely used for testing this type of problem, which is used to verify the applicability of the model to a large case study.

5.1. Toy Network

The toy network has four links, four nodes, one OD pair, and one signalised junction (see Figure 1). The network parameters are given in Table A3 in Appendix B. In this test, there are only two paths available, and we assume that the cycle length is fixed and equal to 90 s. The demand is assumed to be 800 veh/h. The effective green-to-cycle ratio, μ, is constrained between a minimum value of 0.2 and a maximum value of 0.8. Under these assumptions, the problem has only two decision variables: μ and ψ₁ (the percentage of path 2 is ψ₂ = 1 − ψ₁).

On each link i, the generalised link cost, c_i, is the sum of the running time, rt_i, and the expected delay, ed_i, both depending on the flow, f_i:

c_i(f_i) = rt_i(f_i) + ed_i(f_i) ∀i.

Running times are calculated using the following function:

rt_i(f_i) = (L_i/V_i) · (1 + (f_i/Cap_i)⁴),

(20)

where:

L_i is the length of link i;
V_i is the free flow speed on link i;
Cap_i is the capacity of link i.

Delays are calculated using the HCM formula [85], assuming a simulation period, T, equal to 1, as follows:

ed_i(f_i) = (0.50 · C_j · (1−eg_i ^j/C_j)²)/(1−((min (1, X_i ^j) · eg_i ^j /C_j)) +
+ 900 ·T · ((X_i ^j −1) + ((X_i ^j−1)² + (4 · X_i ^j /(ACap_i ^j · T))^1/2,

(21)

where, in addition to the terms already defined, ACap_i ^j = μ_i ^j · s_i ^j is the capacity of the approach at intersection j of link i; s_i ^j is the corresponding saturation flow; and X_i ^j = f_i/ACap_i ^j is the corresponding flow-to-capacity ratio.

The delay calculated with the HCM formula is considered valid only if the ratio between flow and approach capacity, ACap_i ^j, is less than 1.20; solutions giving higher values are considered infeasible.

As we only have two variables in this problem, μ and ψ₁, we have tested all possible combinations with a step of 0.01. A total of 6161 combinations were tested, some of which were found to be infeasible due to excessively high values of flow-to-access capacity ratio. The shape of the objective function, expressed in seconds of total travel time, is shown in Figure 2.

It can be seen that the objective function is not convex; in particular, two local minima are found, far apart, one of which is also the global optimum. This test confirms the need to use a multi-start approach; although it is not possible to know whether the solution obtained by the algorithm is the global optimum, the multi-start approach allows for a wider exploration of the solution space since it is possible to find several local optima from which the best one can be selected. The local optima are listed in Table 1.

Clearly, in the simple case study, the optimal solutions involve routing all vehicles on a single path, which is also given the maximum possible value of the effective green. Other tests were carried out with different values of mobility demand and, therefore, of network congestion levels, obtaining the results summarised in Table 2. Only for very high demand (1600 veh/h) is there only one local optimum (see Figure 3).

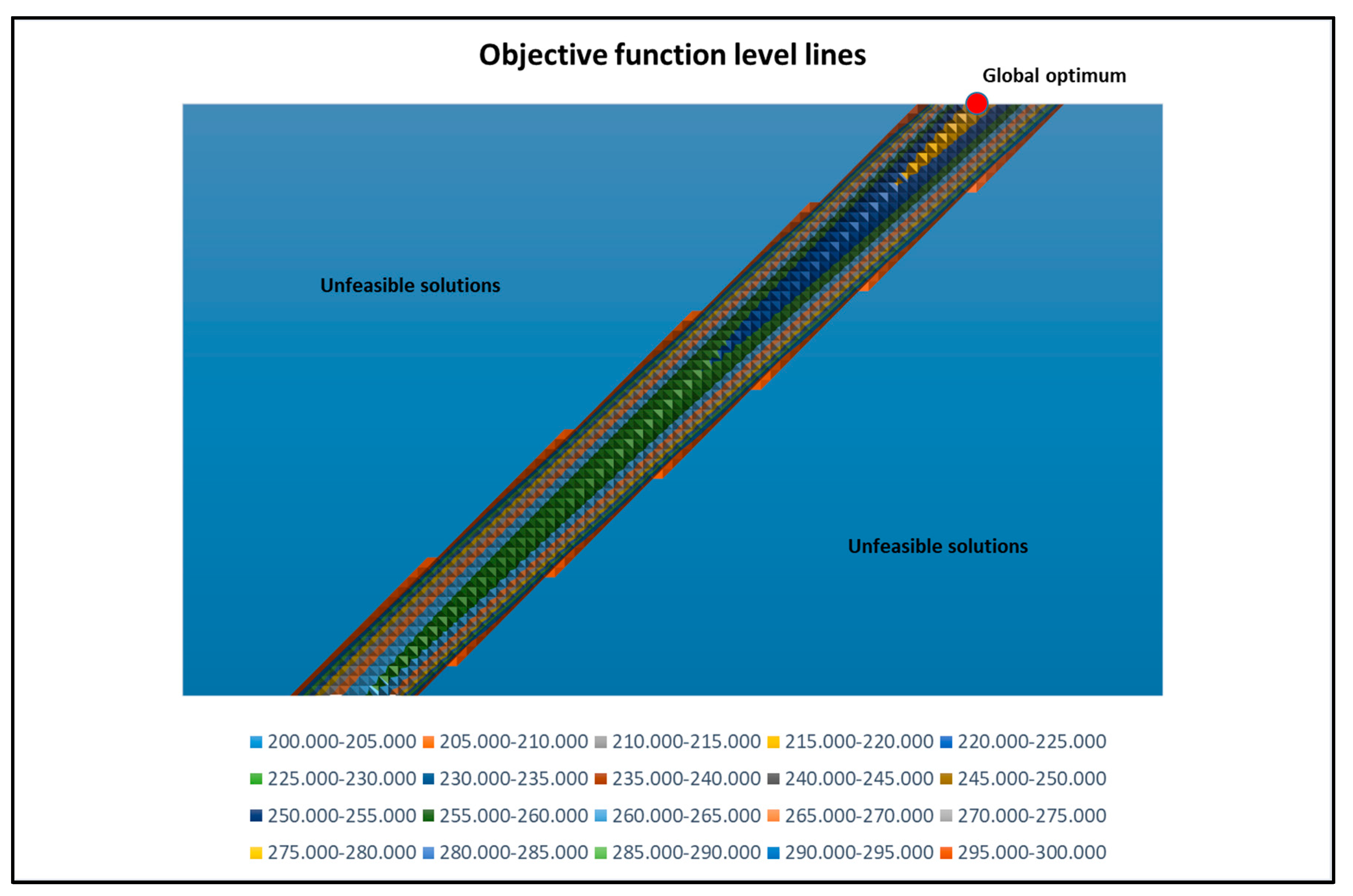
5.2. Small Network

We have tested the proposed approach on the small network shown in Figure 4. It has one OD pair, 14 links, 10 nodes, 4 signalised intersections (all with 2 phases) and 9 possible paths. The decision variables of the problem are 17: 9 ψ_k,od, 4 C_j, and 4 μ_j. Delays were calculated using the HCM formula already used in the previous test.

The characteristics of the links are summarised in Table A4 in Appendix B. We also assume a demand of 1000 veh/h.

We implemented the model in Excel and used the GRG solver to optimise the problem, starting from 23 different initial solutions, generated as described in Section 4. The results are summarised in Table 3. These results show that the multistart algorithm found four different local optima. Solution 2 is the best, with an objective function equal to 171,424 s; the other solutions have objective function values that are not very different (no more than 2%), but with values of the variables that are nonetheless significantly different.

Two further tests were carried out on the same network by increasing the demand to 1500 veh/h and 2000 veh/h to test what happens under conditions of increased congestion. In the first case, six local optima were found, with objective function values varying between 302,564 s and 305,958 s (see Table 4), and with a maximum difference of 1.1%. In the second case, on the other hand, a single optimal solution was found, with an objective function value of 536,318 s (see Table 5). These results seem to show that as the congestion increases, the differences between the locally optimal values decrease until they disappear for high congestion values. Examining the results in Table 5, it can be seen that the same solution is obtained with different values of the ψ_k,od percentages; these different percentages lead to the same traffic flows on the network, representing the system optimal solution.

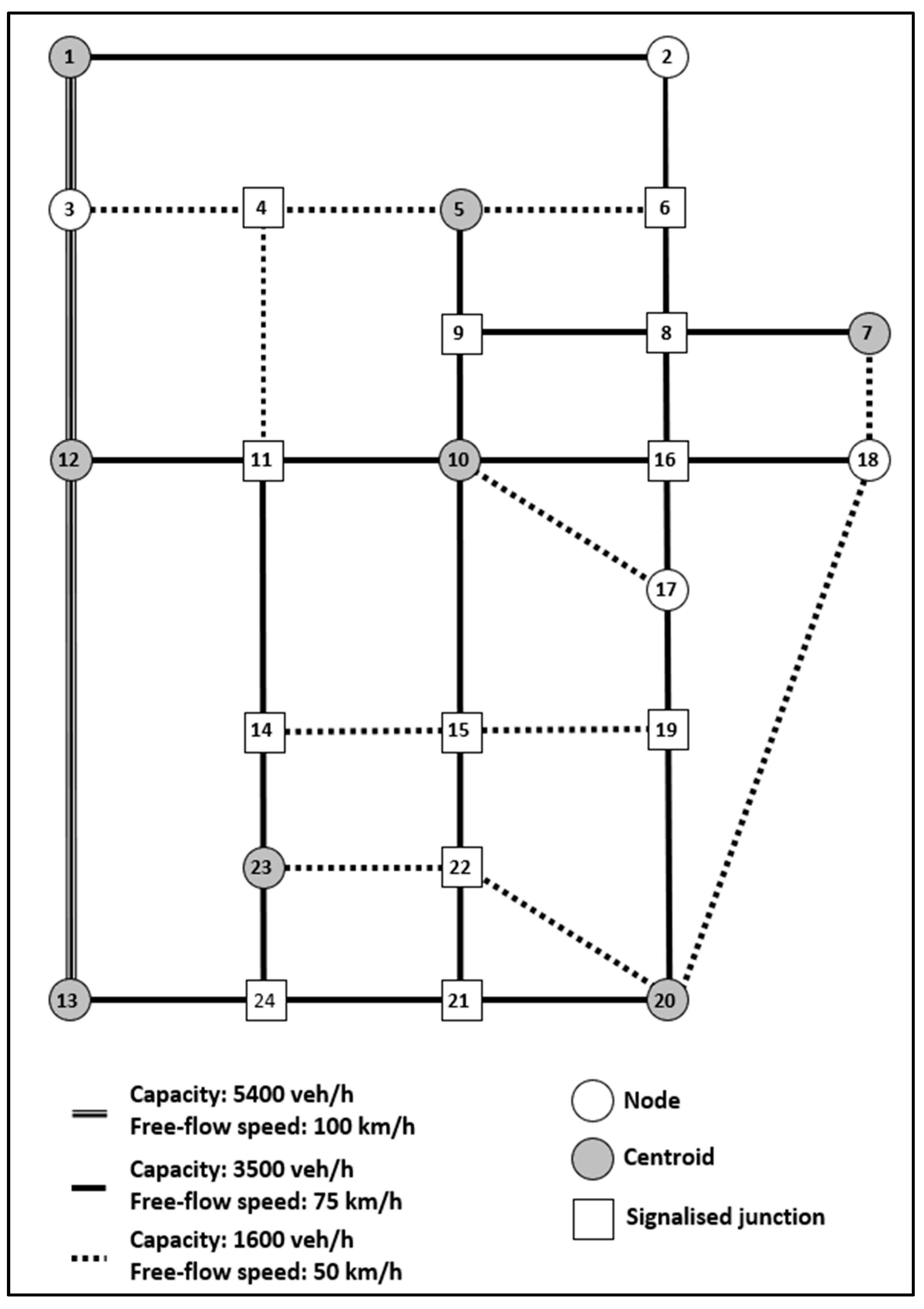
5.3. Sioux Falls Network

Sioux Falls is one of the most widely used networks for testing transport systems [86,87]; it has 76 links (38 road segments) and 24 nodes (see Figure 5). We have assumed that the network has 8 centroid nodes (56 OD pairs, eliminating those of the main diagonal) and 12 signalised junctions. We have also assumed that the saturation flows at intersections are equal to the capacities of the road links (a valid assumption if there is no widening of approaches to intersections). Table A5 in Appendix B summarises the features of the links.

The running times on the links are calculated using Equation (20), while the delays are calculated using Equation (21).

The origin–destination matrix is given in Table A6 in Appendix B, while the number of paths connecting each OD pair is given in Table A7; the average flow/capacity ratio on the network is about 0.3. For each OD pair, all Dial efficient [88] paths were considered.

On this network too, we have implemented the model in Excel and used the GRG solver for its solution. The computation times are acceptable, remaining below 30 s in all the tests carried out. In this case, the multistart approach used 25 initial solutions; the solutions differ in the values of the signal settings, while the initial path choice percentages are always the equiprobable ones for each OD pair. Table A8 in Appendix B shows the values of the signal settings for each initial solution.

The optimisation results have highlighted the following points:

For this level of demand, the duration of the traffic light cycle is an insignificant parameter; in fact, the optimisation procedure leaves it practically unchanged in all the tests carried out, unlike the μ terms, which vary significantly with respect to the initial points.
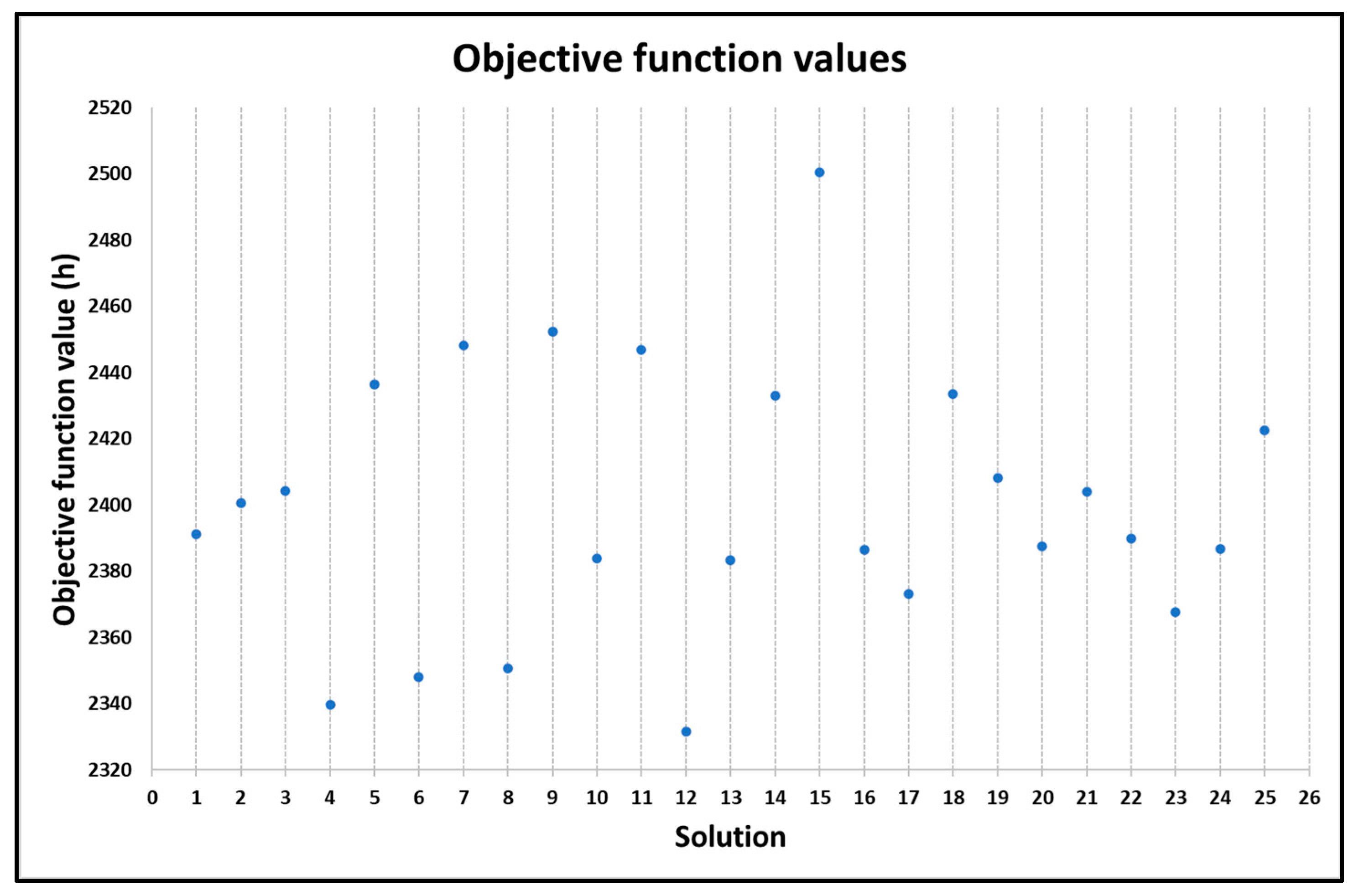
All the solutions have different values of the objective function, as can be seen in Figure 6, although some have very similar values; the best solution is the one obtained from the initial solution 12 (2332 h), while the worst is the one obtained from the initial solution 15 (2500 h). The difference is about 7%.
The traffic flows on the links are different for the different solutions, as can be seen from Figure 7. On some links, the differences are significant (up to 739 veh/h), while on other links, the difference between the traffic flows is less evident (minimum difference 7 veh/h).

The multistart algorithm leads to different solutions depending on the number of initial solutions and how these solutions were generated. Indeed, the non-convex objective function can have many local optima corresponding to even very different solutions. In the experiment shown in detail, the initial solutions were generated as in Table A6, using both defined and randomly generated solutions. Further tests were carried out using the GRG multistart algorithm proposed by Excel to check how much the number of initial solutions could influence the quality of the final solution. Table 6 summarises the objective function values obtained by the GRG multistart algorithm as the number of initial solutions varies, which, in this case, are all randomly generated by the algorithm. The results show that there is, on average, an improvement in the value of the objective function as the number of initial solutions of the multistart procedure increases. This confirms that the objective function is far from being convex. The difference between the local optima found, although not high, is significant; indeed, the maximum variation between the values of the objective function is 1.7%, which is not a negligible value in the context of transport network design problems.

6. Conclusions

Technological innovations are at the heart of the smart city concept, and mobility is one of the fundamental components influencing the quality of life and socioeconomic conditions of citizens. Thanks to the development of green mobility and new technologies, mobility is undergoing profound transformations that can influence lifestyles and the development of the city to increase sustainability.

Autonomous driving is one such technological innovation, together with the concept of MaaS (Mobility as a Service), that has a strong acceleration and can produce significant effects on urban mobility. In this context, this work proposes a methodology for the joint optimisation of traffic light control parameters and autonomous vehicle routes, assuming that both are managed and optimised by a single operator. The proposed approach has been tested on several test networks, showing that the proposed model and algorithm work efficiently and that, since the objective function is not convex, it is necessary to use heuristic algorithms to explore the space of solutions.

There are some practical implications of the centralised control system for both vehicle routes and signal settings. First, the use of a joint optimisation system allows the traffic light control parameters and corresponding vehicle flows to be updated in real time; in practice, this is like solving a continuous network design problem each time, using transport demand as input. This type of approach can have many benefits, first for the community and second for the operator, through reductions in energy and emissions. Users also benefit, as lower costs for the operator (whether public or private) can be matched by lower costs for the trips of users using the system.

This work provides a building block for the construction and implementation of a smart city, with a clear reference to mobility, which is a fundamental and indispensable component. There are two main contributions: (a) the basic idea of being able to jointly manage the routes of autonomous vehicles and the parameters of traffic light regulation, with the aim of achieving a system optimum; (b) the modelling approach that allows the problem to be solved in a time frame compatible with the management of both the transport service and the regulation of intersections.

The limitations of the work should also be mentioned. First, the approach taken is static and therefore useful for assessing the impact of the intervention but not for managing it in real time. The dynamic approach will be the subject of future developments in this research. From the point of view of the results, the networks tested allowed the model and the proposed approach to be evaluated and experimented with, highlighting the need for multistart procedures, as well as the feasibility of the methodology, but the results were not generalisable; indeed, on large real networks, the impact could be different (even better) in terms of system effects, but each network structure could react differently to the application of the procedure. Another critical point is the assumption that there is a single manager of both the fleet of all autonomous vehicles and the control parameters of all traffic lights. This assumption may be valid for small- and medium-sized cities (up to about 100,000 inhabitants), but if the network is very large, it is more likely that there will be several operators of different vehicle fleets, perhaps divided by territory, or several operators competing with each other. These aspects also deserve further investigation in the next phases of this research.

The research perspectives are manifold. First, other algorithms for solving the same problem can be tested and compared, or we could formulate more complex problems to account for different operators. Second, different traffic light control strategies can be considered, e.g., by including offsets in the decision variables. Finally, similar problems can be formulated and solved in the case of mixed traffic (flows of autonomous and conventional vehicles sharing the same network).

Funding

This study was funded by the research project C-Mobility: Technologies for Connected Vehicles (CUP B32C18000240007), co-financed by the European Union, the Italian State, and the Campania Region, under the POR Campania FESR 2014–2020, Priority Axis 1 ‘Research and Innovation’, and by the University of Sannio (FRA 2023).

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The author declares no conflicts of interest.

Appendix A

This appendix summarises notation and terminology.

Table A1. List of acronyms.

Acronyms
AV	Autonomous Vehicle
ENDP	Equilibrium Network Design Problem
GOSS [LOSS]	Global [Local] Optimisation of Signal Settings
GRG	Generalised Reduced Gradient
HCM	Highway Capacity Manual
HDV	Human-Driven Vehicle
MaaS	Mobility as a Service
OD	Origin–Destination
SO	System Optimal
SSDP	Signal Setting Design Problem
VOT	Value Of Time

Table A2. List of symbols and variables.

Symbols and Variables
A	link-path incidence matrix
ACap_i ^j	approach capacity at intersection j of link i
a_i,k	cells of the link-path incidence matrix
c	link cost vector
Cap_i	capacity of link i
c_i	generalised cost on link i
C_j	effective cycle time at intersection j
C_max [C_min]	maximum [minimum] feasible cycle length
d	demand vector
d_od	demand between origin o and destination d
ed_i	expected delay on link i
eg_j¹	effective green time for phase 1 at intersection j
f	link flow vector
f_i	flow on link i
f_SO	system optimum flow vector
g [g^{^}]	vector of the [optimal] signal setting variables
h	path flow vector
h_k	flow on path k
i	index of links
j	index of intersections
k,od	index of a path k connecting od pair
L_i	length of link i
np_od	number of feasible paths connecting od pair
od	origin–destination pair
P	path choice probability matrix
rt_i	running time on link i
S_ψ	feasibility set for ψ_k,od
S_f	feasibility set for system optimum flows
S_g	feasibility set for the signal setting variables
s_i ^j	saturation flow at intersection j of link i
S_od	set of feasible paths connecting od pair
T	simulation period
V_i	free flow speed on link i
X_i ^j	flow to capacity ratio of the approach at intersection j of link i
μ_j	effective green time/cycle ratio for phase 1 at intersection j
μ_max [μ_min]	maximum [minimum] feasible effective green time/cycle ratio
ψ_k,od	percentage of vehicles using path k to travel between o and d
ψ	path percentage matrix
ψ^	matrix of the optimal path percentages

Appendix B

This appendix contains tables showing some data about the test networks.

Table A3. Features of the toy network.

Link	Node_in	Node_fi	Length [km]	Road Capacity [veh/h]	Saturation Flow [veh/h]	Free-Flow Speed [km/h]
1	1	2	0.5	1800	1800	40
2	1	3	0.4	1800	-	40
3	2	4	0.5	1800	-	40
4	3	2	0.2	1800	1800	40

Table A4. Features of the small network.

Link	Length [km]	Capacity [veh/h]	Free-Flow Speed [km/h]
1	0.5	1600	60
2	0.5	1400	60
3	0.3	1400	60
4	0.5	1200	50
5	0.8	1200	50
6	0.6	1200	50
7	0.8	1200	50
8	0.8	1200	50
9	0.3	1200	50
10	0.5	1200	50
11	0.7	1800	80
12	0.6	1200	50
13	0.2	1800	80
14	0.6	1800	80

Table A5. Features of the Sioux Falls network.

Link #	Node_in	Node_fi	Length [km]	Capacity/Saturation Flow [veh/h]	Free-Flow Speed [km/h]
1 [2]	1 [2]	2 [1]	6.0	3500	75
3 [4]	1 [3]	3 [1]	2.0	5400	100
5 [6]	2 [6]	6 [2]	2.0	3500	75
7 [8]	3 [4]	4 [3]	2.0	1600	50
9 [10]	3 [12]	12 [3]	5.0	5400	100
11 [12]	4 [5]	5 [4]	2.0	1600	50
13 [14]	4 [11]	11 [4]	5.0	1600	50
15 [16]	5 [6]	6 [5]	2.0	1600	50
17 [18]	5 [9]	9 [5]	2.5	3500	75
19 [20]	6 [8]	8 [6]	2.5	3500	75
21 [22]	7 [8]	8 [7]	3.0	3500	75
23 [24]	7 [18]	18 [7]	2.5	1600	50
25 [26]	8 [9]	9 [8]	2.0	3500	75
27 [28]	8 [16]	16 [8]	2.5	3500	75
29 [30]	9 [10]	10 [9]	2.5	3500	75
31 [32]	10 [11]	11 [10]	2.0	3500	75
33 [34]	10 [15]	15 [10]	3.0	3500	75
35 [36]	10 [16]	16 [10]	2.0	3500	75
37 [38]	10 [17]	17 [10]	2.5	1600	50
39 [40]	11 [12]	12 [11]	2.0	3500	75
41 [42]	11 [14]	14 [11]	3.0	3500	75
43 [44]	12 [13]	13 [12]	6.0	5400	100
45 [46]	13 [24]	24 [13]	2.0	3500	75
47 [48]	14 [15]	15 [14]	2.0	1600	50
49 [50]	14 [23]	23 [14]	1.5	3500	75
51 [52]	15 [19]	19 [15]	2.0	1600	50
53 [54]	15 [22]	22 [15]	1.5	3500	75
55 [56]	16 [17]	17 [16]	1.5	3500	75
57 [58]	16 [18]	18 [16]	3.0	3500	75
59 [60]	17 [19]	19 [17]	1.5	3500	75
61 [62]	18 [20]	20 [18]	6.7	1600	50
63 [64]	19 [20]	20 [19]	3.0	3500	75
65 [66]	20 [21]	21 [20]	2.0	3500	75
67 [68]	20 [22]	22 [20]	2.5	1600	50
69 [70]	21 [22]	22 [21]	1.5	3500	75
71 [72]	21 [24]	24 [21]	2.0	3500	75
73 [74]	22 [23]	23 [22]	2.0	1600	50
75 [76]	23 [24]	24 [23]	1.5	3500	75

Table A6. OD matrix for the Sioux Falls network.

O\D	1	5	7	10	12	13	20	23
1	-	92.4	231.0	600.6	92.4	231.0	138.6	138.6
5	92.4	-	92.4	462.0	92.4	92.4	46.2	46.2
7	231.0	92.4	-	877.8	323.4	184.8	231.0	92.4
10	600.6	462.0	877.8	-	924.0	877.8	1155.0	831.6
12	92.4	92.4	323.4	924.0	-	600.6	184.8	323.4
13	231.0	92.4	184.8	877.8	600.6	-	277.2	369.6
20	138.6	46.2	231.0	1155.0	231.0	277.2	-	323.4
23	138.6	46.2	92.4	831.6	323.4	369.6	323.4	-

Table A7. Number of Dial efficient paths for the Sioux Falls network.

O\D	1	5	7	10	12	13	20	23
1	-	2	3	6	1	1	10	2
5	2	-	2	1	3	8	8	4
7	3	2	-	3	3	10	3	9
10	6	1	3	-	1	5	5	3
12	1	3	3	1	-	1	10	1
13	1	8	10	5	1	-	1	1
20	10	8	3	5	10	1	-	3
23	2	4	9	3	1	1	3	-

Table A8. Signal settings of the initial solutions (Sioux Falls network).

Intersection →	4		6		8		9		11		14		15		16		19		21		22		24
Solution ↓	C	μ	C	μ	C	μ	C	μ	C	μ	C	μ	C	μ	C	μ	C	μ	C	μ	C	μ	C	μ
1	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50	75	0.50
2	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20	75	0.20
3	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80	75	0.80
4	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50	30	0.50
5	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50	120	0.50
6	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20	30	0.20
7	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20	120	0.20
8	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80	30	0.80
9	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80	120	0.80
10	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80
11	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20	75	0.80	75	0.20
12	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80
13	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20	30	0.80	30	0.20
14	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80
15	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20	120	0.80	120	0.20
16	70	0.53	106	0.34	58	0.45	73	0.54	70	0.72	88	0.71	52	0.78	93	0.29	28	0.56	87	0.34	83	0.53	32	0.67
17	110	0.27	103	0.60	65	0.39	85	0.60	53	0.47	98	0.70	26	0.58	37	0.43	43	0.53	52	0.41	72	0.43	104	0.58
18	78	0.55	118	0.42	75	0.70	93	0.65	106	0.75	63	0.34	47	0.53	65	0.63	62	0.65	30	0.65	108	0.73	117	0.41
19	67	0.60	90	0.35	118	0.55	41	0.27	29	0.46	95	0.22	106	0.46	86	0.78	53	0.65	87	0.56	59	0.44	73	0.35
20	61	0.47	34	0.24	48	0.75	32	0.63	104	0.40	53	0.51	65	0.26	22	0.20	97	0.70	32	0.39	88	0.29	79	0.66
21	40	0.53	27	0.63	84	0.45	82	0.38	103	0.32	111	0.30	115	0.75	65	0.46	48	0.60	60	0.37	86	0.30	77	0.77
22	117	0.38	104	0.54	30	0.77	36	0.52	88	0.72	75	0.60	31	0.50	83	0.51	35	0.55	68	0.40	57	0.37	78	0.28
23	115	0.27	119	0.80	107	0.23	56	0.66	32	0.23	108	0.80	42	0.38	40	0.28	73	0.33	28	0.39	80	0.32	78	0.30
24	27	0.58	28	0.67	98	0.21	46	0.35	93	0.58	49	0.60	64	0.68	120	0.72	67	0.45	50	0.44	113	0.21	90	0.72
25	38	0.29	107	0.56	92	0.36	118	0.33	72	0.59	103	0.36	105	0.54	84	0.42	91	0.74	42	0.70	94	0.38	55	0.73

References

Biyik, C.; Abareshi, A.; Paz, A.; Arce Ruiz, R.; Battarra, R.; Rogers, C.D.F.; Lizarraga, C. Smart Mobility Adoption: A Review of the Literature. J. Open Innov. Technol. Mark. Complex. 2021, 7, 146. [Google Scholar] [CrossRef]
Allam, Z.; Sharifi, A. Research Structure and Trends of Smart Urban Mobility. Smart Cities 2022, 5, 539–561. [Google Scholar] [CrossRef]
Goumiri, S.; Yahiaoui, S.; Djahel, S. Smart Mobility in Smart Cities: Emerging challenges, recent advances and future directions. J. Intell. Transp. Syst. 2024, 1, 1–37. [Google Scholar] [CrossRef]
Medina-Tapia, M.; Robusté, F. Exploring paradigm shift impacts in urban mobility: Autonomous Vehicles and Smart Cities. Transp. Res. Procedia 2018, 33, 203–210. [Google Scholar] [CrossRef]
Gaber, H.; Othman, A.M.; Fahad, A.H. Future of connected autonomous vehicles in smart cities, Solving Urban Infrastructure Problems Using Smart City Technologies. In Solving Urban Infrastructure Problems Using Smart City Technologies. Handbook on Planning, Design, Development, and Regulation; Vacca, J.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 599–611. [Google Scholar]
Golbabaei, F.; Yigitcanlar, T.; Bunker, J. The role of shared autonomous vehicle systems in delivering smart urban mobility: A systematic review of the literature. Int. J. Sustain. Transp. 2021, 15, 731–748. [Google Scholar] [CrossRef]
Manfreda, A.; Ljubi, K.; Groznik, A. Autonomous vehicles in the smart city era: An empirical study of adoption factors important for millennials. Int. J. Inf. Manag. 2021, 58, 102050. [Google Scholar] [CrossRef]
Richter, M.A.; Hagenmaier, M.; Bandte, O.; Parida, V.; Wincent, J. Smart cities, urban mobility and autonomous vehicles: How different cities needs different sustainable investment strategies. Technol. Forecast. Soc. Chang. 2022, 184, 121857. [Google Scholar] [CrossRef]
Pérez-Moure, H.; Lampon, J.; Velando-Rodriguez, M.E.; Rodriguez-Comesana, L. Revolutionizing the road: How sustainable, autonomous, and connected vehicles are changing digital mobility business models. Eur. Res. Manag. Bus. Econ. 2023, 29, 100230. [Google Scholar] [CrossRef]
Gallo, M. Models, algorithms, and equilibrium conditions for the simulation of autonomous vehicles in exclusive and mixed traffic. Simul. Model. Pract. Theory 2023, 129, 102838. [Google Scholar] [CrossRef]
Cascetta, E.; Gallo, M.; Montella, B. Models and algorithms for the optimization of signal settings on urban networks with stochastic assignment models. Ann. Oper. Res. 2006, 144, 301–328. [Google Scholar] [CrossRef]
Magnanti, T.; Wong, R. Network design and transportation planning: Models and algorithms. Transp. Sci. 1984, 18, 181–197. [Google Scholar] [CrossRef]
Cascetta, E.; Gallo, M.; Montella, B. An asymmetric SUE model for the combined assignment-control problem. In Selected Proceedings of 8th WCTR; Pergamon Press: Amsterdam, The Netherlands, 1999; Volume 2, pp. 189–202. [Google Scholar]
Marcotte, P. Network optimization with continuous control parameters. Transp. Sci. 1983, 17, 181–197. [Google Scholar] [CrossRef]
Cantarella, G.E.; Improta, G.; Sforza, A. Road network signal setting: Equilibrium conditions. In Concise Encyclopedia of Traffic and Transportation Systems; Papageorgiou, M., Ed.; Pergamon Press: Amsterdam, The Netherlands, 1991; pp. 366–371. [Google Scholar]
Cantarella, G.E.; Sforza, A. Network design models and methods for urban traffic management. In Urban Traffic Networks—Dynamic Flow Modeling and Control; Gartner, N.H., Improta, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 123–153. [Google Scholar]
Abdelfatah, A.; Mahmassani, H.S. System optimal time-dependent path assignment and signal timing in traffic networks. Transp. Res. Rec. 1999, 1645, 185–193. [Google Scholar] [CrossRef]
Sheffi, Y.; Powell, W.B. Optimal signal settings over transportation networks. J. Transp. Eng. 1983, 109, 824–839. [Google Scholar] [CrossRef]
Heydecker, B.G.; Khoo, T.K. The equilibrium network design problem. In Proceedings of the AIRO’90, Conference on Models and Methods for Decision Support, Sorrento, Italy, 23–28 June 1990; pp. 587–602. [Google Scholar]
Yang, H.; Yagar, S. Traffic assignment and signal control in saturated road networks. Transp. Res. A 1995, 29, 125–139. [Google Scholar] [CrossRef]
Oda, T.; Otokita, T.; Tsugui, T.; Mashiyama, Y. Application of simulated annealing to optimization of traffic signal timings. In Proceedings of the 8th Ifac Symposium on Transportation Systems, Chania, Greece, 16–18 June 1997. [Google Scholar]
Wong, S.C.; Yang, H. Reserve capacity of a signal-controlled road network. Transp. Res. B 1997, 31, 397–402. [Google Scholar] [CrossRef]
Chiou, S.-W. Optimization of area traffic control for equilibrium network flows. Transp. Sci. 1999, 33, 279–289. [Google Scholar] [CrossRef]
Ziyou, G.; Yifan, S. A reserve capacity model of optimal signal control with user-equilibrium route choice. Transp. Res. B 2002, 36, 313–323. [Google Scholar] [CrossRef]
Heydecker, B.G. A decomposition approach for signal optimisation in road networks. Transp. Res. B 1996, 30, 99–114. [Google Scholar] [CrossRef]
Pillai, R.S.; Rathi, A.K.; Cohen, S.L. A restricted branch and bound approach for generating maximum bandwidth signal timing plans for traffic networks. Transp. Res. B 1998, 32, 517–529. [Google Scholar] [CrossRef]
Wey, W.-M. Model formulation and solution algorithm of traffic signal control in an urban network. Comput. Environ. Urban Syst. 2000, 24, 355–377. [Google Scholar] [CrossRef]
Wong, S.C. Group-based optimisation of signal timings using parallel computing. Transp. Res. C 1997, 5, 123–139. [Google Scholar] [CrossRef]
Wong, S.C.; Wong, W.T.; Leung, C.M.; Tong, C.O. Group-based optimization of a time-dependent TRANSYT traffic model for area traffic control. Transp. Res. B 2002, 36, 291–312. [Google Scholar] [CrossRef]
Smith, M.J.; Xiang, Y.; Yarrow, R. Bilevel optimisation of signal timings and road prices on urban road networks. In Proceedings of the 8th Ifac Symposium on Transportation Systems, Chania, Greece, 16–18 June 1997. [Google Scholar]
Abu-Lebdeh, G.; Benekohal, R.F. Design and evaluation of dynamic traffic management strategies for congested conditions. Transp. Res. A 2003, 37, 109–127. [Google Scholar] [CrossRef]
Saraf, R.K. Adaptive Traffic Control Using Neural Networks. Ph.D. Dissertation, Vanderbilt University, Nashville, TN, USA, 1994. [Google Scholar]
Spall, J.C.; Chin, D.C. Traffic-responsive signal timing for system-wide traffic control. Transp. Res. C 1997, 5, 153–163. [Google Scholar] [CrossRef]
Lee, S.; Hazelton, H. Stochastic optimization of combined traffic assignment and signal control junction modelling. In Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Lyon, France, 24–26 July 1996; pp. 713–735. [Google Scholar]
Al-Sharman, M.; Dempster, R.; Daoud, M.A.; Nasr, M.; Raydide, D. Self-Learned Autonomous Driving at Unsignalized Intersections: A Hierarchical Reinforced Learning Approach for Feasible Decision-Making. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12345–12356. [Google Scholar] [CrossRef]
SAE Standard J3016_202104. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles. SAE International Recommended Practice: Warrendale, PA, USA, Revised April 2021, Issued January 2014. 2021. [CrossRef]
Di, X.; Shi, R. A survey on autonomous vehicle control in the era of mixed-autonomy: From physics-based to AI-guided driving policy learning. Transp. Res. C 2021, 125, 103008. [Google Scholar] [CrossRef]
Zhao, C.; Li, L.; Pei, X.; Li, Z.; Wang, F.-Y.; Wu, X. A comparative study of state-of-the-art driving strategies for autonomous vehicles. Accid. Anal. Prev. 2021, 150, 105937. [Google Scholar] [CrossRef] [PubMed]
Makahleh, H.Y.; Ferranti, E.J.S.; Dissanayake, D. Assessing the Role of Autonomous Vehicles in Urban Areas: A Systematic Review of Literature. Future Transp. 2024, 4, 321–348. [Google Scholar] [CrossRef]
D’Emidio, M.; Delfaraz, E.; Di Stefano, G.; Frittella, G.; Vittoria, E. Route Planning Algorithms for Fleets of Connected Vehicles: State of the Art, Implementation, and Deployment. Appl. Sci. 2024, 14, 2884. [Google Scholar] [CrossRef]
Kassens-Noor, E.; Dake, D.; Decaminada, T.; Kotval-K, Z.; Qu, T.; Wilson, M.; Pentland, B. Sociomobility of the 21st century: Autonomous vehicles, planning, and the future city. Transp. Policy 2020, 99, 329–335. [Google Scholar] [CrossRef]
Liu, W.; Hua, M.; Deng, Z.; Meng, Z.; Huang, Y.; Hu, C.; Song, S.; Gao, L.; Liu, C.; Shuai, B.; et al. Systematic Survey of Control Techniques and Applications in Connected and Automated Vehicles. IEEE Internet Things J. 2023, 10, 21892–21916. [Google Scholar] [CrossRef]
Negash, N.M.; Yang, J. Driver Behavior Modeling toward Autonomous Vehicles: Comprehensive Review. IEEE Access 2023, 11, 22788–22821. [Google Scholar] [CrossRef]
Patella, S.M.; Scrucca, F.; Asdrubali, F.; Carrese, S. Carbon Footprint of autonomous vehicles at the urban mobility system level: A traffic simulation-based approach. Transp. Res. D 2019, 74, 189–200. [Google Scholar] [CrossRef]
Ercan, T.; Onat, N.C.; Kaya, N.; Tatari, N.; Eluru, N.; Kucukvar, M. Autonomous electric vehicles can reduce carbon emissions and air pollution in cities. Transp. Res. D 2022, 112, 103472. [Google Scholar] [CrossRef]
Silva, O.; Cordera, R.; Gonzalez-Gonzalez, E.; Nogues, S. Environmental impacts of autonomous vehicles: A review of the scientific literature. Sci. Total Environ. 2022, 830, 154615. [Google Scholar] [CrossRef]
Hasan, M.H.; Van Hentenryck, P. The benefits of autonomous vehicles for community-based trip sharing. Transp. Res. C 2021, 124, 102929. [Google Scholar] [CrossRef]
Carrese, S.; Nigro, M.; Patella, S.M.; Toniolo, E. A preliminary study of the potential impact of autonomous vehicles on residential location in Rome. Res. Transp. Econ. 2019, 75, 55–61. [Google Scholar] [CrossRef]
Moore, M.A.; Lavieri, P.S.; Dias, F.F.; Bhat, C.R. On investigating the potential effects of private autonomous vehicle use on home/work relocations and commute times. Transp. Res. Part C 2020, 110, 166–185. [Google Scholar] [CrossRef]
May, A.D.; Shepherd, S.; Pfaffenbichler, P.; Emberger, G. The potential impacts of automated cars on urban transport: An exploratory analysis. Transp. Policy 2020, 98, 127–138. [Google Scholar] [CrossRef]
Harrison, G.; Stanford, J.; Rakoff, H.; Smith, S.; Shepherd, S.; Barnard, Y.; Innamaa, S. Assessing the influence of connected and automated mobility on the liveability of cities. J. Urban Mobil. 2022, 2, 100034. [Google Scholar] [CrossRef]
Rashidi, T.H.; Waller, T.; Axhausen, K. Reduced value of time for autonomous vehicle users: Myth or reality? Transp. Policy 2020, 95, 30–36. [Google Scholar] [CrossRef]
Tian, Z.; Feng, T.; Timmermans, H.J.P.; Yao, B. Using autonomous vehicles or shared cars? Results of a stated choice experiment. Transp. Res. C 2021, 128, 103117. [Google Scholar] [CrossRef]
Wang, Y.; Cai, P.; Lu, G. Cooperative autonomous traffic organization method for connected automated vehicles in multi-intersection road networks. Transp. Res. C 2020, 111, 458–476. [Google Scholar] [CrossRef]
Sun, W.; Wang, S.; Shao, Y.; Sun, Z.; Levin, M.W. Energy and mobility impacts of connected autonomous vehicles with co-optimization of speed and powertrain on mixed vehicle platoons. Transp. Res. C 2022, 142, 103764. [Google Scholar] [CrossRef]
Zhang, Y.; Ai, Z.; Chen, J.; You, T.; Du, C.; Deng, L. Energy-Saving Optimization and Control of Autonomous Electric Vehicles with Considering Multiconstraints. IEEE Trans. Cybern. 2022, 52, 10869–10881. [Google Scholar] [CrossRef] [PubMed]
Lee, S.; Kim, Y.; Kahng, H.; Lee, S.-K.; Chung, S.; Cheong, T.; Shin, K.; Park, J.; Kim, S.B. Intelligent traffic control for autonomous vehicle systems based on machine learning. Expert Syst. Appl. 2020, 144, 113074. [Google Scholar] [CrossRef]
Rey, D.; Levin, M.W. Blue phase: Optimal network traffic control for legacy and autonomous vehicles. Transp. Res. B 2019, 130, 105–129. [Google Scholar] [CrossRef]
Lazar, D.A.; Biyik, E.; Sadigh, D.; Pedarsani, R. Learning how to dynamically route autonomous vehicles on shared roads. Transp. Res. C 2021, 130, 103258. [Google Scholar] [CrossRef]
Wang, J.; Wang, W.; Ren, G.; Yang, M. Worst-case traffic assignment model for mixed traffic flow of human-driven vehicles and connected and autonomous vehicles by factoring in the uncertain link capacity. Transp. Res. C 2022, 140, 103703. [Google Scholar] [CrossRef]
Guo, Z.; Wang, D.Z.W.; Wang, D. Managing mixed traffic with autonomous vehicles—A day-to-day routing allocation scheme. Transp. Res. C 2022, 140, 103726. [Google Scholar] [CrossRef]
Chen, B.; Sun, D.; Zhou, J.; Wong, W.; Ding, Z. A future intelligent traffic system with mixed autonomous vehicles and human-driven vehicles. Inf. Sci. 2020, 529, 59–72. [Google Scholar] [CrossRef]
Németh, B.; Bede, Z.; Gaspar, P. Control strategy for the optimization of mixed traffic flow with autonomous vehicles. IFAC Pap. 2019, 52, 227–232. [Google Scholar] [CrossRef]
Wang, J.; Peeta, S.; He, X. Multiclass traffic assignment model for mixed traffic flow of human-driven vehicles and connected and autonomous vehicles. Transp. Res. B 2019, 126, 139–168. [Google Scholar] [CrossRef]
Santana, E.F.Z.; Covas, G.; Duarte, F.; Santi, P.; Ratti, C.; Kon, F. Transitioning to a driverless city: Evaluating a hybrid system for autonomous and non-autonomous vehicles. Simul. Model. Pract. Theory 2021, 107, 102210. [Google Scholar] [CrossRef]
Ding, H.; Pan, H.; Bai, H.; Zheng, X.; Chen, J. Driving strategy of connected and autonomous vehicles based on multiple preceding vehicles state estimation in mixed vehicular traffic. Phys. A 2022, 596, 127154. [Google Scholar] [CrossRef]
Zhu, L.; Lu, L.; Wang, X.; Jiang, C.; Ye, N. Operational Characteristics of Mixed-Autonomy Traffic Flow on the Freeway with On- and Off-Ramps and Weaving Sections: An RL-Based Approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13512–13525. [Google Scholar] [CrossRef]
Guo, H.; Chen, Y.; Liu, Y. Shared autonomous vehicle management considering competition with human-driven private vehicles. Transp. Res. C 2022, 136, 103547. [Google Scholar] [CrossRef]
Narayanan, S.; Chaniotakis, E.; Antoniou, C. Modelling reservation-based shared autonomous vehicle services: A dynamic user equilibrium approach. Transp. Res. C 2022, 140, 103651. [Google Scholar] [CrossRef]
Levy, R.; Haddad, J. Cooperative path and trajectory planning for autonomous vehicles on roads without lanes: A laboratory experimental demonstration. Transp. Res. C 2022, 144, 103813. [Google Scholar] [CrossRef]
Wu, L.; Cao, S.; Chen, Y.; Li, J.; Cui, J.; Chang, Y. A cooperative mobility model for multiple autonomous vehicles. Comput. Commun. 2022, 195, 148–161. [Google Scholar] [CrossRef]
Mahmoud, Y.H.; Brown, N.E.; Motallebiaraghi, F.; Koelling, M.; Meyer, R.; Asher, Z.D.; Dontchev, A.; Kolmanovsky, I. Autonomous eco-driving with traffic light and lead vehicle constraints: An application of best constrained interpolation. IFAC-PapersOnLine 2021, 54, 45–50. [Google Scholar] [CrossRef]
Sun, P.; Nam, D.; Jayakrishnan, R.; Jin, W. An eco-driving algorithm based on vehicle to infrastructure (V2I) communications for signalized intersections. Transp. Res. C 2022, 144, 103876. [Google Scholar] [CrossRef]
Talebpour, A.; Mahmassani, H.S. Influence of connected and autonomous vehicles on traffic flow stability and throughput. Transp. Res. C 2016, 71, 143–163. [Google Scholar] [CrossRef]
Tettamanti, T.; Mohammadi, A.; Asadi, H.; Varga, I. A two-level urban traffic control for autonomous vehicles to improve network-wide performance. Transp. Res. Procedia 2017, 27, 913–920. [Google Scholar] [CrossRef]
Stern, R.E.; Chen, Y.; Churchill, M.; Wu, F.; Delle Monache, M.L.; Piccoli, B.; Seibold, B.; Sprinkle, J.; Work, D.B. Quantifying air quality benefits resulting from few autonomous vehicles stabilizing traffic. Transp. Res. D 2019, 67, 351–365. [Google Scholar] [CrossRef]
Miglani, A.; Kumar, N. Deep learning models for traffic flow prediction in autonomous vehicles: A review, solutions, and challenges. Veh. Commun. 2019, 20, 100184. [Google Scholar] [CrossRef]
Liard, T.; Stern, R.; Delle Monache, M.L. Optimal driving strategies for traffic control with autonomous vehicles. IFAC-PapersOnLine 2020, 53, 5322–5329. [Google Scholar] [CrossRef]
Kumakoshi, Y.; Hanabusa, H.; Oguchi, T. Impacts of shared autonomous vehicles: Tradeoff between parking demand reduction and congestion increase. Transp. Res. Interdiscip. Perspect. 2021, 12, 100482. [Google Scholar] [CrossRef]
Zhao, C.; Liao, F.; Li, X.; Du, Y. Macroscopic modeling and dynamic control of on-street cruising-for-parking of autonomous vehicles in a multi-region urban road network. Transp. Res. C 2021, 128, 103176. [Google Scholar] [CrossRef]
Ge, Q.; Han, K.; Liu, X. Matching and routing for shared autonomous vehicles in congestible network. Transp. Res. E 2021, 156, 102513. [Google Scholar] [CrossRef]
Cantarella, G.E. A general fixed-point approach to multimode multi-user equilibrium assignment with elastic demand. Transp. Sci. 1997, 31, 107–128. [Google Scholar] [CrossRef]
Cascetta, E. Transportation Systems Engineering: Theory and Methods; Kluwer Academic Publishers: Dordrecht, The Nederlands, 2001. [Google Scholar]
Gallo, M.; D’Acierno, L.; Montella, B. Global Optimisation of Signal Settings: Meta-heuristic algorithms for solving real-scale problems. In Computer-Based Modelling and Optimization in Transportation; de Sousa, J.F., Rossi, R., Eds.; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2014; Volume 262, pp. 177–193. [Google Scholar]
National Academies of Sciences, Engineering, and Medicine. Highway Capacity Manual 7th Edition: A Guide for Multimodal Mobility Analysis; The National Academies Press: Washington, DC, USA, 2022. [Google Scholar]
Morlok, E.K.; Schofer, J.L.; Pierskalla, W.P.; Marsten, R.E.; Agarwal, S.K.; Stoner, J.W.; Edwards, J.L.; LeBlanc, L.J.; Spacek, D.T. Development and Application of a Highway Network Design Model, Volumes 1 and 2. Final Report: FHWA Contract Number DOT-PH-11-7862; Northwestern University: Evanston, IL, USA, 1973. [Google Scholar]
Suwansirikul, C.; Friesz, T.L.; Tobin, R.L. Equilibrium decomposed optimization: A heuristic for the continuous equilibrium network design problem. Transp. Sci. 1987, 40, 540–542. [Google Scholar] [CrossRef]
Dial, R.B. A Probabilistic Multipath Traffic Assignment Model Which Obviates Path Enumeration. Transp. Res. 1971, 5, 83–111. [Google Scholar] [CrossRef]

Figure 1. Toy network.

Figure 2. Objective function shape (d = 800 veh/h).

Figure 3. Objective function shape (d = 1600 veh/h).

Figure 4. Small network.

Figure 5. Sioux Falls network.

Figure 6. Optimal objective function values.

Figure 7. Traffic flows for the different solutions (different colours correspond to different initial solutions).

Table 1. Local optima.

Solution	μ	ψ₁	Objective Function [s]
1	0.8	1.00	78,649
2	0.2	0.01	86,121

Table 2. Optimal local solutions for different levels of demand.

Demand	Optimal Local Solutions	μ	ψ₁	Objective Function [s]
200	1	0.80	1.00	18,448
200	2	0.20	0.00	20,248
400	1	0.80	1.00	37,206
400	2	0.20	0.00	40,815
600	1	0.80	1.00	56,822
600	2	0.20	0.00	62,289
800	1	0.80	1.00	78,649
800	2	0.20	0.01	86,121
1000	1	0.80	1.00	105,400
1000	2	0.20	0.12	113,747
1200	1	0.80	0.88	138,782
1200	2	0.20	0.17	147,416
1400	1	0.83	0.80	182,350
1400	2	0.20	0.18	192,239
1600	1	0.81	0.80	247,582
1600	2	-	-	-

Table 3. Results on the small network (demand 1000 veh/h).

Variable	1	2	3	4	5	6	7	8	9	10	11	12
μ_{1_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.20	0.80	0.20
μ_{2_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.80	0.20	0.80
μ_{3_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.20	0.80	0.20
μ_{4_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.80	0.20	0.80
C_{1_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{2_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{3_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{4_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
All ψ_k,od	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111
Results	1	2	3	4	5	6	7	8	9	10	11	12
μ_{1_opt}	0.20	0.20	0.20	0.37	0.37	0.20	0.37	0.20	0.37	0.20	0.20	0.20
μ_{2_opt}	0.23	0.23	0.23	0.20	0.37	0.21	0.37	0.25	0.37	0.22	0.23	0.24
μ_{3_opt}	0.20	0.20	0.50	0.80	0.37	0.80	0.37	0.80	0.37	0.20	0.20	0.80
μ_{4_opt}	0.20	0.20	0.20	0.20	0.48	0.20	0.52	0.26	0.52	0.20	0.20	0.20
C_{1_opt}	94.7	94.6	94.8	120.0	120.0	94.7	120.0	94.7	120.0	94.7	94.7	94.7
C_{2_opt}	98.6	98.6	98.8	94.9	120.0	95.6	120.0	101.1	120.0	97.6	98.5	99.9
C_{3_opt}	74.9	74.9	51.8	30.0	120.0	30.0	120.0	30.0	120.0	74.9	81.3	30.0
C_{4_opt}	94.7	94.6	94.7	94.7	120.0	94.3	120.0	101.7	120.0	94.7	94.7	94.5
ψ_{1_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{2_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{3_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{4_opt}	0.447	0.447	0.447	0.447	0.389	0.447	0.389	0.447	0.389	0.447	0.447	0.447
ψ_{5_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{6_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{7_opt}	0.000	0.000	0.000	0.000	0.018	0.000	0.018	0.000	0.018	0.000	0.000	0.000
ψ_{8_opt}	0.000	0.000	0.000	0.000	0.514	0.000	0.514	0.000	0.514	0.000	0.000	0.000
ψ_{9_opt}	0.553	0.553	0.553	0.553	0.079	0.553	0.079	0.553	0.079	0.553	0.553	0.553
Objective function [s]	174,924	174,924	174,924	174,924	171,424	174924.3	171,424	174,924	171,424	174,924	174,924	174,924
Solution	Sol_1	Sol_1	Sol_1	Sol_1	Sol_2	Sol_1	Sol_2	Sol_1	Sol_2	Sol_1	Sol_1	Sol_1
Variable	13	14	15	16	17	18	19	20	21	22	23
μ_{1_start}	0.80	0.20	0.80	0.73	0.38	0.40	0.57	0.33	0.39	0.68	0.78
μ_{2_start}	0.20	0.80	0.20	0.42	0.57	0.66	0.28	0.57	0.36	0.55	0.27
μ_{3_start}	0.80	0.20	0.80	0.30	0.69	0.49	0.73	0.53	0.65	0.76	0.26
μ_{4_start}	0.20	0.80	0.20	0.60	0.44	0.24	0.57	0.34	0.24	0.64	0.51
C_{1_start}	30.0	120.0	120.0	59.0	120.0	59.0	80.0	50.0	66.0	98.0	37.0
C_{2_start}	30.0	120.0	120.0	66.0	108.0	62.0	114.0	77.0	95.0	46.0	108.0
C_{3_start}	30.0	120.0	120.0	104.0	42.0	67.0	40.0	88.0	95.0	72.0	120.0
C_{4_start}	30.0	120.0	120.0	102.0	67.0	112.0	95.0	59.0	106.0	43.0	106.0
All ψ_k,od	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111
Results	13	14	15	16	17	18	19	20	21	22	23
μ_{1_opt}	0.20	0.37	0.37	0.63	0.37	0.20	0.20	0.20	0.22	0.25	0.74
μ_{2_opt}	0.20	0.37	0.37	0.20	0.30	0.23	0.33	0.30	0.20	0.20	0.37
μ_{3_opt}	0.80	0.37	0.38	0.37	0.40	0.31	0.64	0.20	0.54	0.80	0.37
μ_{4_opt}	0.20	0.52	0.52	0.53	0.20	0.52	0.24	0.20	0.52	0.20	0.53
C_{1_opt}	94.9	120.0	120.0	120.0	120.0	94.8	94.7	94.7	97.2	101.2	101.6
C_{2_opt}	94.4	120.0	120.0	95.1	108.0	98.7	114.0	108.6	95.0	94.9	120.0
C_{3_opt}	30.0	120.0	120.0	120.0	42.0	67.0	40.0	87.9	95.0	72.0	120.0
C_{4_opt}	93.8	120.0	120.0	120.0	94.7	120.0	99.4	94.6	120.0	94.7	120.0
ψ_{1_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{2_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{3_opt}	0.000	0.000	0.000	0.398	0.000	0.000	0.000	0.000	0.000	0.000	0.398
ψ_{4_opt}	0.447	0.389	0.389	0.000	0.447	0.401	0.447	0.447	0.401	0.447	0.000
ψ_{5_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{6_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{7_opt}	0.000	0.018	0.018	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{8_opt}	0.000	0.514	0.514	0.517	0.000	0.516	0.000	0.000	0.516	0.000	0.517
ψ_{9_opt}	0.553	0.079	0.079	0.085	0.553	0.083	0.553	0.553	0.083	0.553	0.085
Objective function [s]	174,927	171,424	171,424	171,58	174,924	171,432	174,924	174,924	171,432	174,924	171,58
Solution	Sol_1	Sol_2	Sol_2	Sol_3	Sol_1	Sol_4	Sol_1	Sol_1	Sol_4	Sol_1	Sol_3

Table 4. Results on the small network (demand 1500 veh/h).

Variable	1	2	3	4	5	6	7	8	9	10	11	12
μ_{1_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.20	0.80	0.20
μ_{2_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.80	0.20	0.80
μ_{3_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.20	0.80	0.20
μ_{4_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.80	0.20	0.80
C_{1_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{2_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{3_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{4_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
All ψ_k,od	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111
Results	1	2	3	4	5	6	7	8	9	10	11	12
μ_{1_opt}	0.22	0.46	0.49	0.20	0.47	0.36	0.47	0.47	0.47	0.22	0.47	0.20
μ_{2_opt}	0.40	0.38	0.20	0.24	0.37	0.21	0.37	0.37	0.37	0.40	0.37	0.36
μ_{3_opt}	0.20	0.20	0.23	0.80	0.37	0.80	0.37	0.20	0.37	0.20	0.23	0.80
μ_{4_opt}	0.20	0.21	0.43	0.44	0.42	0.44	0.42	0.42	0.42	0.21	0.42	0.44
C_{1_opt}	97.7	120.0	120.0	95.3	120.0	120.0	120.0	120.0	120.0	97.3	120.0	95.5
C_{2_opt}	120.0	120.0	95.8	100.2	120.0	96.8	120.0	120.0	120.0	120.0	120.0	120.0
C_{3_opt}	94.0	94.6	98.1	30.0	120.0	30.0	120.0	94.4	120.0	94.1	98.5	30.0
C_{4_opt}	95.6	97.2	120.0	120.0	120.0	120.0	120.0	120.0	120.0	97.0	120.0	120.0
ψ_{1_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{2_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{3_opt}	0.000	0.176	0.226	0.000	0.184	0.000	0.184	0.184	0.184	0.000	0.184	0.000
ψ_{4_opt}	0.381	0.273	0.258	0.453	0.266	0.453	0.266	0.266	0.266	0.381	0.266	0.453
ψ_{5_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{6_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{7_opt}	0.134	0.064	0.000	0.000	0.044	0.000	0.044	0.044	0.044	0.134	0.044	0.000
ψ_{8_opt}	0.000	0.003	0.225	0.251	0.218	0.251	0.218	0.218	0.218	0.000	0.218	0.251
ψ_{9_opt}	0.485	0.484	0.290	0.296	0.289	0.296	0.289	0.289	0.289	0.485	0.289	0.296
Objective function [s]	305,748	304,681	302,758	305,958	302,564	305,958	302,564	302,564	302,564	305,748	302,564	305,958
Solution	Sol_1	Sol_2	Sol_3	Sol_4	Sol_5	Sol_4	Sol_5	Sol_5	Sol_5	Sol_1	Sol_5	Sol_4
Variable	13	14	15	16	17	18	19	20	21	22	23
μ_{1_start}	0.80	0.20	0.80	0.73	0.38	0.40	0.57	0.33	0.39	0.68	0.78
μ_{2_start}	0.20	0.80	0.20	0.42	0.57	0.66	0.28	0.57	0.36	0.55	0.27
μ_{3_start}	0.80	0.20	0.80	0.30	0.69	0.49	0.73	0.53	0.65	0.76	0.26
μ_{4_start}	0.20	0.80	0.20	0.60	0.44	0.24	0.57	0.34	0.24	0.64	0.51
C_{1_start}	30.0	120.0	120.0	59.0	120.0	59.0	80.0	50.0	66.0	98.0	37.0
C_{2_start}	30.0	120.0	120.0	66.0	108.0	62.0	114.0	77.0	95.0	46.0	108.0
C_{3_start}	30.0	120.0	120.0	104.0	42.0	67.0	40.0	88.0	95.0	72.0	120.0
C_{4_start}	30.0	120.0	120.0	102.0	67.0	112.0	95.0	59.0	106.0	43.0	106.0
All ψ_k,od	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111
Results	13	14	15	16	17	18	19	20	21	22	23
μ_{1_opt}	0.20	0.47	0.47	0.47	0.47	0.47	0.21	0.22	0.22	0.47	0.47
μ_{2_opt}	0.20	0.37	0.37	0.37	0.37	0.37	0.39	0.40	0.39	0.37	0.37
μ_{3_opt}	0.80	0.37	0.37	0.27	0.24	0.26	0.26	0.20	0.21	0.37	0.37
μ_{4_opt}	0.44	0.42	0.42	0.42	0.42	0.42	0.42	0.20	0.42	0.42	0.42
C_{1_opt}	95.3	120.0	120.0	120.0	120.0	120.0	96.6	96.9	96.9	120.0	120.0
C_{2_opt}	95.7	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
C_{3_opt}	30.0	120.0	120.0	103.9	99.9	102.7	101.2	94.1	95.5	120.0	120.0
C_{4_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	96.1	120.0	120.0	120.0
ψ_{1_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{2_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{3_opt}	0.000	0.184	0.184	0.184	0.184	0.184	0.000	0.000	0.000	0.184	0.184
ψ_{4_opt}	0.453	0.266	0.266	0.266	0.266	0.266	0.380	0.381	0.380	0.266	0.266
ψ_{5_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{6_opt}	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
ψ_{7_opt}	0.000	0.044	0.044	0.044	0.044	0.044	0.114	0.134	0.114	0.044	0.044
ψ_{8_opt}	0.251	0.218	0.218	0.218	0.218	0.218	0.217	0.000	0.217	0.218	0.218
ψ_{9_opt}	0.296	0.289	0.289	0.289	0.289	0.289	0.289	0.485	0.289	0.289	0.289
Objective function [s]	305,958	302,564	302,564	302,564	302,564	302,564	303,662	305,748	303,662	302,564	302,564
Solution	Sol_4	Sol_5	Sol_5	Sol_5	Sol_5	Sol_5	Sol_6	Sol_1	Sol_6	Sol_5	Sol_5

Table 5. Results on the small network (demand 2000 veh/h).

Variable	1	2	3	4	5	6	7	8	9	10	11	12
μ_{1_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.20	0.80	0.20
μ_{2_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.80	0.20	0.80
μ_{3_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.20	0.80	0.20
μ_{4_start}	0.50	0.20	0.80	0.50	0.50	0.20	0.20	0.80	0.80	0.80	0.20	0.80
C_{1_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{2_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{3_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
C_{4_start}	75.0	75.0	75.0	30.0	120.0	30.0	120.0	30.0	120.0	75.0	75.0	30.0
All ψ_k,od	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111
Results	1	2	3	4	5	6	7	8	9	10	11	12
μ_{1_opt}	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48
μ_{2_opt}	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41
μ_{3_opt}	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54
μ_{4_opt}	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44
C_{1_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
C_{2_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
C_{3_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
C_{4_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
ψ_{1_opt}	0.085	0.071	0.101	0.081	0.071	0.054	0.034	0.071	0.059	0.074	0.071	0.071
ψ_{2_opt}	0.071	0.064	0.027	0.060	0.063	0.044	0.099	0.063	0.067	0.060	0.063	0.063
ψ_{3_opt}	0.054	0.074	0.082	0.068	0.076	0.112	0.076	0.076	0.083	0.076	0.076	0.076
ψ_{4_opt}	0.250	0.250	0.250	0.250	0.250	0.250	0.250	0.250	0.250	0.250	0.250	0.250
ψ_{5_opt}	0.018	0.047	0.016	0.060	0.051	0.100	0.031	0.050	0.041	0.047	0.051	0.050
ψ_{6_opt}	0.041	0.032	0.070	0.012	0.030	0.017	0.050	0.031	0.047	0.033	0.030	0.030
ψ_{7_opt}	0.085	0.064	0.057	0.070	0.062	0.027	0.062	0.063	0.055	0.063	0.062	0.063
ψ_{8_opt}	0.126	0.111	0.111	0.087	0.107	0.075	0.163	0.108	0.128	0.107	0.107	0.108
ψ_{9_opt}	0.271	0.286	0.286	0.310	0.290	0.322	0.234	0.289	0.269	0.290	0.290	0.289
Objective function [s]	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318
Solution	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1
Variable	13	14	15	16	17	18	19	20	21	22	23
μ_{1_start}	0.80	0.20	0.80	0.73	0.38	0.40	0.57	0.33	0.39	0.68	0.78
μ_{2_start}	0.20	0.80	0.20	0.42	0.57	0.66	0.28	0.57	0.36	0.55	0.27
μ_{3_start}	0.80	0.20	0.80	0.30	0.69	0.49	0.73	0.53	0.65	0.76	0.26
μ_{4_start}	0.20	0.80	0.20	0.60	0.44	0.24	0.57	0.34	0.24	0.64	0.51
C_{1_start}	30.0	120.0	120.0	59.0	120.0	59.0	80.0	50.0	66.0	98.0	37.0
C_{2_start}	30.0	120.0	120.0	66.0	108.0	62.0	114.0	77.0	95.0	46.0	108.0
C_{3_start}	30.0	120.0	120.0	104.0	42.0	67.0	40.0	88.0	95.0	72.0	120.0
C_{4_start}	30.0	120.0	120.0	102.0	67.0	112.0	95.0	59.0	106.0	43.0	106.0
All ψ_k,od	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111	0.1111
Results	13	14	15	16	17	18	19	20	21	22	23
μ_{1_opt}	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48	0.48
μ_{2_opt}	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41	0.41
μ_{3_opt}	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54	0.54
μ_{4_opt}	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44	0.44
C_{1_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
C_{2_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
C_{3_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
C_{4_opt}	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0	120.0
ψ_{1_opt}	0.070	0.054	0.068	0.019	0.026	0.073	0.048	0.025	0.004	0.118	0.069
ψ_{2_opt}	0.063	0.016	0.069	0.084	0.097	0.063	0.035	0.060	0.165	0.003	0.063
ψ_{3_opt}	0.077	0.140	0.073	0.107	0.087	0.074	0.127	0.125	0.041	0.089	0.077
ψ_{4_opt}	0.250	0.249	0.250	0.250	0.250	0.250	0.250	0.250	0.250	0.250	0.250
ψ_{5_opt}	0.051	0.133	0.077	0.043	0.000	0.049	0.008	0.129	0.023	0.058	0.050
ψ_{6_opt}	0.030	0.010	0.000	0.068	0.092	0.030	0.124	0.000	0.023	0.035	0.032
ψ_{7_opt}	0.062	0.000	0.066	0.032	0.052	0.065	0.011	0.014	0.098	0.050	0.061
ψ_{8_opt}	0.107	0.041	0.084	0.166	0.203	0.107	0.173	0.074	0.202	0.052	0.109
ψ_{9_opt}	0.290	0.356	0.313	0.231	0.194	0.290	0.224	0.323	0.195	0.345	0.288
Objective function [s]	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318	536,318
Solution	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1	Sol_1

Table 6. Values of the objective function for varying the number of initial solutions of the GRG multistart algorithm.

Initial Solutions [#]	Objective Function [h]
5	2326
10	2336
25	2312
50	2314
100	2310
250	2297
500	2295

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Gallo, M. Combined Optimisation of Traffic Light Control Parameters and Autonomous Vehicle Routes. Smart Cities 2024, 7, 1060-1088. https://doi.org/10.3390/smartcities7030045

AMA Style

Gallo M. Combined Optimisation of Traffic Light Control Parameters and Autonomous Vehicle Routes. Smart Cities. 2024; 7(3):1060-1088. https://doi.org/10.3390/smartcities7030045

Chicago/Turabian Style

Gallo, Mariano. 2024. "Combined Optimisation of Traffic Light Control Parameters and Autonomous Vehicle Routes" Smart Cities 7, no. 3: 1060-1088. https://doi.org/10.3390/smartcities7030045

APA Style

Gallo, M. (2024). Combined Optimisation of Traffic Light Control Parameters and Autonomous Vehicle Routes. Smart Cities, 7(3), 1060-1088. https://doi.org/10.3390/smartcities7030045

Article Menu

Combined Optimisation of Traffic Light Control Parameters and Autonomous Vehicle Routes

Highlights

Abstract

1. Introduction

2. Background

2.1. Optimisation of Signal Settings on a Network

2.2. Autonomous Vehicles

2.3. Paper Contribution

3. Model Formulation

4. Solution Algorithm

5. Numerical Results

5.1. Toy Network

5.2. Small Network

5.3. Sioux Falls Network

6. Conclusions

Funding

Data Availability Statement

Conflicts of Interest

Appendix A

Appendix B

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI

O\D	1	5	7	10	12	13	20	23
1	-	2	3	6	1	1	10	2
5	2	-	2	1	3	8	8	4
7	3	2	-	3	3	10	3	9
10	6	1	3	-	1	5	5	3
12	1	3	3	1	-	1	10	1
13	1	8	10	5	1	-	1	1
20	10	8	3	5	10	1	-	3
23	2	4	9	3	1	1	3	-

O\D	1	5	7	10	12	13	20	23
1	-	2	3	6	1	1	10	2
5	2	-	2	1	3	8	8	4
7	3	2	-	3	3	10	3	9
10	6	1	3	-	1	5	5	3
12	1	3	3	1	-	1	10	1
13	1	8	10	5	1	-	1	1
20	10	8	3	5	10	1	-	3
23	2	4	9	3	1	1	3	-

O\D	1	5	7	10	12	13	20	23
1	-	2	3	6	1	1	10	2
5	2	-	2	1	3	8	8	4
7	3	2	-	3	3	10	3	9
10	6	1	3	-	1	5	5	3
12	1	3	3	1	-	1	10	1
13	1	8	10	5	1	-	1	1
20	10	8	3	5	10	1	-	3
23	2	4	9	3	1	1	3	-