Spectral Properties of Water Hammer Wave
Abstract
:1. Introduction: Water Hammer Phenomena
2. Water Hammer Wave
2.1. Theory
2.2. Pressure Losses in the Flow System
3. Data Collection
3.1. Experimental Setup
3.2. Procedure for Collecting Water Hammer Data
3.3. Discharge Data Collection
4. Methods
4.1. The Essence of the Fourier Transform
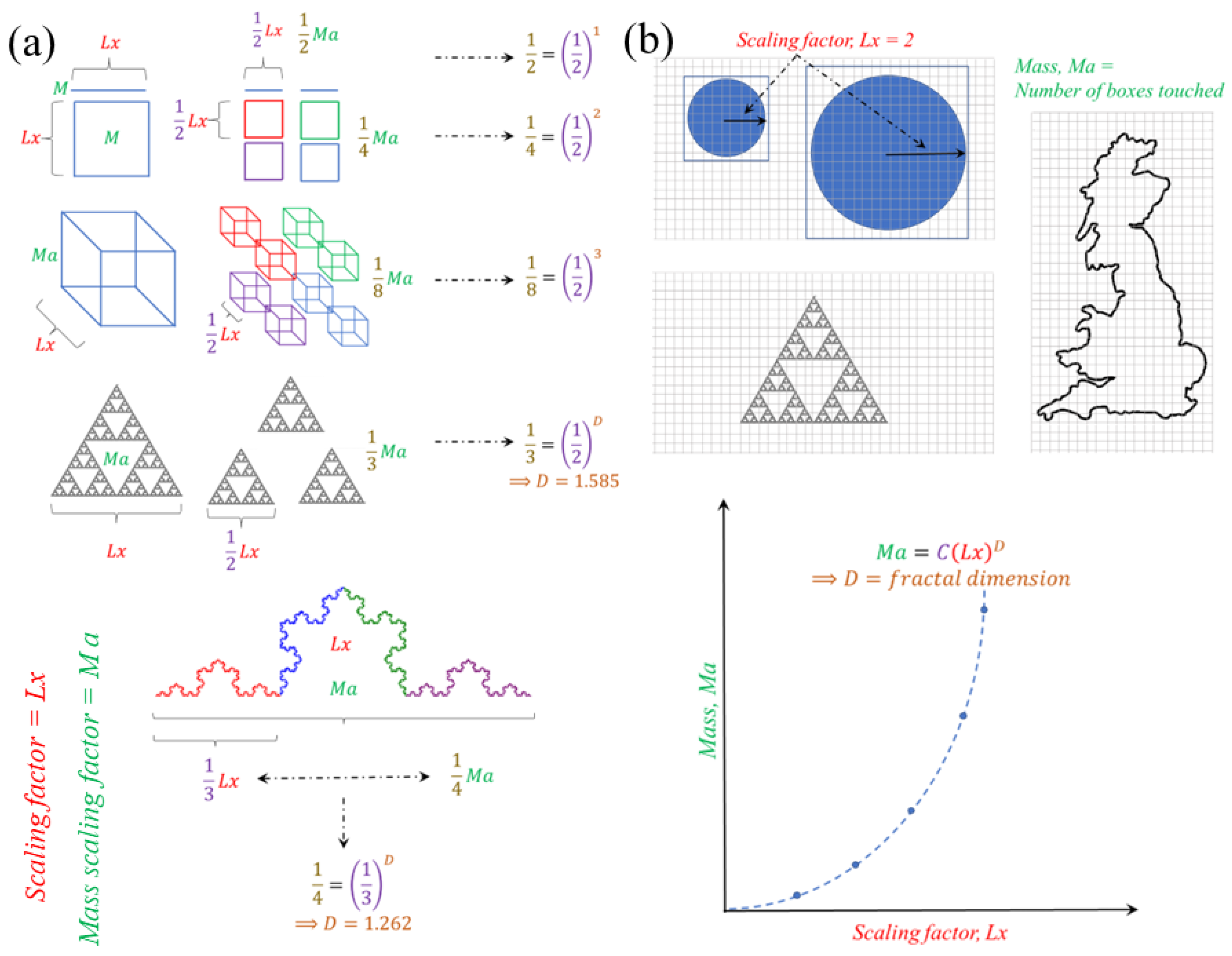
4.2. Roughness in the Form of Fractals
4.3. Power Spectral Density in the Frequency Domain
4.4. Colors of Noise and Hurst Exponent
4.5. Entropy: Approximate Entropy and Sample Entropy
5. Results and Discussion
6. Concluding Remarks
- We explain how the notion of power spectral density can be implemented to understand the behavior of pressure waves generated by the water hammer effect and how the strength of variation is related to the flow rate.
- We propose a method for calculating the fractal behavior of pressure wave time series induced by the water hammer effect. This method may be used to investigate acoustics and design pipe networks.
- We also describe how the concept of entropy can be used to calculate the complexity of a water hammer-induced pressure wave.
- We demonstrate that the response of discharge through the pipe is proportional to the complexity of the pressure wave generated by the water hammer effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sarker, S. Hydraulics Lab Manual. engrXiv 2021. [Google Scholar] [CrossRef]
- Sarker, S. A Short Review on Computational Hydraulics in the context of Water Resources Engineering. Open J. Model. Simul. 2022, 10, 1–31. [Google Scholar] [CrossRef]
- Sarker, S. Water Distribution (Pipe) Network Analysis with WaterCAD. Int. J. Eng. Dev. Res. IJEDR 2021, 9, 149–153. [Google Scholar]
- Guo, Q.; Zhou, J.; Li, Y.; Guan, X.; Liu, D.; Zhang, J. Fluid-structure interaction response of a water conveyance system with a surge chamber during water hammer. Water 2020, 12, 1025. [Google Scholar] [CrossRef] [Green Version]
- Cook, S.S. Erosion by water-hammer. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1928, 119, 481–488. [Google Scholar]
- Kandil, M.; Kamal, A.; El-Sayed, T. Effect of pipematerials on water hammer. Int. J. Press. Vessel. Pip. 2020, 179, 103996. [Google Scholar] [CrossRef]
- Azoury, P.; Baasiri, M.; Najm, H. Effect of valve-closure schedule on water hammer. J. Hydraul. Eng. 1986, 112, 890–903. [Google Scholar] [CrossRef]
- Leishear, R. Fluid Mechanics, Water Hammer, Dynamic Stresses, and Piping Design; ASME Press: New York, NY, USA, 2013. [Google Scholar] [CrossRef] [Green Version]
- Ranjbar, S.; Singh, A. Entropy and intermittency of river bed elevation fluctuations. J. Geophys. Res. Earth Surf. 2020, 125, e2019JF005499. [Google Scholar] [CrossRef]
- Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Critical nodes in river networks. Sci. Rep. 2019, 9, 11178. [Google Scholar] [CrossRef] [Green Version]
- Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Spectral Properties of River Networks. AGUFM 2019, 2019, EP51C–2107. [Google Scholar]
- Sarker, S. Investigating Topologic and Geometric Properties of Synthetic and Natural River Networks Under Changing Climatic. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2021. Available online: https://stars.library.ucf.edu/etd2020/965 (accessed on 20 December 2021).
- Sarker, S. Essence of MIKE 21C (FDM Numerical Scheme): Application on the River Morphology of Bangladesh. Open J. Model. Simul. 2022, 10, 88–117. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, B.K.; Lee, W.R.; Oh, K.Y. Analysis of water hammer in pipelines by partial fraction expansion of transfer function in frequency domain. J. Mech. Sci. Technol. 2010, 24, 1975–1980. [Google Scholar] [CrossRef]
- Reza, A.A.; Sarker, S.; Asha, S.A. An Application of 1-D Momentum Equation to Calculate Discharge in Tidal River: A Case Study on Kaliganga River. Tech. J. River Res. Inst. 2014, 2, 77–86. [Google Scholar]
- Sanderson, G. But what is the Fourier Transform? A visual introduction. 3Blue1Brown. 2018. Available online: https://www.youtube.com/watch?v=r6sGWTCMz2k (accessed on 12 April 2022).
- Rodriguez-Iturbe, I.; Rinaldo, A. Fractal River Basins: Chance and Self-Organization; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature/Revised and Enlarged Edition; Freeman and Co.: New York, NY, USA, 1983. [Google Scholar]
- Sanderson, G. Fractals are typically not self-similar. 3Blue1Brown. 2017. Available online: https://www.youtube.com/watch?v=gB9n2gHsHN4 (accessed on 12 April 2022).
- Bhatt, S.; Dedania, H.; Shah, V.R. Fractal dimensional analysis in financial time series. Int. J. Financ. Manag. 2015, 5, 57–62. [Google Scholar] [CrossRef]
- Han. Fractal Volatility of Financial Time Series; MATLAB Central File Exchange: Natick, MA, USA, 2022. [Google Scholar]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 13. [Google Scholar]
- Gardner, W.A.; Robinson, E.A. Statistical Spectral Analysis—A Nonprobabilistic Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Pilgram, B.; Kaplan, D.T. A comparison of estimators for 1f noise. Phys. D Nonlinear Phenom. 1998, 114, 108–122. [Google Scholar] [CrossRef]
- Norton, M.P.; Karczub, D.G. Fundamentals of Noise and Vibration Analysis for Engineers; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Krapf, D.; Lukat, N.; Marinari, E.; Metzler, R.; Oshanin, G.; Selhuber-Unkel, C.; Squarcini, A.; Stadler, L.; Weiss, M.; Xu, X. Spectral content of a single non-Brownian trajectory. Phys. Rev. X 2019, 9, 011019. [Google Scholar] [CrossRef] [Green Version]
- Krapf, D.; Marinari, E.; Metzler, R.; Oshanin, G.; Xu, X.; Squarcini, A. Power spectral density of a single Brownian trajectory: What one can and cannot learn from it. New J. Phys. 2018, 20, 023029. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Hudson, R.L. The (Mis)behavior of Markets: A Fractal View of Risk, Ruin, and Reward; Basic Books: New York, NY, USA, 2005. [Google Scholar]
- Mandelbrot, B.B. Self-affine fractals and fractal dimension. Phys. Scr. 1985, 32, 257. [Google Scholar] [CrossRef]
- Gneiting, T.; Schlather, M. Stochastic models that separate fractal dimension and the Hurst effect. SIAM Rev. 2004, 46, 269–282. [Google Scholar] [CrossRef] [Green Version]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pincus, S.; Kalman, R.E. Irregularity, volatility, risk, and financial market time series. Proc. Natl. Acad. Sci. USA 2004, 101, 13709–13714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarker, S.; Sarker, T.; Raihan, S.U. Comprehensive Understanding of the Planform Complexity of the Anastomosing River and the Dynamic Imprint of the River’s Flow: Brahmaputra River in Bangladesh. Preprints 2022. [Google Scholar] [CrossRef]
- Delgado-Bonal, A.; Marshak, A.; Yang, Y.; Holdaway, D. Analyzing changes in the complexity of climate in the last four decades using MERRA-2 radiation data. Sci. Rep. 2020, 10, 922. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 6. [Google Scholar] [CrossRef] [Green Version]
- Sarker, S. Understanding the Complexity and Dynamics of Anastomosing River Planform: A Case Study of Brahmaputra River in Bangladesh. In Proceedings of the AGU 2021 Fall Meeting, New Orleans, LA, USA, 28 November 2021. [Google Scholar] [CrossRef]
- Hillhouse, G. What is Water Hammer? Practical Engineering. 2017. Available online: https://practical.engineering/blog/2018/7/24/what-is-a-water-hammer (accessed on 12 April 2022).





| Q = V/t m/s | Static Bar | Time (t) sec | |||||
|---|---|---|---|---|---|---|---|
| D | |||||||
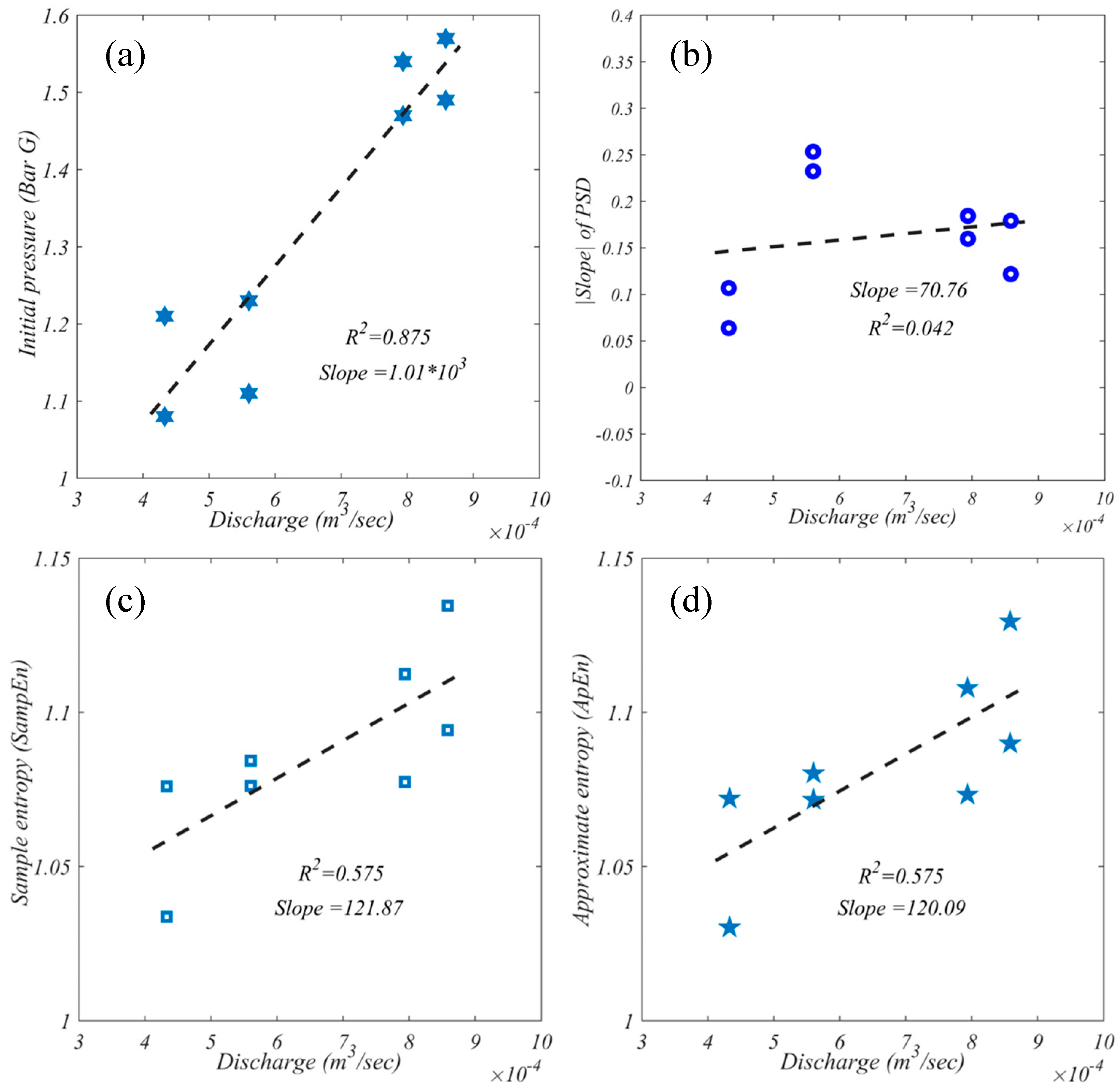
| 0.000433 | 1.21 | −0.1068 | 1.076 | 1.072 | 1.8688 | 0.1312 | 46.2 |
| 0.000858 | 1.57 | −0.1791 | 1.1346 | 1.1295 | 1.8807 | 0.1193 | 23.3 |
| 0.000794 | 1.54 | −0.1844 | 1.1125 | 1.1079 | 1.8710 | 0.1290 | 25.2 |
| 0.00056 | 1.23 | −0.2534 | 1.0843 | 1.0802 | 1.8522 | 0.1478 | 35.7 |
| Q = V/t m/s | Static Bar | Time (t) sec | |||||
| D | |||||||
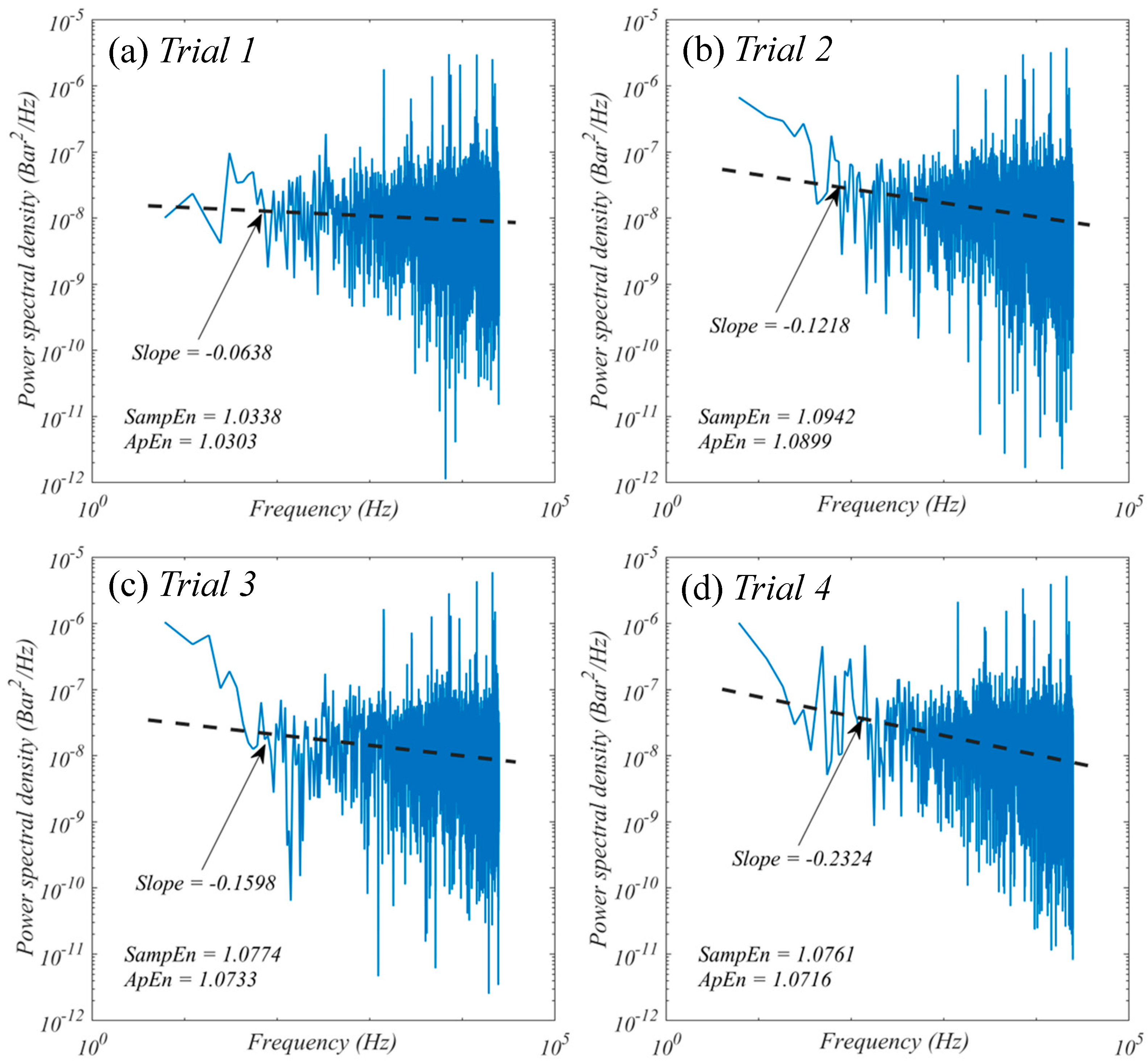
| 0.000433 | 1.08 | −0.0638 | 1.0338 | 1.0303 | 1.855 | 0.1450 | 46.2 |
| 0.000858 | 1.49 | −0.1218 | 1.0942 | 1.0899 | 1.8562 | 0.1438 | 23.3 |
| 0.000794 | 1.47 | −0.1598 | 1.0774 | 1.0733 | 1.8471 | 0.1529 | 25.2 |
| 0.00056 | 1.11 | −0.2324 | 1.0761 | 1.0716 | 1.830 | 0.1700 | 35.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarker, S.; Sarker, T. Spectral Properties of Water Hammer Wave. Appl. Mech. 2022, 3, 799-814. https://doi.org/10.3390/applmech3030047
Sarker S, Sarker T. Spectral Properties of Water Hammer Wave. Applied Mechanics. 2022; 3(3):799-814. https://doi.org/10.3390/applmech3030047
Chicago/Turabian StyleSarker, Shiblu, and Tonmoy Sarker. 2022. "Spectral Properties of Water Hammer Wave" Applied Mechanics 3, no. 3: 799-814. https://doi.org/10.3390/applmech3030047





