Surface Topological Plexcitons: Strong Coupling in a Bi2Se3 Topological Insulator Nanoparticle-Quantum Dot Molecule
Abstract
:1. Introduction
2. Topological Insulator Nanoparticle Subjected to Light
2.1. Permittivity Model
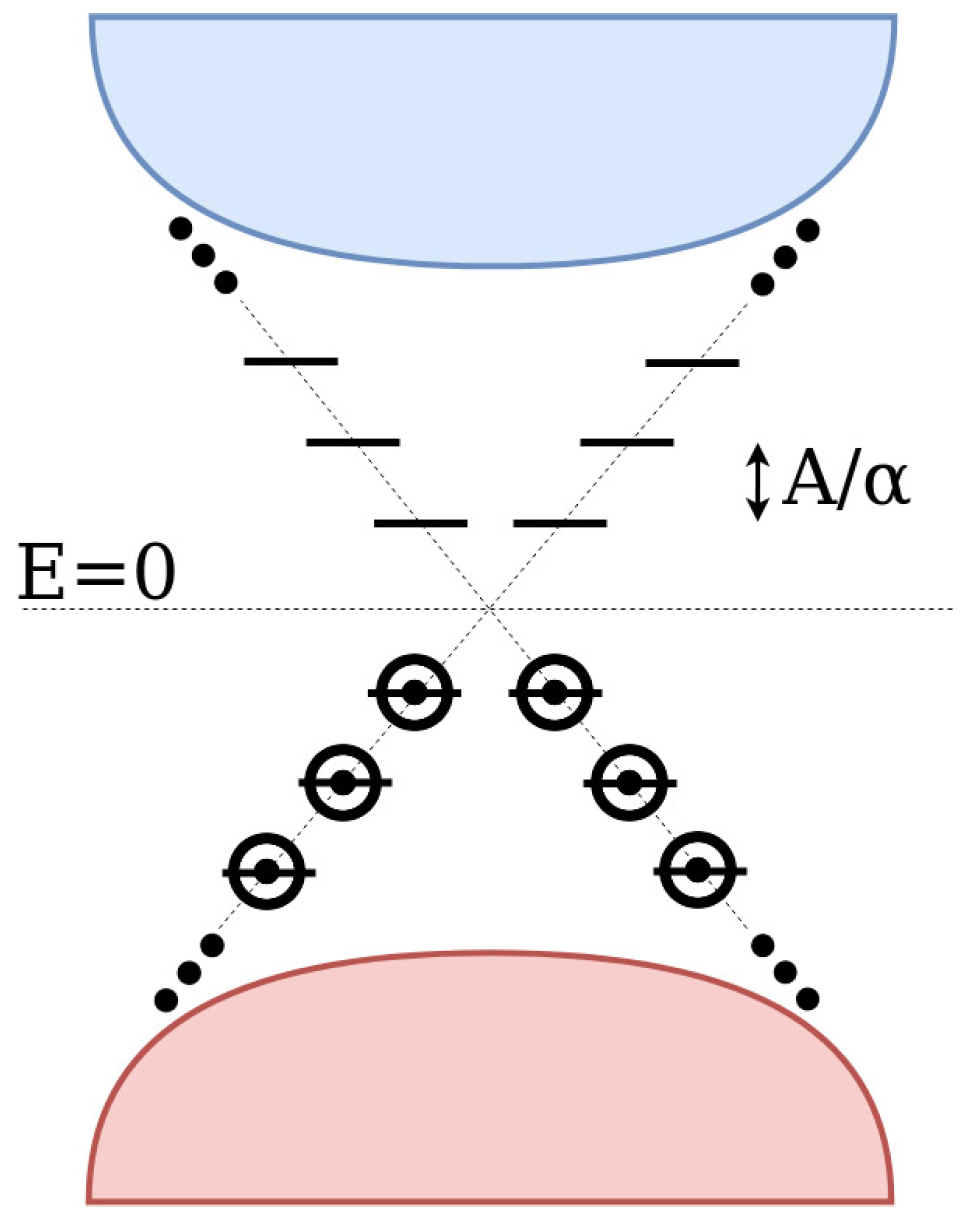
2.2. The SToP Mode
3. Interacting TINP-QE
3.1. The Model
3.2. Dipole Approximation
3.3. Interaction Picture and Rotating Wave Approximation
3.4. Time Evolution of the QE States
3.5. Absorption of the System
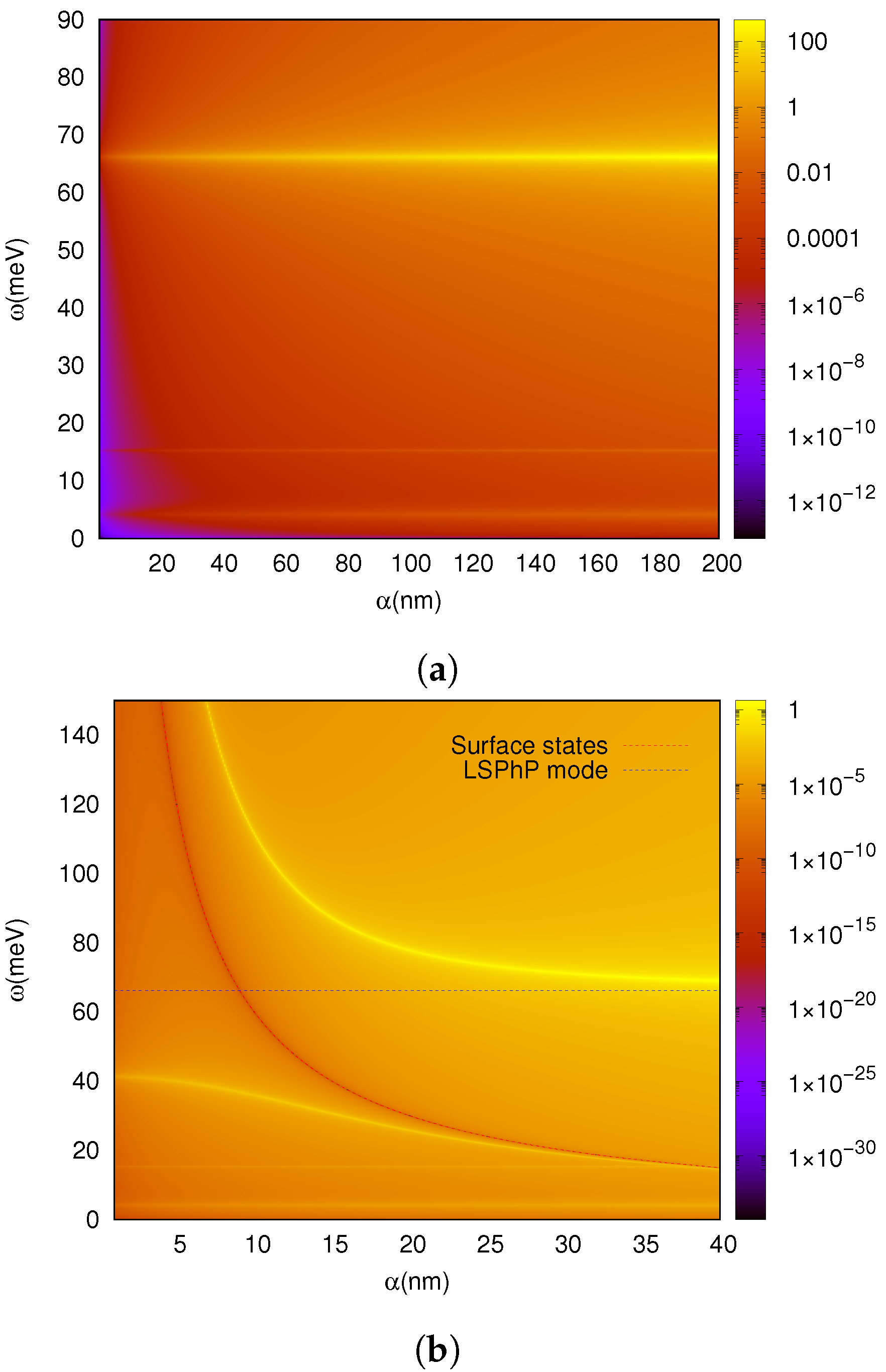
4. Numerical Results and Discussion
4.1. Problem Parameters
4.2. Method of Study
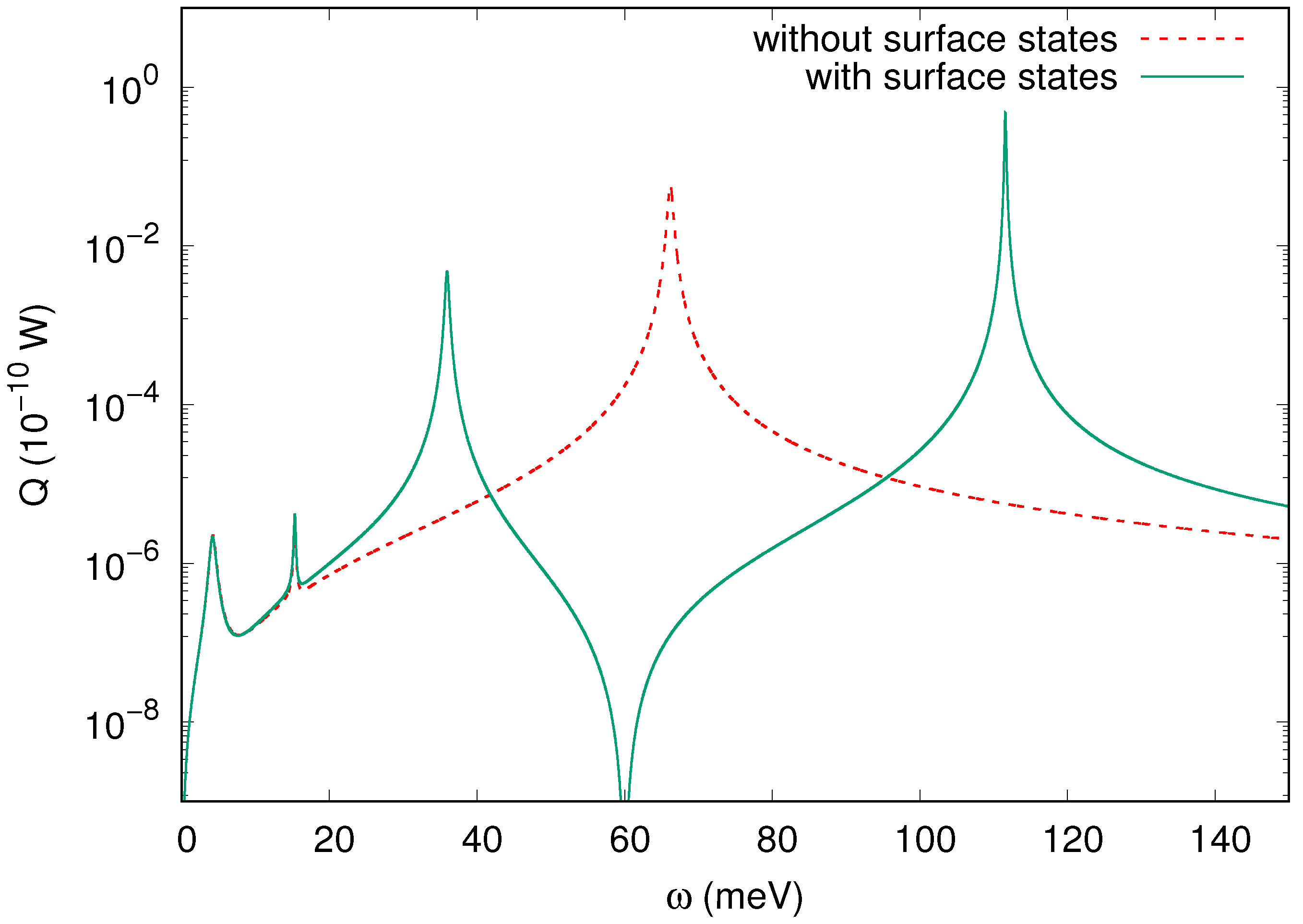
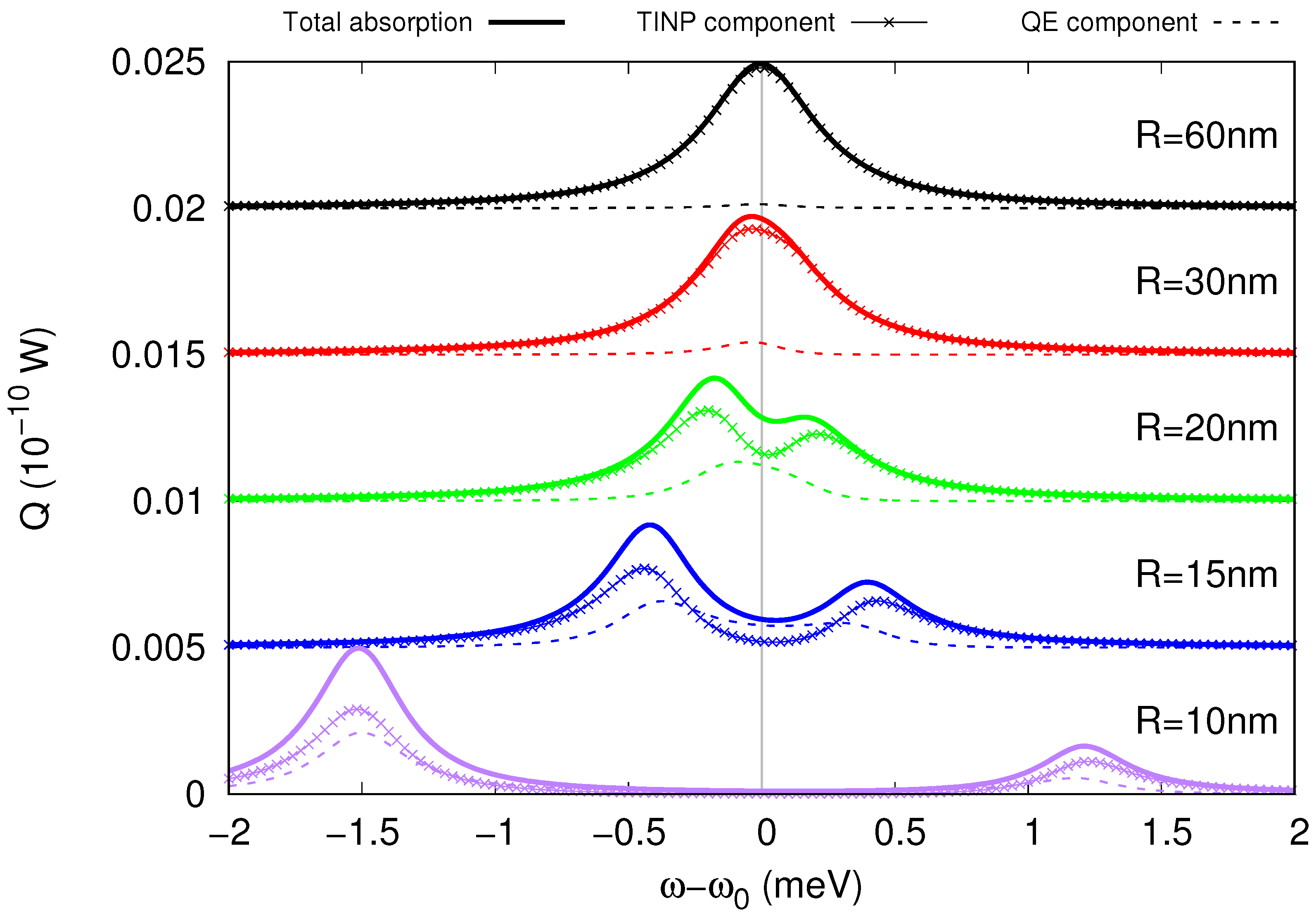
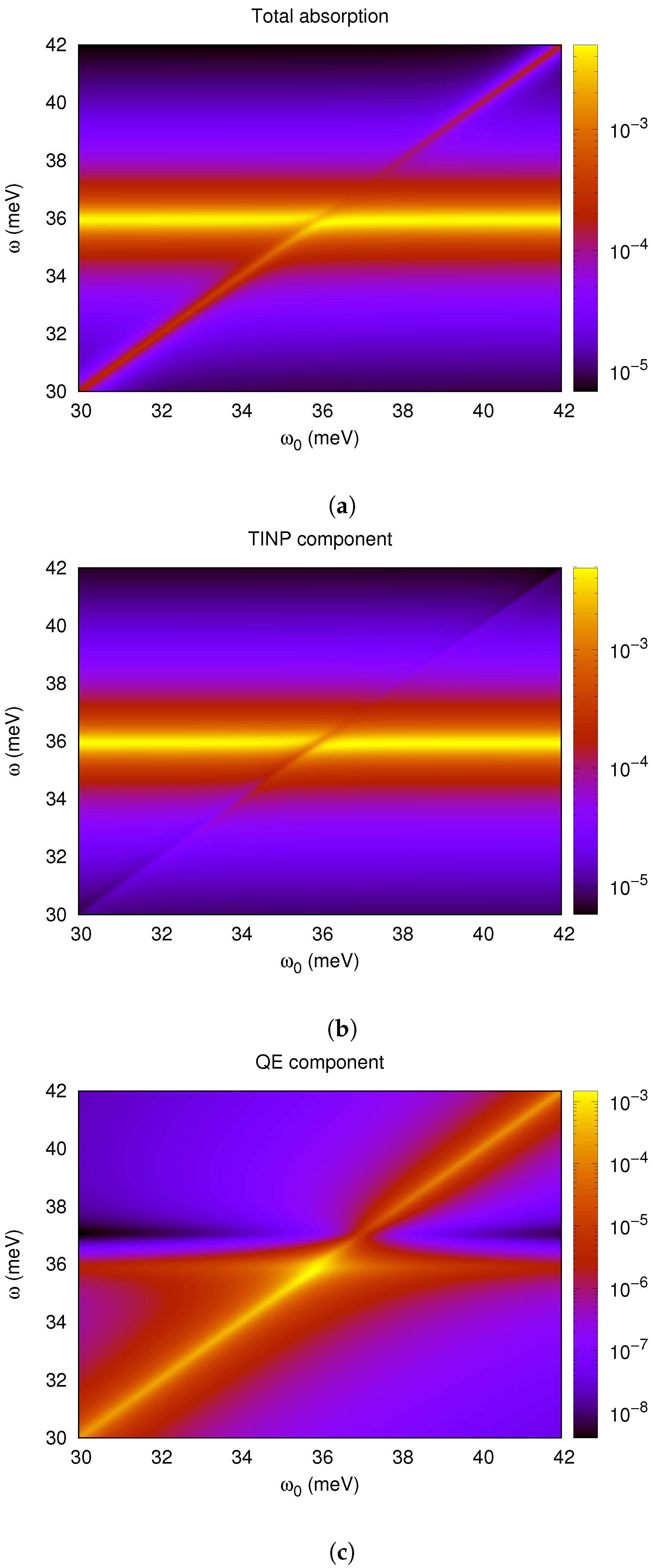
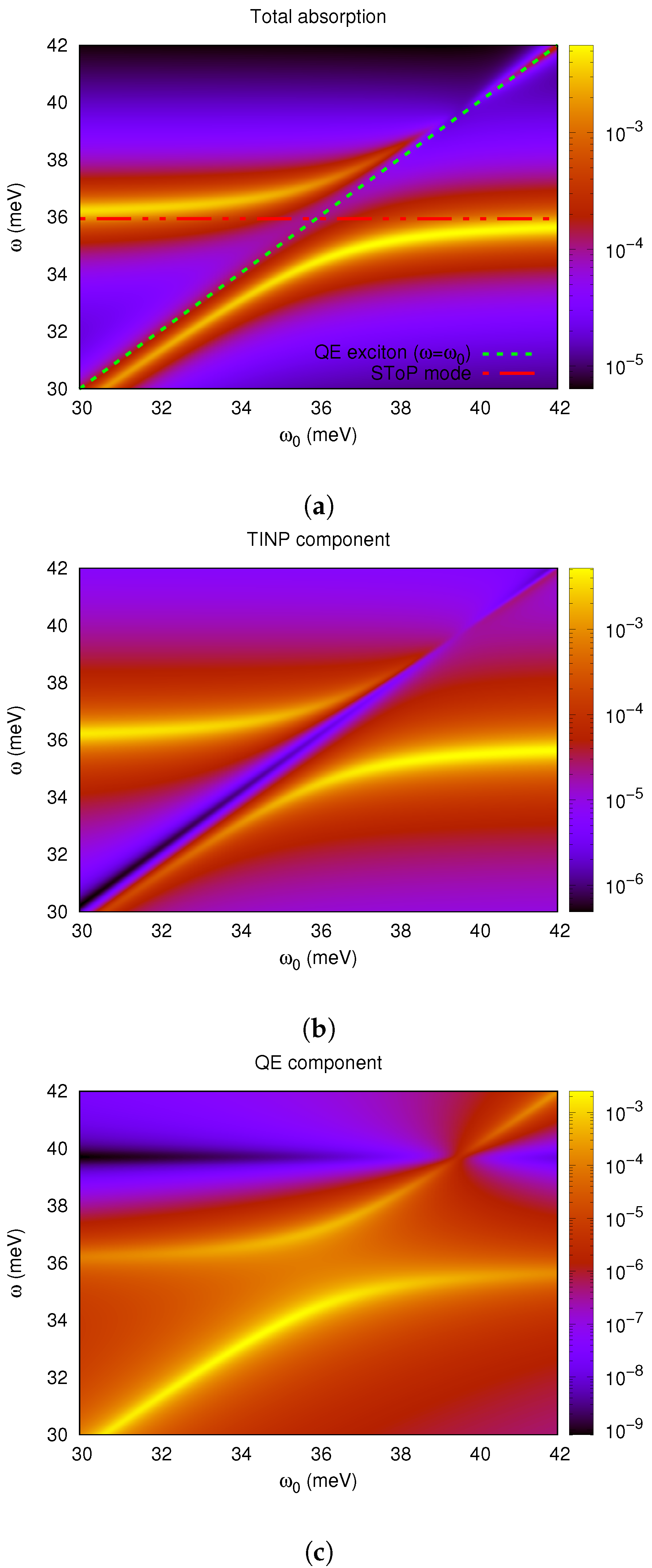
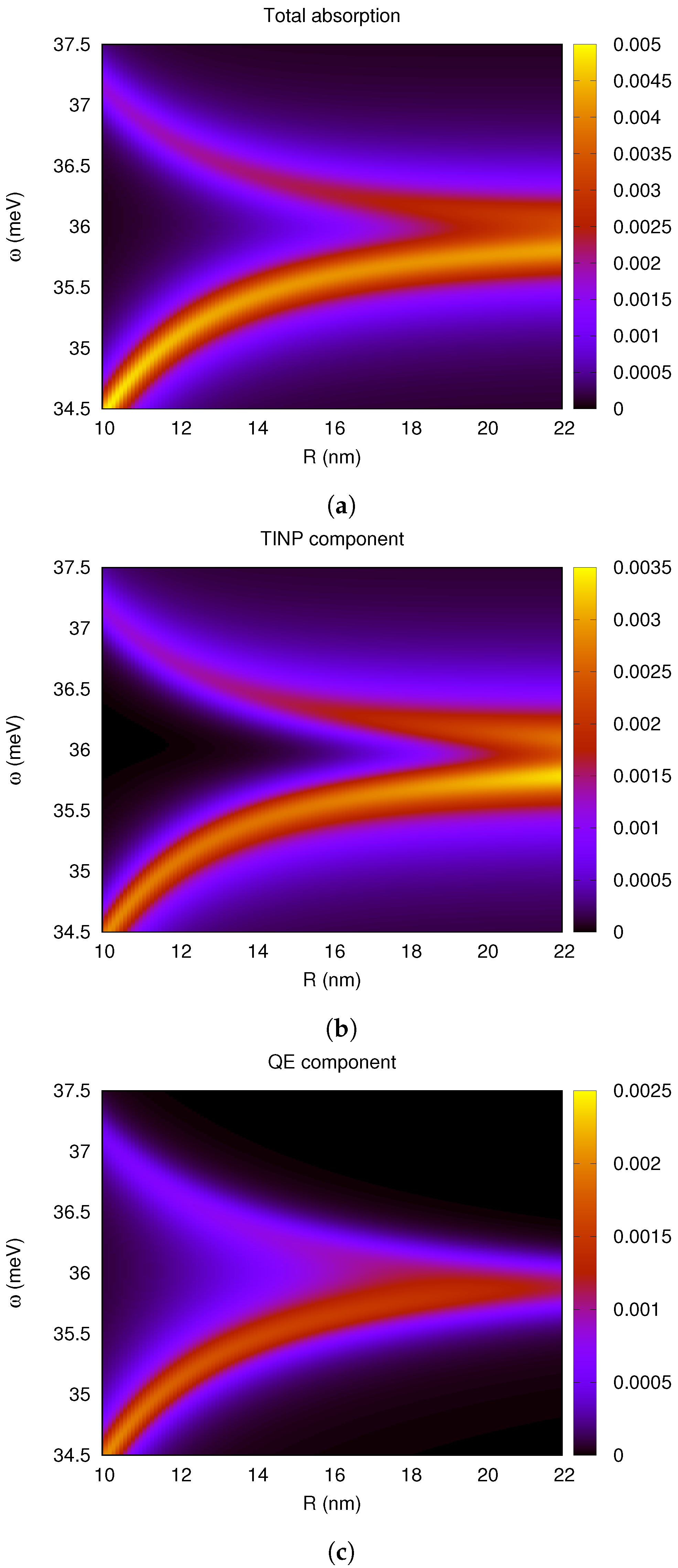
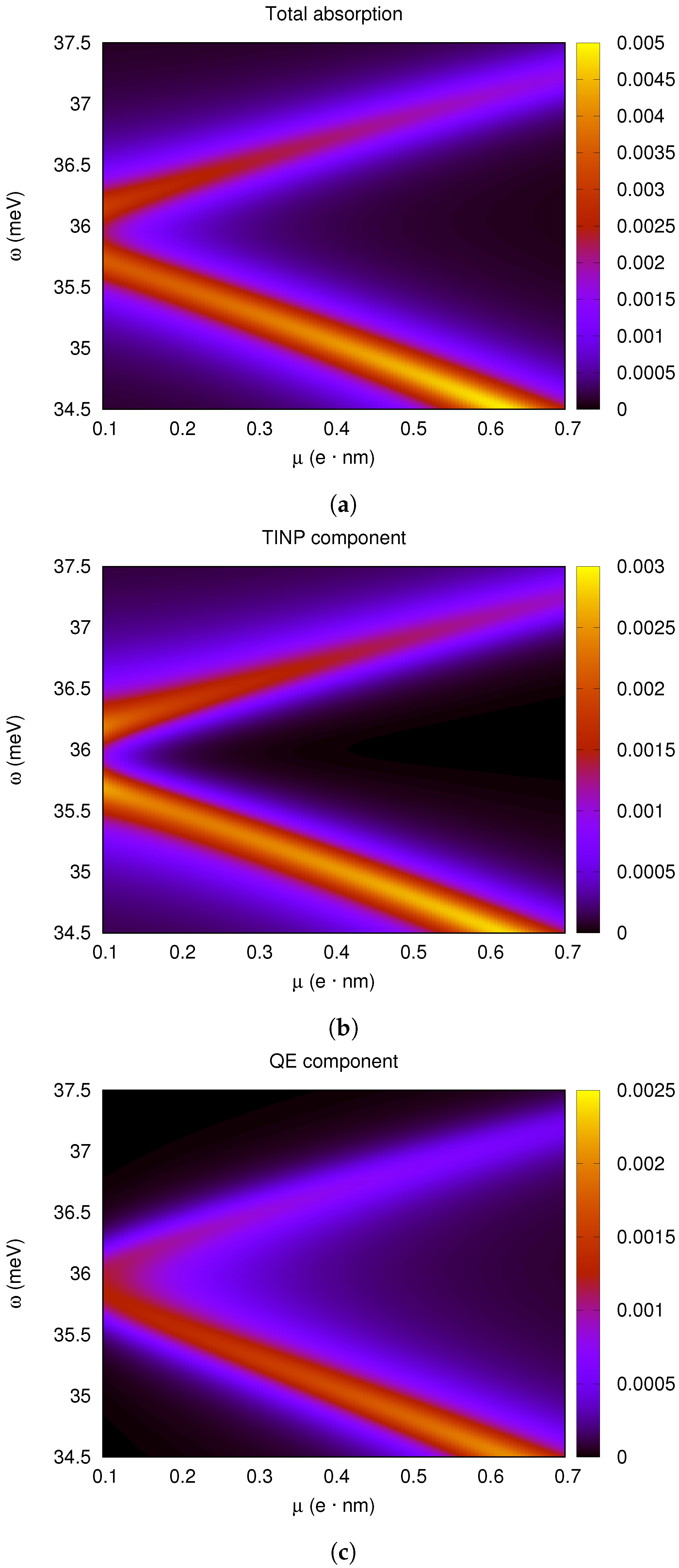
4.3. Strong Coupling between the SToP Mode and the Exciton
4.4. Outlook
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dovzhenko, D.S.; Ryabchuk, S.V.; Rakovich, Y.P.; Nabiev, I.R. Light–matter interaction in the strong coupling regime: Configurations, conditions and applications. Nanoscale 2018, 10, 3589–3605. [Google Scholar] [CrossRef]
- Yu, X.; Yuan, Y.; Xu, J.; Yong, K.; Qu, J.; Song, J. Strong Coupling in Microcavity Structures: Principle, Design, and Practical Application. Laser Photonics Rev. 2019, 13, 1800219. [Google Scholar] [CrossRef]
- Rice, P.R.; Carmichael, H.J. Photon statistics of a cavity-QED laser: A comment on the laser–phase-transition analogy. Phys. Rev. A 1994, 50, 4318–4329. [Google Scholar] [CrossRef]
- Hertzog, M.; Wang, M.; Mony, J.; Börjesson, K. Strong light–matter interactions: A new direction within chemistry. Chem. Soc. Rev. 2019, 48, 937–961. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Yu, H.; Peng, Y.; Yang, Y.; Li, Z.Y. Plasmon-enhanced light–matter interactions and applications. NPJ Comput. Mater. 2019, 5, 45. [Google Scholar] [CrossRef]
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kling, M.F. Roadmap on plasmonics. IOP J. Opt. 2018, 20, 043001. [Google Scholar] [CrossRef]
- Atwater, H.A. The Promise of Plasmonics. Sci. Am. Spec. Ed. 2007, 17, 56–63. [Google Scholar] [CrossRef]
- Verma, S.S. Plasmonics in Nanomedicine: A Review. Glob. J. Nanomed. 2018, 4, 2573–2574. [Google Scholar] [CrossRef]
- Tame, M.S.; McEnery, K.R.; Özdemir, S.K.; Lee, J.; Maier, S.A.; Kim, M.S. Quantum Plasmonics. Nat. Phys. 2013, 9, 329–340. [Google Scholar] [CrossRef]
- Törmä, P.; Barnes, W.L. Strong Coupling between surface plasmon polaritons and emitters: A review. Rep. Prog. Phys. 2015, 78, 013901. [Google Scholar] [CrossRef]
- Bellessa, J.; Bonnand, C.; Plenet, J.C.; Mugnier, J. Strong Coupling between Surface Plasmons and Excitons in an Organic Semiconductor. Phys. Rev. Lett. 2004, 93, 036404. [Google Scholar] [CrossRef]
- Dintinger, J.; Klein, S.; Bustos, F.; Barnes, W.L.; Ebbesen, T.W. Strong coupling between surface plasmon-polaritons and organic molecules in subwavelength hole arrays. Phys. Rev. B 2005, 71, 035424. [Google Scholar] [CrossRef]
- Dintinger, J.; Klein, S.; Ebbesen, T.W. Molecule–Surface Plasmon Interactions in Hole Arrays: Enhanced Absorption, Refractive Index Changes, and All-Optical Switching. Adv. Mater. 2006, 18, 1267–1270. [Google Scholar] [CrossRef]
- Sugawara, Y.; Kelf, T.A.; Baumberg, J.J.; Abdelsalam, M.E.; Bartlett, P.N. Strong Coupling between Localized Plasmons and Organic Excitons in Metal Nanovoids. Phys. Rev. Lett. 2006, 97, 266808. [Google Scholar] [CrossRef]
- Wurtz, G.A.; Evans, P.R.; Hendren, W.; Atkinson, R.; Dickson, W.; Pollard, R.J.; Zayats, A.V.; Harrison, W.; Bower, C. Molecular Plasmonics with Tunable Exciton–Plasmon Coupling Strength in J-Aggregate Hybridized Au Nanorod Assemblies. Nano Lett. 2007, 7, 1297–1303. [Google Scholar] [CrossRef]
- Chovan, J.; Perakis, I.E.; Ceccarelli, S.; Lidzey, D.G. Controlling the interactions between polaritons and molecular vibrations in strongly coupled organic semiconductor microcavities. Phys. Rev. B 2008, 78, 045320. [Google Scholar] [CrossRef]
- Fofang, N.T.; Park, T.H.; Neumann, O.; Mirin, N.A.; Norlander, P.; Halas, N.J. Plexcitonic Nanoparticles: Plasmon-Exciton Coupling in Nanoshell-J-Aggregate Complexes. Nano Lett. 2008, 8, 3481–3487. [Google Scholar] [CrossRef]
- Bellessa, J.; Symonds, C.; Vynck, K.; Lemaitre, A.; Brioude, A.; Beaur, L.; Valvin, P. Giant Rabi splitting between localized mixed plasmon-exciton states in a two-dimensional array of nanosize metallic disks in an organic semiconductor. Phys. Rev. B 2009, 80, 033303. [Google Scholar] [CrossRef]
- Schlather, A.E.; Large, N.; Urban, A.S.; Nordlander, P.; Halas, N.J. Near-Field Mediated Plexcitonic Coupling and Giant Rabi Splitting in Individual Metallic Dimers. Nano Lett. 2013, 13, 3281–3286. [Google Scholar] [CrossRef] [PubMed]
- Pockrand, I.; Swalen, J.D.; Santo, R.; Brillante, A.; Philpott, M.R. Optical properties of organic dye monolayers by surface plasmon spectroscopy. J. Chem. Phys. 1978, 69, 4001–4011. [Google Scholar] [CrossRef]
- Hakala, T.K.; Toppari, J.J.; Kuzyk, A.; Pettersson, M.; Tikkanen, H.; Kunttu, H.; Törmä, P. Vacuum Rabi Splitting and Strong-Coupling Dynamics for Surface-Plasmon Polaritons and Rhodamine 6G Molecules. Phys. Rev. Lett. 2009, 103, 053602. [Google Scholar] [CrossRef]
- Väkeväinen, A.I.; Moerland, R.J.; Rekola, H.T.; Eskelinen, A.P.; Martikainen, J.P.; Kim, D.H.; Törmä, P. Plasmonic Surface Lattice Resonances at the Strong Coupling Regime. Nano Lett. 2014, 14, 1721–1727. [Google Scholar] [CrossRef]
- Gomez, D.E.; Vernon, K.C.; Mulvaney, P.; Davis, T.J. Surface Plasmon Mediated Strong Exciton–Photon Coupling in Semiconductor Nanocrystals. Nano Lett. 2010, 10, 274–278. [Google Scholar] [CrossRef]
- Gomez, D.E.; Vernon, K.C.; Mulvaney, P.; Davis, T.J. Coherent superposition of exciton states in quantum dots induced by surface plasmons. Appl. Phys. Lett. 2010, 96, 073108. [Google Scholar] [CrossRef]
- Manuel, A.P.; Kirkey, A.; Mahdia, N.; Shankar, K. Plexcitonics–fundamental principles and optoelectronic applications. J. Mater. Chem. C 2019, 7, 1821–1853. [Google Scholar] [CrossRef]
- Yuen-Zhou, J.; Saikin, S.K.; Zhu, T.; Onbasli, M.C.; Ross, C.A.; Bulovic, V.; Baldo, M.A. Plexciton Dirac points and topological modes. Nat. Commun. 2016, 7, 11783. [Google Scholar] [CrossRef] [PubMed]
- Politano, A.; Viti, L.; Vitiello, M.S. Optoelectronic devices, plasmonics and photonics with topological insulators. APL Mater. 2017, 5, 035504. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Topological Insulators. Rev. Mod. Phys 2010, 82, 3045. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L. Topological Insulators and Topological Superconductors; Princeton University Press: Princeton, NI, USA, 2013. [Google Scholar]
- Moore, J.E. The Birth of Topological Insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef]
- Qi, X.; Zhang, S. Topological Insulators and Superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photon. Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Jongbum, K.; Gururaj, N.; Naresh, E.; Urcan, G.; Alexandra, B. Plasmonic Resonances in Nanostructured Transparent Conducting Oxide Films. Sel. Top. Quantum Electron. IEEE J. 2013, 19, 4601907. [Google Scholar] [CrossRef]
- Naik, G.V.; Schroeder, J.L.; Ni, X.; Kildishev, A.V.; Sands, T.D.; Boltasseva, A. Titanium nitride as a plasmonic material for visible and near-infrared wavelengths. Opt. Mater. Express 2012, 2, 478–479. [Google Scholar] [CrossRef]
- Luo, X.; Qiu, T.; Lu, W.; Ni, Z. Plasmons in graphene: Recent progress and applications. Mater. Sci. Eng. R Rep. 2013, 74, 351–376. [Google Scholar] [CrossRef]
- Karch, A. Surface Plasmons and Topological Insulators. Phys. Rev. B Condens. Matter 2011, 83, 245432. [Google Scholar] [CrossRef]
- Stauber, T.; Gómez-Santos, O.G.; Brey, L. Plasmonics in topological insulators: Spin-charge separation, the influence of the inversion layer, and phonon-plasmon coupling. ACS Photonics 2017, 4, 2978–2988. [Google Scholar] [CrossRef]
- Pietro, P.D.; Ortolani, M.; Limaj, O.; Gaspare, A.D.; Giliberti, V.; Giorgianni, F.; Brahlek, M.; Bansal, N.; Koirala, N.; Oh, S.; et al. Observation of Dirac plasmons in a topological insulator. Nat. Nanotechnol. 2013, 8, 556–560. [Google Scholar] [CrossRef]
- Jiang, Z.; Rösner, M.; Groenewald, R.E.; Haas, S. Localized Plasmons in Topological Insulators. arXiv 2019, arXiv:1907.12432v2. [Google Scholar] [CrossRef]
- Siroki, G.; Lee, D.K.K.; Haynes, P.D.; Giannini, V. Single-electron induced surface plasmons on a topological nanoparticle. Nat. Commun. 2016, 7, 12375. [Google Scholar] [CrossRef]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Phys. Rev. Lett. 2009, 5, 398–402. [Google Scholar] [CrossRef]
- Gleb, S.; Haynes, P.D.; Lee, D.K.; Vincenzo, G. Protection of surface states in topological nanoparticles. Phys. Rev. Mat. 2017, 1, 024201. [Google Scholar] [CrossRef]
- Imura, K.; Yoshimura, Y.; Takane, Y.; Fukui, T. Spherical topological insulator. Phys. Rev. B 2012, 86, 235119. [Google Scholar] [CrossRef]
- Liu, C.; Qi, X.; Zhang, H.; Dai, X.; Fang, Z.; Zhang, S. Model Hamiltonian for topological insulators. Phys. Rev. B 2010, 82, 045122. [Google Scholar] [CrossRef]
- Artuso, R.D.; Bryant, G.W. Strongly coupled quantum dot-metal nanoparticle systems: Exciton-induced transparency, discontinuous response, and suppression as driven quantum oscillator effects. Phys. Rev. B 2010, 82, 195419. [Google Scholar] [CrossRef]
- Karplus, R.; Schwinger, J. A Note on Saturation in Microwave Spectroscopy. Phys. Rev. 1948, 73, 1020. [Google Scholar] [CrossRef]
- Yariv, A. Quantum Electronics, Appendix 4: Quantum Mechanical Derivation of Nonlinear Optical Constants; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles, Chapter 5: Particles Small Compared with the Wavelength, Section 5.2: The Electrostatics Approximation; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Zhang, W.; Govorov, A.O.; Bryant, G.W. Semiconductor-Metal Nanoparticle Molecules: Hybrid Excitons and the Nonlinear Fano Effect. Phys. Rev. Lett. 2006, 97, 146804. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.Y.; Zhang, W.; Duan, S.Q.; Zhao, X.G.; Govorov, A.O. Optical properties of coupled metal-semiconductor and metal-molecule nanocrystal complexes: Role of multipole effects. Phys. Rev. B 2008, 77, 165301. [Google Scholar] [CrossRef]
- Artuso, R.D.; Bryant, G.W. Optical Response of Strongly Coupled Quantum Dot-Metal Nanoparticle Systems: Double Peaked Fano Structure and Bistability. Nano Lett. 2008, 8, 2106–2111. [Google Scholar] [CrossRef]
- Paspalakis, E.; Evangelou, S.; Terzis, A.F. Control of excitonic population inversion in a coupled semiconductor quantum dot–metal nanoparticle system. Phys. Rev. B 2013, 87, 235302. [Google Scholar] [CrossRef]
- Yang, W.; Chen, A.; Huang, Z.; Lee, R. Ultrafast optical switching in quantum dot-metallic nanoparticle hybrid systems. Opt. Express 2015, 23, 13032–13040. [Google Scholar] [CrossRef]
- Zibik, E.A.; Grange, T.; Carpenter, B.A.; Porter, N.E.; Ferreira, R.; Bastard, G.; Stehr, D.; Winnerl, S.; Helm, M.; Liu, H.Y.; et al. Long lifetimes of quantum-dot intersublevel transitions in the terahertz range. Nat. Mater. Lett. 2009, 8, 803–807. [Google Scholar] [CrossRef]
- Moroz, A. A hidden analytic structure of the Rabi model. Ann. Phys. 2014, 340, 252–266. [Google Scholar] [CrossRef]
- Kockum, A.F.; Miranowicz, A.; Liberato, S.D.; Savasta, S.; Nori, F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19–40. [Google Scholar] [CrossRef]
- Rider, M.S.; Sokolikova, M.; Hanham, S.M.; Navarro-Cia, M.; Haynes, P.D.; Lee, D.K.K.; Daniele, M.; Guidi, M.C.; Mattevi, C.; Lupi, S.; et al. Experimental signature of a topological quantum dot. Nanoscale 2020, 12, 22817–22825. [Google Scholar] [CrossRef]
- Bergman, D.J.; Stockman, I.M. Surface Plasmon Amplification by Stimulated Emission of Radiation: Quantum Generation of Coherent Surface Plasmons in Nanosystems. Phys. Rev. Lett. 2003, 90, 027402. [Google Scholar] [CrossRef]
- Denning, E.V.; Iles-Smith, J.; Gregersen, N.; Mork, J. Phonon effects in quantum dot single-photon sources. Opt. Mater. Express 2020, 10, 222–239. [Google Scholar] [CrossRef]
- Denning, E.V.; Iles-Smith, J.; Mork, J. Quantum light-matter interaction and controlled phonon scattering in a photonic Fano cavity. Phys. Rev. B 2019, 100, 214306. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kountouris, G.; Yannopapas, V. Surface Topological Plexcitons: Strong Coupling in a Bi2Se3 Topological Insulator Nanoparticle-Quantum Dot Molecule. Optics 2024, 5, 101-120. https://doi.org/10.3390/opt5010008
Kountouris G, Yannopapas V. Surface Topological Plexcitons: Strong Coupling in a Bi2Se3 Topological Insulator Nanoparticle-Quantum Dot Molecule. Optics. 2024; 5(1):101-120. https://doi.org/10.3390/opt5010008
Chicago/Turabian StyleKountouris, George, and Vassilios Yannopapas. 2024. "Surface Topological Plexcitons: Strong Coupling in a Bi2Se3 Topological Insulator Nanoparticle-Quantum Dot Molecule" Optics 5, no. 1: 101-120. https://doi.org/10.3390/opt5010008
APA StyleKountouris, G., & Yannopapas, V. (2024). Surface Topological Plexcitons: Strong Coupling in a Bi2Se3 Topological Insulator Nanoparticle-Quantum Dot Molecule. Optics, 5(1), 101-120. https://doi.org/10.3390/opt5010008






