The Static and Dynamic Behavior of Steel Storage Tanks over Different Types of Clay Soil
Abstract
:1. Introduction
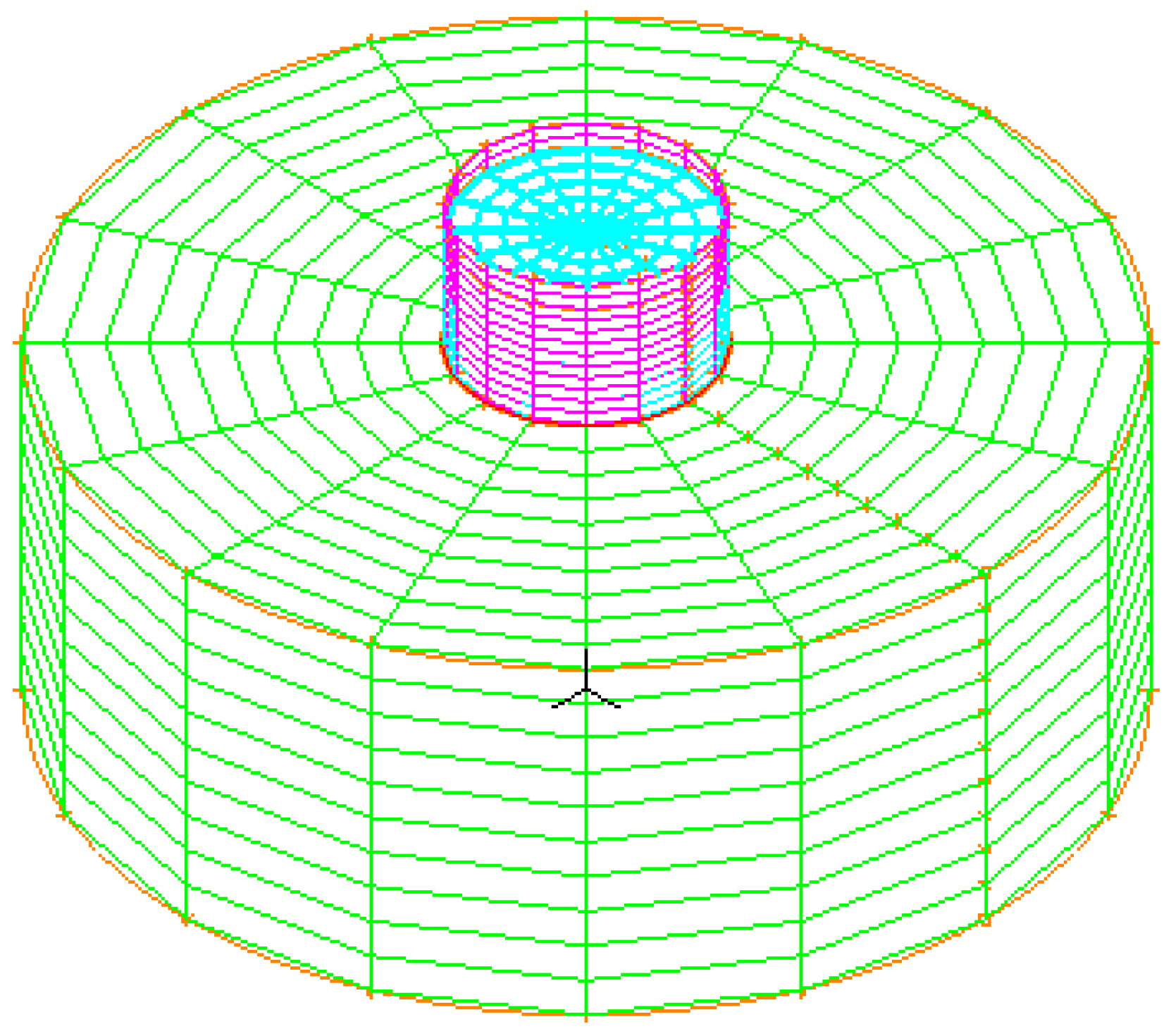
2. FE Modeling
2.1. Elements
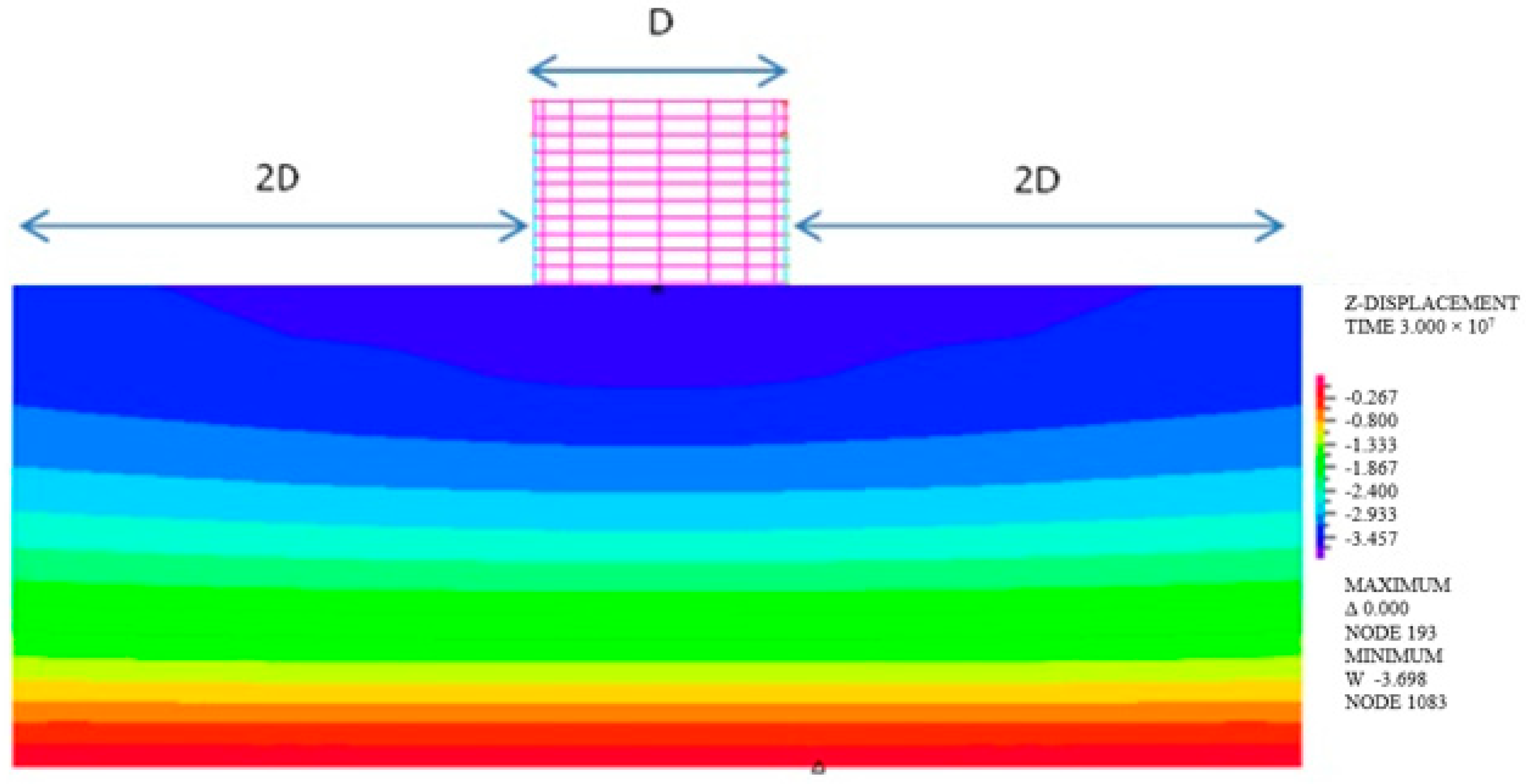
2.2. Boundary Conditions
2.3. Materials
2.4. Procedures of the FE Analysis
2.5. Details of the Studied Tanks
3. Results of the Static Analysis
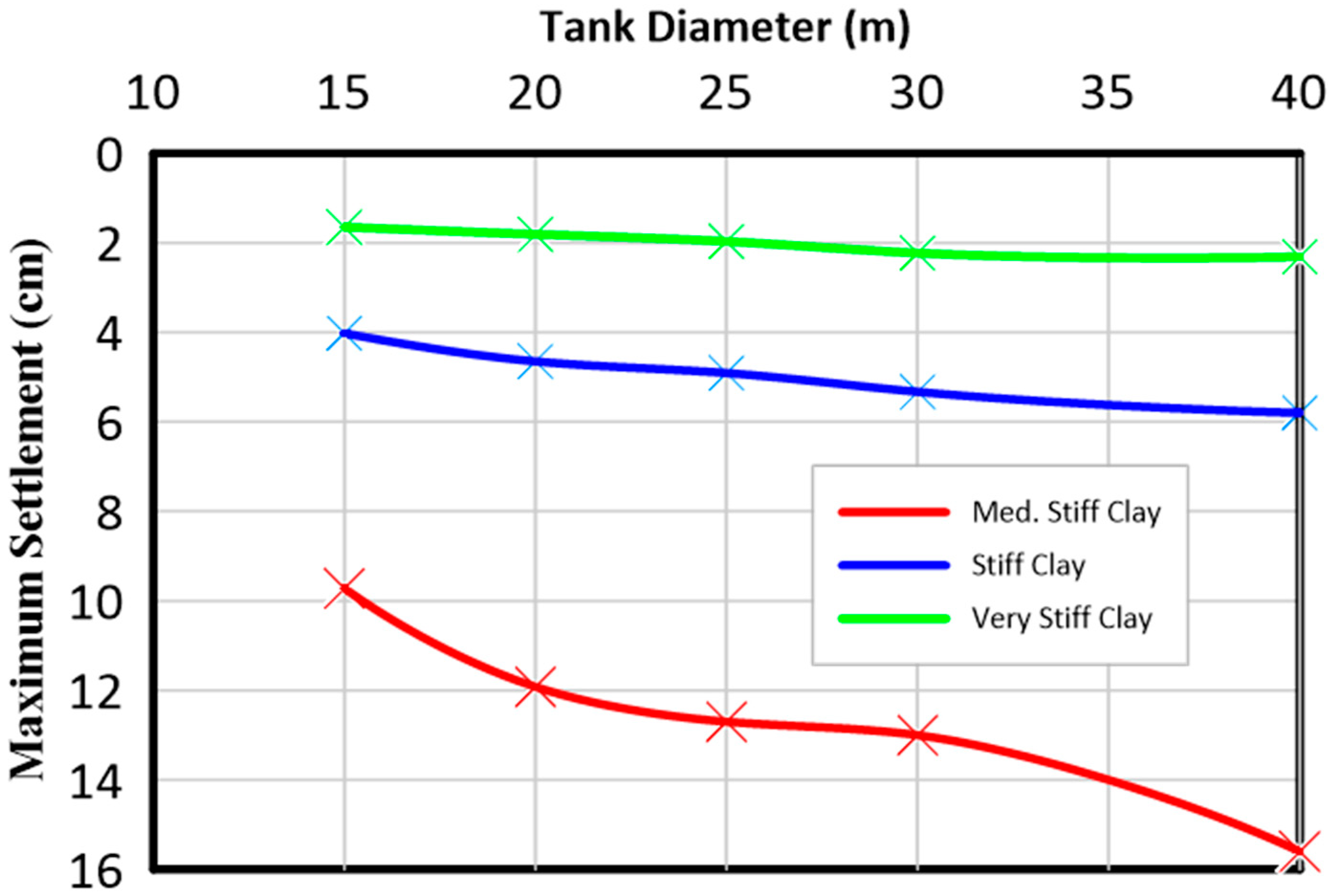
3.1. The Consolidation Settlement under the Base Plate of the Tank
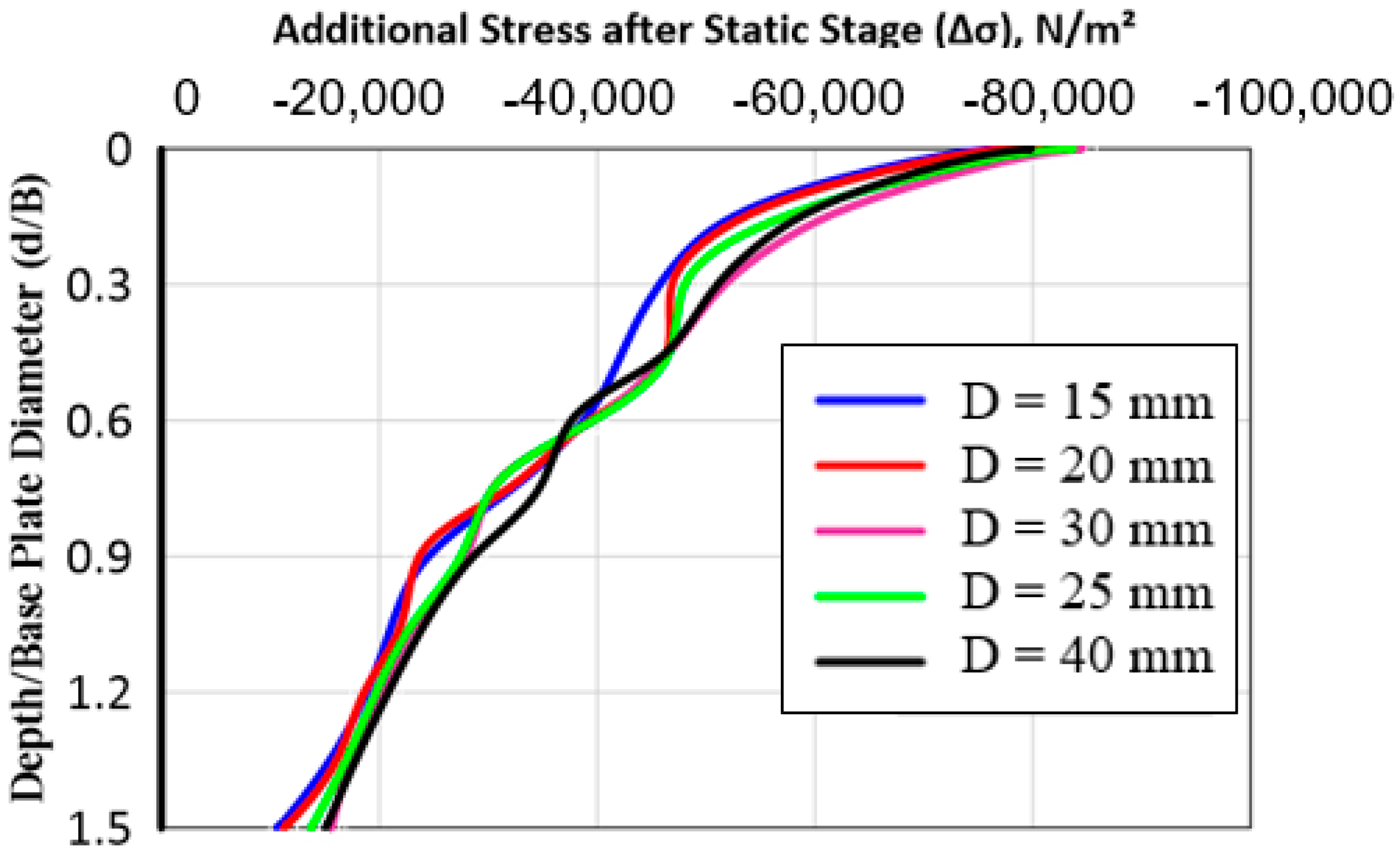
3.2. The Vertical Stress within the Soil Media
4. Results of the Dynamic Analysis
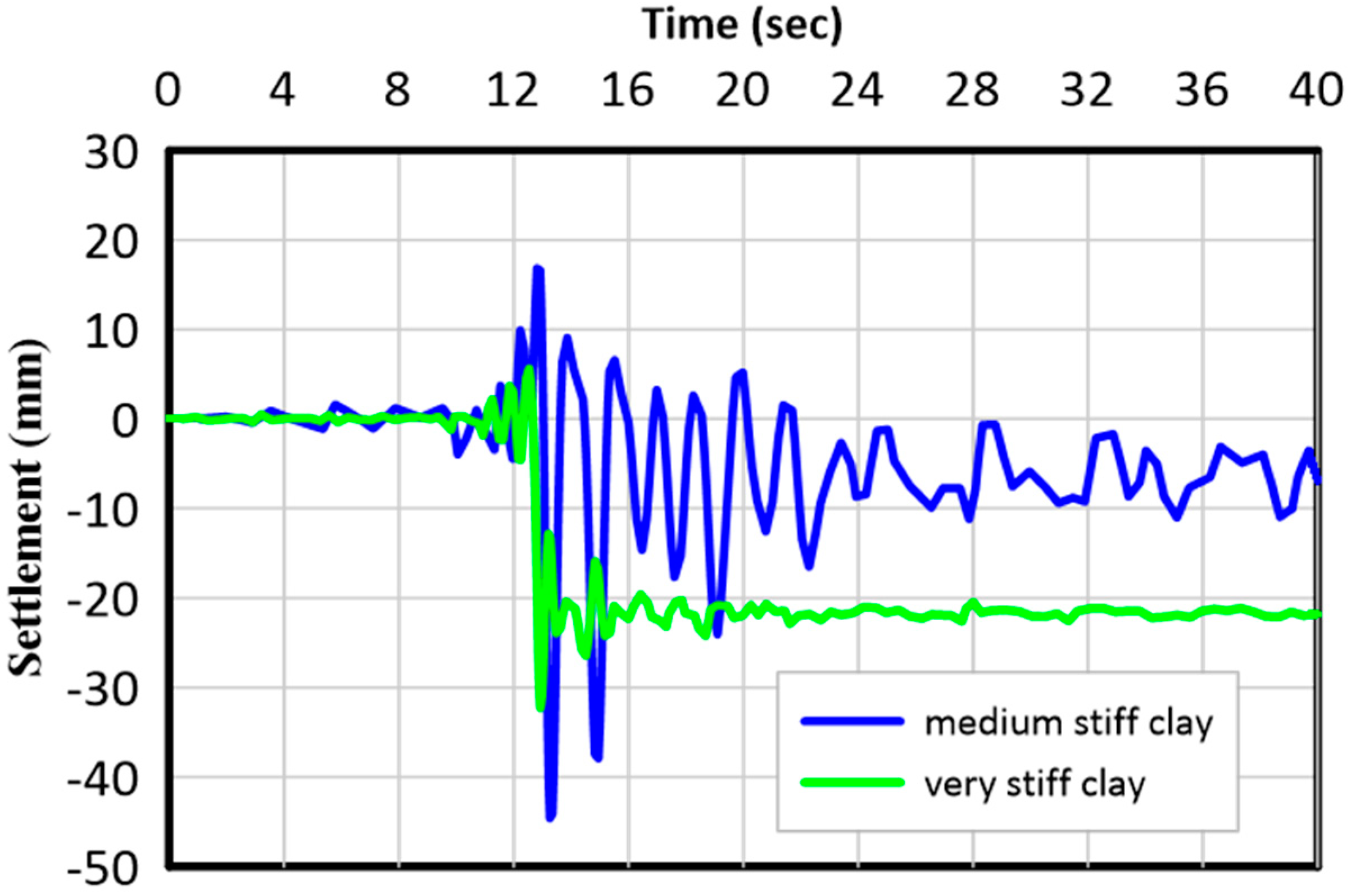
4.1. The Settlement under the Tank Base Plate
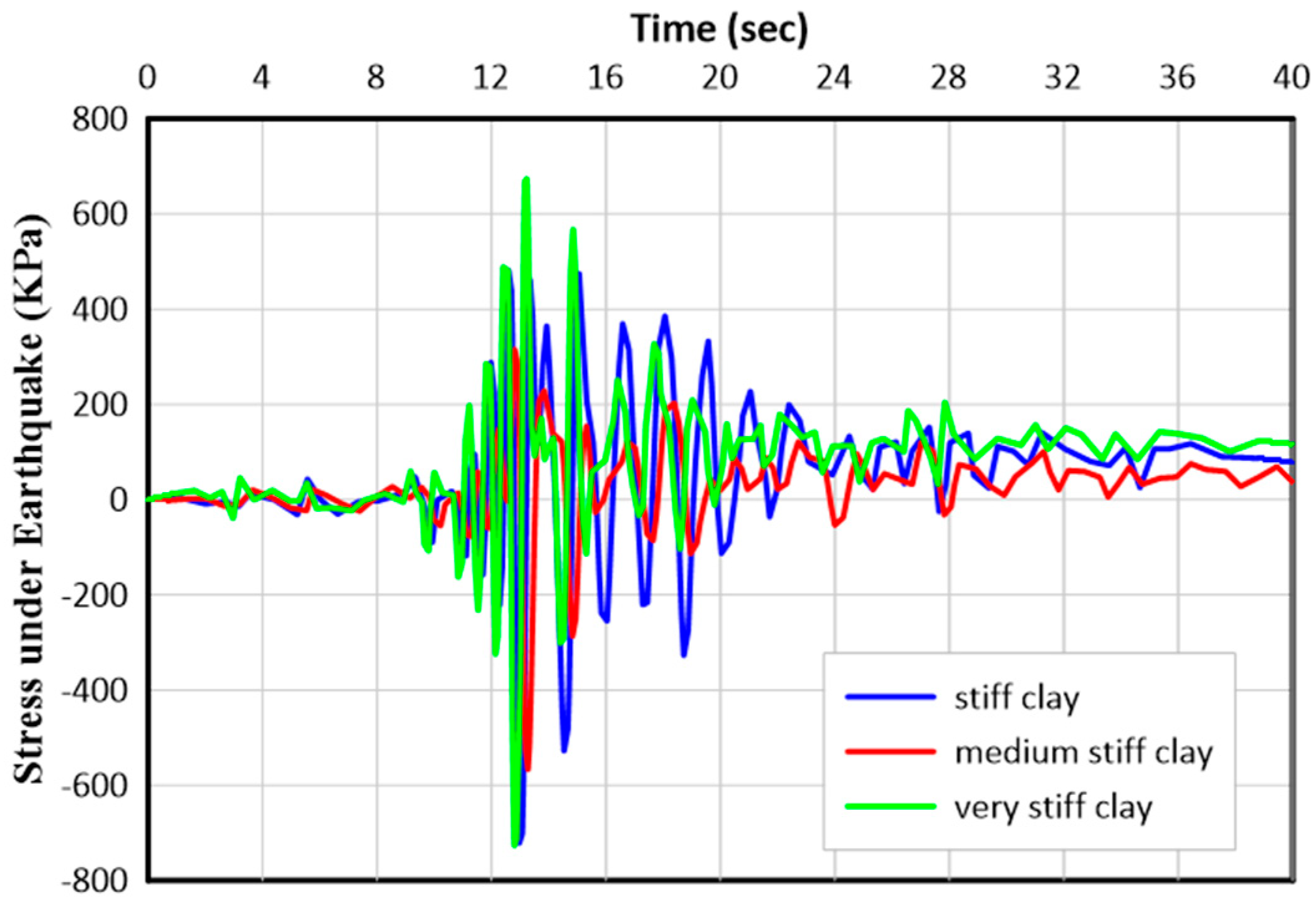
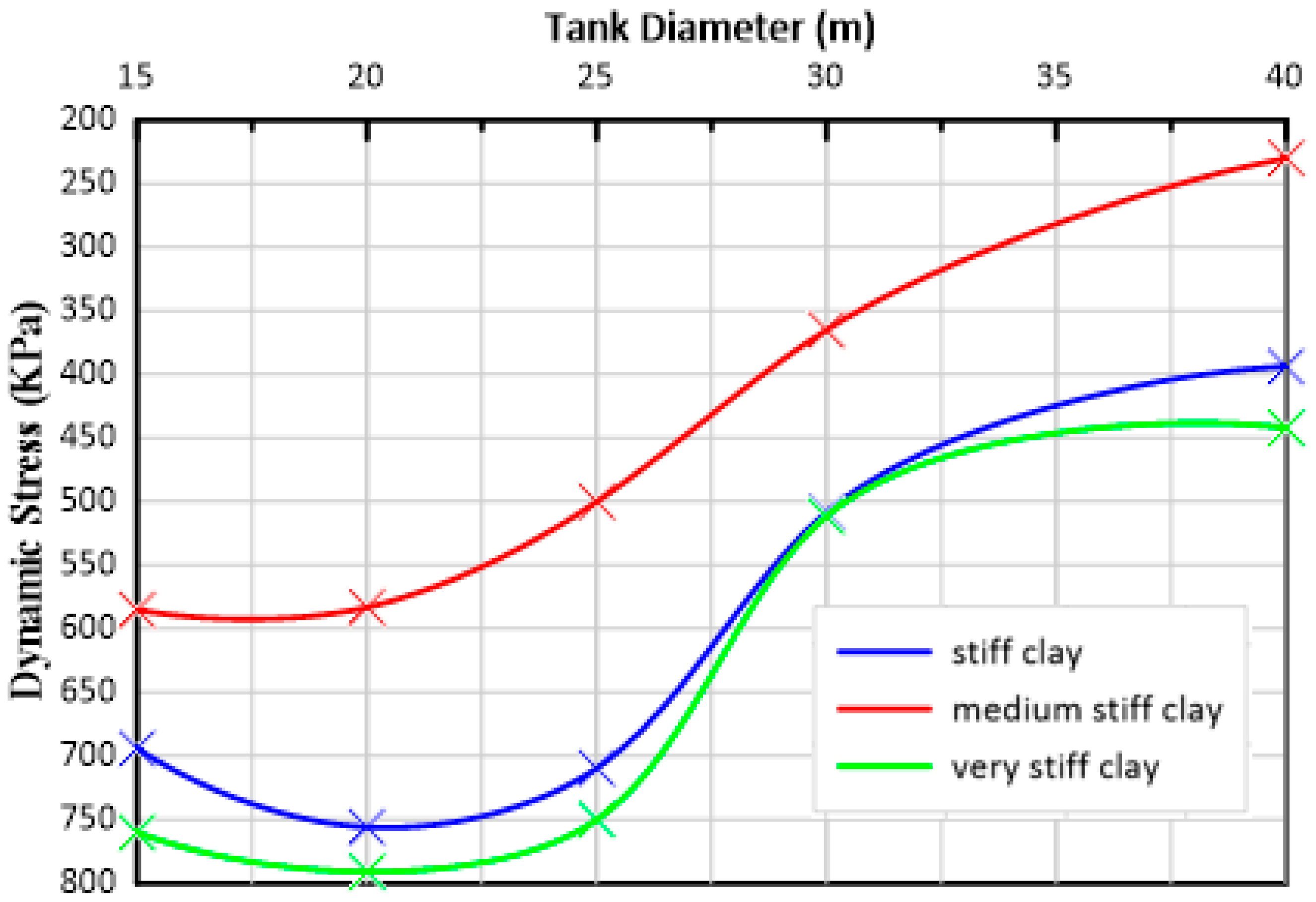
4.2. The Vertical Stresses within the Soil Media
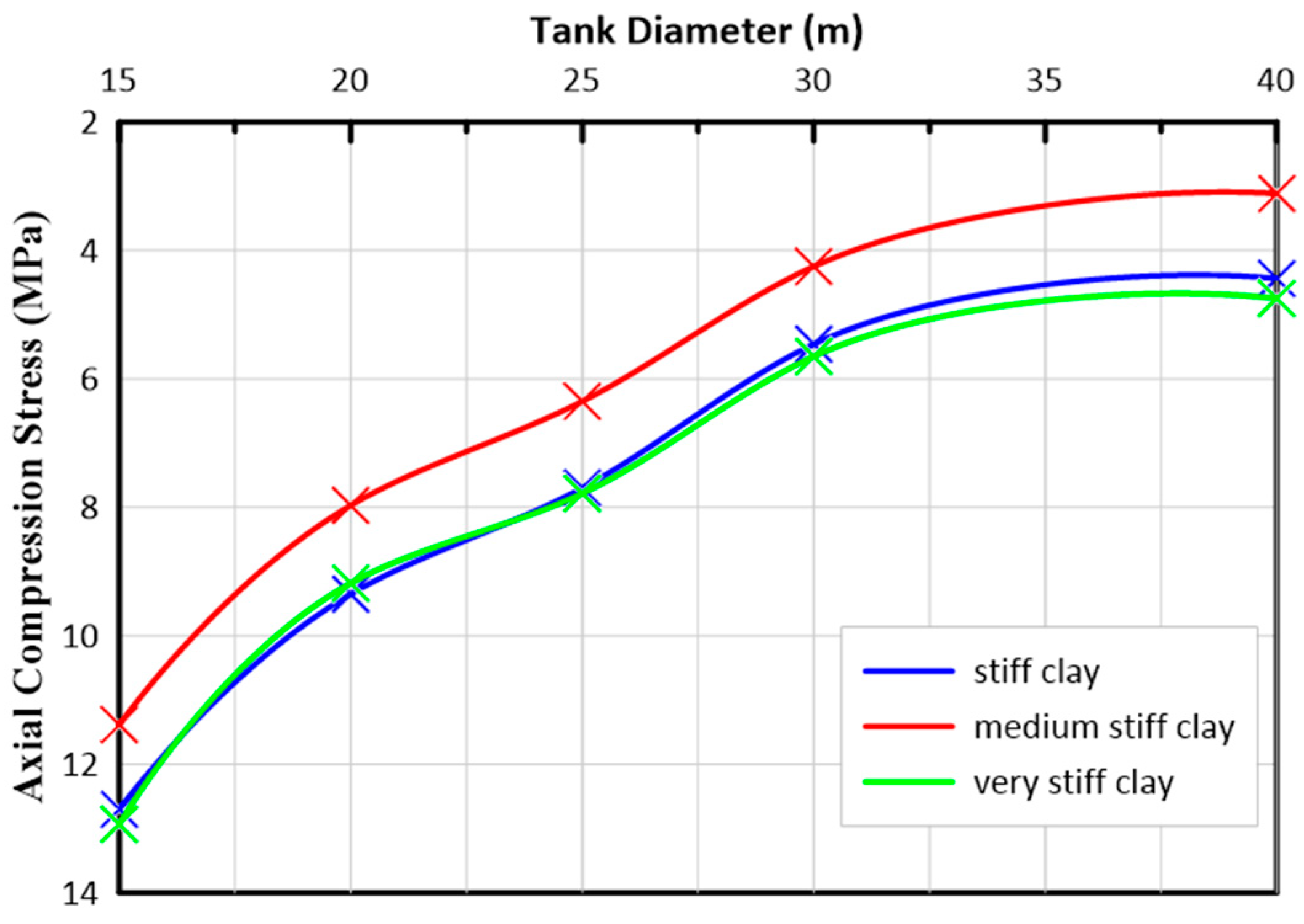
4.3. The Axial Compressive Stresses in the Tank Shells
5. Conclusions
- The settlement under static loading increases with increasing the tank diameter for all cases of different types of clay. Increasing the tank diameter from 15 m to 40 m causes a 60% increase in the total settlement for the case of medium-stiff clay. However, the increases are 44% and 40% for the cases of stiff clay and very stiff clay soils, respectively.
- The vertical static stresses just under the tank are the maximum because of the additional stress that comes from the tank and fluid weights. However, these values decrease gradually (about 18.9%, 18.5%, 16.4%, 13.8%, and 12.8% of the stress values under the tank base) whenever the soil depth under the tank goes down for all cases. These results confirm the empirical results that consider 15% of the stress can be reached at a depth of 1.5 of the footing width.
- The soil under the tanks has a noticeable effect on the dynamic behavior of the studied tanks. The tanks resting over the medium-stiff clay (the weakest soil) give a lower permanent settlement after the earthquake because of its low elastic modulus which leads to the absorption of the earthquake waves in comparison to the other types of soil.
- There are 29.6% and 35.6% increases in the peak dynamic stresses under the tanks in the cases of stiff clay and very stiff clay soils, respectively. The maximum values of the dynamic vertical stresses occur at a time around 13.02 s, which is close to the peak ground acceleration of the earthquake.
- The tanks resting over medium-stiff clay soil (weakest soil) show the minimum values of the axial compression stresses in the tank shells because of the low elastic modulus of this soil which leads to the absorption of the earthquake waves in comparison to the other types of soils. Moreover, decreasing the tank diameter from 40 m to 15 m causes significant increases in the axial compression stress by 265%, 186%, and 172% for the tanks resting over medium-stiff clay, stiff clay, and very stiff clay soils, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marr, A.W.; Ramos, J.A.; Lambe, W.T. Criteria for settlement of tanks. J. Geotech. Eng. Div. 1982, 108, 1017–1039. [Google Scholar] [CrossRef]
- D’orazio, T.B.; Duncan, J.M. Differential settlements in steel tanks. J. Geotech. Eng. 1987, 113, 967–983. [Google Scholar] [CrossRef]
- Chandrakar, P.; Bokare, P.S. A Review—Comparison between Response Spectrum Method and Time History Method for Dynamic Analysis of Multistoried Building. Int. J. Sci. Res. (IJSR) 2015, 6, 244–247. [Google Scholar]
- Jacobsen, L.S.; Ayre, R.S. Hydrodynamic Experiments with Rigid Cylindrical Tanks Subjected to Transient Motions. Bull. Seismol. Soc. Am. 1951, 41, 313–346. [Google Scholar] [CrossRef]
- Ma, D.C.; Liu, W.K.; Gvildys, J.; Chang, Y.W. Seismic Behavior of Liquid-Filled Shells. Nucl. Eng. Des. 1982, 70, 437–455. [Google Scholar] [CrossRef]
- Sánchez, H.S.; Salas, C.C.; Domínguez, A.M. Structural behavior of liquid filled storage tanks of large capacity placed in seismic zones of high risk in Mexico. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Konstandakopoulou, F.D.; Hatzigeorgiou, G.D. Water and Wastewater Steel Tanks under Multiple Earthquakes. Soil Dyn. Earthq. Eng. 2017, 100, 445–453. [Google Scholar] [CrossRef]
- Spritzer, J.M.; Guzey, S. Nonlinear Numerical Evaluation of Large Open-Top Aboveground Steel Welded Liquid Storage Tanks Excited by Seismic Loads. Thin-Walled Struct. 2017, 119, 662–676. [Google Scholar] [CrossRef]
- Hosseinzadeh, N.; Kazem, H.; Ghahremannejad, M.; Ahmadi, E.; Kazem, N. Comparison of API650-2008 Provisions with FEM Analyses for Seismic Assessment of Existing Steel Oil Storage Tanks. J. Loss Prev. Process Ind. 2013, 26, 666–675. [Google Scholar] [CrossRef]
- API 650; Welded Tanks for Oil Storage. American Petroleum Institute: Washington, DC, USA, 2014.
- Hamdan, F.H. Seismic Behavior of Cylindrical Steel Liquid Storage Tanks. J. Constr. Steel Res. 2000, 53, 307–333. [Google Scholar] [CrossRef]
- EN 1998-4, Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC; Eurocode 8: Design of Structures for Earthquake Resistance—Part 4: Silos, Tanks and Pipelines. The European Union: Maastricht, The Netherlands, 2006.
- Mehretehran, A.M.; Maleki, S. 3D Buckling Assessment of Cylindrical Steel Silos of Uniform Thickness under Seismic Action. Thin-Walled Struct. 2018, 131, 654–667. [Google Scholar] [CrossRef]
- Lupattelli, A.; Kita, A.; Salciarini, D.; Venanzi, I.; Ubertini, F. Effects of the soil–structure interaction and seismic vertical component on the response of a concrete surge tank. Structures 2023, 55, 310–323. [Google Scholar] [CrossRef]
- Minoglou, M.K.; Hatzigeorgiou, G.D.; Papagiannopoulos, G.A. Heuristic optimization of cylindrical thin-walled steel tanks under seismic loads. Thin-Walled Struct. 2013, 64, 50–59. [Google Scholar] [CrossRef]
- Hjorteset, K.; Wernli, M.; LaNier, M.W.; Hoyle, K.A.; Oliver, W.H. Development of large-scale precast, prestressed concrete liquefied natural gas storage tanks. PCI J. 2013, 58, 40–54. [Google Scholar] [CrossRef]
- ADINA R&D, Inc. ADINA System 9.6.0; ADINA R&D, Inc.: Watertown, MA, USA, 2019. [Google Scholar]
- Zienkiewicz, O.C.; Shiomi, T. Dynamic behavior of saturated porous media; the generalized biot formulation and its numerical solution. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 71–96. [Google Scholar] [CrossRef]
- Salem, T.N. Analysis of Offshore Piles. Ph.D. Thesis, Zagazig University, Zagazig, Egypt, 1997. [Google Scholar]
- Virella, J.C.; Godoy, L.A.; Suárez, L.E. Dynamic buckling of anchored steel tanks subjected to horizontal earth-quake excitation. J. Constr. Steel Res. 2006, 62, 521–531. [Google Scholar] [CrossRef]
- ASTM A516/A516M-10; Standard Specification for Pressure Vessel Plates, Carbon Steel, for Moderate- and Lower-Temperature Service. ASTM International: West Conshohocken, PA, USA, 2015.
- Liu, M.D.; Carter, J.P. Structured CamClay Model. Can. Geotech. J. 2002, 39, 1313–1332. [Google Scholar] [CrossRef]
- Abed, A. Numerical Modeling of Expansive Soil Behavior. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2008. [Google Scholar]
- California Department of Conservation. The 1989 Loma Prieta Earthquake; California Department of Conservation: Sacramento, CA, USA, 1989. [Google Scholar]
- ECP 202; Egyptian Code for Soil Mechanics—Design and Construction of Foundations; Part 4. Deep Foundations: Cairo, Epygt, 2005.





| Properties | Medium-Stiff Clay | Stiff Clay | Very Stiff Clay | Concrete | Steel |
| Poisson’s ratio, (Ʋ) | 0.40 | 0.40 | 0.40 | 0.20 | 0.29 |
| Unit weight, (Ƴ) kN/m3 | 17.0 | 19.0 | 20.0 | 25.0 | 78.0 |
| Elastic modulus, (E), MPa | 6.0 | 15.0 | 25.0 | 2 × 104 | 2 × 105 |
| Kappa (κ) | 0.017 | 0.01 | 0.0047 | - | - |
| Lambda (λ) | 0.088 | 0.043 | 0.023 | - | - |
| Tank Identification | Tank Diameter, D (m) | Aspect Ratio, H/D | Shell Thickness, t (mm) | Bottom Plate Thickness, ta (mm) |
| 1 | 40 | 0.25 | 12 | 8 |
| 2 | 30 | 0.33 | 10 | 8 |
| 3 | 25 | 0.40 | 9 | 6 |
| 4 | 20 | 0.50 | 8 | 6 |
| 5 | 15 | 0.67 | 6 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salem, T.N.; El-Zohairy, A.; Abdelbaset, A.M. The Static and Dynamic Behavior of Steel Storage Tanks over Different Types of Clay Soil. CivilEng 2023, 4, 1169-1181. https://doi.org/10.3390/civileng4040064
Salem TN, El-Zohairy A, Abdelbaset AM. The Static and Dynamic Behavior of Steel Storage Tanks over Different Types of Clay Soil. CivilEng. 2023; 4(4):1169-1181. https://doi.org/10.3390/civileng4040064
Chicago/Turabian StyleSalem, Tarek N., Ayman El-Zohairy, and Ahmed M. Abdelbaset. 2023. "The Static and Dynamic Behavior of Steel Storage Tanks over Different Types of Clay Soil" CivilEng 4, no. 4: 1169-1181. https://doi.org/10.3390/civileng4040064






