Two Repetitions May Be Enough! Reliability of Movement Timing in Physical Fitness Exercises Performed by Young, Trained Adults Using Inertial Sensors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
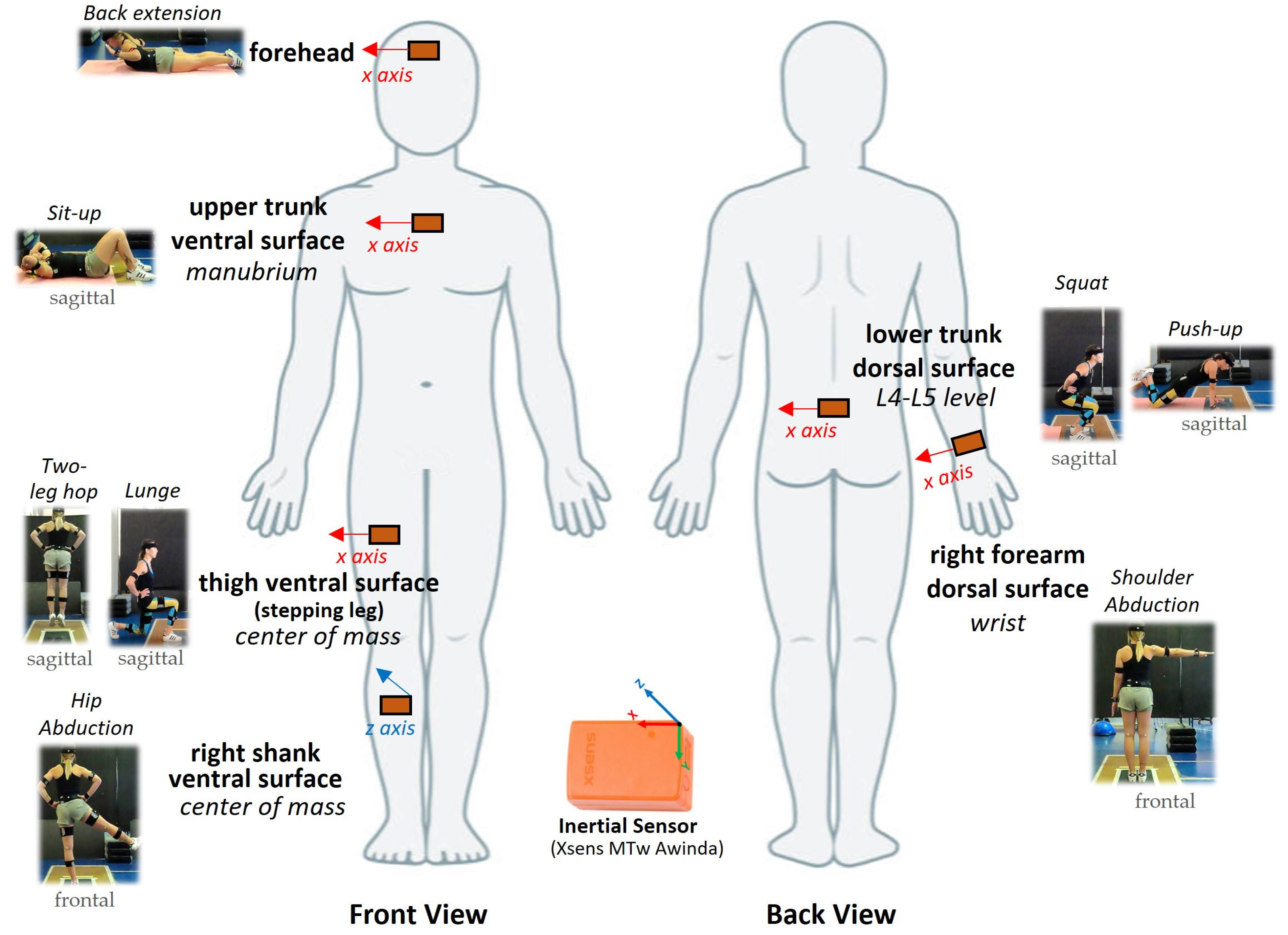
2.2. Experimental Procedure
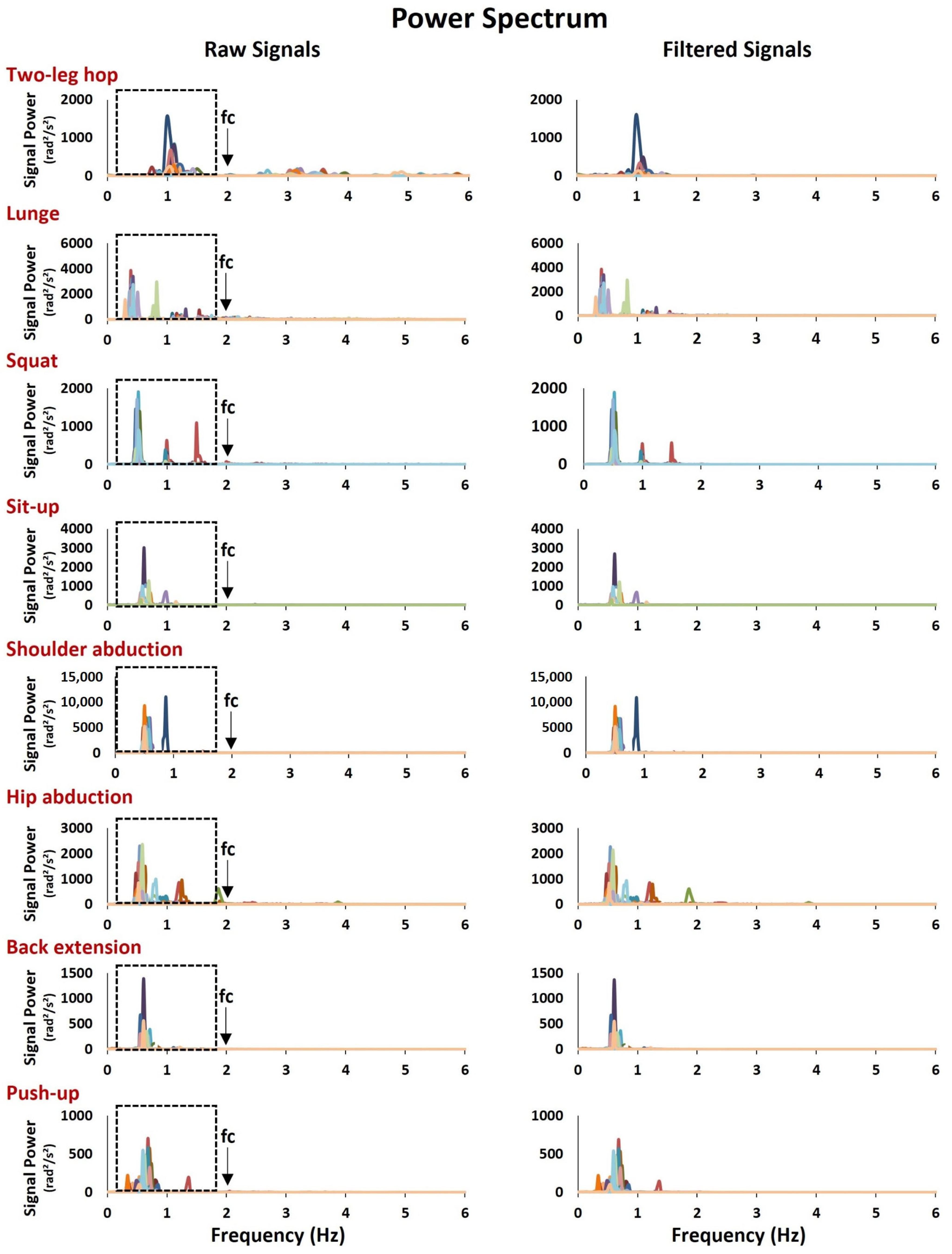
2.2.1. Data Collection and Analysis
2.2.2. Temporal Variables
2.3. Statistical Analysis
2.3.1. Relative Reliability
2.3.2. Absolute Reliability
3. Results
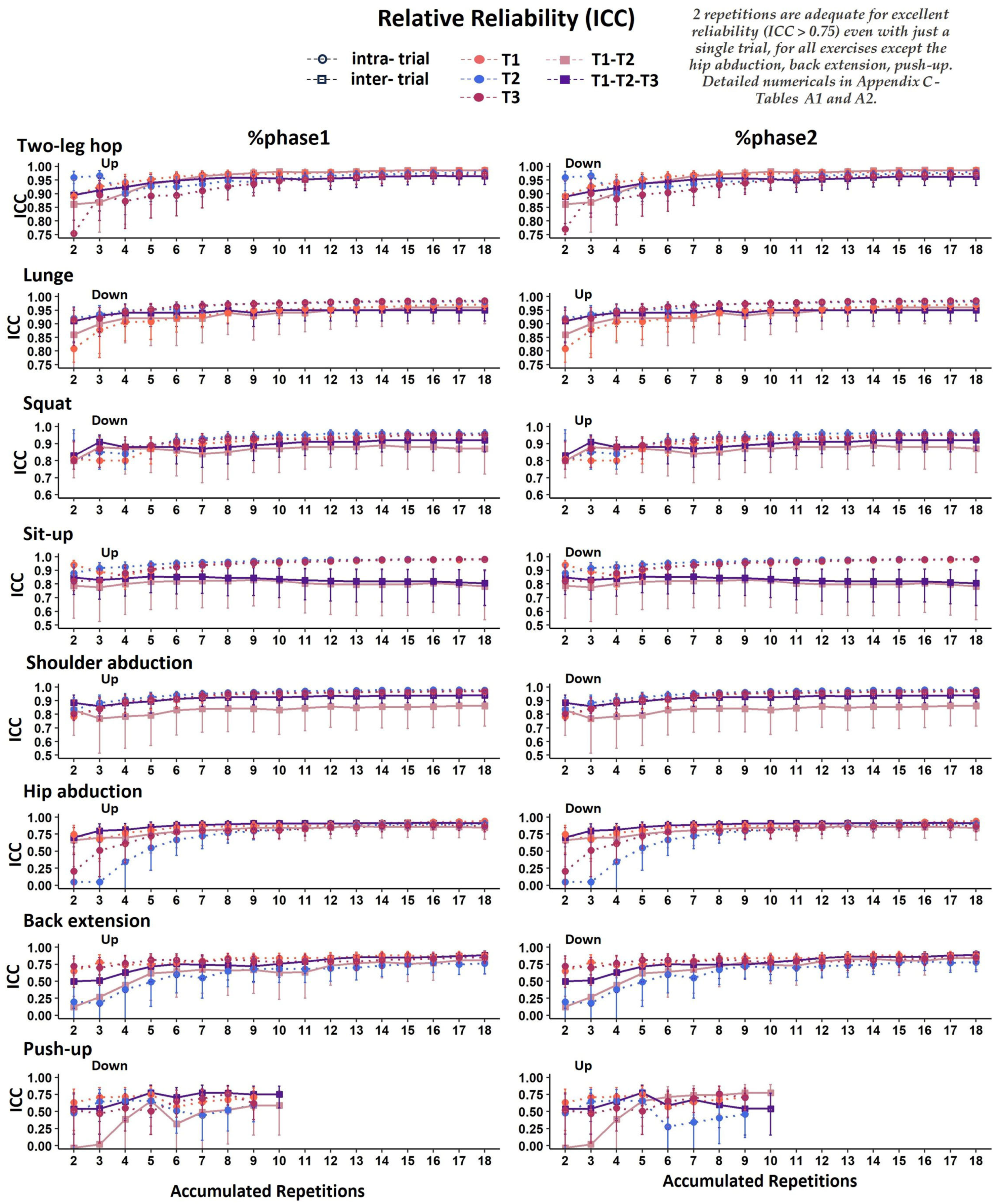
3.1. Relative Temporal Reliability
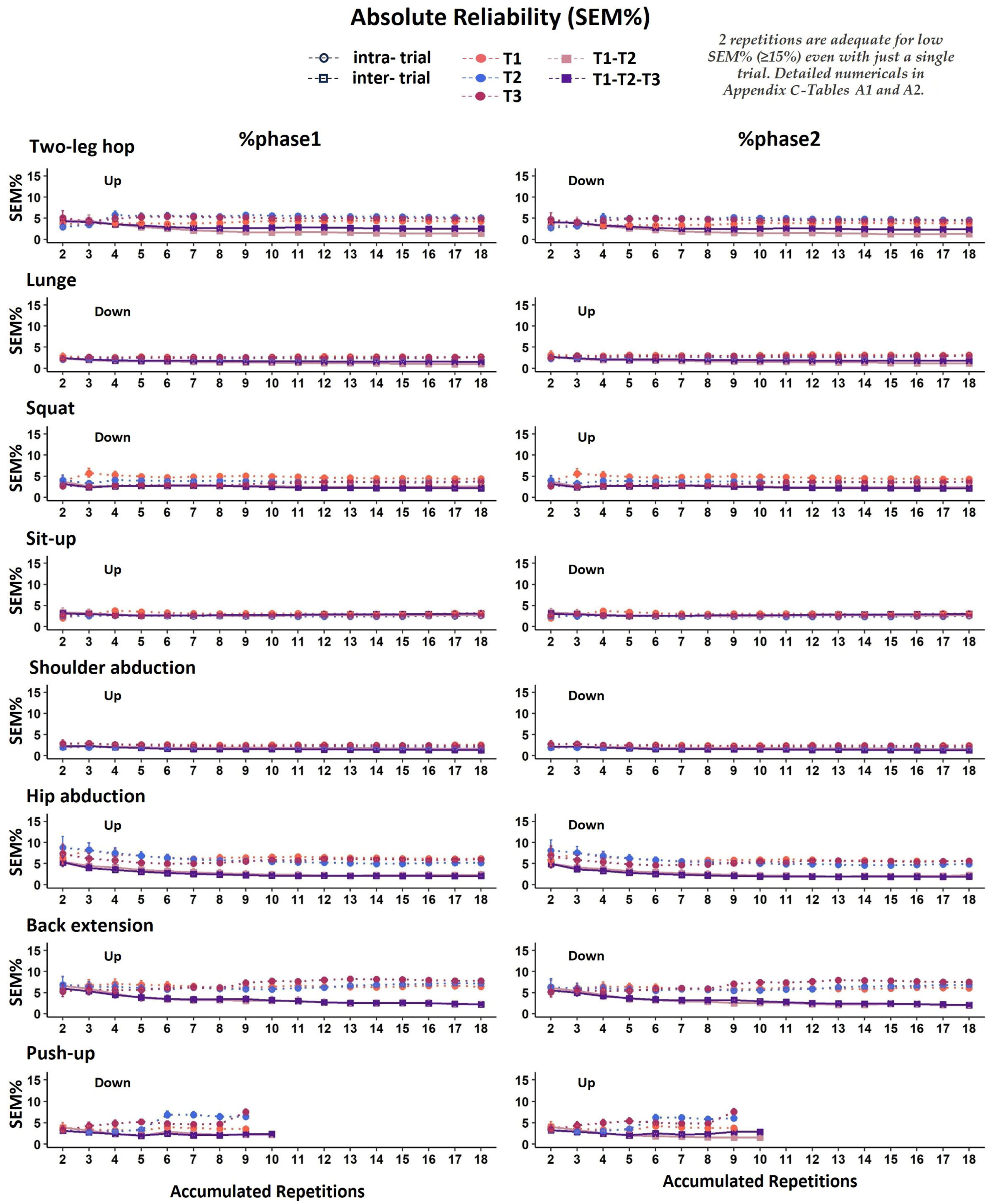
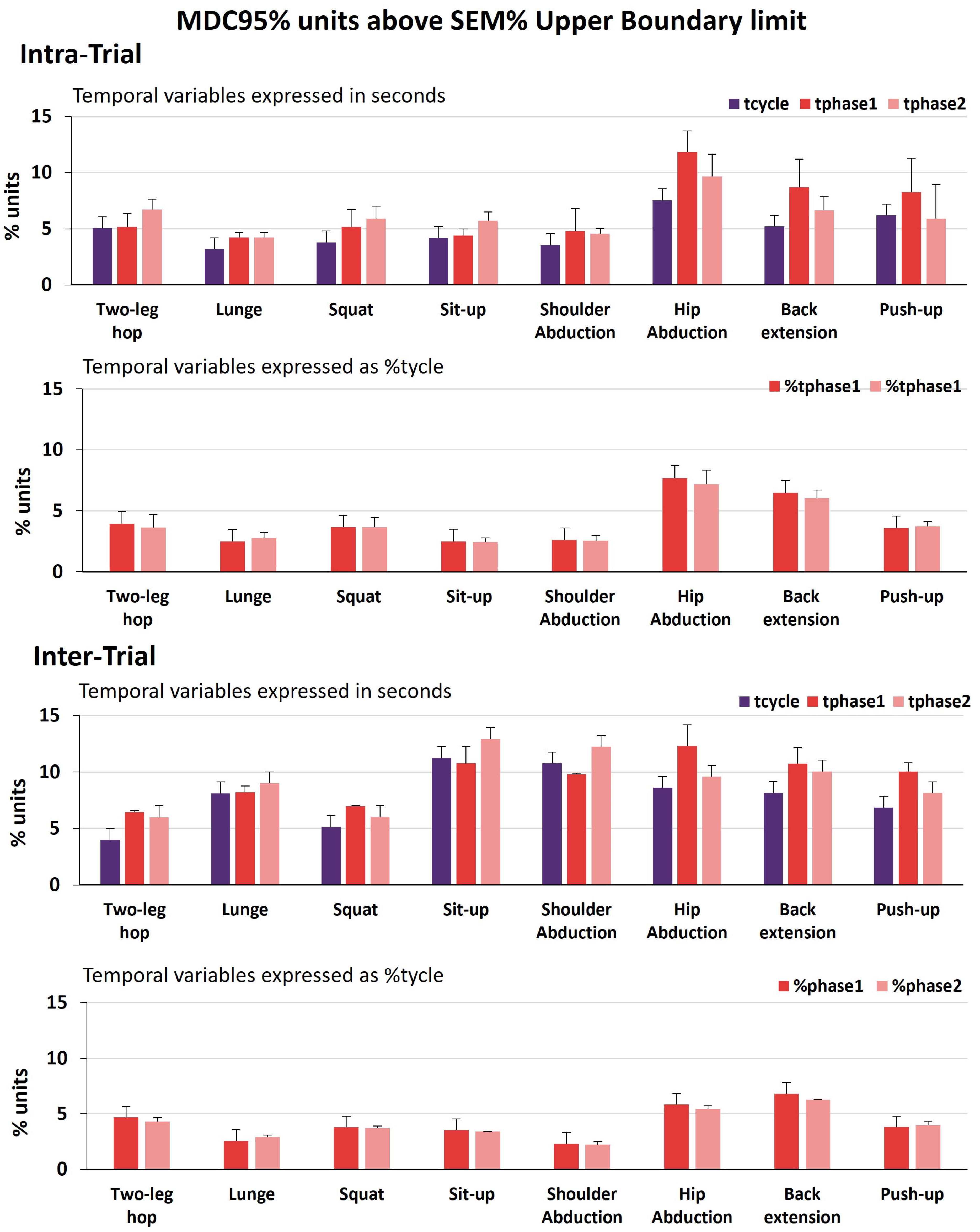
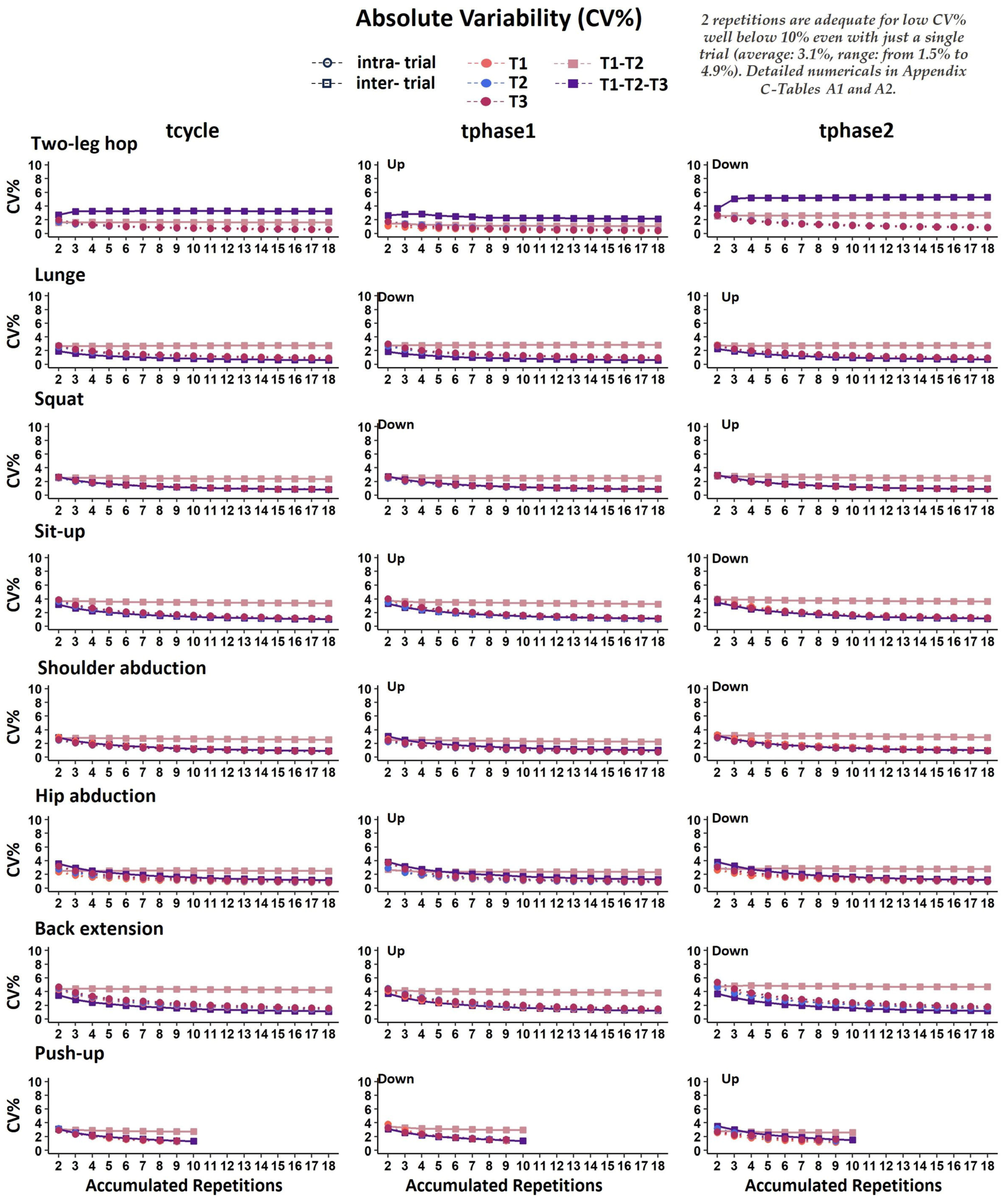
3.2. Absolute Temporal Reliability
4. Discussion
4.1. Relative Temporal Reliability
4.2. Absolute Temporal Reliability
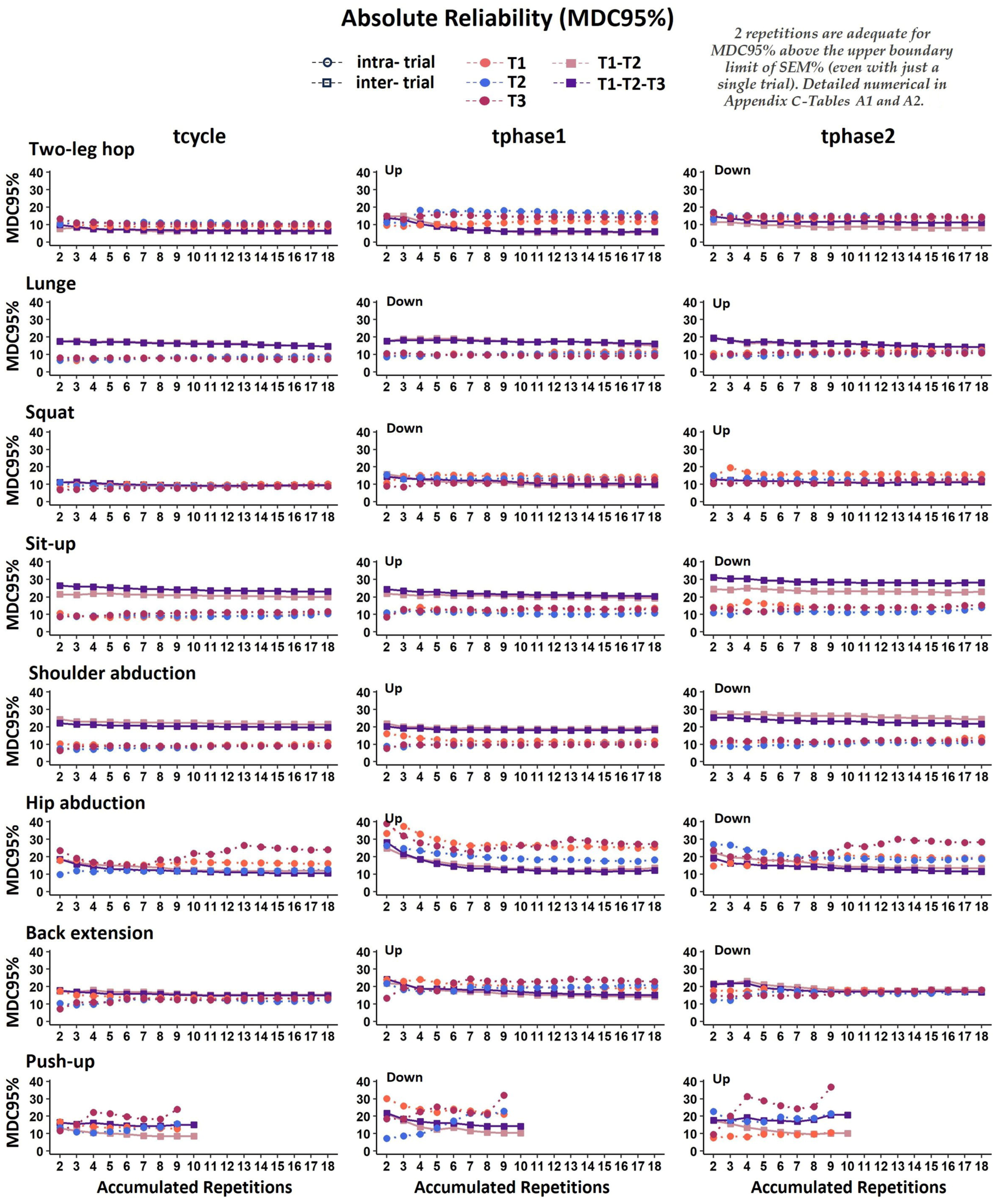
4.3. Required Repetitions for Reliable Temporal Measures
4.4. Practical Application
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B
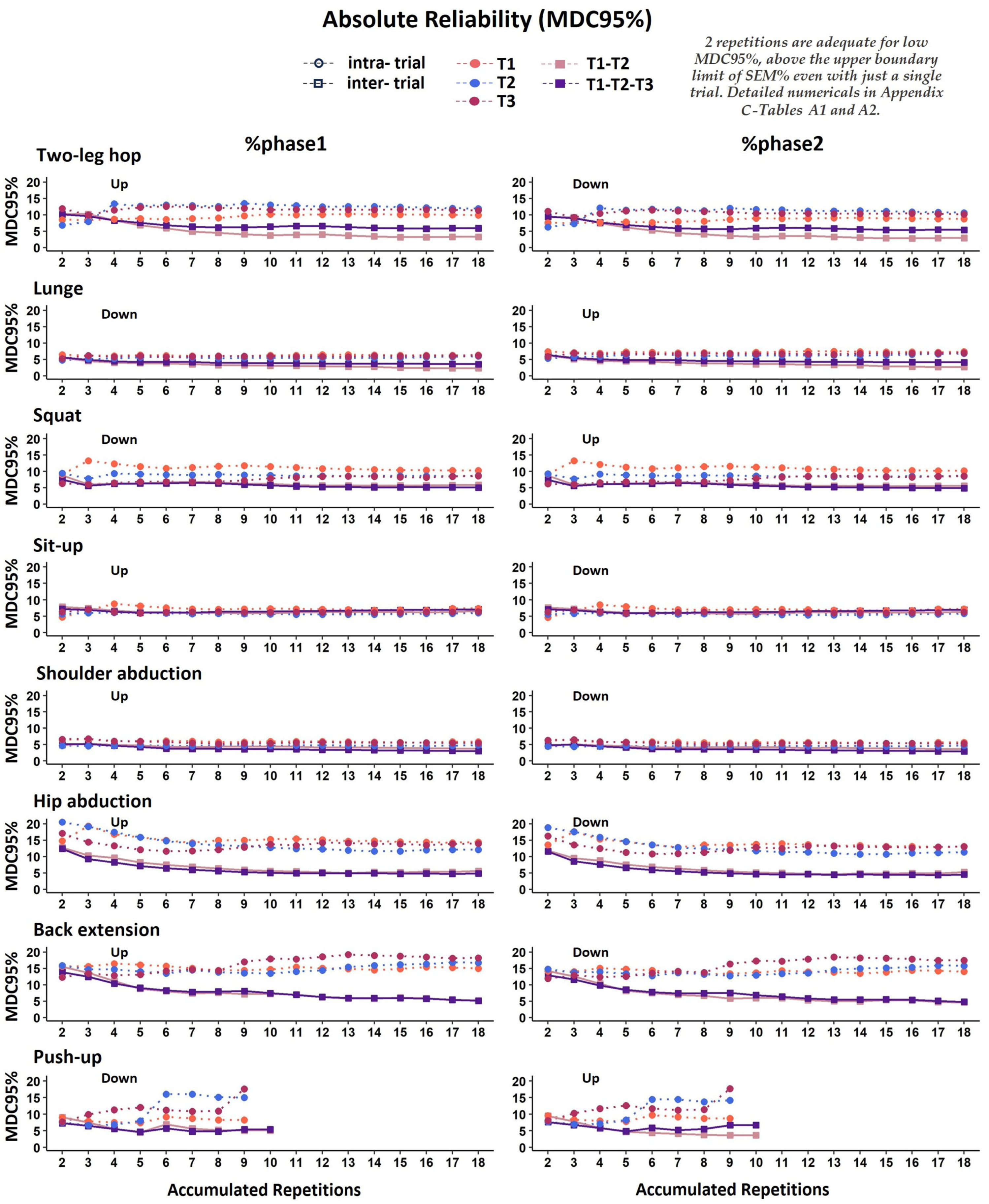
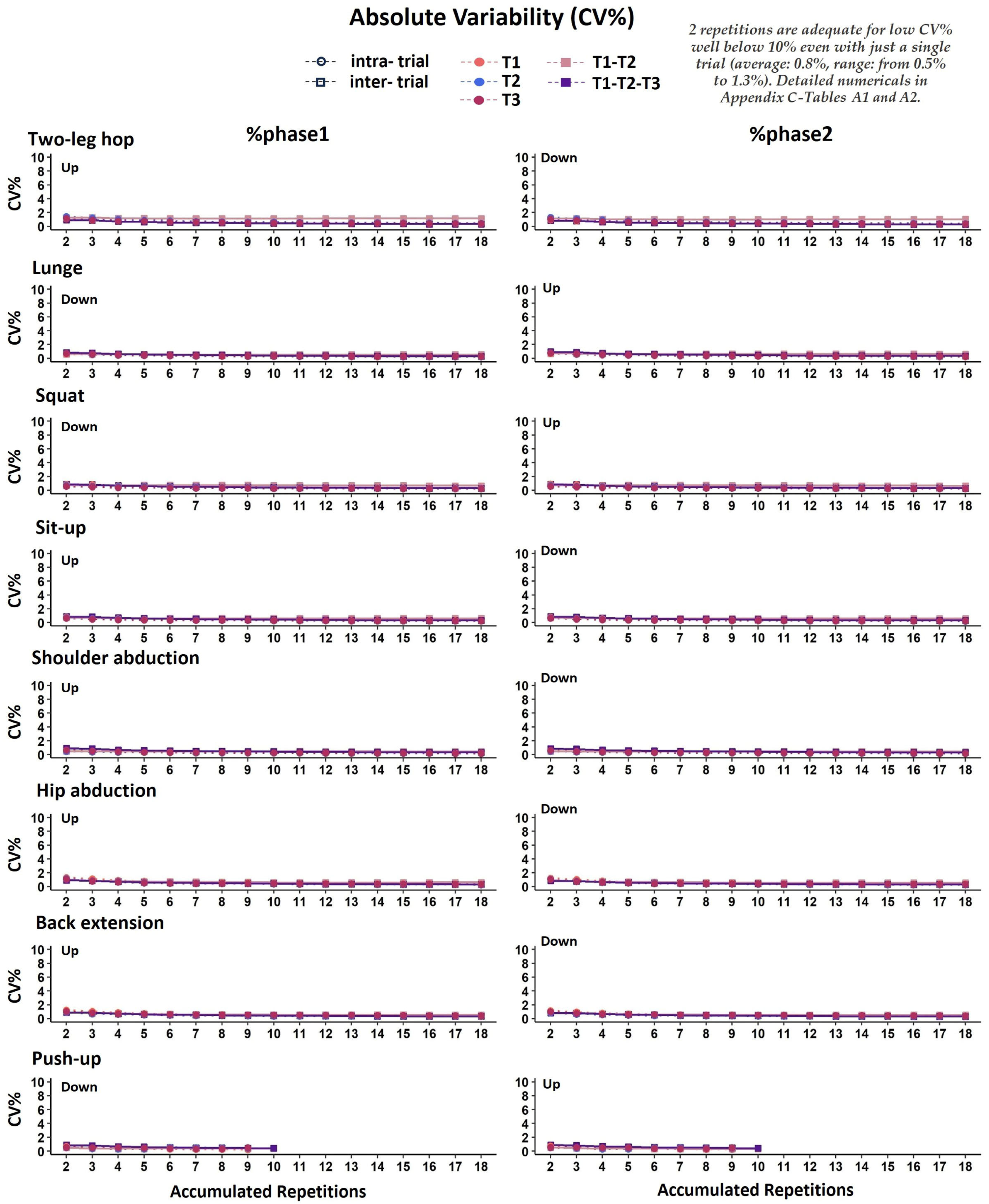
Appendix C
| Intra-Trial Measures | Number of Repetitions (ICC/SEM%/MDC95%/CV%) | ICC (95% CI) | SEM% | MDC95% | CV% | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T1 | T2 | T3 | T1 | T2 | T3 | T1 | T2 | T3 | T1 | T2 | T3 | ||
| Movement Measures Expressed in Seconds (tcycle, tphase1, tphase2) | ||||||||||||||||
| Two-leg hop | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.92 (0.82 0.96) | 0.93 (0.85 0.97) | 0.92 (0.82 0.96) | 4.8 | 4.5 | 5.7 | 11.2 | 10.4 | 13.3 | 1.6 | 1.7 | 2.0 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.86 (0.75 0.93) | 0.92 (0.83 0.96) | 0.86 (0.75 0.94) | 4.1 | 4.8 | 6.4 | 9.6 | 11.2 | 14.9 | 1.1 | 1.7 | 1.7 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.93 (0.85 0.97) | 0.96 (0.91 0.98) | 0.93 (0.84 0.97) | 7.0 | 5.6 | 7.3 | 16.3 | 13.0 | 17.0 | 2.6 | 2.6 | 2.7 | |
| Lunge | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.99 (0.98 1.00) | 0.99 (0.98 1.00) | 0.99 (0.97 0.99) | 2.9 | 2.9 | 3.5 | 6.7 | 6.7 | 8.1 | 2.7 | 2.6 | 2.7 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.96 0.99) | 0.98 (0.97 0.99) | 0.98 (0.96 0.99) | 4.0 | 3.7 | 4.5 | 9.4 | 8.6 | 10.5 | 2.8 | 2.7 | 3.0 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.96 0.99) | 0.98 (0.97 0.99) | 0.98 (0.96 0.99) | 4.5 | 3.7 | 3.9 | 10.6 | 8.7 | 9.2 | 2.8 | 2.7 | 2.7 | |
| Squat | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.97 0.99) | 0.97 (0.93 0.99) | 0.99 (0.96 0.99) | 3.4 | 4.7 | 3.0 | 7.8 | 11.0 | 6.9 | 2.5 | 2.6 | 2.7 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.97 (0.95 0.99) | 0.94 (0.87 0.97) | 0.98 (0.94 0.99) | 4.6 | 6.6 | 3.8 | 10.7 | 15.5 | 8.9 | 2.6 | 2.5 | 2.7 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.96 (0.91 0.98) | 0.95 (0.90 0.98) | 0.98 (0.95 0.99) | 6.2 | 6.4 | 4.5 | 14.4 | 15.0 | 10.4 | 2.8 | 2.9 | 2.9 | |
| Sit-up | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.99 (0.98 0.99) | 0.99 (0.98 1.00) | 0.99 (0.98 1.00) | 4.6 | 3.8 | 3.7 | 10.7 | 8.9 | 8.6 | 3.8 | 3.7 | 3.9 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.99 (0.98 0.99) | 0.99 (0.97 0.99) | 0.99 (0.98 1.00) | 4.4 | 4.7 | 3.6 | 10.3 | 11.0 | 8.5 | 4.0 | 3.5 | 4.0 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.96 0.99) | 0.99 (0.97 0.99) | 0.98 (0.96 0.99) | 6.0 | 4.7 | 5.9 | 14.1 | 11.0 | 13.7 | 4.0 | 3.9 | 3.9 | |
| Shoulder Abduction | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.96 0.99) | 0.98 (0.97 0.99) | 0.99 (0.98 1.00) | 4.4 | 3.2 | 2.7 | 10.3 | 7.4 | 6.4 | 2.9 | 2.5 | 2.6 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.94 (0.87 0.97) | 0.97 (0.93 0.99) | 0.99 (0.97 0.99) | 6.9 | 3.8 | 3.3 | 16.1 | 8.9 | 7.6 | 2.6 | 2.3 | 2.5 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.97 0.99) | 0.98 (0.97 0.99) | 0.98 (0.95 0.99) | 4.6 | 3.9 | 4.8 | 10.7 | 9.1 | 11.1 | 3.3 | 2.8 | 2.9 | |
| Hip Abduction | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.90 (0.78 0.95) | 0.98 (0.96 0.99) | 0.91 (0.80 0.96) | 7.7 | 4.2 | 10.1 | 17.9 | 9.8 | 23.6 | 2.4 | 2.8 | 3.2 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.78 (0.43 0.87) | 0.86 (0.69 0.93) | 0.78 (0.53 0.89) | 14.3 | 11.3 | 14.8 | 33.4 | 26.3 | 29.0 | 2.9 | 2.9 | 3.7 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.95 (0.89 0.98) | 0.88 (0.74 0.94) | 0.90 (0.79 0.95) | 6.4 | 11.6 | 10.2 | 14.8 | 27.1 | 23.8 | 2.7 | 3.3 | 3.1 | |
| Back Extension | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.95 0.99) | 0.99 (0.98 1.00) | 1.00 (0.99 1.00) | 7.4 | 4.5 | 3.1 | 17.4 | 10.4 | 7.3 | 4.3 | 4.5 | 4.7 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.94 (0.88 0.97) | 0.96 (0.92 0.98) | 0.99 (0.97 0.99) | 10.3 | 9.3 | 5.7 | 23.9 | 21.8 | 13.3 | 4.1 | 4.5 | 4.4 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.98 (0.96 0.99) | 0.99 (0.98 1.00) | 0.99 (0.98 0.99) | 7.6 | 5.3 | 6.3 | 17.8 | 12.3 | 14.8 | 4.8 | 4.7 | 5.4 | |
| Push-up | tcycle | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.95 (0.90 0.98) | 0.97 (0.94 0.99) | 0.98 (0.95 0.99) | 7.2 | 5.7 | 5.0 | 16.8 | 13.4 | 11.7 | 3.1 | 3.2 | 2.9 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.89 (0.78 0.95) | 0.99 (0.98 1.00) | 0.95 (0.89 0.98) | 12.9 | 3.1 | 8.0 | 30.2 | 7.2 | 18.6 | 3.8 | 3.3 | 3.2 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.99 (0.97 0.99) | 0.92 (0.83 0.96) | 0.98 (0.96 0.99) | 3.3 | 9.7 | 4.1 | 7.7 | 22.7 | 9.5 | 2.6 | 3.2 | 2.7 | |
| Movement Measures Expressed as %tcycle (%tphase1, %tphase2) | ||||||||||||||||
| Two-leg hop | %tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.89 (0.76 0.95) | 0.96 (0.91 0.98) | 0.75 (0.47 0.89) | 3.6 | 2.9 | 5.1 | 8.5 | 6.8 | 11.9 | 1.1 | 1.4 | 1.1 |
| %tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.89 (0.76 0.95) | 0.96 (0.91 0.98) | 0.77 (0.49 0.90) | 3.3 | 2.7 | 4.8 | 7.6 | 6.3 | 11.1 | 1.0 | 1.3 | 1.1 | |
| Lunge | %tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.81 (0.60 0.91) | 0.92 (0.83 0.96) | 0.91 (0.82 0.96) | 2.8 | 2.1 | 2.3 | 6.5 | 4.8 | 5.3 | 0.6 | 0.7 | 0.7 |
| %tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.81 (0.60 0.91) | 0.92 (0.83 0.96) | 0.91 (0.82 0.96) | 3.2 | 2.3 | 2.5 | 7.4 | 5.4 | 5.9 | 0.7 | 0.8 | 0.8 | |
| Squat | %tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.81 (0.59 0.91) | 0.80 (0.26 0.83) | 0.80 (0.58 0.90) | 3.9 | 4.1 | 2.7 | 9.1 | 9.4 | 6.3 | 0.9 | 0.7 | 0.6 |
| %tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.81 (0.59 0.91) | 0.80 (0.26 0.83) | 0.80 (0.58 0.90) | 3.9 | 4.0 | 2.7 | 9.2 | 9.3 | 6.2 | 0.9 | 0.7 | 0.6 | |
| Sit-up | %tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.94 (0.87 0.97) | 0.88 (0.74 0.94) | 0.82 (0.62 0.92) | 2.0 | 2.5 | 2.7 | 4.8 | 5.7 | 6.3 | 0.8 | 0.7 | 0.6 |
| %tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.94 (0.87 0.97) | 0.88 (0.74 0.94) | 0.82 (0.62 0.92) | 2.0 | 2.4 | 2.7 | 4.7 | 5.5 | 6.3 | 0.8 | 0.7 | 0.6 | |
| Shoulder Abduction | %tphase1 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.78 (0.59 0.88) | 0.84 (0.66 0.92) | 0.80 (0.59 0.91) | 2.8 | 2.0 | 2.9 | 6.5 | 4.6 | 6.6 | 0.6 | 0.5 | 0.6 |
| %tphase2 | 2/2/2/2 | 2/2/2/2 | 2/2/2/2 | 0.78 (0.54 0.90) | 0.84 (0.66 0.92) | 0.80 (0.59 0.91) | 2.7 | 1.9 | 2.7 | 6.2 | 4.5 | 6.4 | 0.6 | 0.5 | 0.6 | |
| Hip Abduction | %phase1 | 4/2/2/2 | 8/2/2/2 | 6/2/2/2 | 0.77 (0.59 0.88) | 0.77 (0.77 0.93) | 0.78 (0.63 0.88) | 6.3 | 8.8 | 7.3 | 14.8 | 20.5 | 17.1 | 1.3 | 1.2 | 1.1 |
| %phase2 | 4/2/2/2 | 8/2/2/2 | 6/2/2/2 | 0.77 (0.59 0.88) | 0.77 (0.77 0.93) | 0.78 (0.63 0.88) | 5.8 | 8.1 | 7.0 | 13.6 | 18.9 | 16.3 | 1.2 | 1.1 | 1.0 | |
| Back Extension | %phase1 | 5/2/2/2 | 15/2/2/2 | 4/2/2/2 | 0.75 (0.58 0.87) | 0.75 (0.60 0.93) | 0.76 (0.57 0.87) | 6.7 | 6.8 | 5.3 | 15.7 | 15.9 | 12.3 | 1.2 | 0.9 | 1.0 |
| %phase2 | 5/2/2/2 | 15/2/2/2 | 4/2/2/2 | 0.75 (0.58 0.87) | 0.75 (0.60 0.93) | 0.76 (0.57 0.87) | 6.1 | 6.4 | 5.1 | 14.2 | 14.8 | 11.9 | 1.1 | 0.9 | 1.0 | |
| Push-up | %phase1 | 5/2/2/2 | 4/2/2/2 | 8/2/2/2 | 0.75 (0.57 0.87) | 0.75 (0.40 0.82) | 0.76 (0.60 0.87) | 3.8 | 3.2 | 3.3 | 9.0 | 7.5 | 7.7 | 0.7 | 0.5 | 0.5 |
| %phase2 | 5/2/2/2 | 4/2/2/2 | 8/2/2/2 | 0.75 (0.57 0.87) | 0.75 (0.40 0.82) | 0.76 (0.60 0.87) | 4.1 | 3.3 | 3.5 | 9.5 | 7.7 | 8.1 | 0.7 | 0.5 | 0.6 | |
| Inter-trial Measures | Number of Repetitions (ICC/SEM%/MDC95%/CV%) | ICC (95% CI) | SEM% | MDC95% | CV% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1–T2 | T1–T2–T3 | T1–T2 | T1–T2–T3 | T1–T2 | T1–T2–T3 | T1–T2 | T1–T2–T3 | T1–T2 | T1–T2–T3 | ||
| Movement Measures Expressed in Seconds (tcycle, tphase1, tphase2) | |||||||||||
| Two-leg hop | tcycle | 2/2/2/2 | 2/2/2/2 | 0.96 (0.91 0.98) | 0.96 (0.92 0.98) | 3.3 | 4.2 | 7.6 | 9.8 | 1.6 | 2.7 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.76 (0.75 0.89) | 0.87 (0.76 0.94) | 6.3 | 5.9 | 14.7 | 13.7 | 1.4 | 2.6 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.97 (0.92 0.98) | 0.96 (0.92 0.98) | 4.9 | 6.3 | 11.4 | 14.7 | 2.5 | 3.6 | |
| Lunge | tcycle | 2/2/2/2 | 2/2/2/2 | 0.91 (0.75 0.96) | 0.93 (0.85 0.97) | 7.5 | 7.5 | 17.6 | 17.4 | 2.7 | 1.9 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.91 (0.72 0.96) | 0.94 (0.85 0.97) | 7.6 | 7.6 | 17.7 | 17.7 | 2.7 | 1.9 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.90 (0.78 0.96) | 0.93 (0.86 0.97) | 8.4 | 8.3 | 19.6 | 19.3 | 2.8 | 2.3 | |
| Squat | tcycle | 2/2/2/2 | 2/2/2/2 | 0.95 (0.75 0.93) | 0.97 (0.91 0.93) | 4.8 | 4.8 | 11.1 | 11.1 | 2.5 | 2.7 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.90 (0.75 0.93) | 0.95 (0.88 0.93) | 6.8 | 6.2 | 15.8 | 14.4 | 2.5 | 2.7 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.95 (0.86 0.93) | 0.97 (0.93 0.93) | 5.5 | 5.5 | 12.9 | 12.9 | 2.8 | 2.9 | |
| Sit-up | tcycle | 2/2/2/2 | 2/2/2/2 | 0.94 (0.89 0.97) | 0.94 (0.89 0.97) | 9.3 | 11.4 | 21.6 | 26.6 | 3.7 | 3.2 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.94 (0.88 0.97) | 0.95 (0.91 0.98) | 9.4 | 10.5 | 21.9 | 24.4 | 3.8 | 3.3 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.94 (0.87 0.97) | 0.92 (0.85 0.96) | 10.5 | 13.3 | 24.5 | 31.0 | 3.9 | 3.5 | |
| Shoulder Abduction | tcycle | 2/2/2/2 | 2/2/2/2 | 0.80 (0.41 0.92) | 0.88 (0.73 0.95) | 10.4 | 9.5 | 24.3 | 22.2 | 2.8 | 2.9 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.79 (0.34 0.92) | 0.88 (0.70 0.95) | 9.4 | 8.7 | 21.9 | 20.3 | 2.5 | 3.1 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.81 (0.48 0.92) | 0.89 (0.75 0.95) | 11.8 | 10.8 | 27.5 | 25.3 | 3.2 | 3.1 | |
| Hip Abduction | tcycle | 2/2/2/2 | 2/2/2/2 | 0.89 (0.70 0.95) | 0.93 (0.85 0.97) | 8.0 | 8.0 | 18.6 | 18.6 | 2.6 | 3.6 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.82 (0.59 0.92) | 0.87 (0.75 0.93) | 10.7 | 12.1 | 24.9 | 28.2 | 2.7 | 3.8 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.88 (0.73 0.94) | 0.93 (0.84 0.97) | 9.6 | 8.2 | 22.5 | 19.2 | 2.9 | 3.8 | |
| Back Extension | tcycle | 2/2/2/2 | 2/2/2/2 | 0.97 (0.91 0.99) | 0.98 (0.96 0.99) | 7.4 | 7.6 | 17.3 | 17.8 | 4.4 | 3.5 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.95 (0.91 0.98) | 0.96 (0.94 0.98) | 9.4 | 10.4 | 21.9 | 24.2 | 4.2 | 3.7 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.96 (0.87 0.98) | 0.97 (0.95 0.99) | 9.3 | 9.2 | 21.8 | 21.4 | 4.7 | 3.7 | |
| Push-up | tcycle | 2/2/2/2 | 2/2/2/2 | 0.96 (0.87 0.98) | 0.96 (0.93 0.98) | 5.6 | 7.0 | 13.0 | 16.4 | 3.1 | 3.1 |
| tphase1 | 2/2/2/2 | 2/2/2/2 | 0.92 (0.78 0.97) | 0.95 (0.90 0.97) | 9.2 | 9.3 | 21.5 | 21.8 | 3.5 | 3.1 | |
| tphase2 | 2/2/2/2 | 2/2/2/2 | 0.93 (0.86 0.97) | 0.95 (0.91 0.98) | 7.5 | 7.6 | 17.5 | 17.6 | 2.8 | 3.5 | |
| Movement Measures Expressed as %tcycle (%tphase1, %tphase2) | |||||||||||
| Two-leg hop | %phase1 | 2/2/2/2 | 2/2/2/2 | 0.86 (0.70 0.94) | 0.90 (0.80 0.95) | 4.4 | 4.3 | 10.3 | 10.1 | 1.2 | 0.9 |
| %phase2 | 2/2/2/2 | 2/2/2/2 | 0.86 (0.70 0.94) | 0.89 (0.79 0.95) | 4.0 | 4.1 | 9.3 | 9.5 | 1.1 | 0.8 | |
| Lunge | %phase1 | 2/2/2/2 | 2/2/2/2 | 0.86 (0.71 0.93) | 0.91 (0.83 0.95) | 2.4 | 2.4 | 5.5 | 5.6 | 0.6 | 0.8 |
| %phase2 | 2/2/2/2 | 2/2/2/2 | 0.86 (0.71 0.93) | 0.91 (0.83 0.95) | 2.7 | 2.7 | 6.3 | 6.3 | 0.7 | 0.9 | |
| Squat | %phase1 | 2/2/2/2 | 2/2/2/2 | 0.80 (0.70 0.86) | 0.83 (0.75 0.91) | 3.8 | 3.2 | 8.8 | 7.5 | 0.7 | 0.9 |
| %phase2 | 2/2/2/2 | 2/2/2/2 | 0.80 (0.70 0.86) | 0.83 (0.75 0.91) | 3.7 | 3.2 | 8.7 | 7.4 | 0.7 | 0.9 | |
| Sit-up | %phase1 | 2/2/2/2 | 2/2/2/2 | 0.79 (0.55 0.90) | 0.85 (0.72 0.92) | 3.4 | 3.1 | 7.9 | 7.3 | 0.7 | 0.9 |
| %phase2 | 2/2/2/2 | 2/2/2/2 | 0.79 (0.55 0.90) | 0.85 (0.72 0.92) | 3.3 | 3.1 | 7.7 | 7.1 | 0.7 | 0.9 | |
| Shoulder Abduction | %phase1 | 2/2/2/2 | 2/2/2/2 | 0.83 (0.64 0.92) | 0.89 (0.79 0.94) | 2.1 | 2.2 | 4.8 | 5.1 | 0.5 | 0.9 |
| %phase2 | 2/2/2/2 | 2/2/2/2 | 0.83 (0.64 0.92) | 0.89 (0.79 0.94) | 2.0 | 2.1 | 4.6 | 4.9 | 0.5 | 0.9 | |
| Hip Abduction | %phase1 | 5/2/2/2 | 2/2/2/2 | 0.75 (0.47 0.89) | 0.80 (0.63 0.90) | 5.5 | 5.3 | 12.8 | 12.4 | 1.0 | 0.9 |
| %phase2 | 5/2/2/2 | 2/2/2/2 | 0.75 (0.47 0.89) | 0.80 (0.63 0.90) | 5.1 | 5.0 | 11.8 | 11.6 | 0.9 | 0.9 | |
| Back Extension | %phase1 | 13/2/2/2 | 5/2/2/2 | 0.77 (0.52 0.89) | 0.76 (0.56 0.88) | 6.7 | 6.0 | 15.5 | 13.9 | 0.9 | 0.9 |
| %phase2 | 12/2/2/2 | 5/2/2/2 | 0.79 (0.57 0.90) | 0.76 (0.56 0.88) | 6.1 | 5.6 | 14.2 | 13.0 | 0.8 | 0.9 | |
| Push-up | %phase1 | 5/2/2/2 | 5/2/2/2 | 0.75 (0.28 0.83) | 0.78 (0.59 0.89) | 3.9 | 3.1 | 9.1 | 7.3 | 0.5 | 0.9 |
| %phase2 | 5/2/2/2 | 5/2/2/2 | 0.75 (0.28 0.83) | 0.78 (0.59 0.89) | 4.1 | 3.3 | 9.5 | 7.6 | 0.5 | 0.9 | |
References
- Allseits, E.K.; Lučarević, J.; Gailey, R.; Agrawal, V.; Gaunaurd, I.; Bennett, C.L. The Development and Concurrent Validity of a Real-Time Algorithm for Temporal Gait Analysis Using Inertial Measurement Units. J. Biomech. 2017, 55, 27–33. [Google Scholar] [CrossRef]
- Cudejko, T.; Button, K.; Al-Amri, M. Validity and Reliability of Accelerations and Orientations Measured Using Wearable Sensors during Functional Activities. Sci. Rep. 2022, 12, 14619. [Google Scholar] [CrossRef] [PubMed]
- Emmanouil, A.; Rousanoglou, E.; Georgaki, A.; Boudolos, K. Concurrent Validity of Inertially Sensed Measures during Voluntary Body Sway in Silence and While Exposed to a Rhythmic Acoustic Stimulus: A Pilot Study. Digit. Biomark. 2021, 5, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.-C.; Hsu, Y.; Shih, K.-S.; Lu, J. Real-Time GAIT Cycle Parameter Recognition Using a Wearable Accelerometry System. Sensors 2011, 11, 7314–7326. [Google Scholar] [CrossRef] [PubMed]
- Ader, L.G.M.; Greene, B.R.; McManus, K.; Tubridy, N.; Caulfield, B. Short Bouts of Gait Data and Body-Worn Inertial Sensors Can Provide Reliable Measures of Spatiotemporal Gait Parameters from Bilateral Gait Data for Persons with Multiple Sclerosis. Biosensors 2020, 10, 128. [Google Scholar] [CrossRef]
- Ader, L.G.M.; Greene, B.R.; McManus, K.; Caulfield, B. Reliability of Inertial Sensor Based Spatiotemporal Gait Parameters for Short Walking Bouts in Community Dwelling Older Adults. Gait Posture 2021, 85, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Bourke, A.K.; Scotland, A.; Lipsmeier, F.; Gossens, C.; Lindemann, M. Gait Characteristics Harvested during a Smartphone-Based Self-Administered 2-Minute Walk Test in People with Multiple Sclerosis: Test-Retest Reliability and Minimum Detectable Change. Sensors 2020, 20, 5906. [Google Scholar] [CrossRef] [PubMed]
- Cormack, S.J.; Newton, R.U.; McGuigan, M.R.; Doyle, T. Reliability of Measures Obtained during Single and Repeated Countermovement Jumps. Int. J. Sports Physiol. Perform. 2008, 3, 131–144. [Google Scholar] [CrossRef] [PubMed]
- Hamill, J.; McNiven, S.L. Reliability of Selected Ground Reaction Force Parameters during Walking. Hum. Mov. Sci. 1990, 9, 117–131. [Google Scholar] [CrossRef]
- Racic, V.; Pavic, A.; Brownjohn, J.M. Number of Successive Cycles Necessary to Achieve Stability of Selected Ground Reaction Force Variables during Continuous Jumping. J. Sports Sci. Med. 2009, 8, 639. [Google Scholar]
- Oliveira, A.S.; Pirscoveanu, C.-I. Implications of Sample Size and Acquired Number of Steps to Investigate Running Biomechanics. Sci. Rep. 2021, 11, 3083. [Google Scholar] [CrossRef] [PubMed]
- Connaboy, C.; Coleman, S.; Moir, G.L.; Sanders, R. Measures of Reliability in the Kinematics of Maximal Undulatory Underwater Swimming. Med. Sci. Sports Exerc. 2010, 42, 762–770. [Google Scholar] [CrossRef]
- Venek, V.; Kranzinger, S.; Schwameder, H.; Stöggl, T. Human Movement Quality Assessment Using Sensor Technologies in Recreational and Professional Sports: A Scoping Review. Sensors 2022, 22, 4786. [Google Scholar] [CrossRef]
- Cuesta-Vargas, A.; Galán-Mercant, A.; Williams, J.M. The Use of Inertial Sensors System for Human Motion Analysis. Phys. Ther. Rev. 2010, 15, 462–473. [Google Scholar] [CrossRef] [PubMed]
- Soulard, J.; Vaillant, J.; Balaguier, R.; Vuillerme, N. Spatio-Temporal Gait Parameters Obtained from Foot-Worn Inertial Sensors Are Reliable in Healthy Adults in Single- and Dual-Task Conditions. Sci. Rep. 2021, 11, 10229. [Google Scholar] [CrossRef] [PubMed]
- Forrester, S.E. Selecting the Number of Trials in Experimental Biomechanics Studies. Int. Biomech. 2015, 2, 62–72. [Google Scholar] [CrossRef]
- King, A.C.; Hannan, K.B. Segment Coordination Variability during Double Leg Bodyweight Squats at Different Tempos. Int. J. Sports Med. 2019, 40, 725–731. [Google Scholar] [CrossRef]
- Šerbetar, I. Establishing Some Measures of Absolute and Relative Reliability of a Motor Tests. Croat. J. Educ. 2014, 17, 37–48. [Google Scholar] [CrossRef]
- Grgic, J.; Schoenfeld, B.J.; Skrepnik, M.; Davies, T.B.; Mikulic, P. Effects of Rest Interval Duration in Resistance Training on Measures of Muscular Strength: A Systematic Review. Sports Med. 2018, 48, 137–151. [Google Scholar] [CrossRef]
- Atkinson, G.; Nevill, A.M. Statistical Methods For Assessing Measurement Error (Reliability) in Variables Relevant to Sports Medicine. Sports Med. 1998, 26, 217–238. [Google Scholar] [CrossRef]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef]
- Fleiss, J.L. The Design and Analysis of Clinical Experiments; Willey: New York, NY, USA, 1986. [Google Scholar]
- Pedersen, B.S.; Kristensen, M.T.; Josefsen, C.O.; Lykkegaard, K.L.; Jønsson, L.R.; Pedersen, M.M. Validation of Two Activity Monitors in Slow and Fast Walking Hospitalized Patients. Rehabil. Res. Pract. 2022, 2022, 9230081. [Google Scholar] [CrossRef] [PubMed]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Weir, J.P. Quantifying Test-Retest Reliability Using the Intraclass Correlation Coefficient and the SEM. J. Strength Cond. Res. 2005, 19, 231. [Google Scholar] [CrossRef] [PubMed]
- Kribus-Shmiel, L.; Zeilig, G.; Sokolovski, B.; Plotnik, M. How Many Strides Are Required for a Reliable Estimation of Temporal Gait Parameters? Implementation of a New Algorithm on the Phase Coordination Index. PLoS ONE 2018, 13, e0192049. [Google Scholar] [CrossRef] [PubMed]
- Widler, K.; Glatthorn, J.F.; Bizzini, M.; Impellizzeri, F.M.; Munzinger, U.; Leunig, M.; Maffiuletti, N.A. Assessment of Hip Abductor Muscle Strength. A Validity and Reliability Study. J. Bone Jt. Surg. Am. Vol. 2009, 91, 2666–2672. [Google Scholar] [CrossRef] [PubMed]
- Shimano, T.; Kraemer, W.J.; Spiering, B.A.; Volek, J.S.; Hatfield, D.L.; Silvestre, R.; Vingren, J.L.; Fragala, M.S.; Maresh, C.M.; Fleck, S.J.; et al. Relationship between the Number of Repetitions and Selected Percentages of One Repetition Maximum in Free Weight Exercises in Trained and Untrained Men. J. Strength Cond. Res. 2006, 20, 819. [Google Scholar] [CrossRef]
- Stergiou, N.; Decker, L.M. Human Movement Variability, Nonlinear Dynamics, and Pathology: Is There a Connection? Hum. Mov. Sci. 2011, 30, 869–888. [Google Scholar] [CrossRef]
- Bruton, A.; Conway, J.; Holgate, S.T. Reliability: What Is It, and How Is It Measured? Physiotherapy 2000, 86, 94–99. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emmanouil, A.; Rousanoglou, E.; Boudolos, K. Two Repetitions May Be Enough! Reliability of Movement Timing in Physical Fitness Exercises Performed by Young, Trained Adults Using Inertial Sensors. Biomechanics 2024, 4, 84-108. https://doi.org/10.3390/biomechanics4010006
Emmanouil A, Rousanoglou E, Boudolos K. Two Repetitions May Be Enough! Reliability of Movement Timing in Physical Fitness Exercises Performed by Young, Trained Adults Using Inertial Sensors. Biomechanics. 2024; 4(1):84-108. https://doi.org/10.3390/biomechanics4010006
Chicago/Turabian StyleEmmanouil, Analina, Elissavet Rousanoglou, and Konstantinos Boudolos. 2024. "Two Repetitions May Be Enough! Reliability of Movement Timing in Physical Fitness Exercises Performed by Young, Trained Adults Using Inertial Sensors" Biomechanics 4, no. 1: 84-108. https://doi.org/10.3390/biomechanics4010006







