1.1. Background
Nowadays, energy and environmental issues are among the most pressing challenges facing humanity, yet they remain difficult to resolve. Non-renewable energy sources are expensive to exploit and will eventually run out [
1], so over-reliance on these sources is not a sustainable way to progress. The other issue in terms of the environment is global warming, which is caused primarily by the emission of greenhouse gases, especially carbon dioxide (CO
2) [
2]. It is reported that fossil fuel power generation and construction industries account for a large portion of the world’s CO
2 emissions [
3,
4]. Therefore, developing clean energy solutions and improving emissions from the construction sector are crucial steps for countries to meet carbon emission standards.
Renewable energy accounted for about 29% of global electricity generation in 2020, according to the International Energy Agency’s (IEA) report on global electricity [
3]. While this is a significant increase from previous years, it still represents a relatively small proportion of the world’s total electricity generation. Nevertheless, the growth in renewable energy is a positive sign and a highlight. As the demand for renewable energy continues to rise, photovoltaic solar power generation has become a promising area of development. However, constructing a solar farm requires special foundation systems to support the weight of the solar panels as well as lateral load action on these panels caused by wind.
H-shaped steel piles are commonly employed in modern solar farms as conventional pile structures. However, as highlighted by Rajapakse [
5], when H-shaped steel is “unplugged”, it has a small end bearing capacity but a large side friction, which is equivalent to a shaft resist pile. When subjected to lateral loads, their resistance mechanism predominantly depends on the flange area to counteract the lateral force. Nevertheless, the options for enhancing the horizontal capacity of H-shaped steel piles in the face of increased lateral loads are quite limited and costly. For instance, when increasing the flange width to improve the lateral capacity, the whole pile shafts will need to be increased, whereas only the top pile area requires such improvement, which will consequently lead to material waste and increased cost. In contrast, helical pipe piles offer a viable alternative by introducing a single helical plate to enhance the overall horizontal bearing capacity. The functioning principle of helical pipe piles is akin to that of an anchor, as they anchor into the soil, providing substantial bearing capacity. Consequently, the implementation of helical pipe piles offers a highly dependable solution, ensuring reliable bearing capacity while simultaneously minimizing material and financial wastage.
Spagnoli and de Hollanda Cavalcanti Tsuha [
6] have emphasized the preference for helical pipe piles over ordinary piles in practical applications. These piles offer numerous advantages, including swift and noise-free installation, low maintenance requirements, and the ability to be easily installed in confined spaces and even on slopes. Additionally, helical piles exhibit convenient disassembly and reusability, making them highly versatile. They can be effectively employed in challenging scenarios with difficult water tables and deliver ample compression and tensile capacity [
6,
7,
8,
9,
10,
11]. Furthermore, Vignesh and Mayakrishnan [
11] have highlighted the diverse applications of helical pipe piles, which include serving as uplift resistance in tunnel support systems, foundations for transmission towers, excavation support, and both land and offshore structures. Moreover, Vignesh and Mayakrishnan [
11] consider helical pipe piles as an ideal and cost-effective choice for underwater structures, particularly for ensuring stability in submarine pipelines.
The use of screw piles or helical pipe piles can be traced back to 1838, when Alexander Mitchell employed them to support the Maplin Sands Lighthouse on the Thames [
8]. However, the construction of helical pipe piles has faced significant challenges due to its intricate torsion-based construction method, impeding its development and research. The advent of hydraulic torque has brought attention to helical pipe piles and initiated preliminary research and development efforts [
8].
Various computational methods have been developed to determine the pull and compressive capacity of helical pipe piles in cohesive and non-cohesive soils, including the individual method (b) and the cylindrical method [
8,
11,
12,
13,
14]. Field tests conducted by Lutenegger [
15] have yielded results consistent with the laboratory tests conducted by Rao and Prasad [
16]. When the spacing ratio (SR), defined as the helical plate spacing divided by the helical plate diameter, is 1.5, it has been observed that the behavior of helical pipe piles exhibits individual plate bearing [
17]. In soft to medium-hard clay, Rao et al. [
17] determined that the optimal pull-out state of helical piles should have an SR value between 1 and 1.5. Hird and Stanier [
18] found that when SR = 1.5, the compressive capacity of a pile with three helical plates was greater than that of a pile with one helical plate. Merifield [
19] demonstrated that when SR is 1.58, the failure mechanism of helical piles transitions from cylindrical shear mode to single-board load mode.
Apart from the SR, there are many factors that may lead to changes in the bearing capacity of the helical pile, such as embedment ratios (H/D, the ratio of the depth between the top screw and the ground to the diameter of the top screw plate). Vignesh and Mayakrishnan [
11] pointed out that the increase in H/D will increase the bearing capacity, but the research results of Merifield [
19] showed that when H/D > 4, the increase in bearing capacity becomes less obvious. Trofimenkov and Mariupolskii [
20] showed that the damage to the soil on the helical pile of a single helical plate depends on H/D, and the critical value of H/D refers to the depth of the helical plate that leads to the damage to the soil. Trofimenkov and Mariupolskii [
20] obtained the critical value of H/D of the helical pile through experiments (H/D = 4–5 in clay; H/D = 5–6 in sand). Vignesh and Mayakrishnan [
11] pointed out that when H/D > critical value of H/D, the damage to the helical pile will not cause surface uplift. In this case, the load is transferred from the pile to the soil through the helical plate and shaft, and the bearing capacity depends on the depth of the helical plate. When H/D < the critical value of H/D, the soil mass of the helical plate will bulge in the limit state. In addition, the research results of Nazir et al. [
21] and El-Rahim et al. [
7] also pointed out that the embedment depth of the helical plate would also affect its axial bearing capacity. Perko [
8] suggested that the depth of the helical plate should be large enough, and placing the helical plate too close to the surface would cause shallow damage.
Merifield [
19] highlighted the somewhat unsatisfactory state of current knowledge regarding the design of helical anchors, which has remained largely unchanged over the past two decades. Despite the increasing popularity of helical pipe piles in the field of engineering and the growing demand for screw piles, there remains an insufficient amount of research conducted on helical pipe piles. Consequently, there is a need for further studies to bridge these research gaps [
11,
22,
23].
While Prasad and Rao [
24] investigated the lateral load capacity of helical pipe piles and found that their horizontal bearing capacity was 1.2–1.5 times that of helical plate piles, Abdrabbo and Wakil [
25] have emphasized the scarcity of research on helical pipe piles under lateral load. Several factors, including spiral plates, soil characteristics, diameter, number, and spacing of spiral blades, can influence the horizontal bearing capacity of helical pipe piles [
25].
In the application of actual solar farms, helical piles have the advantages of high cost effectiveness, fast installation speed, strong tensile strength, environmental protection, etc., so they have been used in solar farms in Canada, the United States, and China to solve the problem of frost [
26]. Sirivachiraporan and Wattanachannarong [
27] also pointed out the use of helical piles in some solar farms in Thailand to improve carrying capacity. However, in the past application, the main purpose was to improve the axial bearing capacity through helical piles. Helical piles are ideal foundations for application in solar farms, and the application in solar farms has obvious capacity improvement [
28]. However, Li et al. [
12] pointed out in 2022 that the research on helical piles’ horizontal bearing capacity is limited and further research is needed. Therefore, to gain a better understanding of the horizontal capacity of helical pipe piles, this study conducted relevant research on the impact of soil parameters on helical pipe pile performance through numerical simulations utilizing ABAQUS (2022) software.
1.2. Research Purpose and Significance
Previous research indicates that further investigation is necessary to gain a comprehensive understanding of helical piles and their potential applications. With the aim of providing robust support for the solar energy industry, this study seeks to analyze and compare the lateral ultimate bearing capacity of helical pipe piles and steel pipe piles in clay under horizontal load. To achieve this goal, the study will utilize ABAQUS software to conduct finite element analysis and simulate various types of clay’s geological conditions through numerical simulation.
With the advancement of science and technology and the increasing global focus on clean energy, solar farms have found practical applications worldwide.
Figure 1 depicts a conventional solar farm in New Zealand, where the solar panels are stationary and lack the ability to rotate. Observing the figure reveals that, due to this fixed orientation, the solar panels cannot consistently maintain optimal positioning as the sun’s position changes.
To enhance the efficiency of solar panels, a United States-based company has introduced an innovative solar system that employs a “tracker” mechanism to control panel rotation. This technology ensures that the solar panel plane maintains a vertical angle with sunlight by tracking the sun’s movement, as illustrated in
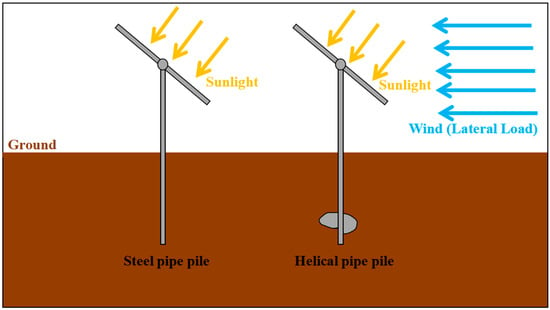
Figure 2. The optimization of solar farms’ efficiency is achieved through precise control of the “tracker”. However, the ensuing problem is that when the rotation angle of the solar panel is too large, the contact area between the solar panel and the wind becomes larger, which requires a higher horizontal bearing capacity of the pile at the bottom of the solar panel.
To promote the sustainable development of clean energy (solar energy), and the application and promotion of the “tracker” system, this paper compares two types of piles to investigate their lateral bearing capacity: one with a helical plate and the other without. Additionally, the study examines the effects of varying clay parameters on the Young’s modulus and cohesion of the soil.
In consideration of material application in civil engineering, this study has selected a minimum standard outside diameter (O.D.) of 76.1 mm for piles. However, future research will also include larger O.D. piles available on the market as a variable for comparison.
Although helical pipe piles are becoming increasingly prevalent in the construction industry, their application scope remains limited worldwide. In light of this, this study seeks to showcase the advantages of helical pipe piles in enhancing horizontal ultimate bearing capacity through finite element analysis, building on current in-depth analysis and research into their applications in construction.