Strategic Analysis of the Pricing Mechanisms in an Online Book Supply Chain in the Presence of Reference Price Effects
Abstract
:1. Introduction
2. Literature Review
3. Model Setup
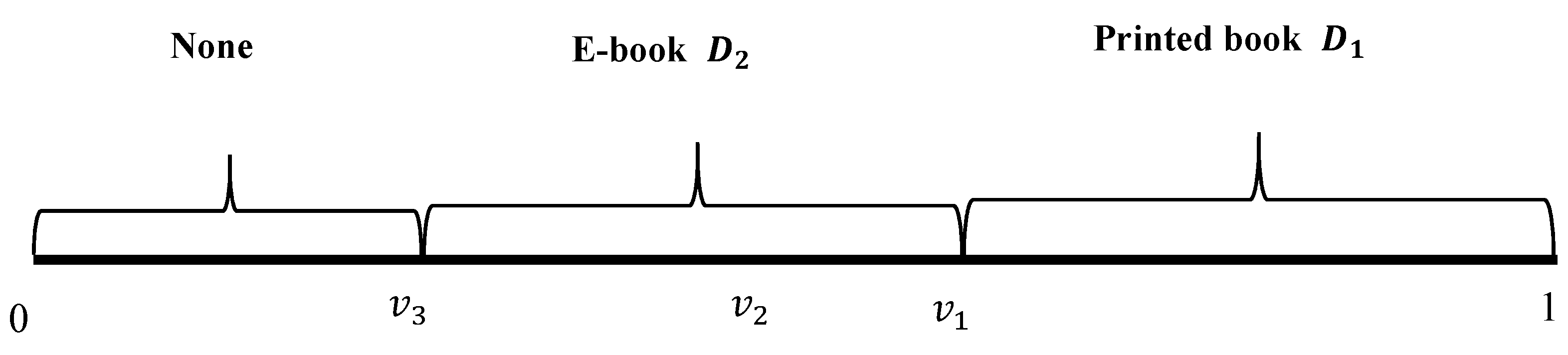
3.1. Consumer
3.2. Profit Function
4. Analysis
4.1. Benchmark without Reference Price Effects
- (i)
- when, the retailer will undercut the cover price. The optimal prices are:,and.
- (ii)
- when, the retailer will set the retail price in compliance with the cover price. The optimal prices areand.
4.2. Model with Reference Price Effects
- (i)
- Whenthe publisher only publishes printed books and the optimal prices areand
- (ii)
- When, the publisher publishes both versions of the book and the optimal prices are: and.
- (iii)
- When, the publisher publishes both versions of book and the optimal prices are:=and=.
- (iv)
- When, the optimal prices are,and.
- (v)
- When, the publishers will not sell the book.
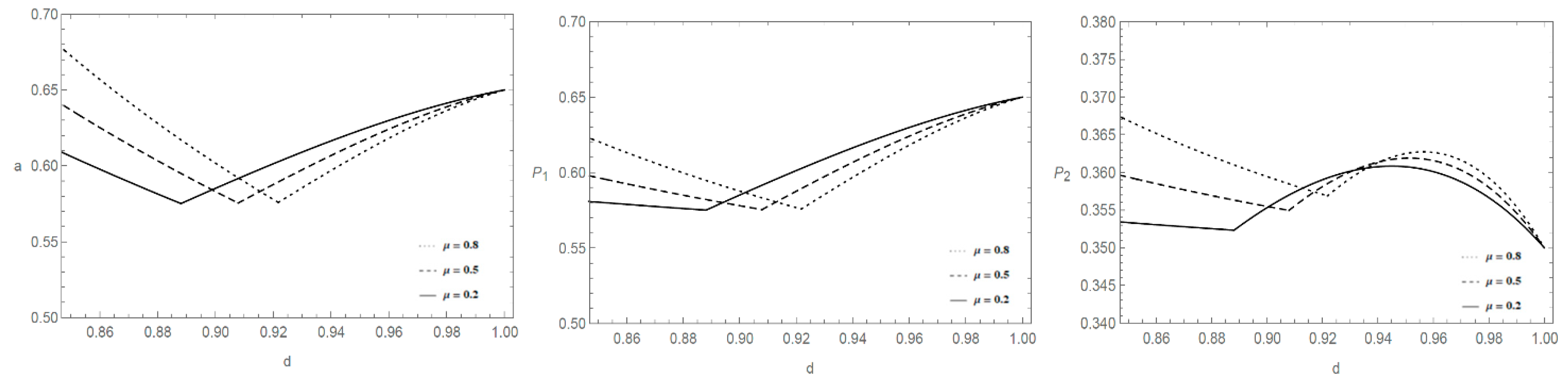
4.3. The Effects of Wholesale Discount Rate
4.4. Reference Price Effects
5. Extension: Reference Price for E-Books
- (1)
- whenandthe retailer will undercut the cover price.
- (2)
- if, whenthe retailer will set the retail price to coincide with the cover price.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Case 1:m = 0, n = 0
- Case 2:
- Case 3:
- Case 4:
- Case 1:
- Case 2:
- Case 3:
- Case 4:
- An alternative time sequence of main model
- Case 1:
- Case 2:
- Case 3:
- Case 4:h
References
- Cheng, Y.; Dong, C.; Liu, R. The coexistence of printed book and electronic book in a book supply chain. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017; pp. 1421–1425. [Google Scholar]
- Lu, Q.H.; Shi, V.; Huang, J.Z. Who benefit from agency model: A strategic analysis of pricing models in distribution channels of physical books and e-books. Eur. J. Oper. Res. 2018, 264, 1074–1091. [Google Scholar] [CrossRef]
- Hua, G.; Cheng, T.C.E.; Wang, S. Electronic books: To “E” or not to “E”? A strategic analysis of distribution channel choices of publishers. Int. J. Prod. Econ. 2011, 129, 338–346. [Google Scholar] [CrossRef]
- Count, S.D. Global Book Printing Market Is Anticipated to Reach Values of around $49 Billion by 2024, Growing at A CAGR of More than 1% during 2020–2024. Available online: https://www.comserveonline.com/news-releases/global-book-printing-market-is-anticipated-to-reach-values-of-around-49-billion-by-2024-growing-at-a-cagr-of-more-than-1-during-2020-2024/10027601 (accessed on 19 March 2021).
- Fabrizi, S.; Lippert, S.; Puppe, C.; Rosenkranz, S. Manufacturer suggested retail prices, loss aversion and competition. J. Econ. Psychol. 2016, 53, 141–153. [Google Scholar] [CrossRef]
- Rosenkranz, S. The Manufacturer’s Suggested Retail Price; Utrecht School of Economics: Utrecht, The Netherlands, 2003. [Google Scholar]
- Malekian, Y.; Rasti-Barzoki, M. A game theoretic approach to coordinate price promotion and advertising policies with reference price effects in a two-echelon supply chain. J. Retail. Consum. Serv. 2019, 51, 114–128. [Google Scholar] [CrossRef]
- Bruttel, L. The Effects of Non-Binding Retail-Price Recommendations on Consumer and Retailer Behavior; Thurgauer Wirtschaftsinstitut, Universität Konstanz: Konstanz, Germany, 2014. [Google Scholar]
- Ariely, D.; Loewenstein, G.; Prelec, D. “Coherent Arbitrariness”: Stable Demand Curves Without Stable Preferences. Q. J. Econ. 2003, 118, 73–106. [Google Scholar] [CrossRef] [Green Version]
- Corson-Knowles, T. 9 Amazon Book Promotion Programs that Can Help You Sell More Books Every Day. Available online: https://www.tckpublishing.com/amazon-book-promotion-programs/ (accessed on 19 March 2021).
- Department, S.R. Which Product Category Interests You Most in Terms of Discounts? Available online: https://www.statista.com/statistics/858043/discount-interest-germany/ (accessed on 19 March 2021).
- Wanat, G. Factors Contributing to the Decision to Purchase a Book in Poland in 2019. Available online: https://www.statista.com/statistics/1077726/poland-factors-in-buying-books/ (accessed on 19 March 2021).
- De los Santos, B.; Kim, I.K.; Lubensky, D. Do MSRPs decrease prices? Int. J. Ind. Organ. 2018, 59, 429–457. [Google Scholar] [CrossRef]
- Atasoy, O.; Morewedge, C.K. Digital Goods Are Valued Less Than Physical Goods. J. Consum. Res. 2018, 44, 1343–1357. [Google Scholar] [CrossRef] [Green Version]
- Sehn, T.C.M.; Fragoso, S. The synergy between eBooks and printed books in Brazil. Online Inf. Rev. 2015, 39, 401–415. [Google Scholar] [CrossRef]
- Mooney, S. Digital object identifiers for eBooks: What are we identifying? Publ. Res. Q. 2001, 17, 29–36. [Google Scholar] [CrossRef]
- De Young, N. How Digital Content Resellers are Impacting Trade Book Publishing. Publ. Res. Q. 2009, 25, 139–146. [Google Scholar] [CrossRef]
- Ramaiah, C.K. An overview of electronic books: A bibliography. Electron. Libr. 2005, 23, 17–44. [Google Scholar] [CrossRef] [Green Version]
- Bounie, D.; Eang, B.; Sirbu, M.; Waelbroeck, P. Superstars and outsiders in online markets: An empirical analysis of electronic books. Electron. Commer. Res. Appl. 2013, 12, 52–59. [Google Scholar] [CrossRef]
- Chen, H.L.; Hu, Y.J.; Smith, M.D. The Impact of E-book Distribution on Print Sales: Analysis of a Natural Experiment. Manag. Sci. 2019, 65, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Lin, Z.; Xu, L.; Swain, A. “Do the electronic books reinforce the dynamics of book supply chain market?”–A theoretical analysis. Eur. J. Oper. Res. 2015, 245, 591–601. [Google Scholar] [CrossRef]
- Li, F.; Li, S.L.; Gu, J.R. Whether to Delay the Release of eBooks or Not? An Analysis of Optimal Publishing Strategies for Book Publishers. J. Theor. Appl. Electron. Commer. Res. 2019, 14, 124–137. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Tang, W. Analysis of Network Effect in the Competition of Self- Publishing Market. J. Theor. Appl. Electron. Commer. Res. 2020, 15, 50–68. [Google Scholar] [CrossRef]
- Hao, L.; Fan, M. An Analysis of Pricing Models in the Electronic Book Market. MIS Q. 2014, 38, 1017–1032. [Google Scholar] [CrossRef]
- Tan, Y.L.; Carrillo, J.E. Strategic Analysis of the Agency Model for Digital Goods. Prod. Oper. Manag. 2017, 26, 724–741. [Google Scholar] [CrossRef]
- Wang, R.X. When Prospect Theory Meets Consumer Choice Models: Assortment and Pricing Management with Reference Prices. Manuf. Serv. Oper. Manag. 2018, 20, 583–600. [Google Scholar] [CrossRef]
- Winer, R.S. A Reference Price Model of Brand Choice for Frequently Purchased Products. J. Consum. Res. 1986, 13, 250–256. [Google Scholar] [CrossRef]
- Zha, Y.; Zhang, L.; Xu, C.; Zhang, T. A two-period pricing model with intertemporal and horizontal reference price effects. Int. Trans. Oper. Res. 2018, 28, 1417–1440. [Google Scholar] [CrossRef]
- Rajendran, K.N.; Tellis, G.J. Contextual and Temporal Components of Reference Price. J. Mark. 1994, 58, 22–34. [Google Scholar] [CrossRef]
- DellaVigna, S. Psychology and Economics: Evidence from the Field. J. Econ. Lit. 2009, 47, 315–372. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.H.; Lim, N.; Camerer, C.F. Modeling the Psychology of Consumer and Firm Behavior with Behavioral Economics. J. Mark. Res. 2006, 43, 307–331. [Google Scholar] [CrossRef] [Green Version]
- Andres-Martinez, M.E.; Gomez-Borja, M.A.; Mondejar-Jimenez, J.A. A model to evaluate the effects of price fairness perception in online hotel booking. Electron. Commer. Res. 2014, 14, 171–187. [Google Scholar] [CrossRef]
- Chen, K.H.; Zha, Y.; Alwan, L.C.; Zhang, L. Dynamic pricing in the presence of reference price effect and consumer strategic behaviour. Int. J. Prod. Res. 2020, 58, 546–561. [Google Scholar] [CrossRef]
- Zhao, N.G.; Wang, Q.; Cao, P.; Wu, J. Dynamic pricing with reference price effect and price-matching policy in the presence of strategic consumers. J. Oper. Res. Soc. 2019, 70, 2069–2083. [Google Scholar] [CrossRef]
- Fibich, G.; Gavious, A.; Lowengart, O. Explicit solutions of optimization models and differential games with nonsmooth (asymmetric) reference-price effects. Oper. Res. 2003, 51, 721–734. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, X.; Hu, P. Technical Note—Dynamic Pricing with Gain-Seeking Reference Price Effects. Oper. Res. 2016, 64, 150–157. [Google Scholar] [CrossRef]
- Popescu, I.; Wu, Y.Z. Dynamic pricing strategies with reference effects. Oper. Res. 2007, 55, 413–429. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, D.; Zhang, C. The influence of reference effect on pricing strategies in revenue management settings. Int. Trans. Oper. Res. 2017, 24, 907–924. [Google Scholar] [CrossRef] [Green Version]
- Bi, W.J.; Li, G.; Liu, M.Q. Dynamic pricing with stochastic reference effects based on a finite memory window. Int. J. Prod. Res. 2017, 55, 3331–3348. [Google Scholar] [CrossRef]
- Greenleaf, E.A. The Impact of Reference Price Effects on the Profitability of Price Promotions. Mark. Sci. 1995, 14, 82–104. [Google Scholar] [CrossRef]
- Fibich, G.; Gavious, A.; Lowengart, O. Optimal price promotion in the presence of asymmetric reference-price effects. Manag. Decis. Econ. 2007, 28, 569–577. [Google Scholar] [CrossRef]
- Lin, Z.B. Price promotion with reference price effects in supply chain. Transp. Res. E-Log. 2016, 85, 52–68. [Google Scholar] [CrossRef]
- Zhang, J.; Chiang, W.Y.K.; Liang, L. Strategic pricing with reference effects in a competitive supply chain. Omega 2014, 44, 126–135. [Google Scholar] [CrossRef]
- Buehler, S.; Gartner, D.L. Making Sense of Nonbinding Retail-Price Recommendations. Am. Econ. Rev. 2013, 103, 335–359. [Google Scholar] [CrossRef] [Green Version]
- Puppe, C.; Rosenkranz, S. Why Suggest Non-Binding Retail Prices? Economica 2011, 78, 317–329. [Google Scholar] [CrossRef] [Green Version]
- Leeper, D. Book Distributors and Book Wholesalers: What’s the Difference? Available online: https://www.bookmobile.com/opinion/book-distributors-and-book-wholesalers-whats-the-difference/ (accessed on 19 March 2021).
- Martin, K. Understanding Wholesale Discounte When Self-Publishing a Book. Available online: https://www.self-pub.net/blog/understanding-wholesale-discounts-when-self-publishing-a-book/ (accessed on 19 March 2021).
- Kunst, A.U.S. Consumers Attitude towards Cheaper e-Books April 2017. Available online: https://www.statista.com/statistics/707093/attitude-e-books-cheaper-than-printed-version/ (accessed on 19 March 2021).
- Thaler, R. Mental Accounting and Consumer Choice. Mark. Sci. 1985, 4, 199–214. [Google Scholar] [CrossRef]
- Amaldoss, W.; He, C. Reference-Dependent Utility, Product Variety, and Price Competition. Manag. Sci. 2018, 64, 4302–4316. [Google Scholar] [CrossRef] [Green Version]
- Sacco, A.; De Giovanni, P. Channel coordination with a manufacturer controlling the price and the effect of competition. J. Bus. Res. 2019, 96, 97–114. [Google Scholar] [CrossRef]
- Cachon, G.P.; Lariviere, M.A. Supply chain coordination with revenue-sharing contracts: Strengths and limitations. Manag. Sci. 2005, 51, 30–44. [Google Scholar] [CrossRef] [Green Version]
- De Giovanni, P. Coordination in a distribution channel with decisions on the nature of incentives and share-dependency on pricing. J. Oper. Res. Soc. 2017, 67, 1034–1049. [Google Scholar] [CrossRef]
- Clerides, S.K. Book value: Intertemporal pricing and quality discrimination in the US market for books. Int. J. Ind. Organ. 2002, 20, 1385–1408. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Loss Aversion in Riskless Choice: A Reference-Dependent Model. Q. J. Econ. 1991, 106, 1039–1061. [Google Scholar] [CrossRef]



| Variable | Description |
|---|---|
| V | Consumers’ willingness to pay for a printed book, |
| The consumers’ acceptance level of an e-book, | |
| The degree of consumers’ concern about a discount, | |
| The publisher’s wholesale discount rate of the printed book, | |
| The sales discount rate of a printed book, | |
| The wholesale price of a printed book, | |
| The publisher’s profit | |
| The online retailer’s profit | |
| The demand for printed book | |
| The demand for e-book | |
| Decision Variables | |
| The cover price of printed book | |
| The retail price of printed book | |
| The retail price of e-book | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Zeng, Y. Strategic Analysis of the Pricing Mechanisms in an Online Book Supply Chain in the Presence of Reference Price Effects. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 1492-1516. https://doi.org/10.3390/jtaer16050084
Hou W, Zeng Y. Strategic Analysis of the Pricing Mechanisms in an Online Book Supply Chain in the Presence of Reference Price Effects. Journal of Theoretical and Applied Electronic Commerce Research. 2021; 16(5):1492-1516. https://doi.org/10.3390/jtaer16050084
Chicago/Turabian StyleHou, Wenhua, and Yuwen Zeng. 2021. "Strategic Analysis of the Pricing Mechanisms in an Online Book Supply Chain in the Presence of Reference Price Effects" Journal of Theoretical and Applied Electronic Commerce Research 16, no. 5: 1492-1516. https://doi.org/10.3390/jtaer16050084
APA StyleHou, W., & Zeng, Y. (2021). Strategic Analysis of the Pricing Mechanisms in an Online Book Supply Chain in the Presence of Reference Price Effects. Journal of Theoretical and Applied Electronic Commerce Research, 16(5), 1492-1516. https://doi.org/10.3390/jtaer16050084






