Optimal Recommendation Strategies for AI-Powered E-Commerce Platforms: A Study of Duopoly Manufacturers and Market Competition
Abstract
:1. Introduction
2. Literature Review
2.1. Recommendation Systems
2.2. Duopoly Competition
2.3. Platform Operations
3. The Model
3.1. The Manufacturers and Platform
3.2. Market Demand
3.3. Timing of the Game
3.4. Assumptions and Limitations
4. Equilibrium Analysis
4.1. Mode NN
- (i)
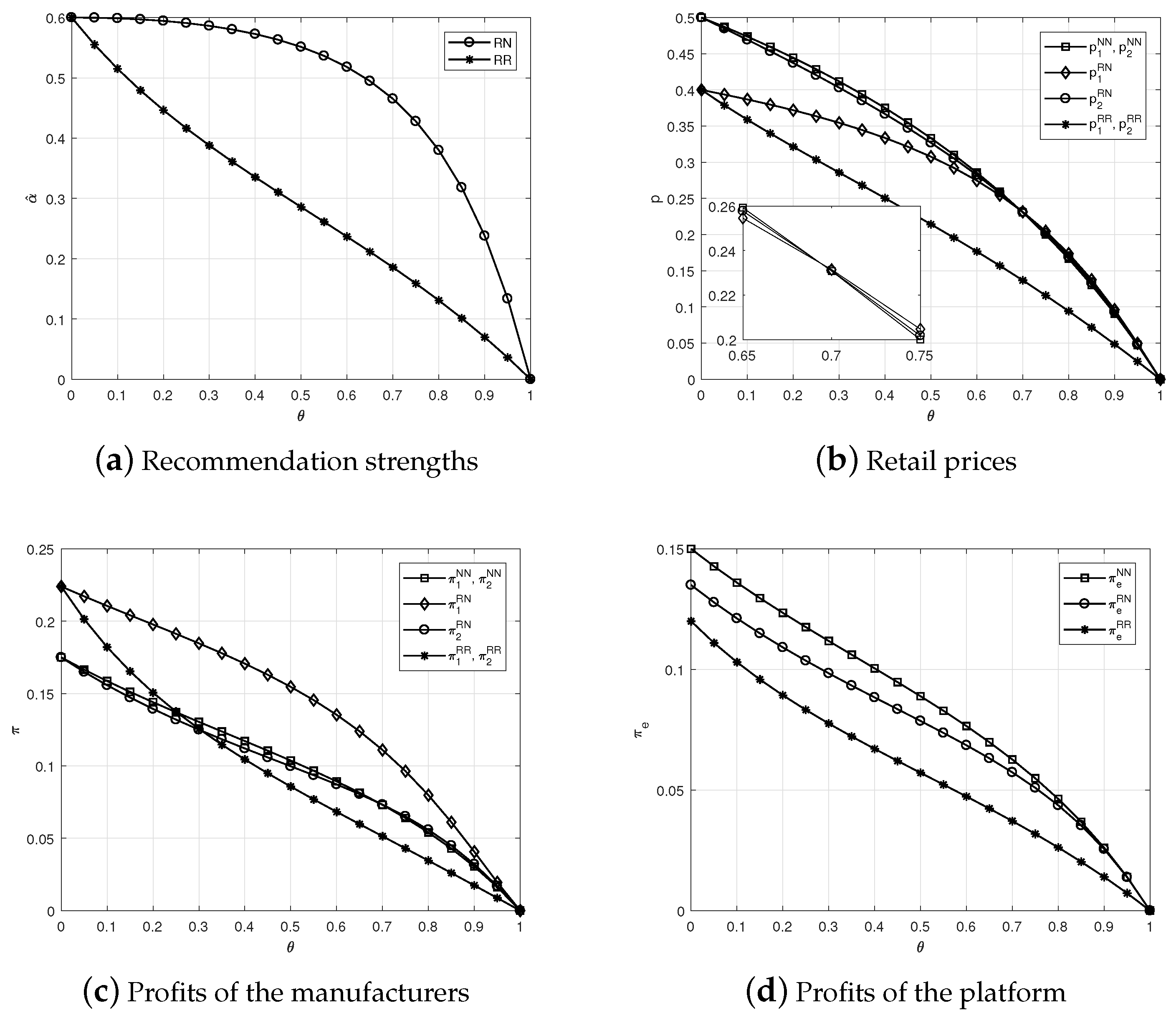
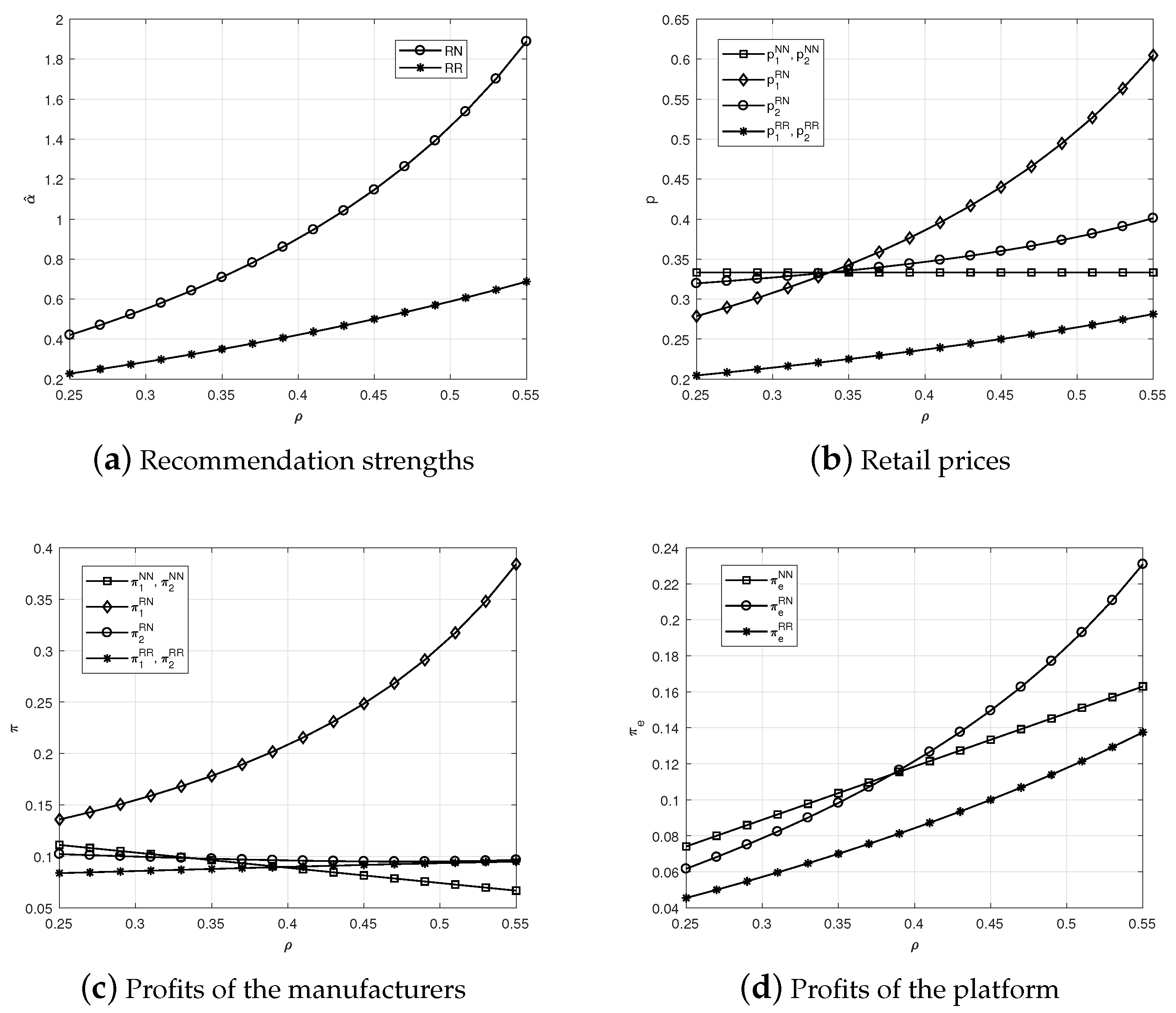
- The equilibrium prices and decrease with product substitutability θ. The profits of the manufacturers and platform , and decrease with θ.
- (ii)
- The profits of the manufacturers and decrease with ρ, whereas increases with ρ.
4.2. Mode RN
- (i)
- The equilibrium prices , and recommendation strength decrease with product substitutability θ.
- (ii)
- , and increase with commission rate ρ. When , or and , the profit of manufacturer who is recommended increases with ρ; when , or and , decreases with ρ. The profit of platform increases with ρ.
- (i)
- If , ; if , .
- (ii)
- When , if , ; if , . When , .
4.3. Mode RR
- (i)
- The equilibrium prices , and recommendation strength decrease with product substitutability θ. The profits of manufacturers , and platform decrease with θ.
- (ii)
- , and increase with commission rate ρ. When , or and , and increase with ρ; when , or and , and decrease with ρ. Moreover, the profit of platform increases with ρ.
5. Equilibrium Comparison
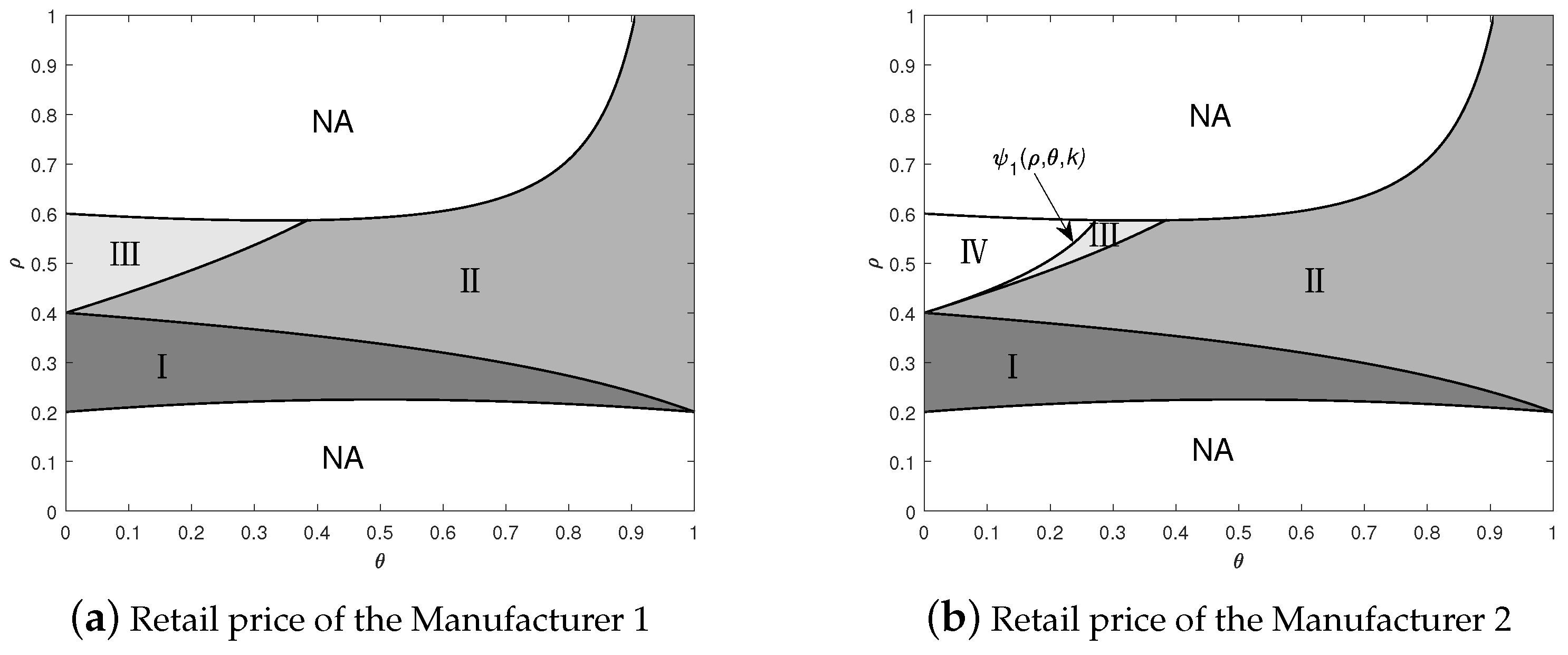
- (i)
- If , ; if , .
- (ii)
- If , ; if , .
- (iii)
- always holds.
- (i)
- If , ; if , .
- (ii)
- If , ; if , .
- (iii)
- If , ; otherwise, ,where .
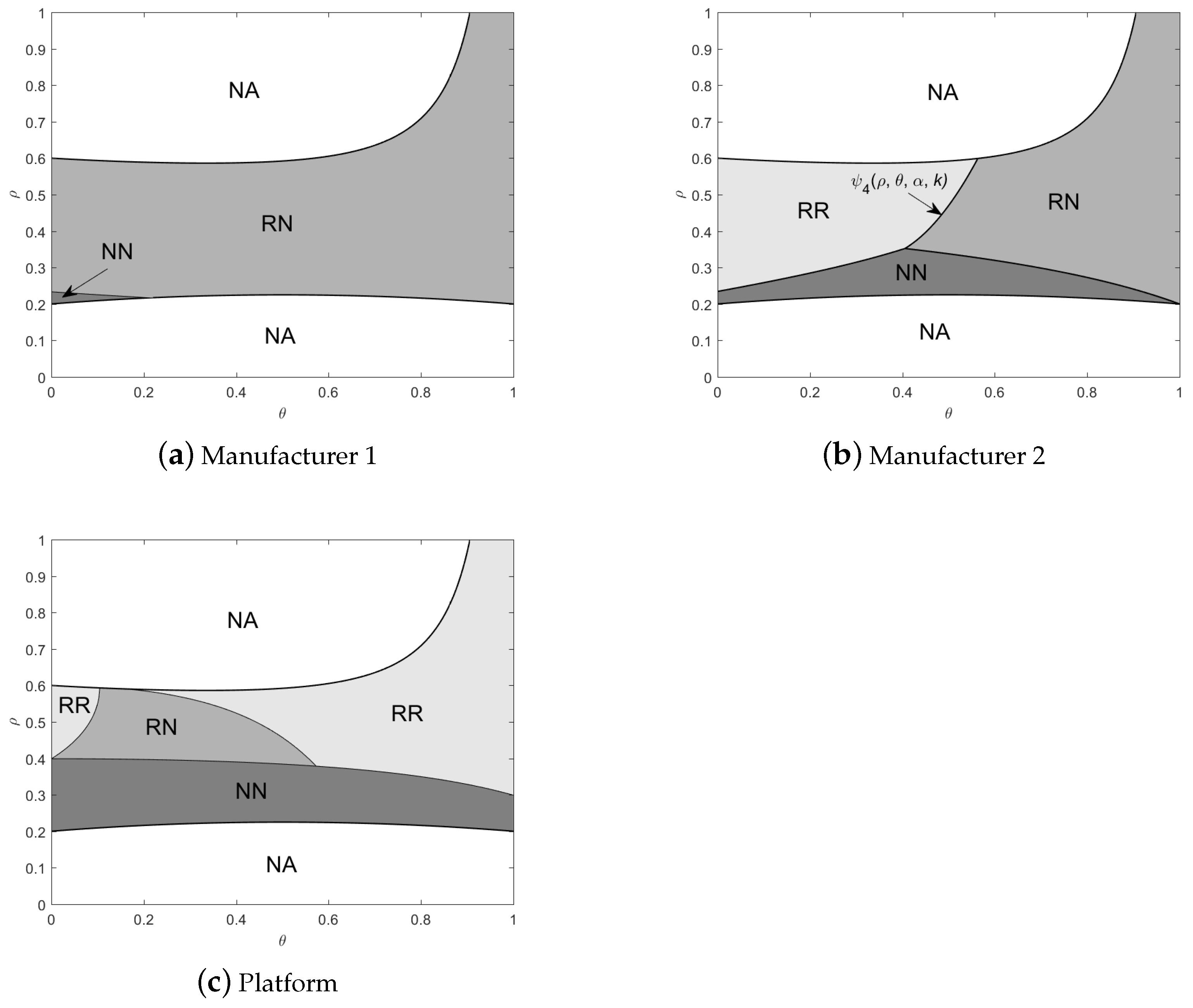
- (i)
- If , ; if , .
- (ii)
- If , ; if , .
- (iii)
- always holds.
- (i)
- If , ; if , .
- (ii)
- If , ; if , .
- (iii)
- If , ; otherwise, , where .
- (i)
- If , ;if , .
- (ii)
- If , ; if , .
- (iii)
- If , we have ; if , .
6. Conclusions and Discussion
6.1. Conclusions
6.2. Discussion
6.3. Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Hosanagar, K.; Fleder, D.; Lee, D.; Buja, A. Will the global village fracture into tribes? Recommender systems and their effects on consumer fragmentation. Manag. Sci. 2014, 60, 805–823. [Google Scholar] [CrossRef]
- Lee, D.; Hosanagar, K. How do product attributes and reviews moderate the impact of recommender systems through purchase stages? Manag. Sci. 2021, 67, 524–546. [Google Scholar] [CrossRef]
- Ettl, M.; Harsha, P.; Papush, A.; Perakis, G. A data-driven approach to personalized bundle pricing and recommendation. Manuf. Serv. Oper. Manag. 2020, 22, 461–480. [Google Scholar] [CrossRef]
- Zhou, C.; Leng, M.; Liu, Z.; Cui, X.; Yu, J. The impact of recommender systems and pricing strategies on brand competition and consumer search. Electron. Commer. Res. Appl. 2022, 53, 1–15. [Google Scholar] [CrossRef]
- Wu, H.; Cai, G.; Chen, J.; Sheu, C. Online manufacturer referral to heterogeneous retailers. Prod. Oper. Manag. 2015, 24, 1768–1782. [Google Scholar] [CrossRef]
- Dogan, O. A recommendation system in e-commerce with profit-support fuzzy association rule mining (p-farm). J. Theor. Appl. Electron. Commer. Res. 2023, 18, 831–847. [Google Scholar] [CrossRef]
- Adomavicius, G.; Bockstedt, G.; Curley, S.; Zhang, J. Effects of online recommendations on consumers willingness to pay. Inf. Syst. Res. 2018, 29, 84–102. [Google Scholar] [CrossRef]
- Yoon, N.; Lee, H.-K. Ai recommendation service acceptance: Assessing the effects of perceived empathy and need for cognition. J. Theor. Appl. Electron. Commer. Res. 2023, 16, 1912–1928. [Google Scholar] [CrossRef]
- Zhou, B.; Zou, T. Competing for recommendations: The strategic impact of personalized product recommendations in online marketplaces. Mark. Sci. 2022, 41, 1–17. [Google Scholar]
- Ghose, A.; Mukhopadhyay, T.; Rajan, U. The impact of internet referral services on a supply chain. Inf. Syst. Res. 2007, 18, 300–319. [Google Scholar] [CrossRef]
- Li, L.; Chen, J.; Raghunathan, S. Recommender system rethink: Implications for an electronic marketplace with competing manufacturers. Inf. Syst. Res. 2018, 29, 1003–1023. [Google Scholar] [CrossRef]
- Jeuland, A.P.; Shugan, S.M. Managing channel profits. Mark. Sci. 1983, 2, 239–272. [Google Scholar] [CrossRef]
- Choi, S.C. Price competition in a channel structure with a common retailer. Mark. Sci. 1991, 10, 271–296. [Google Scholar] [CrossRef]
- Huang, H.; Ke, H.; Wang, L. Equilibrium analysis of pricing competition and cooperation in supply chain with one common manufacturer and duopoly retailers. Int. J. Prod. Econ. 2016, 178, 12–21. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, J.; Zhou, C.; Ren, Y. Strategic business mode choices for e-commerce platforms under brand competition. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 1769–1790. [Google Scholar] [CrossRef]
- Wang, R.; Nan, G.; Chen, L.; Li, M. Channel integration choices and pricing strategies for competing dual-channel retailers. IEEE Trans. Eng. Manag. 2020, 69, 2260–2274. [Google Scholar] [CrossRef]
- Jena, S.K.; Sarmah, S. Price competition and co-operation in a duopoly closed-loop supply chain. Int. J. Prod. Econ. 2014, 156, 346–360. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, M.; Chen, G.; Chen, X. The effect of implementing trade-in strategy on duopoly competition. Eur. J. Oper. Res. 2016, 248, 856–868. [Google Scholar] [CrossRef]
- Tang, F.; Dai, Y.; Ma, Z.-J.; Choi, T.-M. Trade-in operations under retail competition: Effects of brand loyalty. Eur. J. Oper. Res. 2023, 310, 397–414. [Google Scholar] [CrossRef]
- Wei, J.; Lu, J.; Zhao, J. Interactions of competing manufacturers leader-follower relationship and sales format on online platforms. Eur. J. Oper. Res. 2020, 280, 508–522. [Google Scholar] [CrossRef]
- Ding, Y.; Gao, X.; Huang, C.; Shu, J.; Yang, D. Service competition in an online duopoly market. Omega 2018, 77, 58–72. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.; Liu, M. E-tailers procurement strategies for drop-shipping: Simultaneous vs. sequential approach to two manufacturers. Transport. Res. Part E Logist. Transport. Res. 2019, 130, 108–127. [Google Scholar] [CrossRef]
- Shen, Y.; Willems, S.P.; Dai, Y. Channel selection and contracting in the presence of a retail platform. Prod. Oper. Manag. 2019, 28, 1173–1185. [Google Scholar] [CrossRef]
- Zhen, X.; Xu, S. Who should introduce the third-party platform channel under different pricing strategies? Eur. J. Oper. Res. 2022, 299, 168–182. [Google Scholar] [CrossRef]
- Mantin, B.; Krishnan, H.; Dhar, T. The strategic role of third-party marketplaces in retailing. Prod. Oper. Manag. 2014, 23, 1937–1949. [Google Scholar] [CrossRef]
- Lu, Q.; Shi, V.; Huang, J. Who benefit from agency model: A strategic analysis of pricing models in distribution channels of physical books and e-books. Eur. J. Oper. Res. 2018, 264, 1074–1091. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, R.; Yan, Y.; Li, X. Promotional pricing and online business model choice in the presence of retail competition. Omega 2020, 94, 1–13. [Google Scholar] [CrossRef]
- Zhou, C.; Li, X.; Ren, Y.; Yu, J. How do fairness concern and power structure affect competition between e-platforms and third-party sellers? IEEE Trans. Eng. Manag. 2023, 2023, 1–17. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, Q.; He, X. Contract and product quality in platform selling. Eur. J. Oper. Res. 2019, 272, 928–944. [Google Scholar] [CrossRef]
- Choi, T.-M.; Guo, S.; Liu, N.; Shi, X. Optimal pricing in on-demand-service-platform-operations with hired agents and risk-sensitive customers in the blockchain era. Eur. J. Oper. Res. 2020, 284, 1031–1042. [Google Scholar] [CrossRef]
- Zhang, T.; Li, P.; Wang, N. Multi-period price competition of blockchain-technology-supported and traditional platforms under network effect. Int. J. Prod. Res. 2021, 61, 3829–3843. [Google Scholar] [CrossRef]
- Anderson, E.G., Jr.; Parker, G.G.; Tan, B. Platform performance investment in the presence of network externalities. Inf. Syst. Res. 2014, 25, 152–172. [Google Scholar] [CrossRef]
- Taylor, T.A. On-demand service platforms. Manuf. Serv. Oper. Manag. 2018, 20, 704–720. [Google Scholar] [CrossRef]
- Zha, Y.; Li, Q.; Huang, T.; Yu, Y. Strategic information sharing of online platforms as resellers or marketplaces. Mark. Sci. 2022, 2022, 1–99. [Google Scholar] [CrossRef]
- Tsunoda, Y.; Zennyo, Y. Platform information transparency and effects on third-party suppliers and offline retailers. Prod. Oper. Manag. 2021, 30, 4219–4235. [Google Scholar] [CrossRef]
- Martinez-de Albéniz, V.; Pinto, C.; Amorim, P. Driving supply to marketplaces: Optimal platform pricing when suppliers share inventory. Manuf. Serv. Oper. Manag. 2022, 24, 2367–2386. [Google Scholar] [CrossRef]
- Spence, M. Product differentiation and welfare. Am. Econ. Rev. 1976, 66, 407–414. [Google Scholar]
- Cai, G.; Dai, Y.; Zhou, S. Exclusive channels and revenue sharing in a complementary goods market. Mark. Sci. 2012, 31, 172–187. [Google Scholar] [CrossRef]
| Zone | Comparison |
|---|---|
| I | |
| II | |
| III |
| Zone | Comparison |
|---|---|
| I | |
| II | |
| III | |
| IV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Li, H.; Zhang, L.; Ren, Y. Optimal Recommendation Strategies for AI-Powered E-Commerce Platforms: A Study of Duopoly Manufacturers and Market Competition. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1086-1106. https://doi.org/10.3390/jtaer18020055
Zhou C, Li H, Zhang L, Ren Y. Optimal Recommendation Strategies for AI-Powered E-Commerce Platforms: A Study of Duopoly Manufacturers and Market Competition. Journal of Theoretical and Applied Electronic Commerce Research. 2023; 18(2):1086-1106. https://doi.org/10.3390/jtaer18020055
Chicago/Turabian StyleZhou, Chi, He Li, Linlin Zhang, and Yufei Ren. 2023. "Optimal Recommendation Strategies for AI-Powered E-Commerce Platforms: A Study of Duopoly Manufacturers and Market Competition" Journal of Theoretical and Applied Electronic Commerce Research 18, no. 2: 1086-1106. https://doi.org/10.3390/jtaer18020055
APA StyleZhou, C., Li, H., Zhang, L., & Ren, Y. (2023). Optimal Recommendation Strategies for AI-Powered E-Commerce Platforms: A Study of Duopoly Manufacturers and Market Competition. Journal of Theoretical and Applied Electronic Commerce Research, 18(2), 1086-1106. https://doi.org/10.3390/jtaer18020055






