Direct Mail or Bonded Warehouse? Logistics Mode Selection in Cross-Border E-Commerce under Exchange Rate Risk
Abstract
:1. Introduction
- How should suppliers determine the overseas warehouse stock under demand and exchange rate uncertainties?
- How should suppliers choose the logistics mode under demand and exchange rate uncertainties?
2. Literature Review
2.1. Cross-Border E-Commerce Logistics Operations
2.2. Exchange Rate Risk Management
2.3. Robust Inventory Management
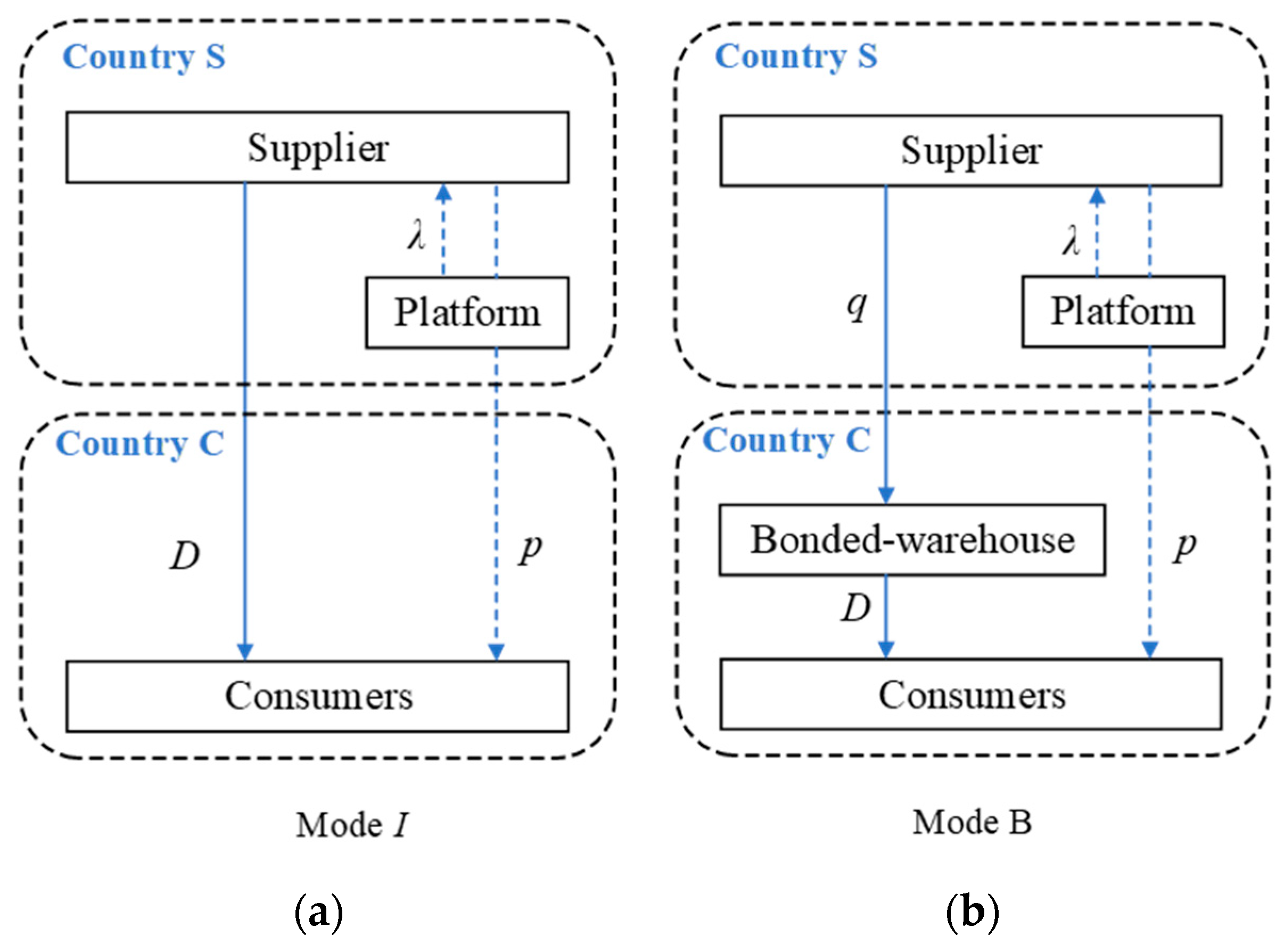
3. Model Description
3.1. Bonded Warehouse Mode
3.2. Direct Mail Mode
4. Analysis
4.1. Optimal Inventory Analysis for Mode B
- (i)
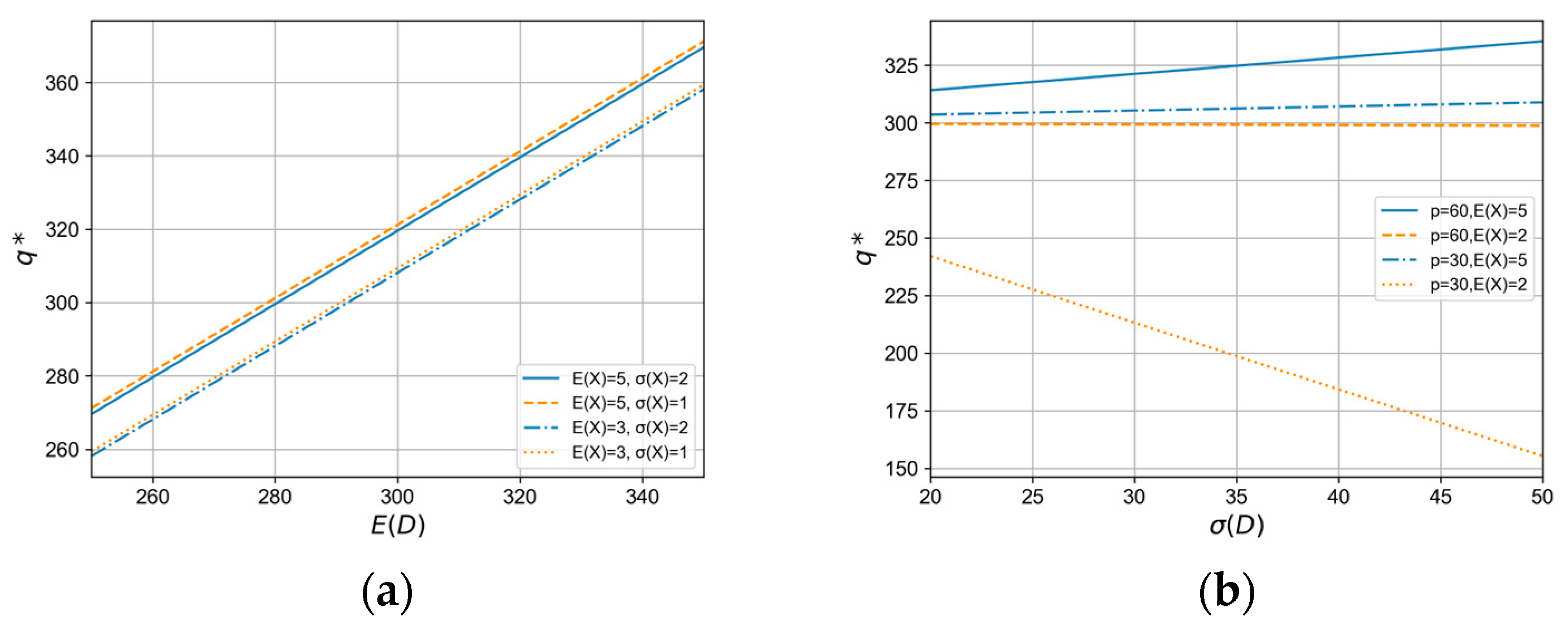
- When the constraint is satisfied, the optimal stocking quantity increases monotonically with the mean value of demand . The monotonicity of with depends on . Specifically, if , increases with . If , decreases with .
- (ii)
- When the constraint is satisfied, the supplier’s profit under mode B varies with the mean value of demand also depends on . If , increases with , if , decreases with . Supplier profit under mode B monotonically decreases with the standard deviation of demand .
- (i)
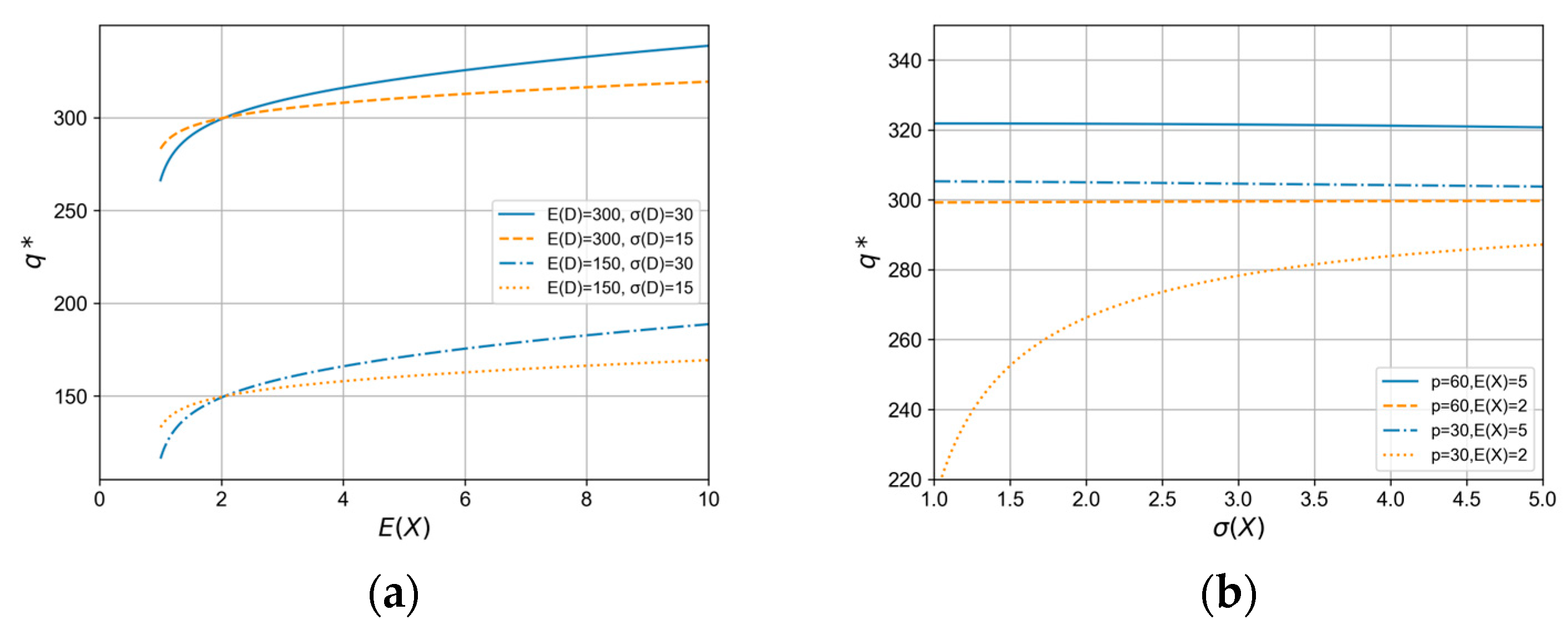
- When the constraint is satisfied, the optimal stocking quantity increases monotonically with the mean value of the exchange rate . The monotonicity of with respect to depends on , if , decreases with , if , increases with .
- (ii)
- When the constraint is satisfied, is a convex function of and decreases monotonically with .
- (i)
- When the constraint is satisfied, the optimal inventory level decreases monotonically with and , but increases monotonically with .
- (ii)
- When the constraint is satisfied, the supplier’s profit is a convex function of , , and .
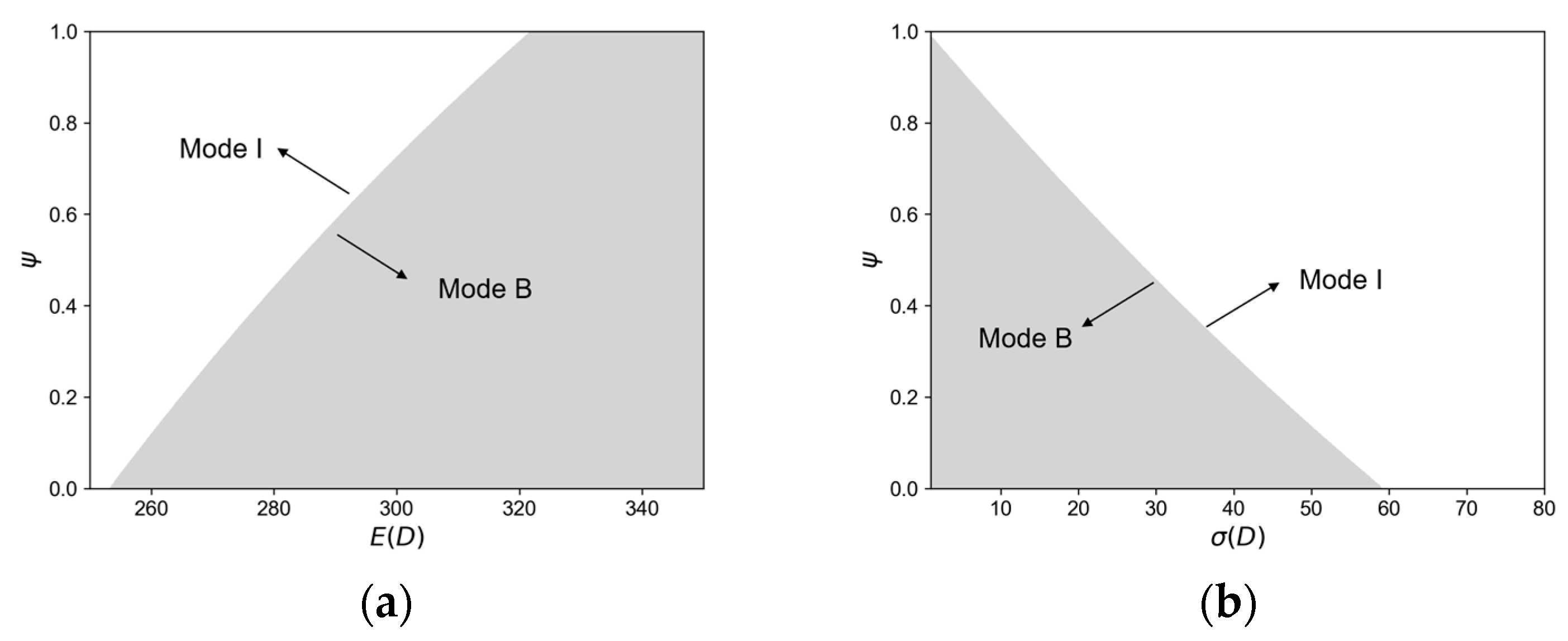
4.2. Logistics Mode Analysis
- (i)
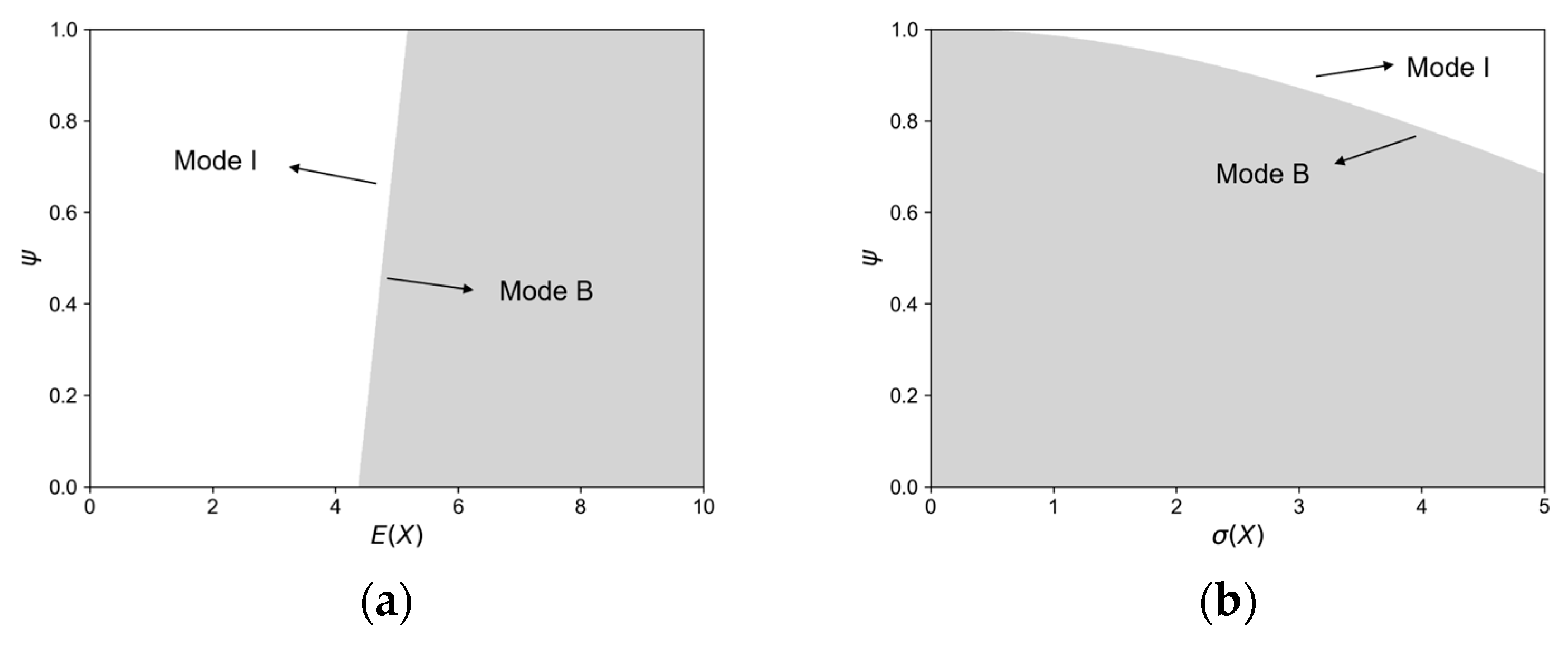
- When the constraint is satisfied, if , . If , . Where .
- (ii)
- When the constraint is satisfied, if , . If , . Where .
- (i)
- Satisfying the constraint , the effect of the mean value of the exchange rate on the logistics mode needs to be discussed in separate cases:
- Case 1. When , we can obtain no matter how the mean value of the exchange rate changes.
- Case 2. When , if , or if .
- Case 3. If , .
- Where
- (ii)
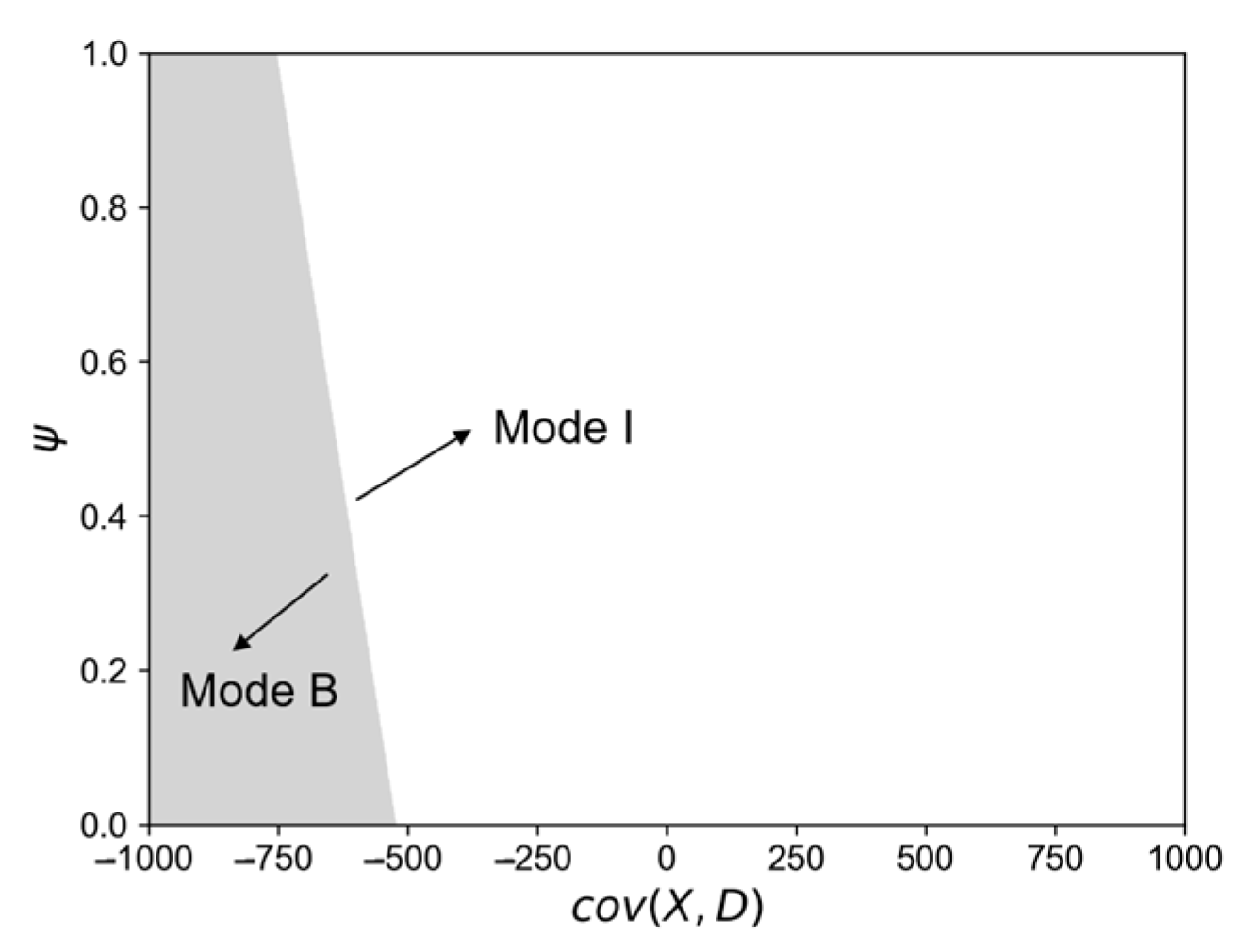
- Satisfying the constraint , when , . When , .
- Case 1: When , if , and are positively correlated, .
- Case 2: When , if , the correlation between and changes from positive to negative, .
- Case 3: When , if cov , the correlation between and changes from negative to positive, .
- Case 4: When , if , and are negatively correlated, .
- Where , .
5. Numerical Studies
5.1. Analysis of Mode B
5.2. Comparison of Logistics Modes
5.3. Impact of Partial Distribution Information on Optimal Results
6. Conclusions
6.1. Main Conclusions
- (i)
- The optimal inventory level for mode B increases monotonically with the mean value of demand and exchange rate. As market demand increases, suppliers increase their overseas warehouse inventory to meet higher market demand. The average exchange rate represents the average exchange rate of the two countries’ currencies, and an increase in the average exchange rate means that the currency of the supplier’s country depreciates, which is more favorable for export, so the supplier will increase the stocking quantity of overseas warehouses to satisfy the overseas market. The impact of demand and exchange rate volatility on the supplier’s overseas warehouse inventory depends on the product’s profit margin. Specifically, when demand volatility increases, suppliers increase high-profit products and decrease low-profit products. When exchange rate volatility increases, suppliers reduce high-profit products and increase low-profit products to cope with exchange rate risk.
- (ii)
- The levels of mean value of demand and exchange rate influence the supplier’s logistics mode choice. When market demand is low, mode I provides higher flexibility and lower operating costs, leading suppliers to prefer mode I. On the contrary, when the level of market demand is high, mode B becomes more economical. Centralized storage can reduce unit logistics costs and improve logistics efficiency, and suppliers prefer mode B. This conclusion is consistent with the current logistics practice. For instance, sellers of special handicrafts or custom-made goods on platforms like Etsy or Shopify typically tend to use mode I due to their smaller order volumes. Large CBEC platforms such as Tmall Global and JD International usually employ mode B to handle large volumes of orders. The impact of exchange rate averaging on the logistics mode also depends on the logistics cost trade-off. When the cost of mode B has a clear advantage, suppliers will always choose mode B. When the cost advantage of mode B decreases, if the exchange rate stabilizes within a specific range, suppliers will choose mode I; otherwise, they will choose mode B.
- (iii)
- There is consistency in the impact of exchange rate and market demand fluctuations on suppliers’ logistics mode. When both exchange rate and demand volatility are low, indicating a relatively stable market, suppliers can use mode B to optimize cost structure and improve overall supply chain efficiency. Conversely, when exchange rate and demand risks increase, market uncertainty rises. In this environment, mode I offers higher flexibility and quicker response capability, better adapting to demand and exchange rate fluctuations, leading suppliers to choose mode I. This finding is not only consistent with Zha et al. [9] and Zhang et al. [3] on the impact of demand fluctuations on logistics mode choice but also the first systematic exploration of the impact of exchange rate fluctuations on suppliers’ logistics mode choice, which provides a theoretical basis and decision-making support for CBEC companies to formulate logistics strategies in the face of exchange rate changes.
- (iv)
- The correlation between exchange rate and demand affects supplier profit and, subsequently, the logistics mode choice. When the correlation is high, exchange rate fluctuations can quickly influence demand, resulting in the instability of demand. At this time, suppliers may prefer mode I to respond directly to demand changes and seize sales opportunities quickly. When the correlation is low, it indicates that market demand is less sensitive to exchange rate fluctuations and that consumer purchasing behavior is more stable. At this time, adopting mode B can provide full play to the advantages of logistics costs, improving logistics efficiency through centralized inventory management and batch order processing, providing more stable supply chain management.
6.2. Managerial Implications
- (i)
- Suppliers should consider product profit margins and market risk to optimize their product portfolios. For high-profit products, increase inventory during periods of high demand volatility to ensure customer demand is met during market peaks, thus seizing profit opportunities. Conversely, inventory should be reduced during high exchange rate volatility to avoid profit losses caused by exchange rate fluctuations. For low-profit products, adopt the opposite strategy. This approach maintains profits while reducing the risk associated with market uncertainties. In addition, suppliers should closely monitor market demand changes and dynamically adjust the amount of stock in overseas warehouses to reduce inventory risk. Different inventory strategies should be adopted to respond to exchange rate changes. Increase inventory during currency depreciation to capitalize on export benefits and reduce export inventory during currency appreciation.
- (ii)
- Choosing an appropriate logistics mode to respond to changes in market demand. When the level of market demand is low and market fluctuations are high, suppliers should adopt mode I to improve the flexibility of response to the market. Mode I is suitable for quickly responding to small orders and testing new markets, reducing the risk of overinvestment and inventory backlog. When market demand is high, and market volatility is low, mode B should be prioritized to reduce unit logistics costs and improve operational efficiency through centralized storage and batch processing. This not only optimizes the cost structure but also strengthens market supply stability. To summarize, CBEC companies should regularly conduct market demand analysis, combine sales data with market trend forecasts, and adjust inventory and logistics deployment accordingly. Additionally, flexible logistics channels should be established to determine the appropriate logistics mode based on market demand, ensuring a balance between cost efficiency and market response speed.
- (iii)
- Selecting an appropriate logistics mode to cope with exchange rate fluctuations. When the logistics cost of overseas warehouses has apparent advantages, maintaining the overseas warehouse mode is a reasonable choice as it controls costs while ensuring supply chain efficiency. However, suppose the cost advantage of overseas warehousing decreases, for example, due to local policy changes, rising operating costs, etc. In that case, suppliers should re-evaluate the cost-effectiveness of both logistics modes and choose the most suitable one based on the extent of exchange rate appreciation or depreciation. When exchange rate volatility is low, a stable market environment allows for the use of the overseas warehouse mode to optimize costs and improve supply chain efficiency. Conversely, when exchange rate risk increases, suppliers should adopt mode I to mitigate risks with its inventory flexibility and quick market response capability. CBEC companies should enhance exchange rate forecasting and increase logistics flexibility, adjusting logistics strategies based on exchange rate trends.
- (iv)
- CBEC companies should consider the correlation between exchange rates and demand when choosing a logistics mode. Different logistics modes are selected according to the high or low correlation between exchange rate and demand in order to maximize market response speed, cost efficiency, and risk management. Mode I is suitable for markets with a high correlation between exchange rates and demand, allowing quick adaptation to environmental changes, such as in luxury goods. Mode B is more suitable for markets with relatively stable demand or less sensitive to exchange rate fluctuations, such as necessities. The correlation between exchange rates and demand is closely related to product attributes and industries. Therefore, CBEC companies should conduct market analysis for different industries and product types, designing and implementing efficient logistics solutions for different product categories.
6.3. Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The Proof of Theorem 1
Appendix A.2. The Proof of Proposition 1
- (i)
- , so increases monotonically with the mean market demand .
- (ii)
- . Since the sign of is undetermined, we need further analysis:
- Case 1. When , , indicating increases monotonically with .
- Case 2. When , , indicating decreases monotonically with .
- (iii)
- . Then we have:
- Case 1. When ,, indicating increases monotonically with .
- Case 2. When , , indicating decreases monotonically with .
- (iv)
- , indicating decreases monotonically with .
Appendix A.3. The Proof of Proposition 2
- (i)
- , so increases monotonically with the mean exchange rate .
- (ii)
- , Then we have:
- Case 1. When , , indicating decreases monotonically with .
- Case 2. When , , indicating increases monotonically with .
- (iii)
- , which cannot be determined as positive or negative. , indicating is a convex function with respect to .
- (iv)
- , indicating decreases monotonically with .
Appendix A.4. The Proof of Proposition 3
- (i)
- , so decreases monotonically with .
- (ii)
- , so decreases monotonically with .
- (iii)
- , so increases monotonically with .
- (i)
- , , so is a convex function with respect to .
- (ii)
- ,, so is a convex function with respect to .
- (iii)
- , , so is a convex function with respect to .
Appendix A.5. The Proof of Proposition 4
- (i)
- . Setting gives . Given the constraint , we have:
- Case 1. When ,, so .
- Case 2. When ,, so .
- (ii)
- . Setting gives . Given the constraint , we have:
- Case 1. When ,, so .
- Case 2. When ,, so .
Appendix A.6. The Proof of Proposition 5
- (i)
- , which cannot be determined as positive or negative. , this shows that is a convex function with respect to , indicating the existence of a minimum point. Setting , we find the extremum point . Substituting into the function , we obtain the minimum value . Since we cannot determine the sign of , further case analysis is required. Setting gives .
- Case 1. When , , , so .
- Case 2. When , , this means the minimum value of is less than zero, indicating can be both positive and negative. Setting , we find the zero points and . Where . If or , , so . If , , so .
- (ii)
- . Therefore, decreases monotonically with . Setting , we get . Given the constraint , we have:
- Case 1. When , , so .
- Case 2. When , , so .
Appendix A.7. The Proof of Proposition 6
References
- Niu, B.Z.; Chen, K.L.; Chen, L.; Ding, C.; Yue, X.H. Strategic waiting for disruption forecasts in cross-border e-commerce operations. Prod. Oper. Manag. 2021, 30, 2840–2857. [Google Scholar] [CrossRef]
- Li, X.F.; Ma, J.; Li, S. Intelligence customs declaration for cross-border e-commerce based on the multi-modal model and the optimal window mechanism. Ann. Oper. Res. 2022, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.M.; Zha, X.Y.; Dan, B.; Liu, Y.; Sui, R.H. Logistics mode selection and information sharing in a cross-border e-commerce supply chain with competition. Eur. J. Oper. Res. 2024, 314, 136–151. [Google Scholar] [CrossRef]
- Belt and Road Portal. China’s Cross-Border e-Commerce Imports and Exports Total 2.38 Trillion Yuan in 2023, up 15.6 Percent. Available online: https://www.yidaiyilu.gov.cn/p/0JPOMQMJ.html (accessed on 15 June 2024).
- Global e-Commerce Sales Reach $6.3 Trillion by 2023. Available online: https://www.ennews.com/news-65332.html (accessed on 15 June 2024).
- Wang, M.; Zhao, L.D.; Herty, M. Logistics service sharing of sellers on an e-commerce platform considering the behavior of carbon emission pooling. Electron. Commer. Res. Appl. 2023, 59, 101267. [Google Scholar] [CrossRef]
- Amazon. Standard Selling Expenses. Available online: https://sell.amazon.com/zh/pricing (accessed on 15 June 2024).
- Does Tmall Global Require a Commission for Opening a Store? Can Individuals Open a Store? Available online: https://www.xeeger.com/article/23726 (accessed on 15 June 2024).
- Zha, X.Y.; Zhang, X.M.; Liu, Y.; Dan, B. Bonded-warehouse or direct-mail? Logistics mode choice in a cross-border e-commerce supply chain with platform information sharing. Electron. Commer. Res. Appl. 2022, 54, 101181. [Google Scholar] [CrossRef]
- Niu, B.Z.; Ruan, Y.Y. Self-reliant shipping to mitigate disruption risk in the direct-delivery channel: Will the e-tailer’s bonded-warehouse channel also benefit? Marit. Policy Manag. 2023, 1–28. [Google Scholar] [CrossRef]
- Song, B.; Yan, W.; Zhang, T.J. Cross-border e-commerce commodity risk assessment using text mining and fuzzy rule-based reasoning. Adv. Eng. Inform. 2019, 40, 69–80. [Google Scholar] [CrossRef]
- Shao, B.J.; Cheng, Z.D.; Wan, L.J.; Yue, J. The impact of cross border E-tailer’s return policy on consumer’s purchase intention. J. Retail. Consum. Serv. 2021, 59, 102367. [Google Scholar] [CrossRef]
- Shi, X.; Wang, H. Design of the cost allocation rule for joint replenishment to an overseas warehouse with a piecewise linear holding cost rate. Oper. Res. Int. J. 2022, 22, 4905–4929. [Google Scholar] [CrossRef]
- Hazarika, B.B.; Mousavi, R. Review of Cross-Border E-Commerce and Directions for Future Research. J. Glob. Inf. Manag. 2022, 30, 1–18. [Google Scholar] [CrossRef]
- Chen, X.; Li, B.; Song, D.P.; Wang, M.X. Influences of risk-aversion behavior and purchasing option in a cross-border dual-channel supply chain. Int. Trans. Oper. Res. 2023, 1–30. [Google Scholar] [CrossRef]
- The 2022 “Cross-border E-commerce Financial Services Report”. Available online: https://www.ebrun.com/report/512935.shtml (accessed on 15 June 2024).
- Zhiou Technology IPO: Relies on Overseas e-Commerce Amazon, Exchange Loss Exceeds 70 Million with Capital Risk. Available online: https://m.thepaper.cn/baijiahao_20576220 (accessed on 15 June 2024).
- US Dollar Index Edges Lower, Yen Expected to Appreciate Significantly—2024 Global Forex Market Outlook. Available online: https://www.163.com/dy/article/IP7U82Q805199DKK.html (accessed on 15 June 2024).
- Wang, X.; Xie, J.; Fan, Z.P. B2C cross-border E-commerce logistics mode selection considering product returns. Int. J. Prod. Res. 2021, 59, 3841–3860. [Google Scholar] [CrossRef]
- Niu, B.Z.; Chen, L.Y.; Wang, J.M. Ad valorem tariff vs. specific tariff: Quality-differentiated e-tailers’ profitability and social welfare in cross-border e-commerce. Omega 2022, 108, 102584. [Google Scholar] [CrossRef]
- Zhang, M.D.; Pratap, S.; Zhao, Z.H.; Prajapati, D.; Huang, G.Q. Forward and reverse logistics vehicle routing problems with time horizons in B2C e-commerce logistics. Int. J. Prod. Res. 2021, 59, 6291–6310. [Google Scholar] [CrossRef]
- Xie, F.J.; Feng, R.C.; Zhou, X.Y. Research on the optimization of cross-border logistics paths of the “belt and road” in the inland regions. J. Adv. Transport. 2022, 2022, 5776334. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K.; Chen, B.; Zhou, J.; Miao, L. Analysis of logistics service supply chain for the One Belt and One Road initiative of China. Transport. Res. E Log. 2018, 117, 23–39. [Google Scholar] [CrossRef]
- Ren, S.; Choi, T.M.; Lee, K.M.; Lin, L. Intelligent service capacity allocation for cross-border-E-commerce related third-party-forwarding logistics operations: A deep learning approach. Transport. Res. E Log. 2020, 134, 101834. [Google Scholar] [CrossRef]
- Han, S.H.; Chen, S.; Yang, K.; Li, H.C.; Yang, F.J.; Luo, Z.W. Free shipping policy for imported cross-border e-commerce platforms. Ann. Oper. Res. 2024, 335, 1537–1566. [Google Scholar] [CrossRef]
- Giuffrida, M.; Mangiaracina, R.; Perego, A.; Tumino, A. Cross-border B2C e-commerce to China: An evaluation of different logistics solutions under uncertainty. Int. J. Phys. Distrib. Log. Manag. 2020, 50, 355–378. [Google Scholar] [CrossRef]
- Kim, K.K.; Park, K.S. Transferring and sharing exchange-rate risk in a risk-averse supply chain of a multinational firm. Eur. J. Oper. Res. 2014, 237, 634–648. [Google Scholar] [CrossRef]
- Ogunranti, G.A.; Ceryan, O.; Banerjee, A. Buyer-supplier currency exchange rate flexibility contracts in global supply chains. Eur. J. Oper. Res. 2021, 288, 420–435. [Google Scholar] [CrossRef]
- Kazaz, B.; Dada, M.; Moskowitz, H. Global Production Planning Under Exchange-Rate Uncertainty. Manag. Sci. 2005, 51, 1101–1119. [Google Scholar] [CrossRef]
- Park, J.H.; Kazaz, B.; Webster, S. Risk mitigation of production hedging. Prod. Oper. Manag. 2017, 26, 1299–1314. [Google Scholar] [CrossRef]
- Gheibi, S.; Kazaz, B.; Webster, S. Capacity reservation and sourcing under exchange-rate uncertainty. Decis. Sci. 2021, 54, 257–276. [Google Scholar] [CrossRef]
- Li, S.L.; Wang, L.T. Outsourcing and capacity planning in an uncertain global environment. Eur. J. Oper. Res. 2010, 207, 131–141. [Google Scholar] [CrossRef]
- Liu, Z.G.; Nagurney, A. Supply chain outsourcing under exchange rate risk and competition. Omega 2011, 39, 539–549. [Google Scholar] [CrossRef]
- Hu, X.L.; Motwani, J.G. Minimizing downside risks for global sourcing under price-sensitive sensitive stochastic demand, exchange rate uncertainties, and supplier capacity constraints. Int. J. Prod. Econ. 2014, 147, 398–409. [Google Scholar] [CrossRef]
- Park, J.; Kazaz, B.; Webster, S. Technical note-pricing below cost under exchange-rate risk. Prod. Oper. Manag. 2016, 25, 153–159. [Google Scholar] [CrossRef]
- Ding, Q.; Dong, L.X.; Kouvelis, P. On the integration of production and financial hedging decisions in global markets. Oper. Res. 2007, 55, 470–489. [Google Scholar] [CrossRef]
- Arcelus, F.J.; Gor, R.; Srinivasan, G. Foreign exchange transaction exposure in a newsvendor setting. Eur. J. Oper. Res. 2013, 227, 552–557. [Google Scholar] [CrossRef]
- Anson, J.; Boffa, M.; Matthias, H. Consumer arbitrage in cross-border e-commerce. Rev. Int. Econ. 2019, 27, 1234–1251. [Google Scholar] [CrossRef]
- Gabrel, V.; Murat, C.; Thiele, A. Recent advances in robust optimization: An overview. Eur. J. Oper. Res. 2014, 235, 471–483. [Google Scholar] [CrossRef]
- Scarf, H. A min-max solution to an inventory problem. In Studies in the Mathematical Theory of Inventory and Production; Stanford University Press: Stanford, CA, USA; California, CA, USA, 1958; pp. 201–209. Available online: https://www.cambridge.org/core/journals/mathematical-gazette/article/abs/studies-in-the-mathematical-theory-of-inventory-and-production-by-k-j-arrow-s-karlin-and-h-scarf-pp-x-340-70s-1958-stanford-university-press-oup-london/1E93D92940792E412A9586692E541ADF (accessed on 15 June 2024).
- Gallego, G.; Moon, I. The distribution free newsboy problem: Review and extensions. J. Oper. Res. Soc. 1993, 44, 825–834. [Google Scholar] [CrossRef]
- Moon, I.; Gallego, G. Distribution free procedures for some inventory models. J. Oper. Res. Soc. 1994, 45, 651–658. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Golany, B.; Nemirovski, A.; Vial, J.P. Retailer-supplier flexible commitments contracts: A robust optimization approach. Manuf. Serv. Oper. Manag. 2005, 7, 248–271. [Google Scholar] [CrossRef]
- Qiu, R.Z.; Shang, J. Robust optimization for risk-averse multi-period inventory decision with partial demand distribution information. Int. J. Prod. Res. 2014, 52, 7472–7495. [Google Scholar] [CrossRef]
- Murray, C.C.; Gosavi, A.; Talukdar, D. The multi-product price-setting newsvendor with resource capacity constraints. Int. J. Prod. Econ. 2012, 138, 148–158. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, W.; Sarin, S.C. Robust multi-product newsvendor model with uncertain demand and substitution. Eur. J. Oper. Res. 2021, 293, 190–202. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, L.; Luo, X.G. On the optimal solution of a distributionally robust multi-product newsvendor problem. J. Oper. Res. Soc. 2022, 74, 2578–2592. [Google Scholar] [CrossRef]
- Chen, L.; He, S.M.; Zhang, S.Z. Tight Bounds for Some Risk Measures, with Applications to Robust Portfolio Selection. Oper. Res. 2011, 59, 847–865. [Google Scholar] [CrossRef]
- Yu, H.; Yan, X.L. Advance selling under uncertain supply and demand: A robust newsvendor perspective. Int. Trans. Oper. Res. 2022, 31, 2672–2715. [Google Scholar] [CrossRef]
- Bai, Q.G.; Xu, J.T.; Gong, Y.M.; Satyaveer, S.C. Robust decisions for regulated sustainable manufacturing with partial demand information: Mandatory emission capacity versus emission tax. Eur. J. Oper. Res. 2022, 298, 874–893. [Google Scholar] [CrossRef]
- Koçyiğit, C.; Iyengar, G.; Kuhn, D.; Wiesemann, W. Distributionally robust mechanism design. Manag. Sci. 2020, 66, 159–189. [Google Scholar] [CrossRef]
- Chen, L.; Dong, T.; Peng, J.; Ralescu, D. Uncertainty analysis and optimization modeling with application to supply chain management: A systematic review. Mathematics 2023, 11, 2530. [Google Scholar] [CrossRef]
- Fu, Q.; Sim, C.K.; Teo, C.P. Profit sharing agreements in decentralized supply chains: A distributionally robust approach. Oper. Res. 2018, 66, 500–513. [Google Scholar] [CrossRef]
- Zhong, Y.G.; Liu, J.; Zhou, Y.W.; Cao, B.; Cheng, T.C.E. Robust contract design and coordination under consignment contracts with revenue sharing. Int. J. Prod. Econ. 2022, 253, 2672–2715. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, W.J. Regret in the newsvendor model with demand and yield randomness. Prod. Oper. Manag. 2021, 30, 4176–4197. [Google Scholar] [CrossRef]
- Perakis, G.; Roels, G. Regret in the newsvendor model with partial information. Oper. Res. 2008, 56, 188–203. [Google Scholar] [CrossRef]
- Ha, A.Y.; Luo, H.; Shang, W. Supplier encroachment, information sharing, and channel structure in online retail platforms. Prod. Oper. Manag. 2021, 31, 1235–1251. [Google Scholar] [CrossRef]
- What Are the Charging Standards of AliExpress? An Introduction to the Cost Composition and Calculation Method! Available online: https://www.amzdh.com/smtwem/4634.html (accessed on 15 June 2024).
- Gao, F.; Su, X. Omnichannel retail operations with buy-online-and-pick-up-in-store. Manag. Sci. 2017, 63, 2478–2492. [Google Scholar] [CrossRef]
- Jiang, L.; Anupindi, R. Customer-driven vs. retailer-driven search: Channel performance and implications. Manuf. Serv. Oper. Manag. 2010, 12, 102–119. [Google Scholar] [CrossRef]
- Lee, C.M.; Hsu, S.L. The effect of advertising on the distribution-free newsboy problem. Int. J. Prod. Econ. 2011, 129, 217–224. [Google Scholar] [CrossRef]
- The Japanese Yen Exchange Rate Plummets! The Lowest Price in 34 Years Boosts Luxury Goods Sales! Available online: https://baijiahao.baidu.com/s?id=1797588656965601257&wfr=spider&for=pc (accessed on 15 June 2024).
| Literature | CBEC Supply Chain | Inventory Risk | Exchange Rate Risk | Partial Distribution Information | Logistics Mode |
|---|---|---|---|---|---|
| [1] | ✓ | ||||
| [3] | ✓ | ✓ | ✓ | ||
| [9] | ✓ | ✓ | ✓ | ||
| [10] | ✓ | ✓ | |||
| [12] | ✓ | ✓ | |||
| [15] | ✓ | ✓ | |||
| [26] | ✓ | ✓ | ✓ | ||
| [27] | ✓ | ||||
| [28] | ✓ | ✓ | |||
| This paper | ✓ | ✓ | ✓ | ✓ | ✓ |
| Notation | Description |
|---|---|
| , the commission rate paid by the supplier to the platform | |
| Suppliers’ overseas warehouse stock quantity (decision variable) | |
| Unit product selling price | |
| Unit product cost | |
| Supplier’s unit logistics cost under the bonded warehouse mode | |
| Supplier’s unit logistics cost under the direct mail mode | |
| , denotes the logistics cost advantage of the bonded warehouse mode | |
| The exchange rate at the beginning of the selling season: 1 unit of currency in country can be exchanged for units of currency in country | |
| The exchange rate at the time of settlement by the supplier: 1 unit of currency in country can be exchanged for units of currency in country |
| Main Factors | Trend | Logistics Mode Choice |
|---|---|---|
| Mean value of demand | Low market demand | Mode I |
| High market demand | Mode B | |
| Demand volatility | Low market volatility | Mode B |
| High market volatility | Mode I | |
| Mean value of exchange rate | The logistics cost advantage of mode B is significant | Mode B |
| The logistics cost advantage of mode B is minimal and the mean value of the exchange rate is too low or too high | Mode B | |
| The logistics cost advantage of mode B is minimal, and the mean value of the exchange rate remains stable within a certain threshold | Mode I | |
| Exchange rate volatility | Low exchange rate volatility | Mode B |
| High exchange rate volatility | Mode I | |
| Exchange rate and demand correlation | High correlation | Mode I |
| Low correlation | Mode B |
| σ(X) | σ(D) | Optimal Profit (Normal Distribution) | Optimal Profit (Partial Distribution Information) | Profit Loss Ratio |
|---|---|---|---|---|
| 2 | 5 | 159,845.01 | 133,109.30 | 20.09% |
| 10 | 163,612.02 | 132,178.61 | 23.78% | |
| 15 | 167,379.03 | 131,247.91 | 27.53% | |
| 20 | 171,146.04 | 130,317.21 | 31.33% | |
| 25 | 174,913.06 | 129,386.52 | 35.19% | |
| 30 | 178,680.07 | 128,455.82 | 39.10% | |
| 3 | 5 | 159,845.01 | 132,915.80 | 20.26% |
| 10 | 163,612.02 | 131,791.61 | 24.14% | |
| 15 | 167,379.03 | 130,667.41 | 28.10% | |
| 20 | 171,146.04 | 129,543.22 | 32.12% | |
| 25 | 174,913.06 | 128,419.02 | 36.20% | |
| 30 | 178,680.07 | 127,294.83 | 40.4% | |
| 4 | 5 | 159,845.01 | 132,690.75 | 20.46% |
| 10 | 163,612.02 | 131,341.49 | 24.57% | |
| 15 | 167,379.03 | 129,992.24 | 28.76% | |
| 20 | 171,146.04 | 128,642.99 | 33.04% | |
| 25 | 174,913.06 | 127,293.73 | 37.41% | |
| 30 | 178,680.07 | 125,944.48 | 41.87% | |
| 5 | 5 | 159,845.01 | 132,447.45 | 20.69% |
| 10 | 163,612.02 | 130,854.91 | 25.03% | |
| 15 | 167,379.03 | 129,262.36 | 29.49% | |
| 20 | 171,146.04 | 127,669.82 | 34.05% | |
| 25 | 174,913.06 | 126,077.27 | 38.73% | |
| 30 | 178,680.07 | 124,484.73 | 43.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yu, H.; Sun, C. Direct Mail or Bonded Warehouse? Logistics Mode Selection in Cross-Border E-Commerce under Exchange Rate Risk. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 2312-2342. https://doi.org/10.3390/jtaer19030112
Li X, Yu H, Sun C. Direct Mail or Bonded Warehouse? Logistics Mode Selection in Cross-Border E-Commerce under Exchange Rate Risk. Journal of Theoretical and Applied Electronic Commerce Research. 2024; 19(3):2312-2342. https://doi.org/10.3390/jtaer19030112
Chicago/Turabian StyleLi, Xiaoyi, Hui Yu, and Caihong Sun. 2024. "Direct Mail or Bonded Warehouse? Logistics Mode Selection in Cross-Border E-Commerce under Exchange Rate Risk" Journal of Theoretical and Applied Electronic Commerce Research 19, no. 3: 2312-2342. https://doi.org/10.3390/jtaer19030112
APA StyleLi, X., Yu, H., & Sun, C. (2024). Direct Mail or Bonded Warehouse? Logistics Mode Selection in Cross-Border E-Commerce under Exchange Rate Risk. Journal of Theoretical and Applied Electronic Commerce Research, 19(3), 2312-2342. https://doi.org/10.3390/jtaer19030112






