Channel Integration Through a Wireless Applet and an E-Commerce Platform
Abstract
1. Introduction
- (1)
- How does the OMO system influence market coverage with respect to the legacy system?
- (2)
- Does the OMO system outperform the legacy system, and if so, when?
- (3)
- How does product digitization impact the value of ommichannelization?
2. Literature Review
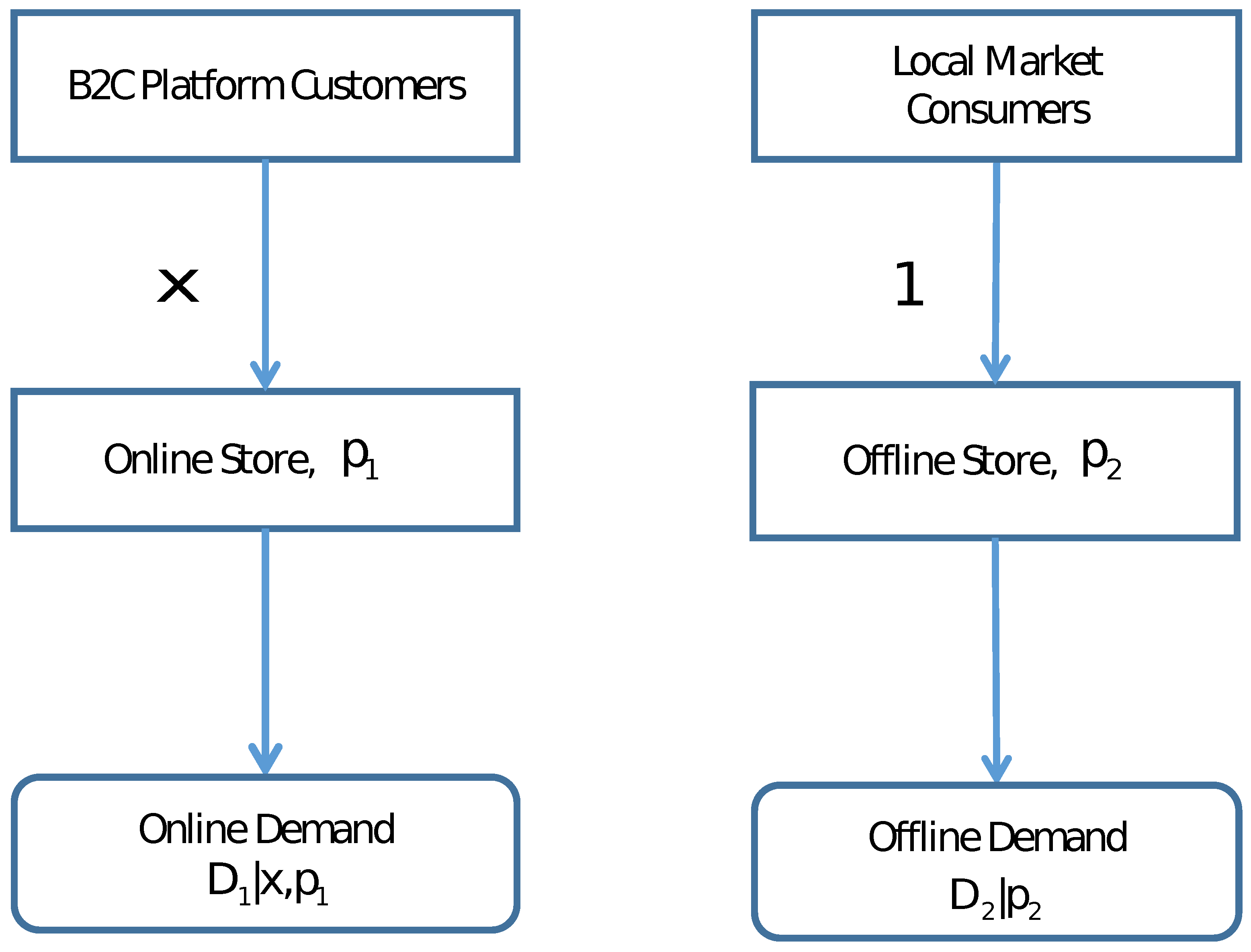
3. Legacy Channel Systems
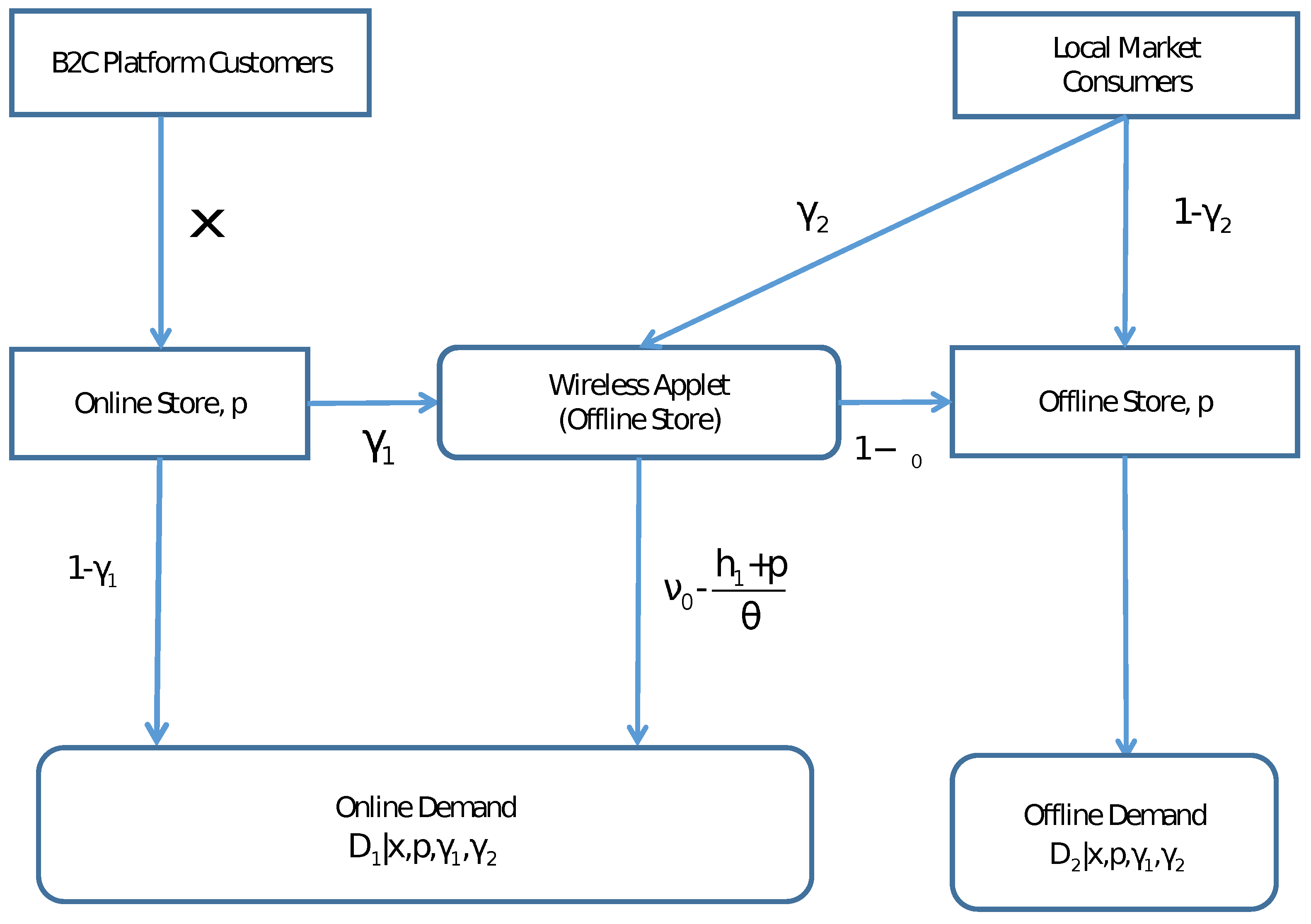
4. The Online–Merge–Offline Channel System
- 1.
- Demand generated by sole-channel potential customers
- 2.
- Demand generated by omnichannelized potential customers
- (i)
- If or , any potential customer with also satisfies . Such a potential customer eventually buys from the offline store and contributes to the demand there. Hence, all the potential customers in Group A lead to a demand of at the offline store.
- (ii)
- If or , only a potential customer with satisfies the conditions required to purchase the product from the offline store. Hence, the potential customers in Group A lead to a demand of in the offline store.
- (i)
- , or, , then a potential customer with does not satisfy . Thus, no demand is generated to purchase through the applet from the potential customers in Group B.
- (ii)
- , or, , only a potential customer with purchases the product. Therefore, a demand of is generated from the potential customers in Group B to purchase through the applet.
- 3.
- Total Demand
- (1)
- when ,
- (2)
- when ,
5. The Perfect OMO Model
5.1. System Performance
5.2. Value of Omnichannelization
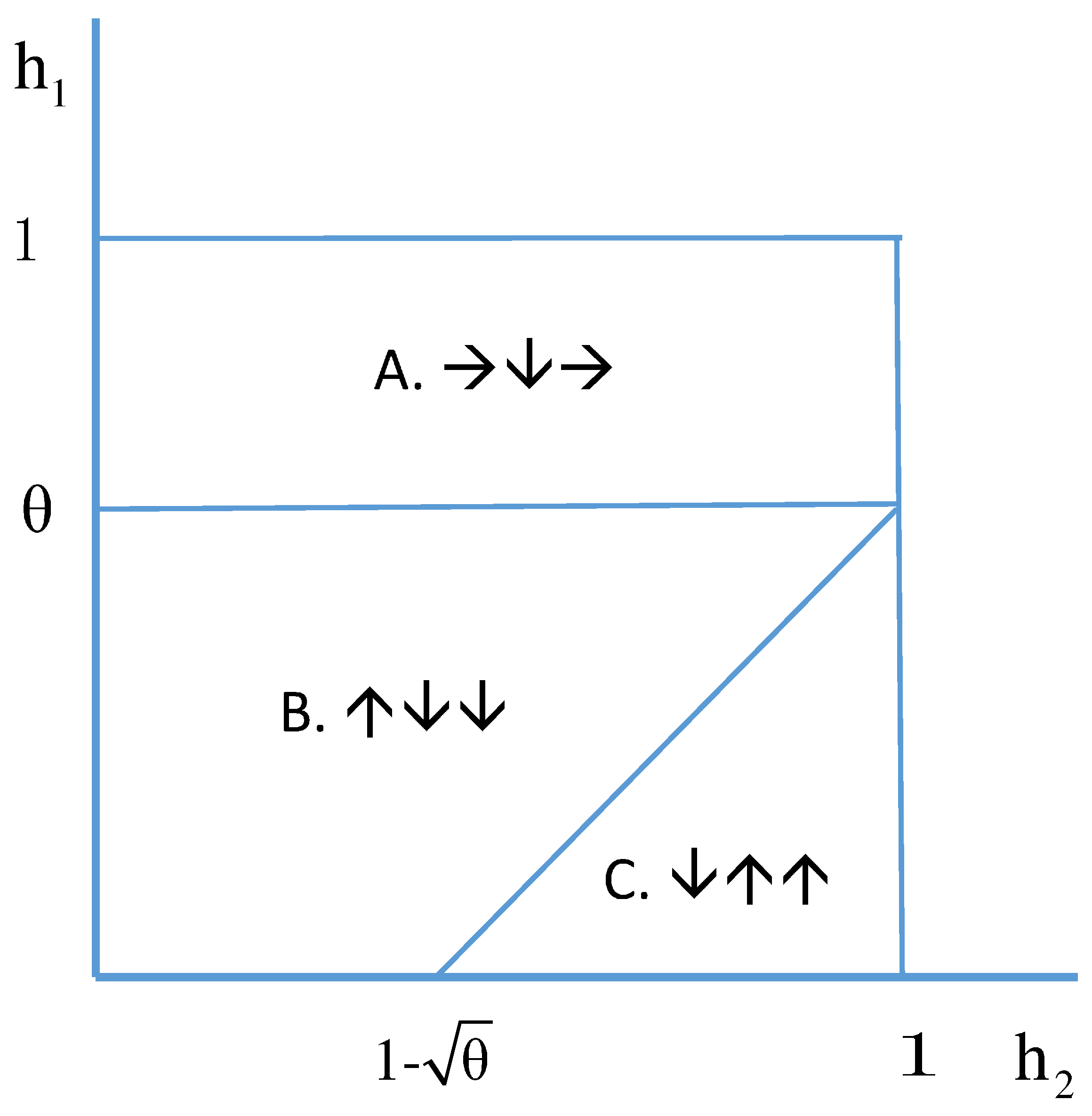
6. General Omnichannelization Rates
6.1. Properties
- (2)
- If the retail price satisfies , the optimal number of potential customers and the retail price can be calculated as follows:
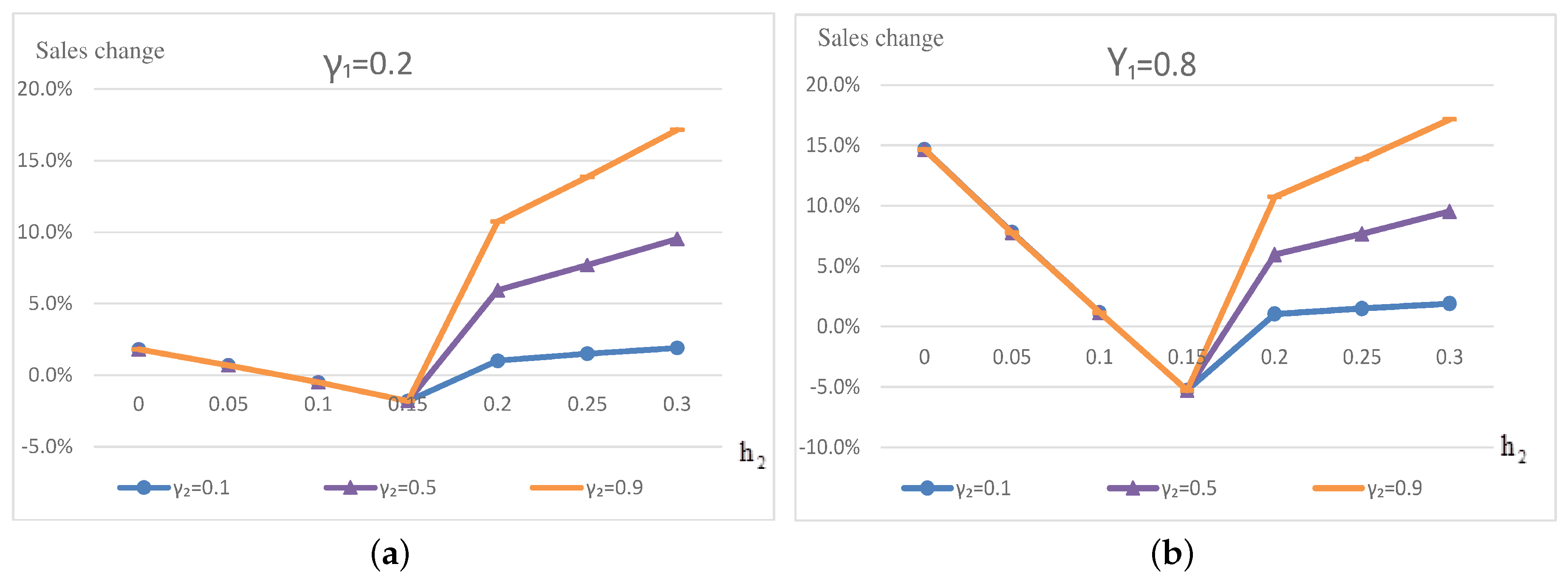
6.2. The Effect of Omnichannelization Rates
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
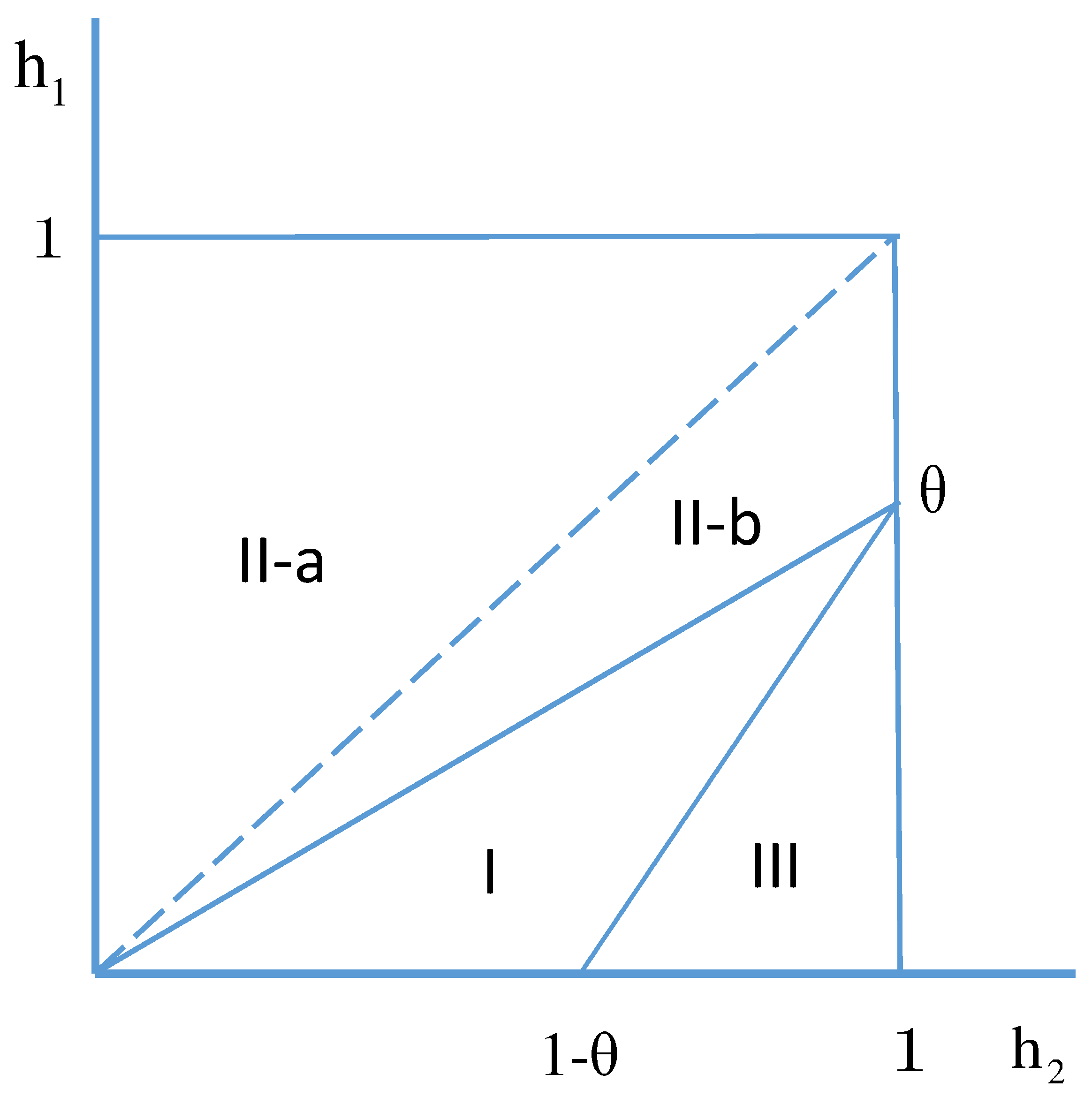
- 1.
- Region II-a
- 2.
- Region II-b
- (1)
- Case 1:
- (2)
- Case 2:
- (3)
- We observe that as , so . It is also noted that and that ; thus, .
- (I)
- (II)
- (1)
- if , then ;
- (2)
- if , then
- (a)
- (b)
- (2)
- In region III of Figure 3, . For the legacy system, ; for the OMO system, . Therefore, , and
- (a)
- If , then
- (b)
- If , then
- (a)
- If , then
- (b)
- If , then
- Region III
References
- Hartung, A. The 9 Reasons Why Amazon Buying Whole Foods Is a Good Idea. 2017. Available online: https://www.forbes.com/sites/adamhartung/2017/06/16/the-9-reasons-why-amazon-buying-whole-foods-is-a-good-idea/?sh=5b31ccf46f15 (accessed on 9 March 2025).
- Alizila. Letter to the Shareholders. 2016. Available online: https://www.alizila.com/letter-to-shareholders-from-executive-chairman-jack-ma/ (accessed on 9 March 2025).
- Conley, P. US Ecommerce Sales and Market Size. 2023. Available online: https://www.digitalcommerce360.com/article/us-ecommerce-sales/ (accessed on 9 March 2025).
- Ma, Y. E-Commerce Share of Retail Sales in Goods China 2014–2022. 2023. Available online: https://www.statista.com/statistics/1129915/china-ecommerce-share-of-retail-sales/ (accessed on 9 March 2025).
- Tang, P.; Chen, J.; Raghunathan, S. Physical stores as warehouses for online channels: Implications for channel choices under competition. Inf. Syst. Res. 2023, 34, 1554–1581. [Google Scholar]
- Weinswig, D. CEO Xiaodong Chen on How Working with Alibaba Has Changed Chinese Retailer Intime. Forbes. 2018. Available online: https://www.forbes.com/sites/deborahweinswig/2018/08/02/exclusive-interview-with-ceo-of-leading-chinese-retailer-xiaodong-chen/?sh=36c87b9db9c5 (accessed on 9 March 2025).
- Verhoef, P.; Kannan, P.; Inman, J. From multi-channel retailing to omni-channel retailing: Introduction to the special issue on multi-channel retailing. J. Retail. 2015, 91, 174–181. [Google Scholar]
- Keeney, R. The value of Internet commerce to the customer. Manag. Sci. 1999, 45, 533–542. [Google Scholar]
- Chiang, W.; Chhajed, D.; Hess, J. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, 1–20. [Google Scholar]
- Brynjolfsson, E.; Smith, M. Frictionless commerce? A comparison of Internet and conventional retailers. Manag. Sci. 2000, 46, 563–585. [Google Scholar]
- Chintagunta, P.; Chu, J.; Cebollada, J. Quantifying transaction costs in online/offline grocery channel choice. Mark. Sci. 2012, 31, 96–114. [Google Scholar]
- Cavallo, A. Are online and offline prices similar? Evidence from large multi-channel retailers. Am. Econ. Rev. 2017, 107, 283–303. [Google Scholar]
- Wiesel, T.; Pauwels, K.; Arts, J. Marketing’s profit impact: Quantifying online and off-line funnel progression. Mark. Sci. 2011, 30, 604–611. [Google Scholar]
- Pauwels, K.; Leeflang, P.; Teerling, M.; Huizingh, K. Does online information drive offline revenue? Onl+y for specific products and consumer segments! J. Retail. 2011, 87, 1–17. [Google Scholar]
- Avery, J.; Steenburgh, Y.; Deighton, J.; Caravella, M. Adding bricks to clicks: Predicting the patterns of cross-channel elasticities over time. J. Mark. 2012, 76, 96–111. [Google Scholar]
- Pauwels, K.; Neslin, S. Building with bricks and mortar: The revenue impact of opening physical stores in a multichannel environment. J. Retail. 2015, 91, 182–197. [Google Scholar]
- Wang, K.; Goldfarb, A. Can offline stores drive online sales? J. Mark. 2017, LIV, 706–719. [Google Scholar]
- Dzyabura, D.; Jagabathula, S.; Muller, E. Accounting for discrepancies between online and offline product evaluations. Mark. Sci. 2019, 38, 88–106. [Google Scholar]
- Kauffman, R.; Lee, D.; Lee, J.; Yoo, B. A Hybrid firm’s pricing strategy in electronic commerce under channel migration. Int. J. Electron. Commer. 2009, 14, 11–54. [Google Scholar]
- Chen, Y.; Dai, Y.; Zhang, Z.; Zhang, K. Managing multirooming: Why wniform price can be optimal for a monopoly retailer and can be uniformly lower. Manag. Sci. 2024, 70, 3102–3122. [Google Scholar]
- Herhasusen, D.; Binder, J.; Schoegel, M.; Herrmann, A. Integrating bricks with clicks: Retailer-level and channel-level outcomes of online-offline channel integration. J. Retail. 2015, 91, 309–325. [Google Scholar]
- Bell, D.; Gallino, S.; Moreno, A. Offline showrooms in omnichannel retail: Demand and operational benefits. Manag. Sci. 2018, 64, 1629–1651. [Google Scholar]
- Jing, B. Showrooming and webrooming: Information externalities between online and offline sellers. Mark. Sci. 2018, 37, 469–483. [Google Scholar]
- Zhang, D.; Dai, H.; Dong, L.; Wu, Q.; Guo, L.; Lin, X. The value of pop-up stores on retailing platforms: Evidence from a field experiment with Alibaba. Manag. Sci. 2019, 65, 5142–5151. [Google Scholar]
- Bell, D.; Gallino, S.; Moreno, A. Customer supercharging in experience-centric channels. Manag. Sci. 2020, 66, 4096–4107. [Google Scholar]
- Cao, J.; So, K.; Yin, S. Impact of an online-to-store channel on demand allocation, pricing and profitability. Eur. J. Oper. Res. 2016, 248, 234–245. [Google Scholar]
- Gao, F.; Su, X. Omnichannel retail operations with buy-online-and-pick-up-in-store. Manag. Sci. 2017, 63, 2478–2492. [Google Scholar]
- Gallino, S.; Moreno, A. Integration of online and offline channels in retail: The impact of sharing reliable inventory availability information. Manag. Sci. 2014, 60, 1434–1451. [Google Scholar]
- Flavián, C.; Gurrea, R.; Orús, C. Choice confidence in the webrooming purchase process: The inpract of online positive reviews and the motivation to touch. J. Consum. Behav. 2016, 15, 459–476. [Google Scholar]
- Flavián, C.; Gurrea, R.; Orús, C. Feeling confidence and smart with webrooming: Understanding the consumer’s path to satisfaction. J. Interact. Mark. 2019, 47, 1–15. [Google Scholar]
- Kleinlercher, K.; Linzmajer, M.; Verhoef, P.; Rudolph, T. Antecedents of webrooming in omnichannel retailing. Front. Psychol. 2020, 11, 606798. [Google Scholar]
- Xu, H.; Wu, X.; Liu, Y. Modelling offline expansion strategies of online companies. Kybernetes 2022, 51, 302–322. [Google Scholar]
- Lemon, K.; Verhoef, P. Understanding customer experience throughout the customer journey. J. Mark. 2016, 80, 69–96. [Google Scholar]
- Herhausen, D.; Kleinlercher, K.; Verhoef, P.; Emrich, O.; Rudolph, T. Loyalty Formation for Different Customer Journey Segments. J. Retail. 2019, 95, 9–29. [Google Scholar]
- Timoumi, A.; Gangwar, M.; Mantrala, M. Cross-channel effects of omnichannel retail marketing strategies: A review of extant data-driven research. J. Retail. 2022, 98, 133–151. [Google Scholar]
- Neslin, S. The omnichannel continuum: Integrating online and offline channels along the customer journey. J. Retail. 2022, 98, 111–132. [Google Scholar]
- Weber, A.; Maier, E. Reducing competitive research shopping with cross-channel delivery. Int. J. Electron. Commer. 2020, 24, 78–106. [Google Scholar]
- Hübner, A.; Hense, J.; Dethlefs, C. The revival of retail stores via omnichannel operations: A literature review and research framework. Eur. J. Oper. Res. 2022, 302, 799–818. [Google Scholar]
- Acquila-Natale, E.; Chaparro-Peláez, J.; Del-Río-Carazo, L.; Cuenca-Enrique, C. Do or die? The effects of COVID-19 on channel integration and digital transformation of large clothing and apparel retailers in Spain. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 439–457. [Google Scholar] [CrossRef]
- Baldivia, M.; Chowdhury, S. Adapting business models in the age of omnichannel transformation: Evidence from the small retail businesses in Australia. J. Theor. Appl. Electron. Commer. Res. 2025, 20, 1. [Google Scholar] [CrossRef]
- Iglesias-Pradas, S.; Acquila-Natale, E. The future of E-Commerce: Overview and prospects of multichannel and omnichannel retail. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 656–667. [Google Scholar] [CrossRef]
- Grossman, G.; Shapiro, C. Informative advertising with differentiated products. Rev. Econ. Stud. 1984, 51, 63–81. [Google Scholar]
- Cattani, K.; Gill, W.; Heese, H.S.; Swaminathan, J. Boiling frogs: Pricing strategies for a manufacturer adding a direct channel that competes with the traditional channel. Prod. Oper. Manag. 2006, 15, 40–56. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y. Channel Integration Through a Wireless Applet and an E-Commerce Platform. J. Theor. Appl. Electron. Commer. Res. 2025, 20, 51. https://doi.org/10.3390/jtaer20010051
Shen Y. Channel Integration Through a Wireless Applet and an E-Commerce Platform. Journal of Theoretical and Applied Electronic Commerce Research. 2025; 20(1):51. https://doi.org/10.3390/jtaer20010051
Chicago/Turabian StyleShen, Yuelin. 2025. "Channel Integration Through a Wireless Applet and an E-Commerce Platform" Journal of Theoretical and Applied Electronic Commerce Research 20, no. 1: 51. https://doi.org/10.3390/jtaer20010051
APA StyleShen, Y. (2025). Channel Integration Through a Wireless Applet and an E-Commerce Platform. Journal of Theoretical and Applied Electronic Commerce Research, 20(1), 51. https://doi.org/10.3390/jtaer20010051





