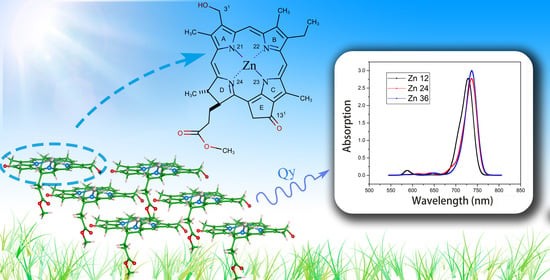
Quantum Chemical Simulation of the Qy Absorption Spectrum of Zn Chlorin Aggregates for Artificial Photosynthesis
Abstract
:1. Introduction
2. Computational Methods
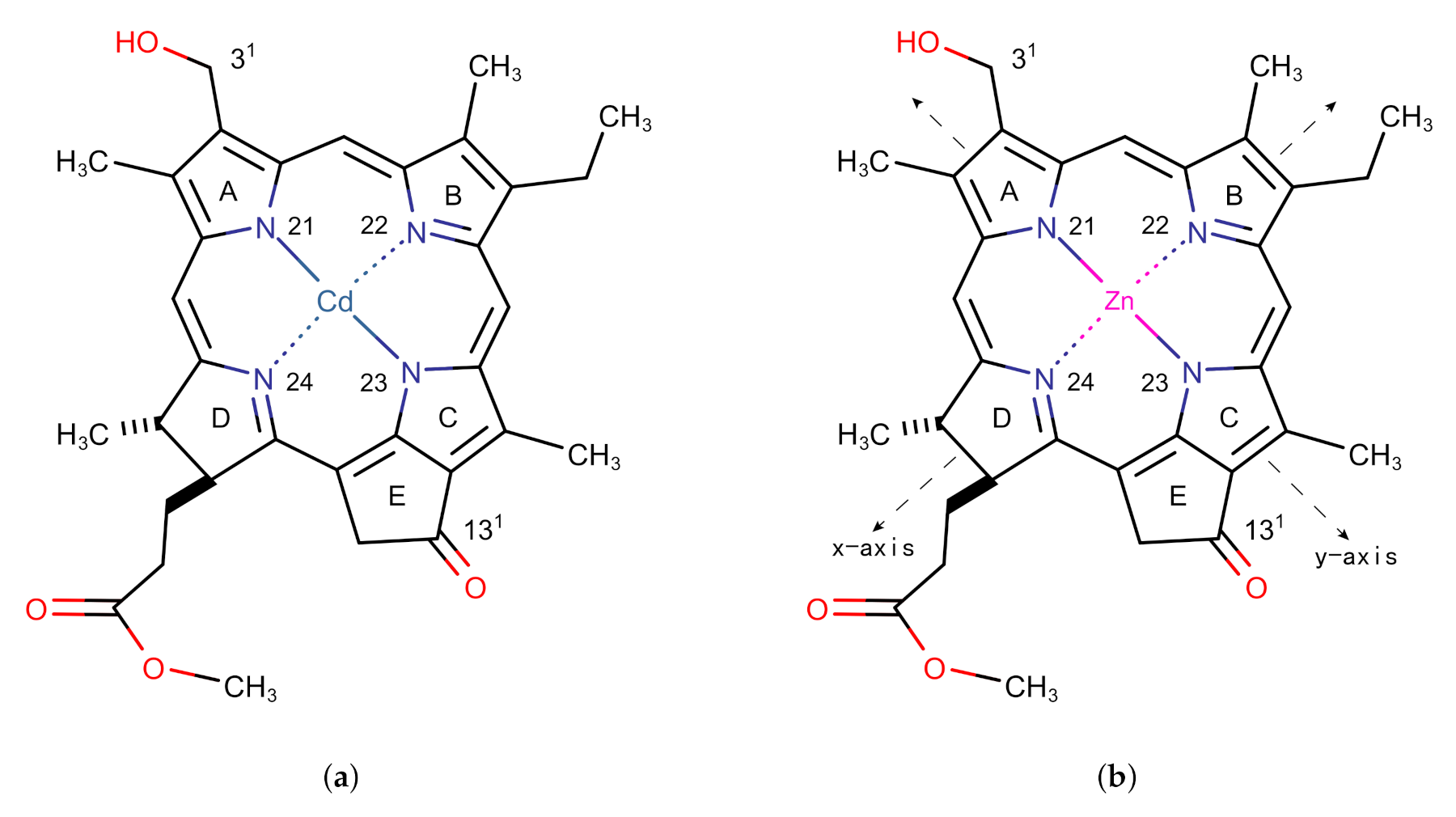
2.1. The Structure and Excitation Energy of the Znchl Monomer
2.2. Exciton Hamiltonian
2.3. Coupling Strength
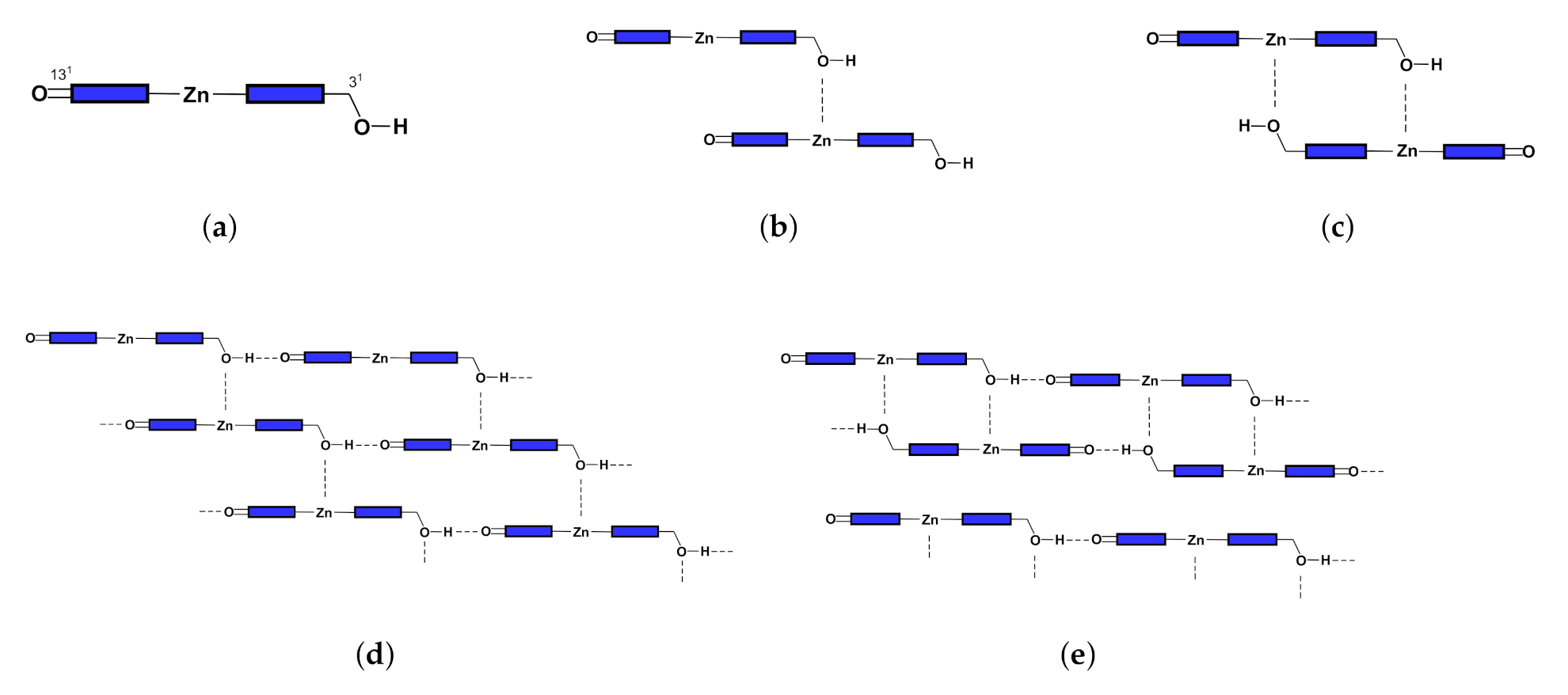
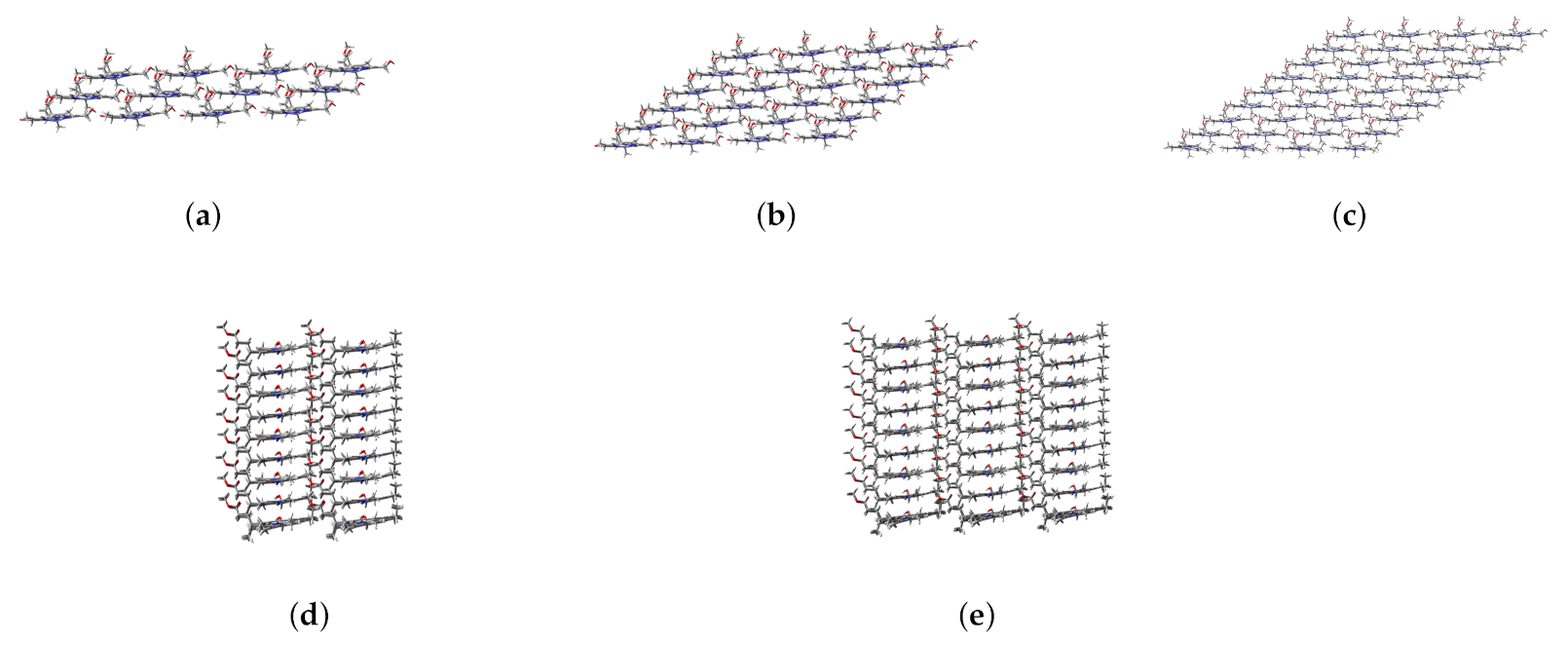
2.4. Structure and Absorption Spectrum of Aggregate
3. Results and Discussion
3.1. The Znchl Monomer and THF-Znchl
3.2. Aggregate
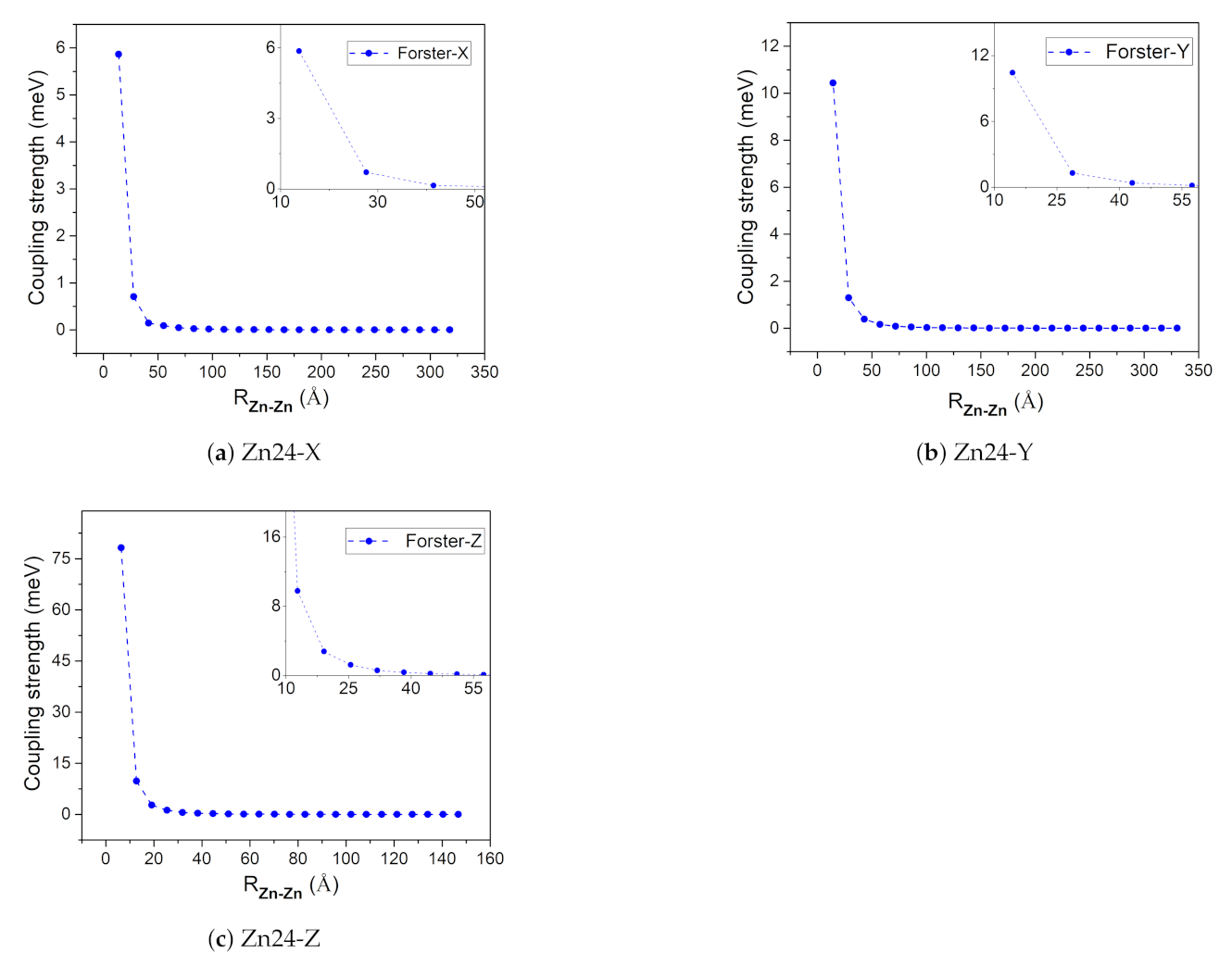
3.2.1. Coupling Strength and QTAIM Properties
3.2.2. Spectral Simulation of Aggregates
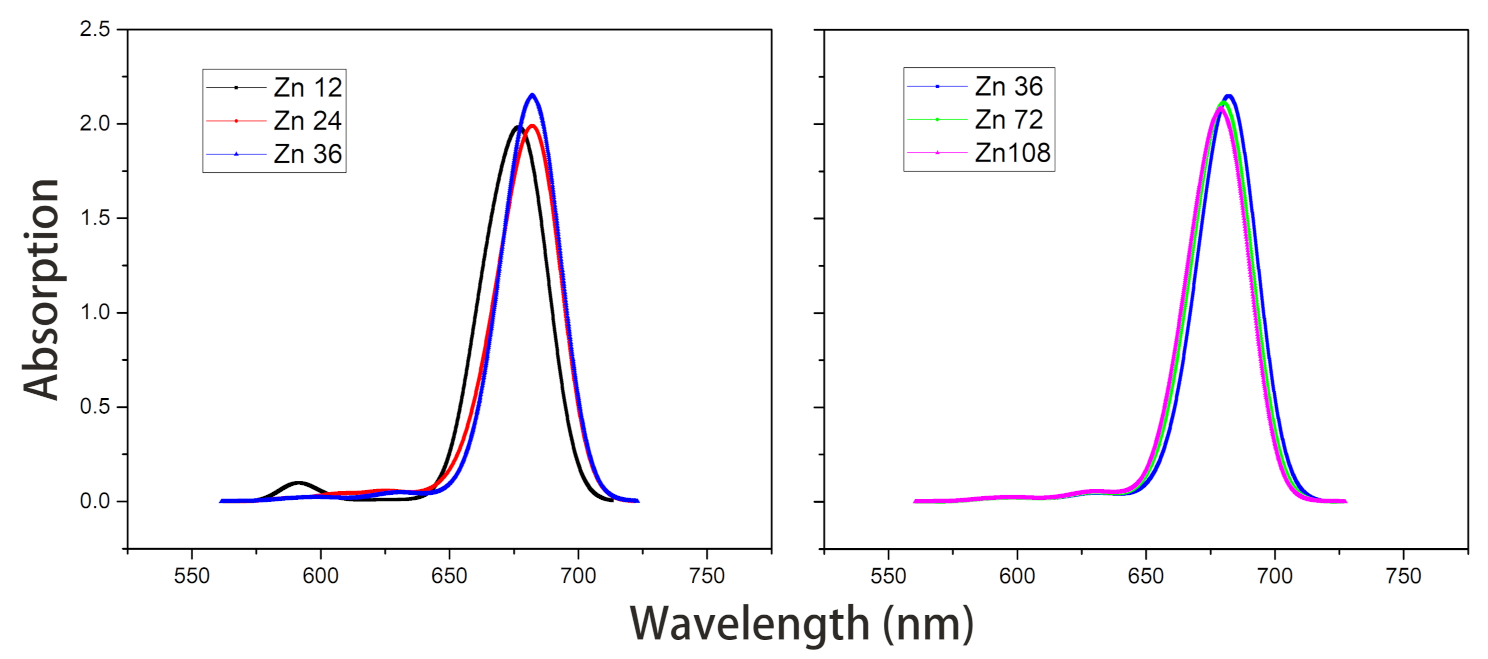
- Under the point dipole approximation, the transition dipole moment and site energy of Znchl monomer in a aggregate were calculated in vacuum. From the transition dipole moment of 5.00 Debye, the coupling strength between two molecules in the open dimer was estimated to be about –65 meV.The peak positions in the absorption spectra of Zn12, Zn24, and Zn36 (see Figure 8) were 676, 681, and 682 nm, respectively, being gradually red-shifted with the extension of the aggregate in the z-axis direction. However, the absorption spectrum is blue-shifted by an expansion in the x-axis. For example, compared with the absorption peak of the Zn36 model (682 nm), the peaks of Zn72 and Zn108 aggregates were blue-shifted by 2 nm (680 nm) and 4 nm (678 nm), respectively.The average site energy and the corresponding wavelength of 36 molecules in the Zn36 aggregate were, respectively, 1.973 eV and 628 nm; the experimental values were 1.917 eV and 647 nm for the Znchl monomer [15]. Thus, the absorption peak of Zn36 is red-shifted by 54 nm in theory relative to the former wavelength; however, it is not consistent with the experimental peak of 92 nm [15].
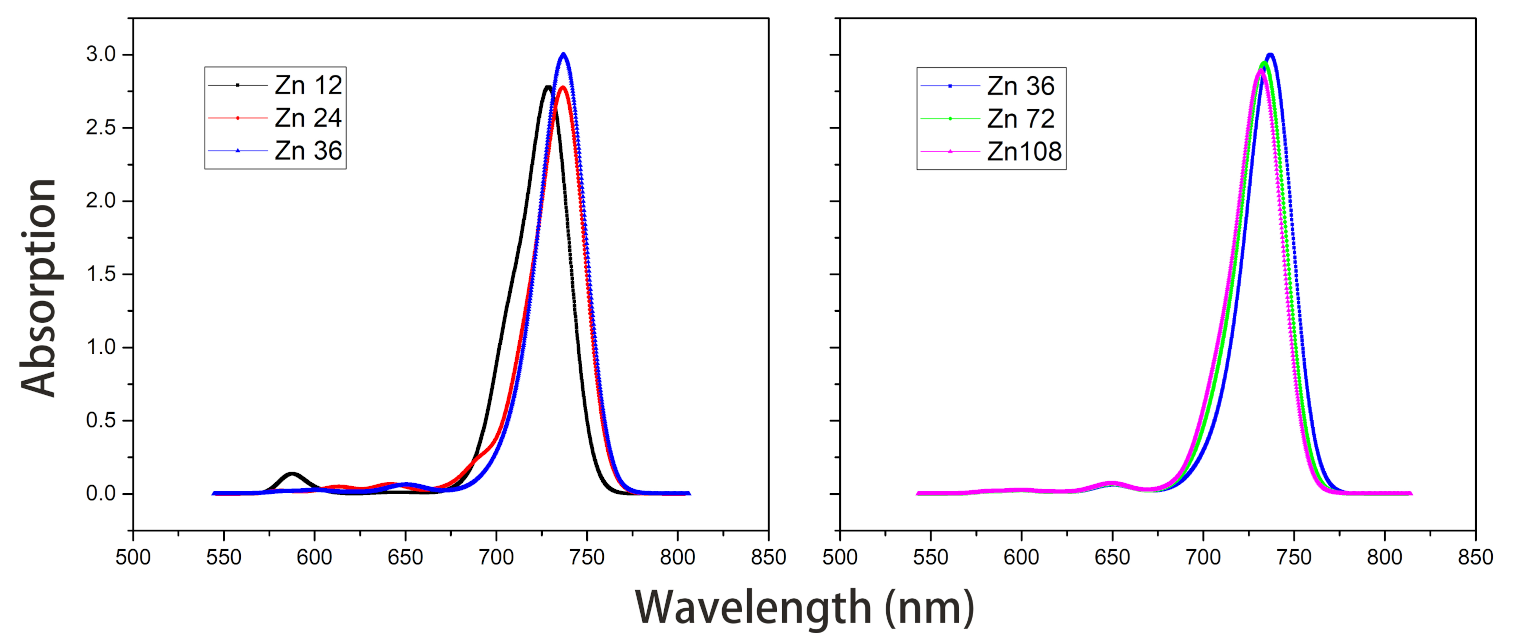
- The Zn aggregate was experimentally measured in a 1% (vol/vol) THF–hexane solution [15]. In order to simulate the experimental conditions, the Znchl monomer in the aggregates was calculated with the SMD implicit mixed solvent model. The obtained transition dipole moment was 6.18 Debye, this being significantly larger than the 5.00 Debye in the vacuum, and the coupling strength between two molecules in the open dimer was about –98 meV.The peaks in the absorption spectra of Zn12, Zn24, and Zn36 (see Figure 9) were 729, 736, and 737 nm, respectively, so the absorption spectrum of Zn36 tends to a limit value. Similarly to the vacuum case, the extension of the aggregate in the z-axis direction may gradually red-shift the absorption spectrum, and the extension in the x-axis from Zn36 to Zn72 (734 nm) leads to a blue-shift of only 3 nm. Compared with the average absorption peak at 645 nm of 36 molecules in the Zn36 aggregate, the absorption peak of the Zn36 aggregate is red-shifted by 90 nm, being in good agreement with the experimental one of 92 nm [15].
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Bchl | bacteriochlorophyll |
| BCP | bond critical point |
| DOOP | out-of-plane distance |
| HOMO | the highest occupied molecular orbitals |
| LUMO | the lowest unoccupied molecular orbitals |
| QTAIM | quantum theory of atoms in molecules |
| SMD | implicit solvation model based on density |
| TDDFT | time-dependent density functional theory |
| Zn-zdimer | Zn-centered chlorin dimer stacked in z-direction |
| Znchl | Zn-centered chlorin |
References
- Oostergetel, G.T.; van Amerongen, H.; Boekema, E.J. The chlorosome: A prototype for efficient light harvesting in photosynthesis. Photosynth. Res. 2010, 104, 245–255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blankenship, R.E. Molecular Mechanisms of Photosynthesis; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Pishchalnikov, R.; Shubin, V.; Razjivin, A. Single molecule fluorescence spectroscopy of psi trimers from arthrospira platensis: A computational approach. Molecules 2019, 24, 822. [Google Scholar] [CrossRef] [Green Version]
- Balaban, T.S.; Tamiaki, H.; Holzwarth, A.R. Chlorins Programmed for Self-Assembly. In Supermolecular Dye Chemistry; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2005; pp. 1–38. [Google Scholar]
- Balaban, T.S. Tailoring porphyrins and chlorins for self-assembly in biomimetic artificial antenna systems. Acc. Chem. Res. 2005, 38, 612–623. [Google Scholar] [CrossRef]
- Ganapathy, S.; Sengupta, S.; Wawrzyniak, P.K.; Huber, V.; Buda, F.; Baumeister, U.; Würthner, F.; de Groot, H.J.M. Zinc chlorins for artificial light-harvesting self-assemble into antiparallel stacks forming a microcrystalline solid-state material. Proc. Natl. Acad. Sci. USA 2009, 106, 11472–11477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linnanto, J.M.; Korppi-Tommola, J.E.I. Exciton description of chlorosome to baseplate excitation energy transfer in filamentous anoxygenic phototrophs and green sulfur bacteria. J. Phys. Chem. B 2013, 117, 11144–11161. [Google Scholar] [CrossRef] [PubMed]
- Pšenčík, J.; Ikonen, T.P.; Laurinmäki, P.; Merckel, M.C.; Butcher, S.J.; Serimaa, R.E.; Tuma, R. Lamellar organization of pigments in chlorosomes, the light harvesting complexes of green photosynthetic bacteria. Biophys. J. 2004, 87, 1165–1172. [Google Scholar] [CrossRef] [Green Version]
- Oostergetel, G.T.; Reus, M.; Chew, A.G.M.; Bryant, D.A.; Boekema, E.J.; Holzwarth, A.R. Long-range organization of bacteriochlorophyll in chlorosomes of Chlorobium tepidum investigated by cryo-electron microscopy. FEBS Lett. 2007, 581, 5435–5439. [Google Scholar] [CrossRef] [Green Version]
- Ganapathy, S.; Oostergetel, G.T.; Wawrzyniak, P.K.; Reus, M.; Chew, A.G.M.; Buda, F.; Boekema, E.J.; Bryant, D.A.; Holzwarth, A.R.; De Groot, H.J.M. Alternating syn-anti bacteriochlorophylls form concentric helical nanotubes in chlorosomes. Proc. Natl. Acad. Sci. USA 2009, 106, 8525–8530. [Google Scholar] [CrossRef] [Green Version]
- Tamiaki, H. Supramolecular structure in extramembraneous antennae of green photosynthetic bacteria. Coord. Chem. Rev. 1996, 148, 183–197. [Google Scholar] [CrossRef]
- Leiger, K.; Linnanto, J.M.; Freiberg, A. Establishment of the Qy Absorption Spectrum of Chlorophyll a Extending to Near-Infrared. Molecules 2020, 25, 3796. [Google Scholar] [CrossRef] [PubMed]
- Janik-Zabrotowicz, E.; Arczewska, M.; Prochniewicz, P.; Świetlicka, I.; Terpiłowski, K. Stability of Chlorophyll a Monomer Incorporated into Cremophor EL Nano-Micelles under Dark and Moderate Light Conditions. Molecules 2020, 25, 5059. [Google Scholar] [CrossRef]
- Tamiaki, H.; Amakawa, M.; Shimono, Y.; Tanikaga, R.; Holzwarth, A.R.; Schaffner, K. Synthetic zinc and magnesium chlorin aggregates as models for supramolecular antenna complexes in chlorosomes of green photosynthetic bacteria. Photochem. Photobiol. 1996, 63, 92–99. [Google Scholar] [CrossRef]
- Miyatake, T.; Tamiaki, H. Self-aggregates of natural chlorophylls and their synthetic analogues in aqueous media for making light-harvesting systems. Coord. Chem. Rev. 2010, 254, 2593–2602. [Google Scholar] [CrossRef]
- Sengupta, S.; Würthner, F. Chlorophyll J-aggregates: From bioinspired dye stacks to nanotubes, liquid crystals, and biosupramolecular electronics. Acc. Chem. Res. 2013, 46, 2498–2512. [Google Scholar] [CrossRef] [PubMed]
- Cogdell, R.J.; Gall, A.; Köhler, J. The architecture and function of the light-harvesting apparatus of purple bacteria: From single molecules to in vivo membranes. Q. Rev. Biophys. 2006, 39, 227–324. [Google Scholar] [CrossRef] [PubMed]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett 1984, 52, 997. [Google Scholar] [CrossRef]
- Casida, M.E. Recent Advances in Density Functional Methods; World Scientific: Singapore, 1995; Volume 1, p. 155. [Google Scholar]
- Yin, S.; Dahlbom, M.G.; Canfield, P.J.; Hush, N.S.; Kobayashi, R.; Reimers, J.R. Assignment of the Qy absorption spectrum of photosystem-I from Thermosynechococcus elongatus based on CAM-B3LYP calculations at the PW91-optimized protein structure. J. Phys. Chem. B 2007, 111, 9923–9930. [Google Scholar] [CrossRef]
- Linnanto, J.; Korppi-Tommola, J. Quantum chemical simulation of excited states of chlorophylls, bacteriochlorophylls and their complexes. Phys. Chem. Chem. Phys. 2006, 8, 663–687. [Google Scholar] [CrossRef] [PubMed]
- Mirkovic, T.; Ostroumov, E.E.; Anna, J.M.; Van Grondelle, R.; Scholes, G.D. Light absorption and energy transfer in the antenna complexes of photosynthetic organisms. Chem. Rev. 2017, 117, 249–293. [Google Scholar] [CrossRef]
- de Boer, I.; Matysik, J.; Amakawa, M.; Yagai, S.; Tamiaki, H.; Holzwarth, A.R.; de Groot., H.J.M. MAS NMR structure of a microcrystalline Cd-bacteriochlorophyll d analogue. J. Am. Chem. Soc. 2003, 125, 13374–13375. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theoret. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* basis set for third-row atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davydov, A.S. Theory of Molecular Excitons; Springer: New York, NY, USA, 1971. [Google Scholar]
- Förster, T. Zwischenmolekulare energiewanderung und fluoreszenz. Ann. Phys. 1948, 437, 55–75. [Google Scholar] [CrossRef]
- Scholes, G.D.; Curutchet, C.; Mennucci, B.; Cammi, R.; Tomasi, J. How Solvent Controls Electronic Energy Transfer and Light Harvesting. J. Phys. Chem. B 2007, 111, 6978–6982. [Google Scholar] [CrossRef]
- Krueger, B.P.; Scholes, G.D.; Fleming, G.R. Calculation of couplings and energy-transfer pathways between the pigments of LH2 by the ab initio transition density cube method. J. Phys. Chem. B 1998, 102, 5378–5386. [Google Scholar] [CrossRef]
- Hsu, C.P.; Walla, P.J.; Head-Gordon, M.; Fleming, G.R. The role of the S1 state of carotenoids in photosynthetic energy transfer: The light-harvesting complex II of purple bacteria. J. Phys. Chem. B 2001, 105, 11016–11025. [Google Scholar] [CrossRef]
- Linnanto, J.; Korppitommola, J.; Helenius, V.M. Electronic States, Absorption Spectrum and Circular Dichroism Spectrum of the Photosynthetic Bacterial LH2 Antenna of Rhodopseudomonas acidophila as Predicted by Exciton Theory and Semiempirical Calculations. J. Phys. Chem. B 1999, 103, 8739–8750. [Google Scholar] [CrossRef]
- Madjet, M.E.; Abdurahman, A.; Renger, T.h. Intermolecular Coulomb couplings from ab initio electrostatic potentials: Application to optical transitions of strongly coupled pigments in photosynthetic antennae and reaction centers. J. Phys. Chem. B 2006, 110, 17268–17281. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.P.; You, Z.Q.; Chen, H.C. Characterization of the short-range couplings in excitation energy transfer. J. Phys. Chem. C 2008, 112, 1204–1212. [Google Scholar] [CrossRef]
- Prokhorenko, V.I.; Steensgaard, D.B.; Holzwarth, A.R. Exciton theory for supramolecular chlorosomal aggregates: 1. Aggregate size dependence of the linear spectra. Biophys. J. 2003, 85, 3173–3186. [Google Scholar] [CrossRef] [Green Version]
- Linnanto, J.M.; Korppi-Tommola, J.E.I. Investigation on chlorosomal antenna geometries: Tube, lamella and spiral-type self-aggregates. Photosynth. Res. 2008, 96, 227–245. [Google Scholar] [CrossRef] [PubMed]
- Steinmann, C.; Kongsted, J. Electronic energy transfer in polarizable heterogeneous environments: A systematic investigation of different quantum chemical approaches. J. Chem. Theory Comput. 2015, 11, 4283–4293. [Google Scholar] [CrossRef] [Green Version]
- Kimura, A.; Itoh, S. Theoretical model of exciton states and ultrafast energy transfer in heliobacterial Type I homodimeric reaction center. J. Phys. Chem. B 2018, 122, 11852–11859. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The CP2K Developers Group. Available online: http://www.cp2k.org (accessed on 18 December 2020).
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09 Revision E.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Rappoport, D.; Furche, F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Sirohiwal, A.; Berraud-Pache, R.; Neese, F.; Izsák, R.; Pantazis, D.A. Accurate computation of the absorption spectrum of chlorophyll a with pair natural orbital coupled cluster methods. J. Phys. Chem. B 2020, 124, 8761–8771. [Google Scholar] [CrossRef] [PubMed]
- Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density—Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. 1984, 23, 627–628. [Google Scholar] [CrossRef]
- Macchi, P.; Proserpio, M.D.; Sironi, A. Experimental Electron Density in a Transition Metal Dimer: Metal-Metal and Metal-Ligand Bonds. J. Am. Chem. Soc. 1998, 120, 13429–13435. [Google Scholar] [CrossRef]
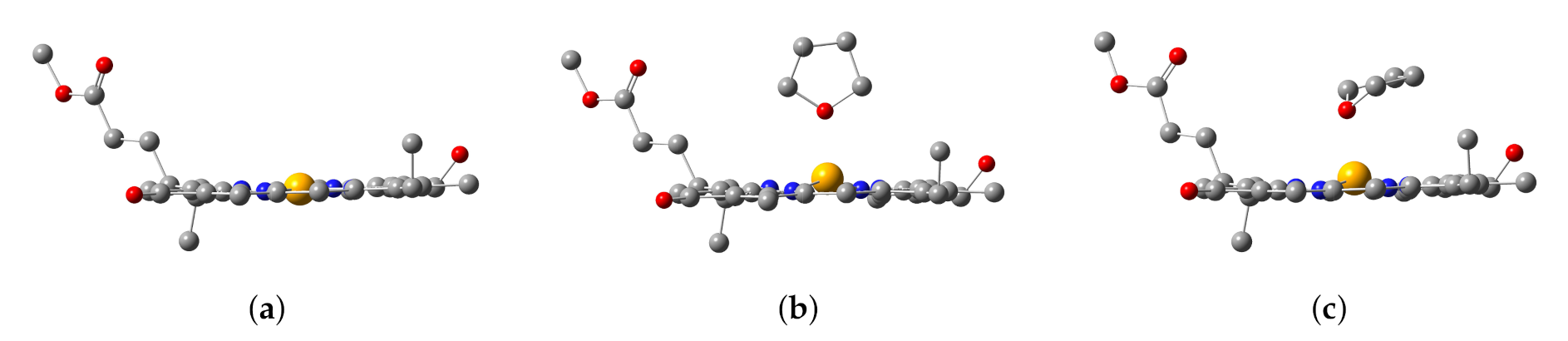
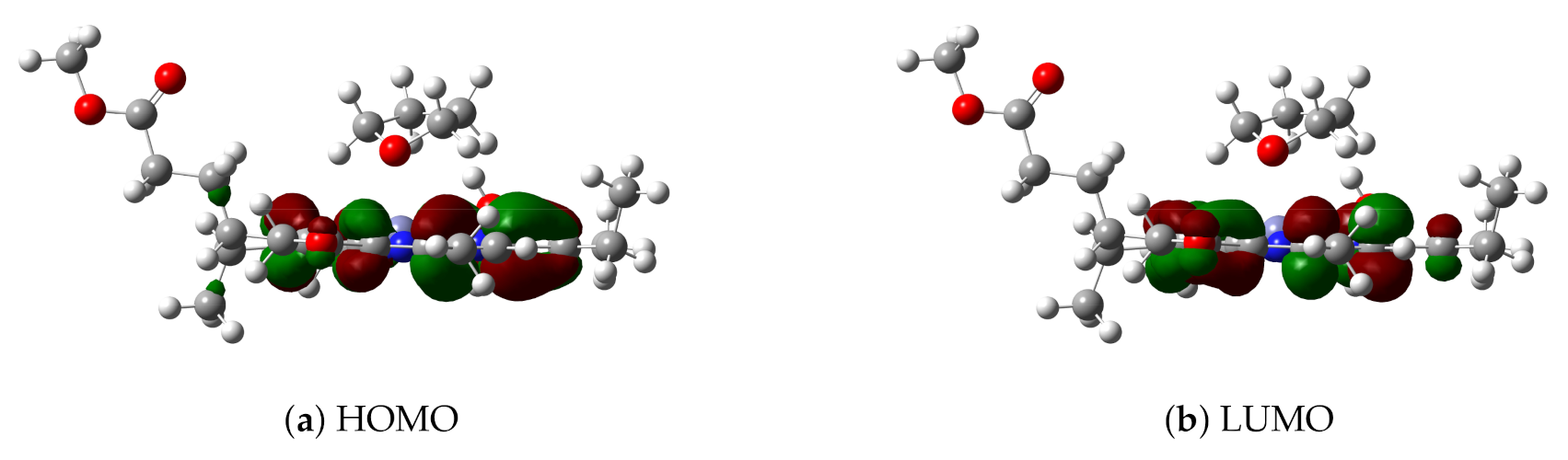
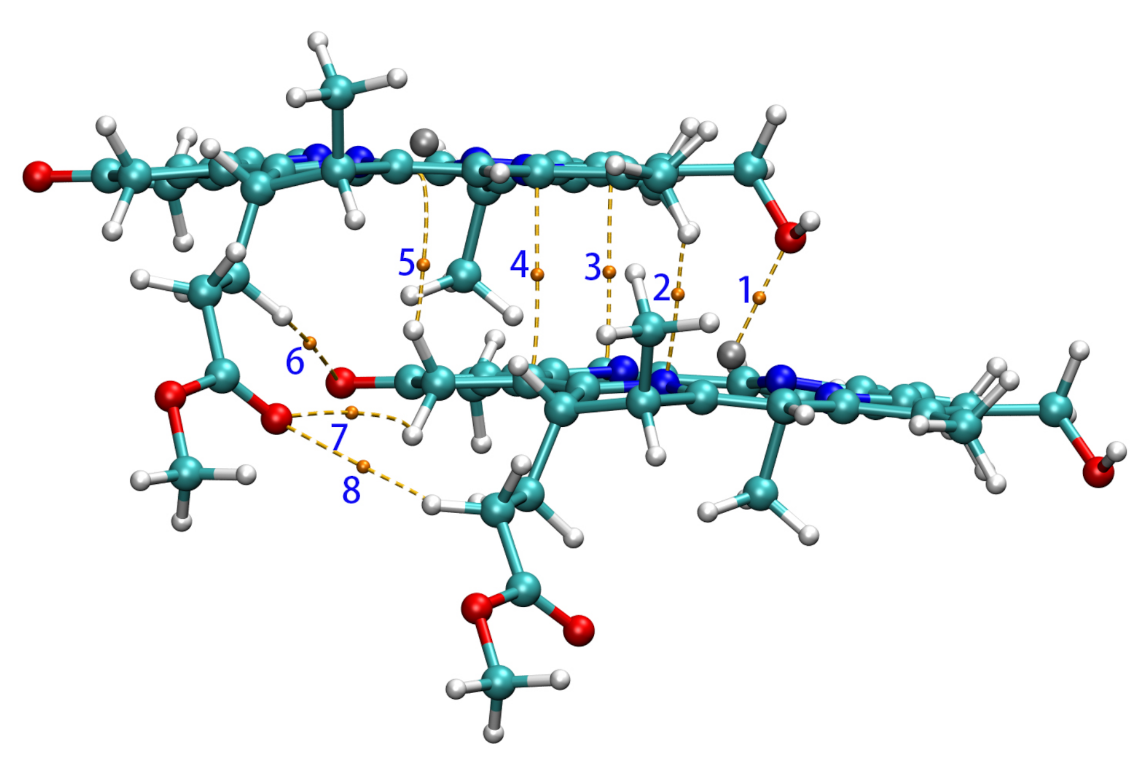
| Structural Parameter | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| Zn-N21 Zn-N22 Zn-N23 Zn-N24 | 1.979 2.050 1.972 2.190 1.219 1.212 | 2.016 2.080 2.011 2.224 1.220 1.212 | 2.014 2.074 1.998 2.193 1.219 1.212 |
| N21-Zn-N22 N22-Zn-N23 N23-Zn-N24 N24-Zn-N21 N21-Zn-N23 | 92.4 88.8 88.6 90.2 178.1 | 90.5 87.2 86.9 88.8 158.3 | 90.8 87.2 88.3 88.9 160.8 |
| DOOP | 0.03 | 0.38 | 0.33 |
| Functional | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|
| /eV ( /nm) | f | /eV (/nm) | f | /eV (/nm) | f | |
| in THF solvent | ||||||
| LC-PBE B97X CAM-B3LYP | 1.902 (652) 1.938 (640) 2.038 (608) | 0.28 0.29 0.32 | 1.892 (655) 1.927 (643) 2.027 (612) | 0.25 0.26 0.30 | 1.879 (660) 1.915 (648) 2.018 (614) | 0.26 0.27 0.30 |
| in vacuum | ||||||
| LC-PBE B97X CAM-B3LYP | 1.935 (641) 1.977 (627) 2.089 (594) | 0.19 0.19 0.21 | 1.924 (644) 1.965 (631) 2.076 (597) | 0.17 0.18 0.19 | 1.909 (650) 1.951 (635) 2.067 (600) | 0.17 0.18 0.19 |
| Expt. [14] | 1.917 eV (647 nm) | |||||
| Property | BCP1 | BCP2 | BCP3 | BCP4 | BCP5 | BCP6 | BCP7 | BCP8 |
|---|---|---|---|---|---|---|---|---|
| 0.0458 −0.0021 0.0572 | 0.0082 0.0012 0.0055 | 0.0051 0.0007 0.0030 | 0.0046 0.0007 0.0028 | 0.0072 0.0007 0.0043 | 0.0028 0.0006 0.0019 | 0.0023 0.0006 0.0016 | 0.0014 0.0004 0.0010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Suo, B.; Yin, S.; Zou, W. Quantum Chemical Simulation of the Qy Absorption Spectrum of Zn Chlorin Aggregates for Artificial Photosynthesis. Molecules 2021, 26, 1086. https://doi.org/10.3390/molecules26041086
Wang Z, Suo B, Yin S, Zou W. Quantum Chemical Simulation of the Qy Absorption Spectrum of Zn Chlorin Aggregates for Artificial Photosynthesis. Molecules. 2021; 26(4):1086. https://doi.org/10.3390/molecules26041086
Chicago/Turabian StyleWang, Zhimo, Bingbing Suo, Shiwei Yin, and Wenli Zou. 2021. "Quantum Chemical Simulation of the Qy Absorption Spectrum of Zn Chlorin Aggregates for Artificial Photosynthesis" Molecules 26, no. 4: 1086. https://doi.org/10.3390/molecules26041086
APA StyleWang, Z., Suo, B., Yin, S., & Zou, W. (2021). Quantum Chemical Simulation of the Qy Absorption Spectrum of Zn Chlorin Aggregates for Artificial Photosynthesis. Molecules, 26(4), 1086. https://doi.org/10.3390/molecules26041086