1. Introduction
The flutter phenomenon is a dynamic instability that arises in lifting structures. It starts when the velocity becomes greater than a critical speed value, namely the flutter boundary. The fluid does not absorb the structure’s energy anymore but increases it as the damping becomes negative in value, causing a condition of fatigue or damage to the structure. The amplitude of the flutter oscillations can grow indefinitely in the linear model, particularly for divergent flutter, or reach a constant amplitude, such as with limit cycle oscillations (LCOs), when there are stiffness or aerodynamic nonlinearities, like in the actual case. By studying the variation of the damping ratio with the airstream velocity, it is possible to recognize different types of flutter [
1] such as soft flutter, which is characterized by a slight slope of the damping ratio–speed curve, and hard flutter, which presents an abrupt variation of the damping ratio beyond the critical point and the hump mode, which is characterized by an initial reduction of damping that becomes negative in value and then increases to become positive again, describing a closed flutter region. The danger in reaching flutter instability is not only related to the high amplitude that can be encountered, but also to the fatigue effect and the increase of the control surface’s freeplay that it can cause. Over the years, many measures have been taken to prevent the rise of aeroelastic vibration phenomena. These can be mainly divided into two categories: passive and active methods. The study of mass balance belongs to the category of passive methods. The dimension and the position of masses strongly influence the amplitude and the frequency of flutter oscillations and modify the coupling mechanism between the bending and torsional vibration modes. A possible passive solution may be reached by moving the center of mass of each structural element of the wing closer to the axis of elasticity (AE) or by installing some concentrated masses to modify the wing’s moment of inertia, with the aim of reducing the amount of energy extracted from the fluid [
2]. The modern methods used for flutter suppression are active methods. These use the data recorded from sensors installed on the structure, such as accelerometers, that are elaborated by a control system to properly move some aerodynamic surfaces or to implement other changes in the structure shape in order to obtain the desired dynamic behavior. The first examples of technology for the control of aeroelastic oscillations were based on the movement of aerodynamic surfaces, such as the trailing edge flap, by means of servo-hydraulic systems [
3]. However, hydraulic systems present some drawbacks, such as the multiple conversions of the energy from one type to another, (e.g., from mechanical to hydraulic and to mechanical again). Conversions of energy lead to losses which, in turn, require higher nominal power of the system and higher weight as well. Lastly, it has to be said that hydraulic systems usually do not reach high bandwidth values. Thus, considering that aeroelastic phenomena are characterized by high frequencies, it follows that they might not be suitable for flutter suppression. The above-mentioned problems have motivated a growing interest in deformation-induced actuators, such as piezoelectric actuators. These, in fact, allow one to obtain mechanical power directly from electric energy. However, piezoelectric actuation does not allow for obtaining large displacements; thus, amplification mechanisms are to be studied. The first attempts of piezoelectric actuation were related to the use of bimorph beams realized by bonding two piezoelectric layers such that when an electric voltage is applied, one stretches while the other contracts, and bending deformations of the beam are obtained. Applications of this technology have been studied for the active control of helicopter blade twist by Waltz and Chopra [
4] and for the flutter suppression of cantilever wings by Heeg [
5]. An innovative method for wing oscillation control consists of the integration of actuators into the structure such that the geometry of the structure itself can be modified, usually in terms of the airfoil camber. This technology is called morphing actuation and has been studied since the 1990s, a period in which greater knowledge of piezoelectric materials was acquired, allowing the modeling of these materials in thin patches that can be integrated into the structure. The first studies that aimed at verifying the feasibility of piezoelectric morphing actuation were carried out by Lazarus et al. [
6] along with numerous other scholars. However, they focused on the realization of all-movable aerodynamic surfaces not specifically designed for aeroelastic suppression. On the contrary, the technology presented by Fichera et al. [
7] was specifically designed for aeroelastic suppression. They proposed a trailing edge morphing actuator capable of a 25 Hz bandwidth and a ±15° maximum equivalent rotation. It is made of two panels: one is an Macro-Fiber Composite-MFC piezo patch sandwich, which is the active part of the actuator, while the other is made of an aluminum alloy. Both panels are fixed on the wing box on one end and on a slider on the other end. In particular, the slider has airfoil trailing edge geometry and allows the two panels to slide in the deformed configuration. Other works dealing with piezoelectric actuation for aeroelastic suppression are based on the installation of piezo patches on the structure’s surface. The actuation of the patches is combined with modern control techniques in order to obtain a robust suppression system [
8].
Other simpler configurations of piezoelectric actuation deal with the use of piezoelectric stacks. Piezo stacks are made by overlapping several piezoelectric layers in order to obtain a rod able to elongate or compress after the application of an electric voltage. Since this configuration does not allow one to obtain large displacements, some amplification mechanisms have been studied. Among others, there are the so-called X and V configurations. The mechanism presented by Hall and Prechtl [
9] is based on an X configuration that allows amplification of the compression deformation of the stacks, resulting in a vertical displacement. On the other hand, the amplification mechanism proposed by Ardelean and Clark [
10] takes advantage of two piezoelectric stacks arranged in a V configuration. The latter configuration is the one selected for the investigation carried out in the present study.
In order to realize the flutter suppression of the airfoil, using the movement of aerodynamic surfaces, many studies have been carried out over the years, and some solutions were reported in the following. In the work of Chen et al. [
11], a two-degrees-of-freedom airfoil was considered, while the presence of both the leading edge and trailing edge aerodynamic surfaces was taken into account only in the expressions of the aerodynamic loads. The control method used by Chen et al. [
11] was based on a sliding mode controller (SMC) (i.e., a nonlinear state feedback controller capable of changing its own structure when the system assumes different states). Thus, this controller presents robustness properties to external disturbances and uncertainties. However, the conventional SMC assumes that the controller could switch from one value to another instantaneously, and this is not possible in real-life applications due to the presence of delays. Therefore, the same authors proposed a high-order sliding mode controller (HOSMC) that was introduced after the backstepping procedure. In this way, a continuous input is provided to the controller [
12]. In the studies of Na et al. [
13] and Yang et al. [
14], the model of a three-degrees-of-freedom airfoil was taken into account. Thus, the dynamic of the aerodynamic surface was considered. The control strategy proposed by Na et al. [
13] was based on an LQR control implementing full-state feedback. Again, this leads to the necessity of having a system that is completely observable. The authors introduced the presence of measure noises and output disturbances, and thus a linear quadratic Gaussian (LQG) controller associated with a sliding mode observer has been implemented, since this architecture is capable of noise decoupling and shows robustness properties to disturbances. Yang et al. [
14] instead specified that the LQR and LQG controllers are based on mathematical knowledge of the disturbances. Thus, when there are some uncertainties, these strategies lose robustness. In order to take into account the uncertainties in the design of the controller, Yang et al. [
14] proposed
loop shaping, which is implemented by defining a generalized plant that encloses all the dynamic features to be controlled, such as sensors and actuator dynamics and so on, and introducing two different input vectors, namely the control input vector and the exogenous input vector. Then, the disturbance–output transfer function is defined, and the minimization problem of its infinity norm is solved. In the works of Wang et al. [
15] and Zhang et al. [
16], neural networks were associated with a full-state feedback–feedforward controller. This strategy has been studied by Bemelli-Zazzera et al. [
17], too. They introduced the use of dynamic neural networks that were capable of changing their own weights through active training in order to adapt to the parameter variation during the normal functioning of the system. In the work of Andrievsky et al. [
18], simple adaptive control (SAC) was implemented for the flutter suppression of an airfoil using an implicit reference model (IRM) and the pacification theorem. The authors implemented an adaptive control capable of flutter suppression in both the cases of the presence of actuator delays and the lack thereof.
Recent works dealing with active flutter suppression, carried out in the framework of projects financed by the European Union and the USA, have been presented. In the work carried out by Takarics and Vanek [
19], a low-order, control-oriented LPV model of the aircraft was obtained using the bottom-up approach. The order of the nonlinear aeroservoelastic model subsystems is reduced, paying attention to capture accurately the flutter modes. Then, the controller is designed considering a polytopic LPV representation. In the work proposed by Waitman and Marcos [
20], a high-fidelity, nonlinear aeroservoelastic model of the FLEXOP aircraft was considered, and three
optimal controllers were tuned and scheduled for different true airspeed values, increasing the damping of the flutter modes at these velocities. This approach led to a flutter boundary increase of 30%. Another recent work carried out by Theis et al. [
21] dealt with the flutter suppression of the mini MUTT aircraft model, built at the University of Minnesota. The
loop shaping method was used in order to design a controller that presented good robustness to a wide variety of uncertainties. Pusch [
22] studied a method based on the blending of control inputs and measurement outputs to isolate individual aeroelastic modes in order to use SISO controllers. In Schmidt et al. [
23], the authors presented a study on drone flight dynamics, taking into account aeroelastic effects modeled by using the mean–axis formulation and quasi-steady aerodynamics. The rigid and aeroelastic model of the drone has since been used to study several controllers for autopiloting, considering the flutter instability as well.
In this work, one of the objectives is to present an FEM model of a V-stack piezoelectric actuator for the flutter suppression of an airfoil. Thus, the finite element model of the actuator is first introduced, and the behavior of the FEM model is compared with the experimental data in order to validate it. The second aim is to propose a heuristic method called population decline swarm optimization for tuning a simple control strategy based on a filtered PID controller by looking for the minimization of the integral of time absolute error (ITAE). This approach is used to set gain scheduling of the controller parameters in order to realize a velocity-dependent flutter suppression system and extend the flight envelope of the airfoil.
This paper is organized as follows. In
Section 2, the numerical model of a three-degrees-of-freedom airfoil is described, and the augmented state space model for the time domain analysis is introduced. In
Section 3, the actuator is studied, introducing the finite element formulation of the piezo stacks. Starting from the state space model, the transfer function that relates the actuator tip’s vertical displacement to the input voltage is computed. In
Section 4, the tuning of the gain scheduling-filtered PID controller is done. The filtered PID controller is tuned using the
algorithm by minimizing the ITAE of the error of the pitch angle. In order to set up an adaptive control in the velocity, the gain scheduling approach is introduced, and the optimization algorithm is used to find the optimal controllers for different velocity values. In
Section 5, the open loop analysis of the system for the identification of the flutter boundary is first carried out. Then, the validation of the static and dynamic behavior of the actuator is done. Moreover, the convergence results of the
optimization procedure are also shown. At last, the comparison between open-loop and closed-loop responses is presented, and some critical situations are simulated in order to study the performance of the closed-loop system.
2. 3DOF Airfoil Model
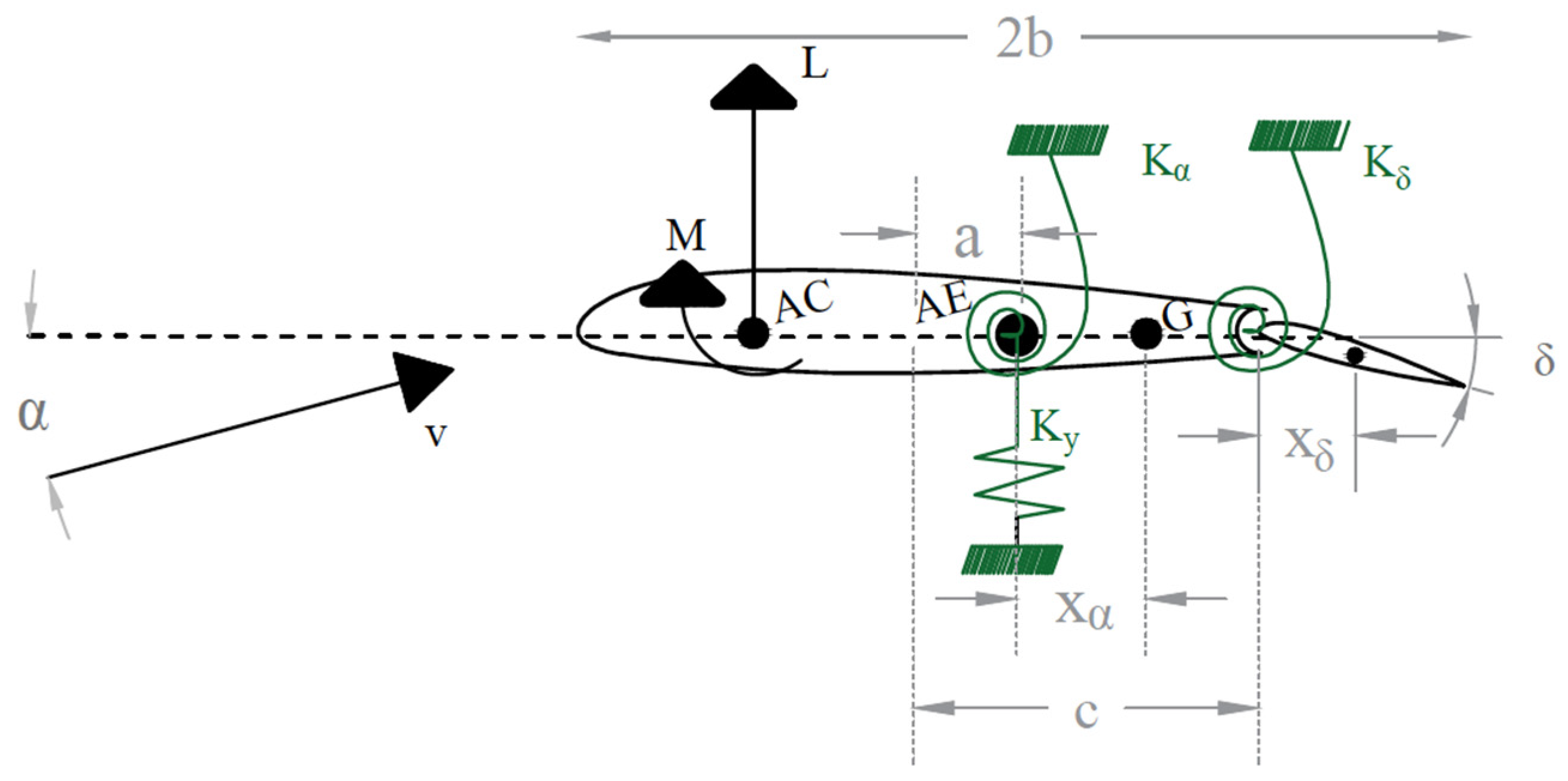
In order to study the flutter phenomenon, a simplification was introduced by reducing the wing to its representative mean airfoil and, as a consequence, a two-dimensional structural model could be considered. The torsional deformability of the wing, which was considered as a beam with a thin-walled section, was simulated by a spring of stiffness
placed in the axis of elasticity (AE), which represented the constraint. The flexional stiffness was simulated by the heave spring
. Due to the presence of the flap a third spring of stiffness,
was introduced in order to take into account the hinge behavior. In this way the three-degrees-of-freedom concentrated parameters model of the wing, shown in
Figure 1, was obtained. Of course, this model had to be considered as a first approximation of the structure, useful for the preliminary studies carried out in this work.
In order to obtain the equations of motion of the three-degrees-of-freedom (3DOF) airfoil, the balance between the inertial, elastic and aerodynamic forces was imposed, writing the system in Equation (1) [
24]. The nonlinear stiffness term
was also considered in order to take into account that nonlinear effects could arise for large displacements, introducing the limit cycle oscillation phenomenon:
where
and
are the pitch and flap rotation angles, respectively, while
is the plunge displacement,
and
are the inertia moments,
and
are the static moments,
is the total mass of the wing and the support blocks,
is the lift force and
and
are the aerodynamic moments acting on the airfoil and on the flap, respectively.
In order to carry out the stability analysis of the airfoil, it could be useful to take into account the nondimensional equations of motion. Thus, the first and the second equations of the system in (1) were divided by the term
, while the third equation was divided by the term
, obtaining the following system:
where
and
,
are the uncoupled natural frequencies,
and
are the gyration radius divided by the semi-chord of the airfoil
and
is the nonlinear stiffness coefficient, such that
.
In order to obtain the state space model of the system, it was convenient to write the system in matrix form at first (see Equation (3)). The generalized displacement vector
, the generalized force vector
and the matrices
and
, namely the generalized inertia matrix and the stiffness matrix that are reported in
Appendix A, were defined:
In order to introduce the structural damping contribution, the procedure described by Liu and Dowell [
25] was followed, and the damping factors obtained experimentally were treated in the numerical model as modal damping factors. The structural damping matrix was written as
where
is the modal matrix, while the modal damping matrix was defined as
where
,
and
are the modal masses, the coupled natural frequencies and the measured damping ratios, respectively.
Once the matrices were defined, the model could be written as
Before defining the state space representation of the analyzed problem, the aerodynamic force model must be introduced.
2.1. Aerodynamic Model
The aerodynamic model considered in this work was the one formulated by Theodorsen [
26] for an oscillating airfoil. It was based on the potential flow theory and on the hypothesis that the amplitude of the oscillations is so small that they can be treated as perturbations. According to this theory, the aerodynamic force and moments are functions of the Lagrangian parameters and of the Theodorsen constants
, reported in
Appendix B. The aerodynamic loads were written as follows:
where it appears that the Theodorsen function of the reduced frequency
, where
is the airstream velocity and
is the frequency of the motion. The Theodorsen function was defined as a function of the Hankel function of the second kind as follows:
The structural and aerodynamic formulation discussed is suitable for the analysis of the system in the frequency domain, from which information about the flutter boundary can be obtained. For the aim of this work, it was convenient to introduce time domain analysis. The Duhamel formulation [
27] that allows for modeling the arbitrary motion of the airfoil instead of the simple harmonic one was thus introduced by writing the circulatory contribution to the aerodynamic loads as follows:
where
and
have values
,
,
and
[
27].
By integrating parts of Equation (11), a simplified expression of
was obtained:
In addition, using the Padè approximation, it could be written as a second-order differential equation, where the two aerodynamic augmented states
and
appear (see Equation (13)):
2.2. Augmented State Space Form
The numerical model of the 3DOF airfoil belongs to the class of parameter varying systems, as it depends on the velocity of the airstream. Considering a fixed speed value, the 3DOF model could be considered as a time-invariant system, and thus the augmented state space formulation could be used for the time domain tuning of the controller, introducing the state vector
and writing Equations (6)–(9) in matrix form:
Then, the dynamic matrix
was computed. The state input matrix
was defined, taking into account that the input was the flap deflection
. Thus,
was a column matrix equal to the second column of the dynamic matrix. Lastly, the output state matrix
was imposed to be the identity matrix in the hypothesis of ideal sensors for all the variables. The augmented state space model is written as follows:
where the term
takes into account the nonlinear stiffness contribution.
4. Gain-Scheduled Filtered PID Active Controller
The control architecture chosen in this work and shown in
Figure 5 was based on an output feedback scheme based on a filtered Proportional-Integral-Derivative fPID controller that presented some benefits. This type of controller presented a simplicity in implementation and installation and, moreover, it only requested one output measure, thus asking for the implementation of only one sensor device and allowing us to avoid the complication of the controller scheme introduced by, for instance, state observers. These are some of the reasons that currently still motivate the use of PID controllers in the industry [
30]. Moreover, the PID controller had a fixed structure, and the problem reduced to the tuning of its parameters, which were made in this work using a population decline swarm optimization
algorithm. The principal issue of choosing a PID controller is that it is not adaptive with the system’s change of parameters. In this work, in order to make the controller adaptive in velocity, a gain scheduling (GS) approach was used.
The filtered PID controller acted by minimizing the error function
, being
, because the aim was to stabilize the system. The reference signal sent to the actuator was the voltage input, and it was computed as the sum of three terms: one proportional to the current error, one proportional to the time integral of the error, ensuring the system reached the desired setpoint, and the last term proportional to the filtered error time derivative [
30]:
where
is the solution of the following first-order differential equation:
The choice of a controller with all three components was related to the peculiarities of each term. In fact, a proportional-only controller could not make the system able to reach the setpoint. By increasing the proportional gain, the difference between the actual and desired values could be reduced, but the system would encounter more oscillations for the rapid transient; thus, the integral contribution was added. At least, the derivative terms allowed the system to tackle the rapid transient easily, as the derivative gave information on the evolution of the error. Thus, the controller was able to forecast and fill the eventual delays, leading to a reduction of the oscillation amplitude.
The controller parameters, namely , and , had to be tuned in such a way that no instabilities due to the control were introduced, and the flap displacement had to be able to stabilize the airfoil in the shortest time. In order to obtain the PID controller at the flutter speed, a algorithm was used, and the fitness function to be minimized was chosen to be the integral of time absolute error (ITAE).
It is worth noting that that, strictly speaking, heuristic optimizers did not find the actual optimum, but their solution was always the best parameter configuration among all the other configurations that were tested. This means that the controller might be suboptimal because it is just the best among the tested ones. This is particularly true when a flat region of the performance index is found. Thus, considering that the PID tuning was gained via a numeric metaheuristic approach, the obtained controller was to be considered as a suboptimal one. With regard to the objective function, it should be noted that the ITAE was chosen because it had the ability to highlight the divergence error that occurred when incorrect controller parameters were used and the flutter vibration started increasing slowly. The mathematical expression of the fitness function is the following:
where
is the instant of perturbation and
is the time window chosen for the computation of the function, being large enough to include the entire transient response, but not too much to affect the computational cost of the algorithm. In this study, it was imposed to be
s and
s.
Each particle
at each iteration
was defined in the algorithm by four coordinates
, and the minimization problem was expressed as follows:
where the research space limits were chosen by a preliminary trial and error approach.
As the speed can vary, the 3DOF airfoil model is a parameter varying system, and for this family of dynamic systems, the simplest method to obtain adaptive controllers is the gain scheduling (GS) method. The GS method was implemented by defining a set of controllers tuned for different working conditions of the system, which were identified by an appropriate scheduling variable, in this case the airstream speed. However, each controller guaranteed the desired performance only locally, and thus an interpolation of the controller parameters had to be introduced [
31]. The gain scheduling control architecture used is shown in
Figure 6.
In order to compute the scheduling table, the algorithm was used for different velocity values, and the optimal PID controller for each one was found. A set of linear, time-invariant sub-optimal controller parameters was obtained, and a linear interpolation of the PID parameters was introduced to obtain a parameter-varying controller.