Groundwater Quality Evaluation of the Dawu Water Source Area Based on Water Quality Index (WQI): Comparison between Delphi Method and Multivariate Statistical Analysis Method
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Single Factor Evaluation
3.2. Full Index Analysis
3.3. Delphi Method Analysis
3.4. Principal Component Analysis
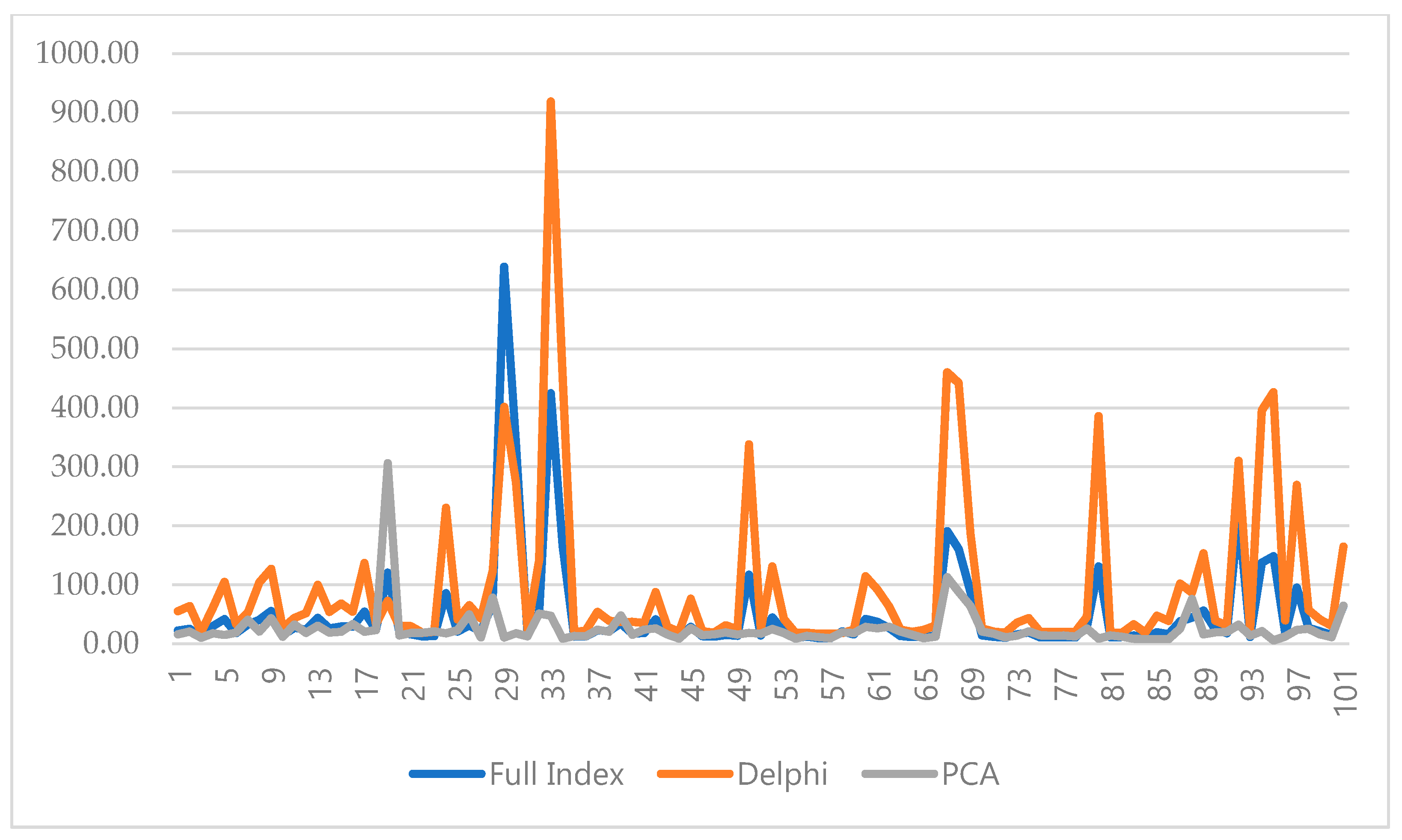
3.5. Evaluation and Comparison
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Döll, P.; Fiedler, K. Global-scale modeling of groundwater recharge. Hydrol. Earth Syst. Sci. 2008, 12, 863–885. [Google Scholar] [CrossRef] [Green Version]
- Hou, D.; Li, G.; Nathanail, P. An emerging market for groundwater remediation in China: Policies, statistics, and future outlook. Front. Environ. Sci. Eng. 2018, 12. [Google Scholar] [CrossRef]
- MEE. Bulletin on the State of China’s Ecology and Environment, China; MEE: Beijing, China, 2019. [Google Scholar]
- Gao, Z.; Zhang, H.; Feng, J.; Lu, T.; Yang, L.; Sun, J.; Shi, M. Dynamic evolution of karst water levels and its controlling and influencing factors in Northern China: A case study in the Dawu water source area. Carbonates Evaporites 2020, 35. [Google Scholar] [CrossRef]
- Noori, R.; Berndtsson, R.; Hosseinzadeh, M.; Adamowski, J.F.; Abyaneh, M.R. A critical review on the application of the National Sanitation Foundation Water Quality Index. Environ. Pollut. 2019, 244, 575–587. [Google Scholar] [CrossRef] [PubMed]
- Horton, R.K. An index number system for rating water quality. J. Water Pollut. Control Fed. 1965, 37, 300–306. [Google Scholar]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Tozer, R.G. A water quality index—Do we dare? Water Sew Works 1970, 117, 339–343. [Google Scholar]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; O’Connor, M. A Water Quality Index—Crashing the Psychological Barrier. Indic. Environ. Qual. 1972, 1, 173–178. [Google Scholar] [CrossRef]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Landwehr, J.M. Validating the WQI. In Proceedings of the National Meeting of American Society of Civil Engineers on WATER Resources Engineering, Washington, DC, USA, 29 January–2 February 1973. [Google Scholar]
- Deininger, R.A.; Maciunas, J.M. Water Quality Index for Public Water Supplies; University of Michigan: Ann Arbor, MI, USA, 1971. [Google Scholar]
- Linstone, H.A.; Murray, T. The Delphi Method: Techniques and Applications; Addison Wesley Reading: Boston, MA, USA, 1975. [Google Scholar]
- House, M.A. A water quality index for river management. J. Water Environ. Manag. 1989, 3, 336–344. [Google Scholar] [CrossRef]
- House, M.A. Water quality indices as indexs of ecosystem change. Environ. Monit. Assess. 1990, 5, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Bouslah, S.; Djemili, L.; Houichi, L. Water quality index assessment of Koudiat Medouar Reservoir, northeast Algeria using weighted arithmetic index method. J. Water Land Dev. 2017, 35, 221–228. [Google Scholar] [CrossRef]
- MRC. An Assessment of Water Quality in the Lower Mekong Basin; MRC Technology Paper; Mekong River Commission: Vientiane, Laos, 2008; p. 70. [Google Scholar]
- Bhatt, J.P.; Pandit, M.K. A macro-invertebrate based new biotic index to monitor river quality. Curr. Sci. 2010, 99, 196–203. [Google Scholar]
- Lumb, A.; Sharma, T.C.; Bibeault, J.F. A Review of Genesis and Evolution of Water Quality Index (WQI) and Some Future Directions. Water Qual. Expo. Health 2011, 3, 11–24. [Google Scholar] [CrossRef]
- Machiwal, D.; Islam, A.; Kamble, T. Trends and probabilistic stability index for evaluating groundwater quality: The case of quaternary alluvial and quartzite aquifer system of India. J. Environ. Manag. 2019, 237, 457–475. [Google Scholar] [CrossRef] [PubMed]
- Mahapatra, S.S.; Sahu, M.; Patel, R.K.; Panda, B.N. Prediction of Water Quality Using Principal Component Analysis. Water Qual. Expo. Health 2012, 4, 93–104. [Google Scholar] [CrossRef]
- Fathy, S.A.H.; Hamid, F.F.A.; Shreadah, M.A.; Mohamed, L.A.; El-Gazar, M.G. Application of Principal Component Analysis for Developing Water Quality Index for Selected Coastal Areas of Alexandria Egypt. Resour. Environ. 2012, 2, 297–305. [Google Scholar] [CrossRef] [Green Version]
- Yotova, G.; Varbanov, M.; Tcherkezova, E.; Tsakovski, S. Water quality assessment of a river catchment by the composite water quality index and self-organizing maps. Ecol. Indic. 2021, 120, 106872. [Google Scholar] [CrossRef]
- NHC; SAC. Standard Examination Methods for Drinking Water; GB/T5750; NHC; SAC: Beijing, China, 2006.
- AQSIQ; SAC. Standards for Groundwater Quality; GT14848-2017; AQSIQ; SAC: Beijing, China, 2017. [Google Scholar]
- NHC; SAC. Standards for Drinking Water Quality; GB5749-2006; NHC; SAC: Beijing, China, 2006.
- The European Commission Environment. The Drinking Water Directive (DWD), Council Directive 98/83/EC; The European Commission Environment: Brussels, Belgium, 1998. [Google Scholar]
- WHO. Guidelines for Drinking-Water Quality, 4th ed.; World Health Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Musa, H.D.; Yacob, M.R.; Abdullah, A.M.; Ishak, M.Y. Delphi Method of Developing Environmental Well-being Indexs for the Evaluation of Urban Sustainability in Malaysia. Procedia Environ. Sci. 2015, 30, 244–249. [Google Scholar] [CrossRef] [Green Version]
- Cheshmidari, M.N.; Ardakani, A.H.H.; Alipor, H.; Shojaei, S. Applying Delphi method in prioritizing intensity of flooding in Ivar watershed in Iran. Spat. Inf. Res. 2017, 25, 173–179. [Google Scholar] [CrossRef]
- Moreira, D.G.; Costello, J.T.; Brito, C.J.; Adamczyk, J.G.; Ammer, K.; Bach, A.J.; Costa, C.M.; Eglin, C.; Fernandes, A.A.; Fernández-Cuevas, I.; et al. Thermographic imaging in sports and exercise medicine: A Delphi study and consensus statement on the measurement of human skin temperature. J. Therm. Biol. 2017, 69, 155–162. [Google Scholar] [CrossRef]
- Strand, J.; Carson, R.T.; Navrud, S.; Ortiz-Bobea, A.; Vincent, J.R. Using the Delphi method to value protection of the Amazon rainforest. Ecol. Econ. 2017, 131, 475–484. [Google Scholar] [CrossRef]
- Varndell, W.; Fry, M.; Lutze, M.; Elliot, D. Use of the Delphi method to generate guidance in emergency nursing practice: A systematic review. Int. Emerg. Nurs. 2020, 100867. [Google Scholar] [CrossRef]
- Vega, M.; Pardo, R.; Barrado, E.; Debán, L. Assessment of seasonal and polluting effects on the quality of river water by exploratory data analysis. Water Res. 1998, 32, 3581–3592. [Google Scholar] [CrossRef]
- Liu, C.; Lin, K.; Kuo, Y. Application of factor analysis in the assessment of groundwater quality in a blackfoot disease area in Taiwan. Sci. Total Environ. 2003, 313, 77–89. [Google Scholar] [CrossRef]
- Simeonov, V.; Stratis, J.A.; Samara, C.; Zachariadis, G.; Voutsa, D.; Anthemidis, A.; Sofoniou, M.; Kouimtzis, T. Assessment of the surface water quality in Northern Greece. Water Res. 2003, 37, 4119–4124. [Google Scholar] [CrossRef]
- Singh, K.P.; Malik, A.; Mohan, D.; Sinha, S. Multivariate statistical techniques for the evaluation of spatial and temporal variations in water quality of Gomti River (India)—A case study. Water Res. 2004, 38, 3980–3992. [Google Scholar] [CrossRef] [PubMed]
- Trabelsi, R.; Zouari, K. Coupled geochemical modeling and multivariate statistical analysis approach for the assessment of groundwater quality in irrigated areas: A study from North Eastern of Tunisia. Groundw. Sustain. Dev. 2019, 8, 413–427. [Google Scholar] [CrossRef]
- Abdelaziz, S.; Gad, M.I.; El Tahan, A.H.M. Groundwater quality index based on, P.CA: Wadi El-Natrun; Egypt. J. Afr. Earth Sci. 2020, 172, 103964. [Google Scholar] [CrossRef]
- Bouderbala, A.; Remini, B.; Hamoudi, A.S.; Pulido-Bosch, A. Application of Multivariate Statistical Techniques for Characterization of Groundwater Quality in the Coastal Aquifer of Nador; Tipaza (Algeria). Acta Geophys. 2016, 64, 670–693. [Google Scholar] [CrossRef] [Green Version]
- Roberts, N.M.; Tikoff, B.; Davis, J.R.; Stetson-Lee, T. The utility of statistical analysis in structural geology. J. Struct. Geol. 2019, 125, 64–73. [Google Scholar] [CrossRef]
- Masoud, A.M.; Ali, M.H. Coupled multivariate statistical analysis and, WQI approaches for groundwater quality assessment in Wadi El-Assiuty downstream area; Eastern Desert; Egypt. J. Afr. Earth Sci. 2020, 172, 103982. [Google Scholar] [CrossRef]
- Suhas, S.; Chaudhary, J.K. A Comparative Study of Fuzzy Logic and, WQI for Groundwater Quality Assessment. Procedia Comput. Sci. 2020, 171, 1194–1203. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, S.; Li, H.; Fu, K.; Xu, Y. Groundwater pollution source identification and apportionment using, P.MF and, P.CA-APCA-MLR receptor models in a typical mixed land-use area in Southwestern China. Sci. Total Environ. 2020, 741, 140383. [Google Scholar] [CrossRef]
- Guido, R.C. A tutorial review on entropy-based handcrafted feature extraction for information fusion. Inf. Fusion 2018, 41, 161–175. [Google Scholar] [CrossRef]
- Cole, C. Calculating the information content of an information process for a domain expert using Shannon’s mathematical theory of communication-A preliminary analysis. Inf. Process. Manag. 1997, 33, 715–726. [Google Scholar] [CrossRef]
- Zou, Z.H.; Yun, Y.; Li, H.; Fu, K.; Xu, Y. Entropy method for determination of weight of evaluating indexs in fuzzy synthetic evaluation for water quality assessment. J. Environ. Sci. 2006, 18, 1020–1023. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, W. A relative entropy method to measure non-exponential random data. Phys. Lett. A 2015, 379, 95–99. [Google Scholar] [CrossRef]
- Hasan, M.S.U.; Rai, A.K. Groundwater quality assessment in the Lower Ganga Basin using entropy information theory and GIS. J. Clean. Prod. 2020, 274, 123077. [Google Scholar] [CrossRef]
- Li, P.; Wu, J.; Qian, H.; Lyu, X.; Liu, H. Origin and assessment of groundwater pollution and associated health risk: A case study in an industrial park, northwest China. Environ. Geochem. Health 2014, 36, 693–712. [Google Scholar] [CrossRef]
- Qiu, W.H. Management Decision and Applied Entropy; China Machine Press: Beijing, China, 2002; pp. 193–196. [Google Scholar]
- Pan, G.; Xu, Y.; Yu, Z.; Song, S.; Zhang, Y. Analysis of river health variation under the background of urbanization based on entropy weight and matter-element model: A case study in Huzhou City in the Yangtze River Delta, China. Environ. Res. 2015, 139, 31–35. [Google Scholar] [CrossRef]
- Ma, Z.; Li, H.; Ye, Z.; Wen, J.; Hu, Y.; Liu, Y. Application of modified water quality index (WQI) in the assessment of coastal water quality in main aquaculture areas of Dalian, China. Mar. Pollut. Bull. 2020, 157, 111285. [Google Scholar] [CrossRef]
- Nong, X.; Shao, D.; Zhong, H.; Liang, J. Evaluation of water quality in the South-to-North Water Diversion Project of China using the water quality index (WQI) method. Water Res. 2020, 178, 115781. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Unit | Min. | Max. | Mean | Chinese Standards | WFD | WHO Guidelines (2011) |
|---|---|---|---|---|---|---|---|
| Na+ | mg/L | 4.9839 | 913.3225 | 41.0366 | 200 | 200 | 200 |
| NH4+–N | mg/L | 0.0200 | 29.6567 | 0.5087 | 0.5 | 0.5 | —— |
| Fe | mg/L | 0.0000 | 6.1300 | 0.6632 | 0.3 | 0.2 | —— |
| Cl− | mg/L | 12.0060 | 2152.3590 | 133.9351 | 250 | 250 | —— |
| SO42− | mg/L | 54.3220 | 920.7760 | 131.0471 | 250 | 250 | —— |
| pH | —— | 7.01 | 8.48 | 7.50 | 6.5–8.5 | 6.5–9.5 | —— |
| TH | mg/L | 276.5610 | 2286.1430 | 482.5170 | 450 | —— | —— |
| TDS | mg/L | 321.9000 | 3846.4300 | 625.9090 | 1000 | —— | —— |
| COD (Mn) | mg/L | 0.5000 | 57.4000 | 2.2400 | 3 | —— | —— |
| F− | mg/L | 0.0720 | 0.5247 | 0.2331 | 1 | 1.5 | 1.5 |
| NO3−–N | mg/L | 0.0182 | 91.7497 | 11.6870 | 10 | 50 | 11 |
| NO2−–N | mg/L | 0.0030 | 6.1300 | 0.2973 | 1 | 0.5 | 0.9 |
| Al | mg/L | 0.0010 | 0.5240 | 0.0321 | 0.2 | 0.2 | —— |
| Mn | mg/L | 0.0001 | 2.6463 | 0.1389 | 0.1 | 0.05 | —— |
| Hg | mg/L | 0.0001 | 0.0069 | 0.0002 | 0.001 | 0.001 | 0.006 |
| Pb | mg/L | 0.0001 | 0.0149 | 0.0009 | 0.01 | 0.01 | 0.01 |
| Mo | mg/L | 0.0001 | 0.0646 | 0.0031 | 0.07 | —— | —— |
| Ag | mg/L | 0.0000 | 0.0005 | 0.0001 | 0.05 | —— | —— |
| Ni | mg/L | 0.0001 | 0.0254 | 0.0020 | 0.02 | 0.02 | 0.07 |
| tetrachloromethane | mg/L | 0.0001 | 0.0597 | 0.0010 | 0.002 | 0.004 | |
| benzene | mg/L | 0.0002 | 2.6000 | 0.0390 | 0.01 | 0.01 | 0.01 |
| methylbenzene | mg/L | 0.0001 | 0.0648 | 0.0010 | 0.7 | —— | 0.7 |
| chloroethylene | mg/L | 0.0004 | 0.4510 | 0.0086 | 0.005 | 0.0005 | 0.0003 |
| 1,1-dichloroethylene | mg/L | 0.0001 | 0.0932 | 0.0027 | 0.03 | —— | —— |
| dichloromethane | mg/L | 0.0002 | 0.0097 | 0.0004 | 0.02 | —— | 0.02 |
| 1,2-dichloroethylene | mg/L | 0.0000 | 0.1858 | 0.0054 | 0.05 | —— | 0.05 |
| 1,2-dichloroethane | mg/L | 0.0002 | 0.0633 | 0.0020 | 0.03 | 0.003 | 0.03 |
| trichloroethylene | mg/L | 0.0001 | 0.2035 | 0.0085 | 0.07 | 0.01 | 0.02 |
| 1,2-dichloropropane | mg/L | 0.0002 | 0.4643 | 0.0107 | —— | —— | 0.04 |
| 1,1,2-trichloroethane | mg/L | 0.0001 | 0.9990 | 0.0261 | 2 | —— | —— |
| tetrachloroethylene | mg/L | 0.0001 | 0.3291 | 0.0061 | 0.04 | 0.01 | 0.04 |
| chlorobenzene | mg/L | 0.0001 | 0.0321 | 0.0010 | 0.3 | —— | —— |
| ethylbenzene | mg/L | 0.0001 | 0.3510 | 0.0038 | 0.3 | —— | 0.3 |
| xylene(total) | mg/L | 0.0000 | 0.4778 | 0.0054 | 0.5 | —— | 0.5 |
| styrene | mg/L | 0.0001 | 0.0209 | 0.0003 | 0.02 | —— | 0.02 |
| paradichlorobenzene | mg/L | 0.0001 | 0.0018 | 0.0001 | 0.3 | —— | 0.3 |
| o-dichlorobenzene | mg/L | 0.0001 | 0.0010 | 0.0001 | 1 | —— | 1 |
| trichlorobenzene (total) | mg/L | 0.0000 | 0.4778 | 0.0107 | 0.02 | —— | —— |
| Index | Rate | Index | Rate | Index | Rate | Index | Rate |
|---|---|---|---|---|---|---|---|
| Na+ | 1.98% | NO3−–N | 49.50% | tetra-chloromethane | 4.95% | 1,1,2-trichloroethane | 9.90% |
| NH4+–N | 3.96% | NO2−–N | 9.90% | benzene | 4.95% | tetra-chloroethylene | 1.98% |
| Fe | 42.57% | Al | 0.99% | methylbenzene | 0.00% | chlorobenzene | 0.00% |
| Cl− | 9.90% | Mn | 10.89% | chloroethylene | 2.97% | ethylbenzene | 0.99% |
| SO42− | 5.94% | Hg | 0.99% | 1,1-dichloroethylene | 2.97% | xylene (total) | 0.00% |
| pH | 0.00% | Pb | 1.98% | dichloromethane | 0.00% | styrene | 0.99% |
| TH | 31.68% | Mo | 0.00% | 1,2-dichloroethylene | 2.97% | para-dichlorobenzene | 0.00% |
| TDS | 9.90% | Ag | 0.00% | 1,2-dichloroethane | 1.98% | o-dichlorobenzene | 0.00% |
| COD (Mn) | 6.93% | Ni | 0.99% | trichloroethylene | 4.95% | trichlorobenzene (total) | 0.00% |
| F− | 0.00% | 1,2-dichloropropane | 7.92% |
| Component | Initial Eigenvalue | Extraction Sums of Squared Loadings | Rotation Sums of Squared Loadings | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | Variance % | Accumulation % | Total | Variance % | Accumulation % | Total | Variance % | Accumulation % | |
| 1 | 11.091 | 29.188 | 29.188 | 11.091 | 29.188 | 29.188 | 6.803 | 17.903 | 17.903 |
| 2 | 6.165 | 16.224 | 45.412 | 6.165 | 16.224 | 45.412 | 6.794 | 17.880 | 35.783 |
| 3 | 3.721 | 9.791 | 55.203 | 3.721 | 9.791 | 55.203 | 4.853 | 12.771 | 48.554 |
| 4 | 2.720 | 7.159 | 62.362 | 2.720 | 7.159 | 62.362 | 3.297 | 8.676 | 57.230 |
| 5 | 2.464 | 6.484 | 68.845 | 2.464 | 6.484 | 68.845 | 2.839 | 7.472 | 64.702 |
| 6 | 2.067 | 5.438 | 74.284 | 2.067 | 5.438 | 74.284 | 2.660 | 6.999 | 71.701 |
| 7 | 1.643 | 4.324 | 78.607 | 1.643 | 4.324 | 78.607 | 2.024 | 5.326 | 77.026 |
| 8 | 1.477 | 3.886 | 82.493 | 1.477 | 3.886 | 82.493 | 1.997 | 5.256 | 82.283 |
| 9 | 1.088 | 2.863 | 85.356 | 1.088 | 2.863 | 85.356 | 1.168 | 3.073 | 85.356 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| xylene (total) | 0.975 | ||||||||
| styrene | 0.970 | ||||||||
| methylbenzene | 0.935 | ||||||||
| trichlorobenzene (total) | 0.895 | ||||||||
| Ni | 0.757 | ||||||||
| TH | 0.671 | ||||||||
| Mn | 0.516 | ||||||||
| dichloromethane | 0.956 | ||||||||
| 1,2-dichloroethylene | 0.932 | ||||||||
| 1,2-dichloroethane | 0.886 | ||||||||
| chloroethylene | 0.886 | ||||||||
| 1,1,2-trichloroethane | 0.851 | ||||||||
| chlorobenzene | 0.817 | ||||||||
| 1,1-dichloroethylene | 0.780 | ||||||||
| o-dichlorobenzene | 0.981 | ||||||||
| ethylbenzene | 0.976 | ||||||||
| benzene | 0.918 | ||||||||
| paradichlorobenzene | 0.807 | ||||||||
| Na+ | 0.935 | ||||||||
| TDS | 0.860 | ||||||||
| Cl− | 0.851 | ||||||||
| pH | −0.494 | ||||||||
| NO3−–N | 0.894 | ||||||||
| NH4+–N | 0.868 | ||||||||
| NO2−–N | 0.755 | ||||||||
| COD (Mn) | 0.729 | ||||||||
| tetrachloromethane | 0.962 | ||||||||
| 1,2-dichloropropane | 0.756 | ||||||||
| trichloroethylene | 0.668 | ||||||||
| tetrachloroethylene | 0.494 | ||||||||
| Mo | 0.795 | ||||||||
| SO42− | 0.751 | ||||||||
| F− | 0.595 | ||||||||
| Ag | 0.386 | ||||||||
| Al | 0.919 | ||||||||
| Pb | 0.664 | ||||||||
| Fe | 0.586 | ||||||||
| Hg | 0.906 |
| WQI Range | Type | Classification |
|---|---|---|
| <20 | Excellent | Ⅰ |
| 25–50 | Good | Ⅱ |
| 50–100 | Poor | Ⅲ |
| 100–150 | Very poor | Ⅳ |
| >150 | Unsuitable | Ⅴ |
| Full Index | Delphi | PCA 2 | |||
|---|---|---|---|---|---|
| WQI 1 | Classification | WQI | Classification | WQI | Classification |
| 22.84 | I | 55.33 | III | 15.96 | I |
| 25.58 | II | 63.89 | III | 20.88 | I |
| 12.17 | I | 20.00 | I | 10.19 | I |
| 30.14 | II | 61.58 | III | 18.05 | I |
| 41.84 | II | 105.16 | IV | 15.17 | I |
| 18.34 | I | 33.44 | II | 19.21 | I |
| 32.76 | II | 52.68 | III | 40.68 | II |
| 40.98 | II | 104.18 | IV | 20.78 | I |
| 55.58 | III | 127.24 | IV | 43.19 | II |
| 14.91 | I | 26.91 | II | 12.29 | I |
| 27.24 | II | 44.14 | II | 32.89 | II |
| 24.01 | I | 52.20 | III | 18.84 | I |
| 43.92 | II | 99.81 | III | 30.51 | II |
| 26.37 | II | 54.18 | III | 19.07 | I |
| 29.59 | II | 68.50 | III | 20.58 | I |
| 29.12 | II | 54.61 | III | 33.39 | II |
| 54.70 | III | 136.76 | IV | 20.59 | I |
| 23.99 | I | 33.11 | II | 23.23 | I |
| 120.63 | IV | 72.80 | III | 305.92 | V |
| 19.37 | I | 29.75 | II | 14.32 | I |
| 16.01 | I | 30.02 | II | 18.16 | I |
| 12.63 | I | 18.79 | I | 18.80 | I |
| 13.15 | I | 20.34 | I | 21.34 | I |
| 85.67 | III | 230.50 | V | 18.03 | I |
| 20.72 | I | 41.54 | II | 23.18 | I |
| 31.55 | I I | 65.52 | III | 49.84 | II |
| 21.59 | I | 43.20 | II | 11.05 | I |
| 67.14 | III | 122.41 | IV | 78.29 | III |
| 638.88 | V | 401.38 | V | 10.75 | I |
| 341.01 | V | 273.59 | V | 18.09 | I |
| 13.67 | I | 25.35 | II | 12.81 | I |
| 53.21 | III | 143.58 | IV | 51.25 | III |
| 424.70 | V | 918.88 | V | 47.55 | II |
| 165.20 | IV | 458.78 | V | 8.77 | I |
| 12.05 | I | 20.55 | I | 13.21 | I |
| 12.48 | I | 22.18 | I | 13.00 | I |
| 22.96 | I | 54.40 | III | 24.04 | I |
| 21.08 | I | 39.31 | II | 20.60 | I |
| 34.52 | II | 37.02 | II | 47.88 | II |
| 17.4 | I | 37.32 | II | 15.56 | I |
| 18.35 | I | 35.41 | II | 24.15 | I |
| 41.61 | II | 87.58 | III | 26.13 | II |
| 19.03 | I | 28.75 | II | 15.73 | I |
| 10.55 | I | 20.32 | I | 8.86 | I |
| 28.66 | II | 76.3 | III | 26.58 | II |
| 12.91 | I | 21.41 | I | 14.67 | I |
| 12.14 | I | 19.08 | I | 16.01 | I |
| 15.21 | I | 31.42 | II | 19.38 | I |
| 13.53 | I | 24.56 | I | 15.91 | I |
| 117.02 | IV | 337.95 | V | 18.58 | I |
| 14.27 | I | 23.39 | I | 17.05 | I |
| 44.92 | II | 131.1 | IV | 25.26 | I |
| 21.36 | I | 42.38 | II | 18.56 | I |
| 9.89 | I | 18.32 | I | 8.87 | I |
| 12.18 | I | 18.8 | I | 13.52 | I |
| 9.78 | I | 17.28 | I | 11.41 | I |
| 9.52 | I | 16.83 | I | 9.78 | I |
| 21.27 | I | 18.22 | I | 19.92 | I |
| 16.19 | I | 24.26 | I | 18.48 | I |
| 42.33 | II | 114.27 | IV | 28.77 | I |
| 37.55 | II | 92.62 | III | 26.26 | I |
| 26.95 | II | 63.77 | III | 29.04 | I |
| 13.38 | I | 24.03 | I | 20.75 | I |
| 11.59 | I | 20.47 | I | 15.3 | I |
| 11.25 | I | 23.88 | I | 9.53 | I |
| 14.5 | I | 30.54 | II | 12.16 | I |
| 191.04 | IV | 460.18 | V | 112.91 | IV |
| 160.41 | IV | 441.96 | V | 88.36 | III |
| 88.39 | III | 187.84 | V | 64.06 | III |
| 14.21 | I | 25.95 | II | 20.87 | I |
| 11.87 | I | 20.93 | I | 17.18 | I |
| 10.43 | I | 19.11 | I | 11.22 | I |
| 16.21 | I | 36.06 | II | 13.88 | I |
| 19.55 | I | 43.63 | II | 21.08 | I |
| 10.81 | I | 19.74 | I | 14.47 | I |
| 10.77 | I | 19.75 | I | 13.62 | I |
| 10.78 | I | 19.97 | I | 14.02 | I |
| 10.74 | I | 20.44 | I | 12.37 | I |
| 30.07 | II | 46.18 | II | 25.8 | II |
| 131.06 | IV | 385.95 | V | 8.84 | I |
| 11.21 | I | 18.37 | I | 14.25 | I |
| 11.59 | I | 18.82 | I | 12.16 | I |
| 14.22 | I | 33.25 | II | 8.47 | I |
| 9.23 | I | 19.1 | I | 7.74 | I |
| 19.87 | I | 47.65 | II | 7.71 | I |
| 16.59 | I | 39.14 | II | 8.11 | I |
| 38.38 | I | 102.29 | IV | 25.78 | II |
| 44.43 | II | 86.78 | III | 76.04 | III |
| 56.47 | III | 153.27 | V | 16.27 | I |
| 24.99 | I | 39.23 | II | 19.42 | I |
| 18.01 | I | 31.55 | II | 19.96 | I |
| 217.71 | V | 310.11 | V | 32.54 | II |
| 11.83 | I | 19.46 | I | 13.99 | I |
| 137.77 | IV | 395.92 | V | 21.51 | I |
| 148.56 | IV | 426.33 | V | 5.95 | I |
| 17.73 | I | 39.81 | II | 12.42 | I |
| 95.06 | III | 269.26 | V | 23.62 | I |
| 26.85 | II | 57.67 | III | 25.44 | II |
| 21.22 | I | 41.21 | II | 16.09 | I |
| 14.58 | I | 30.47 | II | 11.57 | I |
| 64.42 | III | 164.69 | V | 64.82 | III |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhu, H.; Cui, X.; Wang, W.; Luan, X.; Chen, L.; Cui, Z.; Zhang, L. Groundwater Quality Evaluation of the Dawu Water Source Area Based on Water Quality Index (WQI): Comparison between Delphi Method and Multivariate Statistical Analysis Method. Water 2021, 13, 1127. https://doi.org/10.3390/w13081127
Liu Z, Zhu H, Cui X, Wang W, Luan X, Chen L, Cui Z, Zhang L. Groundwater Quality Evaluation of the Dawu Water Source Area Based on Water Quality Index (WQI): Comparison between Delphi Method and Multivariate Statistical Analysis Method. Water. 2021; 13(8):1127. https://doi.org/10.3390/w13081127
Chicago/Turabian StyleLiu, Zhizheng, Henghua Zhu, Xiaowei Cui, Wei Wang, Xiaoyu Luan, Lu Chen, Zhaojie Cui, and Long Zhang. 2021. "Groundwater Quality Evaluation of the Dawu Water Source Area Based on Water Quality Index (WQI): Comparison between Delphi Method and Multivariate Statistical Analysis Method" Water 13, no. 8: 1127. https://doi.org/10.3390/w13081127
APA StyleLiu, Z., Zhu, H., Cui, X., Wang, W., Luan, X., Chen, L., Cui, Z., & Zhang, L. (2021). Groundwater Quality Evaluation of the Dawu Water Source Area Based on Water Quality Index (WQI): Comparison between Delphi Method and Multivariate Statistical Analysis Method. Water, 13(8), 1127. https://doi.org/10.3390/w13081127





