Reduction of CO2 Emissions in Steelmaking by Means of Utilization of Steel Plant Waste Heat to Stabilize Seasonal Cooling Water Temperature
Abstract
:1. Introduction
1.1. Heat Recovery in Steelmaking
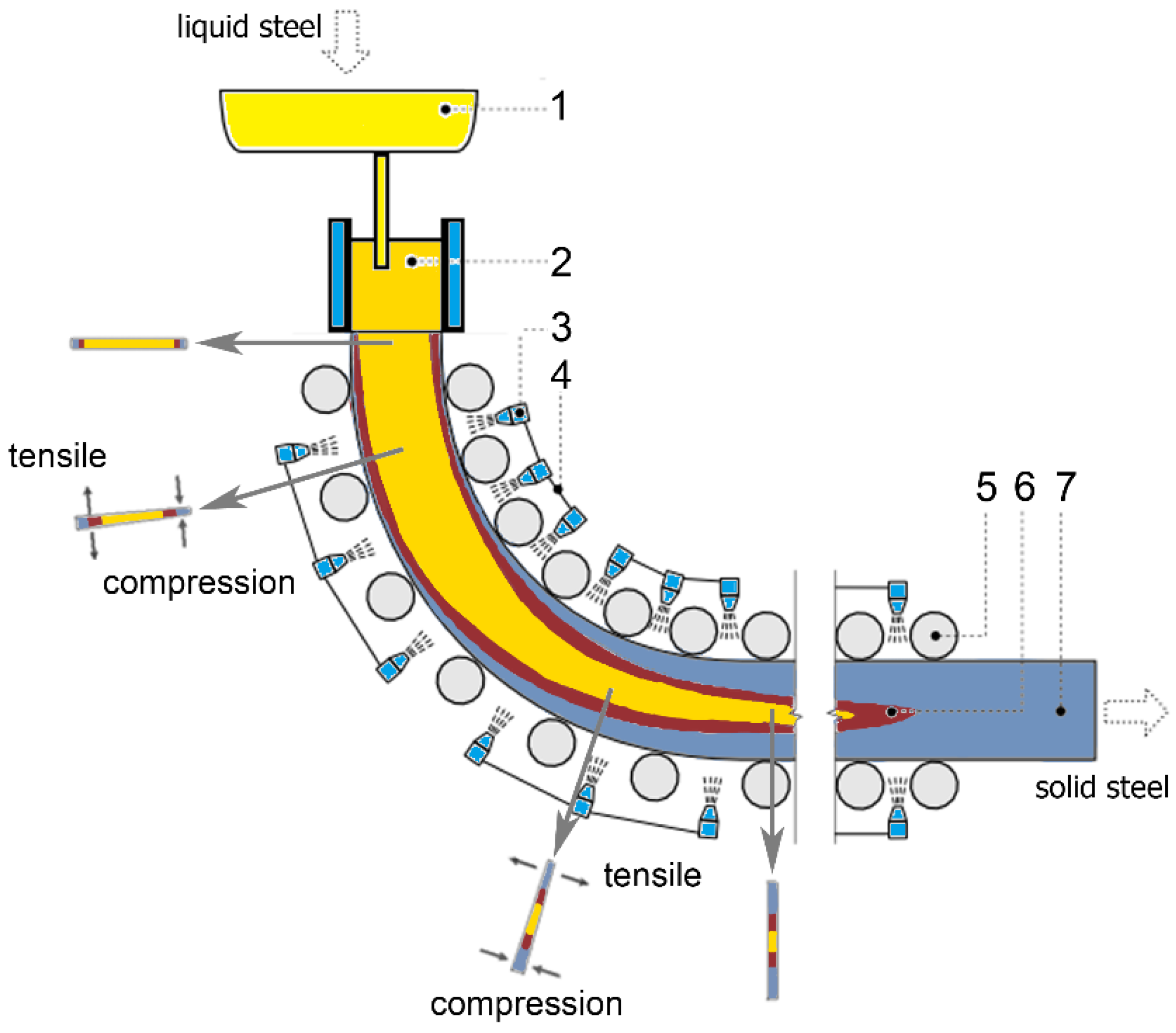
1.2. Continuous Casting Process
1.3. Simulation Models
1.4. Aim of the Paper and Applied Methods
2. Methods
2.1. Modelling of Continuous Casting Process
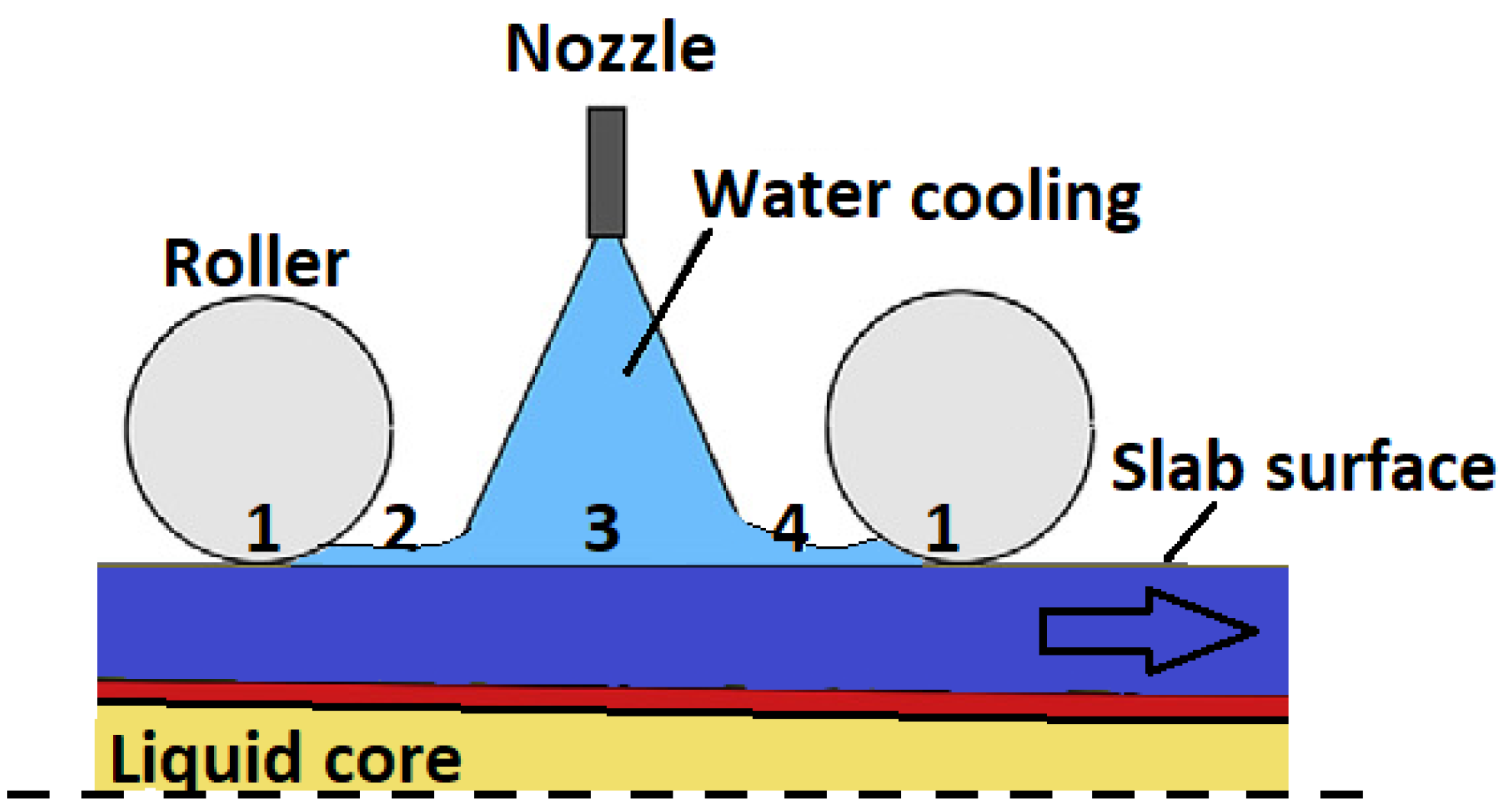
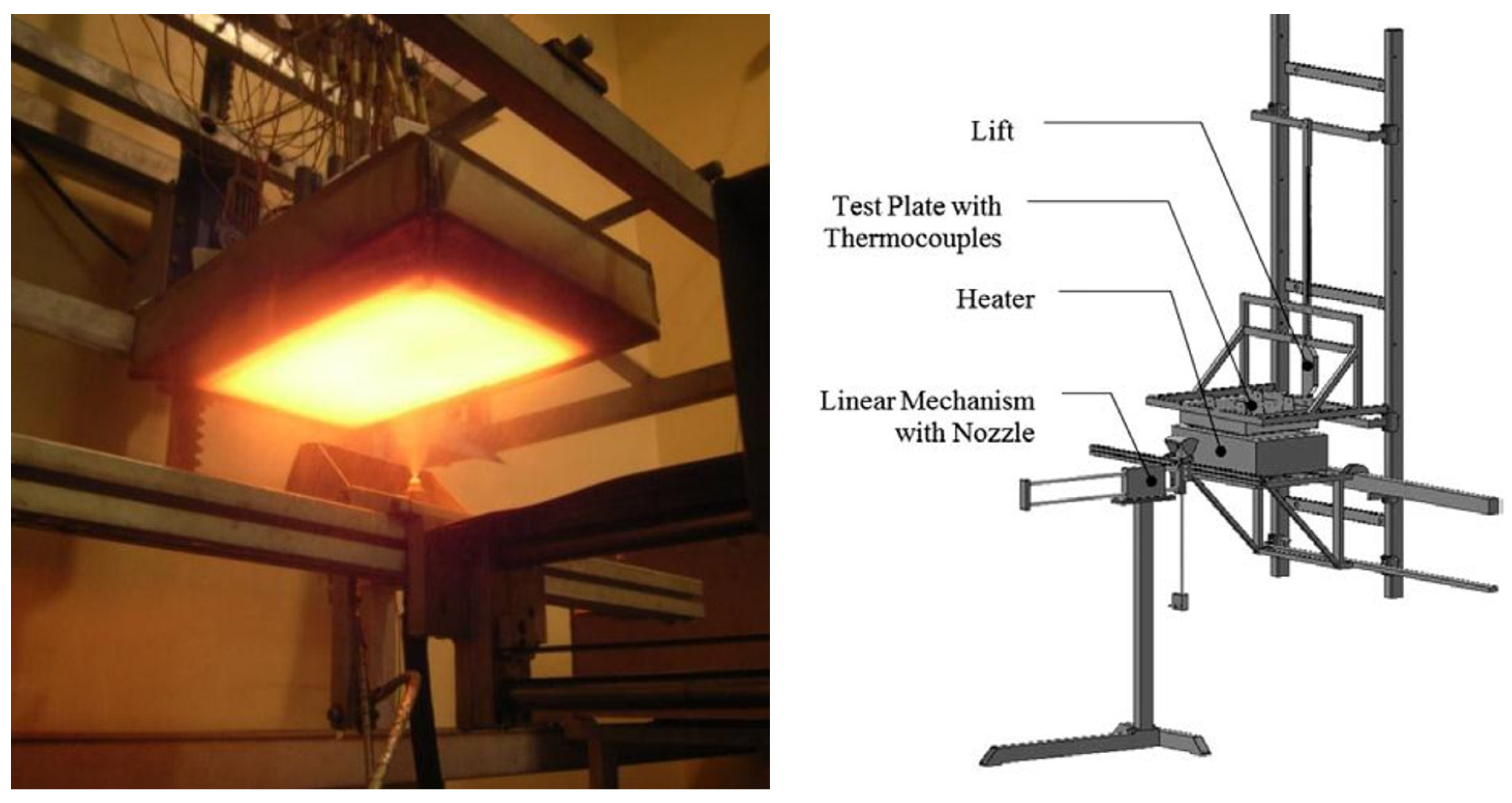
2.2. Experimental Setup and HTC Measurement
3. Results and Discussion
4. Conclusions
- Cooling water stabilization throughout the seasons, which also stabilizes the surface slab/billet temperatures and can preserve high steel quality (for billet and slab casting).
- By using the BrDSM, the optimal water cooling temperature can be found in the sense of minimizing cooling water consumption (for billet casting).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Steel Association. The White Book of Steel; Pyramidion.be. 2012. Available online: http://www.voestalpine.com/ (accessed on 11 September 2019).
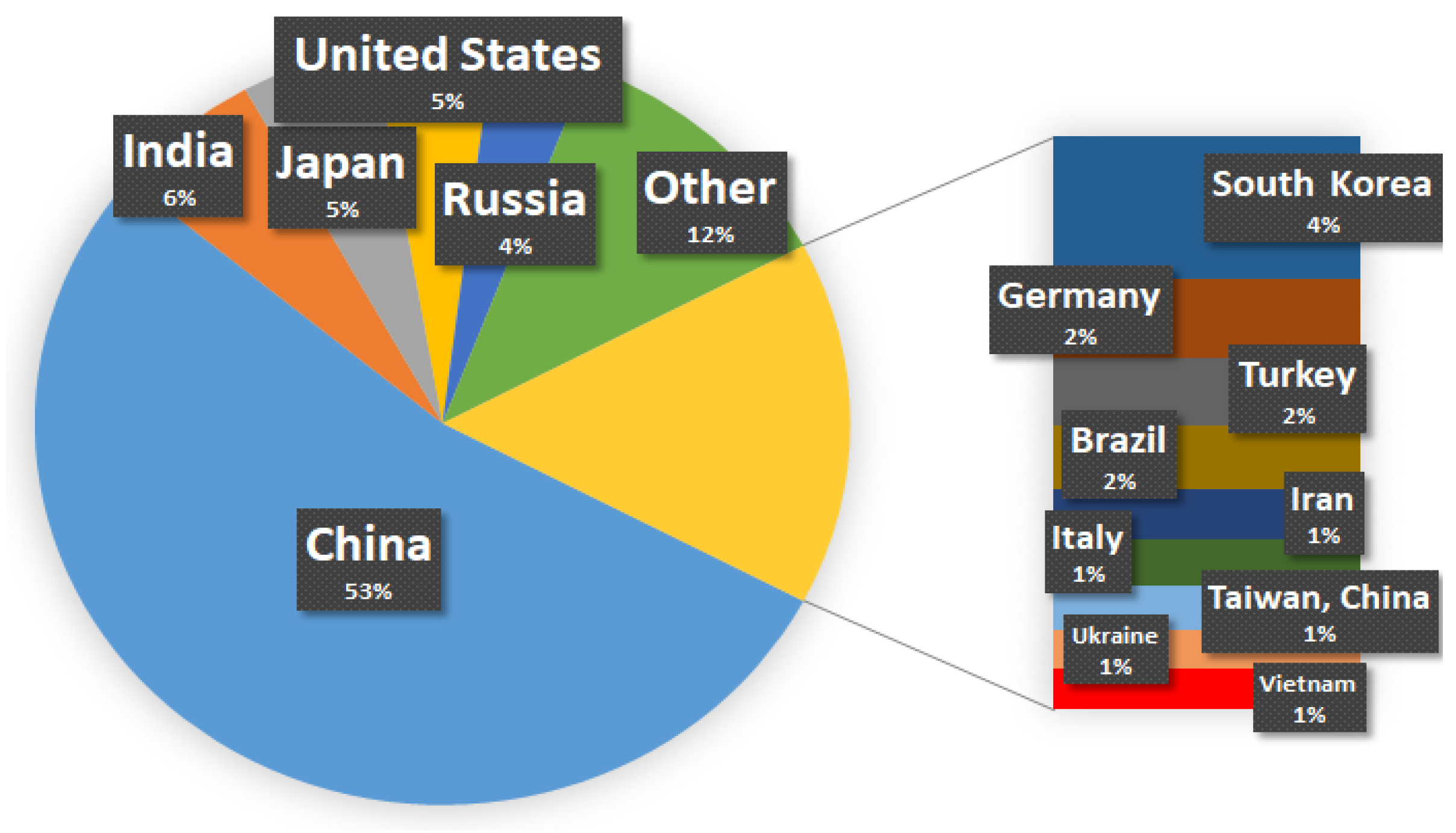
- World Steel in Figures; World steel association: Brussels, Belgium, 2020.
- Penn, J.; Pennerstorfer, P.; Jungbauer, A. New Generation of Continuous Casting Plants with Intelligent Manufacturing Strategy. Berg-und Hüttenmännische Monatshefte 2018, 163, 11–17. [Google Scholar] [CrossRef]
- European Environment Agency. Environmental Pressures of Heavy Metal Releases from Europe’s Industry. Available online: https://www.eea.europa.eu/ (accessed on 24 May 2018).
- Jouhara, H.; Khordehgah, N.; Almahmoud, S.; Delpech, B.; Chauhan, A.; Tassou, S.A. Waste heat recovery technologies and applications. Therm. Sci. Eng. Prog. 2018, 6, 268–289. [Google Scholar] [CrossRef]
- López Pérez, S.; Herrero López, S.; Ubieta Astigarraga, E.; del Hoyo Arce, I.; Gómez de Arteche Botas, M.; Iturralde Iñarga, J. Design of a Radiant Heat Capturing Device for Steel Mills. J. Sustain. Dev. Energy Water Environ. Syst. 2019. [Google Scholar] [CrossRef]
- Keplinger, T.; Haider, M.; Steinparzer, T.; Patrejko, A.; Trunner, P.; Haselgrübler, M. Dynamic simulation of an electric arc furnace waste heat recovery system for steam production. Appl. Therm. Eng. 2018, 135, 188–196. [Google Scholar] [CrossRef]
- Brandt, C.H.; Schüler, N.; Gaderer, M.; Kuckelkorn, J.M. Development of a thermal oil operated waste heat exchanger within the off-gas of an electric arc furnace at steel mills. Appl. Therm. Eng. 2014, 66, 335–345. [Google Scholar] [CrossRef]
- McBrien, M.; Serrenho, A.C.; Allwood, J.M. Potential for energy savings by heat recovery in an integrated steel supply chain. Appl. Therm. Eng. 2016, 103, 592–606. [Google Scholar] [CrossRef] [Green Version]
- Birat, J.P.; Chow, C.; Emi, T.; Emling, W.H.; Fastert, H.P.; Fitzel, H. The Making, Shaping, Treating of Steel: Casting Volume, 11th ed.; Cramb, A.W., Ed.; The AISE Steel Foundation: Pittsburgh, PA, USA, 2003; p. 1000. [Google Scholar]
- Sulaiman, H. Steel in automotive industry–the view from the supply chain. In Proceedings of the METEC & 2nd ESTAD 2015, Dusseldorf, Germany, 15–19 June 2015; pp. 1–8. [Google Scholar]
- Dahmen, B. Economical and flexible tailor-made solutions for the production of new steel grades. In Proceedings of the METEC & 2nd ESTAD 2015, Dusseldorf, Germany, 15–19 June, 2015; pp. 1–8. [Google Scholar]
- Miśkiewicz, R.; Wolniak, R. Practical Application of the Industry 4.0 Concept in a Steel Company. Sustainability 2020, 12, 5776. [Google Scholar] [CrossRef]
- Gonzalez, M.; Goldschmit, M.B.; Assanelli, A.P.; Dvorkin, E.N.; Berdaguer, E.F. Modeling of the Solidification Process in a Continuous Casting Installation for Steel Slabs. Metall. Mater. Trans. B 2003, 34, 455–473. [Google Scholar] [CrossRef]
- Louhenkilpi, S. Chapter 1.8—Continuous Casting of Steel, In Treatise on Process Metallurgy; Seshadri, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 373–434. [Google Scholar]
- Mauder, T.; Stetina, J. High Quality Steel Casting by Using Advanced Mathematical Methods. Metals 2019, 8, 1019. [Google Scholar] [CrossRef] [Green Version]
- Jansto, G.S. Steelmaking and Continuous Casting Process Metallurgy Factors Influencing Hot Ductility Behavior of Niobium Bearing Steels. In Proceedings of the METAL 2013, Brno, Czech Republic, 15–17 May 2013; pp. 32–39. [Google Scholar]
- Klimes, L.; Charvat, P.; Bohunsky, T.; Klemes, J.J.; Stetina, J. Possibilities for the Reduction of Water Consumption in Steel Industry and Continuous Steel Casting: An Overview. Chem. Eng. Trans. 2019, 76, 211–216. [Google Scholar] [CrossRef]
- Doctor, Y.N.; Patil, B.T.; Darekar, A.M. Review of Optimization Aspects for Casting Processes. Int. J. Sci. Res. 2015, 4, 2364–2368. [Google Scholar]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of digital twin about concepts, technologies, and industrial applications. J. Manuf. Syst. 2020, 346–361. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Science and Engineering of Casting Solidification, 2nd ed; Springer Science: New York, NY, USA, 2009; 402p. [Google Scholar]
- Meng, Y.; Thomas, B.G. Heat-Transfer and Solidification Model of Continuous Slab Casting: CON1D. Metall. Mater. Trans. B 2003, 34, 685–705. [Google Scholar] [CrossRef]
- Alizadeh, M.; Edris, H.; Shafyei, A. Mathematical Modeling of Heat Transfer for Steel Continuous Casting. Int. J. ISSI 2006, 3, 7–16. [Google Scholar]
- Tieu, A.K.; Kim, I.S. Simulation of the continuous casting process by a mathematical model. Int. J. Mech. Sci. 1997, 39, 185–192. [Google Scholar] [CrossRef]
- BrDSM. Brno Dynamic Solidification Model e BrDSM: Software for Modelling, Simulating and Control of Continuous Casting of Steel. 2016. Available online: www.continuouscasting.info (accessed on 20 May 2021).
- Santos, C.A.; Spim, J.A.; Garcia, A. Mathematical modelling and optimization strategies (genetic algorithm and knowledge base) applied to the continuous casting of steel. Eng. Appl. Artif. Intell. 2003, 16, 511–527. [Google Scholar] [CrossRef]
- Ji, Z.; Wang, B.; Xie, Z.; Lai, Z. Ant Colony Optimization Based Heat Transfer Coefficient Identification for Secondary Cooling Zone of Continuous Caster. In Proceedings of the 2007 IEEE International Conference on Integration Technology, Shenzhen, China, 20–24 March 2007; pp. 558–562. [Google Scholar] [CrossRef]
- Zheng, P.; Guo, J.; Hao, X.-J. Hybrid Strategies for Optimizing Continuous Casting Process of Steel. In Proceedings of the 2004 IEEE International Conference on Industrial Technology (ICIT), Hammamet, Tunisia, 8–10 December 2004; pp. 1156–1161. [Google Scholar] [CrossRef]
- Mauder, T.; Sandera, C.; Stetina, J.; Seda, M. Optimization of Quality of Continuously Cast Steel Slabs by Using Firefly Algorithm. Mater. Tehnol. 2011, 45, 347–350. [Google Scholar]
- Heat Transfer and Fluid FLow Laboratory. Heatlab. Available online: https://www.heatlab.cz/ (accessed on 20 May 2021).
- Mauder, T.; Sandera, C.; Stetina, J. Optimal control algorithm for continuous casting process by using fuzzy logic. Steel Res. Int. 2015, 86, 785–798. [Google Scholar] [CrossRef]
- Totten, G.E.; Bates, C.E.; Clinton, N.A. Handbook of Quenchants and Quenching Technology; Haddad, M.T., Ed.; ASM International: Materials Park, OH, USA, 1993; 507p. [Google Scholar]
- Ramírez, L.A.; Muñoz, D.F.; Palomar, M.; Romero-Romo, M.A.; Gonzalez, T.J. Heat removal analysis on steel billets and slabs produced by continuous casting using numerical simulation. Int. J. Adv. Manuf. Technol. 2017, 93, 1545–1565. [Google Scholar] [CrossRef] [Green Version]
- Ha, J.S.; Cho, J.R.; Lee, B.Y.; Ha, M.Y. Numerical Analysis on Secondary Cooling and Bulging in the Continuous Casting of Slabs. J. Mater. Process. Technol. 2001, 113, 257–261. [Google Scholar] [CrossRef]
- Raudensky, M.; Bohacek, J. Leidenfrost Phenomena at Hot Sprayed Surface. In Proceedings of the 7th ECI Int. Conference on Boiling Heat Transfer, Santa Catarina, Brazil, 3–7 May 2009; Volume 36959, pp. 355–359. [Google Scholar] [CrossRef]
- Bernardin, J.D.; Mudawar, I. The Leidenfrost Point: Experimental Study and Assessment of Existing Models. ASME J. Heat Transf. 1999, 121, 894–903. [Google Scholar] [CrossRef]
- Raudensky, M.; Hnizdil, M.; Hwang, J.Y.; Lee, S.H.; Kim, S.Y. Influence of the Water Temperature on the Cooling Intensity of Mist Nozzles in Continuous Casting. Mater. Tehnol. 2012, 46, 311–315. [Google Scholar]
- Pohanka, M.; Bellerova, H.; Raudensky, M. Experimental Technique for Heat Transfer Measurements on Fast moving Sprayed Surfaces. J. ASTM Int. 2009, 6, 1–9. [Google Scholar] [CrossRef]
- Hnizdil, M.; Raudensky, M. Influence of Water Temperature on the Cooling Intensity During Continuous Casting and Hot Rolling. In Proceedings of the METAL 2012, Brno, Czech Republic, 23–25 May 2012; pp. 1–6. [Google Scholar]
- Zhou, J.; Tsai, H.L.; Wang, P.C. Transport Phenomena and Keyhole Dynamics during Pulsed Laser Welding. ASME J. Heat Transf. 2006, 128, 680–690. [Google Scholar] [CrossRef]
- Kulkarni, M.S.; Babu, A.S. Managing quality in continuous casting process using product quality model and simulated annealing. J. Mater. Process. Technol. 2005, 166, 294–306. [Google Scholar] [CrossRef]


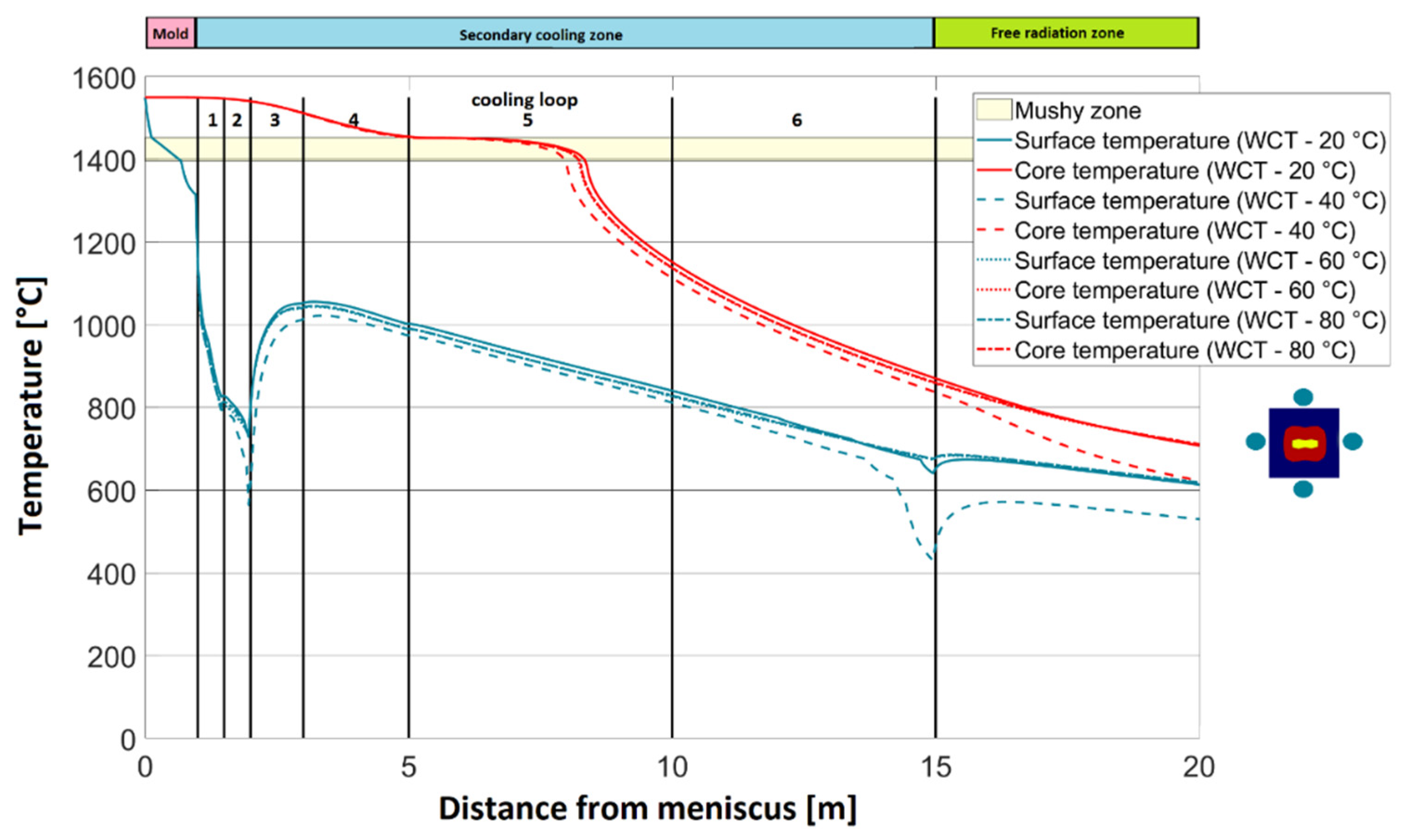
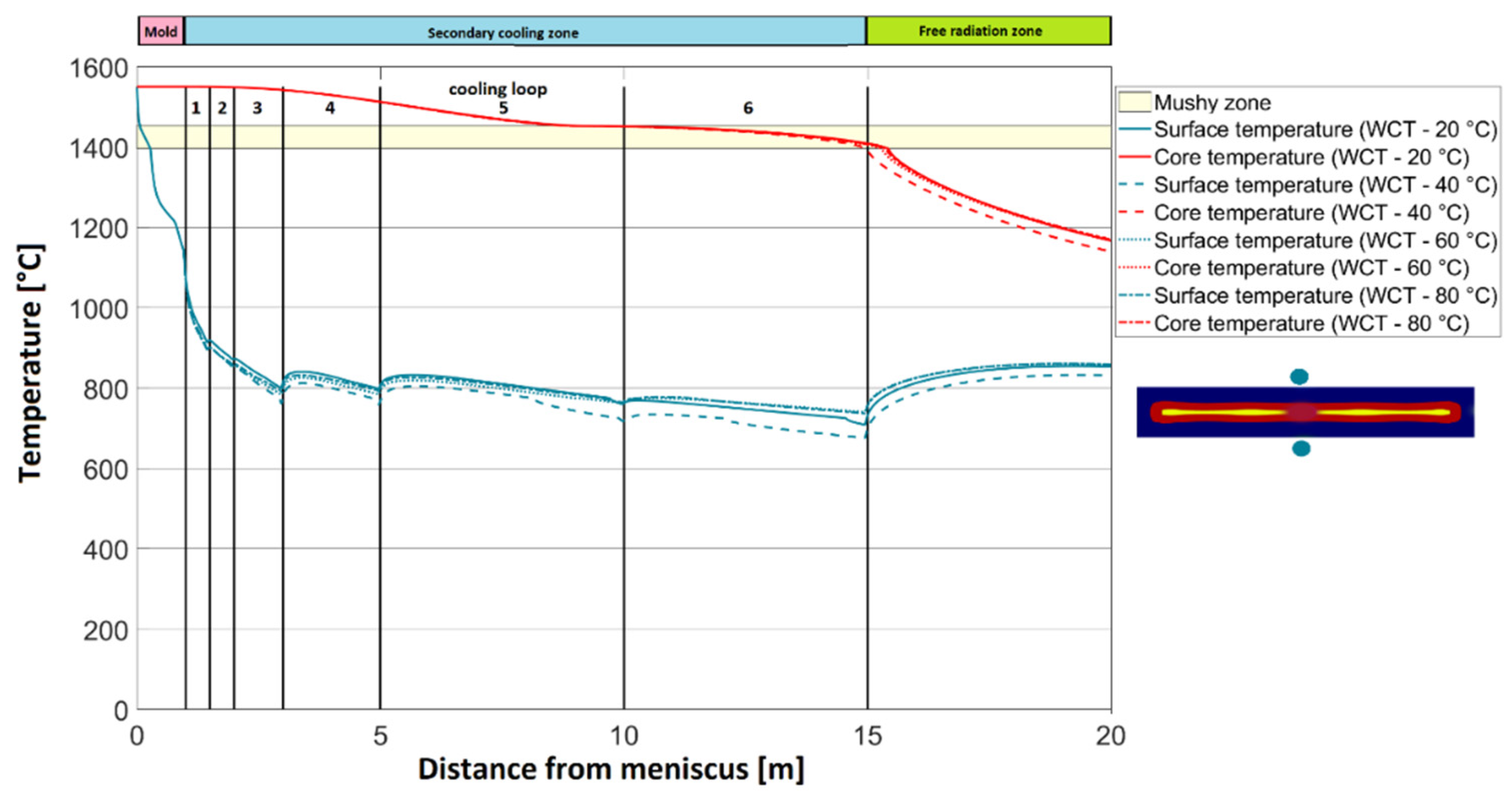
| Specific Heat Capacity | Thermal Conductivity | Density | |
|---|---|---|---|
| Liquid steel | 780 J/kgK | 22 W/mK | 6900 kg/m3 |
| Solid steel | 700 J/kgK | 22 W/mK | 7200 kg/m3 |
| Liquidus temperature | 1453 °C | ||
| Solidus temparature | 1396 °C | ||
| Latent heat | 247 kJ/kgK |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauder, T.; Brezina, M. Reduction of CO2 Emissions in Steelmaking by Means of Utilization of Steel Plant Waste Heat to Stabilize Seasonal Cooling Water Temperature. Sustainability 2021, 13, 5957. https://doi.org/10.3390/su13115957
Mauder T, Brezina M. Reduction of CO2 Emissions in Steelmaking by Means of Utilization of Steel Plant Waste Heat to Stabilize Seasonal Cooling Water Temperature. Sustainability. 2021; 13(11):5957. https://doi.org/10.3390/su13115957
Chicago/Turabian StyleMauder, Tomas, and Michal Brezina. 2021. "Reduction of CO2 Emissions in Steelmaking by Means of Utilization of Steel Plant Waste Heat to Stabilize Seasonal Cooling Water Temperature" Sustainability 13, no. 11: 5957. https://doi.org/10.3390/su13115957
APA StyleMauder, T., & Brezina, M. (2021). Reduction of CO2 Emissions in Steelmaking by Means of Utilization of Steel Plant Waste Heat to Stabilize Seasonal Cooling Water Temperature. Sustainability, 13(11), 5957. https://doi.org/10.3390/su13115957







