Recent Advances in Photoalignment Liquid Crystal Polarization Gratings and Their Applications
Abstract
:1. Introduction
2. Operation Principles
3. Device Fabrication
3.1. LC Alignment
3.1.1. Surface Photoalignment
3.1.2. Bulk Photoalignment
3.2. Polarization Holography
3.2.1. Interference Methods
3.2.2. Imprint Methods
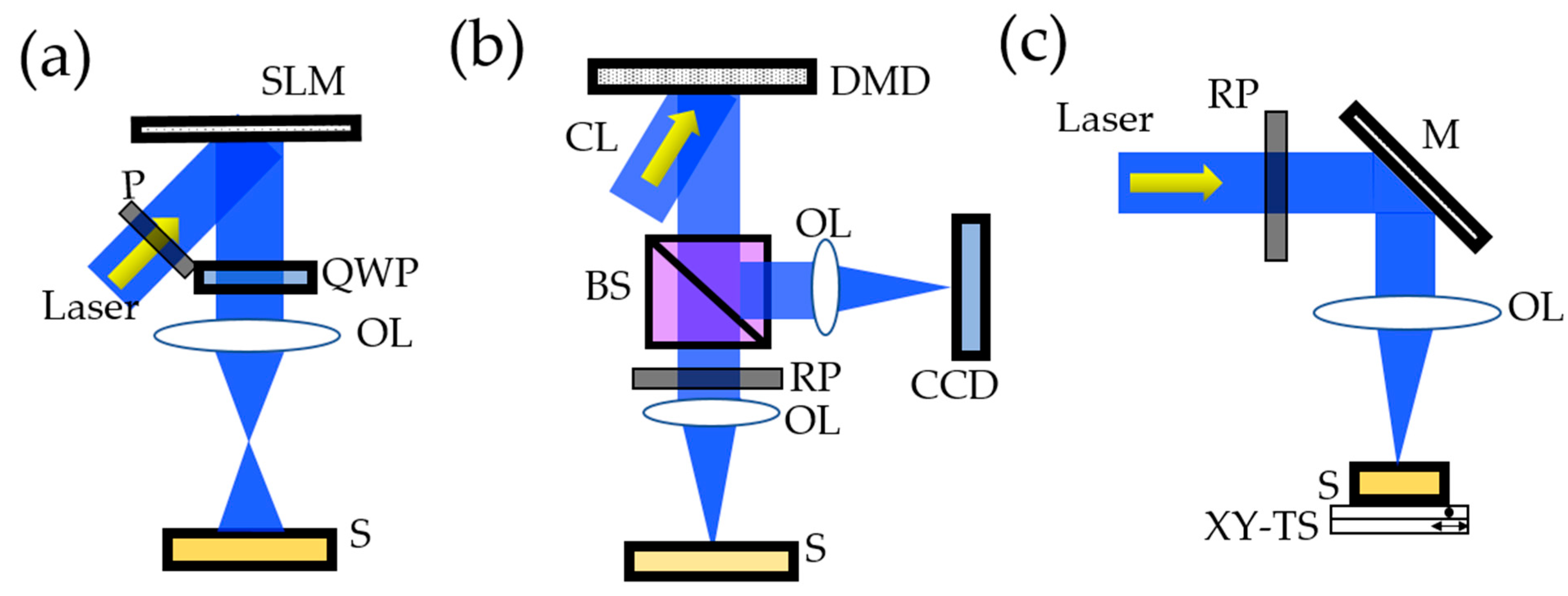
3.2.3. Digital Methods
4. Applications
4.1. Multi-Functional Photonic Devices
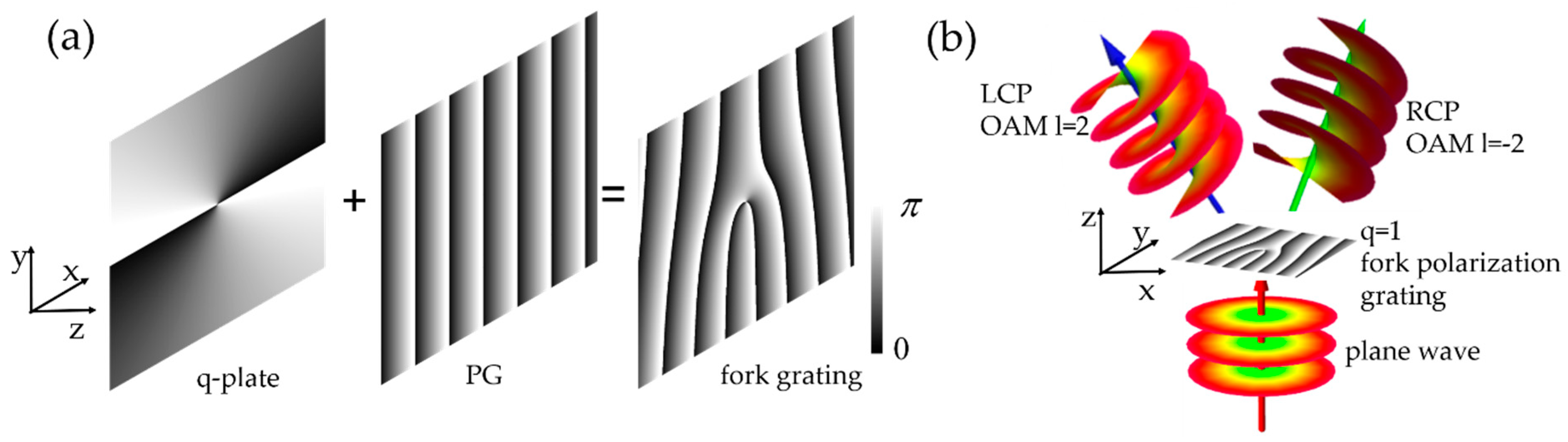
4.1.1. Orbital Angular Momentum Generator and Controller
4.1.2. Spin Hall Meta-Lens
4.2. Information Processing and Displays
4.2.1. Beam Steering System
4.2.2. Edge Detection
4.2.3. High Transmittance Holographic Polarizer
4.2.4. Enlarging the Eyebox for Near-Eye Display
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cincotti, G. Polarization gratings: Design and applications. IEEE J. Quantum Electron. 2003, 39, 1645–1652. [Google Scholar] [CrossRef]
- Crawford, G.P.; Eakin, J.N.; Radcliffe, M.D.; Callan-Jones, A.; Pelcovits, R.A. Liquid-crystal diffraction gratings using polarization holography alignment techniques. J. Appl. Phys. 2005, 98, 123102. [Google Scholar] [CrossRef] [Green Version]
- Hooper, I.R.; Sambles, J.R. Dispersion of surface plasmon polaritons on short-pitch metal gratings. Phys. Rev. B 2002, 65, 165432. [Google Scholar] [CrossRef] [Green Version]
- Gorodetski, Y.; Biener, G.; Niv, A.; Kleiner, V.; Hasman, E. Space-variant polarization manipulation for far-field polarimetry by use of subwavelength dielectric gratings. Opt. Lett. 2005, 30, 2245–2247. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Space-variant Pancharatnam-Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 2002, 27, 1141–1143. [Google Scholar] [CrossRef]
- Gori, F. Measuring Stokes parameters by means of a polarization grating. Opt. Lett. 1999, 24, 584–586. [Google Scholar] [CrossRef] [PubMed]
- Oh, C. Broadband Polarization Gratings for Efficient Liquid Crystal Display, Beam Steering, Spectropolarimetry, and Fresnel Zone Plate. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2009. [Google Scholar]
- Honma, M.; Nose, T. Twisted nematic liquid crystal polarization grating with the handedness conservation of a circularly polarized state. Opt. Express 2012, 20, 18449–18458. [Google Scholar] [CrossRef] [PubMed]
- Kawai, K.; Sasaki, T.; Noda, K.; Sakamoto, M.; Kawatsuki, N.; Ono, H. Holographic binary grating liquid crystal cells fabricated by one-step exposure of photocrosslinkable polymer liquid crystalline alignment substrates to a polarization interference ultraviolet beam. Appl. Opt. 2015, 54, 6010–6018. [Google Scholar] [CrossRef] [PubMed]
- Serak, S.V.; Roberts, D.E.; Hwang, J.Y.; Nersisyan, S.R.; Tabiryan, N.V.; Bunning, T.J.; Steeves, D.M.; Kimball, B.R. Diffractive waveplate arrays. J. Opt. Soc. Am. B 2017, 34, B56–B63. [Google Scholar] [CrossRef]
- Escuti, M.J.; Oh, C.; Sanchez, C.; Bastiaansen, C.; Broer, D.J. Simplified spectropolarimetry using reactive mosogen polarization gratings. In Proceedings of the Imaging Spectrometry XI, SPIE Optics + Photonics, San Diego, CA, USA, 13–17 August 2006; Shen, S.S., Lewis, P.E., Eds.; SPIE Press: Bellingham, WA, USA, 2006; Volume 6302, p. 630207. [Google Scholar]
- Nikolova, L.; Todorov, T. Diffraction efficiency and selectivity of polarization holographic recording. Opt. Acta 1984, 31, 579–588. [Google Scholar] [CrossRef]
- Zhan, T.; Lee, Y.H.; Tan, G.; Xiong, J.; Yin, K.; Gou, F.; Zou, J.; Zhang, N.; Zhao, D.; Yang, J.; et al. Pancharatnam-Berry optical elements for head-up and near-eye displays. J. Opt. Soc. Am. B 2019, 36, D52–D65. [Google Scholar] [CrossRef]
- Nersisyan, S.R.; Tabiryan, N.V.; Steeves, D.M.; Kimball, B.R. Characterization of optically imprinted polarization gratings. Appl. Opt. 2009, 48, 4062–4067. [Google Scholar] [CrossRef]
- Fu, W.; Zhou, Y.; Yuan, Y.; Lin, T.; Zhou, Y.; Huang, H.; Fan, F.; Wen, S. Generalization of Pancharatnam-Berry phase interference theory for fabricating phase-integrated liquid crystal optical elements. Liq. Cryst. 2020, 47, 369–376. [Google Scholar] [CrossRef]
- Chen, P.; Ji, W.; Wei, B.Y.; Hu, W.; Chigrinov, V.; Lu, Y.Q. Generation of arbitrary vector beams with liquid crystal polarization converters and vector-photoaligned q-plates. Appl. Phys. Lett. 2015, 107, 241102. [Google Scholar] [CrossRef]
- Lee, D.; Kwak, K.; Jhun, C.G.; Choi, H.S.; Song, J.K. Maskless fabrication of film-patterned-retarder (FPR) using wedged liquid crystal cell. IEEE Photonics J. 2019, 11, 7001508. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Li, S.; Zhou, P.; Zhan, T.; Chen, Q.; Su, Y.; Wu, S.T. Single-exposure fabrication of tunable Pancharatnam-Berry devices using a dye-doped liquid crystal. Opt. Express 2019, 27, 9054–9060. [Google Scholar] [CrossRef] [Green Version]
- Fu, W.; Zhou, Y.; Yuan, Y.; Lin, T.; Zhou, Y.; Huang, H.; Fan, F.; Wen, S. Symmetric Airy vortex and symmetric Airy vector beams. Liq. Cryst. 2020, 47, 369–376. [Google Scholar] [CrossRef]
- Kim, J.; Li, Y.; Miskiewicz, M.N.; Oh, C.; Kudenov, M.W.; Escuti, M.J. Fabrication of ideal geometric-phase holograms with arbitrary wavefronts. Optica 2015, 2, 958–964. [Google Scholar] [CrossRef]
- Wen, B.; Petschek, R.G.; Rosenblatt, C. Nematic liquid-crystal polarization gratings by modification of surface alignment. Appl. Opt. 2002, 41, 1246–1250. [Google Scholar] [CrossRef]
- He, Z.; Gou, F.; Chen, R.; Yin, K.; Zhan, T.; Wu, S.T. Liquid Crystal Beam Steering Devices: Principles, Recent Advances, and Future Developments. Crystals 2019, 9, 292. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Yin, Y.; Yuan, Y.; Lin, T.; Huang, H.; Yao, L.; Wang, X.; Tam, A.M.W.; Fan, F.; Wen, S. Liquid crystal pancharatnam-Berry phase lens with spatially separated focuses. Liq. Cryst. 2019, 46, 995–1000. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, H.; Chen, C.F.; Zhao, J.; Li, G.; Wu, Q.; Luo, H.; Wen, S.; Liu, Z. Optical edge detection based on high-efficiency dielectric metasurface. Proc. Natl. Acad. Sci. USA 2019, 116, 11137. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.; Zhan, T.; Zou, J.; Fan, F.; Wu, S.T. Maxwellian near-eye display with an expanded eyebox. Opt. Express 2020, 28, 38616–38625. [Google Scholar] [CrossRef]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 1956, 44, 247–262. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. A 1984, 392, 45–57. [Google Scholar]
- Goldstein, D. Polarized Light, 2nd ed.; Marcel Dekker: New York, NY, USA, 2003; pp. 226–227. [Google Scholar]
- Oh, C.; Escuti, M.J. Achromatic diffraction from polarization gratings with high efficiency. Opt. Lett. 2008, 33, 2287–2289. [Google Scholar] [CrossRef]
- Zou, J.; Zhan, T.; Xiong, J.; Wu, S.T. Broadband wide-view Pancharatnam-Berry phase deflector. Opt. Express 2020, 28, 4921–4927. [Google Scholar] [CrossRef]
- Moharam, M.G.; Young, L. Criterion for Bragg and Raman-Nath diffraction regimes. Appl. Opt. 1978, 17, 1757–1759. [Google Scholar] [CrossRef]
- Gao, K.; McGinty, C.; Payson, H.; Berry, S.; Vornehm, J.; Finnemeyer, V.; Roberts, B.; Bos, P. High-efficiency large-angle Pancharatnam phase deflector based on dual-twist design. Opt. Express 2017, 25, 6283–6293. [Google Scholar] [CrossRef]
- Xiang, X.; Kim, J.; Escuti, M.J. Bragg polarization gratings for wide angular bandwidth and high efficiency at steep deflection angles. Sci. Rep. 2018, 8, 7202. [Google Scholar] [CrossRef] [Green Version]
- Sakhn, O.; Gritsai, Y.; Sahm, H.; Stumpe, J. Fabrication and performance of efficient thin circular polarization gratings with Bragg properties using bulk photo-alignment of a liquid crystalline polymer. Appl. Phys. B 2018, 124, 52. [Google Scholar] [CrossRef]
- Xiong, J.; Wu, S.T. Rigorous coupled-wave analysis of liquid crystal polarization gratings. Opt. Express 2020, 28, 35960–35971. [Google Scholar] [CrossRef]
- Xiang, X.; Kim, J.; Komanduri, R.; Escuti, M.J. Nanoscale liquid crystal polymer Bragg polarization gratings. Opt. Express 2017, 25, 19298–19308. [Google Scholar] [CrossRef] [Green Version]
- Weng, Y.; Xu, D.; Zhang, Y.; Li, X.; Wu, S.T. Polarization volume grating with high efficiency and large diffraction angle. Opt. Express 2016, 24, 17746–17759. [Google Scholar] [CrossRef]
- Lee, Y.H.; Yin, K.; Wu, S.T. Reflective polarization volume gratings for high efficiency waveguide-coupling augmented reality displays. Opt. Express 2017, 25, 27008–27014. [Google Scholar] [CrossRef]
- Yin, K.; Zhan, T.; Xiong, J.; He, Z.; Wu, S.T. Polarization volume gratings for near-eye displays and novel photonic devices. Crystals 2020, 10, 561. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, W.; Yu, Y.; Wang, Q.; Mu, Q.; Li, S.; Chen, J. Twisting structures in liquid crystal polarization gratings and lenses. Crystals 2021, 11, 243. [Google Scholar] [CrossRef]
- Kgelnik, H. Imaging of optical modes—Resonators with internal lenses. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Magnusson, R.; Graylord, T.K. Analysis of multiwave diffraction of thick gratings. J. Opt. Soc. Am. 1977, 67, 1165–1170. [Google Scholar] [CrossRef]
- Xiang, X.; Escuti, M.J. Numerical analysis of Bragg regime polarization gratings by rigorous coupled-wave analysis. In Proceedings of the Practical Holography XXXI: Materials and Applications, SPIE OPTO, San Francisco, CA, USA, 28 January–2 February 2017; Bjelkhagen, H.I., Bove, V.M., Eds.; SPIE Press: Bellingham, WA, USA, 2017; 10127, p. 101270D. [Google Scholar]
- Xiang, X.; Escuti, M.J. Numerical analysis of Bragg polarization gratings. J. Opt. Soc. Am. B 2019, 36, D1–D8. [Google Scholar] [CrossRef]
- Xiang, X.; Escuti, M.J. Numerical modeling of polarization gratings by rigorous coupled wave analysis. In Proceedings of the Emerging Liquid Crystal Technologies XI, SPIE OPTO, San Francisco, CA, USA, 13–18 February 2016; Chien, L.-C., Broer, D.J., Kikuchi, H., Tabiryan, N.V., Eds.; SPIE Press: Bellingham, WA, USA, 2016; Volume 9769, p. 976918. [Google Scholar]
- Ishiguro, M.; Sato, D.; Shishido, A.; Ikeda, T. Bragg-type polarization gratings fromed in thick polymer films containing azobezene and tolane moieties. Langmuir 2007, 23, 332–338. [Google Scholar] [CrossRef] [PubMed]
- Honma, M.; Nose, T. Polarization-independent liquid crystal grating fabricated by microrubbing process. Jpn. J. Appl. Phys. 2003, 42, 6992–6997. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoneya, M.; Yokoyama, H. Tristable nematic liquid-crystal device using micropatterned surface alignment. Nature 2002, 420, 159–162. [Google Scholar] [CrossRef]
- Lee, C.H.; Yoshida, H.; Miura, Y.; Fujii, A.; Ozaki, M. Local liquid crystal alignment on patterned micrograting structures photofabricated by two photon excitation direct laser writing. Appl. Phys. Lett. 2008, 93, 173509. [Google Scholar] [CrossRef]
- He, Z.; Tan, G.; Chanda, D.; Wu, S.T. Novel liquid crystal photonic devices enabled by two-photon polymerization. Opt. Express 2019, 27, 11472–11491. [Google Scholar] [CrossRef]
- Chigrinov, V.G.; Kozenkov, V.M.; Kwok, H.S. Photoalignment of Liquid Crystalline Materials: Physics and Applications; John Wiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Ichimura, K. Photoalignment of liquid-crystal systems. Chem. Rev. 2000, 100, 1847–1874. [Google Scholar] [CrossRef] [PubMed]
- Culbreath, C.; Glazar, N.; Yokoyama, H. Note: Automated maskless micro-multidomain photoalignment. Rev. Sci. Instrum. 2011, 82, 126107. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Jiang, M.; Peng, C.; Sun, K.; Yaroshchuk, O.; Lavrentovich, O.; Wei, Q.H. High-resolution and high-throughput plasmonic photopatterning of complex molecular orientations in liquid crystals. Adv. Mater. 2016, 28, 2353–2358. [Google Scholar] [CrossRef]
- Ichimura, K.; Suzuki, Y.; Seki, T.; Hosoki, A.; Aoki, K. Reversible change in alignment mode of nematic liquid crystals regulated photochemically by command surfaces modified with an azobenzene monolayer. Langmuir 1988, 4, 1214–1216. [Google Scholar] [CrossRef]
- Shteyner, E.A.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.-S.; Afanasyev, A.D. Submicron-scale liquid crystal photo-alignment. Soft Matter 2013, 9, 5160–5165. [Google Scholar] [CrossRef]
- Chen, J.; Bos, P.J.; Vithana, H.; Johnson, D.L. An electrooptically controlled liquid-crystal diffraction grating. Appl. Phys. Lett. 1995, 67, 2588–2590. [Google Scholar] [CrossRef]
- Komanduri, R.K.; Escuti, M.J. High efficiency reflective liquid crystal polarization gratings. Appl. Phys. Lett. 2009, 95, 091106. [Google Scholar] [CrossRef] [Green Version]
- Komanduri, R.K.; Oh, C.; Escuti, M.J. Reflective liquid crystal polarization gratings with high efficiency and small pitch. In Proceedings of the Liquid Crystals XII, Photonic Devices + Applications, San Francisco, CA, USA, 10–14 August 2008; Khoo, I.C., Ed.; SPIE Press: Bellingham, WA, USA, 2008; Volume 7050, p. 70500J. [Google Scholar]
- Emoto, A.; Matsumoto, T.; Yamashita, A.; Shioda, T.; Ono, H.; Kawatsuki, N. Large birefringence and polarization holographic gratings formed in photocross-linkable polymer liquid crystals comprising bistolane mesogenic side groups. J. Appl. Phys. 2009, 106, 073505. [Google Scholar] [CrossRef]
- Ono, H.; Emoto, A.; Takahashi, F.; Kawatsuki, N.; Hasegawa, T. High stable polarization gratings in photocrosslinkable polymer liquid crystals. J. Appl. Phys. 2003, 94, 1298–1303. [Google Scholar] [CrossRef]
- Kim, J.; Komanduri, R.K.; Escuti, M.J. A compact holographic recording setup for tuning pitch using polarizing prisms. In Proceedings of the Practical Holography XXVI: Materials and Applications, SPIE OPTO, San Francisco, CA, USA, 21–26 January 2012; Bjelkhagen, H.I., Bove, V.M., Eds.; SPIE Press: Bellingham, WA, USA, 2012; Volume 8281, p. 82810R. [Google Scholar]
- Miskiewicz, M.N.; Kim, J.; Li, Y.; Komanduri, R.K.; Escuti, M.J. Progress on large-area polarization grating fabrication. In Proceedings of the Acquisition, Tracking, Pointing, and Laser Systems Technologies XXVI, SPIE Defense, Security, and Sensing, Baltimore, MD, USA, 23–27 April 2012; Thompson, W.E., McManamon, P.F., Eds.; SPIE Press: Bellingham, WA, USA, 2012; Volume 8395, p. 83950G. [Google Scholar]
- Huang, Y.H.; Li, M.S.; Ko, S.W.; Fuh, A.Y.G. Helical wavefront and beam shape modulated by advanced liquid crystal q-plate fabricated via photoalignment and analyzed by Michelson’s interference. App. Opt. 2013, 52, 6557–6561. [Google Scholar] [CrossRef] [PubMed]
- Zhan, T.; Xiong, J.; Lee, Y.H.; Chen, R.; Wu, S.T. Fabrication of Pancharatnam-Berry phase optical elements with highly stable polarization holography. Opt. Express 2019, 27, 2632–2642. [Google Scholar] [CrossRef] [Green Version]
- Provenzano, C.; Pagliusi, P.; Cipparrone, G. Electrically tunable two-dimensional liquid crystals gratings induced by polarization holography. Opt. Express 2007, 15, 5872–5878. [Google Scholar] [CrossRef]
- Nys, I.; Beeckman, J.; Neyts, K. Switchable 3D liquid crystal grating generated by periodic photo-alignment on both substrates. Soft Matter 2015, 11, 7802–7808. [Google Scholar] [CrossRef]
- Nys, I.; Nersesyan, V.; Beeckman, J.; Neyts, K. Complex liquid crystal superstructures induced by periodic photo-alignment at top and bottom substrates. Soft Matter 2018, 14, 6892–6902. [Google Scholar] [CrossRef]
- Amano, R.; Salamon, P.; Yokokawa, S.; Kobayashi, F.; Sasaki, Y.; Fujii, S.; Buka, A.; Araoka, F.; Orihara, H. Tunable two-dimensional polarization grating using a self-organized micropixelated liquid crystal structure. RSC Adv. 2018, 8, 41472–41479. [Google Scholar] [CrossRef] [Green Version]
- Burrow, G.M.; Gaylord, T.K. Multi-beam interference advances and applications: Nano-electronics, photonic crystals, metamaterials, subwavelength structures, optical trapping, and biomedical structures. Micromachines 2011, 2, 221–257. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, Y.J.; Song, F.; Chigrinov, V.G.; Kwok, H.S.; Hu, M.; Luo, D.; Sun, X.W. Photoalignment-induced two-dimensional liquid crystal polarization structure via multi-beam polarization interferometry. Opt. Express 2018, 26, 7683–7692. [Google Scholar] [CrossRef]
- Shi, Y.; Lai, Y.; Liu, Y.J.; Chigrinov, V.G.; Kwok, H.S.; Hu, M.; Luo, D.; Sun, X.W. Two-dimensional liquid crystal polarization grating via linearly polarized light modified multi-beam polarization interferometry. Opt. Express 2019, 27, 13061–13071. [Google Scholar] [CrossRef]
- Ruiz, U.; Provenzano, C.; Pagliusi, P.; Cipparrone, G. Pure two-dimensional polarization patterns for holographic recording. Opt. Lett. 2012, 37, 311–313. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, U.; Pagliusi, P.; Provenzano, C.; Shibaev, V.P.; Cipparrone, G. Supramolecular chiral structures: Smart polymer organization guided by 2D polarization light patterns. Adv. Funct. Mater. 2012, 22, 2964–2970. [Google Scholar] [CrossRef]
- Du, T.; Fan, F.; Tam, A.M.W.; Sun, J.T.; Chigrinov, V.G.; Hwok, H.S. Complex nanoscale-ordered liquid crystal polymer film for high transmittance holographic polarizer. Adv. Mater. 2015, 27, 7191–7195. [Google Scholar] [CrossRef]
- Zhao, X.; Boussaid, F.; Bermak, A.; Chigrinov, V.G. Thin photo-patterned micropolarizer array for CMOS image sensors. IEEE Photonics J. 2009, 21, 805–807. [Google Scholar]
- Schadt, M.; Seiberle, H.; Schuster, A. Optical patterning of multi-domain liquid-crystal display with wide viewing angles. Nature 1996, 381, 212–215. [Google Scholar] [CrossRef]
- Hsiang, E.L.; Li, Y.; He, Z.; Zhan, T.; Zhang, C.; Lan, Y.F.; Dong, Y.; Wu, S.T. Enhancing the efficiency of color conversion micro-LED display with a patterned cholesteric liquid crystal polymer film. Nanomaterials 2020, 10, 2430. [Google Scholar] [CrossRef]
- Zhao, C.X.; Fan, F.; Du, T.; Chigrinov, V.G.; Hwok, H.S. Multilayer photo-aligned thin-film structure for polarizing photonics. Opt. Lett. 2015, 40, 2993–2996. [Google Scholar] [CrossRef] [Green Version]
- Fan, F. Liquid Crystal Patterned Photoalignment: Methods and Applications. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, 2013. [Google Scholar]
- Seiberle, H.; Schmitt, K.; Schadt, M. Multidomain LCDs and complex optical retarders generated by photo-alignment. Proc. Eurodisp. 1999, 99, 6–9. [Google Scholar]
- Li, Y.; Zhan, T.; Wu, S.T. Flat cholesteric liquid crystal polymeric lens with low f-number. Opt. Express 2020, 28, 5875–5882. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Escuti, M.J. Polarization grating exposure method with easily tunable period via dual rotating polarization grating masks. J. Opt. Soc. Am. B 2019, 36, D42–D46. [Google Scholar] [CrossRef]
- Tam, A.M.; Fan, F.; Du, T.; Hu, W.; Zhang, W.; Zhao, C.; Wang, X.; Ching, K.L.; Li, G.; Luo, H.; et al. Bifocal optical-vortex lens with sorting of the generated nonseparable spin-orbital angular-momentum states. Phys. Rev. Appl. 2017, 7, 034010. [Google Scholar] [CrossRef]
- Fan, F.; Du, T.; Srivastava, A.K.; Lu, W.; Chigrinov, V.; Kwok, H.S. Axially symmetric polarization converter made of patterned liquid crystal quarter wave plate. Opt. Express 2012, 20, 23036–23043. [Google Scholar] [CrossRef]
- Davis, J.A.; Moreno, I.; Tsai, P. Polarization eigenstates for twisted-nematic liquid-crystal displays. Appl. Opt. 1998, 37, 937–945. [Google Scholar] [CrossRef] [PubMed]
- Stalder, M.; Schadt, M. Linearly polarized light with axial symmetry generated by liquid-crystal polarization converters. Opt. Lett. 1996, 21, 1948–1950. [Google Scholar] [CrossRef]
- Yeh, P.; Gu, C. Optics of Liquid Crystal Displays; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 67. [Google Scholar]
- Chen, D.; Zhao, H.; Yan, K.; Xu, D.; Guo, Q.; Sun, L.; Wu, F.; Chigrinov, V.G.; Kwok, H.S. Interference-free and single exposure to generate continuous cycloidal alignment for large-area liquid crystal devices. Opt. Express 2019, 27, 29332–29339. [Google Scholar] [CrossRef]
- Sio, L.D.; Roberts, D.E.; Liao, Z.; Nersisyan, S.; Uskova, O.; Wickboldt, L.; Tabiryan, N.; Ateeves, D.M.; Kimball, B.R. Digital polarization holography advancing geometrical phase optics. Opt. Express 2016, 24, 18297–18306. [Google Scholar] [CrossRef]
- Wu, H.; Hu, H.C.; Lin, X.W.; Zhu, G.; Choi, J.W.; Chigrinov, V.; Lu, Y.Q. Arbitrary photo-patterning in liquid crystal alignments using DMD based lithography system. Opt. Express 2012, 20, 16684–16689. [Google Scholar] [CrossRef] [Green Version]
- Ji, W.; Lee, C.H.; Chen, P.; Hu, W.; Ming, Y.; Zhang, L.; Lin, T.H.; Chigrinov, V.; Lu, Y.Q. Meta-q-plate for complex beam shaping. Sci. Rep. 2016, 6, 25528. [Google Scholar] [CrossRef] [Green Version]
- Miskiewicz, M.N.; Escuti, M.J. Direct-writing of complex liquid crystal patterns. Opt. Express 2014, 22, 12691–12706. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Song, H.; Zhang, R.; Manukyan, K.; Li, L.; Zhao, Z.; Pang, K.; Liu, C.; Almaiman, A.; Rock, R.; et al. Experimental mitigation of atmospheric turbulence effect using pre-signal combing for uni- and bi-directional free-space optical links with two 100-Gbit/s OAM-multiplexed channels. J. Lightwave Technol. 2020, 38, 8289. [Google Scholar] [CrossRef]
- Xie, G.; Song, H.; Zhao, Z.; Milione, G.; Ren, Y.; Liu, C.; Zhang, R.; Bao, C.; Li, L.; Wang, Z.; et al. Using A complex optical-angular-momentum spectrum to measure object parameters. Opt. Lett. 2017, 42, 4482–4485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Zhang, R.; Zhao, Z.; Xie, G.; Liao, P.; Pang, K.; Song, H.; Liu, C.; Ren, Y.; Labroille, G.; et al. High-capacity free-space optical communications between a ground transmitter and a ground receiver via a UAV using multiplexing of multiple orbital-angular-momentum beams. Sci. Rep. 2017, 7, 17427. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef] [Green Version]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Nori, F.; Zayats, A.V. Spin-orbit interactions of light. Nat. Photonics 2015, 9, 796–808. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Pancharatnam-Berry phase optical elements for wave front shaping in the visible domain: Switchable helical mode generation. Appl. Phys. Lett. 2006, 88, 221102. [Google Scholar] [CrossRef] [Green Version]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical Spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef] [Green Version]
- Slussarenko, S.; Murauski, A.; Du, T.; Chigrinov, V.; Marrucci, L.; Santamato, E. Tunable liquid crystal q-plates with arbitrary topological charge. Opt. Express 2011, 19, 4085–4090. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, T.; Yuan, Y.; Zhou, Y.; Fu, W.; Huang, H.; Yao, L.; Fan, F.; Wen, S. Bragg reflective polychromatic vector beam generation from opposite-handed cholesteric liquid crystals. Opt. Lett. 2019, 44, 2720–2723. [Google Scholar] [CrossRef]
- Lin, T.; Zhou, Y.; Yuan, Y.; Fu, W.; Yao, L.; Huang, H.; Fan, F.; Wen, S. Transflective spin-orbital angular momentum conversion device by three-dimensional multilayer liquid crystalline materials. Opt. Express 2018, 26, 29244–29252. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Wei, B.Y.; Ji, W.; Ge, S.J.; Hu, W.; Xu, F.; Chirgrinov, V.; Lu, Y.Q. Arbitrary and reconfigurable optical vortex generation: A high-efficiency technique using director-varying liquid crystal fork gratings. Photonics Res. 2015, 3, 133–139. [Google Scholar] [CrossRef]
- Wei, B.; Zhang, Y.; Li, P.; Liu, S.; Hu, W.; Lu, Y.; Wu, Y.; Dou, X.; Zhao, J. Liquid-crystal splitter for generating and separating autofocusing and antodefocusing circular Airy beams. Opt. Express 2020, 28, 26151–26160. [Google Scholar] [CrossRef]
- Duan, W.; Chen, P.; Ge, S.J.; Wei, B.Y.; Hu, W.; Lu, Y.Q. Helicity-dependent forked vortex lens based on photo-patterned liquid crystals. Opt. Express 2017, 25, 14059–14064. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, H.; Hu, G.; Luo, H.; Wen, S.; Liu, Z. Broadband photonic spin Hall meta-lens. ACS Nano 2018, 12, 82–88. [Google Scholar] [CrossRef]
- Kwon, K.C.; Lim, Y.T.; Shin, C.W.; Erdenebat, M.U.; Hwang, J.M.; Kim, N. Enhanced depth-of-field of an integral imaging microscope using a bifocal holographic optical element-micro lens array. Opt. Lett. 2017, 42, 3209–3212. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Yin, K.; Li, K.; Wu, S.T. Holographic optical elements for augmented reality: Principles, present status, and future perspectives. Adv. Photonics Res. 2020, 1, 2000049. [Google Scholar] [CrossRef]
- Yin, K.; He, Z.; Wu, S.T. Reflective polarization volume lens with small f-number and large diffraction angle. Adv. Opt. Mater. 2020, 8, 2000170. [Google Scholar] [CrossRef]
- Kim, J.; Oh, C.; Serati, S.; Escuti, M.J. Wide-angle, nonmechanical beam steering with high throughput utilizing polarization gratings. Appl. Opt. 2011, 50, 2636–2639. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Miskiewicz, M.N.; Serati, S.; Escuti, M.J. Nonmechanical laser beam steering based on polymer polarization gratings: Design optimization and demonstration. J. Lightwave Technol. 2015, 33, 2068–2077. [Google Scholar] [CrossRef]
- Kim, J.; Oh, C.; Escuti, M.J.; Hosting, L.; Serati, S. Wide-angle, nonmechanical beam steering using thin liquid crystal polarization gratings. In Advanced Wavefront Control: Methods, Devices, and Applications VI; SPIE: Bellingham, WA, USA, 2008; Volume 7093, p. 709302. [Google Scholar]
- Gou, F.; Peng, F.; Ru, Q.; Lee, Y.H.; Chen, H.; He, Z.; Zhan, T.; Vodopyanov, K.L.; Wu, S.T. Mid-wave infrared beam steering based on high-efficiency liquid crystal diffractive waveplates. Opt. Express 2017, 25, 22404–22410. [Google Scholar] [CrossRef]
- Chen, H.; Weng, Y.; Xu, D.; Tabiryan, N.V.; Wu, S.T. Beam steering for virtual/augmented reality displays with a cycloidal diffractive waveplate. Opt. Express 2016, 24, 7287–7298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oh, C.; Kim, J.; Muth, J.; Serati, S.; Escuti, M.J. High-throughput continuous beam steering using rotating polarization gratings. IEEE Photonics Technol. Lett. 2010, 22, 200–202. [Google Scholar] [CrossRef]
- Mehrl, D.J.; Liu, Z.C.; Storrs, M. Synchronous detection method for obtaining directional gradients of images. Opt. Lett. 1991, 17, 346–348. [Google Scholar] [CrossRef]
- He, S.; Zhou, J.; Chen, S.; Shu, W.; Luo, H.; Wen, S. Spatial differential operation and edge detection based on the geometric spin Hall effect of light. Opt. Lett. 2020, 45, 877–880. [Google Scholar] [CrossRef]
- He, S.; Zhou, J.; Chen, S.; Shu, W.; Luo, H.; Wen, S. Wavelength-independent optical fully differential operation based on the spin-orbit interaction of light. APL. Photonics 2020, 5, 036105. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; He, S.; Zhou, J.; Chen, S.; Wen, S.; Luo, H. Goos-Hanchen effect enabled optical differential operation and image edge detection. Appl. Phys. Lett. 2020, 116, 211103. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Wu, Y.; Li, T.; Fan, F.; Huang, H.; Wen, S. Optical edge detection with adjustable resolution based on liquid crystal polarization gratings. Chin. Opt. Lett. 2020, 18, 093501. [Google Scholar] [CrossRef]
- Li, T.; Yang, Y.; Liu, X.; Wu, Y.; Zhou, Y.; Huang, S.; Li, X.; Huang, H. Enhanced optical edge detection based on a Pancharatnam-Berry flat lens with a large focal length. Opt. Lett. 2020, 45, 3681–3684. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Qian, H.; Zhao, J.; Tang, M.; Wu, Q.; Lei, M.; Luo, H.; Wen, S.; Chen, S.; Liu, Z. Two-dimensional optical spatial differentiation and high-contrast imaging. Natl. Sci. Rev. 2020, 8, nwaa176. [Google Scholar] [CrossRef]
- Kim, J.; Komanduri, R.K.; Lawler, K.F.; Kekas, D.J.; Escuti, M.J. Efficient and monolithic polarization conversion system based on a polarization grating. Appl. Opt. 2020, 51, 4852–4857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seo, E.; Kee, H.C.; Kim, Y.; Jeong, S.; Choi, H.; Lee, S. Polarization conversion system using a polymer polarization grating. SID Int. Symp. Dig. Tech. Pap. 2011, 42, 540–543. [Google Scholar] [CrossRef] [Green Version]
- Kramida, G. Resolving the vergence-accommodation conflict in head-mounted displays. IEEE Trans. Vis. Comput. Graph. 2016, 22, 1912–1931. [Google Scholar] [CrossRef]
- Zhan, T.; Xiong, J.; Zou, J.; Wu, S.T. Multifocal displays: Review and prospect. PhotoniX 2020, 1, 10. [Google Scholar] [CrossRef] [Green Version]
- Lanman, D.; Luebke, D. Near-eye light field displays. ACM Trans. Graph. 2013, 32, 220. [Google Scholar] [CrossRef]
- Maimone, A.; Georgiou, A.; Kollin, J.S. Holographic near-eye displays for virtual and augmented reality. ACM Trans. Graph. 2017, 36, 85. [Google Scholar] [CrossRef]
- He, Z.; Yin, K.; Fan-Chiang, K.H.; Wu, S.T. Enlarging the eyebox of Maxwellian displays with a customized liquid crystal Dammann grating. Crystals 2021, 11, 195. [Google Scholar] [CrossRef]
- Fan, F.; Yao, L.; Wang, X.; Shi, L.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S.; Wen, S. Ferroelectric liquid crystal Dammann grating by patterned photoalignment. Crystals 2017, 7, 79. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Li, Y.; Li, K.; Wu, S.T. Aberration-free pupil steerable Maxwellian display for augmented reality with cholesteric liquid crystal holographic lenses. Opt. Lett. 2021, 46, 1760–1763. [Google Scholar] [CrossRef]
- Yoo, C.; Bang, K.; Jang, C.; Kim, D.; Lee, C.K.; Sung, G.; Lee, H.S.; Lee, B. Dual-focal waveguide see-through near-eye display with polarization-dependent lenses. Opt. Lett. 2019, 44, 1920–1923. [Google Scholar] [CrossRef] [PubMed]
- Yoo, C.; Bang, K.; Chae, M.; Lee, B. Extended-viewing-angle waveguide near-eye display with a polarization-dependent steering combiner. Opt. Lett. 2020, 45, 2870–2873. [Google Scholar] [CrossRef] [PubMed]
- Yin, K.; He, Z.; Li, K.; Wu, S.T. Doubling the FOV of AR displays with a liquid crystal polarization-dependent combiner. Opt. Express 2021, 29, 11512–11519. [Google Scholar] [CrossRef] [PubMed]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, T.; Xie, J.; Zhou, Y.; Zhou, Y.; Yuan, Y.; Fan, F.; Wen, S. Recent Advances in Photoalignment Liquid Crystal Polarization Gratings and Their Applications. Crystals 2021, 11, 900. https://doi.org/10.3390/cryst11080900
Lin T, Xie J, Zhou Y, Zhou Y, Yuan Y, Fan F, Wen S. Recent Advances in Photoalignment Liquid Crystal Polarization Gratings and Their Applications. Crystals. 2021; 11(8):900. https://doi.org/10.3390/cryst11080900
Chicago/Turabian StyleLin, Tiegang, Jin Xie, Yingjie Zhou, Yaqin Zhou, Yide Yuan, Fan Fan, and Shuangchun Wen. 2021. "Recent Advances in Photoalignment Liquid Crystal Polarization Gratings and Their Applications" Crystals 11, no. 8: 900. https://doi.org/10.3390/cryst11080900
APA StyleLin, T., Xie, J., Zhou, Y., Zhou, Y., Yuan, Y., Fan, F., & Wen, S. (2021). Recent Advances in Photoalignment Liquid Crystal Polarization Gratings and Their Applications. Crystals, 11(8), 900. https://doi.org/10.3390/cryst11080900





