Molecular Dynamics and Machine Learning in Catalysts
Abstract
:1. Introduction
2. Molecular Dynamics
2.1. Introduction of Molecular Dynamics
2.1.1. Ab initio Molecular Dynamics
2.1.2. Reactive Force Field Molecular Dynamics
2.2. Application of AIMD and ReaxFF
2.2.1. The Growth of the Carbon Materials
2.2.2. Dehydrogenation and Hydrogenation
2.2.3. Oxidation Reaction
2.2.4. Segregation and Restructuring
2.2.5. Discussion
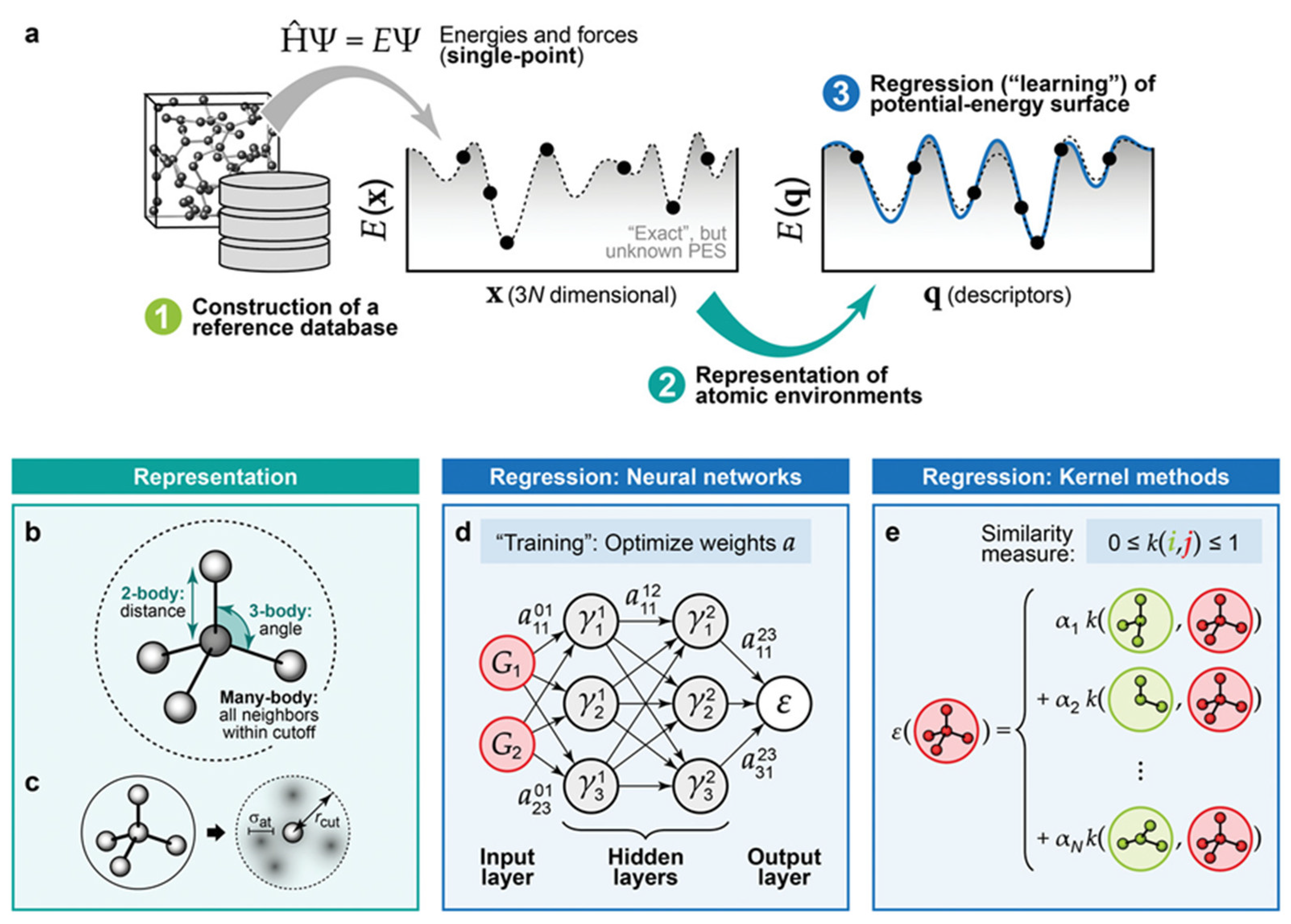
3. Machine Learning in Catalysts
3.1. Introduction of Methods
3.2. Applications of Machine Learning in Catalysis
3.2.1. Machine Learning Potentials
3.2.2. The Development of Descriptors
3.3. Discussion
| Descriptor | Class of Catalyst | Reaction | Optimal Catalyst(s) Identified |
|---|---|---|---|
| d-band center [157] | Transition metals, transition metal alloys | ORR | Pt and Pd [172] |
| eg occupancy [155] | Transition metal oxides | ORR | Pt3Ni [173], LaCoO3 (t2g5eg1) and LaNiO3(t2g6eg1) |
| t2g occupancy [168] | Transition metal oxides | OER | CuCoO2, PtCoO2 |
| O p-band ceter [174] | Transition metal oxides | OER | (Pr0.5Ba0.5)CoO3 |
| Evac vacancy formation energy [154] | Core shell transition metal nanoparticles | ORR | Pd3Cu1@Pt (core@shell) |
| Esurf surface energy [155] | Pure metals | Hydrogen evolution reaction | Pt |
| Esurf surface energy [156] | Transition metal carbides | Hydrogen evolution reaction | Pt/Mo2C |
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiao, J.; Liu, Y.; Hong, F.; Zhang, J. A review of catalysts for the electroreduction of carbon dioxide to produce low-carbon fuels. Chem. Soc. Rev. 2014, 43, 631–675. [Google Scholar] [CrossRef]
- Sahraie, N.R.; Kramm, U.I.; Steinberg, J.; Zhang, Y.; Thomas, A.; Reier, T.; Paraknowitsch, J.-P.; Strasser, P. Quantifying the density and utilization of active sites in non-precious metal oxygen electroreduction catalysts. Nat. Commun. 2015, 6, 8618. [Google Scholar] [CrossRef] [Green Version]
- Francke, R.; Schille, B.; Roemelt, M. Homogeneously Catalyzed Electroreduction of Carbon Dioxide-Methods, Mechanisms, and Catalysts. Chem. Rev. 2018, 118, 4631–4701. [Google Scholar] [CrossRef]
- Zhao, Z.; Lu, W.; Yang, R.; Zhu, H.; Dong, W.; Sun, F.; Jiang, Z.; Lyu, Y.; Liu, T.; Du, H.; et al. Insight into the Formation of Co@Co2C Catalysts for Direct Synthesis of Higher Alcohols and Olefins from Syngas. ACS Catal. 2018, 8, 228–241. [Google Scholar] [CrossRef]
- Elgrishi, N.; Kurtz, D.A.; Dempsey, J.L. Reaction Parameters Influencing Cobalt Hydride Formation Kinetics: Implications for Benchmarking H2-Evolution Catalysts. J. Am. Chem. Soc. 2017, 139, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Arandiyan, H.; Gao, X.; Li, J. Recent Advances in Catalysts for Methane Combustion. Catal. Surv. Asia 2015, 19, 140–171. [Google Scholar] [CrossRef]
- Thoda, O.; Xanthopoulou, G.; Vekinis, G.; Chroneos, A. Review of Recent Studies on Solution Combustion Synthesis of Nanostructured Catalysts. Adv. Eng. Mater. 2018, 20, 1800047. [Google Scholar] [CrossRef]
- Sun, W.; Gong, B.; Pan, J.; Wang, Y.; Xia, H.; Zhang, H.; Dai, Q.; Wang, L.; Wang, X. Catalytic combustion of CVOCs over Cr Ti1- oxide catalysts. J. Catal. 2020, 391, 132–144. [Google Scholar] [CrossRef]
- Frontera, P.; Macario, A.; Ferraro, M.; Antonucci, P. Supported Catalysts for CO2 Methanation: A Review. Catalysts 2017, 7, 59. [Google Scholar] [CrossRef]
- Li, R.; Zhang, W.; Zhou, K. Metal–Organic-Framework-Based Catalysts for Photoreduction of CO2. Adv. Mater. 2018, 30, 1705512. [Google Scholar] [CrossRef]
- Millet, M.-M.; Algara-Siller, G.; Wrabetz, S.; Mazheika, A.; Girgsdies, F.; Teschner, D.; Seitz, F.; Tarasov, A.; Levchenko, S.V.; Schlögl, R.; et al. Ni Single Atom Catalysts for CO2 Activation. J. Am. Chem. Soc. 2019, 141, 2451–2461. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chong, C.C.; Cheng, Y.W.; Bukhari, S.N.; Setiabudi, H.D.; Jalil, A.A. Methane dry reforming over Ni/fibrous SBA-15 catalysts: Effects of support morphology (rod-liked F-SBA-15 and dendritic DFSBA-15). Catal Today 2021, 375, 245–257. [Google Scholar] [CrossRef]
- Morshed, M.N.; Behary, N.; Bouazizi, N.; Guan, J.P.; Nierstrasz, V.A. An overview on biocatalysts immobilization on textiles: Preparation, progress and application in wastewater treatment. Chemosphere 2021, 279, 130481. [Google Scholar] [CrossRef] [PubMed]
- Hong, Q.S.; Li, T.Y.; Zheng, S.S.; Chen, H.B.; Ren, W.J.; Chu, H.H.; Xu, K.D.; Mei, Z.W.; Pan, F. Modulating proton binding energy on the tungsten carbide nanowires surfaces for boosting hydrogen evolution in acid. J. Energy Chem. 2021, 62, 610–616. [Google Scholar] [CrossRef]
- Stirling, A.; Nair, N.N.; Lledós, A.; Ujaque, G. Challenges in modelling homogeneous catalysis: New answers from ab initio molecular dynamics to the controversy over the Wacker process. Chem. Soc. Rev. 2014, 43, 4940–4952. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woo, T.K.; Margl, P.M.; Deng, L.; Cavallo, L.; Ziegler, T. Towards more realistic computational modeling of homogenous catalysis by density functional theory: Combined QM/MM and ab initio molecular dynamics. Catal Today 1999, 50, 479–500. [Google Scholar] [CrossRef]
- Paquet, E.; Viktor, H.L. Computational Methods for Ab initio Molecular Dynamics. Adv. Chem. 2018, 2018, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N.; Crespi, V.H. Registry-dependent interlayer potential for graphitic systems. Phys. Rev. B 2005, 71, 235415. [Google Scholar] [CrossRef] [Green Version]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef] [Green Version]
- Chenoweth, K.; van Duin, A.C.T.; Goddard, W.A. ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Hydrocarbon Oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef] [Green Version]
- Zheng, M.; Li, X.; Guo, L. Algorithms of GPU-enabled reactive force field (ReaxFF) molecular dynamics. J. Mol. Graph. Model. 2013, 41, 1–11. [Google Scholar] [CrossRef]
- Guo, F.; Wen, Y.-S.; Feng, S.-Q.; Li, X.-D.; Li, H.-S.; Cui, S.-X.; Zhang, Z.-R.; Hu, H.-Q.; Zhang, G.-Q.; Cheng, X.-L. Intelligent-ReaxFF: Evaluating the reactive force field parameters with machine learning. Comput. Mater. Sci. 2020, 172, 109393. [Google Scholar] [CrossRef]
- Shin, Y.K.; Kwak, H.; Zou, C.; Vasenkov, A.V.; van Duin, A.C.T. Development and Validation of a ReaxFF Reactive Force Field for Fe/Al/Ni Alloys: Molecular Dynamics Study of Elastic Constants, Diffusion, and Segregation. J. Phys. Chem. A 2012, 116, 12163–12174. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Zhou, X.; Yang, T. Hetero-ConvLSTM: A Deep Learning Approach to Traffic Accident Prediction on Heterogeneous Spatio-Temporal Data. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; Association for Computing Machinery: London, UK, 2018; pp. 984–992. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Fidelis, T.T.; Sun, W.-H. Machine Learning in Catalysis, from Proposal to Practicing. ACS Omega 2020, 5, 83–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Han, D.; Hong, Y.; Sun, H.; Zhang, J.; Zhang, J. Machine Learning Enabled Prediction of Mechanical Properties of Tungsten Disulfide Monolayer. ACS Omega 2019, 4, 10121–10128. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Hong, Y.; Hou, B.; Zhang, Z.; Negahban, M.; Zhang, J. Accelerated discoveries of mechanical properties of graphene using machine learning and high-throughput computation. Carbon 2019, 148, 115–123. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Zhang, Z.; Zhang, J.; Zeng, X.C. Machine learning and artificial neural network prediction of interfacial thermal resistance between graphene and hexagonal boron nitride. Nanoscale 2018, 10, 19092–19099. [Google Scholar] [CrossRef] [PubMed]
- Toyao, T.; Maeno, Z.; Takakusagi, S.; Kamachi, T.; Takigawa, I.; Shimizu, K.-I. Machine Learning for Catalysis Informatics: Recent Applications and Prospects. ACS Catal. 2020, 10, 2260–2297. [Google Scholar] [CrossRef]
- Schlexer Lamoureux, P.; Winther, K.T.; Garrido Torres, J.A.; Streibel, V.; Zhao, M.; Bajdich, M.; Abild-Pedersen, F.; Bligaard, T. Machine Learning for Computational Heterogeneous Catalysis. ChemCatChem 2019, 11, 3581–3601. [Google Scholar] [CrossRef] [Green Version]
- Den Breejen, J.P.; Radstake, P.B.; Bezemer, G.L.; Bitter, J.H.; Frøseth, V.; Holmen, A.; de Jong, K.P. On the Origin of the Cobalt Particle Size Effects in Fischer−Tropsch Catalysis. J. Am. Chem. Soc. 2009, 131, 7197–7203. [Google Scholar] [CrossRef]
- Camara, G.A.; De Lima, R.B.; Iwasita, T. Catalysis of ethanol electrooxidation by PtRu: The influence of catalyst composition. Electrochem. Commun. 2004, 6, 812–815. [Google Scholar] [CrossRef]
- Haruta, M. Size- and support-dependency in the catalysis of gold. Catal Today 1997, 36, 153–166. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wang, A.; Zhang, T.; Mou, C.-Y. Catalysis by gold: New insights into the support effect. Nano Today 2013, 8, 403–416. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Wang, X. Rough contact is not always bad for interfacial energy coupling. Nanoscale 2013, 5, 11598–11603. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Li, L.; Zeng, X.C.; Zhang, J. Tuning thermal contact conductance at graphene-copper interface via surface nanoengineering. Nanoscale 2015, 7, 6286–6294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tabor, D.P.; Roch, L.M.; Saikin, S.K.; Kreisbeck, C.; Sheberla, D.; Montoya, J.H.; Dwaraknath, S.; Aykol, M.; Ortiz, C.; Tribukait, H.; et al. Accelerating the discovery of materials for clean energy in the era of smart automation. Nat. Rev. Mater. 2018, 3, 5–20. [Google Scholar] [CrossRef] [Green Version]
- Funes-Ardoiz, I.; Schoenebeck, F. Established and Emerging Computational Tools to Study Homogeneous Catalysis—From Quantum Mechanics to Machine Learning. Chem 2020, 6, 1904–1913. [Google Scholar] [CrossRef]
- Bonk, B.M.; Weis, J.W.; Tidor, B. Machine Learning Identifies Chemical Characteristics That Promote Enzyme Catalysis. J. Am. Chem. Soc. 2019, 141, 4108–4118. [Google Scholar] [CrossRef] [Green Version]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M.; et al. The ReaxFF reactive force-field: Development, applications and future directions. npj Comput. Mater. 2016, 2, 15011. [Google Scholar] [CrossRef]
- Burger, B.; Maffettone, P.M.; Gusev, V.V.; Aitchison, C.M.; Bai, Y.; Wang, X.Y.; Li, X.B.; Alston, B.; Li, B.Y.; Clowes, R.; et al. A mobile robotic chemist. Nature 2020, 583, 237–241. [Google Scholar] [CrossRef]
- Wittkamper, H.; Maisel, S.; Wu, M.; Frisch, J.; Wilks, R.; Grabau, M.; Spiecker, E.; Bar, M.; Gorling, A.; Steinruck, H.; et al. Oxidation induced restructuring of Rh-Ga SCALMS model catalyst systems. J. Chem. Phys. 2020, 153, 104702. [Google Scholar] [CrossRef]
- Pastore, G.; Smargiassi, E.; Buda, F. Theory of ab initiomolecular-dynamics calculations. Phys. Rev. A 1991, 44, 6334–6347. [Google Scholar] [CrossRef]
- Tuckerman, M.E. Ab initio molecular dynamics: Basic concepts, current trends and novel applications. J. Phys.-Condens. Mat. 2002, 14, R1297–R1355. [Google Scholar] [CrossRef]
- Born, M.; Oppenheimer, R. Zur Quantentheorie der Molekeln. Ann. Der Phys. 1927, 389, 457–484. [Google Scholar] [CrossRef]
- Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
- Brockherde, F.; Vogt, L.; Li, L.; Tuckerman, M.E.; Burke, K.; Müller, K.-R. Bypassing the Kohn-Sham equations with machine learning. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hutter, J. Car-Parrinello molecular dynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 604–612. [Google Scholar] [CrossRef]
- Iannuzzi, M.; Laio, A.; Parrinello, M. Efficient Exploration of Reactive Potential Energy Surfaces Using Car-Parrinello Molecular Dynamics. Phys. Rev. Lett. 2003, 90, 238302. [Google Scholar] [CrossRef] [Green Version]
- Martyna, G.J.; Hughes, A.; Tuckerman, M.E. Molecular dynamics algorithms for path integrals at constant pressure. J. Chem. Phys. 1999, 110, 3275–3290. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initiomolecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter. 2009, 21, 395502. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef] [PubMed]
- Andreoni, W.; Curioni, A. New advances in chemistry and materials science with CPMD and parallel computing. Parallel Comput. 2000, 26, 819–842. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comput. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]
- Otaki, H.; Taguchi, Y.; Nishida, N. Molecular Dynamics Simulation of Local Structural Models of PrPSc Reveals How Codon 129 Polymorphism Affects Propagation of PrPSc; Cold Spring Harbor Laboratory: Cold Spring Harbor, NY, USA, 2019. [Google Scholar]
- Osuna, S.; Jiménez-Osés, G.; Noey, E.L.; Houk, K.N. Molecular Dynamics Explorations of Active Site Structure in Designed and Evolved Enzymes. Acc. Chem. Res. 2015, 48, 1080–1089. [Google Scholar] [CrossRef] [PubMed]
- Van Duin, A.C.T.; Strachan, A.; Stewman, S.; Zhang, Q.; Xu, X.; Goddard, W.A. ReaxFFSiO Reactive Force Field for Silicon and Silicon Oxide Systems. J. Phys. Chem. A 2003, 107, 3803–3811. [Google Scholar] [CrossRef] [Green Version]
- Chenoweth, K.; Cheung, S.; van Duin, A.C.T.; Goddard, W.A.; Kober, E.M. Simulations on the Thermal Decomposition of a Poly(dimethylsiloxane) Polymer Using the ReaxFF Reactive Force Field. J. Am. Chem. Soc. 2005, 127, 7192–7202. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Çaǧın, T.; van Duin, A.; Goddard, W.A.; Qi, Y.; Hector, L.G. Adhesion and nonwetting-wetting transition in theAl/α−Al2O3interface. Phys. Rev. B 2004, 69, 045423. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Zybin, S.V.; Sun, H.; Goddard, W.A. ReaxFF-lg: Correction of the ReaxFF Reactive Force Field for London Dispersion, with Applications to the Equations of State for Energetic Materials. J. Phys. Chem. A 2011, 115, 11016–11022. [Google Scholar] [CrossRef]
- Odegard, G.M.; Jensen, B.D.; Gowtham, S.; Wu, J.; He, J.; Zhang, Z. Predicting mechanical response of crosslinked epoxy using ReaxFF. Chem. Phys. Lett. 2014, 591, 175–178. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Shin, Y.K.; Li, S.; Bennett, T.D.; van Duin, A.C.T.; Mauro, J.C. Enabling Computational Design of ZIFs Using ReaxFF. J. Phys. Chem. B 2018, 122, 9616–9624. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Kylasa, S.B.; Aktulga, H.M.; Grama, A.Y. PuReMD-GPU: A reactive molecular dynamics simulation package for GPUs. J. Comput. Phys. 2014, 272, 343–359. [Google Scholar] [CrossRef]
- Aktulga, H.M.; Fogarty, J.C.; Pandit, S.A.; Grama, A.Y. Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques. Parallel Comput. 2012, 38, 245–259. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Huang, X.; Yue, Y.; Wang, J.; Wang, X. Dynamic response of graphene to thermal impulse. Phys. Rev. B 2011, 84, 235416. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wang, X. Thermal transport in bent graphene nanoribbons. Nanoscale 2013, 5, 734–743. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, X.; Xie, H. Phonon energy inversion in graphene during transient thermal transport. Phys. Lett. A 2013, 377, 721–726. [Google Scholar] [CrossRef]
- Zhang, J.; Hong, Y.; Yue, Y. Thermal transport across graphene and single layer hexagonal boron nitride. J. Appl. Phys. 2015, 117, 134307. [Google Scholar] [CrossRef]
- Tessonnier, J.-P.; Su, D.S. Recent Progress on the Growth Mechanism of Carbon Nanotubes: A Review. ChemSusChem. 2011, 4, 824–847. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Xiong, W.; Zhou, Y.S.; Lu, Y.F.; Zeng, X.C. An ab initio study of the nickel-catalyzed transformation of amorphous carbon into graphene in rapid thermal processing. Nanoscale 2016, 8, 9746–9755. [Google Scholar] [CrossRef] [Green Version]
- Fukuhara, S.; Shimojo, F.; Shibuta, Y. Conformation and catalytic activity of nickel-carbon cluster for ethanol dissociation in carbon nanotube synthesis: Ab initio molecular dynamics simulation. Chem. Phys. Lett. 2017, 679, 164–171. [Google Scholar] [CrossRef]
- Neyts, E.C.; van Duin, A.C.; Bogaerts, A. Changing chirality during single-walled carbon nanotube growth: A reactive molecular dynamics/Monte Carlo study. J. Am. Chem. Soc. 2011, 133, 17225–17231. [Google Scholar] [CrossRef]
- Skubic, L.; Sovdat, J.; Teran, N.; Huš, M.; Kopač, D.; Likozar, B. Ab initio Multiscale Process Modeling of Ethane, Propane and Butane Dehydrogenation Reactions: A Review. Catalysts 2020, 10, 1405. [Google Scholar] [CrossRef]
- Jalid, F.; Khan, T.S.; Haider, M.A. CO2 reduction and ethane dehydrogenation on transition metal catalysts: Mechanistic insights, reactivity trends and rational design of bimetallic alloys. Catal. Sci. Technol. 2021, 11, 97–115. [Google Scholar] [CrossRef]
- Jimenez-Orozco, C.; Flórez, E.; Viñes, F.; Rodriguez, J.A.; Illas, F. Critical Hydrogen Coverage Effect on the Hydrogenation of Ethylene Catalyzed by δ-MoC(001): An Ab initio Thermodynamic and Kinetic Study. ACS Catal. 2020, 10, 6213–6222. [Google Scholar] [CrossRef]
- Chenoweth, K.; van Duin, A.C.T.; Persson, P.; Cheng, M.-J.; Oxgaard, J.; Goddard, W.A. Development and Application of a ReaxFF Reactive Force Field for Oxidative Dehydrogenation on Vanadium Oxide Catalysts. J. Phys. Chem. C 2008, 112, 14645–14654. [Google Scholar] [CrossRef] [Green Version]
- Feng, M.; Jiang, X.Z.; Luo, K.H. A reactive molecular dynamics simulation study of methane oxidation assisted by platinum/graphene-based catalysts. Proc. Combust. Inst. 2019, 37, 5473–5480. [Google Scholar] [CrossRef]
- Mattioli, G.; Risch, M.; Amore Bonapasta, A.; Dau, H.; Guidoni, L. Protonation states in a cobalt-oxide catalyst for water oxidation: Fine comparison of ab initio molecular dynamics and X-ray absorption spectroscopy results. Phys. Chem. Chem. Phys. 2011, 13, 15437–15441. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-G.; Yoon, Y.; Glezakou, V.-A.; Li, J.; Rousseau, R. The Role of Reducible Oxide–Metal Cluster Charge Transfer in Catalytic Processes: New Insights on the Catalytic Mechanism of CO Oxidation on Au/TiO2 from ab initio Molecular Dynamics. J. Am. Chem. Soc. 2013, 135, 10673–10683. [Google Scholar] [CrossRef]
- Zhang, Y.R.; van Duin, A.C.T.; Luo, K.H. Investigation of ethanol oxidation over aluminum nanoparticle using ReaxFF molecular dynamics simulation. Fuel 2018, 234, 94–100. [Google Scholar] [CrossRef]
- Mao, Q.; van Duin, A.C.T.; Luo, K.H. Investigation of methane oxidation by palladium-based catalyst via ReaxFF Molecular Dynamics simulation. Proc. Combust. Inst. 2017, 36, 4339–4346. [Google Scholar] [CrossRef] [Green Version]
- Hoppe, S.; Li, Y.; Moskaleva, L.V.; Muller, S. How silver segregation stabilizes 1D surface gold oxide: A cluster expansion study combined with ab initio MD simulations. Phys. Chem. Chem. Phys. 2017, 19, 14845–14853. [Google Scholar] [CrossRef]
- Barnard, L.; Morgan, D. Ab initio molecular dynamics simulation of interstitial diffusion in Ni–Cr alloys and implications for radiation induced segregation. J. Nucl. Mater. 2014, 449, 225–233. [Google Scholar] [CrossRef]
- Chen, J.H.; Martinez, T.J. QTPIE: Charge transfer with polarization current equalization. A fluctuating charge model with correct asymptotics. Chem. Phys. Lett. 2007, 438, 315–320, Erratum in 2008, 463, 288–288. [Google Scholar] [CrossRef]
- Vanduin, A.C.T.; Baas, J.M.A.; Vandegraaf, B. Delft Molecular Mechanics—A New Approach to Hydrocarbon Force-Fields—Inclusion of a Geometry-Dependent Charge Calculation. J. Chem. Soc. Faraday T 1994, 90, 2881–2895. [Google Scholar] [CrossRef]
- Choi, J.; Curl, R.; Thompson, L. Molybdenum nitride catalysts I. Influence of the synthesis factors on structural properties. J. Catal. 1994, 146, 218–227. [Google Scholar] [CrossRef] [Green Version]
- Cecilia, J.A.; Jiménez-Morales, I.; Infantes-Molina, A.; Rodríguez-Castellón, E.; Jiménez-López, A. Influence of the silica support on the activity of Ni and Ni2P based catalysts in the hydrodechlorination of chlorobenzene. Study of factors governing catalyst deactivation. J. Mol. Catal. A Chem. 2013, 368–369, 78–87. [Google Scholar] [CrossRef]
- Garrido-Barros, P.; Matheu, R.; Gimbert-Suriñach, C.; Llobet, A. Electronic, mechanistic, and structural factors that influence the performance of molecular water oxidation catalysts anchored on electrode surfaces. Curr. Opin. Electrochem. 2019, 15, 140–147. [Google Scholar] [CrossRef]
- Zahrt, A.F.; Henle, J.J.; Rose, B.T.; Wang, Y.; Darrow, W.T.; Denmark, S.E. Prediction of higher-selectivity catalysts by computer-driven workflow and machine learning. Science 2019, 363, eaau5631. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Hou, B.; Jiang, H.; Zhang, J. Machine learning and artificial neural network accelerated computational discoveries in materials science. WIREs Comput. Mol. Sci. 2020, 10, e1450. [Google Scholar] [CrossRef]
- Panteleev, J.; Gao, H.; Jia, L. Recent applications of machine learning in medicinal chemistry. Bioorganic Med. Chem. Lett. 2018, 28, 2807–2815. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Hong, Y.; Wang, M.; Xin, G.; Yue, Y.; Zhang, J. Mechanical properties of molybdenum diselenide revealed by molecular dynamics simulation and support vector machine. Phys. Chem. Chem. Phys. 2019, 21, 9159–9167. [Google Scholar] [CrossRef] [PubMed]
- Chen, E.P.; Bondi, R.W.; Michalski, P.J. Model-based Target Pharmacology Assessment (mTPA): An Approach Using PBPK/PD Modeling and Machine Learning to Design Medicinal Chemistry and DMPK Strategies in Early Drug Discovery. J. Med. Chem. 2021, 64, 3185–3196. [Google Scholar] [CrossRef] [PubMed]
- Raccuglia, P.; Elbert, K.C.; Adler, P.D.F.; Falk, C.; Wenny, M.B.; Mollo, A.; Zeller, M.; Friedler, S.A.; Schrier, J.; Norquist, A.J. Machine-learning-assisted materials discovery using failed experiments. Nature 2016, 533, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Jennings, P.C.; Lysgaard, S.; Hummelshøj, J.S.; Vegge, T.; Bligaard, T. Genetic algorithms for computational materials discovery accelerated by machine learning. NPJ Comput. Mater. 2019, 5, 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Zhang, Z. Artificial Neural Network; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 1–35. [Google Scholar]
- Shmilovici, A. Support Vector Machines; Springer: Berlin/Heidelberg, Germany, 2009; pp. 231–247. [Google Scholar]
- Reid, J.P.; Proctor, R.S.J.; Sigman, M.S.; Phipps, R.J. Predictive Multivariate Linear Regression Analysis Guides Successful Catalytic Enantioselective Minisci Reactions of Diazines. J. Am. Chem. Soc. 2019, 141, 19178–19185. [Google Scholar] [CrossRef] [Green Version]
- Pearce, N.D.; Wand, M.P. Penalized Splines and Reproducing Kernel Methods. Am. Stat. 2006, 60, 233–240. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef] [Green Version]
- Back, S.; Tran, K.; Ulissi, Z.W. Toward a Design of Active Oxygen Evolution Catalysts: Insights from Automated Density Functional Theory Calculations and Machine Learning. ACS Catal. 2019, 9, 7651–7659. [Google Scholar] [CrossRef]
- Can, E.; Yildirim, R. Data mining in photocatalytic water splitting over perovskites literature for higher hydrogen production. Appl. Catal. B Environ. 2019, 242, 267–283. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Lee, T.-F.; Chao, P.-J.; Ting, H.-M.; Chang, L.; Huang, Y.-J.; Wu, J.-M.; Wang, H.-Y.; Horng, M.-F.; Chang, C.-M.; Lan, J.-H.; et al. Using Multivariate Regression Model with Least Absolute Shrinkage and Selection Operator (LASSO) to Predict the Incidence of Xerostomia after Intensity-Modulated Radiotherapy for Head and Neck Cancer. PLoS ONE 2014, 9, e89700. [Google Scholar]
- Vovk, V. Kernel Ridge Regression; Springer: Berlin/Heidelberg, Germany, 2013; pp. 105–116. [Google Scholar]
- Awad, M.; Khanna, R. Support Vector Regression; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Werth, J.; Sigman, M.S. Linear Regression Model Development for Analysis of Asymmetric Copper-Bisoxazoline Catalysis. ACS Catal. 2021, 11, 3916–3922. [Google Scholar] [CrossRef]
- Alred, J.M.; Bets, K.V.; Xie, Y.; Yakobson, B.I. Machine learning electron density in sulfur crosslinked carbon nanotubes. Compos. Sci Technol 2018, 166, 3–9. [Google Scholar] [CrossRef]
- Atlas, S.R. Embedding Quantum Statistical Excitations in a Classical Force Field. J. Phys. Chem. A 2021, 125, 3760–3775. [Google Scholar] [CrossRef] [PubMed]
- Bal, K.M.; Neyts, E.C. Quantifying the impact of vibrational nonequilibrium in plasma catalysis: Insights from a molecular dynamics model of dissociative chemisorption. J. Phys. D Appl. Phys. 2021, 54. [Google Scholar] [CrossRef]
- Batra, R.; Sankaranarayanan, S. Machine learning for multi-fidelity scale bridging and dynamical simulations of materials. J. Phys. Mater. 2020, 3, 031002. [Google Scholar] [CrossRef]
- Brickel, S.; Das, A.K.; Unke, O.T.; Turan, H.T.; Meuwly, M. Reactive molecular dynamics for the [Cl-CH3-Br](-) reaction in the gas phase and in solution: A comparative study using empirical and neural network force fields. Electron. Struct 2019, 1, 024002. [Google Scholar] [CrossRef]
- Caro, M.A.; Csanyi, G.; Laurila, T.; Deringer, V.L. Machine learning driven simulated deposition of carbon films: From low-density to diamondlike amorphous carbon. Phys. Rev. B 2020, 102, 174201. [Google Scholar] [CrossRef]
- Chan, H.; Narayanan, B.; Cherukara, M.J.; Sen, F.G.; Sasikumar, K.; Gray, S.K.; Chan, M.K.Y.; Sankaranarayanan, S.K.R.S. Machine Learning Classical Interatomic Potentials for Molecular Dynamics from First-Principles Training Data. J. Phys. Chem. C 2019, 123, 6941–6957. [Google Scholar] [CrossRef]
- Chen, L.; Sukuba, I.; Probst, M.; Kaiser, A. Iterative training set refinement enables reactive molecular dynamics via machine learned forces. RSC Adv. 2020, 10, 4293–4299. [Google Scholar] [CrossRef] [Green Version]
- Daksha, C.M.; Yeon, J.; Chowdhury, S.C.; Gillespie, J.W. Automated ReaxFF parametrization using machine learning. Comput. Mater. Sci. 2021, 187, 110107. [Google Scholar] [CrossRef]
- Djilali, L.; Sanchez, E.N.; Belkheiri, M. Real-time neural sliding mode field oriented control for a DFIG-based wind turbine under balanced and unbalanced grid conditions. IET Renew. Power Gen. 2019, 13, 618–632. [Google Scholar] [CrossRef]
- Elbaz, Y.; Furman, D.; Toroker, M.C. Modeling Diffusion in Functional Materials: From Density Functional Theory to Artificial Intelligence. Adv. Funct. Mater. 2020, 30, 1900778. [Google Scholar] [CrossRef]
- Gaffney, A.M.; An, Q.; Goddard, W.A.; Diao, W.J.; Glazoff, M.V. Toward Concurrent Engineering of the M1-Based Catalytic Systems for Oxidative Dehydrogenation (ODH) of Alkanes. Top. Catal. 2020, 63, 1667–1681. [Google Scholar] [CrossRef]
- Zhu, L.J.; Zhang, Y.L.; Zhang, L.; Zhou, X.Y.; Jiang, B. Unified and transferable description of dynamics of H(2)dissociative adsorption on multiple copper surfacesviamachine learning. Phys. Chem. Chem. Phys. 2020, 22, 13958–13964. [Google Scholar] [CrossRef] [PubMed]
- Zhen, H.J.; Liu, L.; Lin, Z.Z.; Gao, S.Y.; Li, X.L.; Zhang, X. Physically Compatible Machine Learning Study on the Pt-Ni Nanoclusters. J. Phys. Chem. Lett. 2021, 12, 1573–1580. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.Y.; Zhang, Y.L.; Guo, H.; Jiang, B. Towards bridging the structure gap in heterogeneous catalysis: The impact of defects in dissociative chemisorption of methane on Ir surfaces. Phys. Chem. Chem. Phys. 2021, 23, 4376–4385. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.R.; Li, Y.F. Advances in two dimensional electrochemical catalysts for ammonia synthesis. Chin. Sci. B-Chin. 2021, 66, 625–639. [Google Scholar] [CrossRef]
- Unke, O.T.; Chmiela, S.; Sauceda, H.E.; Gastegger, M.; Poltavsky, I.; Schutt, K.T.; Tkatchenko, A.; Muller, K.R. Machine Learning Force Fields. Chem. Rev. 2021, 121, 10142–10186. [Google Scholar] [CrossRef] [PubMed]
- Deringer, V.L.; Caro, M.A.; Csányi, G. Machine Learning Interatomic Potentials as Emerging Tools for Materials Science. Adv. Mater. 2019, 31, 1902765. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef] [PubMed]
- Burkle, M.; Perera, U.; Gimbert, F.; Nakamura, H.; Kawata, M.; Asai, Y. Deep-Learning Approach to First-Principles Transport Simulations. Phys. Rev. Lett. 2021, 126, 177701. [Google Scholar] [CrossRef]
- Wang, P.P.; Xiong, W.J.; Huang, Z.B.; He, Y.L.; Liu, J.M.; Ye, H.P.; Xiao, J.N.; Li, Y.; Fan, D.A.Y.; Chen, S.Q. Diffractive Deep Neural Network for Optical Orbital Angular Momentum Multiplexing and Demultiplexing. IEEE J. Sel. Top. Quant. 2021, 28, 1–11. [Google Scholar] [CrossRef]
- Larizza, L.; Calzari, L.; Alari, V.; Russo, S. Genes for RNA-binding proteins involved in neural-specific functions and diseases are downregulated in Rubinstein-Taybi iNeurons. Neural Regen Res. 2022, 17, 5. [Google Scholar] [CrossRef]
- Lei, L.; Ke, C.; Xiao, K.Y.; Qu, L.H.; Lin, X.; Zhan, X.; Tu, J.Y.; Xu, K.; Liu, Y.J. Identification of different bran-fried Atractylodis Rhizoma and prediction of atractylodin content based on multivariate data mining combined with intelligent color recognition and near-infrared spectroscopy. Spectrochim Acta A 2021, 262, 120119. [Google Scholar] [CrossRef]
- You, D.D.; Shen, X.C.; Liu, G.J.; Wang, G.X. Signal anomaly identification strategy based on Bayesian inference for nuclear power machinery. Mech. Syst. Signal Pr. 2021, 161, 107967. [Google Scholar] [CrossRef]
- Cai, W.S.; Wilson, J.; Song, A.M. Present status of electric-double-layer thin-film transistors and their applications. Flex Print Electron. 2021, 6, 043001. [Google Scholar] [CrossRef]
- Andersson, K.; Oosterlee, C.W. A deep learning approach for computations of exposure profiles for high-dimensional Bermudan options. Appl. Math. Comput. 2021, 408, 126332. [Google Scholar]
- Bartók, A.P.; Kermode, J.; Bernstein, N.; Csányi, G. Machine Learning a General-Purpose Interatomic Potential for Silicon. Phys. Rev. X 2018, 8, 041048. [Google Scholar] [CrossRef] [Green Version]
- Rowe, P.; Csányi, G.; Alfè, D.; Michaelides, A. Development of a machine learning potential for graphene. Phys. Rev. B 2018, 97, 054303. [Google Scholar] [CrossRef] [Green Version]
- Ulissi, Z.W.; Tang, M.T.; Xiao, J.; Liu, X.; Torelli, D.A.; Karamad, M.; Cummins, K.; Hahn, C.; Lewis, N.S.; Jaramillo, T.F.; et al. Machine-Learning Methods Enable Exhaustive Searches for Active Bimetallic Facets and Reveal Active Site Motifs for CO2 Reduction. ACS Catal. 2017, 7, 6600–6608. [Google Scholar] [CrossRef] [Green Version]
- Al-Resayes, S.I.; Azam, M.; Trzesowska-Kruszynska, A.; Kruszynski, R.; Soliman, S.M.; Mohapatra, R.K.; Khan, Z. Structural and Theoretical Investigations, Hirshfeld Surface Analyses, and Cytotoxicity of a Naphthalene-Based Chiral Compound. ACS Omega 2020, 5, 27227–27234. [Google Scholar] [CrossRef]
- Deimel, M.; Reuter, K.; Andersen, M. Active Site Representation in First-Principles Microkinetic Models: Data-Enhanced Computational Screening for Improved Methanation Catalysts. Acs Catal. 2020, 10, 13729–13736. [Google Scholar] [CrossRef]
- Gong, L.L.; Zhang, D.T.; Shen, Y.; Wang, X.W.; Zhang, J.; Han, X.; Zhang, L.P.; Xia, Z.H. Enhancing both selectivity and activity of CO2 conversion by breaking scaling relations with bimetallic active sites anchored in covalent organic frameworks. J. Catal. 2020, 390, 126–134. [Google Scholar] [CrossRef]
- Ma, S.C.; Liu, Z.P. Machine Learning for Atomic Simulation and Activity Prediction in Heterogeneous Catalysis: Current Status and Future. ACS Catal. 2020, 10, 13213–13226. [Google Scholar] [CrossRef]
- Migliaro, I.; Cundari, T.R. Density Functional Study of Methane Activation by Frustrated Lewis Pairs with Group 13 Trihalides and Group 15 Pentahalides and a Machine Learning Analysis of Their Barrier Heights. J. Chem. Inf. Model. 2020, 60, 4958–4966. [Google Scholar] [CrossRef] [PubMed]
- Miyahara, Y.; Fukutsuka, T.; Abe, T.; Miyazaki, K. Dual-Site Catalysis of Fe-Incorporated Oxychlorides as Oxygen Evolution Electrocatalysts. Chem. Mater. 2020, 32, 8195–8202. [Google Scholar] [CrossRef]
- Wang, H.Y.; Zhang, Y.T.; Yan, F.F.; Zhang, H.C. Insight into the Structures and Electrocatalytic Activities of PdAg Alloy on RGO in the Oxidation of Ethanol, Ethylene Glycol and Glycerol. Catal Lett. 2021, 151, 1796–1804. [Google Scholar] [CrossRef]
- Yao, M.K.; Shi, Z.H.; Zhang, P.; Ong, E.E.J.; Jiang, J.Z.; Ching, W.Y.; Li, N. Density Functional Theory Study of Single Metal Atoms Embedded into MBene for Electrocatalytic Conversion of N-2 to NH3. ACS Appl. Nano Mater. 2020, 3, 9870–9879. [Google Scholar] [CrossRef]
- Yuan, S.; Li, Y.D.; Peng, J.Y.; Questell-Santiago, Y.M.; Akkiraju, K.; Giordano, L.; Zheng, D.J.; Bagi, S.; Roman-Leshkov, Y.; Shao-Horn, Y. Conversion of Methane into Liquid Fuels-Bridging Thermal Catalysis with Electrocatalysis. Adv. Energy Mater. 2020, 10, 2002154. [Google Scholar] [CrossRef]
- Sinthika, S.; Waghmare, U.V.; Thapa, R. Structural and Electronic Descriptors of Catalytic Activity of Graphene-Based Materials: First-Principles Theoretical Analysis. Small 2018, 14, 1703609. [Google Scholar] [CrossRef] [PubMed]
- Timoshenko, J.; Frenkel, A.I. “Inverting” X-ray Absorption Spectra of Catalysts by Machine Learning in Search for Activity Descriptors. ACS Catal. 2019, 9, 10192–10211. [Google Scholar] [CrossRef]
- Zhuang, H.; Tkalych, A.J.; Carter, E.A. Surface energy as a descriptor of catalytic activity. J. Phys. Chem. C 2016, 120, 23698–23706. [Google Scholar] [CrossRef]
- Jacobs, R.; Booske, J.; Morgan, D. Understanding and controlling the work function of perovskite oxides using density functional theory. Adv. Funct. Mater. 2016, 26, 5471–5482. [Google Scholar] [CrossRef] [Green Version]
- Hwang, S.J.; Yoo, S.J.; Shin, J.; Cho, Y.-H.; Jang, J.H.; Cho, E.; Sung, Y.-E.; Nam, S.W.; Lim, T.-H.; Lee, S.-C. Supported core shell electrocatalysts for fuel cells: Close encounter with reality. Sci. Rep. 2013, 3, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Suntivich, J.; Gasteiger, H.A.; Yabuuchi, N.; Nakanishi, H.; Goodenough, J.B.; Shao-Horn, Y. Design principles for oxygen-reduction activity on perovskite oxide catalysts for fuel cells and metal–air batteries. Nat. Chem. 2011, 3, 546–550. [Google Scholar] [CrossRef]
- Toyoda, K.; Hinogami, R.; Miyata, N.; Aizawa, M. Calculated descriptors of catalytic activity for water electrolysis anode: Application to delafossite oxides. J. Phys. Chem. C 2015, 119, 6495–6501. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Theoretical surface science and catalysis—Calculations and concepts. Adv. Catal. 2000, 45, 71–129. [Google Scholar]
- Takahashi, K.; Miyazato, I.; Nishimura, S.; Ohyama, J. Unveiling Hidden Catalysts for the Oxidative Coupling of Methane based on Combining Machine Learning with Literature Data. ChemCatChem 2018, 10, 3223–3228. [Google Scholar] [CrossRef]
- Fung, V.; Zhang, J.; Juarez, E.; Sumpter, B.G. Benchmarking graph neural networks for materials chemistry. NPJ Comput. Mater. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Ye, W.; Zuo, Y.; Zheng, C.; Ong, S.P. Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals. Chem. Mater. 2019, 31, 3564–3572. [Google Scholar] [CrossRef] [Green Version]
- Schweidtmann, A.M.; Rittig, J.G.; König, A.; Grohe, M.; Mitsos, A.; Dahmen, M. Graph Neural Networks for Prediction of Fuel Ignition Quality. Energy Fuels 2020, 34, 11395–11407. [Google Scholar] [CrossRef]
- Louis, S.-Y.; Zhao, Y.; Nasiri, A.; Wang, X.; Song, Y.; Liu, F.; Hu, J. Graph convolutional neural networks with global attention for improved materials property prediction. Phys. Chem. Chem. Phys. 2020, 22, 18141–18148. [Google Scholar] [CrossRef]
- Ghanekar, P.; Deshpande, S.; Greeley, J. Adsorbate Chemical Environment-Based Machine Learning Framework for Heterogeneous Catalysis; Cambridge University Press (CUP): Cambridge, UK, 2021. [Google Scholar]
- Ramsundar, B.; Leswing, K. Molecular machine learning with DeepChem. Abstr. Pap. Am. Chem. S 2019, 257. [Google Scholar]
- Ramsundar, B. Molecular machine learning with DeepChem. Abstr. Pap. Am. Chem. S 2018, 255. Available online: https://www.proquest.com/openview/9c0e06a343233b48d962991d19873ed8/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 15 September 2021).
- Zhang, J.; Zhao, J.; Lin, H.N.; Tan, Y.Y.; Cheng, J.X. High-Speed Chemical Imaging by Dense-Net Learning of Femtosecond Stimulated Raman Scattering. J. Phys. Chem. Lett. 2020, 11, 8573–8578. [Google Scholar] [CrossRef]
- Minnich, A.J.; McLoughlin, K.; Tse, M.; Deng, J.; Weber, A.; Murad, N.; Madej, B.D.; Ramsundar, B.; Rush, T.; Calad-Thomson, S.; et al. AMPL: A Data-Driven Modeling Pipeline for Drug Discovery. J. Chem. Inf. Model. 2020, 60, 1955–1968. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.W.; Kramer, S.T.; Fang, M.J.; Qiu, Y.K.; Wu, Z.; Xu, D. A self-attention based message passing neural network for predicting molecular lipophilicity and aqueous solubility. J. Cheminformatics 2020, 12, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitsuno, H.; Okuwaki, K.; Ito, M.; Mochizuki, Y. Development of Educational Scratch Program for Machine Learning for Students in Chemistry Course. J. Comput. Chem.-Jpn. 2019, 18, 126–128. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Ramsundar, B.; Feinberg, E.N.; Gomes, J.; Geniesse, C.; Pappu, A.S.; Leswing, K.; Pande, V. MoleculeNet: A benchmark for molecular machine learning. Chem. Sci. 2018, 9, 513–530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jonsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- Stamenkovic, V.; Mun, B.S.; Mayrhofer, K.J.; Ross, P.N.; Markovic, N.M.; Rossmeisl, J.; Greeley, J.; Nørskov, J.K. Changing the activity of electrocatalysts for oxygen reduction by tuning the surface electronic structure. Angew. Chem. 2006, 118, 2963–2967. [Google Scholar] [CrossRef]
- Grimaud, A.; May, K.J.; Carlton, C.E.; Lee, Y.-L.; Risch, M.; Hong, W.T.; Zhou, J.; Shao-Horn, Y. Double perovskites as a family of highly active catalysts for oxygen evolution in alkaline solution. Nat. Commun. 2013, 4, 1–7. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhu, Y.; Wu, Y.; Chen, C.; Hong, Y.; Yue, Y.; Zhang, J.; Hou, B. Molecular Dynamics and Machine Learning in Catalysts. Catalysts 2021, 11, 1129. https://doi.org/10.3390/catal11091129
Liu W, Zhu Y, Wu Y, Chen C, Hong Y, Yue Y, Zhang J, Hou B. Molecular Dynamics and Machine Learning in Catalysts. Catalysts. 2021; 11(9):1129. https://doi.org/10.3390/catal11091129
Chicago/Turabian StyleLiu, Wenxiang, Yang Zhu, Yongqiang Wu, Cen Chen, Yang Hong, Yanan Yue, Jingchao Zhang, and Bo Hou. 2021. "Molecular Dynamics and Machine Learning in Catalysts" Catalysts 11, no. 9: 1129. https://doi.org/10.3390/catal11091129
APA StyleLiu, W., Zhu, Y., Wu, Y., Chen, C., Hong, Y., Yue, Y., Zhang, J., & Hou, B. (2021). Molecular Dynamics and Machine Learning in Catalysts. Catalysts, 11(9), 1129. https://doi.org/10.3390/catal11091129








