1. Introduction
Metaheuristics have demonstrated their efficacy in recent years in handling complex problems, especially complex combinatorial challenges. There are several examples in biology [
1], logistics [
2], civil engineering [
3], and machine learning [
4], among others. Despite the increased efficiency, and in part due to the vast scale of many combinatorial problems, it is also vital to maintain the strength of metaheuristic approaches. Thus, hybrid techniques have been employed to enhance metaheuristic algorithmic performance.
Among the main approaches of how to integrate metaheuristics, has been found hybrid heuristics, [
5], where multiple metaheuristic algorithms are merged to boost their capabilities. In [
6], for example, the authors employed simulated annealing-based genetic and tabu-search-based genetic algorithms to address the ordering planning problem. The hybrid approaches were compared to the traditional approaches in this study, with the hybrid approaches outperforming the traditional approaches. In [
7], the cuckoo search and firefly algorithm search methods are combined in order to avoid getting the procedure stuck in local optimum. The hybrid algorithm was applied to a job schedulers problem in high-performance computing systems. When compared to traditional policies, the results indicated significant reductions in server energy consumption.
Another interesting hybrid approach, [
8], is matheuristics, which combines mathematical programming approaches with metaheuristic algorithms. The vehicle routing problem, for example, was studied utilizing mixed-integer linear programming and metaheuristic techniques in [
9]. These methods, generally, do not take advantage of the auxiliary data created by metaheuristics in order to obtain more reliable results. In the solution-finding process, metaheuristics provide useful accessory data, which may be used to inform machine learning approaches. The area of artificial intelligence and in particular machine learning has grown important in recent times applying in different areas [
10,
11,
12]. Machine learning approaches combined with metaheuristic algorithms is a novel area of research that has gained traction in recent years [
13].
According to [
13,
14], there are three primary areas in which machine learning algorithms utilize metaheuristic data: low-level integrations, high-level integrations, and optimization problems. A current area of research in low-level integrations is the construction of binary versions of algorithms that operate naturally in continuous space. In [
15], a state-of-the-art of the different binarization techniques is developed in which two main groups stand out. The first group corresponds to general binarization techniques in which the movements of the metaheuristics are not modified, but rather after its execution, the binarization of the solutions is applied. The second group corresponds to modifications applied directly to the movement of metaheuristics. The first group has the advantage that the procedure is used for any continuous metaheuristic, the second, when the adjustments are carried out in an adequate way, have good performance. There are examples of integration between machine learning and metaheuristics in this domain. In [
16,
17], the binary versions of the cuckoo search algorithm were generated using the k-nearest neighbor technique. These binary versions were applied to multidimensional knapsack and set covering problems, respectively. Whereas in the field of civil engineering [
18,
19], hybrid methods were proposed that utilizes db-scan and k-means, respectively, as a binarization method and is used to optimize the emission of CO
of retaining walls.
In accordance with low-level integration between machine learning and metaheuristics, in this article, a hybrid approach was used that combines a cuckoo search algorithm with the unsupervised k-means technique to obtain a binary version of the continuous cuckoo search algorithm. The suggested approach combines these two strategies with the objective of obtaining a robust binary version through the use of the data acquired during the execution of the metaheuristic. The proposed algorithm was applied to the set-union knapsack problem. The set union knapsack problem (SUKP) [
20] is a generalization of the classical knapsack problem. SUKP has received attention from researchers in recent years [
21,
22,
23] due to its interesting applications [
24,
25], as well as the difficulty of being able to solve it efficiently. In SUKP, there is a set of items where each item has a profit. Additionally, each item associates a set of elements where each element has a weight that is associated with the knapsack constraint. In the literature, it is observed that the algorithms that have addressed SUKP are mainly improved metaheuristics and have allowed obtaining results in reasonable times. When applying a metaheuristic in its standard form to SUKP, these algorithms have had limitations such as stability and decreased performance as the instance grows in size. For example, in [
26], different transfer functions were used and evaluated with small and medium SUKP instances. This effect is observed when the algorithms are applied to standard SUKP instances, additionally, to increase the challenge in [
27], a new set of benchmark problems was recently generated. All previous, leads to exploring hybrid techniques in order to strengthen the performance of the algorithm. The following are the contributions made by this work:
- 1.
A new greedy initiation operator is proposed.
- 2.
The k-means technique, proposed in [
28], is used to binarize the cuckoo search (CS) algorithm, tuned and applied for the first time to the SUKP. Additionally, a random binarization operator is designed and two transition probabilities are applied to evaluate the contribution of k-means in the final result. It should be noted that the binarization method allows generating binary versions of other continuous swarm intelligence metaheuristics.
- 3.
A new local search operator is proposed to improve the exploitation of the search space.
- 4.
The results obtained by the hybrid algorithm are compared with different algorithms that have addressed SUKP. It should be noted that the standard SUKP instances and the new instances proposed in [
27] were solved.
The following is a summary of the contents:
Section 2 delves into the set-union knapsack problem and its applications. The k-means cuckoo search algorithm and the local search operator are described in
Section 3. In
Section 4, the detail of the numerical experiments and comparisons are developed. Finally, the conclusions and potential lines of research are discussed in
Section 5.
2. The Set Union Knapsack Problem
The Set-Union Knapsack Problem (SUKP) is a generalized knapsack model with the following definition. First, let
U be a set of
n elements with each element
having a weight
> 0. Let
V be a set of m items with each item
being a subset of elements
and having a profit
. Finally, for a knapsack with capacity
C, SUKP entails identifying a set of items
that maximizes the total profit of S while guaranteeing that the total weight of the components of S does not exceed the capacity C of the knapsack. Being the elements belonging to the set
S, the decision variables of the problem. It is worth noting that an elements weight is only tallied once, even if it corresponds to several chosen items in S. SUKP may be written mathematically as follows:
subject to:
In reviewing the literature SUKP has been found to have interesting applications, for example in [
24]. The goal of this application is to improve the scalability of cybernetic systems robustness. Given a centralized cyber system with a fixed memory capacity that holds a collection of profit-generating services (or requests), each of which contains a set of data objects. When a data object is activated, it consumes a particular amount of memory, and using the same data object several times does not result in increased memory consumption (An important condition of SUKP). The goal is to choose a subset of services from among the candidate services that maximizes the total profit of those services while keeping the total memory required by the underlying data objects within the cyber system’s memory capacity. The SUKP model, in which an item corresponds to a service with its profit and an element relates to a data object with its memory usage, is a convenient way to structure this application (element weight). Finding the optimal solution to the ensuing SUKP problem is thus comparable to solving the data allocation problem.
Another interesting application is related to the rendering of an animated crow in real-time [
29]. In the article, the authors present a method to accelerate the visualization of large crowds of animated characters. They adopt a caching system that enables a skinned key-pose (elements) to be re-used by multi-pass rendering, between multiple agents and across multiple frames, an interpolative approach that enables key-pose blending to be supported. In this problem, each item corresponds to a crowd member. Applications are also found in data stream compression through the use of bloom filters [
25].
SUKP is an
-hard problem [
20] that has been tackled by a variety of methods. In [
20,
30], theoretical studies using greedy approaches or dynamic programming are found. An integer linear programming model was developed in [
31] and applied to small instances of 85 and 100 items, finding the optimal solutions.
Metaheuristic algorithms have also addressed SUKP. In [
32], the authors use an artificial bee colony technique to tackle SUKP. In addition, this algorithm integrates a greedy operator with the aim of addressing infeasible solutions. In [
33], the authors designed an enhanced moth search algorithm. To improve its efficiency, this algorithm incorporates an integrating differential mutation operator. The Jaya algorithm was employed in [
34]. Additionally, a differential evolution technique was incorporated to enhance exploration capability. The Cauchy mutation is used to boost its exploitation ability. Furthermore, an enhanced repair operator has been designed to repair the infeasible solutions. In [
26], the effectiveness of different transfer functions is studied in order to binarize the moth metaheuristics. A local search operator is designed in [
35] and applied to long-scale instances of SUKP. The article proposes three strategies that conform to the adaptive tabu search framework and efficiently solve new instances of SUKP. In [
36], the grey wolf optimizer (GWO) algorithm is adapted to address binary problems. For the algorithm to be robust, traditional binarization methods are not used. To replicate the GWO leadership hierarchy technique, a multiple parent crossover is established with two distinct dominance tactics. In addition, an adaptive mutation with an exponentially decreasing step size is used to avoid early convergence and achieve a balance of intensification and diversification.
3. The Machine Learning Cuckoo Search Algorithm
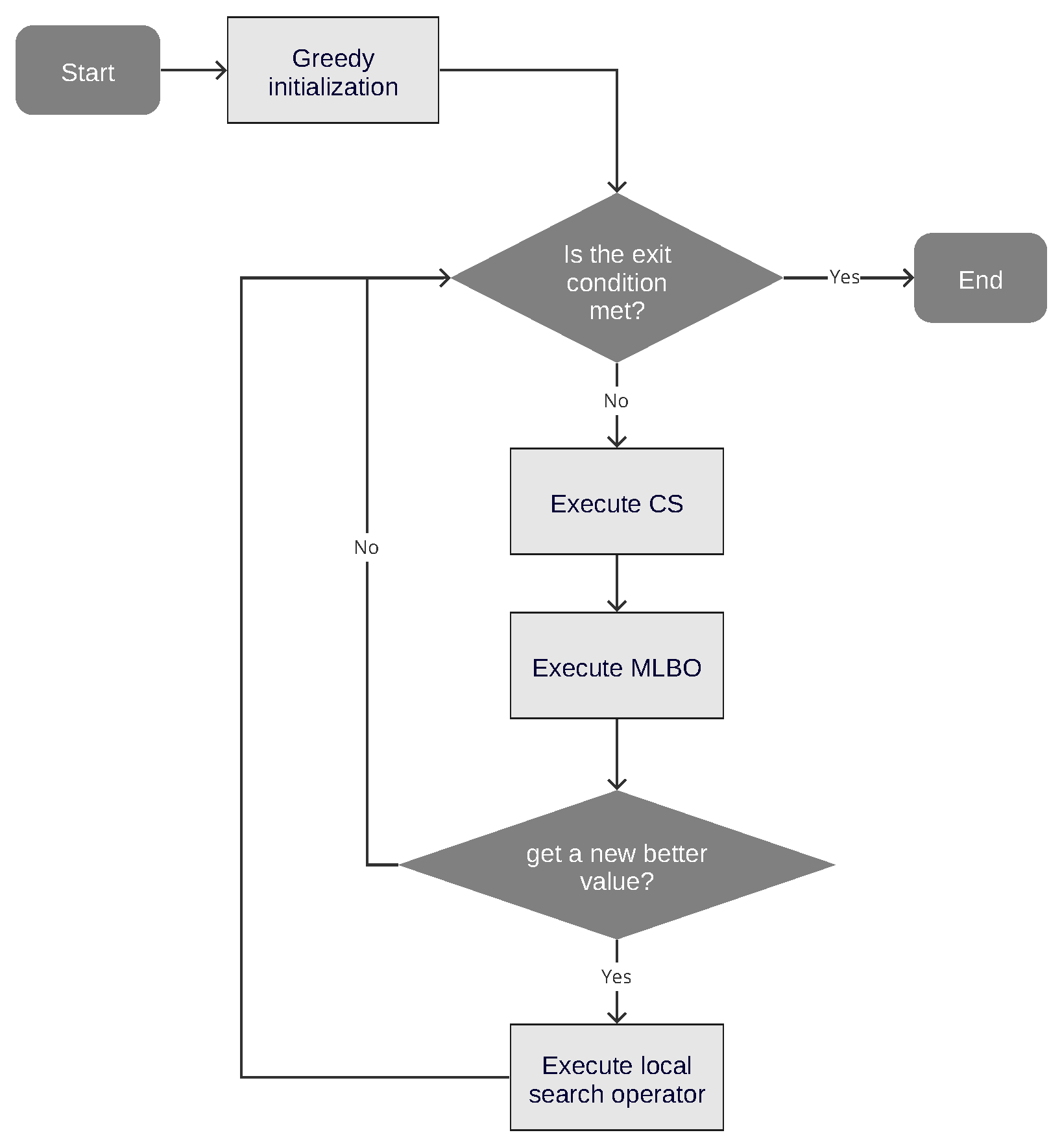
This section describes the machine learning binary cuckoo search algorithm used to solve the SUKP problem. This hybrid algorithm consists of three main operators: A greedy initialization operator detailed in
Section 3.1. CS is then used to develop the optimization. Here, it should be noted that CS is going to produce results with values in
and therefore they must be binarized. Then, a machine learning binarization operator performs the binarization of the solutions generated by the cuckoo search algorithm, and which uses the unsupervised k-means technique. This operator is detailed in
Section 3.2. Finally, a local search operator is applied when the condition of finding a new maximum is met. The logic of the local search operator is detailed in
Section 3.3.
Figure 1 shows the flowchart of the binary machine learning cuckoo search algorithm. It is also worth noting that CS can be replaced by any other continuous swarm intelligence metaheuristic.
3.1. Greedy Initialization Operator
The objective of this operator is to build the solutions that will start the search process. For this, the items are ordered using the ratio defined in Equation (
3). As input to the operator,
is utilized, and it contains the elements ordered by
r from highest to lowest. As output, a valid solution,
, is obtained.
In line 4, a blank
solution is initialized, then in line 5 the fulfillment of the constraint by
is validated. While the weight of the solution items (
), Equation (
2), is not equal or greater thab the knapsack constraint (
), a random number
is generated in line 6, and compare it in line 7 with
. If
is greater than
, an element of
is added in line 8, fulfilling the order. Otherwise, in line 11, a random item is chosen, then add it to the solution, and in line 12 remove it from
. Once the knapsack is full, the solution needs to be cleaned up in line 15, as it is greater than or equal to
. In the case that it is the same, it does not take action. In the event that it is greater, the items of
must be ordered using r defined in Equation (
3) and it is removed in order starting with the smallest and checking the constraint in each elimination. Once the constraint is fulfilled, the procedure stops and the solution
is returned. The pseudo-code is shown in Algorithm 1.
| Algorithm 1 Greedy initialization operator |
- 1:
Function initSolutions() - 2:
Input
- 3:
Output
- 4:
- 5:
while (weightSol < knapsackSize) do - 6:
getRandom() - 7:
if
then - 8:
) - 9:
) - 10:
else - 11:
) - 12:
) - 13:
end if - 14:
end while - 15:
cleanSol() - 16:
return
|
3.2. Machine Learning Binarization Operator
The machine learning binarization operator (MLBO) is responsible for the binarization process. This receives as input the list of solutions obtained from the previous iteration, the metaheuristic (), in this case CS, the best solution obtained, so far, and the transition probability for each cluster, . To this list , in line 4, the is applied, in this case it corresponds to CS. From the result of applying to , the absolute value of velocities, , is obtained. These velocities correspond to the transition vector obtained by applying MH to the list of solutions. The set of all velocities is clustered in line 5, using k-means (getKmeansClustering), in this particular case K = 5.
So, for each
and each dimension
j, a cluster is assigned and each cluster is associated with a transition probability (
), ordered by the value of the cluster centroid. For this case the transition probabilities used were [0.1, 0.2, 0.4, 0.8, 0.9]. Then for the set of points that belong to the cluster with the smallest centroid, which is represented by the green color in
Figure 2, the transition probability 0.1 was associated. For the group of blue points that obtained the centroid with the highest value, a transition probability of 0.9 was associated. The smaller the value of the centroid, the smaller the value of
are associated with it. Then, in line 8, for each
, a transition probability
is associated and and later on line 9 compared with a random number
. In the case that
, then it is updated considering the best value, line 10, and otherwise, it is not updated, line 12. Once all the solutions have been updated, each of them is cleaned up using the process explained in
Section 3.1. In the case of a new best value is obtained, in line 19, a local search operator is executed. This local search operator is detailed in the following section. Finally, the updated list of solutions
and the best solution
are returned. The pseudo-code is shown in Algorithm 2.
| Algorithm 2 Machine learning binarization operator (MLBO). |
- 1:
Function MLBO(, , , ) - 2:
Input , , - 3:
Output , - 4:
getAbsValueVelocities(, ) - 5:
getKmeansClustering(, K) - 6:
for (each in ) do - 7:
for (each in ) do - 8:
= getClusterProbability(, ) - 9:
ifthen - 10:
Update considering the best. - 11:
else - 12:
Do not update the item in - 13:
end if - 14:
end for - 15:
cleanSol() - 16:
end for - 17:
getBest() - 18:
if > then - 19:
execLocalSearch() - 20:
- 21:
end if - 22:
return,
|
3.3. Local Search Operator
According to
Figure 1, the local search operator is executed every time the metaheuristic finds a new best value. As input, the local search operator receives the new best values (
), and as a first stage, it uses it to obtain the items that belong and do not belong to
, line 4 of Algorithm 3. These two lists of items are iterated,
times, performing a swap without repetition, line 7 of Algorithm 3. Once the swap is carried out, the conditions are evaluated: it will improve the profit and that the weight of the knapsack is less than or equal to
. If both conditions are met, the
is updated by
, to finally return
.
| Algorithm 3 Local search. |
- 1:
Function LocalSearch() - 2:
Input
- 3:
Output
- 4:
getItems() - 5:
i = 0 - 6:
while (i < T) do - 7:
swap(, ) - 8:
if and then - 9:
- 10:
end if - 11:
i += 1 - 12:
end while - 13:
return
|
4. Results
This section details the experiments conducted with MLBO and cuckoo search metaheuristic, to determine the proposed algorithms effectiveness and contribution when applied to a -hard combinatorial problem. This specific version of MLBO that cuckoo search uses will be denoted by MLCSBO. The SUKP was chosen as a benchmark problem because it has been approached by several algorithms and is not trivial to solve in small, medium and large instances. However, it should be emphasized that the MLBO binarization technique is easily adaptable to other optimization algorithms. The optimization algorithm chosen was CS because it is a simple-to-parameterize algorithm that has been used to solve a wide variety of optimization problems.
Python 3.6 was used to build the algorithm, as well as a PC running Windows 10 with a Core i7 processor and 16 GB of RAM. To evaluate whether the difference is statistically significant, the Wilcoxon signed-rank test was used. Additionally, 0.05 was utilized as the significance level. The test is chosen in accordance with the methodology outlined in [
37,
38]. The Shapiro–Wilk normality test is used initially in this process. If one of the populations is not normal and both have the same number of points, the Wilcoxon signed-rank test is proposed to determine the difference. In the experiments, the Wilcoxon test was used to compare the MLCSBO results with the other variants or algorithms used in pairs. For comparison, the complete list of results was always used. Further, in the case of the experiment in
Section 4.2, since there are multiple comparisons and in order to correct for these comparisons, a post hoc test was performed with the Holm–Bonferroni correction. The statsmodels and scipy libraries of Python were used to develop the tests. Each instance was resolved 30 times in order to acquire the best value and average indicators. Additionally, the average time (in seconds) required for the algorithm to find the optimal solution is reported for each instance.
The first set of instances were proposed in [
39]. These instances have between 85 and 500 items and elements. These instances are characterized by two parameters. A first parameter
, which represents the density in the matrix, where
means the item
i includes to the
j element. A second parameter
, which represents the capacity ratio
C over the total weight of the elements. Then, a SUKP instance is named as
. The second group of instances was introduced in [
27], and in this case, they contain between 585 and 1000 items and elements. The form was built following the same previous structure.
4.1. Parameter Setting
The methods described in [
28,
40] was used to pick the parameters. To make an appropriate parameter selection, this methodology employs four metrics specified by the Equations (
4)–(
7). Values were generated using the instances 100_85_0.10_0.75, 100_100_0.15_0.85, and 85_100_0.10_0.75. Each parameter combination was run ten times. The collection of parameters that have been explored and selected is presented in
Table 1. To determine the configuration, the polygon area obtained from the four metric radar chart is calculated for each setting. The configuration that obtained the largest area was selected. In the case of the transition probabilities, only the probability of the third cluster was varied considering the values [0.4, 0.5], the rest of the values were considered constant.
- 1.
The difference in percentage terms between the best value achieved and the best known value:
- 2.
The percentage difference between the worst value achieved and the best value known:
- 3.
The percentage departure of the obtained average value from the best-known value:
- 4.
The convergence time used in the execution:
4.2. Insight into Binary Algorithm
The objective of this section is to determine the contribution of the MLCSBO operator and the local search operator in the final result of the optimization. To address this challenge, a random operator is designed that aims to replace MLBO in
Figure 1 with an operator that performs random transitions. In particular, two configurations are studied Random-05, which has a 50% chance of making a transition, and Random-03, which has a 30% chance of making a transition. Additionally, the configuration with and without a local search operator is studied. Each of the algorithms is evaluated for its performance without (NL) and with the local search operator.
The results are shown in
Table 2 and
Table 3 and
Figure 3. From
Table 2, it can be deduced that the best values obtained are for MLCSBO, which has the binarization mechanism based on k-means. The above for both indicators average and best value. When comparing MLCSBO-NL, note that MLCSBO-NL does not have the local search operator, with Random-03-NL and Random-05-NL, it is noted that MLCSBO-NL is more robust in the averages and best values. This allows evaluating the effect of incorporating k-means with respect to a random binarization operator in the optimization result. Furthermore, MLCSBO-NL works better than Random-03 and Random-05, where the latter incorporate the local search operator. On the other hand, when analyzing the contribution of the local operator, it is observed that each time it is incorporated generates an improvement in both the averages and the best values. First the Wilcoxon statistical test was applied, where MLCSBO is compared with the other variations. The statistical test indicates that the differences are significant between MLCSBO and the other variations analyzed. However, as there are multiple comparisons, the
p-values were corrected using the Holm–Bonferroni test. For this correction, the experiments of the operators Random-03 and Random-05 were treated as independent groups. In
Figure 3, we see that the highest time is for MLCSBO. In particular, Random-05-NL, which corresponds on average to the best performer, is 18.8% faster than MLCSBO. On the other hand, MLCSBO-NL which does not have the local search operator is 7.4% faster than MLCSBO.
In
Figure 3 and
Table 4, the
%-Gap, defined in Equation (
8), with respect to the best known value is compared of the different variants developed in this experiment. The comparison is made through box plots. In Figure, it is observed that MLCSBO has a more robust behavior than the rest, since it obtains better values and smaller dispersions than the other variants. On the other hand, the variants that obtain the worst performance correspond to those that have the random binarization operator and do not use the local search operator.
Additionally, the significance has been analyzed using the Wilcoxon test for the other variants. The details of the results are shown in
Table 5. In each cell of the table, the
p-values of best|average are written. In the table, it is observed that the difference of MLCSBO-NL with respect to the Random variants is not significant in the best indicator, but it is significant in the average indicator. The same goes for Random03 with respect to Random05. However, when analyzing Random03-NL with respect to Random05-NL, there is no significant difference in any of the indicators.
4.3. Algorithm Comparisons
This section compares MLCSBO performance to that of other algorithms that have tackled SUKP. Different forms of approximations were used in the comparative selection. A genetic algorithm (GA), in which uniform mutation, point cross-over, and roulette wheel selection operators were used. In particular, the cross-over probability was
and the mutation probability was selected at
. An artificial bee colony (ABC
, BABC), where the parameters used were a = 5 and limit defined as
, and a binary evolution technique (binDE) with factor
and crossover constant in 0.3, were adapted in [
32] to tackle the SUKP. In [
41], a weighted superposition attraction algorithm (bSWA), with parameters
,
, and
, is proposed to solve SUKP. Two variations gPSO and gPSO* of particle swam optimization algorithm were proposed in [
22]. In the case of gPSO, the init parameters used were
,
, and
. In the case of gPSO*,
and
. An artificial search agent with cognitive intelligence (intAgents) was proposed in [
42], where the parameters used are,
,
,
, and
. Finally, the DH-Jaya algorithm was designed in [
34], with parameters
,
, and
. In
Table 6 and
Table 7, the comparisons of the 30 smallest instances of SUKP are presented.
Table 8 shows the results for the 30 largest instances. In the latter case, only results were found for BABC and DH-Jaya reported in the literature.
Consider
Table 6 and
Table 7, which summarize the results for the 30 smallest instances. MLCSBO had the best value in 27 of the 30 cases. After that, GWOrbd has 16 best values, DH-Jaya has 11 best values, and GWOfbd also has 11 best values. It is possible that more than one algorithm gets the best value in some cases, in which case they are repeated in the accounting. This shows a good performance of the MLCSBO algorithm with respect to the other algorithms both in finding the best values as well as in reproducing these systematically. However, when the results for the 30 largest instances are analyzed, which are shown in
Table 8, it is observed that the good performance obtained by MLCSBO is not repeated. In the case of larger instances, DH-Jaya is observed to perform better than MLCSBO. In the case of the best value indicator, DH-Jaya obtains 22 best values and MLCSBO 10. Even more, so when the average indicator is compared, MLCSBO gets 4 best averages and DH-Jaya, 26. To make sure there was an exploit problem on the local search operator, in these cases
T was changed to 800, however, no improvements were obtained. The latter raises the suspicion that the decrease in performance in large cases is related to the exploration of the algorithm.
5. Conclusions
In this research, a hybrid k-means cuckoo search algorithm has been proposed. This hybrid binarization method applies the k-means technique to binarize the solutions generated by the cuckoo search algorithm. Additionally, in order for the procedure to be efficient, it was reinforced with a greedy initialization algorithm and with a local search operator. The proposed hybrid technique was used to solve cases of the set-union knapsack problem on a medium and large scale. The role of binarization and local search operators was investigated. To do this, a random operator was designed using two transition probabilities Random03 and Random05, which were compared in different situations. Finally, when the proposed approach is compared with several state-of-the-art methods, it is observed that the proposed algorithm is capable of improving the previous results in most cases. We highlight that the proposed algorithm uses a general binarization framework based on k-means and which can be easily adapt different metaheuristics and integrate with initiation and local search operators and in this particular case solve SUKP giving reasonable results.
According to the behavior of MLCSBO, it is observed that in the first 30 instances, it performed robustly, significantly outperforming the algorithms used in the comparison. However, in the 30 largest instances, their efficiency was not as clear when compared to the algorithms that had solved these instances. When it came to increasing the exploitation capacity of the local search operator, increasing T, there were no improvements. The above suggests three ideas for new lines of research. The first idea is to improve the search space exploration, this can be achieved using different solution initiation mechanisms, in MLBO, a greedy initialization operator was used. The second idea, thinking that the algorithm could be trapped in local optimum, the incorporation of a perturbation operator can be investigated. At this point, it can also consider the use of machine learning techniques such as the k-nearest neighborhood. Finally, the last idea aims to explore other binarization techniques based on other clustering algorithms or some other binarization strategies.