Next Article in Journal
Clioquinol Decreases Levels of Phosphorylated, Truncated, and Oligomerized Tau Protein
Next Article in Special Issue
DFT Quantum-Chemical Calculation of Thermodynamic Parameters and DSC Measurement of Thermostability of Novel Benzofuroxan Derivatives Containing Triazidoisobutyl Fragments
Previous Article in Journal
Hetero/Homo-Complexes of Sucrose Transporters May Be a Subtle Mode to Regulate Sucrose Transportation in Grape Berries
Previous Article in Special Issue
Substructural Approach for Assessing the Stability of Higher Fullerenes
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 22
Issue 21
10.3390/ijms222112067
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Cubic Octa-Carbon: Quantum-Chemical Design of Molecular Structure and Potential Way of Its Synthesis from Cubane

by
Denis V. Chachkov
1 and
Oleg V. Mikhailov
2,*
1
Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences–Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, Lobachevskii Street 2/31, 420111 Kazan, Russia
2
Analytical Chemistry, Certification and Quality Management Department, Kazan National Research Technological University, K. Marx Street 68, 420015 Kazan, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2021, 22(21), 12067; https://doi.org/10.3390/ijms222112067
Submission received: 22 September 2021 / Revised: 30 October 2021 / Accepted: 5 November 2021 / Published: 8 November 2021
(This article belongs to the Special Issue Simple Substances of Non-metals: Molecular Structures Modeling with Using DFT and More Advanced Methods of Quantum Chemistry)
Browse Figures
Versions Notes

Abstract

:
Quantum-chemical calculation of most important parameters of molecular and electronic structures of octa-carbon C8 having cubic form (bond lengths, bond and torsion angles) using CCSD(T)/QZVP and DFT B3PW91/QZVP methods, has been carried out. NBO analysis data and HOMO/LUMO images for this compound are presented, too. Good agreement was found between the structural data obtained using the above two quantum-chemical methods and, also, with corresponding experimental data. Also, the standard thermodynamic parameters of formation of cubic C8 considered here, and namely standard enthalpy ΔfH0(298K), entropy Sf0(298K) and Gibbs’ energy ΔfG0(298K) of formation for this compound were calculated. By using this data, a theoretically possible variant of the synthesis of this compound by dehydrogenation of cubane C8H8 is considered, and the thermodynamic characteristics of each of the four stages of this process have been calculated. It is noted that each of the four stages of this process is characterized by a very high (about 500 kJ/mol) enthalpy of activation, as a result of that, for their realization within a sufficiently short time, the use of appropriate catalysts is necessary.

1. Introduction

Carbon, alone, among all chemical elements is known to be the only one whose atoms’ number of valence orbitals, number of valence electrons and maximum possible coordination numbers of each coincide with each other. Due to this unique circumstance, it can form long homochain structures containing many hundreds and thousands of atoms. For this element, in addition to the allotropic modifications well and long known to all science—graphite and diamond—a very significant number of other varieties are known, such as carbyne, glassy carbon, various shapes of nanotubes, nanofibers, astralenes, numerous fullerenes (containing, in a molecule, between 60 and several hundred carbon atoms) and amorphous carbon [1,2,3,4,5,6,7,8,9,10]. At the beginning of the twenty-first century another unique modification of this chemical element was obtained—graphene, the structure of which can be considered as one plane of layered graphite, separated from its bulk crystal [1,11,12,13,14,15,16,17]. All these modifications of carbon contain a very significant (at least several dozen) number of atoms in their structural units; nevertheless, according to the data given in [1], there is quite a lot of information in the literature on allotropic modifications of carbon containing a small (less than 10) number of atoms. One of the most interesting modifications of this type is octa-carbon C8, for the molecular structure of which the cubic form seems to be the most probable. This substance can serve as a very useful precursor for the organic synthesis of a number of cubane derivatives, for example, polycyclic framework compounds containing articulated cubane fragments; seems to be very promising for use in a number of branches of technology, in particular, as “building blocks” for new nanodevices, which, in turn, can be implemented to create digital memory systems; the possibility of using it in the creation of catalysts for various physicochemical processes is not excluded. The synthesis of such a compound, however, has not yet been experimentally carried out; though there are many works devoted to the theoretical calculation of its molecular and/or electronic structure, carried out mainly using DFT, HF, or even semiempirical methods (see, in particular, [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]). In this regard, the purpose of this work is to perform a quantum-chemical calculation of the molecular structure of this compound by a more rigorous ab initio quantum-chemical method, namely CCSD (T)/QZVP, as well as to theoretically consider the possibility of its synthesis based on a chemical compound that also has cubic structure, namely, cubane C8H8.

2. Calculation Method

The quantum-chemical calculation of molecular structures of octa-carbon molecule having C8 composition was carried out using the CCSD(T)/QZVP method, combining the common QZVP extended quadruple zeta split-valence basis set [33,34] and the coupled cluster method, using both single and double substitutions, including triple excitation non-iterative CCSD(T) [35,36,37,38]. The given method is one of the most accurate and reliable quantum-chemical methods for calculating the molecular structures of various chemical compounds (in particular, p-elements) and considers electron correlation very well. Along with this, for comparison, we also calculated the parameters of the molecular structure of C8 using the much less time-consuming DFT method, namely DFT B3PW91/QZVP level, which, combined with QZVP and B3PW91 functionality [39,40] and according to data in [41], has minimal values of so-called “normal error” in comparison with other variants of the DFT method. Calculations were performed with the Gaussian09 program package [42]. To visualize the results of our calculations, we used the ChemCraft software, Version 1.8.
The initial structures of the C8 molecules for carrying out quantum-chemical calculations are shown in Scheme 1:
The choice of these six structures was determined by the next two factors: firstly, of the valence possibilities of the carbon atom (which can bind with one, two, three, or four neighboring atoms by means of three chemical bonds, according to the exchange mechanism of chemical bond formation); secondly, by these structures’ having the greatest typicality as compared with other structures of eight atoms. That is why, in particular, the hexagonal bipyramid, the dodecahedron and plane bicyclic structure containing articulated six-numbered and four-numbered rings, were not included in the number of initial structures because, here, as well as in other permissible eight-atomic structures, each carbon atom’s being bound to neighboring carbon atoms by exactly four chemical bonds is impossible to achieve. The correspondence of the found stationary points to energy minima was proved, in all cases, by calculating the second derivatives of the energies with respect to atoms’ coordinates; all equilibrium structures corresponding to the minima on the potential energy surfaces have only positive frequencies.
Calculations of the structural parameters of the intermediates and transition states of the theoretically possible reaction for the production of C8, and namely, the reaction of the stepwise dehydrogenation of cubane C8H8, were carried out using the B3PW91/QZVP method, since the use of the coupled-cluster method, CCSD(T)/QZVP, to solve this problem would require very large time and energy costs, far beyond our technical capabilities. In all cases, frequencies of normal vibrations were calculated; in the case of transient states, the first frequency was imaginary and corresponded to the motion of the atoms involved in the reaction. To confirm the correspondence of the found transition states to the studied reaction from each transition state, a descent towards the reagents and reaction products was carried out (IRC procedure in Gaussian09). Of note is that, at the second stage of the dehydrogenation process (i.e., when the second hydrogen molecule is split off), the reaction could already only proceed at those carbon atoms that are chemically bonded to those in C8H6 molecules deprived of hydrogen atoms. The transition state of the dehydrogenation reaction, in the formation of which hydrogen molecules would be split off from those carbon atoms that were not linked by the above-mentioned chemical bonds, was not found during the calculations.
The values of the standard thermodynamic characteristics of the carbon-containing compounds under study were calculated using the G4 method described, in detail, in [43]. All quantum-chemical calculations were carried out in the Joint Supercomputer Center of the Russian Academy of Sciences-Branch of Federal Scientific Center ”Scientific Research Institute for System Analysis of the RAS” (http://www.jscc.ru).

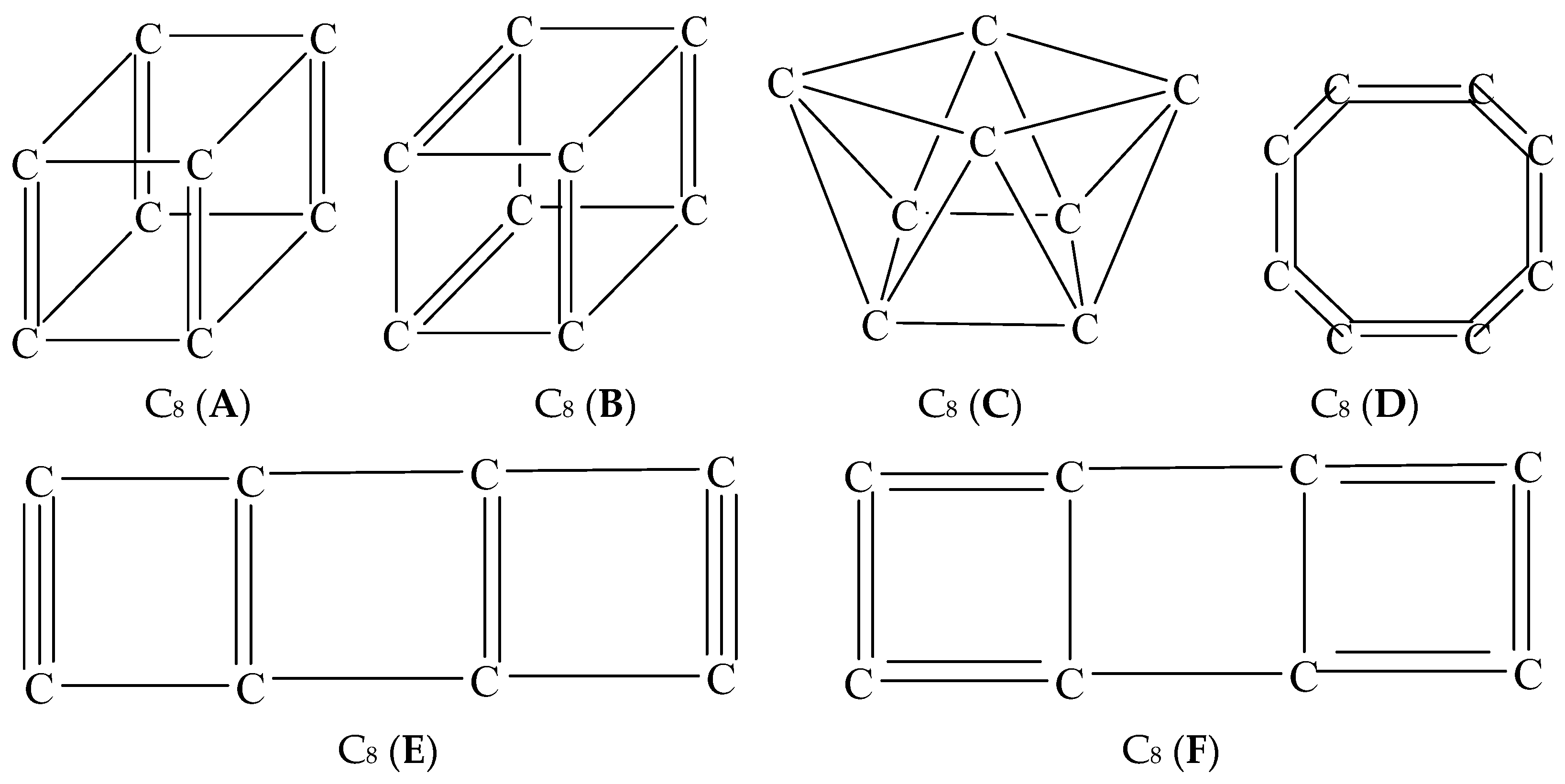
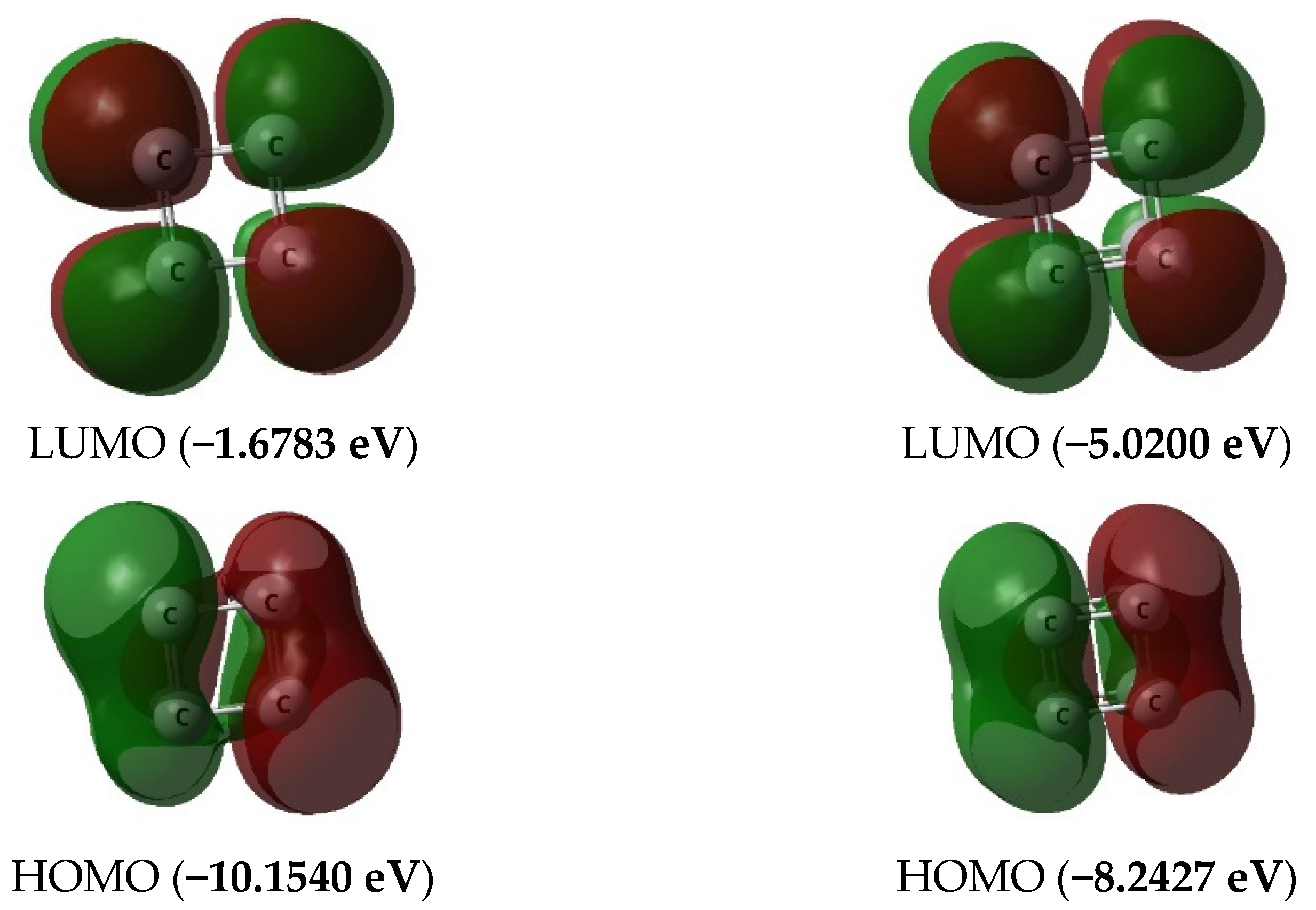
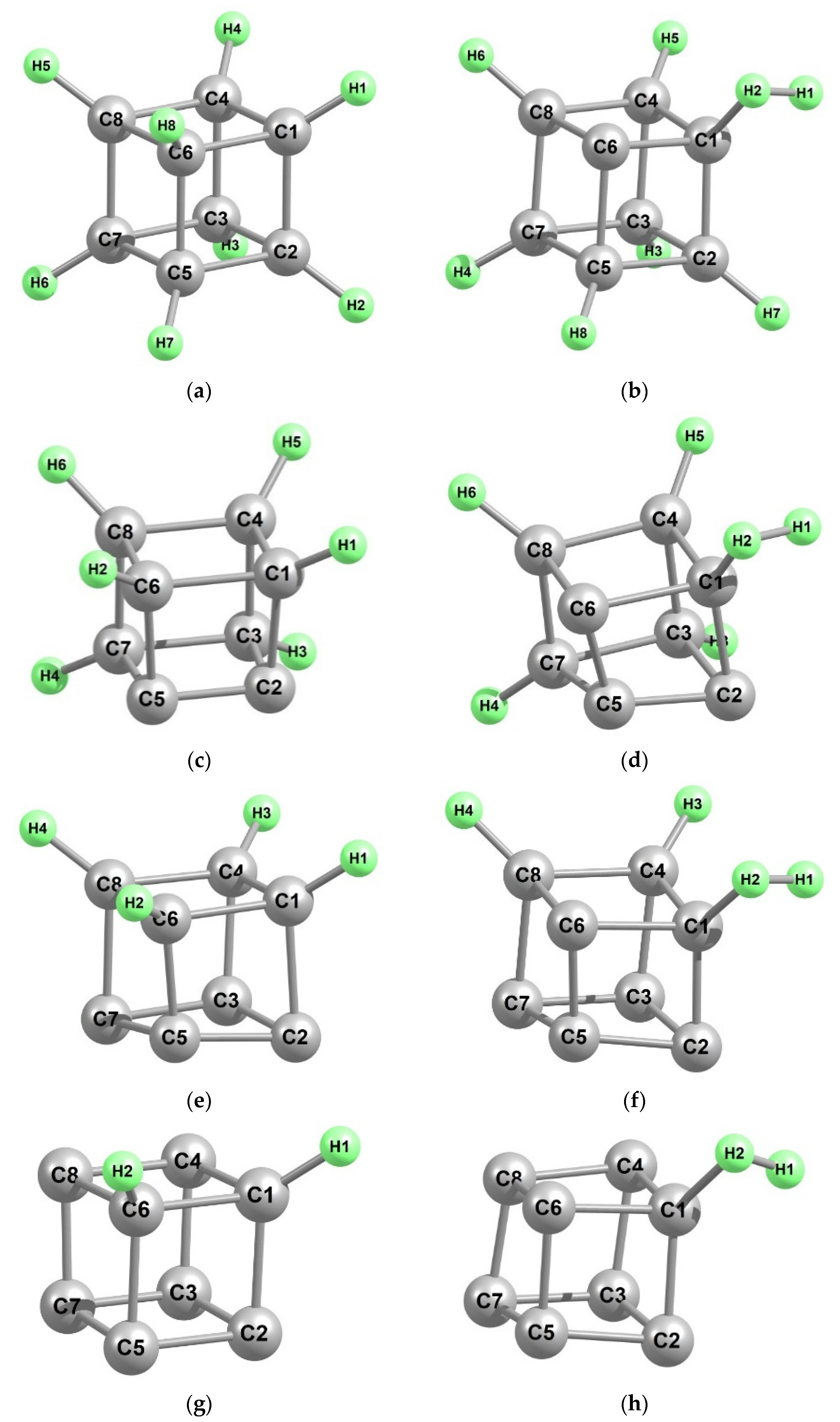
3. Results and Discussion

According to the results of our calculations, the most stable of these six structures of octa-atomic carbon molecule mentioned above, is C8 (A), in the form of the cube. The image of the molecular structure of this compound calculated by CCSD(T)/QZVP method is shown in Figure 1.
The geometric parameters of this molecular structure calculated with the given methods (bond lengths, bond angles and some torsion angles) are presented in Table 1. As can be seen from these data, quantitatively, the values of similar parameters are very close to each other (the difference between these two structures’ bond lengths between their carbon atoms is no more than 2 pm, and, between their bond and torsion (dihedral) angles, no more than 0.4°). However, there is a very clear qualitative difference between the CCSD(T)/QZVP and DFT B3PW91/QZVP structures: in the former, the bond lengths and angles between carbon atoms are generally not the same (although some of them coincide), whereas, in the latter, they are the same (Table 1). The reasons for this qualitative difference between the results of calculations by the CCSD(T)/QZVP and DFT B3PW91/QZVP methods are most likely associated with the Jahn–Teller effect, and namely, the instability of a highly symmetric structure containing degenerate states of electrons to deformations that lower its symmetry. The point symmetry group D4h was obtained during the calculation by the DFT B3PW91/QZVP method; in the course of the calculations using the CCSD(T)/QZVP method we obtained the point symmetry group C1, i.e., a lack of symmetry. Note, in this connection, that within the CCSD(T)/QZVP molecular structure itself the maximum difference between the lengths of carbon–carbon bonds is 0.5 pm, between the bond angles is 0.7°, and between torsion angles is 0.4°; compared with the values of these parameters themselves, these differences look very insignificant.
The images of the highest occupied (HOMO) and lowest vacant (LUMO) molecular orbitals obtained using the above quantum chemical methods are presented in Figure 2. As can be seen therein, the forms of the given MOs obtained by these different methods are very similar to each other, wherein, however, the energies of these MOs are very different from each other. Most likely this difference is associated with a well-known feature of the DFT methods, and namely—due to some approximations that simplify the calculation of the electron correlation—the underestimation, in particular, of the difference in the HOMO-LUMO energies. That is why the data of the coupled-cluster method (CCSD), in the given case, should be considered much more reliable.
NBO analysis data of the C8 structures within each of these methods are presented in Table 2. As follows from these data, in the case of using the CCSD(T)/QZVP method, a weakly pronounced polarization of carbon atoms occurs, some of which carry an insignificant (about 0.01 electron charge unit (ē)) positive charge, and some of which carry the same slight negative charge. This feature, as was noted above, is also most likely a result of the Jahn–Teller effect. In the DFT B3PW91/QZVP calculations, the charges on each of the eight carbon atoms, with an accuracy of four significant digits after the decimal, are zero (Table 2).
According to our calculations of the standard thermodynamic parameters of the isobaric process (the standard enthalpy of formation ΔfH0(298K), the standard entropy of formation S0f (298K), and the standard Gibbs energy of formation ΔfG0(298K)) by the G4 method for the C8 molecule, their values are 1871.6 kJ/mol, 348.7 J/mol·K and 1767.6 kJ/mol, respectively. As it can be seen from these data, ΔfH0(298K) and ΔfG0(298K) values are positive (and very significant in modulus), and cannot be obtained for the most stable modification of elemental carbon, graphite, according to the classical canons of thermodynamics. In this connection, it seems advisable to consider the possibility of obtaining cubic octa-carbon in some other way, and one of the most promising methods is the stepwise dehydrogenation of the saturated polycyclic hydrocarbon, cubane C8H8, which was first obtained more than 50 years ago [44,45] and, by its own the spatial structure, is the compound closest to octa-carbon, according to the general scheme shown in Figure 3.
In accordance with calculation by the DFT B3PW91/QZVP method, the carbon–carbon bond lengths in the cubane molecule are 156.1 pm, the carbon–hydrogen bonds are 108.7 pm, the bond angles are 90.0° and 125.2°, for CCC and CCH, respectively. These values are in very good agreement with the experimental values of these parameters found in [46,47] (157.1 pm, 108.2 pm, 90.0° and 125.0°, respectively). The noted good agreement allows us to assert that, using this method, it is possible to adequately describe the specificity of the dehydrogenation reaction of C8H8 to C8, including the molecular structures of intermediates and transient states TSn (so-called “activated complexes”). The indicated molecular structures are shown in Figure 4, some of their geometric parameters and negative frequency characteristic of the transient states TSn are presented in Table 3 and in Supplementary Materials. As can be seen, the formation of any of the four TSn transient states is accompanied by a rather pronounced deformation of the cubic structure of the initial C8H8; at the same time, interestingly, in the series TS1–TS2–TS3–TS4, the carbon–carbon bond lengths, as compared to those in cubane, first decrease, then increase, then decrease again and increase again; a similar situation takes place for the carbon–hydrogen bond lengths. The interatomic distances (H1H2), on the contrary, in the same row decrease monotonically (Table 3). In connection with this deformation, the change in the bond angles formed by carbon atoms located in the adjacent vertices of the hexahedron (distorted cube) also looks quite natural, one part of which becomes greater than 90°, while the other part is less than 90°, although the deviation in the values of both these and of other angles from 90° is, as a rule, not more than 5°.
The decomposition reaction of cubane, according to the C8H8 → C8 + 4H2 general scheme in both the solid and the gas phase, proceeds with an increase in the total volume of the reaction system (due to the formation of gaseous hydrogen), and therefore, according to the classical canons of thermodynamics, should be accompanied by an increase in the entropy of the reaction system. On the other hand, this reaction is endothermic (according to our calculation, its standard enthalpy is 1325.6 kJ, its standard entropy is 514.1 J/K, and its standard Gibbs’s energy is 1172.4 kJ), so its implementation is provided by the entropy factor. Using the classical Gibbs—Helmholtz equation for the isobaric process ΔrG0(T) = ΔrH0(298 K)–TΔrS0(298 K) (where ΔrH0(298 K) and ΔrS0(298 K) are the changes in enthalpy and entropy as a result of a chemical process referred to standard conditions, T is the process temperature in K, ΔrG0(T) is the dependence of the Gibbs’s free energy on the temperature T), it is easy to find that this reaction can proceed at a temperature T ≥ 2578.5 K. A similar situation is observed for individual stages of this reaction with the sequential formation of compounds C8H6, C8H4, C8H2 and C8 (see Figure 3).
As can be seen from the data presented in Figure 3b and Table 3, each of the four successive stages of the cubane dehydrogenation reaction is characterized by high values of activation enthalpies and, at the same time, rather low values of activation entropies, as a result of which the energy barriers for the formation of transient states are very significant, wherein the realization of each of these stages is due to the entropy factor, so that all of them can be realized only at sufficiently high temperatures (more than 2000 K). However, even at such high temperatures, the rates of these reactions are likely to be insufficient for their practical implementation within a sufficiently short time, and if so, then in order to increase them, it will be necessary to search for appropriate catalysts for these very reactions.

4. Conclusions

As it can be seen from the above, both the used independent quantum-chemical calculation methods—CCSD(T)/QZVP and DFT B3PW91/QZVP—unequivocally indicate the existence of cubic octa-carbon as the most stable of all possible carbon modifications having a C8 composition, wherein the quantitative parameters of the molecular structure (bond lengths, bond and torsion (dihedral) angles) of this carbon modification, calculated using these methods, turn out to be very close to each other, though, qualitatively, they are different; according to the data of the first of these methods, as similar parameters are different (though insignificantly), but, according to the second, they are the same (Table 1). Taking into account the fact that, in reality, all carbon atoms in the cubic structure of C8 should most likely be equivalent to each other, we can expect that the real structure of cubic octa-carbon C8 should be some kind of intermediate variant between the structures obtained as a result of our quantum-chemical calculations using the above independent methods. The assessment of the thermodynamic characteristics of the reaction carried out in this article (from the use of which, in principle, cubic octa-carbon can be obtained, namely, the dehydrogenation of cubane C8H8) indicates the reality of such a reaction, albeit under rather harsh conditions (i.e., at a high temperature) and with the obligatory use of a catalyst to ensure its flow at a sufficiently high rate. The goal, now, is to confirm all this experimentally.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/ijms222112067/s1.

Author Contributions

Conceptualization, O.V.M.; Methodology, O.V.M. and D.V.C.; Software, D.V.C.; Validation, O.V.M. and D.V.C.; Formal Analysis, O.V.M. and D.V.C.; Investigation, O.V.M. and D.V.C.; Resources, D.V.C.; Data Curation, D.V.C.; Writing-Original Draft Preparation, O.V.M. and D.V.C.; Writing—Review and Editing, O.V.M.; Visualization, O.V.M. and D.V.C.; Supervision, O.V.M.; Project Administration, O.V.M.; Funding Acquisition, D.V.C. All authors have read and agreed to the published version of the manuscript.

Funding

Contribution of author Chachkov D.V. was funded by the state assignment to the Federal State Institution “Scientific Research Institute for System Analysis of the Russian Academy of Sciences” for scientific research (http://www.jscc.ru).

Institutional Review Board Statement

Not applicable.

Acknowledgments

All quantum-chemical calculations were performed at the Joint Supercomputer Center of Russian Academy of Sciences—Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” that is acknowledgement for technical support. Also, this study was carried using the equipment of the Center of Collective Use “Nanomaterials and Nanotechnology” of the Kazan National Research Technological University.

Conflicts of Interest

The authors declare that they have no conflict of interest, financial or otherwise.

References

  1. Kharisov, B.I.; Kharissova, O.V. Carbon Allotropes: Metal-Complex Chemistry, Properties and Applications; Springer Nature AG: Cham, Switzerland, 2019; ISBN 978-3-030-03504-4. [Google Scholar] [CrossRef]
  2. Belenkov, E.A.; Mavrinsky, V.V. Crystal structure of a perfect carbyne. Crystallogr. Rep. 2008, 53, 83–87. [Google Scholar] [CrossRef]
  3. Pan, B.; Xiao, J.; Li, J.; Liu, P.; Wang, C.; Yang, G. Carbyne with finite length: The one-dimensional sp carbon. Sci. Adv. 2015, 1, e1500857. [Google Scholar] [CrossRef] [Green Version]
  4. Shi, L.; Rohringer, P.; Suenaga, K.; Niimi, K.S.Y.; Kotakoski, J.; Meyer, J.; Peterlik, H.; Wanko, M.; Jahangirov, S.; Rubio, A.; et al. Confined linear carbon chains as a route to bulk carbyne. Nat. Mater. 2016, 15, 634–639. [Google Scholar] [CrossRef]
  5. Schueller, O.J.A.; Brittain, S.T.; Whitesides, G.M. Fabrication of glassy carbon microstructures by pyrolysis of microfabricated polymeric precursors. Adv. Mater. 1997, 9, 477–480. [Google Scholar] [CrossRef]
  6. Jorio, A.; Dresselhaus, M.S.; Dresselhaus, G.; Gogotsi, Y. Carbon Nanotubes: Advanced Topics in the Synthesis, Structure, Properties and Applications, 1st ed; Springer: Berlin, Germany, 2008; ISBN 978-3-540-72864-1. [Google Scholar] [CrossRef]
  7. Tibbetts, G.; Lake, M.; Strong, K.; Rice, B. A review of the fabrication and properties of vapor-grown carbon nanofiber/polymer composites. Compos. Sci. Technol. 2007, 67, 1709–1718. [Google Scholar] [CrossRef]
  8. Khamatgalimov, A.; Kovalenko, V. Substructural Approach for Assessing the Stability of Higher Fullerenes. Int. J. Mol. Sci. 2021, 22, 3760. [Google Scholar] [CrossRef]
  9. McCulloch, D.G.; McKenzie, D.R.; Goringe, C.M. Ab initio simulations of the structure of amorphous carbon. Phys. Rev. 2000, B61, 2349. [Google Scholar] [CrossRef]
  10. Robertson, J. Diamond-like amorphous carbon. Mater. Sci. Eng. R Rep. 2002, 37, 129–281. [Google Scholar] [CrossRef] [Green Version]
  11. Katsnelson, M.; Novoselov, K. Graphene: New bridge between condensed matter physics and quantum electrodynamics. Solid State Commun. 2007, 143, 3–13. [Google Scholar] [CrossRef] [Green Version]
  12. Geim, A.K.; Novoselov, K. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
  13. Ghuge, A.D.; Shirode, A.R.; Kadam, V.J. Graphene: A comprehensive review. Curr. Drug Targets 2017, 18, 724–733. [Google Scholar] [CrossRef]
  14. Wu, J.; Pisula, W.; Mullen, K. Graphenes as potential material for electronics. Chem. Rev. 2007, 107, 718–747. [Google Scholar] [CrossRef]
  15. Yu, X.; Cheng, H.; Zhang, M.; Zhao, Y.; Qu, L.; Shi, G. Graphene-based smart materials. Nature Rev. Mater. 2017, 2, 17046. [Google Scholar] [CrossRef]
  16. Novoselov, K.S. Technology: Rapid progress in producing graphene. Nature 2014, 505, 291. [Google Scholar] [CrossRef] [Green Version]
  17. Van den Brink, J. Graphene: From strength to strength. Nat. Nanotechnol. 2007, 2, 199–201. [Google Scholar] [CrossRef] [PubMed]
  18. Krishnan, R.; Binkley, J.S. Structure, stability, and fragmentation of small carbon clusters. J. Chem. Phys. 1987, 87, 2191–2197. [Google Scholar]
  19. Martin, J.M.L.; Francois, J.P.; Gijbels, R. Ab initio study of the infrared spectra of linear Cn clusters (n = 6–9). J. Chem. Phys. 1990, 93, 8850–8861. [Google Scholar] [CrossRef]
  20. Martin, J.M.L.; Francois, J.P.; Gijbels, R. A critical comparison of MINDO/3, MNDO, AM1, and PM3 for a model problem: Carbon clusters C2-C10. An ad hoc reparametrization of MNDO well suited for the accurate prediction of their spectroscopic constants. J. Comput. Chem. 1991, 12, 52–70. [Google Scholar] [CrossRef]
  21. Parasuk, V.; Almlöf, J. The electronic and molecular structure of carbon clusters: C8 and C10. Theor. Chim. Acta 1992, 83, 227–237. [Google Scholar] [CrossRef]
  22. Hutter, J.; Luethi, H.P.; Diederich, F. Structures and vibrational frequencies of the carbon molecules C2-C18 calculated by density functional theory. J. Am. Chem. Soc. 1994, 116, 750–756. [Google Scholar] [CrossRef]
  23. Tseng, S.; Shen, M.; Yu, C. A MNDO study of carbon clusters with specifically fitted parameters. Theor. Chim. Acta 1995, 92, 269–280. [Google Scholar] [CrossRef]
  24. Martin, J.M.L.; El-Yazal, J.; Francois, J.-P. Structure and vibrational spectra of carbon clusters Cn (n = 2–10, 12, 14, 16, 18) using density functional theory including exact exchange. Chem. Phys. Lett. 1995, 242, 570–579. [Google Scholar] [CrossRef]
  25. Martin, J.M.L.; Taylor, P.R. Structure and Vibrations of Small Carbon Clusters from Coupled-Cluster Calculations. J. Phys. Chem. 1996, 100, 6047–6056. [Google Scholar] [CrossRef]
  26. Wang, S.L.; Rittby, C.M.L.; Graham, W.R.M. Detection of cyclic carbon clusters. II. Isotopic study of the 𝜈12(e𝑢) mode of cyclic C8 in solid Ar. J. Chem. Phys. 1997, 107, 7025–7033. [Google Scholar] [CrossRef]
  27. Nyrönen, T.H.; Reijo Suontamo, R. An MO study of neutral C high-symmetry clusters. Chem. Phys. Lett. 1997, 280, 227–232. [Google Scholar] [CrossRef]
  28. Jones, R.O. Density functional study of carbon clusters C2n (2 ≤ n ≤ 16). I. Structure and bonding in the neutral clusters. J. Chem. Phys. 1999, 110, 5189–5200. [Google Scholar] [CrossRef] [Green Version]
  29. Sharapa, D.; Hirsch, A.; Meyer, B.; Clark, T. Cubic C8: An Observable Allotrope of Carbon? ChemPhysChem 2015, 16, 2165–2171. [Google Scholar] [CrossRef] [Green Version]
  30. Varandas, A.J.C. Even numbered carbon clusters: Cost-effective wavefunction-based method for calculation and automated location of most structural isomers. Eur. Phys. J. D 2018, 72, 134. [Google Scholar] [CrossRef]
  31. Rocha, C.M.R.; Li, J.; Varandas, A.J.C. Difficulties and Virtues in Assessing the Potential Energy Surfaces of Carbon Clusters via DMBE Theory: Stationary Points of Cκ (κ = 2−10) at the Focal Point. J. Phys. Chem. A 2019, 123, 3121–3130. [Google Scholar] [CrossRef]
  32. Chaglayan, B.; Huran, A.W.; Amor, N.B.; Brumas, V.; Evangelisti, S.; Leininger, T. Spherical aromaticity and electron delocalization in C8 and B4N4 cubic systems. Theor. Chem. Acc. 2019, 138, 5. [Google Scholar] [CrossRef]
  33. Schaefer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
  34. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
  35. Pople, A.; Krishnan, R.; Schlegel, H.B.; Binkley, J.S. Electron Correlation Theories and Their Application to the Study of Simple Reaction Potential Surfaces. Int. J. Quantum Chem. 1978, 14, 545–560. [Google Scholar] [CrossRef]
  36. Bartlett, R.J.; Purvis, G.D., III. Many-body perturbation-theory, coupled-pair many-electron theory, and importance of quadruple excitations for correlation problem. Int. J. Quantum Chem. 1978, 14, 561–581. [Google Scholar] [CrossRef]
  37. Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model—The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
  38. Pople, J.A.; Head-Gordon, M.; Krishnan, R. Quadratic configuration interaction—A general technique for determining electron correlation energies. J. Chem. Phys. 1987, 87, 5968–5975. [Google Scholar] [CrossRef]
  39. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Revs. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
  40. Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Revs. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [Green Version]
  41. Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef]
  42. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.01; Gaussian Inc.: Wallingford, UK, 2009. [Google Scholar]
  43. Ochterski, J.W. Thermochemistry in Gaussian; Gaussian Inc.: Wallingford, UK, 2000. [Google Scholar]
  44. Eaton, P.E. Cubanes: Starting materials for the chemistry of the 1990s and the new century. Angew. Chem. Int. Ed. 1992, 31, 1421–1436. [Google Scholar] [CrossRef]
  45. Biegasiewicz, K.F.; Griffiths, J.R.; Savage, G.P.; Tsanaktsidis, J.; Priefer, R. Cubane: 50 Years Later. Chem. Rev. 2015, 115, 6719–6745. [Google Scholar] [CrossRef] [PubMed]
  46. Hedberg, L.; Hedberg, K.; Eaton, P.E.; Nodari, N.; Robiette, A.G. Bond lengths and quadratic force field for cubane. J. Am. Chem. Soc. 1991, 113, 1514–1517. [Google Scholar] [CrossRef]
  47. Schubert, W.; Yoshimine, M.; Pacansky, J. Ab initio self-consistent field calculations on the structure of cubane, cubene, and the cubyl radical. J. Phys. Chem. 1981, 85, 1340–1342. [Google Scholar] [CrossRef]
Ijms 22 12067 sch001 550
Scheme 1. Potential molecular structures of octa-carbon: C8 (A) and C8 (B)—cubes, C8 (C)—square antiprism, C8 (D)—octagon, C8 (E) and C8 (F)—a combination of three rectangles with four common vertices.
Scheme 1. Potential molecular structures of octa-carbon: C8 (A) and C8 (B)—cubes, C8 (C)—square antiprism, C8 (D)—octagon, C8 (E) and C8 (F)—a combination of three rectangles with four common vertices.
Ijms 22 12067 sch001
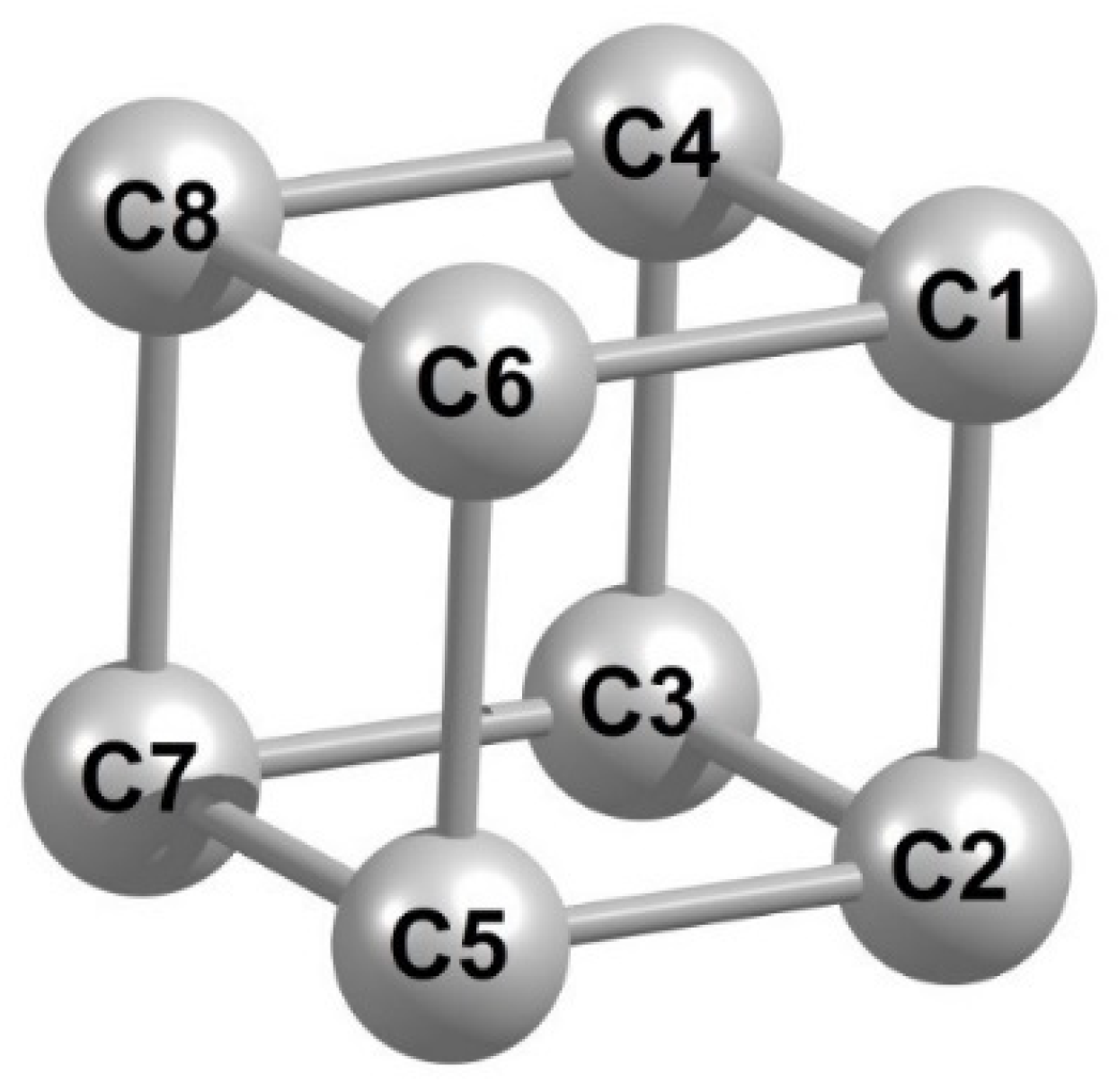
Ijms 22 12067 g001 550
Figure 1. Molecular structure of theoretically possible polymorphic modification of elemental carbon C8 according to data of quantum-chemical calculation with using CCSD(T)/QZVP method.
Figure 1. Molecular structure of theoretically possible polymorphic modification of elemental carbon C8 according to data of quantum-chemical calculation with using CCSD(T)/QZVP method.
Ijms 22 12067 g001
Ijms 22 12067 g002 550
Figure 2. The images of the highest occupied (HOMO) and lowest vacant (LUMO) molecular orbitals obtained by CCSD(T)/QZVP (left) and DFT B3PW91/QZVP (right).
Figure 2. The images of the highest occupied (HOMO) and lowest vacant (LUMO) molecular orbitals obtained by CCSD(T)/QZVP (left) and DFT B3PW91/QZVP (right).
Ijms 22 12067 g002
Ijms 22 12067 g003 550
Figure 3. Scheme of the probable dehydrogenation reaction of cubane C8H8 with the formation of cubic octa-carbon C8 (a) and the energetic profile of this reaction (b) (TS1, TS2, TS3, TS4 are various transient states).
Figure 3. Scheme of the probable dehydrogenation reaction of cubane C8H8 with the formation of cubic octa-carbon C8 (a) and the energetic profile of this reaction (b) (TS1, TS2, TS3, TS4 are various transient states).
Ijms 22 12067 g003
Ijms 22 12067 g004 550
Figure 4. The images of molecular structures of cubane C8H8 (a), intermediates C8H6 (c), C8H4 (e), C8H2 (g) and transient states TS1 (b), TS2 (d), TS3 (f), TS4 (h) of reactions of its dehydrogenation.
Figure 4. The images of molecular structures of cubane C8H8 (a), intermediates C8H6 (c), C8H4 (e), C8H2 (g) and transient states TS1 (b), TS2 (d), TS3 (f), TS4 (h) of reactions of its dehydrogenation.
Ijms 22 12067 g004
Table
Table 1. Geometric parameters of the molecular structure of C8 molecule calculated by the CCSD(T)/QZVP and DFT B3PW91/QZVP calculation methods.
Table 1. Geometric parameters of the molecular structure of C8 molecule calculated by the CCSD(T)/QZVP and DFT B3PW91/QZVP calculation methods.
ParameterCalculated byParameterCalculated by
CCSD(T)/QZVPB3PW91/QZVPCCSD(T)/QZVPB3PW91/QZVP
Carbon–Carbon Bond Lengths, pm
(C1C4)148.3146.7(C7C5)148.0146.7
(C4C8)148.0146.7(C5C2)148.6146.7
(C8C6)148.2146.7(C1C2)148.3146.7
(C6C1)148.1146.7(C3C4)148.3146.7
(C2C3)148.3146.7(C5C6)148.5146.7
(C3C7)148.5146.7(C7C8)148.5146.7
Bond Angles, deg
(C1C4C8)90.490.0(C5C6C1)90.490.0
(C4C8C6)89.690.0(C6C1C2)89.890.0
(C8C6C1)90.390.0(C6C5C7)89.990.0
(C6C1C4)89.790.0(C5C7C8)90.290.0
(C2C5C7)89.990.0(C7C8C6)89.890.0
(C5C7C3)90.390.0(C8C6C5)90.190.0
(C1C2C3)90.290.0(C7C8C4)89.890.0
(C2C3C4)89.890.0(C8C4C3)90.490.0
(C3C4C1)90.290.0(C4C3C7)89.790.0
(C6C1C4)89.790.0(C3C7C8)90.190.0
(C1C2C5)90.390.0(C7C8C4)89.890.0
(C2C5C6)89.990.0(C8C4C3)90.490.0
Selected Torsion (Dihedral) Angles, deg
(C1C4C8C6)–0.20.0(C1C2C7C8)0.00.0
(C1C4C3C2)0.40.0(C4C6C5C3)0.20.0
(C1C2C5C6)0.00.0(C1C2C3C7)–90.1–90.0
(C2C3C7C5)–0.20.0(C2C5C6C8)90.390.0
(C5C6C8C7)–0.40.0(C5C6C8C4)–90.2–90.0
(C3C4C8C7)0.20.0(C7C8C4C1)–90.0–90.0
Table
Table 2. NBO analysis data for the cubic octa-carbon C8 calculated by the CCSD(T)/QZVP and DFT B3PW91/QZVP methods.
Table 2. NBO analysis data for the cubic octa-carbon C8 calculated by the CCSD(T)/QZVP and DFT B3PW91/QZVP methods.
Calculation
Method		Effective Charge on Carbon Atoms, in Units of Electron Charge (ē)
C1C2C3C4C5C6C7C8
CCSD(T)/QZVP−0.0104+0.0099−0.0098+0.0102−0.0097+0.0102+0.0099−0.0103
B3PW91/QZVP0.00000.00000.00000.00000.00000.00000.00000.0000
Table
Table 3. Enthalpy of activation (ΔH#, kJ/mol), Gibbs’s energy of activation (ΔG#, kJ/mol), entropy of activation (ΔS#, J/mol·K) under standard conditions, standard enthalpy of reaction (ΔHr, kJ), the standard Gibbs’s energy of the reaction (ΔGr, kJ), the standard entropy of the reaction (ΔSr, J/K), some geometric parameters and negative frequency characteristic of the transient states TSn (n = 1–4, see Figure 3 and Figure 4) of the dehydrogenation process cubane calculated by the DFT B3PW91/QZVP method.
Table 3. Enthalpy of activation (ΔH#, kJ/mol), Gibbs’s energy of activation (ΔG#, kJ/mol), entropy of activation (ΔS#, J/mol·K) under standard conditions, standard enthalpy of reaction (ΔHr, kJ), the standard Gibbs’s energy of the reaction (ΔGr, kJ), the standard entropy of the reaction (ΔSr, J/K), some geometric parameters and negative frequency characteristic of the transient states TSn (n = 1–4, see Figure 3 and Figure 4) of the dehydrogenation process cubane calculated by the DFT B3PW91/QZVP method.
Transition Stage (TSn)TS1TS2TS3TS4
ΔH#
ΔG#
ΔS#		534.4
527.5
23.0		506.9
504.5
8.0		478.2
476.3
6.5		448.2
446.5
5.9
ΔHr
ΔGr
ΔSr		314.8
271.4
145.6		337.3
298.6
129.6		326.2
287.8
128.8		347.3
314.5
110.1
r(H1H2), pm90.990.485.284.3
r(C1H1), pm140.2134.3144.4137.6
r(C1H2), pm125.5124.4132.8134.5
r(C2H2), pm197.2209.4218.9219.2
r(C1C2), pm155.0160.7157.7154.4
∠H1C1H2, deg39.640.735.536.1
∠H2C1C2, deg88.793.797.498.5
ν1, cm−1−1569−1258−1144−1022
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Chachkov, D.V.; Mikhailov, O.V. Cubic Octa-Carbon: Quantum-Chemical Design of Molecular Structure and Potential Way of Its Synthesis from Cubane. Int. J. Mol. Sci. 2021, 22, 12067. https://doi.org/10.3390/ijms222112067

AMA Style

Chachkov DV, Mikhailov OV. Cubic Octa-Carbon: Quantum-Chemical Design of Molecular Structure and Potential Way of Its Synthesis from Cubane. International Journal of Molecular Sciences. 2021; 22(21):12067. https://doi.org/10.3390/ijms222112067

Chicago/Turabian Style

Chachkov, Denis V., and Oleg V. Mikhailov. 2021. "Cubic Octa-Carbon: Quantum-Chemical Design of Molecular Structure and Potential Way of Its Synthesis from Cubane" International Journal of Molecular Sciences 22, no. 21: 12067. https://doi.org/10.3390/ijms222112067

APA Style

Chachkov, D. V., & Mikhailov, O. V. (2021). Cubic Octa-Carbon: Quantum-Chemical Design of Molecular Structure and Potential Way of Its Synthesis from Cubane. International Journal of Molecular Sciences, 22(21), 12067. https://doi.org/10.3390/ijms222112067

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop