The research study was primarily dependent on computer simulations in EnergyPlus Version 8 to replicate the typical Malawian urban residential building’s thermal behaviour and then study the impacts of various envelope configurations on the thermal comfort conditions registered in the building. A total of seven building envelope features were identified including Floor Thickness (FT), Wall R-value (WR), Roof R-value (RR), Glazing Insulation (GL), Ventilation Bricks Infiltration (BI), Wall Transparency Ratio (TR) and Window Overhang (WO). These features were studied at four levels in their order of diminishing R-values.
3.1. Construction of Simulation Model
Basing on statistics regarding the size of urban households in Malawi, a building model was developed for this study to represent the typical urban residential building in Malawi as closely as possible. The model spread over a total floor area of 95.8 m2 including two bed rooms, one living room, one shower room, one toilet and one kitchen.
The typical urban residential building in Malawi is a single family dwelling unit having an average size of about five persons with two rooms for sleeping [
40].
The
Figure 2 below show the floor plan and elevations of the building model:
Urban residential building construction uses relatively simple materials and technologies. According to the NSO [
40], the widely used construction materials are cement, unburnt bricks and iron sheets for building floors, walls and roofs respectively.
Table 1 below shows the urban residential buildings’ construction materials by proportion of the urban residential building stock.
For purposes of this study, the typical urban residential building is made of mass concrete floor slabs with a thickness of 150 mm. The Walls are made of burnt bricks. Typically, the walls are solid with thicknesses of 230 mm and 115 mm for external and internal walls respectively. A 13 mm layer of sand and cement plaster is applied on the internal side of the walls. The walls are punctuated with glazed steel framed windows. Three-millimetre clear glass is used for the glazing. Two air bricks of size 215 mm × 140 mm are fixed above every window on the opposite top ends. Ceilings are made of Nulite ceiling boards. The roofs, which are mostly either gable or hipped, are made of a timber framework and covered with Iron Sheets having 0.3 mm thickness and pitches ranging from 7°–45°.
Despite the fact that unburnt bricks feature prominently in urban residential building construction, this study’s characterization of a typical residential building opts for burnt bricks on account of their superior structural capabilities.
Table 2 below shows the thermal properties of the materials.
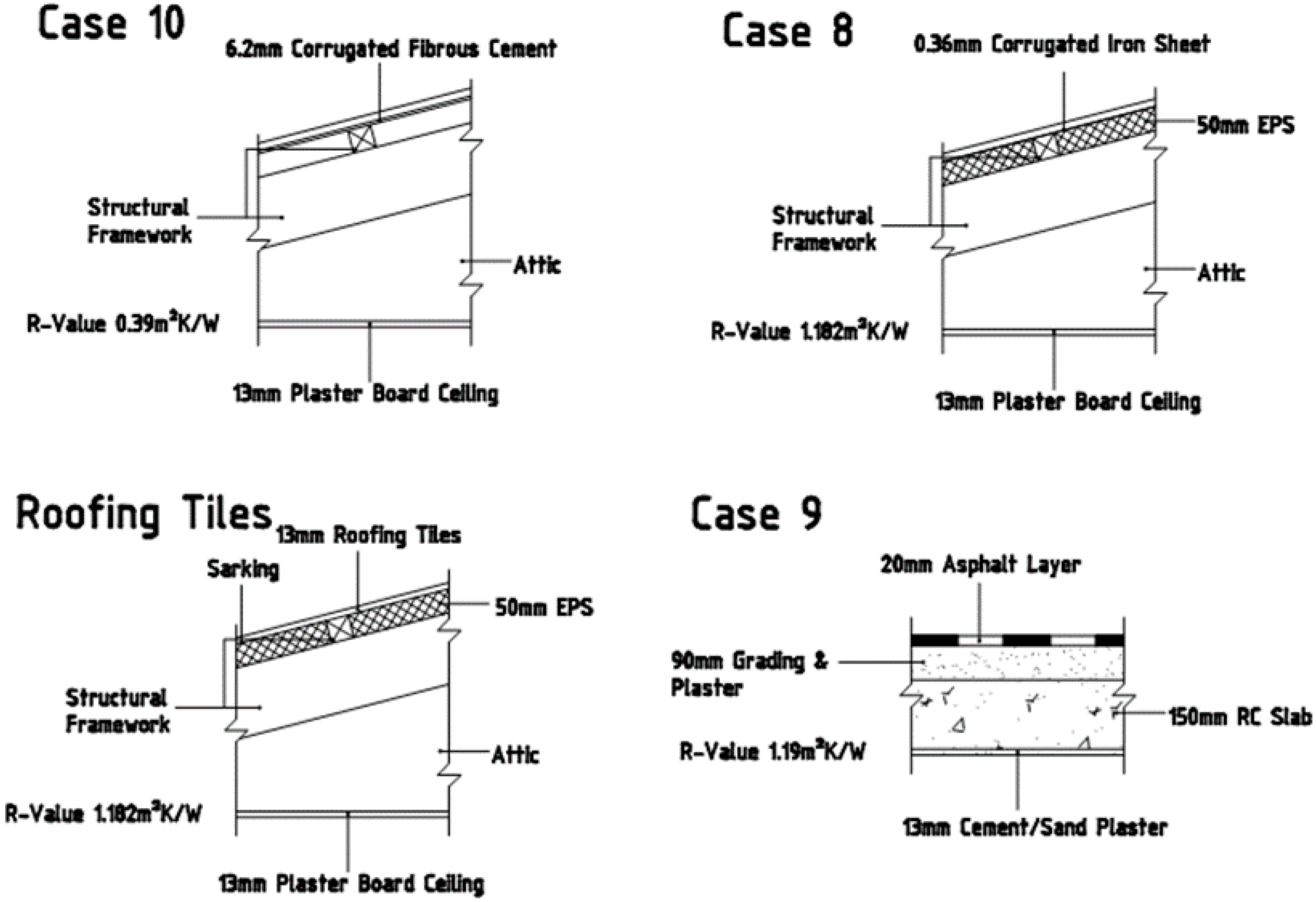
A total of seven envelope features were systematically manipulated and the impacts on the thermal performance of the buildings observed. These features included Floor Thickness, Wall R-value, Roof R-value, Window Glazing Insulation, Air Infiltration through air bricks, Wall Transparency Ratio and Window Overhang depth.
During the systematic manipulation, four levels of each of the envelope design features were studied to understand their impact on the thermal comfort conditions registered in the building models.
Table 3 below shows the envelope design features and their values at each of their levels of study.
3.2. Simulation Procedures
The urban residential building under consideration in this study is a naturally ventilated building. There was not going to be any use of mechanical equipment to control the indoor thermal environment. For this reason, in the simulation control, it was expressly specified that the simulation runs were to only cater for the weather file run periods. The other calculations such as zone sizing, system sizing, plant sizing and sizing periods were not going to be necessary.
The building model was developed in the context of an urban environment. In EnergyPlus, its terrain was thus classified as being in the City.
EnergyPlus requires the input of the geographical location of the model before a simulation can run. Ideally, this study’s models’ location should have been specified as being in Malawi seeing that it is grounded in that context. However, presently, there does not exist a geographical location accompanied with an EnergyPlus readable weather file from any Malawian City. Alternatively, a closer location to Malawi was then identified, one whose climatic design data is not very different from that of Malawian urban areas. This location is Harare City in Zimbabwe.
Zimbabwe is located along longitude 20°00′ S and latitude 30°00′ E. Malawi on the other hand is located along longitude 13°30′ S and latitude 34°00′ E.
Figure 3 shows the geographical location of Zimbabwe in relation to Malawi.
Malawi has a sub-tropical climate characterised by a warm-wet season stretching from November to April. A relatively cold, dry season spans across May and August with temperatures falling to between 4 °C and 10 °C. A hot season stretches from September to October with average temperatures scaling up to 37 °C [
42].
The climatic conditions in Zimbabwe are very similar to those of Malawi owing to the two countries’ geographical location. The ASHRAE Handbook [
43] provides the consolidated climatic design information for Zimbabwe as shown in the
Table 4,
Table 5 and
Table 6 below.
Where DB—Dry Bulb Temperature, °C, DP—Dew Point temperature, °C, WB—Wet Bulb Temperature, °C, WS—Wind Speed, m/s, Enth—Enthalpy, kJ/kg, HR—Humidity Ratio, grams of moisture per kilogram of dry air, MCDB—Mean Coincident Dry Bulb Temperature, °C, MCWB—Mean Coincident Wet Bulb Temperature, °C, MCWS—Mean Coincident Wind Speed, m/s, PCWD—Prevailing Coincident Wind Direction, °, 0 = North, 90 = East. The percentages denote annual cumulative frequency of occurrence.
A comparison of mean monthly temperatures for Harare City in Zimbabwe and the three Malawian Cities of Mzuzu, Lilongwe and Blantyre shows of the similarity in these countries’ climatic conditions as presented in
Figure 4 below.
It can be seen from the figure that the temperatures of Mzuzu and Lilongwe Cities are very close to those of Harare City in Zimbabwe. A statistical validation exercise later on in the study proved the applicability of the Harare EnergyPlus weather file for use in relation to the Malawian Cities of Mzuzu and Lilongwe.
The simulation was run across the year from 1 January through to 31 December.
In the schedule types and limits, five data types were used namely occupancy, occupant activity level, availability of facilities, temperature and finally, humidity.
The Malawi National Statistics Office [
40] reports that the average household size in Malawi is 5. Basing on the household size, this study makes some key assumptions that such a household comprises of two spouses and three dependents, both the spouses belong to the working class, the three dependents are all school-attending individuals and that the entire household goes to worship on Sundays.
In Malawi, a typical working day spans across 8 h, from 08:00–17:00 or 7:30–16:30, with a break at midday. School starts at 7:30 and runs up to 15:00. Thus, during the week, the building occupancy is intermittent. Weekends are mostly for resting at home. However, many households spend the entire Saturday or Sunday mornings at places of worship. Worship services usually run from 08:00 –12:00.
The occupant activity levels were obtained from ASHRAE [
44]. The activity levels that were used in this study are shown in the
Table 7 below:
Compact schedules were used to describe the operation of each of the key elements in the building model including the intermittency in occupancy, occupant activity levels, equipment use, operation of window openings, lighting requirements and several other dynamics.
Choice of the model materials was based on the data gathered about the typical residential building construction in Malawi. A number of materials were used in the variations of the typical residential building model including burnt Bricks, Sand and Cement Plaster, Iron sheets, Concrete, Nulite ceiling boards, Cement Screed and others. These materials had to be changed with varying model construction requirements.
A total of seven thermal zones were created in the typical urban residential building model. They included Living Room, Bedroom 1 and 2, Kitchen, Passage, Shower and Toilet.
Figure 5 below shows these thermal zones.
The green colour indicates internal boundary conditions and the blue indicates external boundary conditions.
For purposes of ensuring ease of management of the simulation environment and enhancing accuracy of results, this study zeroed in on a singly zoned model. This model had one thermal zone, the living room, which was extracted from the full model of the typical residential building. The singly zoned model is shown in
Figure 6 below:
Seeing that it was a singly zoned model, all its walls took on external boundary conditions unlike the case in the full model.
However, for purposes of validating the simulation results, it was the full model that was used. This was done so as to replicate the thermal conditions in the typical residential building as closely as possible.
The internal gains in the thermal zones were attributed to the building occupants, lights and electric equipment. This model catered for a family of 4. Each room had a compact fluorescent lamp. The kitchen had an electric cooking stove, a microwave and a refrigerator. The living room had a TV screen and a mini hi-fi. The internal gains can be summarized as shown in the
Table 8 below:
Using the Zone Air Flow model, it was possible to specify the various amounts of infiltration and natural ventilation flow rates through the air bricks and windows. For purposes of this study, the air flow through the air bricks was considered as infiltration. This was because the air bricks’ operational surface areas were very small in comparison to those of the windows such that it was only appropriate to consider them together with unintended openings in the building envelope through which infiltration primarily occurs. According to ASHRAE [
44] the flow rate of air forced through ventilation inlet openings by wind is given by the following expression:
where: Q = Air Flow rate in m
3·s
−1, C
v = Effectiveness of opening, assumed to be 0.5 to 0.6 for perpendicular winds and 0.25 to 0.35 for diagonal winds, A = Free Area of inlet in m
2, U = Wind Speed in m·s
−1.
3.3. Experimental Validation of Simulation Model
The simulation model was experimentally validated to check its appropriateness to the climatic design conditions prevalent in Malawi. To do this, hourly temperatures were recorded from typical residential buildings selected in the three major cities in Malawi namely Mzuzu, Lilongwe and Blantyre with Köppen-Geiger climate classifications of Csb, Csa and Cwa respectively.
The recorded results were then compared to the simulated results. The ASHRAE Handbook [
44], provides statistical tools for evaluating the accuracy of Indoor Air Quality predictions such that the correlation coefficient, r, of predictions and measurements should be 0.9 or greater.
In each of the three cities, an urban residential building with a characterization similar to the study’s model as described in
Section 3.1, was identified. Fundamentally, the selected buildings shared four similar aspects with the study’s building model namely the envelope construction details including the element composition and materials, the occupant family size and occupancy intermittency, internal loading factors and finally, the location within the urban fabric. It is important to note that these buildings were strictly naturally ventilated.
Data loggers were then placed in four different thermal zones within the residential buildings including the Living Room, two Bedrooms, and the Kitchen. The Data loggers were placed in a generally central location within the thermal zones on raised platforms above the floor and away from direct solar insolation. These Data loggers possessed an ability to measure and store up to 32,000 temperature readings. Their temperature measurement range was −35 °C~80 °C, with an accuracy of ±0.3 °C, a resolution of 0.1 °C and a negligible long term drift.
For purposes of the validation exercise, this study was only interested in the ambient temperatures during the course of the day over a period of 15 h from 05:00 to 20:00.
The data collected from each City was then compared to the simulation results obtained for a corresponding day in EnergyPlus simulations using the model and simulation procedures described in
Section 3.2. According to ASHRAE, such simulation results can only be valid if the correlation coefficient, r, is equal to or greater than 0.9.
Owing to the resource constraints, the validation exercise was only limited to readings obtained from a single zone, the Living Room zone. A more elaborate validation exercise encompassing all the readings from all the building zones may provide the subject for further research. Nonetheless, it can be said that a validation of readings from a single zone alone can inspire confidence in the results. Several studies in the past have used a single zone only for validation of results [
24,
45,
46,
47].
The correlation coefficients of results for the three cities show that the simulation model is valid for the two cities of Mzuzu and Lilongwe while that for Blantyre fails to pass the validation test.
Table 9 shows the validation results.
The failure of the Blantyre City results in the validation test derives from the notable differences that exist in the climatic conditions between the City and Harare City in Zimbabwe, whose weather file was adopted for use in the simulation process.
Figure 4 provided insight into this discrepancy.
3.4. Optimization Methodology
A comprehensive review of the literature showed that there are three methods that have been widely employed in building thermal design optimization research. They include Fuzzy Sets [
46], Algorithms [
48,
49] and Orthogonal Arrays [
47,
50].
The present study adopted the optimization method used by [
47,
50] involving the use of orthogonal arrays, statistical analyses and the listing method. This optimization method was chosen on account of its affordable computational requirement as opposed to the other methodologies which despite having higher efficiencies, come with a very high computational cost.
Orthogonal arrays provide a method for designing experiments to investigate how different parameters affect the mean and variance of a process performance characteristic that defines how well the process is functioning [
51]. The flow of work when using orthogonal arrays is presented in
Figure 7 below:
The first task was to identify the building envelope features to be studied in the course of the research work and then set the levels at which they would be studied. Seven features were identified including Floor Thickness (FT), Wall R-value (WR), Roof R-value (RR), Glazing Insulation (GL), Ventilation Bricks Infiltration (BI), Wall Transparency Ratio (TR) and Window Overhang (WO). These features were studied at four levels in the order of diminishing R-values as presented in the
Table 3.
Prior to conducting a comprehensive run of simulations to determine the optimal features, it is important to study the significance of each of the parameters towards the building’s thermal comfort performance. In order to do this, the first round of simulation runs is limited to only the highest and lowest values of the parameters. An understanding of the significance helps in determining the control levels at a later stage.
For the present study, a suitable orthogonal array was found to be the L32 array. The array was completed using the seven parameters and then simulations in EnergyPlus were conducted accordingly. The
Figure A1 shows the completed L32 array.
For the purposes of this study, the optimal combination of features would be the one that yielded the least amount of discomfort hours on the building users.
Using the results from this round of simulations, an Analysis of Variance was conducted to ascertain the significance of each of the parameters and their interactions. The levels of the parameters with the least amount of registered discomfort hours were then used as the control levels for a final round of simulations where each parameter had all its four levels studied while all the others parameter values remained constrained to the control values. The combination of parameters in Case 18 registered the least amount of discomfort hours. Therefore, these values would provide the control values during the final comprehensive simulation runs.
Finally, the annual thermal behaviour registered by the optimal combination was then closely analysed to see if there could be any further improvements to it.
Analysis of Variance
The results from the first round of simulations at the highest and lowest levels were subjected to an Analysis of Variance (ANOVA). The analysis showed that of the parameters that were studied, the air infiltration through the ventilation bricks constituted the most significant parameter registering a variance ratio of 526.36. The analysis of results for the all the parameters are presented in the
Table 10 below.
A summary of the discomfort hours registered at each of the two levels of the seven parameters is provided in
Table 11 below.
The parameter levels registering the minimum amount of discomfort hours were then adopted as control levels for the next round of simulations which were planned using the listing method. These levels can be seen where the discomfort hours are in bold face in the table above. Using the listing method, the next round of simulations was then planned as presented in the
Table 12 below.
The simulation results showed that the combination of features in Case 5 yielded the least amount of discomfort hours. For the purpose of this study, this combination would be the optimal set of envelope design features. This combination was singled out and then closely analysed to examine any potential for further development which could yield even lesser discomfort hours.