Surrogate Models Applied to Optimized Organic Rankine Cycles
Abstract
:1. Introduction
- Appling surrogate techniques to replace an entire optimization model instead of part of it as usually reported in the literature;
- Evaluating the effect of different inputs used to represent heat source characteristics on the surrogates;
- Making a comparison between stochastic and deterministic surrogates.
2. Methodology
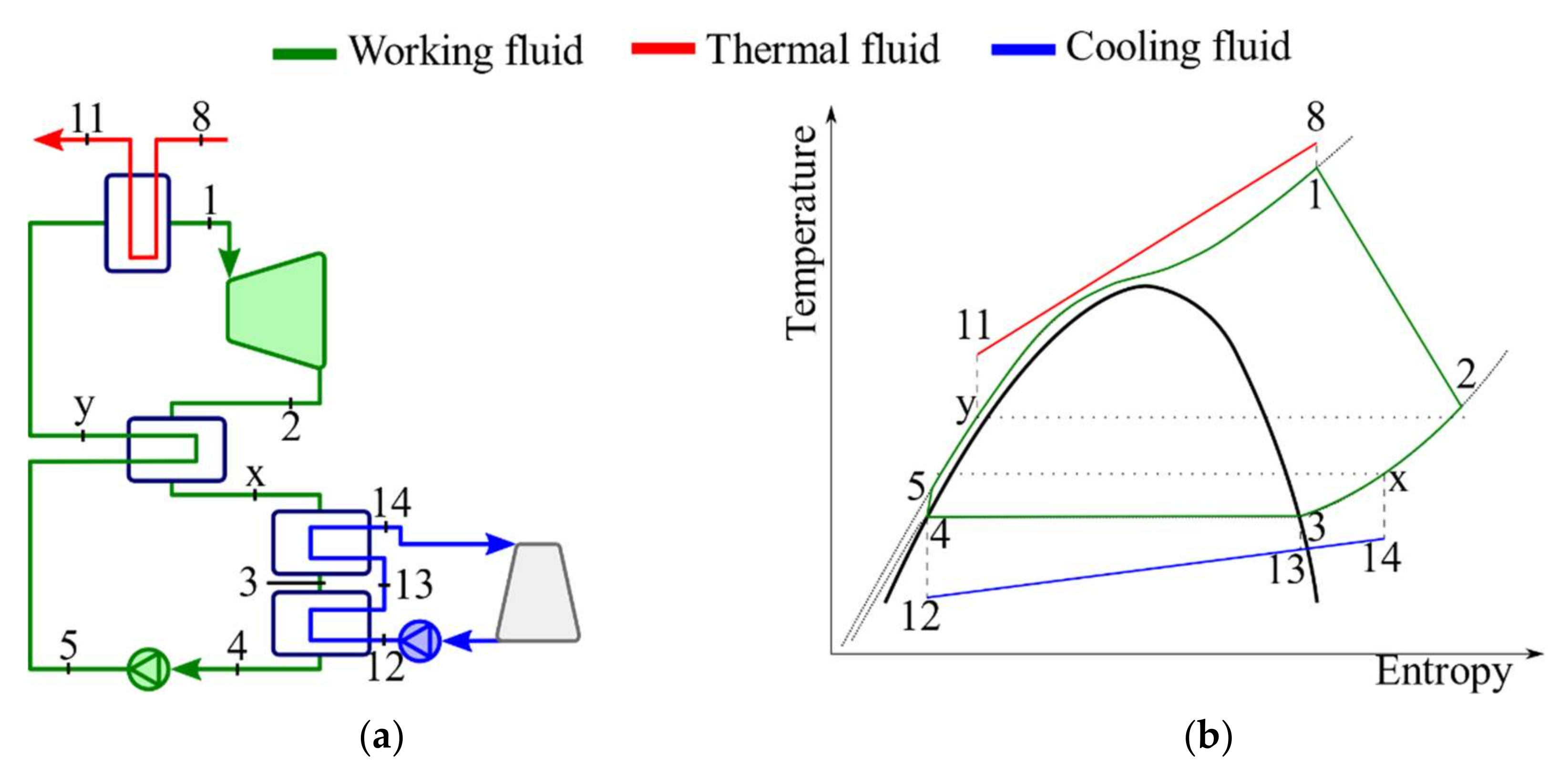
2.1. Thermodynamic Model
2.2. Plate Heat Exchangers Models
2.3. Economic Model
2.4. Thermodynamic-Economic Optimization
2.5. Surrogates for Optimized ORCs
3. Results and Discussion
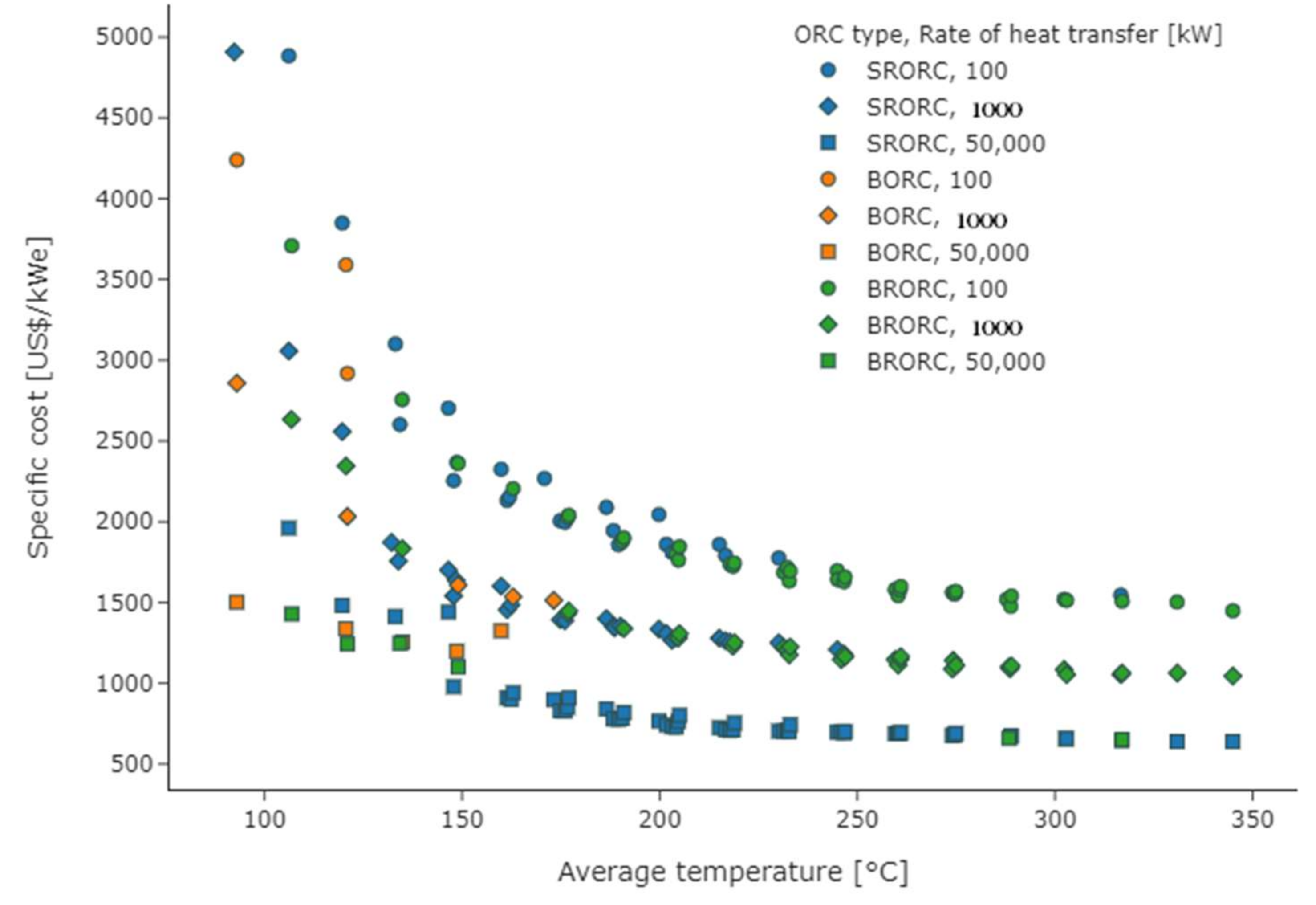
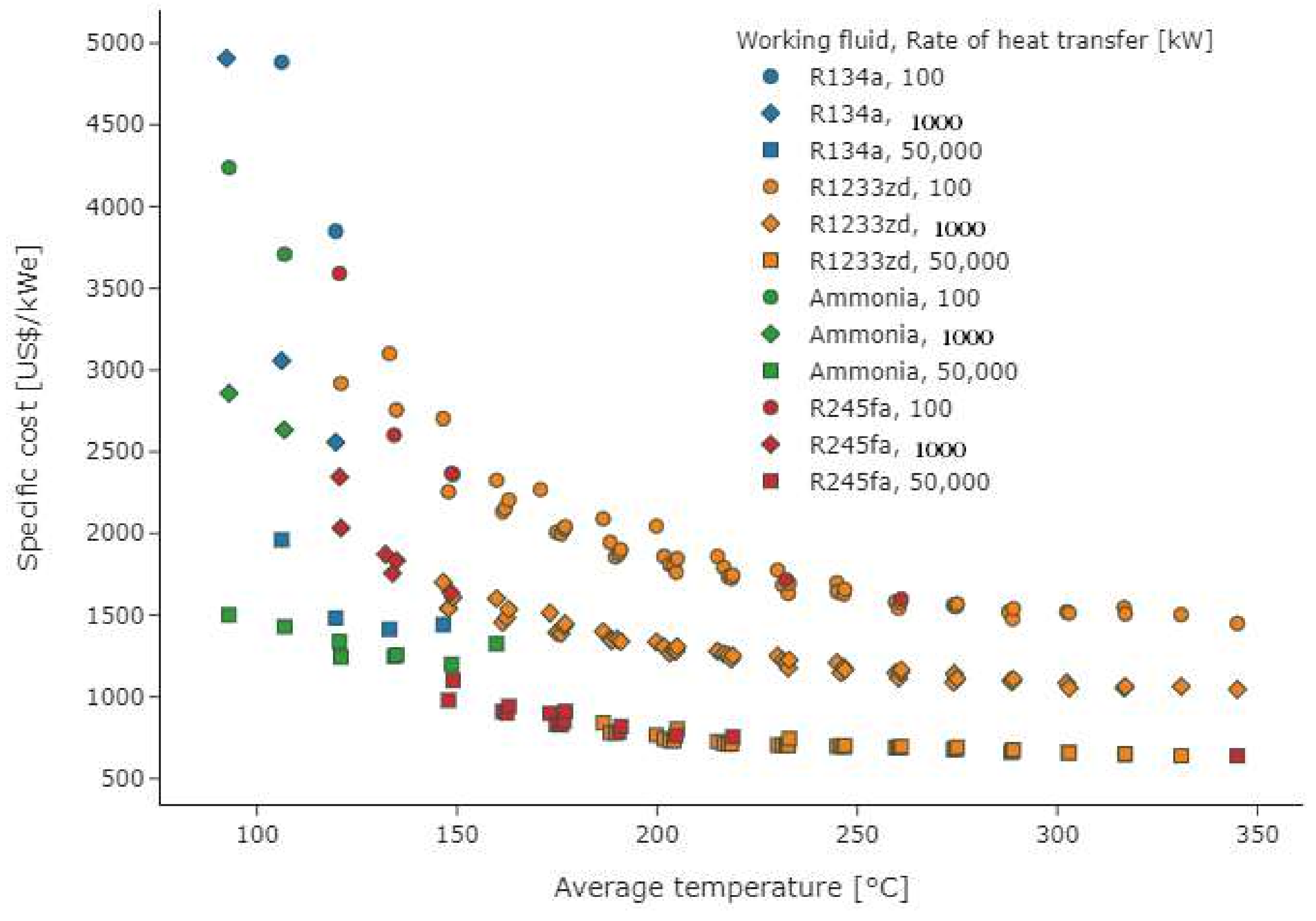
3.1. Thermodynamic-Economic Optimization
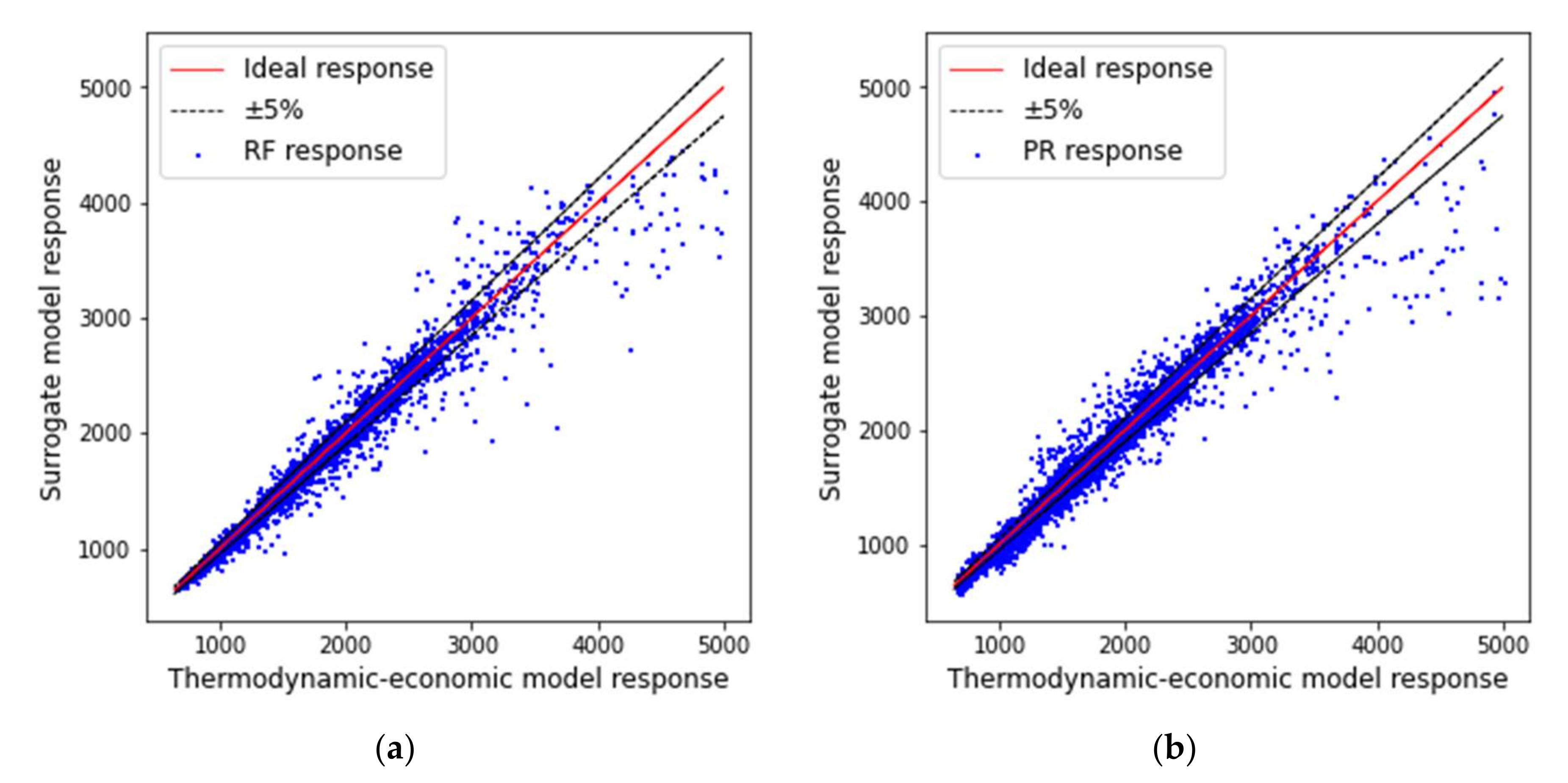
3.2. Surrogates for Optimized ORCs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Invernizzi, C.M. Closed Power Cycles. In Lecture Notes in Energy; Springer: London, UK, 2013; Volume 11, ISBN 978-1-4471-5139-5. [Google Scholar]
- Spencer, L. A comprehensive review of small solar-powered heat engines: Part I. A history of solar-powered devices up to 1950. Sol. Energy 1989, 43, 191–196. [Google Scholar] [CrossRef]
- Spencer, L. A comprehensive review of small solar-powered heat engines: Part II. Research since 1950—“conventional” engines up to 100 kW. Sol. Energy 1989, 43, 197–210. [Google Scholar] [CrossRef]
- Spencer, L. A comprehensive review of small solar-powered heat engines: Part III. Research since 1950—“unconventional” engines up to 100 kW. Sol. Energy 1989, 43, 211–225. [Google Scholar] [CrossRef]
- Babatunde, A.F.; Sunday, O.O. A Review of Working Fluids for Organic Rankine Cycle (ORC) Applications. IOP Conf. Series: Mater. Sci. Eng. 2018, 413, 012019. [Google Scholar] [CrossRef]
- Quoilin, S.; Broek, M.V.D.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef] [Green Version]
- Tartière, T.; Astolfi, M. A World Overview of the Organic Rankine Cycle Market. Energy Procedia 2017, 129, 2–9. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Khennich, M.; Galanis, N. Optimal Design of ORC Systems with a Low-Temperature Heat Source. Entropy 2012, 14, 370–389. [Google Scholar] [CrossRef] [Green Version]
- Hettiarachchi, H.M.; Golubovic, M.; Worek, W.M.; Ikegami, Y. Optimum design criteria for an Organic Rankine cycle using low-temperature geothermal heat sources. Energy 2007, 32, 1698–1706. [Google Scholar] [CrossRef]
- Shengjun, Z.; Huaixin, W.; Tao, G. Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation. Appl. Energy 2011, 88, 2740–2754. [Google Scholar] [CrossRef]
- Loni, R.; Mahian, O.; Najafi, G.; Sahin, A.Z.; Rajaee, F.; Kasaeian, A.; Mehrpooya, M.; Bellos, E.; le Roux, W.G. A critical review of power generation using geothermal-driven organic Rankine cycle. Therm. Sci. Eng. Prog. 2021, 25, 101028. [Google Scholar] [CrossRef]
- Drescher, U.; Brüggemann, D. Fluid selection for the Organic Rankine Cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar] [CrossRef]
- Liu, H.; Shao, Y.; Li, J. A biomass-fired micro-scale CHP system with organic Rankine cycle (ORC)—Thermodynamic modelling studies. Biomass Bioenergy 2011, 35, 3985–3994. [Google Scholar] [CrossRef]
- Jang, Y.; Lee, J. Optimizations of the organic Rankine cycle-based domestic CHP using biomass fuel. Energy Convers. Manag. 2018, 160, 31–47. [Google Scholar] [CrossRef]
- Jing, L.; Gang, P.; Jie, J. Optimization of low temperature solar thermal electric generation with Organic Rankine Cycle in different areas. Appl. Energy 2010, 87, 3355–3365. [Google Scholar] [CrossRef]
- Quoilin, S.; Orosz, M.; Hemond, H.; Lemort, V. Performance and design optimization of a low-cost solar organic Rankine cycle for remote power generation. Sol. Energy 2011, 85, 955–966. [Google Scholar] [CrossRef] [Green Version]
- Garg, P.; Orosz, M.S. Economic optimization of Organic Rankine cycle with pure fluids and mixtures for waste heat and solar applications using particle swarm optimization method. Energy Convers. Manag. 2018, 165, 649–668. [Google Scholar] [CrossRef]
- Wu, D.; Zuo, J.; Liu, Z.; Han, Z.; Zhang, Y.; Wang, Q.; Li, P. Thermodynamic analyses and optimization of a novel CCHP system integrated organic Rankine cycle and solar thermal utilization. Energy Convers. Manag. 2019, 196, 453–466. [Google Scholar] [CrossRef]
- Vélez, F.; Segovia, J.J.; Martin, M.C.; Antolín, G.; Chejne, F.; Quijano, A. A technical, economical and market review of organic Rankine cycles for the conversion of low-grade heat for power generation. Renew. Sustain. Energy Rev. 2012, 16, 4175–4189. [Google Scholar] [CrossRef]
- Apostol, V.; Pop, H.; Dobrovicescu, A.; Prisecaru, T.; Alexandru, A.; Prisecaru, M. Thermodynamic Analysis of ORC Configurations Used for WHR from a Turbocharged Diesel Engine. Procedia Eng. 2015, 100, 549–558. [Google Scholar] [CrossRef] [Green Version]
- Akman, M.; Ergin, S. Thermo-environmental analysis and performance optimisation of transcritical organic Rankine cycle system for waste heat recovery of a marine diesel engine. Ships Offshore Struct. 2020, 16, 1104–1113. [Google Scholar] [CrossRef]
- Varshil, P.; Deshmukh, D. A comprehensive review of waste heat recovery from a diesel engine using organic rankine cycle. Energy Rep. 2021, 7, 3951–3970. [Google Scholar] [CrossRef]
- Astolfi, M.; Romano, M.C.; Bombarda, P.; Macchi, E. Binary ORC (organic Rankine cycles) power plants for the exploitation of medium–low temperature geothermal sources—Part A: Thermodynamic optimization. Energy 2014, 66, 423–434. [Google Scholar] [CrossRef]
- Da Silva, J.A.; Seifert, V.; de Morais, V.O.; Tsolakis, A.; Herreros, J.; Torres, E. Exergy evaluation and ORC use as an alternative for efficiency improvement in a CI-engine power plant. Sustain. Energy Technol. Assess. 2018, 30, 216–223. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Zhou, N.J.; Guo, J.; Wang, X.Y. Fluid selection and parametric optimization of organic Rankine cycle using low temperature waste heat. Energy 2012, 40, 107–115. [Google Scholar] [CrossRef]
- Li, Y.-R.; Wang, J.-N.; Du, M.-T. Influence of coupled pinch point temperature difference and evaporation temperature on performance of organic Rankine cycle. Energy 2012, 42, 503–509. [Google Scholar] [CrossRef]
- Mazetto, B.M.; Da Silva, J.A.M.; Junior, S.D.O. Are ORCs a Good Option for Waste Heat Recovery in a Petroleum Refinery? Int. J. Thermodyn. 2015, 18, 161. [Google Scholar] [CrossRef] [Green Version]
- Astolfi, M.; Romano, M.C.; Bombarda, P.; Macchi, E. Binary ORC (Organic Rankine Cycles) power plants for the exploitation of medium–low temperature geothermal sources—Part B: Techno-economic optimization. Energy 2014, 66, 435–446. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Comparison between regenerative organic Rankine cycle (RORC) and basic organic Rankine cycle (BORC) based on thermoeconomic multi-objective optimization considering exergy efficiency and levelized energy cost (LEC). Energy Convers. Manag. 2015, 96, 58–71. [Google Scholar] [CrossRef]
- Song, J.; Loo, P.; Teo, J.; Markides, C. Thermo-Economic Optimization of Organic Rankine Cycle (ORC) Systems for Geothermal Power Generation: A Comparative Study of System Configurations. Front. Energy Res. 2020, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 9780470060681. [Google Scholar]
- Pires, T.S.; Cruz, M.E.; Colaço, M.J. Response surface method applied to the thermoeconomic optimization of a complex cogeneration system modeled in a process simulator. Energy 2013, 52, 44–54. [Google Scholar] [CrossRef]
- Riyanto, H.; Martowibowo, S.Y. Optimization of Organic Rankine Cycle Waste Heat Recovery for Power Generation in a Cement Plant via Response Surface Methodology. Int. J. Technol. 2015, 6, 938. [Google Scholar] [CrossRef]
- Zhang, X.S.; Yang, B.; Yu, T.; Jiang, L. Dynamic Surrogate Model Based Optimization for MPPT of Centralized Thermoelectric Generation Systems under Heterogeneous Temperature Difference. IEEE Trans. Energy Convers. 2020, 35, 966–976. [Google Scholar] [CrossRef]
- Kazemian, A.; Basati, Y.; Khatibi, M.; Ma, T. Performance prediction and optimization of a photovoltaic thermal system integrated with phase change material using response surface method. J. Clean. Prod. 2021, 290, 125748. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bég, O.A.; Parsa, A.B.; Nazari, F. Analysis and optimization of a transcritical power cycle with regenerator using artificial neural networks and genetic algorithms. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 701–717. [Google Scholar] [CrossRef]
- Luo, Y.; Hu, Y.; Lu, T. Efficient optimized design of solar power tower plants based on successive response surface methodology. Int. J. Low-Carbon Technol. 2019, 14, 475–486. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory System Advisor Model 2020. Available online: https://sam.nrel.gov/ (accessed on 1 October 2021).
- De Araújo, L.R. O uso do Método de Superfície de Resposta na Otimização Termoeconômica de Superestruturas Modeladas em Software Comercial para Projeto de Sistemas de Recuperação de Calor Residual em Motores Diesel Estacionários; Universidade Federal do Espírito Santo: Espírito Santo, Brazil, 2020. [Google Scholar]
- Kazemian, M.E.; Nassab, S.A.G. Thermodynamic Analysis and Statistical Investigation of Effective Parameters for Gas Turbine Cycle using the Response Surface Methodology. Int. J. Eng. 2020, 33, 894–905. [Google Scholar] [CrossRef]
- Dincer, I.; Zamfirescu, C. Conventional Power Generating Systems. In Advanced Power Generation Systems; Elsevier BV: Amsterdam, The Netherlands, 2014; pp. 199–310. [Google Scholar]
- Moens, L.; Blake, D.M. Advanced Heat Transfer and Thermal Storage Fluids. In Proceedings of the International Solar Energy Conference, Orlando, FL, USA, 6–12 August 2005; pp. 791–793. [Google Scholar]
- Jiménez-Arreola, M.; Wieland, C.; Romagnoli, A. Direct vs. indirect evaporation in Organic Rankine Cycle (ORC) systems: A comparison of the dynamic behavior for waste heat recovery of engine exhaust. Appl. Energy 2019, 242, 439–452. [Google Scholar] [CrossRef]
- Tascioni, R. Advanced Modeling of a Micro Solar CHP System for Residential Applications; Sapienza—University of Rome: Rome, Italy, 2021. [Google Scholar]
- Wang, T. The gas and steam turbines and combined cycle in IGCC systems. In Integrated Gasification Combined Cycle (IGCC) Technologies; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 497–640. ISBN 9780081001851. [Google Scholar]
- Leeper, S. Wet Cooling Towers—Rule-of-Thumb; U.S. Department of Energy: Washington, DC, USA, 1981. [Google Scholar]
- Cortinovis, G.F.; Ribeiro, M.T.; Paiva, J.L.; Song, T.W.; Pinto, J.M. Integrated analysis of cooling water systems: Modeling and experimental validation. Appl. Therm. Eng. 2009, 29, 3124–3131. [Google Scholar] [CrossRef]
- Pontes, R.F.; Yamauchi, W.M.; Silva, E.K. Analysis of the effect of seasonal climate changes on cooling tower efficiency, and strategies for reducing cooling tower power consumption. Appl. Therm. Eng. 2019, 161, 114148. [Google Scholar] [CrossRef]
- Kakaç, S.; Liu, H.; Pramuanjaroenkij, A. Heat Exchangers: Selection, Rating, and Thermal Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2012; Volume 6, ISBN 1439849900. [Google Scholar]
- Yu, G.; Shu, G.; Tian, H.; Wei, H.; Liang, X. Multi-approach evaluations of a cascade-Organic Rankine Cycle (C-ORC) system driven by diesel engine waste heat: Part B-techno-economic evaluations. Energy Convers. Manag. 2016, 108, 596–608. [Google Scholar] [CrossRef]
- Lim, T.-W.; Choi, Y.-S.; Lee, C.-K. Design of plate heat exchangers for use in medium temperature organic Rankine cycles. Heat Mass Transf. 2018, 55, 165–174. [Google Scholar] [CrossRef]
- Martin, H. A theoretical approach to predict the performance of chevron-type plate heat exchangers. Chem. Eng. Process. Process. Intensif. 1996, 35, 301–310. [Google Scholar] [CrossRef]
- Kim, I.-K.; Park, J.-H.; Kwon, Y.-H.; Kim, Y.-S. Experimental Study on R-410a Evaporation Heat Transfer Characteristics in Oblong Shell and Plate Heat Exchanger. Heat Transf. Eng. 2007, 28, 633–639. [Google Scholar] [CrossRef]
- Yan, Y.-Y.; Lio, H.-C.; Lin, T.-F. Condensation heat transfer and pressure drop of refrigerant R-134a in a plate heat exchanger. Int. J. Heat Mass Transf. 1999, 42, 993–1006. [Google Scholar] [CrossRef]
- Karellas, S.; Schuster, A.; Leontaritis, A.-D. Influence of supercritical ORC parameters on plate heat exchanger design. Appl. Therm. Eng. 2012, 33-34, 70–76. [Google Scholar] [CrossRef]
- Huang, J.; Sheer, T.J.; Bailey-McEwan, M. Heat transfer and pressure drop in plate heat exchanger refrigerant evaporators. Int. J. Refrig. 2012, 35, 325–335. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, version 10.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [Green Version]
- Vogel, E.; Küchenmeister, C.; Bich, E.; Laesecke, A. Reference Correlation of the Viscosity of Propane. J. Phys. Chem. Ref. Data 1998, 27, 947–970. [Google Scholar] [CrossRef]
- Marsh, K.N.; Perkins, A.R.A.; Ramires, M.L.V. Measurement and Correlation of the Thermal Conductivity of Propane from 86 K to 600 K at Pressures to 70 MPa. J. Chem. Eng. Data 2002, 47, 932–940. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995; ISBN 978-0-471-58467-4. [Google Scholar]
- Thermoflow Inc. Thermoflex; Thermoflow Inc.: Jacksonville, FL, USA, 2021. [Google Scholar]
- Benítez-Hidalgo, A.; Nebro, A.J.; García-Nieto, J.; Oregi, I.; Del Ser, J. jMetalPy: A Python framework for multi-objective optimization with metaheuristics. Swarm Evol. Comput. 2019, 51, 100598. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Ostertagová, E. Modelling using Polynomial Regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef] [Green Version]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Yusof, Y. A Comparison of Normalization Techniques in Predicting Dengue Outbreak. Int. Conf. Bus. Econ. Res. 2010, 1, 345–349. [Google Scholar]
- Raymaekers, J.; Rousseeuw, P.J. Transforming variables to central normality. Mach. Learn. 2021, 1–23. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. Int. Jt. Conf. Artif. Intell. 1995, 14, 1137–1145. [Google Scholar]

| Fluid | Molecular Formula | Type | ODP | GWP | Safety Group | Evaporation Temperature 1 (°C) | Critical Temperature (°C) | Critical Pressure (bar) |
|---|---|---|---|---|---|---|---|---|
| D4 | Dry | 0 | - | A2 | 175.74 | 313.35 | 13.47 | |
| R134a | Wet | 0 | 1370 | A1 | −26.07 | 101.06 | 40.59 | |
| R245fa | Isentropic | 0 | 1050 | B1 | 15.05 | 153.86 | 36.51 | |
| Ammonia | Wet | 0 | 0 | B2 | −33.32 | 132.25 | 113.33 | |
| R1233zd | Isentropic | 0 | 1 | A1 | 18.26 | 166.45 | 36.24 | |
| SES36 | Dry | 0 | 3710 | A1 | 35.72 | 177.55 | 28.49 |
| Input Parameter | Lower Bound | Upper Bound |
|---|---|---|
| 60 °C | 340 °C | |
| 70 °C | 350 °C | |
| 100 kWt | 50,000 kWt |
| Parameter | Description | Value | Reference |
|---|---|---|---|
| Ambient dry bulb temperature | 27.1 °C | ||
| Ambient pressure | 1.007 bar | ||
| Ambient relative humidity | 79.9% | ||
| Expander isentropic efficiency | 53% | [45] | |
| Pump isentropic efficiency | 70% | [45] | |
| Transmission efficiency | 95% | [45] | |
| Generator/motor efficiency | 90% | [45] | |
| Cooling fluid inlet temperature | 40 °C | ||
| Cooling fluid outlet temperature | 50 °C |
| Condition | Equation | Reference |
|---|---|---|
| No phase change | [53] | |
| Evaporation | [54] | |
| Condensation | [55] | |
| Supercritical state | [56] |
| Condition | Equation | Reference |
|---|---|---|
| No phase change/Supercritical state | [50] | |
| Evaporation | [57] | |
| Condensation | [55] |
| Constraint | Range |
| Pinch point temperature difference | |
| Turbine pressure difference | |
| Quality during expansion | |
| Heat exchangers pressure drop |
| Variable | Description | Lower Bound | Upper Bound | Unit |
|---|---|---|---|---|
| Evaporation pressure | 4.01325 | 42 | bar | |
| Condensation pressure | 1.01325 | bar | ||
| Turbine inlet temperature | °C | |||
| Recuperator outlet temperature at cold side | °C | |||
| Evaporator plate width | 0.3048 | 4.572 | m | |
| Condenser plate width | 0.3048 | 4.572 | m | |
| Recuperator plate width | 0.3048 | 4.572 | m | |
| Evaporator working fluid velocity | 0.2 | 2.0 | m/s | |
| Condenser working fluid velocity | 0.2 | 2.0 | m/s | |
| Recuperator working fluid velocity | 0.2 | 2.0 | m/s |
| Variable | Input/Output | Type |
|---|---|---|
| Heat transfer fluid | Input | Categorical |
| Working fluid | Input | Categorical |
| ORC configuration | Input | Categorical |
| Thermal fluid inlet temperature () | Input | Numeric |
| Thermal fluid outlet temperature () | Input | Numeric |
| Rate of heat transfer () | Input | Numeric |
| Specific cost () | Output | Numeric |
| Electrical efficiency () | Output | Numeric |
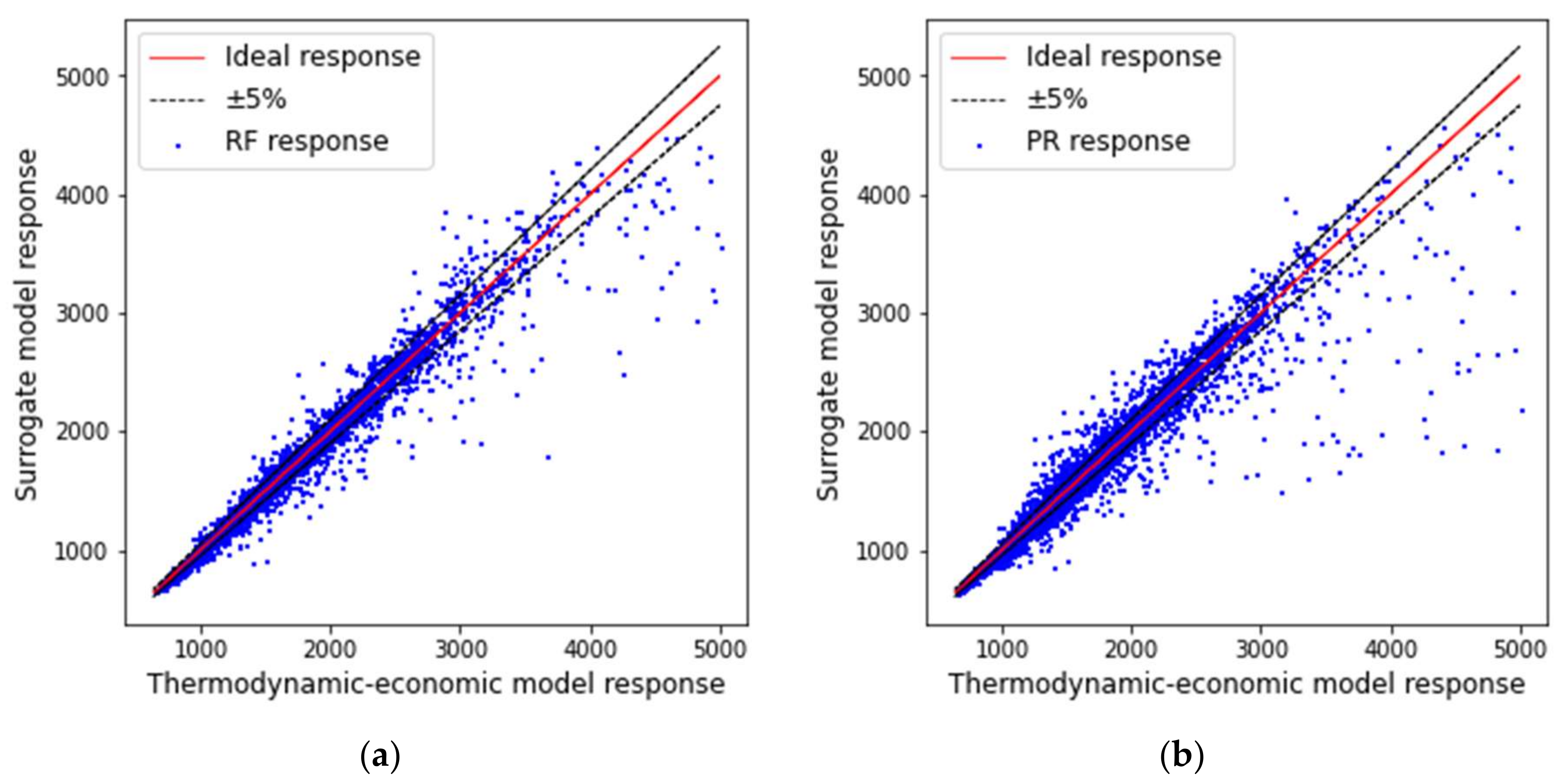
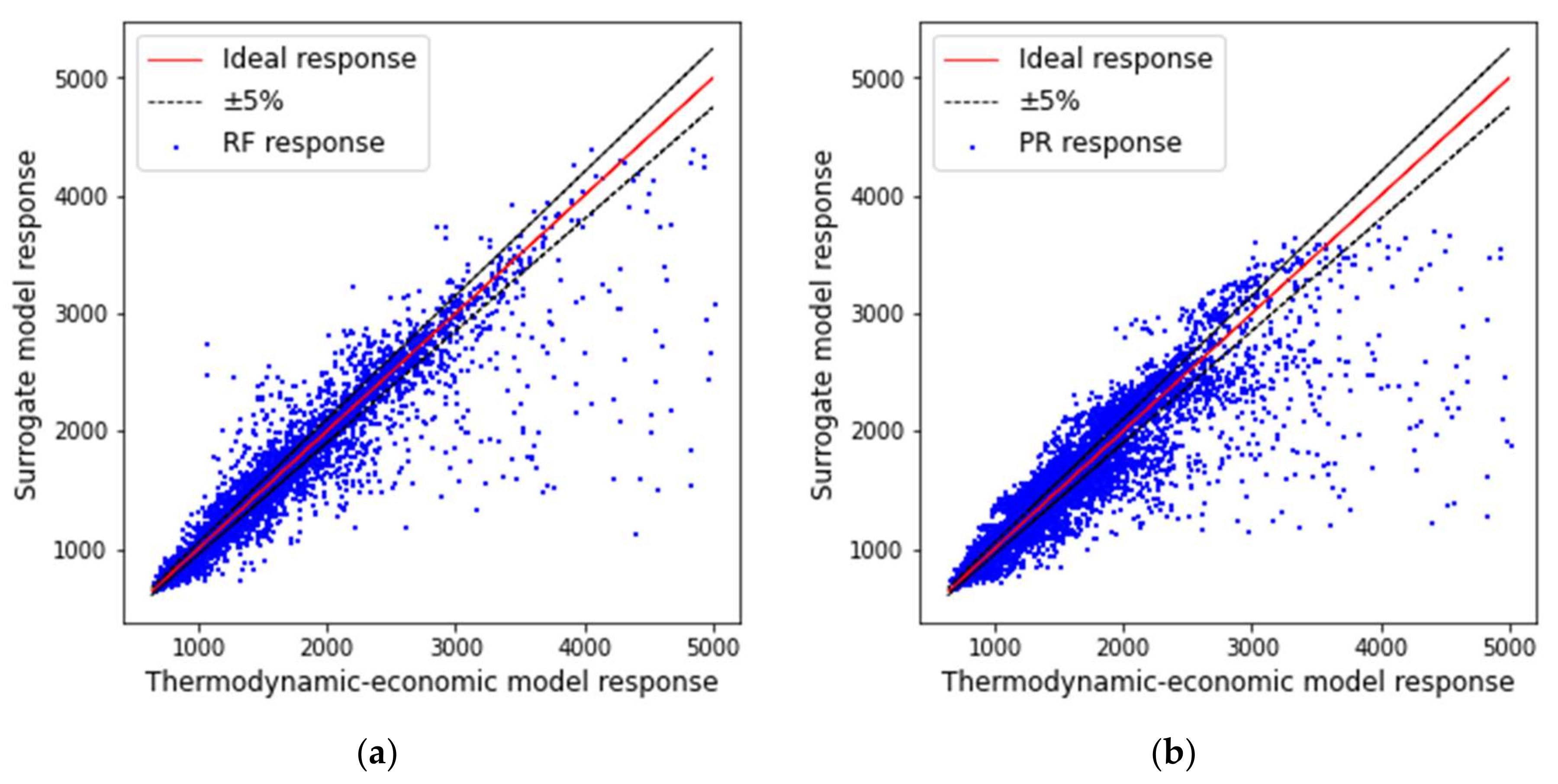
| Model | Input Data | Output | Training R-Square | Validation R-Square | Cases with Error ≤ 5% |
|---|---|---|---|---|---|
| RF | , and | Specific cost | 0.98 ± 0.00 | 0.97 ± 0.00 | (88.10 ± 0.42)% |
| PR | , and | Specific cost | 0.96 ± 0.00 | 0.96 ± 0.00 | (75.01 ± 0.99)% |
| RF | , and | Efficiency | 0.99 ± 0.00 | 0.98 ± 0.00 | (81.18 ± 0.86)% |
| PR | , and | Efficiency | 0.97 ± 0.00 | 0.97 ± 0.00 | (75.72 ± 0.54)% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilasboas, I.F.; dos Santos, V.G.S.F.; Ribeiro, A.S., Jr.; da Silva, J.A.M. Surrogate Models Applied to Optimized Organic Rankine Cycles. Energies 2021, 14, 8456. https://doi.org/10.3390/en14248456
Vilasboas IF, dos Santos VGSF, Ribeiro AS Jr., da Silva JAM. Surrogate Models Applied to Optimized Organic Rankine Cycles. Energies. 2021; 14(24):8456. https://doi.org/10.3390/en14248456
Chicago/Turabian StyleVilasboas, Icaro Figueiredo, Victor Gabriel Sousa Fagundes dos Santos, Armando Sá Ribeiro, Jr., and Julio Augusto Mendes da Silva. 2021. "Surrogate Models Applied to Optimized Organic Rankine Cycles" Energies 14, no. 24: 8456. https://doi.org/10.3390/en14248456
APA StyleVilasboas, I. F., dos Santos, V. G. S. F., Ribeiro, A. S., Jr., & da Silva, J. A. M. (2021). Surrogate Models Applied to Optimized Organic Rankine Cycles. Energies, 14(24), 8456. https://doi.org/10.3390/en14248456






