Prediction of Placental Barrier Permeability: A Model Based on Partial Least Squares Variable Selection Procedure
Abstract
:1. Introduction
2. Results and Discussion
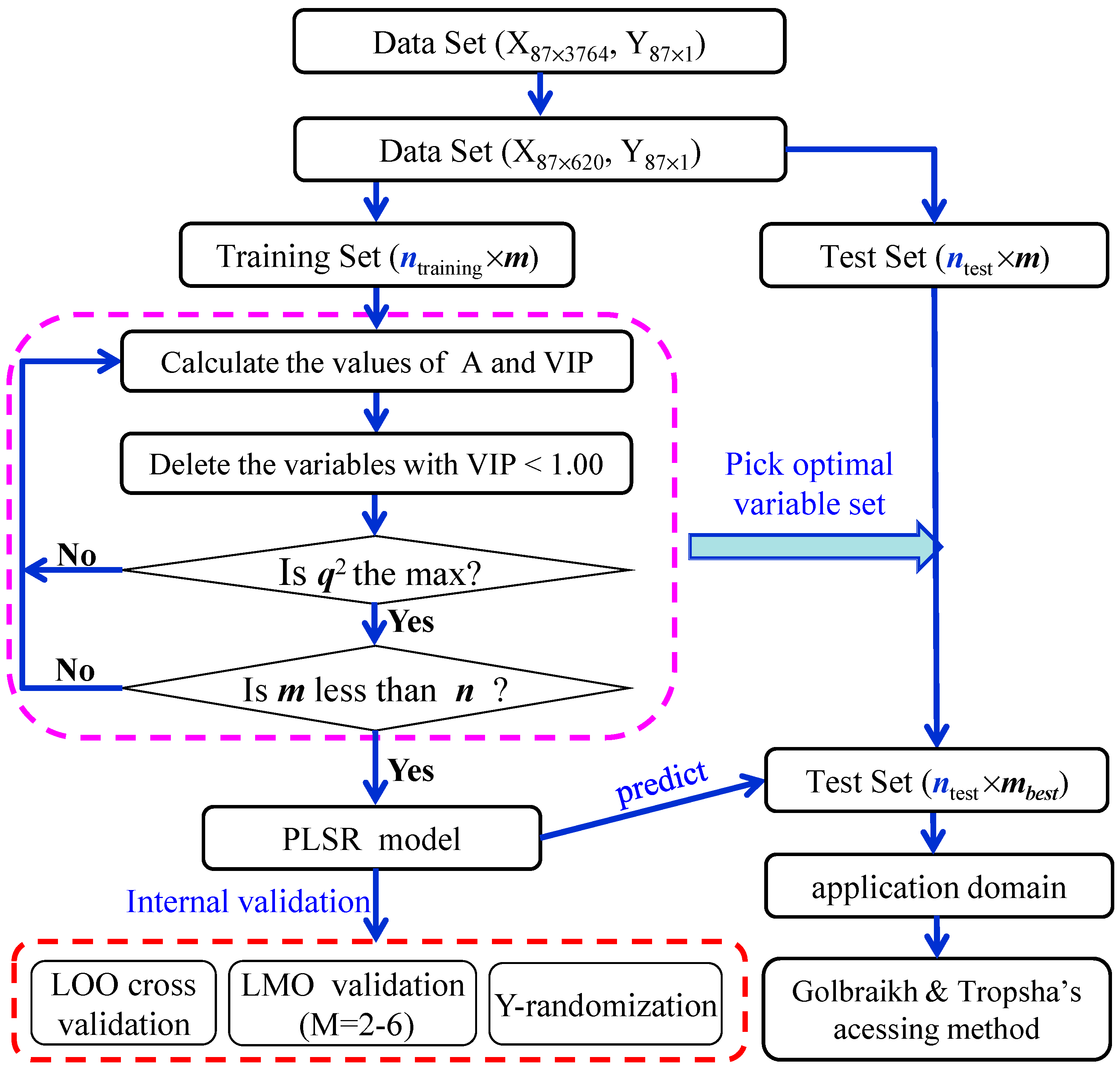
2.1. PLS Variable Selection
| m | A | r2 | RMSE | q2 | RMSV |
|---|---|---|---|---|---|
| 620 | 8 | 0.9801 | 0.04 | 0.3715 | 0.25 |
| 396 | 7 | 0.9716 | 0.05 | 0.5569 | 0.20 |
| 286 | 8 | 0.9745 | 0.05 | 0.6532 | 0.18 |
| 235 | 8 | 0.9751 | 0.05 | 0.6773 | 0.17 |
| 195 | 7 | 0.9573 | 0.06 | 0.6984 | 0.16 |
| 163 | 7 | 0.9651 | 0.06 | 0.7445 | 0.15 |
| 137 | 7 | 0.9518 | 0.07 | 0.7153 | 0.16 |
| 115 | 7 | 0.9368 | 0.07 | 0.6941 | 0.17 |
| 100 | 7 | 0.9264 | 0.08 | 0.6831 | 0.17 |
| 85 | 7 | 0.9302 | 0.08 | 0.7125 | 0.16 |
| 79 | 7 | 0.9341 | 0.08 | 0.7560 | 0.15 |
| 73 | 7 | 0.9258 | 0.08 | 0.7330 | 0.15 |
| 67 | 7 | 0.9169 | 0.09 | 0.7022 | 0.16 |
| 62 | 7 | 0.9138 | 0.09 | 0.7271 | 0.16 |
| 58 | 7 | 0.9110 | 0.09 | 0.7208 | 0.16 |
| 55 | 7 | 0.9115 | 0.09 | 0.7303 | 0.15 |
| 48 | 7 | 0.9064 | 0.09 | 0.7323 | 0.15 |
| 42 | 7 | 0.8525 | 0.11 | 0.6655 | 0.17 |
| 39 | 5 | 0.8115 | 0.13 | 0.6350 | 0.18 |
| 34 | 5 | 0.7845 | 0.14 | 0.6138 | 0.19 |
| Type of Descriptor | m | Name of Descriptor |
|---|---|---|
| Constitutional indices | 4 | Me, O%, nO, nHet |
| Topological indices | 3 | DELS, DECC, Psi_i_A |
| Connectivity indices | 1 | X0Av |
| Information indices | 3 | SIC1,AAC, IC1 |
| 2D matrix-based descriptor | 5 | TI2_L, SM5_X, Chi_Dz(p), SM1_Dz(p), SM6_B(s) |
| 2D autocorrelations | 11 | MATS3v, GATS1e, ATSC2s, MATS1e, ATSC3e, ATSC1e, ATSC1s, ATSC3s, MATS8i, GATS3v, GATS1s |
| Burden eigenvalues | 1 | SpMax3_Bh(s) |
| P-VS-like descriptors | 2 | P_VSA_p_2, P_VSA_s_6 |
| Edge adjacency indices | 4 | Eig03_EA(dm), Eig05_EA(dm), Eig06_EA(dm), SpMAD_B(s) |
| Functional group counts | 3 | nRNH2, nHDon, nPyrimidines |
| Atom-centred fragments | 1 | O-057 |
| CAST 2D | 5 | CATS2D_07_DD, CATS2D_04_DD, CATS2D_08_DA CATS2D_05_AP, CATS2D_04_LL |
| 2D atom pairs | 2 | T(O..O), F05[O-O] |
| Molecular properties | 2 | MLOGP, SAdon |
| Drug-like indices | 1 | LLS_01 |
2.2. PLS Regression Model
| No. | Name | CI-Obs. | CI-Cal. | No. | Name | CI-Obs. | CI-Cal. |
|---|---|---|---|---|---|---|---|
| 1 * | Abacavir | 0.47 | 0.62 | 45 | Mefloquine | 1.57 | |
| 2 | Acipimox | 0.25 | 0.38 | 46 | Meropenem | 0.08 | 0.16 |
| 3 * | Acyclovir | 0.17 | 0.09 | 47 | Metaclopramide | 0.40 | 0.65 |
| 4 * | Alanine | 0.30 | 0.40 | 48 | Metformin | 0.34 | 0.44 |
| 5 | Alfentanil | 0.75 | 0.68 | 49 | Methadone | 0.83 | 0.97 |
| 6 | PAH | 0.47 | 0.41 | 50 * | Mezlocilline | 0.14 | –0.08 |
| 7 * | Amprenavir | 0.38 | 0.39 | 51 * | Morphine | 0.63 | 0.36 |
| 8 * | Azidothymidine | 0.29 | 0.15 | 52 | Naloxone | 0.64 | 0.46 |
| 9 | Betamethasone | 0.41 | 0.44 | 53 * | Nicotine | 0.93 | 0.54 |
| 10 | Biotin | 0.35 | 0.43 | 54 | Oseltamivir | 0.13 | 0.28 |
| 11 | Bisheteroypiperazine | 0.72 | 0.65 | 55 | Hydroxyphenytoin | 0.52 | 0.51 |
| 12 | Buprenorphine | 0.29 | 0.32 | 56 | PCB-52 | 0.74 | 0.62 |
| 13 | Cefoperazone | 0.04 | 0.06 | 57 | Pentamidine | 0.04 | 0.04 |
| 14 | Cefpirome | 0.20 | 0.02 | 58 | Phenobarbitone | 0.52 | 0.63 |
| 15 * | Ceftizoxime | 0.12 | 0.04 | 59 * | Prednisolone | 0.38 | 0.46 |
| 16 * | Chloroprocaine | 0.83 | 0.69 | 60 | Propofol | 0.51 | 0.58 |
| 17 | L-Leucine | 0.62 | 0.55 | 61 | Pyridoxal | 0.37 | 0.40 |
| 18 | Lidocaine | 0.91 | 0.96 | 62 | Pyridoxal 5'-phosphate | 0.07 | 0.06 |
| 19 * | Bupivacaine | 0.73 | 0.91 | 63 | Pyridoxine | 0.56 | 0.45 |
| 20 * | Cimetidine | 0.30 | 0.38 | 64 | Pyrimethamine | 1.00 | 1.03 |
| 21 | Clavulanic acid | 0.06 | 0.11 | 65 | Quabain | 0.07 | 0.07 |
| 22 | Cocaethylene | 0.78 | 0.82 | 66 | Ribofl avin | 0.69 | 0.74 |
| 23 | Cocaine | 0.88 | 0.74 | 67 | Rifabutin | 0.37 | 0.42 |
| 24 * | Cortisol | 0.50 | 0.54 | 68 * | Rifampin | 0.12 | 0.76 |
| 25 | Cortisone | 0.74 | 0.63 | 69 | Ritodrine | 0.10 | 0.04 |
| 26 | Creatinine | 0.31 | 0.36 | 70 | Ritonavir | 0.09 | 0.07 |
| 27 | D4T | 0.24 | 0.25 | 71 * | Ropivacaine | 0.75 | 0.94 |
| 28 | DDE | 0.61 | 0.68 | 72 | Rosiglitazone | 0.20 | 0.35 |
| 29 | Dexamethasone | 0.37 | 0.44 | 73 | Salbutamol | 0.40 | 0.30 |
| 30 | Dichlorobenzene | 0.98 | 0.99 | 74 | Saquinavir | 0.05 | 0.09 |
| 31 | Diclofenac | 0.79 | 0.68 | 75 * | S-Ketoprofen | 0.39 | 0.91 |
| 32 * | Didanosine | 0.31 | 0.29 | 76 | SR49059 | 0.31 | 0.33 |
| 33 | Ethanol | 1.07 | 1.05 | 77 | Sufentanil | 0.66 | 0.65 |
| 34 | Fenoterol | 0.10 | 0.18 | 78 | Sulindac | 0.47 | 0.60 |
| 35 | Ganciclovir | 0.17 | 0.08 | 79 | Sulindac sulfide | 0.81 | 0.64 |
| 36 * | Glucose | 0.26 | 0.50 | 80 | Theophylline | 0.80 | 0.64 |
| 37 | Hydralazine | 0.61 | 0.62 | 81 | Thiopental | 0.95 | 0.89 |
| 38 | Indinavir | 0.39 | 0.34 | 82 | Ticarcillin | 0.04 | 0.14 |
| 39 * | Indomethacin | 0.72 | 0.58 | 83 * | Triameterene | 0.85 | 0.80 |
| 40 * | L-Alpha-acetyl-N-normethadol | 0.80 | 0.88 | 84 | Trovafl oxacin | 0.19 | 0.23 |
| 41 | L-Alphacetylmethadol | 0.95 | 0.92 | 85 | Urea | 0.32 | 0.28 |
| 42 | Lamivudine | 0.23 | 0.19 | 86 | Valproic acid | 0.95 | 0.93 |
| 43 | Lysine | 0.35 | 0.29 | 87 | Vinblastine | 0.31 | 0.23 |
| 44 | Lopinavir | 0.73 | 0.60 | 88 | Zalcitabine | 0.22 | 0.34 |

2.3. Internal and External Validation
| Model Parameter | Value | ||
|---|---|---|---|
| A | 7 | ||
| r2 | 0.9064 | ||
| RMSE | 0.09 | ||
| q2(LOO) | 0.7323 | ||
| RMSV | 0.15 | ||
| q2(L2O) | 0.6620 (±0.0195) | ||
| q2(L3O) | 0.6496 (±0.0147) | ||
| q2(L4O) | 0.6638 (±0.0169) | ||
| q2(L5O) | 0.6932 (±0.0148) | ||
| q2(L6O) | 0.5441 (±0.0217) | ||
| Y-Randomization | r2Yrand | 0.3740 (±0.0152) | |
| q2Yrand | −1.1573 (±0.1952) | ||
| rp2 | 0.4201(np = 22) | 0.7656(np = 19) | |
| RMSP | 0.23 | 0.14 | |
2.4. Application Domain

2.5. Mechanistic Interpretation
3. Experimental Section
3.1. Data Collection

3.2. Descriptor Calculation and Pretreatment
3.3. Variable Selection
3.4. Model Development and Validation
3.5. Application Domain
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Collins, T.F. History and evolution of reproductive and developmental toxicology guidelines. Curr. Pharm. Des. 2006, 12, 1449–1465. [Google Scholar] [CrossRef] [PubMed]
- Younglai, E.V.; Wu, Y.J.; Foster, W.G. Reproductive toxicology of environmental toxicants: emerging issues and concerns. Curr. Pharm. Des. 2007, 13, 3005–3019. [Google Scholar] [CrossRef] [PubMed]
- Andrade, S.E.; Gurwitz, J.H.; Davis, R.L.; Chan, K.A.; Finkelstein, J.A.; Fortman, K.; McPhillips, H.; Raebel, M.A.; Roblin, D.; Smith, D.H.; et al. Prescription drug use in pregnancy. Am. J. Obstet. Gynecol. 2004, 191, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Glover, D.D.; Amonkar, M.; Rybeck, B.F.; Tracy, T.S. Prescription, over-the-counter, and herbal medicine use in a rural, obstetric population. Am. J. Obstet. Gynecol. 2003, 188, 1039–1045. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, A.A.; Gilboa, S.M.; Werler, M.M.; Kelley, K.E.; Louik, C.; Hernández-Díaz, S. Medication use during pregnancy, with particular focus on prescription drugs: 1976–2008. Am. J. Obstet. Gynecol. 2011, 205, 51.e1–51.e8. [Google Scholar] [CrossRef] [PubMed]
- Nina, I.; Kenneth, E.T. Drug Metabolism and Transport During Pregnancy: How Does Drug Disposition Change during Pregnancy and What Are the Mechanisms that Cause Such Changes? Drug Metab. Dispos. 2013, 41, 256–262. [Google Scholar] [CrossRef] [PubMed]
- Ventura, S.J.; Abma, J.C.; Mosher, W.D.; Henshaw, S. Estimated pregnancy rates by outcome for the United States, 1990–2004. Natl. Vital Stat. Rep. 2008, 56, 1–25. [Google Scholar] [PubMed]
- David, E.; Riki, L.; Ariel, J.J.; Gernot, D.; Moshe, H. Have We Neglected the Role of Fetal Endothelium in Transplacental Transport? Traffic 2014, 15, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Rubinchik-Stern, M.; Eyal, S. Drug interactions at the human placenta: What is the evidence? Front. Pharmacol. 2012, 3, 126. [Google Scholar] [CrossRef] [PubMed]
- Myllynen, P.; Pasanen, M.; Pelkonen, O. Human placenta: A human organ for developmental toxicology research and biomonitoring. Placenta 2005, 26, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Myllynen, P.; Immonen, E.; Kummu, M.; Vähäkangas, K. Developmental expression of drug metabolizing enzymes and transporter proteins in human placenta and fetal tissues. Expert Opin. Drug Metab. Toxicol. 2009, 5, 1483–1499. [Google Scholar] [CrossRef] [PubMed]
- Vähäkangas, K.; Myllynen, P. Experimental methods to study human transplacental exposure to genotoxic agents. Mutat. Res. 2006, 608, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Myren, M.; Mose, T.; Mathiensen, L.; Knudsen, L.E. The human placenta an alternative for studying foetal exposure. Toxicol. In Vitro 2007, 21, 1332–1340. [Google Scholar] [CrossRef] [PubMed]
- Simon-Hettich, B.; Rothfuss, A.; Steger-Hartmann, T. Use of computer assisted prediction of toxic effects of chemical substances. Toxicology 2006, 224, 156–162. [Google Scholar] [CrossRef] [PubMed]
- Tropsha, A.; Golbraikh, A. Predictive QSAR modeling work flow, model applicability domains, and virtual screening. Curr. Pharm. Des. 2007, 13, 3494–3504. [Google Scholar] [CrossRef] [PubMed]
- Vedani, A.; Dobler, M.; Lill, M.A. In silico prediction of harmful effects triggered by drugs and chemicals. Toxicol. Appl. Pharm. 2005, 207, S398–S407. [Google Scholar] [CrossRef]
- Vedani, A.; Dobler, M.; Lill, M.A. The challenge of predicting drug toxicity in silico. Basic Clin. Pharmacol. Toxicol. 2006, 99, 195–208. [Google Scholar] [CrossRef] [PubMed]
- Zvinavashe, E.; Murk, A.J.; Rietjens, I.M. Promises and pitfalls of quantitative structure–activity relationship approaches for predicting metabolism and toxicity. Chem. Res. Toxicol. 2008, 21, 2229–2236. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.H.; Xia, Z.N.; Qin, L.T.; Liu, S.S. Prediction of blood–brain partitioning: A model based on molecular electronegativity distance vector descriptors. J. Mol. Graph. Model. 2010, 29, 214–220. [Google Scholar] [CrossRef] [PubMed]
- Stepensky, D. Prediction of drug disposition on the basis of its chemical structure. Clin. Pharmacokinet. 2013, 52, 415–431. [Google Scholar] [CrossRef] [PubMed]
- Dobchev, D.A.; Pillai, G.G.; Karelson, M. In silico machine learning methods in drug development. Curr. Top. Med. Chem. 2014, 14, 1913–1922. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.S.; Huang, R.B.; Chou, K.C. Review: Recent advances in QSAR and their applications in predicting the activities of chemical molecules, peptides and proteins for drug design. Curr. Protein Pept. Sci. 2008, 9, 248–259. [Google Scholar] [CrossRef] [PubMed]
- Beck, B.; Geppert, T. Industrial applications of in silico ADMET. J. Mol. Model. 2014, 20, 2322–2325. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.T.; Trossini, G.H. The survey of the use of QSAR methods to determine intestinal absorption and oral bioavailability during drug design. Med. Chem. 2014, 10, 441–448. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Chen, L.; Li, Y.; Tian, S.; Sun, H.; Hou, T. ADMET Evaluation in Drug Discovery. 13. Development of in Silico Prediction Models for P-Glycoprotein Substrates. Mol. Pharm. 2014, 11, 716–726. [Google Scholar] [CrossRef] [PubMed]
- Wenlock, M.C.; Carlsson, L.A. How experimental errors influence drug metabolism and pharmacokinetic QSAR/QSPR models. J. Chem. Inf. Model. 2015, 55, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, M.; Madden, J.C.; Rowe, P.H.; Cronin, M.T.D. Structure-based modeling in reproductive toxicology: (Q)SARs for the placental barrier. SAR QSAR Environ. Res. 2007, 18, 57–76. [Google Scholar] [CrossRef] [PubMed]
- Giaginis, C.; Zira, A.; Theocharis, S.; Tsantili-Kakoulidou, A. Application of quantitative structure-activity relationships for modeling drug and chemical transport across the human placenta barrier: A multivariate data analysis approach. J. Appl. Toxicol. 2009, 29, 724–733. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.H.; Liu, S.S.; Xiao, Q.F.; Qin, L.T.; Xia, Z.N. PLS variable selection procedure in QSAR study on the performance of organic compounds through polyethylene membrane. Acta Chim. Sin. 2011, 10, 1232–1238. [Google Scholar]
- Molecular Operating Environment (MOE); 2013.08; Chemical Computing Group Inc.: Montreal, QC, Canada, 2014.
- Dragon6, 2010. Dragon 6 User’s Manual; Talete srl: Milano, Italy, 2010. Available online: http://www.vcclab.org/lab/edragon/ (accessed on 6 May 2015).
- Eriksson, L.; Johansson, E. Multivariate design and modelling in QSAR. Chemom. Intell. Lab. Syst. 1996, 34, 1–19. [Google Scholar] [CrossRef]
- Eriksson, L.; Johansson, E.; Kettaneh-Wold, N.; Wold, S. Multi-and Megavariate Data Analysis, Principles and Applications; Umetrics AB: Umea, Sweden, 2001. [Google Scholar]
- Giaginis, C.; Theocharis, S.; Tsantili-Kakoulidou, A. Quantitative structure-activity relationships for PPAR-gamma binding and gene transactivation of tyrosine-based agonists using multivariate statistics. Chem. Biol. Drug Des. 2008, 72, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, M.P.; Teran, C.; Saiz-Urra, L.; Teijeira, M. Variable selection methods in QSAR: An overview. Curr. Top. Med. Chem. 2008, 8, 1606–1627. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Chong, I.G.; Jun, C.H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Shahlaei, M.; Fassihi, A.; Saghaie, L.; Zare, A. Prediction of partition coefficient of some 3-hydroxy pyridine-4-one derivatives using combined partial least square regression and genetic algorithm. Res. Pharm. Sci. 2014, 9, 143–153. [Google Scholar] [PubMed]
- Vucicevic, J.; Nikolic, K.; Dobričić, V.; Agbaba, D. Prediction of blood–brain barrier permeation of α-adrenergic and imidazoline receptor ligands using PAMPA technique and quantitative-structure permeability relationship analysis. Eur. J. Pharm. Sci. 2015, 68, 94–105. [Google Scholar] [CrossRef] [PubMed]
- Qin, L.T.; Liu, S.S.; Chen, F.; Xiao, Q.F.; Wu, Q.S. Chemometric model for predicting retention indices of constituents of essential oils. Chemosphere 2013, 90, 300–305. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Zhang, C.T. Review: Prediction of protein structural classes. Crit. Rev. Biochem. Mol. Biol. 1995, 30, 275–349. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Some remarks on protein attribute prediction and pseudo amino acid composition (50th Anniversary Year Review). J. Theor. Biol. 2011, 273, 236–247. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, L.; Jaworska, J.; Worth, A.P.; Cronin, M.T.D.; McDowell, R.M.; Gramatica, P. Methods for reliability and uncertainty assessment and for applicability evaluations of classification- and regression-based QSARs. Environ. Health Perspect. 2003, 111, 1361–1375. [Google Scholar] [CrossRef] [PubMed]
- Wold, S. PLS for multivariate linear modeling. In Chemometric Methods in Molecular Design; Van de Waterbeemd, H., Ed.; Verlag-Chemie: Weinheim, Germany, 1995; Volume 2, pp. 195–218. [Google Scholar]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef] [PubMed]
- Giaginis, C.; Tsantili-Kakoulidou, A.; Theocharis, S. Assessing Drug Transport across the Human Placental Barrier: From in Vivo and in Vitro Measurements to the ex Vivo Perfusion Method and in silico Techniques. Curr. Pharm. Des. 2011, 12, 804–813. [Google Scholar]
- Giaginis, C.; Theocharis, S.; Tsantili-Kakoulidou, A. Current toxicological aspects on drug and chemical transport and metabolism across the human placental barrier. Expert Opin. Drug Metab. Toxicol. 2012, 8, 1263–1275. [Google Scholar] [CrossRef] [PubMed]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; WILEY VCH: New York, NY, USA, 2009. [Google Scholar]
- Giaginis, C.; Zira, A.; Theocharis, S.; Tsantili-Kakoulidou, A. Simple physicochemical properties as effective filters for risk estimation of drug transport across the human placental barrier. Rev. Clin. Pharmacol. Pharmacokinet. 2008, 22, 146–148. [Google Scholar]
- Challier, J.C. Criteria for evaluating perfusing experiments and presentation of the results. Contrib. Gynecol. Obstet. 1985, 13, 77–84. [Google Scholar] [PubMed]
- Challier, J.C.; Guerre-Millo, M.; Nandakumaran, M.; Gerbaut, L.; d’Athis, P. Clearance of compounds of different molecular size in the human placenta in vitro. Biol. Neonate 1985, 48, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Judith, A.S.; Anjali, G.; Scott, M.; Larry, C.; Jeffrey, C.; Joseph, L.A.; Susan, M.R.; Jerrie, S.R. Utilization of an ex vivo human placental perfusion model to predict potential fetal exposure to carboplatin during pregnancy. Am. J. Obstet. Gynecol. 2014, 210, 275.e1–275.e9. [Google Scholar] [PubMed]
- Teófilo, R.F.; Martins, J.P.A.; Ferreira, M.M.C. Sorting variables by using informative vectors as a strategy for feature selection in multivariate regression. J. Chemom. 2009, 23, 32–48. [Google Scholar] [CrossRef]
- Chirico, N.; Gramatica, P. Real external predictivity of QSAR models: How to evaluate it? Comparison of different validation criteria and proposal of using the concordance correlation coefficient. J. Chem. Inf. Model. 2011, 51, 2320–2335. [Google Scholar] [CrossRef] [PubMed]
- Consonni, V.; Ballabio, D.; Todeschini, R. Comments on the definition of the Q2 parameter for QSAR validation. J. Chem. Inf. Model. 2009, 49, 1669–1678. [Google Scholar] [CrossRef] [PubMed]
- Consonni, V.; Ballabio, D.; Todeschini, R. Evaluation of model predictive ability by external validation techniques. J. Chemom. 2010, 24, 194–201. [Google Scholar] [CrossRef]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci. 2003, 22, 69–77. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.-H.; Xia, Z.-N.; Yan, L.; Liu, S.-S. Prediction of Placental Barrier Permeability: A Model Based on Partial Least Squares Variable Selection Procedure. Molecules 2015, 20, 8270-8286. https://doi.org/10.3390/molecules20058270
Zhang Y-H, Xia Z-N, Yan L, Liu S-S. Prediction of Placental Barrier Permeability: A Model Based on Partial Least Squares Variable Selection Procedure. Molecules. 2015; 20(5):8270-8286. https://doi.org/10.3390/molecules20058270
Chicago/Turabian StyleZhang, Yong-Hong, Zhi-Ning Xia, Li Yan, and Shu-Shen Liu. 2015. "Prediction of Placental Barrier Permeability: A Model Based on Partial Least Squares Variable Selection Procedure" Molecules 20, no. 5: 8270-8286. https://doi.org/10.3390/molecules20058270
APA StyleZhang, Y.-H., Xia, Z.-N., Yan, L., & Liu, S.-S. (2015). Prediction of Placental Barrier Permeability: A Model Based on Partial Least Squares Variable Selection Procedure. Molecules, 20(5), 8270-8286. https://doi.org/10.3390/molecules20058270






