Quantitative Structure–Property Relationship (QSPR) Models for a Local Quantum Descriptor: Investigation of the 4- and 3-Substituted-Cinnamic Acid Esterification
Abstract
:1. Introduction


Theoretical Background and Computational Details
2. Methodology
2.1. Synthesis and Characterization
2.2. Computational Methods
2.3. Statistics Analysis
3. Results and Discussion
3.1. Theoretical Calculations

3.2. Step 1: O-Protonation for Acid-Catalyzed 4- or 3-X-Cinnamic Acid Esterification
| X | σp | EHOMO-x2 | EHOMO-x1 | EHOMO | ELUMO | η | η1 | η2 | B3LYP | M06-2X | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔH1298K | O-Charge | ƒ−O | ΔH1298K | O-Charge | ƒ−O | ||||||||||
| (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (kcal/mol) | (kcal/mol) | |||||||
| 1 | H | 0 | −0.4839 | −0.4547 | −0.3241 | 0.034 | −0.1791 | −0.2444 | −0.2590 | −39.35 | −0.609 | −0.114 | −34.23 | −0.614 | −0.104 |
| 2 | 4-NO2 | 0.78 | −0.5032 | −0.4726 | −0.3559 | 0.001 | −0.1785 | −0.2369 | −0.2522 | −29.71 | −0.596 | −0.114 | −24.98 | −0.603 | −0.107 |
| 3 | 3-NO2 | 0.71 | −0.4963 | −0.4676 | −0.3498 | 0.021 | −0.1856 | −0.2445 | −0.2589 | −31.51 | −0.597 | −0.116 | −26.68 | −0.603 | −0.107 |
| 4 | 4-F | 0.15 | −0.4874 | −0.4584 | −0.3288 | 0.034 | −0.1815 | −0.2463 | −0.2608 | −38.08 | −0.608 | −0.112 | −33.04 | −0.613 | −0.103 |
| 5 | 3-F | 0.34 | −0.4894 | −0.4609 | −0.3349 | 0.033 | −0.1838 | −0.2468 | −0.2611 | −36.00 | −0.604 | −0.112 | −30.87 | −0.610 | −0.103 |
| 6 | 4-Cl | 0.23 | −0.4862 | −0.4600 | −0.3274 | 0.035 | −0.1814 | −0.2477 | −0.2608 | −37.97 | −0.607 | −0.103 | −32.47 | −0.612 | −0.095 |
| 7 | 4-CN | 0.70 | −0.4948 | −0.4697 | −0.3440 | 0.015 | −0.1795 | −0.2423 | −0.2549 | −31.92 | −0.599 | −0.105 | −26.77 | −0.605 | −0.099 |
| 8 | 4-OCH3 | −0.28 | −0.4780 | −0.4495 | −0.3053 | 0.031 | −0.1682 | −0.2403 | −0.2546 | −46.04 | −0.616 | −0.098 | −40.24 | −0.620 | −0.089 |
| 9 | 4-OH | −0.46 | −0.4804 | −0.4512 | −0.3096 | 0.030 | −0.1697 | −0.2405 | −0.2551 | −43.97 | −0.614 | −0.103 | −38.60 | −0.618 | −0.093 |
| 10 | 4-CH3 | −0.17 | −0.4809 | −0.4517 | −0.3145 | 0.034 | −0.1742 | −0.2428 | −0.2574 | −42.33 | −0.612 | −0.106 | −36.88 | −0.617 | −0.097 |
| X | σp | EHOMO-x2 | EHOMO-x1 | EHOMO | ELUMO | η | η3 | η4 | B3LYP | M06-2X | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔH2298K | C-Charge | ƒ+C | ΔH2298K | C-Charge | ƒ+C | ||||||||||
| (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (Hartrees) | (kcal/mol) | (kcal/mol) | |||||||
| 1 | H | 0 | −0.8494 | −0.7366 | −0.4652 | −0.133 | −0.1660 | −0.3018 | −0.3582 | 37.50 | 0.809 | −0.165 | 31.09 | 0.854 | −0.187 |
| 2 | 4-NO2 | 0.78 | −0.8703 | −0.7555 | −0.4938 | −0.158 | −0.1678 | −0.2987 | −0.3560 | 27.38 | 0.822 | −0.153 | 21.51 | 0.869 | −0.179 |
| 3 | 3-NO2 | 0.71 | −0.8658 | −0.7513 | −0.4888 | −0.149 | −0.1701 | −0.3013 | −0.3586 | 29.30 | 0.821 | −0.164 | 23.35 | 0.868 | −0.188 |
| 4 | 4-F | 0.15 | −0.8525 | −0.7381 | −0.4682 | −0.135 | −0.1666 | −0.3016 | −0.3588 | 36.18 | 0.806 | −0.163 | 29.90 | 0.851 | −0.185 |
| 5 | 3-F | 0.34 | −0.8575 | −0.7439 | −0.4719 | −0.142 | −0.1651 | −0.3011 | −0.3579 | 34.03 | 0.814 | −0.165 | 27.67 | 0.860 | −0.188 |
| 6 | 4-Cl | 0.23 | −0.8512 | −0.7380 | −0.4590 | −0.138 | −0.1607 | −0.3002 | −0.3568 | 35.98 | 0.805 | −0.157 | 29.26 | 0.851 | −0.179 |
| 7 | 4-CN | 0.70 | −0.8647 | −0.7506 | −0.4753 | −0.154 | −0.1607 | −0.2984 | −0.3554 | 29.70 | 0.817 | −0.155 | 23.36 | 0.864 | −0.178 |
| 8 | 4-OCH3 | −0.28 | −0.8329 | −0.7161 | −0.4391 | −0.120 | −0.1596 | −0.2981 | −0.3565 | 44.38 | 0.785 | −0.152 | 37.31 | 0.829 | −0.171 |
| 9 | 4-OH | −0.46 | −0.8386 | −0.7227 | −0.4467 | −0.124 | −0.1614 | −0.2994 | −0.3574 | 42.28 | 0.790 | −0.155 | 35.68 | 0.835 | −0.176 |
| 10 | 4-CH3 | −0.17 | −0.8425 | −0.7283 | −0.4517 | −0.127 | −0.1623 | −0.3006 | −0.3577 | 40.53 | 0.800 | −0.159 | 33.80 | 0.846 | −0.181 |
| Entry | Correlation | Statistic Parameters, from B3LYP Data | Statistic Parameters, from M06-2X Data | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a n | b r2 | c Sd | d F | e a | f b | a n | b r2 | c Sd | d F | e a | f b | ||
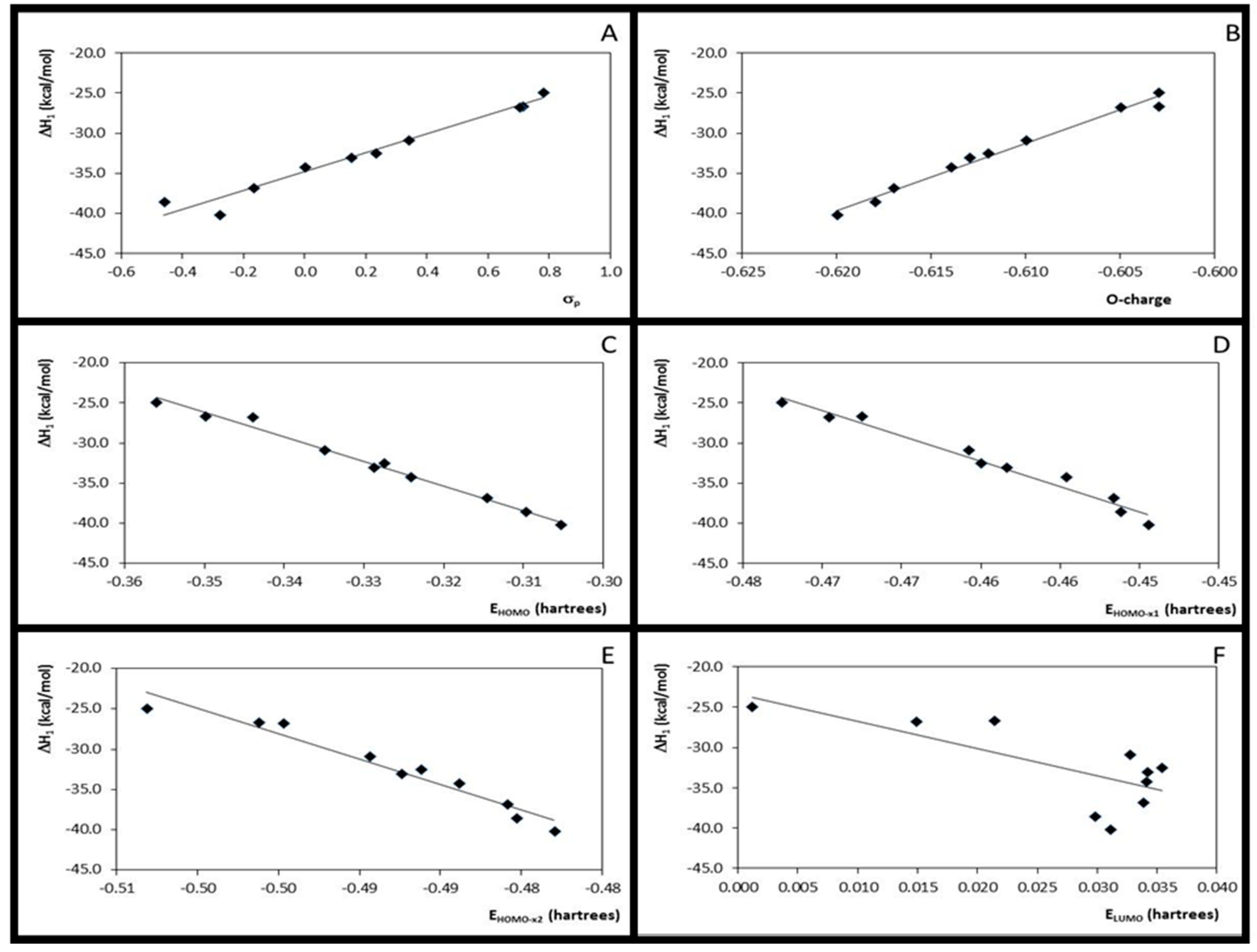
| 1 | ΔH1 × σp | 10 | 0.96 | 1.190 | 183.76 | 12.332 | −40.156 | 10 | 0.97 | 1.012 | 231.80 | 11.773 | −34.831 |
| 2 | ΔH1 × EHOMO | 10 | 0.99 | 0.528 | 967.21 | −322.772 | −144.019 | 10 | 0.99 | 0.600 | 674.59 | −306.266 | −133.368 |
| 3 | ΔH1 × EHOMO-x1 | 10 | 0.97 | 1.085 | 222.72 | −663.279 | −342.544 | 10 | 0.97 | 0.942 | 268.58 | −632.353 | −323.116 |
| 4 | ΔH1 × EHOMO-x2 | 10 | 0.95 | 1.299 | 152.98 | −669.555 | −364.463 | 10 | 0.95 | 1.282 | 141.37 | −635.148 | −342.458 |
| 5 | ΔH1 × ELUMO | 10 | 0.53 | 4.003 | 8.96 | −357.354 | −28.077 | 10 | 0.53 | 3.806 | 8.95 | −339.609 | −23.341 |
| 6 | ΔH1 × η1 | 10 | 0.00 | 5.827 | 0.003 | 30.301 | −30.319 | 10 | 0.00 | 5.540 | 0.002 | 22.962 | −26.891 |
| 7 | ΔH1 × η2 | 10 | 0.00 | 5.821 | 0.021 | 90.116 | −14.488 | 10 | 0.00 | 5.532 | 0.023 | 89.398 | −9.459 |
| 8 | ΔH1 × O-charge | 10 | 0.99 | 0.610 | 722.05 | 774.924 | 432.069 | 10 | 0.98 | 0.687 | 512.40 | 840.187 | 481.298 |
| 9 | O-charge × σ | 10 | 0.96 | 0.001 | 197.14 | 0.016 | −0.609 | 10 | 0.96 | 0.001 | 177.59 | 0.014 | −0.614 |
| 10 | ΔH1 × ƒ−O | 10 | 0.45 | 4.324 | 6.53 | −608.324 | −103.572 | 10 | 0.61 | 3.445 | 12.69 | −669.405 | −99.216 |
3.3. Step 2: The Nucleophilic Attack by Ethanol for Acid-Catalysed 4- or 3-X-Cinnamic Acid Esterification
3.4. Global Reaction: Theoretical and Experimental Data Compared

| Entry | Correlation | Statistic Parameters, from B3LYP Data | Statistic Parameters, from M06-2X Data | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a n | b r2 | c Sd | d F | e a | f b | a n | b r2 | c Sd | d F | e a | f b | ||
| 1 | ΔH2 × σp | 10 | 0.96 | 1.224 | 188.79 | −12.848 | 38.295 | 10 | 0.97 | 1.036 | 236.73 | −12.179 | 31.728 |
| 2 | ΔH2 × EHOMO | 10 | 0.94 | 1.502 | 122.67 | 315.800 | 182.878 | 10 | 0.92 | 1.575 | 97.82 | 295.839 | 167.144 |
| 3 | ΔH2 × EHOMO-x1 | 10 | 0.98 | 0.768 | 491.36 | 440.946 | 361.197 | 10 | 0.98 | 0.784 | 418.70 | 415.698 | 336.128 |
| 4 | ΔH2 × EHOMO-x2 | 10 | 1.00 | 0.395 | 1876.39 | 465.138 | 432.281 | 10 | 0.99 | 0.502 | 1034.83 | 438.358 | 403.016 |
| 5 | ΔH2 × ELUMO | 10 | 0.98 | 0.846 | 404.12 | 442.778 | 96.782 | 10 | 0.98 | 0.716 | 504.41 | 418.814 | 87.044 |
| 6 | ΔH2 × η3 | 10 | 0.00 | 6.065 | 0.010 | 143.048 | 78.656 | 10 | 0.00 | 5.728 | 0.003 | 76.029 | 52.109 |
| 7 | ΔH2 × η4 | 10 | 0.04 | 5.958 | 0.299 | −975.353 | −312.797 | 10 | 0.04 | 5.601 | 0.370 | −1020.168 | −335.244 |
| 8 | ΔH2 × C-charge | 10 | 0.93 | 1.580 | 110.04 | −442.790 | 393.012 | 10 | 0.94 | 1.460 | 115.22 | −390.752 | 362.487 |
| 9 | C-charge × σ | 10 | 0.87 | 0.005 | 55.32 | 0.027 | 0.802 | 10 | 0.88 | 0.005 | 58.93 | 0.029 | 0.847 |
| 10 | ΔH2 × ƒ+C | 10 | 0.03 | 5.987 | 0.22 | 184.019 | 64.947 | 10 | 0.18 | 5.179 | 1.79 | 405.806 | 102.824 |
| Entry | Correlation | Statistic Parameters, from B3LYP Data | |||||
|---|---|---|---|---|---|---|---|
| a n | b r2 | c Sd | d F | e a | f b | ||
| 1 | Yield × σp | 10 | 0.89 | 3.659 | 64.52 | 22.459 | 61.408 |
| 2 | Yield × ΔHr | 9 | 0.88 | 2.823 | 53.91 | −33.197 | 2.085 |
| 3 | σp × ΔHr | 10 | 0.96 | 9.307 | 189.96 | −186.546 | −346.005 |
| 4 | Yield × ΔH1 | 9 | 0.91 | 2.439 | 74.59 | 0.014 | 119.852 |
| 5 | Yield × ΔH2 | 9 | 0.91 | 2.438 | 74.68 | −0.013 | 115.165 |
| 6 | Yield × EHOMO-x2 (CA) g | 9 | 0.88 | 2.870 | 51.93 | −0.914 | −378.864 |
| 7 | Yield × EHOMO-x1 (CA) g | 9 | 0.91 | 2.418 | 76.06 | −0.092 | −358.353 |
| 8 | Yield × EHOMO (CA) g | 9 | 0.90 | 2.613 | 64.10 | −0.045 | −81.343 |
| 9 | Yield × ELUMO (PCA) h | 9 | 0.94 | 2.019 | 112.08 | −0.604 | −16.153 |
| 10 | Yield × O-charge (CA) g | 9 | 0.87 | 2.900 | 50.73 | 1.059 | 709.663 |
| 11 | Yield × C-charge (PCA) h | 10 | 0.80 | 4.816 | 33.86 | 0.748 | −538.252 |
| 12 | Yield × ƒ−O (CA) g | 10 | 0.32 | 9.030 | 3.90 | −0.982 | −40.491 |
| 13 | Yield × η (CA) g | 10 | 0.60 | 6.979 | 11.93 | −1396.507 | −182.887 |
| 14 | Yield × η1 (CA) g | 10 | 0.01 | 10.932 | 0.123 | −379.821 | −26.491 |
| 15 | Yield × η2 (CA) g | 10 | 0.01 | 10.978 | 0.05 | −275.984 | −5.160 |
| 16 | Yield × η (PCA) h | 10 | 0.24 | 9.595 | 2.54 | −1431.193 | −168.858 |
| 17 | Yield × η3 (PCA) h | 10 | 0.00 | 10.997 | 0.03 | −449.46 | −68.993 |
| 18 | Yield × η4 (PCA) h | 10 | 0.05 | 10.726 | 0.43 | 2100.165 | −816.352 |
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Verstrepen, K.J.; Derdelinckx, G.; Dufour, J.P.; Winderickx, J.; Thevelein, J.M.; Pretorius, I.S.; Delvaux, F.R. Flavor-active esters: Adding fruitiness to beer. J. Biosci. Bioeng. 2003, 96, 110–118. [Google Scholar] [CrossRef]
- Parveen, I.; Threadgill, M.D.; Hauck, B.; Donnison, I.; Winters, A. Isolation, identification and quantitation of hydroxycinnamic acid conjugates, potential platform chemicals, in the leaves and stems of Miscanthus-giganteususing LC-ESI-MSn. Phytochemistry 2011, 72, 2376–2384. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mamidi, N.; Sukhamoy, G.; Sahoo, J.; Manna, D. Alkyl cinnamates as regulator for the C1 domain of protein kinase C isoforms. Chem. Phys. Lipids 2012, 165, 320–330. [Google Scholar] [CrossRef] [PubMed]
- Waghamare, S.R.; Gaikwad, H.H. Facile water mediated Wittig reaction approach for the synthesis of bioactive aryl and benzyl cinnamates. J. Chem. Pharm. Res. 2012, 4, 2415–2421. [Google Scholar]
- Promkatkaew, M.; Suramitr, S.; Karpkird, T.; Ehara, M.; Hannongbua, S. Absorption and emission properties of various substituted cinnamic acids and cinnamates, based on TDDFT investigation. Int. J. Quantum Chem. 2013, 113, 542–554. [Google Scholar] [CrossRef]
- Neil, J.L.; Steber, A.L.; Muckle, M.T.; Zaleski, D.P.; Lattanzi, V.; Spezzano, S.; McCarthy, M.C.; Remijan, A.J.; Friedel, D.N.; Weaver, S.L.W.; et al. Spatial distributions and interstellar reaction processes. J. Phys. Chem. A 2011, 115, 6472–6480. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.P.; Tandon, P.; Mishra, P. Some new reaction pathways for the formation of cytosine, in interstellar space—A quantum chemical study. Adv. Space Res. 2013, 51, 797–811. [Google Scholar] [CrossRef]
- Santos, A.C.S.; Echevarria, A. Electronic effects on 13C-NMR chemical shifts of substituted 1,3,4-thiadiazolium salts. Magn. Reson. Chem. 2001, 39, 182–186. [Google Scholar] [CrossRef]
- Echevarria, A.; Nascimento, M.G.; Miller, J. Carbon-13 NMR and azomethine proton NMR spectra of substituted N-benzylideneanilines and Hammett correlations. Magn. Reson. Chem. 1985, 23, 809–813. [Google Scholar] [CrossRef]
- Oliveira, R.C.M.; Bauerfeldt, G.F. Implementation of a variational code for the calculation of rate constants and application to barrier less dissociation and radical recombination reactions: CH3OH = CH3 + OH. Int. J. Quantum Chem. 2012, 112, 3132–3140. [Google Scholar] [CrossRef]
- Bauerfeldt, G.F.; Cardozo, T.M.; Pereira, M.S.; da Silva, C.O. The anomeric effect: The dominance of exchange effects in closed-shell systems. Org. Biomol. Chem. 2013, 11, 299–308. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.B.; Byrd, H.; O’Donnell, S.E.; Davis, E. Hammett parameter and molecular-modeling correlations of substituent effects on esterification kinetics. J. Chem. Educ. 2010, 87, 845–847. [Google Scholar] [CrossRef]
- Borkar, V.T.; Bonde, S.L.; Dangat, V.T.A. Quantitative structure-reactivity assessment of phenols by investigation of rapid iodination kinetics using hydrodynamic voltammetry: Applicability of the Hammett equation in aqueous medium. Int. J. Chem. Kinet. 2013, 45, 693–702. [Google Scholar] [CrossRef]
- Hammett, L. Effect of structure upon the reactions of organic compounds. Benzene derivatives. J. Am. Chem. Soc. 1937, 59, 96–103. [Google Scholar] [CrossRef]
- Sá, M.M.; Ferreira, M.; Caramori, F.F.; Zaramello, L.; Bortoluzzi, A.J.; Faggion, D., Jr.; Domingos, J.B. Investigating the Ritter type reaction of α-methylene-β-hydroxy esters in acidic medium: Evidence for the intermediacy of an allylic cation. Eur. J. Org. Chem. 2013, 23, 5180–5187. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Ramanathan, V.; Mishra, B.K. Influence of the substituents on the CH...π interaction: Benzene-methane complex. J. Phys. Chem. A 2013, 117, 6687–6694. [Google Scholar] [CrossRef] [PubMed]
- Laurence, C.; Gal, J.F. Lewis Basicity and Affinity Scales: Data and Measurement; John Wiley & Sons Ltd.: London, UK, 2010; pp. 1–106. [Google Scholar]
- Pearson, R.G. Hard and soft acids and bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
- Pearson, R.G. Hard and soft acids and bases (HSAB). I. Fundamental principles. J. Chem. Educ. 1968, 45, 581–587. [Google Scholar] [CrossRef]
- Pearson, R.G. Recent advances in the concept of hard and soft acids and bases. J. Chem. Educ. 1987, 64, 561–567. [Google Scholar] [CrossRef]
- Pearson, R.G. Chemical hardness and density functional theory. J. Chem. Sci. 2005, 117, 369–377. [Google Scholar] [CrossRef]
- Klopman, G. Chemical reactivity and the concept of charge- and frontier-controlled reactions. J. Am. Chem. Soc. 1968, 90, 223–334. [Google Scholar] [CrossRef]
- Ho, T.L. Analysis of some synthetic reactions by the HSAB principle. J. Chem. Educ. 1978, 55, 355–360. [Google Scholar] [CrossRef]
- Eryurek, M.; Bayari, S.H.; Yuksel, D.; Hanhan, M.E. Density functional investigation of the molecular structures, vibrational spectra and molecular properties of sulfonated pyridyl imine ligands and their palladium complexes. Comput. Theor. Chem. 2013, 1013, 109–115. [Google Scholar] [CrossRef]
- Anderson, J.S.M.; Melin, J.; Ayres, P.W. Conceptual density-functional theory for general chemical reactions, including those that are neither charge- nor frontier-orbital-controlled. 1. Theory and derivation of a general-purpose reactivity indicator. J. Chem. Theory Comput. 2007, 3, 358–374. [Google Scholar] [CrossRef]
- Allison, T.C.; Tong, Y.Y.J. Application of the condensed Fukui function to predict reactivity in core–shell transition metal nanoparticles. Electrochim. Acta 2013, 101, 334–340. [Google Scholar] [CrossRef]
- Wu, D.; Jia, D.; Liu, A.; Liu, L.; Guo, J. Theoretical study on the reactivity of Lewis pairs PR3/B(C6F5)3 (R = Me, Ph, tBu, C6F5). Chem. Phys. Lett. 2012, 541, 1–6. [Google Scholar] [CrossRef]
- Cárdenas, C. The Fukui potential is a measure of the chemical hardness. Chem. Phys. Lett. 2011, 513, 127–129. [Google Scholar] [CrossRef]
- Méndez, M.; Cedillo, A. Gas phase Lewis acidity and basicity scales for boranes, phosphines and amines based on the formation of donor-acceptor complexes. Comput. Theor. Chem. 2013, 1011, 44–56. [Google Scholar] [CrossRef]
- Pérez, P.; Contreras, R.; Aizman, A. Sites of protonation of N2-substituted N1,N1-dimethyl formamidines from regional reactivity índices. Mol. Struct. TheoChem 1999, 493, 267–273. [Google Scholar] [CrossRef]
- Melin, J.; Aparicio, F.; Subramanian, V.; Galván, M.; Chattaraj, P.K. Is the Fukui function a right descriptor of hard-hard interactions? J. Phys. Chem. A 2004, 108, 2487–2491. [Google Scholar] [CrossRef]
- Da Silva, R.R.; Ramalho, T.C.; Santos, J.M.; Figueroa-Villar, J.D. On the limits of highest-occupied molecular orbital driven reactions: The frontier effective-for-reaction molecular orbital concept. J. Phys. Chem. A 2006, 110, 1031–1040. [Google Scholar] [CrossRef] [PubMed]
- Maksic, Z.; Vianello, R. Comment on the paper “On the limits of highest-occupied molecular orbital driven reactions: The frontier effective-for-reaction molecular orbital concept”. J. Phys. Chem. A 2006, 110, 10651–10652. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, R.R.; Ramalho, T.C.; Santos, J.M.; Figueroa-Villar, J.D. Reply to “Comment on the paper ‘On the limits of highest-occupied molecular orbital driven reactions: The frontier effective-for-reaction molecular orbital concept’”. J. Phys. Chem. A 2006, 110, 10653–10654. [Google Scholar] [CrossRef]
- Da Silva, R.R.; Santos, J.M.; Ramalho, T.C.; Figueroa-Villar, D. Concerning the FERMO concept and Pearson’s hard and soft acid-base principle. J. Braz. Chem. Soc. 2006, 17, 223–226. [Google Scholar] [CrossRef]
- Costa, E.B.; Trsic, M. A quantum chemical study on a set of non-imidazole H3 antihistamine molecules. J. Mol. Graph. Model. 2010, 28, 657–663. [Google Scholar] [CrossRef] [PubMed]
- Fuentealba, P.; David, J.; Guerra, D. Density functional based reactivity parameters: Thermodynamic or kinetic concepts? J. Mol. Struct. TheoChem 2010, 943, 127–137. [Google Scholar] [CrossRef]
- Rodrigues-Santos, C.E.; Echevarria, A. Convenient syntheses of pyrazolo[3,4-b]pyridin-6-ones using either microwave or ultrasound irradiation. Tetrahedron Lett. 2011, 52, 336–340. [Google Scholar] [CrossRef]
- Xu, C.; Chen, G.; Fu, C.; Huang, X. Carbonyl homologation via α-trimethylsilyl β-lactone rearrangements. A nonbasic alternative to the Wittig reaction. Synth. Commun. 1995, 25, 15–20. [Google Scholar]
- Wang, H.; Zhang, K.; Liu, Y.Z.; Lin, M.Y.; Lu, J.X. Electrochemical carboxylation of cinnamate esters in MeCN. Tetrahedron 2008, 64, 314–318. [Google Scholar] [CrossRef]
- Silverstein, R.M.; Webster, F.X. Spectrometric Identification of Organic Compounds, 7th ed.; Wiley: Hoboken, NJ, USA, 2005; p. 502. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Cramer, C.J. Essentials of Computational Chemistry Theories and Models; John Wiley and Sons: Hoboken, UK, 2004; pp. 55–70. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Oliveira, D.B.; Gaudio, A.C. BuildQSAR: A new computer program for QSAR analysis. Quant. Struct. Act. Relatsh. 2000, 19, 599–601. [Google Scholar] [CrossRef]
- The Spectroscopic Data of the Ethyl Cinnamates Esters are Available on the Spectral Database of Organic Compounds in. Available online: http://www.sdbs.db.aist.go.jp (accessed on 11 July 2013).
- Padmanabhan, J.; Parthasarathy, R.; Sarkar, U.; Subramanian, V.; Chattaraj, P.K. Effect of solvation on the condensed Fukui function and the generalized philicity index. Chem. Phys. Lett. 2004, 383, 122–128. [Google Scholar]
- Sample Availability: Not available.
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues-Santos, C.E.; Echevarria, A.; Sant’Anna, C.M.R.; Bitencourt, T.B.; Nascimento, M.G.; Bauerfeldt, G.F. Quantitative Structure–Property Relationship (QSPR) Models for a Local Quantum Descriptor: Investigation of the 4- and 3-Substituted-Cinnamic Acid Esterification. Molecules 2015, 20, 17493-17510. https://doi.org/10.3390/molecules200917493
Rodrigues-Santos CE, Echevarria A, Sant’Anna CMR, Bitencourt TB, Nascimento MG, Bauerfeldt GF. Quantitative Structure–Property Relationship (QSPR) Models for a Local Quantum Descriptor: Investigation of the 4- and 3-Substituted-Cinnamic Acid Esterification. Molecules. 2015; 20(9):17493-17510. https://doi.org/10.3390/molecules200917493
Chicago/Turabian StyleRodrigues-Santos, Cláudio E., Aurea Echevarria, Carlos M. R. Sant’Anna, Thiago B. Bitencourt, Maria G. Nascimento, and Glauco F. Bauerfeldt. 2015. "Quantitative Structure–Property Relationship (QSPR) Models for a Local Quantum Descriptor: Investigation of the 4- and 3-Substituted-Cinnamic Acid Esterification" Molecules 20, no. 9: 17493-17510. https://doi.org/10.3390/molecules200917493
APA StyleRodrigues-Santos, C. E., Echevarria, A., Sant’Anna, C. M. R., Bitencourt, T. B., Nascimento, M. G., & Bauerfeldt, G. F. (2015). Quantitative Structure–Property Relationship (QSPR) Models for a Local Quantum Descriptor: Investigation of the 4- and 3-Substituted-Cinnamic Acid Esterification. Molecules, 20(9), 17493-17510. https://doi.org/10.3390/molecules200917493