Genealogy of Conjugated Acyclic Polyenes
Abstract
:1. Introduction
2. Preliminary Discussions
2.1. Planar Conjugated Acyclic Polyene Isomers
2.2. Mean Length of Conjugation
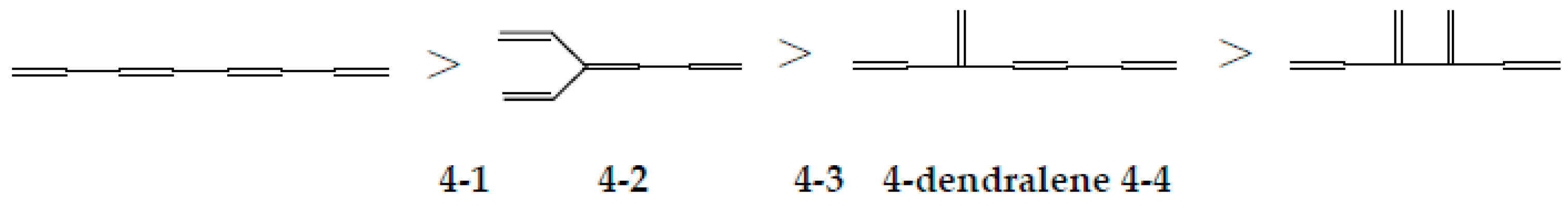
2.3. Hückel Molecular Orbital Method and Eπ
2.4. Topological Index
3. Results and Discussion
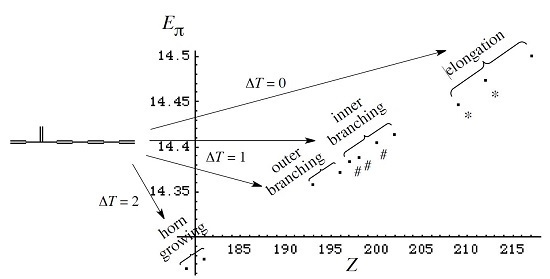
3.1. Vinyl Addition and Horn Growing
- (i)
- Relative stability among the isomers derived by elongation, branching, and horn growing can roughly be estimated according to their respective ΔT value in the reverse of this order.
- (ii)
- ΔL can discriminate between the relative stability of isomers derived by inner and outer branching.
- (iii)
- The lesser stability of outer branching relative to inner branching can be attributed to the short-range conjugation caused by the vinyl group addition, in contrast to the wide-range of the inner branching (elaborated upon later).
3.2. Discriminative Power of Z
- (iv)
- Z-index can accurately discriminate the stability difference among the same type of growing process, while ΔL cannot.
- (v)
- Deep understanding of the structure–stability relation of conjugated acyclic polyenes can be obtained by the complementary discussion with their T, L, and Z values, even without the help of a computer.
3.3. Beyond Conjugated Acyclic Polyenes
 , and
, and  , etc.? Actually, the Zs of 6-3 and 6-4 are calculated to be 11 and 10, respectively, in parallel with their low Eπ values of 6.159 and 6.000 relative to their singlet isomers, 6-1 and 6-2. While we can systematically discuss the stability of all these 6π conjugated systems by using their Z and T values, we are confronted with the difficulty of counting L values for radicals. However, try to expand our definition of L to conjugated acyclic polyene radicals as in Figure 11, where we take the average L of the length of conjugation l for all the possible paths in the given radical. This time, the value of l composed of b CC bonds is tentatively chosen as (b + 1)/2, which is consistent with what has already been defined for stable (singlet) conjugated acyclic polyene molecules.
, etc.? Actually, the Zs of 6-3 and 6-4 are calculated to be 11 and 10, respectively, in parallel with their low Eπ values of 6.159 and 6.000 relative to their singlet isomers, 6-1 and 6-2. While we can systematically discuss the stability of all these 6π conjugated systems by using their Z and T values, we are confronted with the difficulty of counting L values for radicals. However, try to expand our definition of L to conjugated acyclic polyene radicals as in Figure 11, where we take the average L of the length of conjugation l for all the possible paths in the given radical. This time, the value of l composed of b CC bonds is tentatively chosen as (b + 1)/2, which is consistent with what has already been defined for stable (singlet) conjugated acyclic polyene molecules.Conflicts of Interest
Appendix A. Simple Recipe for Calculating the Z-Index of Branched Conjugated Polyenes
| N | G = SN | p(G,k) | ZN | ||||
|---|---|---|---|---|---|---|---|
| k = 0 | 1 | 2 | 3 | 4 | |||
| 1 | ● | 1 | 1 | ||||
| 2 |  | 1 | 1 | 2 | |||
| 3 |  | 1 | 2 | 3 | |||
| 4 |  | 1 | 3 | 1 | 5 | ||
| 5 |  | 1 | 4 | 3 | 8 | ||
| 6 |  | 1 | 5 | 6 | 1 | 13 | |
| 7 |  | 1 | 6 | 10 | 4 | 21 | |
| 8 | 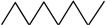 | 1 | 7 | 15 | 10 | 1 | 34 |


References
- Hosoya, H. Mathemaical foundation of organic electron theory—How do π-electrons flow in conjugated systems? J. Mol. Struct. (THEOCHEM) 1999, 461/462, 473–482. [Google Scholar] [CrossRef]
- Hosoya, H. From how to why. Graph-theoretical verification of quantum-mechanical aspects of π-electron behavior in conjugated systems. Bull. Chem. Soc. Jpn. 2003, 76, 2233–2252. [Google Scholar] [CrossRef]
- Hosoya, H. Aromaticity index can predict the stability of polycyclic conjugated hydrocarbons. Monatsh. Chem. 2005, 136, 1037–1054. [Google Scholar] [CrossRef]
- Hosoya, H. How can we explain the stability of conjugated hydrocarbon and heterosubstituted networks by topological descriptors? Curr. Comput. Aided Drug Des. 2010, 6, 225–234. [Google Scholar] [CrossRef]
- Hosoya, H. How can mathematical chemistry contribute to the development of mathematics? Int. J. Philos. Chem. (HYLE) 2013, 19, 87–105. [Google Scholar]
- Hosoya, H. Cross-conjugation at the heart of understanding the electronic theory of organic chemistry. Curr. Org. Chem. 2015, 19, 293–310. [Google Scholar] [CrossRef]
- Hopf, H. Classics in Hydrocarbon Chemistry: Syntheses, Concepts, Perspectives; Wiley-VCH: Weinheim, Germany, 2000; Chapter 11; pp. 251–320. [Google Scholar]
- Gholami, M.; Tykwinski, R.R. Oligomeric and polymeric systems with a cross-conjugated π-framework. Chem. Rev. 2006, 1006, 4997–5027. [Google Scholar] [CrossRef] [PubMed]
- Limacher, P.A.; Lüthi, H.P. Cross-conjugation. Comp. Mol. Sci. 2011, 1, 477–486. [Google Scholar] [CrossRef]
- Dias, J.R. A quantitative metric for conjugation in polyene hydrocarbons having a single classical structure. J. Phys. Chem. A 2014, 118, 10822–10836. [Google Scholar] [CrossRef] [PubMed]
- Gineityte, V. A simple rationale for lowered stabilities of branched and cross-conjugated polyenes. Monatsh. Chem. 2016, 147, 1303–1313. [Google Scholar] [CrossRef]
- Hopf, H.; Sherburn, M.S. (Eds.) Cross Conjugation: Modern Dendralene, Radialene and Fulvene Chemistry; Wiley-VCH: Weinheim, Germany, 2016. [Google Scholar]
- Hosoya, H. Topological index. A newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons. Bull. Chem. Soc. Jpn. 1971, 44, 2332–2339. [Google Scholar] [CrossRef]
- Hosoya, H.; Hosoi, K.; Gutman, I. A topological index for the total π-electron energy. Proof of a generalised Hückel rule for an arbitrary network. Theor. Chim. Acta 1975, 38, 37–47. [Google Scholar] [CrossRef]
- Phelan, N.F.; Orchin, M. Cross-conjugation. J. Chem. Ed. 1968, 45, 633–637. [Google Scholar] [CrossRef]
- Almenningen, A.; Gatial, A.; Grace, D.S.B.; Hopf, H.; Klaeboe, P.; Lehrich, F.; Nielsen, C.J.; Powel, D.L.; Tratteberg, M. The molecular structure of 3-methylene-1,4-pentadiene studied by gaseous electron diffraction, and by vibrational NMR, and ultraviolet spectroscopy. Acta Chem. Scand. 1988, A42, 634–650. [Google Scholar] [CrossRef]
- Norinder, U. Conformational analysis of 3-methylene-1,4-pentadiene using molecular mechanics and quantum mechanical calculations. J. Mol. Struct. (THEOCHEM) 1987, 150, 85–91. [Google Scholar] [CrossRef]
- Cyvin, S.J.; Brunvoll, J.; Brendsdal, E.; Cyvin, B.N. Enumeration of polyene hydrocarbons: A complete mathematical solution. J. Chem. Inf. Comput. Sci. 1995, 35, 743–751. [Google Scholar] [CrossRef]
- Bytautas, I.; Klein, D.J. Formula periodic table for acyclic hydrocarbon isomer classes: Combinatorially averaged graph invariants. Phys. Chem. Chem. Phys. 1999, 1, 5565–5572. [Google Scholar] [CrossRef]
- Bytautas, I.; Klein, D.J. Formula periodic table for the isomer classes of acyclic hydrocarbons—Enumerative and asymptotic characteristics. Croat. Chem. Acta 2000, 73, 331–357. [Google Scholar]
- Knop, J.V.; Muller, W.R.; Szymanski, K.; Trinajstic, N. Computer Generation of Certain Classes of Molecules; SKTH/Kemija u Industriji: Zagreb, Croatia, 1985. [Google Scholar]
- Gutman, I. Acyclic systems with extremal Hückel π-electron energy. Theor. Chim. Acta 1977, 45, 79–87. [Google Scholar] [CrossRef]
- Gutman, I.; Ruscic, B.; Trinajstic, N.; Wilcox, C.F., Jr. Graph theory and molecular orbitals. XII. Acyclic polyenes. J. Chem. Phys. 1975, 62, 3399–3405. [Google Scholar] [CrossRef]
- Hosoya, H. Graphical enumeration of the coefficients of the secular polynomials of the Hückel molecular orbitals. Theor. Chim. Acta 1972, 25, 215–222. [Google Scholar] [CrossRef]
- Hosoya Index. Available online: https://en.wikipedia.org/wiki/Hosoya-index (accessed on 26 May 2017).
- Topological Index. Available online: https://en.wikipedia.org/wiki/Topological index (accessed on 26 May 2017).
- Weisstein, E.W. Hosoya Index. MathWorld-A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/Hosoya Index.html (accessed on 26 May 2017).
- Weisstein, E.W. Topological Index. MathWorld-A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/Topological Index.html (accessed on 26 May 2017).
- Longuet-Higgins, H.C. Resonance structures and MO in unsaturated hydrocarbons. J. Chem. Phys. 1950, 18, 265–274. [Google Scholar] [CrossRef]
- Hess, B.E., Jr.; Schaad, L.J. Hückel molecular orbital n-resonance energies. J. Am. Chem. Soc. 1971, 93, 305–310. [Google Scholar] [CrossRef]
- Schaad, L.J.; Hess, B.E., Jr. Dewar resonance energy. Chem. Rev. 2001, 101, 1465–1476. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I.; Milun, M.; Trinajstic, N. Topological definition of delocalization energy. MATCH 1975, 1, 171–175. [Google Scholar]
- Aihara, J. A new definition of Dewar-type resonance energy. J. Am. Chem. Soc. 1976, 98, 2750–2758. [Google Scholar] [CrossRef]
Sample Availability: Not available. |













| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| No. of isomers | 1 | 1 | 2 | 4 | 11 | 30 | 96 |
| Isomer | Molecular Graph G | Eπ | E(H&S) | Z | PG(x) | T | L |
|---|---|---|---|---|---|---|---|
| 4-1 |  | 9.518 | 9.538 | 34 | x8 − 7x6 + 15x4 – 10x2 +1 | 0 | 4 |
| 4-2 | 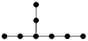 | 9.446 | 9.447 | 32 | x8 − 7x6 + 14x4 – 9x2 +1 | 1 | 3 |
| 4-3 | 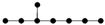 | 9.409 | 9.408 | 31 | x8 − 7x6 + 14x4 – 8x2 +1 | 1 | 2.5 |
| 4-4 | 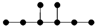 | 9.332 | 9.308 | 29 | x8 − 7x6 + 13x4 – 7x2 +1 | 2 | 2 |
| Type of Growing | Energy Change | ΔT | ΔL |
|---|---|---|---|
| elongation | Stabilization | 0 | + |
| inner branching | small change | +1 | +, 0, – |
| outer branching | Destabilization | +1 | – |
| horn growing | big destabilization | +2 | – – |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosoya, H. Genealogy of Conjugated Acyclic Polyenes. Molecules 2017, 22, 896. https://doi.org/10.3390/molecules22060896
Hosoya H. Genealogy of Conjugated Acyclic Polyenes. Molecules. 2017; 22(6):896. https://doi.org/10.3390/molecules22060896
Chicago/Turabian StyleHosoya, Haruo. 2017. "Genealogy of Conjugated Acyclic Polyenes" Molecules 22, no. 6: 896. https://doi.org/10.3390/molecules22060896
APA StyleHosoya, H. (2017). Genealogy of Conjugated Acyclic Polyenes. Molecules, 22(6), 896. https://doi.org/10.3390/molecules22060896