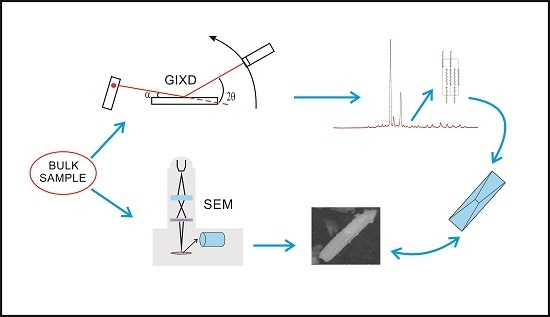
From Intermolecular Interactions to Texture in Polycrystalline Surfaces of 1,?-alkanediols (? = 10–13)
Abstract
:1. Introduction
2. Results and Discussion
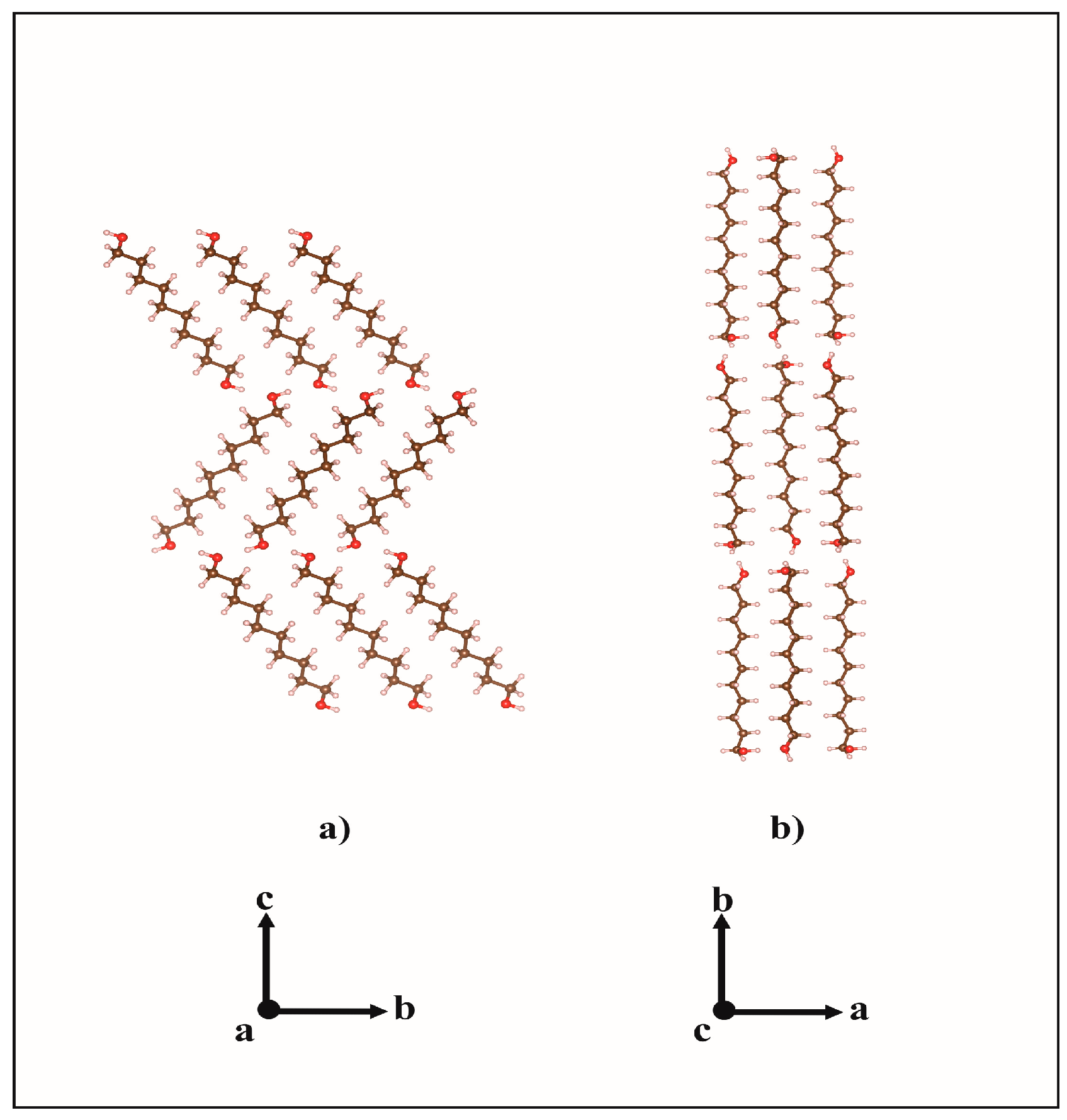
2.1. From Hydrogen Bonds to Herringbone Angle
2.2. Preferred Orientation Analysis
3. Experimental Section
3.1. Samples
3.2. GIXD Data Collection
3.3. Thermal Analysis
4. Structure Determination
4.1. Indexation and Determination of Space Groups (i), and Whole-Pattern Fitting (ii)
4.2. Isomorphic Molecular Replacement (iii), and Lattice Energy Minimization (iv)
4.3. Rigid-Body Rietveld Refinement (v)
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Thalladi, V.H.; Boese, R.; Weiss, H.C. The Melting Point Alternation in α,ω-Alkanediols and α,ω-Alkanediamines: Interplay between Hydrogen Bonding and Hydrophobic Interactions. Angew. Chem. Int. Ed. 2000, 5, 918–922. [Google Scholar] [CrossRef]
- Nakamura, N.; Sato, T. 1,10-Decanediol. Acta Cryst. 1999, 55, 1685–1687. [Google Scholar] [CrossRef]
- Nakamura, N.; Setodi, S.; Ikeya, T. 1,11-Undecanediol. Acta Cryst. 1999, 55, 789–791. [Google Scholar] [CrossRef]
- Nakamura, N.; Setodi, S. 1,12-Dodecanediol. Acta Cryst. 1997, 53, 1885–1887. [Google Scholar] [CrossRef]
- Nakamura, N.; Tanihara, Y.; Takayama, T. 1,13-Tridecanediol. Acta Cryst. 1997, 53, 253–255. [Google Scholar] [CrossRef]
- Nakamura, N.; Sato, T. 1,14-Tetradecanediol. Acta Cryst. 1999, 55, 1687–1689. [Google Scholar] [CrossRef]
- Nakamura, N.; Uno, K.; Watanabe, R.; Ikeya, T.; Ogawa, Y. 1,15-Pentadecanediol. Acta Cryst. 2000, 56, 903–904. [Google Scholar] [CrossRef]
- Nakamura, N.; Yamamoto, T. 1,16-Hexadecanediol. Acta Cryst. 1994, 50, 946–948. [Google Scholar]
- Nakamura, N.; Uno, K.; Ogawa, Y. 1,17-Heptadecanediol. Acta Cryst. 2001, 57, 585–586. [Google Scholar] [CrossRef]
- Nakamura, N.; Watanabe, R. Octadecane-1,18-diol. Acta Cryst. 2001, 57, o136–o138. [Google Scholar] [CrossRef]
- Nakamura, N.; Uno, K.; Ogawa, Y. Nonadecane-1,19-diol. Acta Cryst. 2001, 57, o485–o487. [Google Scholar] [CrossRef]
- Nakamura, N.; Uno, K.; Ogawa, Y. 1,21-Henicosanediol. Acta Cryst. 2000, 56, 1389–1390. [Google Scholar] [CrossRef]
- Uno, K.; Ogawa, Y.; Nakamura, N. Polymorphism of Long-Chain Alkane-α, ω-Diols with an Even Number of Carbon Atoms. Cryst. Growth Des. 2008, 8, 592–599. [Google Scholar] [CrossRef]
- Popovitz-Biro, R.; Majewski, J.; Margulis, L.; Cohen, S.; Leiserowitz, L.; Lahav, M. Inhibition of self-aggregation of α,ω-Docosanediol into 3D Crystallites by “Tailor-Made” amphiphilic auxiliaries. Adv. Mater. 1994, 6, 956–959. [Google Scholar] [CrossRef]
- Majewski, J.; Edgar, R.; Popovitz-Biro, R.; Kjaer, K.; Bouwman, W.G.; Als-Nielsen, J.; Lahav, M.; Leiserowitz, L. Structure Determination in the Twilight Region Between Monolayers and 3-D Crystals; a Grazing Incidence X-Ray Diffraction Study of Nanocrystalline Aggregates of α,ω-Docosanediol at the Air–Water Interface. Angew. Chem. Int. Ed. 1995, 34, 649–652. [Google Scholar] [CrossRef]
- Chavda, S.; Singh, K.; Marangoni, D.G.; Aswal, V.K.; Bahadur, P. Cationic micelles modulated in the presence of α,ω-Alkanediols: A SANS, NMR and conductometric study. J. Surfactants Deterg. 2012, 15, 317–325. [Google Scholar] [CrossRef]
- Wen, M.; Buschhaus, C.; Jetter, R. Nanotubes on plant surfaces: Chemical composition of epicuticular wax crystals on needles of Taxus baccata L. Phytochemistry 2006, 67, 1808–1817. [Google Scholar] [CrossRef] [PubMed]
- Welzel, U.; Ligot, J.; Lamparter, P.; Vermeulen, A.C.; Mittemeijer, E.J. Stress analysis of polycrystalline thin films and surface regions by X-ray diffraction. J. Appl. Cryst. 2005, 38, 1–29. [Google Scholar] [CrossRef]
- Dollase, W.A. Correction of intensities for preferred orientation in powder diffractometry: Application of the March model. J. Appl. Cryst. 1986, 19, 267–272. [Google Scholar] [CrossRef]
- Allen, F.H.; Watson, D.G.; Brommer, L.; Orpen, A.G.; Taylor, R. International Tables of Crystallography, C: Mathematical, Physical and Chemical Tables, 3rd ed.; Springer: Dordrecht, The Netherlands, 2004; p. 790. [Google Scholar]
- Siskos, M.G.; Choudhary, M.I.; Gerothanassis, I.P. Hydrogen Atomic Positions of O-H···O Hydrogen Bonds in Solution and in the Solid State: The Synergy of Quantum Chemical Calculations with 1H-NMR Chemical Shifts and X-ray Diffraction Methods. Molecules 2017, 22, 415. [Google Scholar] [CrossRef] [PubMed]
- Siskos, M.G.; Choudhary, M.I.; Tzakos, A.G.; Gerothanassis, I.P. 1H NMR Chemical shift assignment, structure and conformational elucidation of hypericin with the use of DFT calculations—The challenge of accurate positions of labile hydrogens. Tetrahedron 2016, 72, 8287–8293. [Google Scholar] [CrossRef]
- Deringer, V.L.; Hoepfner, V.; Dronskowski, R. Accurate Hydrogen Positions in Organic Crystals: Assessing a Quantum-Chemical Aide. Cryst. Growth Des. 2012, 12, 1014–1021. [Google Scholar] [CrossRef]
- Ohno, K.; Yoshida, H.; Watanabe, H.; Fujita, T.; Matsura, H. Conformational Study of 1-Butanol by the Combined Use of Vibrational Spectroscopy and ab Initio Molecular Orbital Calculations. J. Phys. Chem. 1994, 98, 6924–6930. [Google Scholar] [CrossRef]
- Desiraju, R.G.; Steiner, T. The weak hydrogen bond. In Structural Chemistry and Biology; Oxford University Press: New York, NY, USA, 2001; pp. 12–15. [Google Scholar]
- Piacente, V.; Ferro, D.; Della-Gatta, G. Heat capacities near room temperature of ten solid alkane-α, ω-diols HO-(CH2)n-OH where n = 6 and 8 ≤ n ≤ 16. Thermochim. Acta 1993, 223, 65–73. [Google Scholar] [CrossRef]
- Piacente, V.; Ferro, D.; Della-Gatta, G. Vaporization enthalpies of five odd-numbered (C7 to C15) α,ω-alkanediols. Thermochim. Acta 1994, 232, 317–321. [Google Scholar] [CrossRef]
- Pertsin, A.T.; Kitaigorodsky, A.I. The atom-atom potential method. In Applications in Organic Molecular Solids; Springer: New York, NY, USA, 1987; pp. 15–26. [Google Scholar]
- Bergerhoff, G.; Berndt, M.; Brandenburg, K.; Degen, T. Concerning inorganic crystal structure types. Acta Cryst. 1999, 55, 147–156. [Google Scholar] [CrossRef]
- De la Flor, G.; Orobengoa, D.; Tasci, E.; Perez-Mato, J.M.; Aroyo, M.I. Comparison of structures applying the tools available at the Bilbao Crystallographic Server. J. Appl. Cryst. 2016, 49, 653–664. [Google Scholar] [CrossRef]
- Aroyo, M.I.; Perez-Mato, J.M.; Capillas, C.; Kroumova, E.; Ivantchev, S.; Madariaga, G.; Kirov, A.; Wondratschek, H. Bilbao Crystallographic Server I: Databases and crystallographic computing programs. Z. Kristallogr. 2006, 221, 15–27. [Google Scholar] [CrossRef]
- Aroyo, M.I.; Kirov, A.; Capillas, C.; Perez-Mato, J.M.; Wondratschek, H. Bilbao Crystallographic Server II: Representations of crystallographic point groups and space groups. Acta Cryst. 2006, 62, 115–128. [Google Scholar] [CrossRef] [PubMed]
- Timofeva, T.V.; Nesterov, V.N.; Dolgushin, F.M.; Zubavichus, Y.V.; Goildshtein, J.T.; Sammet, D.M.; Clark, R.D.; Penn, B.; Sntipin, M.Y. One-pot polymorphism of nonlinear optical materials. First example of organic polytypes. Cryst. Eng. 2000, 3, 263–288. [Google Scholar] [CrossRef]
- Verma, A.R.; Krishna, P. Polymorphism and Polytypism in Crystals; Wiley: Hoboken, NJ, USA, 1966. [Google Scholar]
- Feller, R.K.; Cheetman, A.K. Polytypism, homochirality, interpenetration, and hydrogen-bonding in transition metal (Mn(II), Ni(II), Cu(II), Zn(II)) 5-hydroxyisophthalate coordination polymers containing 4,4′-bipyridyl. Dalton Trans. 2008, 15, 2034–2042. [Google Scholar] [CrossRef] [PubMed]
- Duggirala, N.K.; Kanniah, S.L.; Muppidi, V.K.; Thaimattam, R.; Devarakonda, S. Polytypism in desvenlafaxine succinate monohydrate. Cryst. Eng. Commun. 2009, 11, 989–992. [Google Scholar] [CrossRef]
- Frede, E.; Precht, D. Structure studies on the organic compounds. Kieler Milchw. Forsch. 1974, 26, 325–332. [Google Scholar]
- Precht, D. Kristallstrukturentersuchungen an Fettalkoholen und Röntgenbeugung. Fet. Seif. Anst. 1976, 78, 145–149. [Google Scholar] [CrossRef]
- Kobayashi, M.; Kobayashi, T.; Cho, Y.; Kaneko, F. States of molecular assembly and physical properties of crystalline long chain compounds studied by vibrational spectroscopy. Macromol. Chem. Macromol. Symp. 1986, 5, 1–20. [Google Scholar] [CrossRef]
- Plomp, M.; van Enckevort, W.J.P.; van Hoof, P.J.C.M.; van de Streek, C.J. Morphology of and dislocation movement in n-C40H82 paraffin crystals grown from solution. J. Cryst. Growth 2003, 249, 600–613. [Google Scholar] [CrossRef]
- Rodriguez, M.; Llinares, M.; Doulut, S.; Heitz, A.; Martinez, J. A facile synthesis of chiral N-protected β-amino alcohols. Tetrahedron Lett. 1991, 32, 923–926. [Google Scholar] [CrossRef]
- Nguyen, T.B.; Castanet, A.-S.; Nguyen, T.-H.; Nguyen, K.P.P.; Bardeau, J.-F.; Gibaud, A.; Mortier, J. Synthesis of model long-chain ω-alkenyltrichlorosilanes and triethoxysilanes for the formation of self-assembled monolayers. Tetrahedron 2006, 62, 647–651. [Google Scholar] [CrossRef]
- Mitsunaga, T. X-ray thin-film measurement techniques II. Out-of-plane diffraction measurements. Rigaku J. 2009, 25, 7–12. [Google Scholar]
- Toraya, H.; Huang, T.C.; Wu, Y. Intensity enhancement in asymmetric diffraction with parallel beam synchrotron radiation. J. Appl. Cryst. 1993, 26, 774–777. [Google Scholar] [CrossRef]
- Pola-Albores, F.; Paraguay-Delgado, F.; Antúnez-Flores, W.; Amézaga-Madrid, P.; Ríos-Valdovinos, E.; Miki-Yoshida, M. Microstructural study of ZnO nanostructures by Rietveld analysis. J. Nanomater. 2011, 27, 643126. [Google Scholar] [CrossRef]
- Boultif, A.; Louër, D. Powder pattern indexing with the dichotomy method. J. Appl. Cryst. 2004, 37, 724–731. [Google Scholar] [CrossRef]
- Smith, G.S.; Snyder, R.L. FN: A criterion for rating powder diffraction patterns and evaluating the reliability of powder pattern indexing. J. Appl. Cryst. 1979, 12, 60–65. [Google Scholar] [CrossRef]
- De Wolff, P.M. A simplified criterion for the reliability of powder pattern indexing. J. Appl. Cryst. 1968, 1, 108–113. [Google Scholar] [CrossRef]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J. FULLPROF: A Program for Rietveld Refinement and Pattern Matching Analysis. In Proceedings of the Abstracts of the Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr, Toulouse, France, 16–18 July 1990. [Google Scholar]
- Toraya, H.J. Whole-powder-pattern fitting without reference to a structural model: Application to X-ray powder diffraction data. J. Appl. Cryst. 1986, 19, 440–447. [Google Scholar] [CrossRef]
- Berar, J.F.; Baldinozzi, G. Modeling of line-shape asymmetry in powder diffraction. J. Appl. Cryst. 1993, 26, 128–129. [Google Scholar] [CrossRef]
- Roisnel, T.; Rodriguez-Carvajal, J. WinPLOTR: A Windows tool for powder diffraction pattern analysis. In Proceedings of the European Powder Diffraction EPDIC 7, Barcelona, Spain, 20–23 May 2001. [Google Scholar]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A Generic Force Field for Molecular Simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The general utility Lattice Program (GULP). Mol. Simul. 2003, 24, 291–341. [Google Scholar] [CrossRef]
- Gasteiger, J.; Marsili, M. Iterative partial equalization of orbital electronegativity-a rapid access to atomic charges. Tetrahedron 1990, 36, 3219–3228. [Google Scholar] [CrossRef]
- Rietveld, H.M. Line profiles of neutron powder-diffraction peaks for structure refinement. Acta Cryst. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Cryst. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Toby, B.H. R factors in Rietveld analysis: How good is good enough? Powder Diffr. 2006, 21, 67–70. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds and analyses data are available from all the authors. |







| Crystals | D-H···A | D-H (Å) | H ···A (Å) | D···A (Å) | D-H···A (°) | Ehb (kJ/mol) |
|---|---|---|---|---|---|---|
| DEDOL | Oh-Ho···Oh i | 0.97 | 1.85 | 2.8148 | 176 | −28.15 |
| UNDOL | O2-H2o···O1 ii | 0.96 | 1.75 | 2.7063 | 170 | −27.15 |
| O1-H1o···O2 iii | 0.97 | 1.83 | 2.7968 | 174 | −28.19 | |
| C2-H2a ···O1 iv | 0.95 | 2.68 | 3.4764 | 142 | −3.19 | |
| DODOL | Oh-Ho···Oh i | 0.96 | 1.86 | 2.8254 | 177 | −28.14 |
| TRDOL | O2-H2o···O1 ii | 1.08 a | 1.67 | 2.7440 | 171 | −25.37 |
| O1-H1o···O2 iii | 0.82 a | 1.94 | 2.7470 | 165 | −27.82 | |
| C12-H12b ···O2 iv | 1.09 | 2.54 | 3.4758 | 144 | −3.46 |
| ΔHtr+fus (298 K) (kJ mol−1) a | Tfus (K) | ΔHvap(298 K) (kJ mol−1) | ΔHsub (298 K) (kJ mol−1) | Elatt at (298 K) (kJ mol−1) | |
|---|---|---|---|---|---|
| DEDOL | 37.17 ± 1.58 | 343.27 ± 0.60 | 120.2 ± 4.9 [27] | 157.37 ± 5.15 | −164.53 |
| UNDOL | 36.02 ± 1.42 | 338.85 ± 0.11 | 131.7 ± 4.1 [27] | 167.72 ± 4.34 | −167.07 |
| DODOL | 47.45 ± 1.48 | 352.52 ± 0.35 | 130.5 ± 5.7 [27] | 177.95 ± 5.80 | −165.78 |
| TRDOL | 41.60 ± 1.37 | 351.27 ± 0.43 | 132.8 ± 7.8 [27] | 174.40 ± 7.90 | −170.68 |
| Crystal Properties | DEDOL | UNDOL | DODOL | TRDOL |
|---|---|---|---|---|
| Empirical formula | C10H22O2 | C11H24O2 | C12H26O2 | C13H28O2 |
| Formula weight | 174.28 | 188.31 | 202.34 | 216.36 |
| Range of 2θ (°) | 2–70 | 2–70 | 2–70 | 2–70 |
| Crystal system | Monoclinic | Orthorhombic | Monoclinic | Orthorhombic |
| Space group | P21/c | P212121 | P21/c | P212121 |
| a (Å) | 4.9570 (7) | 7.1154 (8) | 4.9665 (8) | 7.1847 (9) |
| b (Å) | 5.1820 (9) | 32.4798 (3) | 5.1895 (9) | 37.6468 (4) |
| c (Å) | 21.2361 (3) | 5.1402 (6) | 24.5088 (4) | 5.1239 (7) |
| β (°) | 96.6938 (4) | 90.000 | 90.7523 (5) | 90.000 |
| Volume (Å3) | 541.776 (9) | 1187.93 (5) | 630.547 (8) | 1385.91 (7) |
| Z | 2 | 4 | 2 | 4 |
| U a | 0.21474 (5) | 0.06757 (3) | 0.08719 (2) | 0.4460 (1) |
| V a | −0.04840 (9) | −0.02228 (2) | −0.0435 (1) | −0.02944 (5) |
| W a | 0.10096 (3) | 0.1423 (1) | 0.09275 (3) | 0.10261 (2) |
| X b | 0.00316 (5) | 0.00404 (2) | 0.00535 (3) | 0.00809 (4) |
| Eta0 (µ0) b | 0.6954 (2) | 0.6982 (6) | 0.6897 (6) | 0.6925 (4) |
| Rp (%) | 6.70 | 6.88 | 6.98 | 7.51 |
| Rwp (%) | 9.30 | 8.25 | 9.22 | 8.75 |
| χ2 | 4.82 | 4.80 | 6.47 | 7.46 |
| Uoverall (Å2) | 0.1260 (3) | 0.4674 (2) | 0.0556 (2) | 0.1340 (3) |
| r March (hkl) | 0.6068 (-104) 0.4434 (208) | 1.1816 (101) 0.9041 (200) 0.4675 (0 12 1) | 0.6582 (-104) 0.6321 (1 0 10) | 1.3323 (101) |
| Chemical formula | C10H22O2 | C11H24O2 | C12H26O2 | C13H28O2 |
| Formula weight | 174.28 | 188.31 | 202.34 | 216.36 |
| A (Å) | B (Å) | C (Å) | Α (°) | Β (°) | Γ (°) | F (20) a | M (20) a | |
|---|---|---|---|---|---|---|---|---|
| DEDOL | 4.9355 (3) | 4.6817 (8) | 20.4366 (3) | 90 | 95.617 (6) | 90 | 24.0 | 24.5 |
| UNDOL | 6.9843 (8) | 32.1392 (6) | 4.9418 (7) | 90 | 90.000 (2) | 90 | 17.3 | 17.8 |
| DODOL | 5.0704 (2) | 5.1411 (2) | 23.9209 (5) | 90 | 90.315 (8) | 90 | 15.0 | 16.5 |
| TRDOL | 6.9177 (7) | 37.5049 (8) | 5.2351 (2) | 90 | 90.000 (4) | 90 | 21.5 | 18.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luis-Raya, G.; Ramírez-Cardona, M.; Luna-Bárcenas, G.; Hernández-Landaverde, M.A.; Jiménez-Nieto, A.; García-Rivas, J.L.; España-Sánchez, B.L.; Sanchez, I.C. From Intermolecular Interactions to Texture in Polycrystalline Surfaces of 1,?-alkanediols (? = 10–13). Molecules 2017, 22, 956. https://doi.org/10.3390/molecules22060956
Luis-Raya G, Ramírez-Cardona M, Luna-Bárcenas G, Hernández-Landaverde MA, Jiménez-Nieto A, García-Rivas JL, España-Sánchez BL, Sanchez IC. From Intermolecular Interactions to Texture in Polycrystalline Surfaces of 1,?-alkanediols (? = 10–13). Molecules. 2017; 22(6):956. https://doi.org/10.3390/molecules22060956
Chicago/Turabian StyleLuis-Raya, Gilgamesh, Màrius Ramírez-Cardona, Gabriel Luna-Bárcenas, Martín A. Hernández-Landaverde, Adair Jiménez-Nieto, Jose Luis García-Rivas, Beatriz Liliana España-Sánchez, and Isaac C. Sanchez. 2017. "From Intermolecular Interactions to Texture in Polycrystalline Surfaces of 1,?-alkanediols (? = 10–13)" Molecules 22, no. 6: 956. https://doi.org/10.3390/molecules22060956
APA StyleLuis-Raya, G., Ramírez-Cardona, M., Luna-Bárcenas, G., Hernández-Landaverde, M. A., Jiménez-Nieto, A., García-Rivas, J. L., España-Sánchez, B. L., & Sanchez, I. C. (2017). From Intermolecular Interactions to Texture in Polycrystalline Surfaces of 1,?-alkanediols (? = 10–13). Molecules, 22(6), 956. https://doi.org/10.3390/molecules22060956