Mapping Free Energy Pathways for ATP Hydrolysis in the E. coli ABC Transporter HlyB by the String Method
Abstract
1. Introduction
2. Methods
2.1. Theory: MFEP by the String Method in Collective Variables
2.2. Computational Details
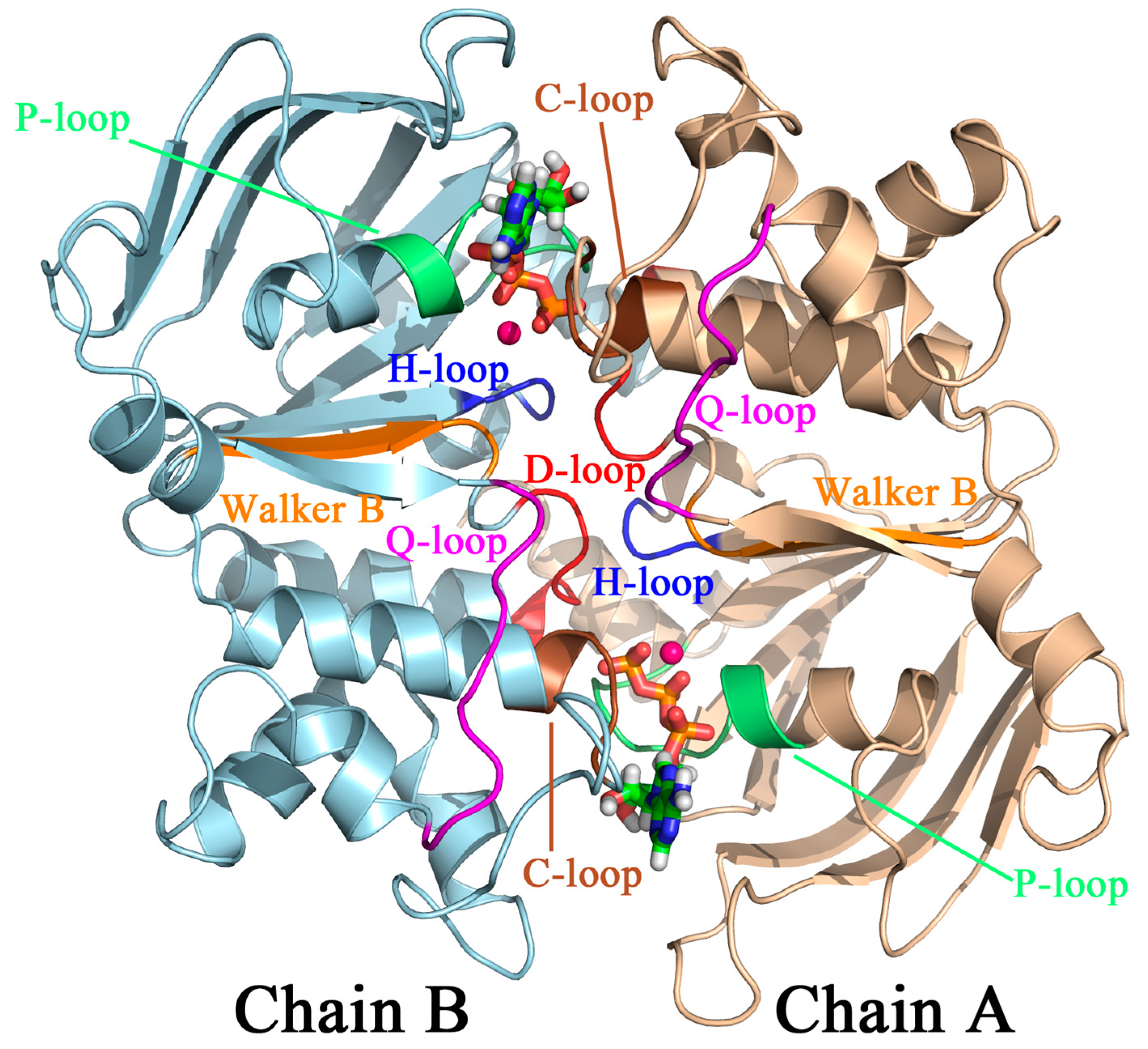
2.2.1. Structural Model, Potential Energy Surface, and General MD Setup
2.2.2. String Simulations
3. Results and Discussion
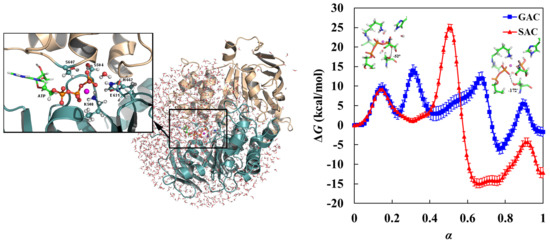
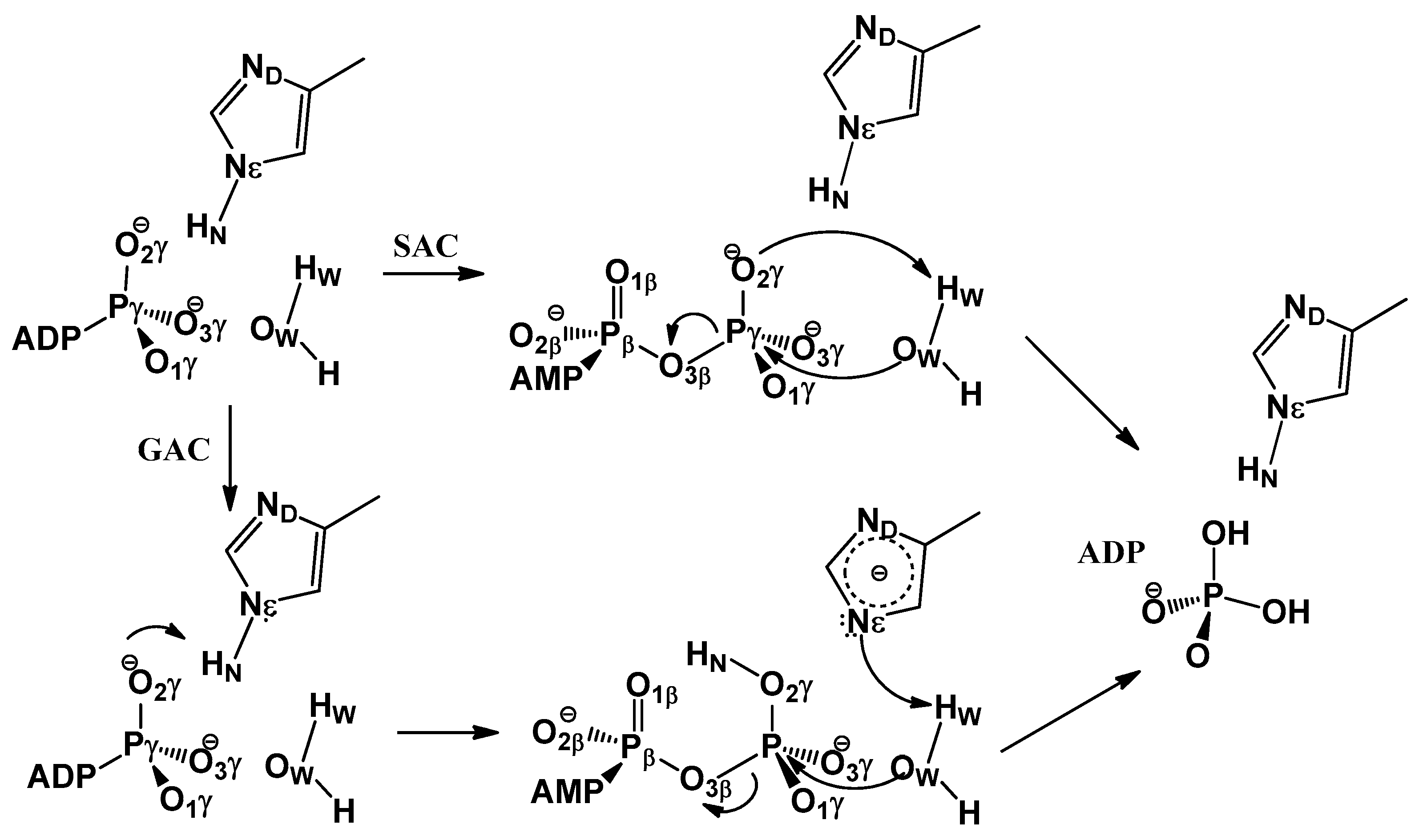
3.1. Free Energy Profile for GAC
3.2. Free Energy Profile for SAC
3.3. GAC Is Preferred over SAC for Catalysis
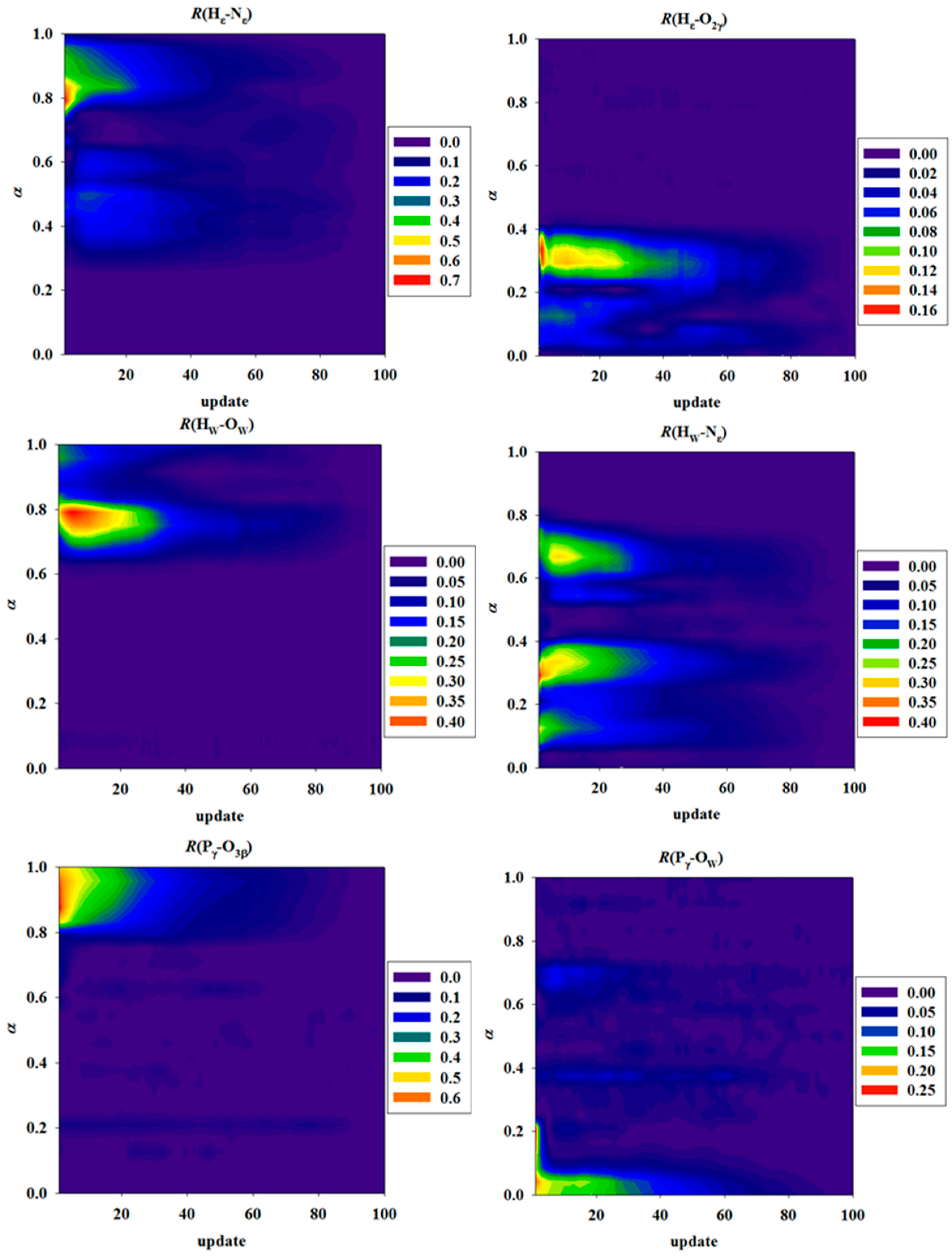
3.4. Convergence of String MFEPs
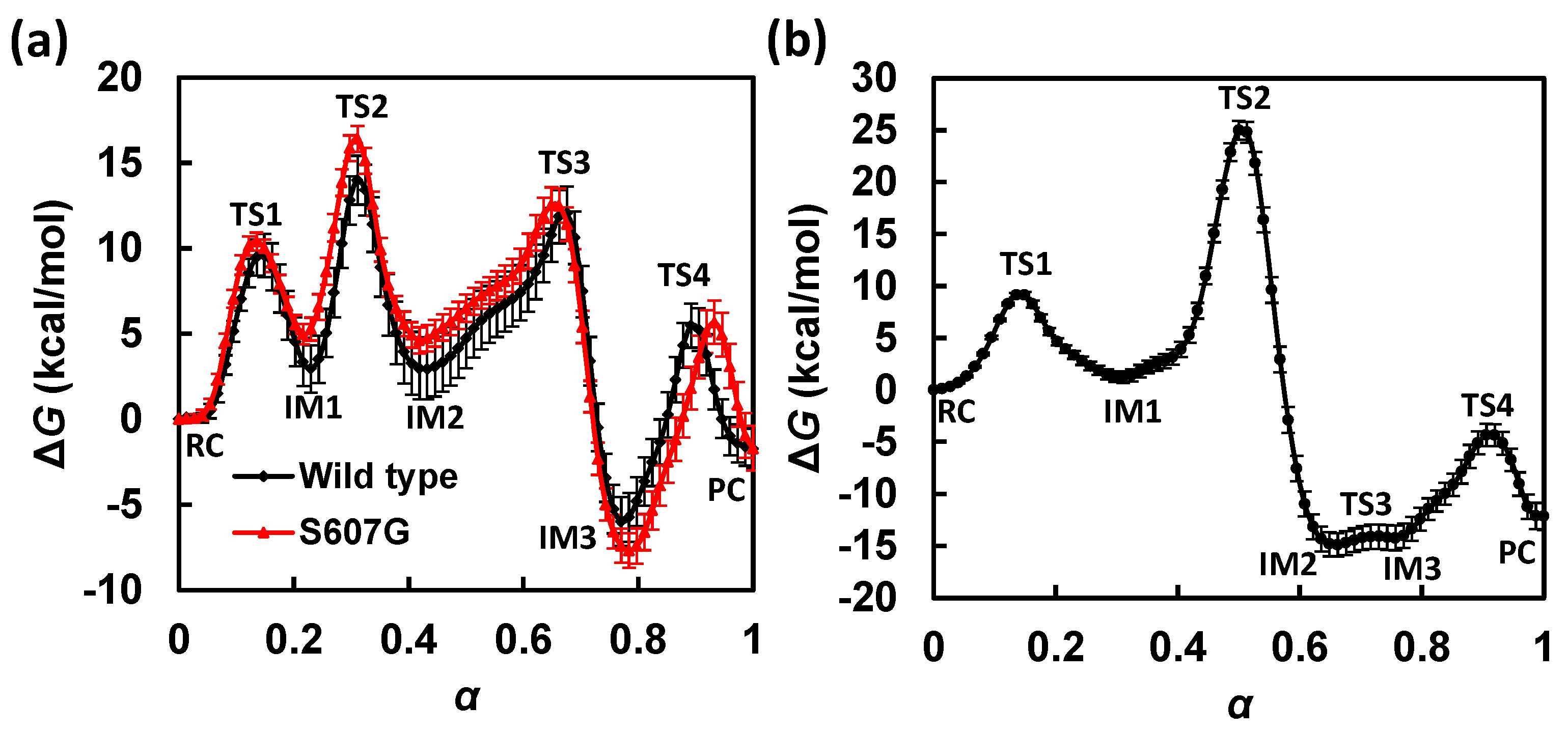
3.5. S607 Displays “Finger Motion” during ATP Hydrolysis
3.6. Free Energy Profile for S607G in Silico Mutation
4. Unresolved Issues
4.1. Protonation State of H-Loop His
4.2. Limitation of Methods
4.3. Solvent Kinetic Isotope Effects
5. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
References
- Davidson, A.L.; Dassa, E.; Orelle, C.; Chen, J. Structure, function, and evolution of bacterial ATP-binding cassette systems. Microbiol. Mol. Biol. Rev. 2008, 72, 317–364. [Google Scholar] [CrossRef] [PubMed]
- Holland, I.B.; Schmitt, L.; Young, J. Type 1 protein secretion in bacteria, the ABC-transporter dependent pathway. Mol. Membr. Biol. 2005, 22, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Zaitseva, J.; Jenewein, S.; Jumpertz, T.; Holland, I.B.; Schmitt, L. H662 is the linchpin of ATP hydrolysis in the nucleotide-binding domain of the ABC transporter HlyB. EMBO J. 2005, 24, 1901–1910. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.M.T.; Mohan, M.S. The metal chelates of riboflavin and riboflavin monophosphate. J. Inorg. Nucl. Chem. 1973, 35, 1749–1755. [Google Scholar] [CrossRef]
- Zaitseva, J.; Holland, I.B.; Schmitt, L. The role of CAPS buffer in expanding the crystallization space of the nucleotide-binding domain of the ABC transporter haemolysin B from Escherichia coli. Acta Cryst. D 2004, 60, 1076–1084. [Google Scholar] [CrossRef] [PubMed]
- Zaitseva, J.; Oswald, C.; Jumpertz, T.; Jenewein, S.; Wiedenmann, A.; Holland, I.B.; Schmitt, L. A structural analysis of asymmetry required for catalytic activity of an ABC-ATPase domain dimer. EMBO J. 2006, 25, 3432–3443. [Google Scholar] [CrossRef] [PubMed]
- Geourjon, C.; Orelle, C.; Steinfels, E.; Blanchet, C.; Deleage, G.; Di Pietro, A.; Jault, J.-M. A common mechanism for ATP hydrolysis in ABC transporter and helicase superfamilies. Trends Biochem. Sci. 2001, 26, 539–544. [Google Scholar] [CrossRef]
- Schmitt, L.; Benabdelhak, H.; Blight, M.A.; Holland, I.B.; Stubbs, M.T. Crystal structure of the nucleotide-binding domain of the ABC-transporter Haemolysin B: Identification of a variable region within ABC helical domains. J. Mol. Biol. 2003, 330, 333–342. [Google Scholar] [CrossRef]
- Story, R.M.; Steitz, T.A. Structure of the recA protein-ADP complex. Nature 1992, 355, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Shyamala, V.; Baichwal, V.; Beall, E.; Ames, G.F.-L. Structure-function analysis of the histidine permease and comparison with cystic fibrosis mutations. J. Biol. Chem. 1991, 266, 18714–18719. [Google Scholar] [PubMed]
- Davidson, A.L.; Sharma, S. Mutation of a single MalK subunit severely impairs maltose transport activity in Escherichia coli. J. Bacteriol. 1997, 179, 5458–5464. [Google Scholar] [CrossRef] [PubMed]
- Schultz, K.M.; Merten, J.A.; Klug, C.S. Characterization of the E506Q and H537A dysfunctional mutants in the E. coli ABC transporter MsbA. Biochemistry 2011, 50, 3599–3608. [Google Scholar] [CrossRef] [PubMed]
- Ernst, R.; Kueppers, P.; Klein, C.M.; Schwarzmueller, T.; Kuchler, K.; Schmitt, L. A mutation of the H-loop selectively affects rhodamine transport by the yeast multidrug ABC transporter Pdr5. Proc. Natl. Acad. Sci. USA 2008, 105, 5069–5074. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Ojeda-May, P.; Pu, J. H-loop histidine catalyzes ATP hydrolysis in the E. coli ABC-transporter HlyB. Phys. Chem. Chem. Phys. 2013, 15, 15811–15815. [Google Scholar] [CrossRef] [PubMed]
- Bourne, H.R. The arginine finger strikes again. Nature 1997, 389, 673–674. [Google Scholar] [CrossRef] [PubMed]
- Abrahams, J.P.; Leslie, A.G.W.; Lutter, R.; Walker, J.E. Structure at 2.8 Å resolution of F1-ATPase from bovine heart mitochondria. Nature 1994, 370, 621–628. [Google Scholar] [CrossRef] [PubMed]
- Rittinger, K.; Walker, P.A.; Eccleston, J.F.; Smerdon, S.J.; Gamblin, S.J. Structure at 1.65 Å of RhoA and its GTPase-activating protein in complex with a transition-state analogue. Nature 1997, 389, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Scheffzek, K.; Ahmadian, M.R.; Kabsch, W.; Wiesmuller, L.; Lautwein, A.; Schmitz, F.; Wittinghofer, A. The Ras-RasGAP complex: Structural basis for GTPase activation and its loss in oncogenic Ras mutants. Science 1997, 277, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Seewald, M.J.; Korner, C.; Wittinghofer, A.; Vetter, I.R. RanGAP mediates GTP hydrolysis without an arginine finger. Nature 2002, 415, 662–666. [Google Scholar] [CrossRef] [PubMed]
- Tesmer, J.J.G.; Berman, D.M.; Gilman, A.G.; Sprang, S.R. Structure of RGS4 bound to AlF4−-activated Giα1: Stabilization of the transition state for GTP hydrolysis. Cell 1997, 89, 251–261. [Google Scholar] [CrossRef]
- Glennon, T.M.; Villa, J.; Warshel, A. How Does GAP Catalyze the GTPase Reaction of Ras?: A Computer Simulation Study. Biochemistry 2000, 39, 9641–9651. [Google Scholar] [CrossRef] [PubMed]
- Maegley, K.A.; Admiraal, S.J.; Herschlag, D. Ras-catalyzed hydrolysis of GTP: A new perspective from model studies. Proc. Natl. Acad. Sci. USA 1996, 93, 8160–8166. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhang, X.C. GTP Hydrolysis Mechanism of Ras-like GTPases. J. Mol. Biol. 2004, 340, 921–932. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Osborne, A.R.; Groll, M.; Rapoport, T.A. RecA-like motor ATPases—Lessons from structures. Biochim. Biophys. Acta 2004, 1659, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2007, 117, 185–199. [Google Scholar] [CrossRef]
- Huang, W.; Liao, J.-L. Catalytic mechanism of the maltose transporter hydrolyzing ATP. Biochemistry 2016, 55, 224–231. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.-L.; Furuta, T.; Sakurai, M. ATP Hydrolysis mechanism in a maltose transporter explored by QM/MM metadynamics simulation. J. Phys. Chem. B 2016, 120, 11102–11112. [Google Scholar] [CrossRef] [PubMed]
- Dall’Acqua, W.; Carter, P. Substrate-assisted catalysis: Molecular basis and biological significance. Protein Sci. 2000, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Schweins, T.; Langen, R.; Warshel, A. Why have mutagenesis studies not located the general base in ras p21. Nat. Struct. Biol. 1994, 1, 476–484. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.E.W.; Vanden-Eijnden, E. Finite temperature string method for the study of rare events. J. Phys. Chem. B 2005, 109, 6688–6693. [Google Scholar]
- Maragliano, L.; Fischer, A.; Vanden-Eijnden, E.; Ciccotti, G. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J. Chem. Phys. 2006, 125, 024106. [Google Scholar] [CrossRef] [PubMed]
- Miller, T.F., III; Vanden-Eijnden, E.; Chandler, D. Solvent coarse-graining and the string method applied to the hydrophobic collapse of a hydrated chain. Proc. Natl. Acad. Sci. USA 2007, 104, 14559–14564. [Google Scholar] [CrossRef] [PubMed]
- Pan, A.C.; Sezer, D.; Roux, B. Finding transition pathways using the string method with swarms of trajectories. J. Phys. Chem. B 2008, 112, 3432–3440. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikov, V.; Karplus, M.; Vanden-Eijnden, E. Free energy of conformational transition paths in biomolecules: The string method and its application to myosin VI. J. Chem. Phys. 2011, 134, 085103. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Hummer, G. Pore opening and closing of a pentameric ligand-gated ion channel. Proc. Natl. Acad. Sci. USA 2010, 107, 19814–19819. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Yang, W. On-the-path random walk sampling for efficient optimization of minimum free-energy path. J. Comput. Chem. 2009, 30, 1649–1653. [Google Scholar] [CrossRef] [PubMed]
- Rosta, E.; Nowotny, M.; Yang, W.; Hummer, G. Catalytic mechanism of RNA backbone cleavage by ribonuclease H from quantum mechanics/molecular mechanics simulations. J. Am. Chem. Soc. 2011, 133, 8934–8941. [Google Scholar] [CrossRef] [PubMed]
- Zinovjev, K.; Ruiz-Pernia, J.J.; Tunon, I. Toward an automatic determination of enzymatic reaction mechanisms and their activation free energies. J. Chem. Theory Comput. 2013, 9, 3740–3749. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Martinez, M.; Field, M.; Crehuet, R. Enzymatic minimum free energy path calculations using swarms of trajectories. J. Phys. Chem. B 2015, 119, 1103–1113. [Google Scholar] [CrossRef] [PubMed]
- Doron, D.; Kohen, A.; Nam, K.; Major, D.T. How accurate are transition states from simulations of enzymatic reactions? J. Chem. Theory Comput. 2014, 10, 1863–1871. [Google Scholar] [CrossRef] [PubMed]
- Ojeda-May, P.; Li, Y.; Ovchinnikov, V.; Nam, K. Role of protein dynamics in allosteric control of the catalytic phosphoryl transfer of insulin receptor kinase. J. Am. Chem. Soc. 2015, 137, 12454–12457. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Fang, D.; Ito, S.; Okamoto, Y.; Ovchinnikov, V.; Cui, Q. QM/MM free energy simulations: Recent progress and challenges. Mol. Simul. 2016, 42, 1056–1078. [Google Scholar] [CrossRef] [PubMed]
- Vanden-Eijnden, E.; Venturoli, M. Revisiting the finite temperature string method for the calculation of reaction tubes and free energies. J. Chem. Phys. 2009, 130, 194103. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.J.P. MOPAC: A semiempirical molecular orbital program. J. Comput. Aided Mol. Des. 1990, 4, 1–105. [Google Scholar] [CrossRef] [PubMed]
- Field, M.J.; Bash, P.A.; Karplus, M.J. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., III; MacKerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Mackerell, A.D.; Feig, M.; Brooks, C.L., III. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Amara, P.; Alhambra, C.; Field, M.J. A generalized hybrid orbital (GHO) method for the treatment of boundary atoms in combined QM/MM calculations. J. Phys. Chem. A 1998, 102, 4714–4721. [Google Scholar] [CrossRef]
- Brooks, C.L., III; Karplus, M. Deformable stochastic boundaries in molecular dynamics. J. Chem. Phys. 1983, 79, 6312–6325. [Google Scholar] [CrossRef]
- Adelman, S.A.; Brooks, C.L., III. Generalized Langevin models and condensed-phase chemical reaction dynamics. J. Phys. Chem. 1982, 86, 1511–1524. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–337. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B. Numerical Recipes in FORTRAN 77. In The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Ross, J. Energy transfer from adenosine triphosphate. J. Phys. Chem. B 2006, 110, 6987–6990. [Google Scholar] [CrossRef] [PubMed]
- Cleland, W.W.; Hengge, A.C. Enzymatic mechanisms of phosphate and sulfate transfer. Chem. Rev. 2006, 106, 3252–3278. [Google Scholar] [CrossRef] [PubMed]
- Lodi, P.J.; Knowles, J.R. Neutral imidazole is the electrophile in the reaction catalyzed by triosephosphate isomerase: Structural origins and catalytic implications. Biochemistry 1991, 30, 6948–6956. [Google Scholar] [CrossRef] [PubMed]
- Florian, J.; Warshel, A. A fundamental assumption about OH- attack in phosphate ester hydrolysis is not fully justified. J. Am. Chem. Soc. 1997, 119, 5473–5474. [Google Scholar] [CrossRef]
- Procko, E.; Ferrin-O’Connell, I.; Ng, S.-L.; Gaudet, R. Distinct structural and functional properties of the ATPase sites in an asymmetric ABC transporter. Mol. Cell 2006, 24, 51–62. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Pu, J. Reaction path force matching: A new strategy of fitting specific reaction parameters for semiempirical methods in combined QM/MM simulations. J. Chem. Theory Comput. 2014, 10, 3038–3054. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Viloca, M.; Truhlar, D.G.; Gao, J. Reaction-path energetics and kinetics of the hydride transfer reaction catalyzed by dihydrofolate reductase. Biochemistry 2003, 42, 13558–13575. [Google Scholar] [CrossRef] [PubMed]
- Poulsen, T.D.; Garcia-Viloca, M.; Gao, J.; Truhlar, D.G. Free energy surface, reaction paths, and kinetic isotope effect of short-chain Acyl-CoA dehydrogenase. J. Phys. Chem. B 2003, 107, 9567–9578. [Google Scholar] [CrossRef]
- Lopez, X.; York, D.M. Parameterization of semiempirical methods to treat nucleophilic attacks to biological phosphates: AM1/d parameters for phosphorus. Theor. Chem. Acc. 2003, 109, 149–159. [Google Scholar] [CrossRef]
- Nam, K.; Cui, Q.; Gao, J.; York, D.M. Specific reaction parametrization of the AM1/d Hamiltonian for phosphoryl transfer reactions: H, O, and P atoms. J. Chem. Theory Comput. 2007, 3, 486–504. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.; Gao, J.; York, D.M. Quantum mechanical/molecular mechanical simulation study of the mechanism of hairpin ribozyme catalysis. J. Am. Chem. Soc. 2008, 130, 4680–4691. [Google Scholar] [CrossRef] [PubMed]
- Kroonblawd, M.P.; Pietrucci, F.; Saitta, A.M.; Goldman, N. Generating converged accurate free energy surfaces for chemical reactions with a force-matched semiempirical Model. J. Chem. Theory Comput. 2018, 14, 2207–2218. [Google Scholar] [CrossRef] [PubMed]
- Nam, K. Acceleration of Ab Initio QM/MM Calculations under periodic boundary conditions by multiscale and multiple time step approaches. J. Chem. Theory Comput. 2014, 10, 4175–4183. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Wu, J.; Yang, W. Multiscale quantum mechanics/molecular mechanics simulations with neural networks. J. Chem. Theory Comput. 2016, 12, 4934–4946. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Sode, O.; Dama, J.F.; Voth, G.A. Simulating protein mediated hydrolysis of ATP and other nucleoside triphosphates by combining QM/MM molecular dynamics with advances in metadynamics. J. Chem. Theory Comput. 2017, 13, 2332–2341. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Chen, M.; Yang, W. Random walk in orthogonal space to achieve efficient free-energy simulation of complex systems. Proc. Natl. Acad. Sci. USA 2008, 105, 20227–20232. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.; Gao, J.; York, D.M. An efficient linear-scaling Ewald method for long-range electrostatic interactions in combined QM/MM calculations. J. Chem. Theory Comput. 2005, 1, 2–13. [Google Scholar] [CrossRef] [PubMed]
- Ojeda-May, P.; Pu, J. Isotropic periodic sum treatment of long-range electrostatic interactions in combined quantum mechanical and molecular mechanical calculations. J. Chem. Theory Comput. 2014, 10, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Ojeda-May, P.; Pu, J. Treating electrostatics with Wolf summation in combined quantum mechanical and molecular mechanical simulations. J. Chem. Phys. 2015, 143, 174111. [Google Scholar] [CrossRef] [PubMed]
- Herdendorf, T.J.; Nelson, S.W. Catalytic mechanism of bacteriophage T4 Rad50 ATP hydrolysis. Biochemistry 2014, 53, 5647–5660. [Google Scholar] [CrossRef] [PubMed]
- Pu, J.; Gao, J.; Truhlar, D.G. Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions. Chem. Rev. 2006, 106, 3140–3169. [Google Scholar] [CrossRef] [PubMed]
- Nikaido, K.; Ames, G.F.-L. One intact ATP-binding subunit is sufficient to support ATP hydrolysis and translocation in an ABC transporter, the histidine permease. J. Biol. Chem. 1999, 274, 26727–26735. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, M.; Hayashi, S.; Schulten, K. On the Mechanism of ATP hydrolysis in F1-ATPase. Biophys. J. 2003, 85, 2253–2266. [Google Scholar] [CrossRef]
- Dittrich, M.; Schulten, K. PcrA helicase, a prototype ATP-driven molecular motor. Structure 2006, 14, 1345–1353. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Yu, X.; Hu, P.; Broyde, S.; Zhang, Y. A Water-mediated and substrate-assisted catalytic mechanism for sulfolobus solfataricus DNA polymerase IV. J. Am. Chem. Soc. 2007, 129, 4731–4737. [Google Scholar] [CrossRef] [PubMed]
- Kiani, F.A.; Fischer, S. Catalytic strategy used by the myosin motor to hydrolyze ATP. Proc. Natl. Acad. Sci. USA 2014, 111, E2947–E2956. [Google Scholar] [CrossRef] [PubMed]
- McCullagh, M.; Saunders, M.G.; Voth, G.A. Unraveling the mystery of ATP hydrolysis in actin filaments. J. Am. Chem. Soc. 2014, 136, 13053–13058. [Google Scholar] [CrossRef] [PubMed]
- Zoghbi, M.E.; Altenberg, G.A. Hydrolysis at one of the two nucleotide-binding sites drives the dissociation of ATP-binding cassette nucleotide-binding domain dimers. J. Biol. Chem. 2013, 288, 34259–34265. [Google Scholar] [CrossRef] [PubMed]
- Hohl, M.; Briand, C.; Grutter, M.G.; Seeger, M.A. Crystal structure of a heterodimeric ABC transporter in its inward-facing conformation. Nat. Struct. Mol. Biol. 2012, 19, 395–402. [Google Scholar] [CrossRef] [PubMed]
- Hohl, M.; Hurlimann, L.M.; Bohm, S.; Schoppe, J.; Grutter, M.G.; Bordignon, E.; Seeger, M.A. Structural basis for allosteric cross-talk between the asymmetric nucleotide binding sites of a heterodimeric ABC exporter. Proc. Natl. Acad. Sci. USA 2014, 111, 11025–11030. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.P.; Kueppers, P.; Hanekop, N.; Schmitt, L. Generating symmetry in the asymmetric ABC transporter Pdr5 from Saccharomyces cerevisiae. J. Biol. Chem. 2014, 289, 15272–15279. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Abele, R.; Tampe, R. Functional non-equivalence of ATP-binding cassette signature motifs in the transporter associated with antigen processing (TAP). J. Biol. Chem. 2004, 279, 46073–46081. [Google Scholar] [CrossRef] [PubMed]
- Ernst, R.; Koch, J.; Horn, C.; Tampe, R.; Schmitt, L. Engineering ATPase activity in the isolated ABC cassette of human TAP1. J. Biol. Chem. 2006, 281, 27471–27480. [Google Scholar] [CrossRef] [PubMed]
- Procko, E.; O’Mara, M.L.; Bennett, W.F.D.; Tieleman, D.P.; Gaudet, R. The mechanism of ABC transporters: General lessons from structural and functional studies of an antigenic peptide transporter. FASEB J. 2009, 23, 1287–1302. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |

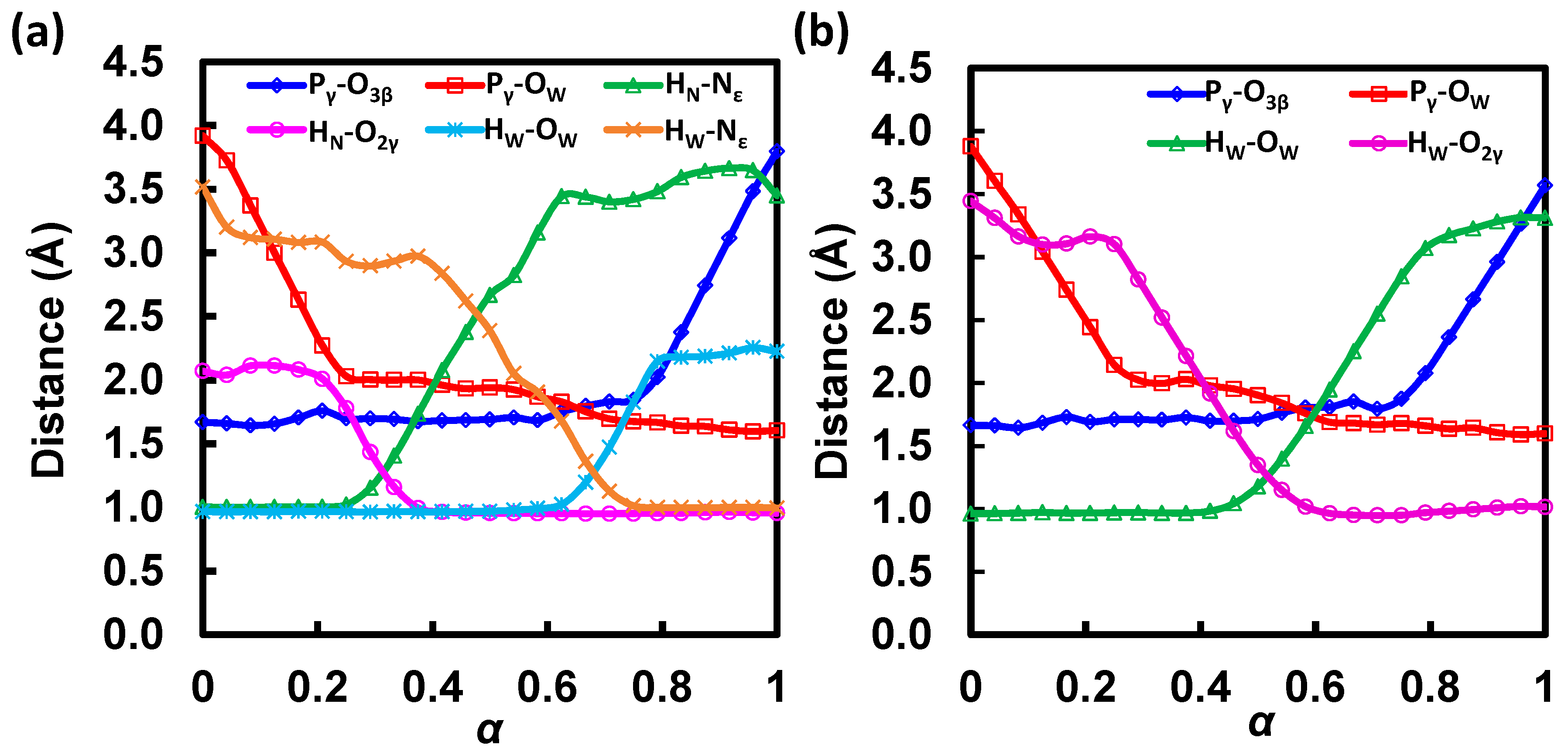

| State | α | ΔG | Pγ-O3β | Pγ-OW | HN-Nε,H662 | HN-O2γ | HW-OW | HW-Nε,H662 |
|---|---|---|---|---|---|---|---|---|
| RC | 0.00 | 0.0 | 1.67 | 3.92 | 1.00 | 2.07 | 0.97 | 3.52 |
| TS1 | 0.15 | 9.6 | 1.68 | 2.79 | 1.00 | 2.10 | 0.97 | 3.09 |
| IM1 | 0.23 | 2.9 | 1.73 | 2.15 | 1.01 | 1.89 | 0.97 | 3.01 |
| TS2 | 0.31 | 14.0 | 1.69 | 2.00 | 1.27 | 1.31 | 0.97 | 2.91 |
| IM2 | 0.43 | 2.9 | 1.68 | 1.95 | 2.19 | 0.96 | 0.97 | 2.75 |
| TS3 | 0.68 | 12.0 | 1.80 | 1.74 | 3.43 | 0.95 | 1.26 | 1.31 |
| IM3 | 0.77 | −6.0 | 1.93 | 1.67 | 3.45 | 0.95 | 1.98 | 1.01 |
| TS4 | 0.89 | 5.5 | 2.89 | 1.62 | 3.65 | 0.96 | 2.20 | 1.00 |
| PC | 1.00 | −1.7 | 3.80 | 1.60 | 3.45 | 0.95 | 2.22 | 1.00 |
| State | α | ΔG | Pγ-O3β | Pγ-OW | HW-OW | HW-O2γ |
|---|---|---|---|---|---|---|
| RC | 0.00 | 0.0 | 1.66 | 3.88 | 0.96 | 3.44 |
| TS1 | 0.14 | 9.1 | 1.69 | 2.97 | 0.97 | 3.10 |
| IM1 | 0.31 | 1.2 | 1.71 | 2.01 | 0.97 | 2.68 |
| TS2 | 0.50 | 25.0 | 1.71 | 1.90 | 1.18 | 1.35 |
| IM2 | 0.66 | −14.9 | 1.85 | 1.68 | 2.22 | 0.95 |
| TS3 | 0.73 | −14.1 | 1.83 | 1.67 | 2.70 | 0.95 |
| IM3 | 0.76 | −14.2 | 1.90 | 1.68 | 2.88 | 0.95 |
| TS4 | 0.91 | −4.3 | 2.88 | 1.62 | 3.27 | 1.00 |
| PC | 1.00 | −12.2 | 3.57 | 1.60 | 3.31 | 1.02 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Ojeda-May, P.; Nagaraju, M.; Kim, B.; Pu, J. Mapping Free Energy Pathways for ATP Hydrolysis in the E. coli ABC Transporter HlyB by the String Method. Molecules 2018, 23, 2652. https://doi.org/10.3390/molecules23102652
Zhou Y, Ojeda-May P, Nagaraju M, Kim B, Pu J. Mapping Free Energy Pathways for ATP Hydrolysis in the E. coli ABC Transporter HlyB by the String Method. Molecules. 2018; 23(10):2652. https://doi.org/10.3390/molecules23102652
Chicago/Turabian StyleZhou, Yan, Pedro Ojeda-May, Mulpuri Nagaraju, Bryant Kim, and Jingzhi Pu. 2018. "Mapping Free Energy Pathways for ATP Hydrolysis in the E. coli ABC Transporter HlyB by the String Method" Molecules 23, no. 10: 2652. https://doi.org/10.3390/molecules23102652
APA StyleZhou, Y., Ojeda-May, P., Nagaraju, M., Kim, B., & Pu, J. (2018). Mapping Free Energy Pathways for ATP Hydrolysis in the E. coli ABC Transporter HlyB by the String Method. Molecules, 23(10), 2652. https://doi.org/10.3390/molecules23102652