Towards a Stochastic Paradigm: From Fuzzy Ensembles to Cellular Functions
Abstract
:1. The Structure-Function Paradigm
(x,y,z) (x,y,z,t)
2. The Ensemble View
{pcs1,…,pcsN} (x,y,z,t)
{kcs1,…,kcsN}
3. Adaptation to Stochastic Cellular Conditions
4. Ambiguity and Redundancy in Sequence, Structure, and Function
5. Functional Promiscuity
6. Conformational Heterogeneity
7. Redundant Sequence Motifs
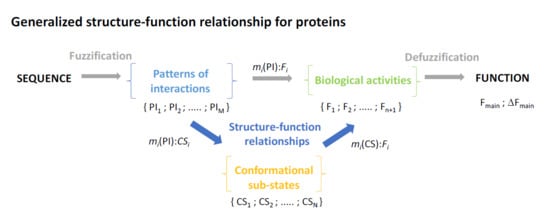
8. Generalized Structure-Function Ensembles
9. Fuzzy Sets Quantify Sequence and Conformation Ambiguities
10. The Stochastic Structure-Function Relationship
11. Conclusion and Outlook
Funding
Conflicts of Interest
References
- Perutz, M.F. Relation between structure and sequence of haemoglobin. Nature 1962, 194, 914–917. [Google Scholar] [CrossRef] [PubMed]
- Kendrew, J.C. Myoglobin and the structure of proteins. Science 1963, 139, 1259–1266. [Google Scholar] [CrossRef] [PubMed]
- Koshland, D.E., Jr. Properties of the active site of enzymes. Ann. N Y Acad. Sci. 1963, 103, 630–642. [Google Scholar] [CrossRef] [PubMed]
- Blake, C.C.; Koenig, D.F.; Mair, G.A.; North, A.C.; Phillips, D.C.; Sarma, V.R. Structure of hen egg-white lysozyme. A three-dimensional Fourier synthesis at 2 Angstrom resolution. Nature 1965, 206, 757–761. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A. Energetics of enzyme catalysis. Proc. Natl. Acad. Sci. USA 1978, 75, 5250–5254. [Google Scholar] [CrossRef] [PubMed]
- Blomberg, R.; Kries, H.; Pinkas, D.M.; Mittl, P.R.; Grutter, M.G.; Privett, H.K.; Mayo, S.L.; Hilvert, D. Precision is essential for efficient catalysis in an evolved Kemp eliminase. Nature 2013, 503, 418–421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frauenfelder, H.; Sligar, S.G.; Wolynes, P.G. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1603. [Google Scholar] [CrossRef] [PubMed]
- Artymiuk, P.J.; Blake, C.C.; Grace, D.E.; Oatley, S.J.; Phillips, D.C.; Sternberg, M.J. Crystallographic studies of the dynamic properties of lysozyme. Nature 1979, 280, 563–568. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, H.; Petsko, G.A.; Tsernoglou, D. Temperature-dependent X-ray diffraction as a probe of protein structural dynamics. Nature 1979, 280, 558–563. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Lewandowski, J.R.; Halse, M.E.; Blackledge, M.; Emsley, L. Protein dynamics. Direct observation of hierarchical protein dynamics. Science 2015, 348, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Fontes, M.R.; Teh, T.; Kobe, B. Structural basis of recognition of monopartite and bipartite nuclear localization sequences by mammalian importin-alpha. J. Mol. Biol. 2000, 297, 1183–1194. [Google Scholar] [CrossRef] [PubMed]
- Diez, M.; Zimmermann, B.; Borsch, M.; Konig, M.; Schweinberger, E.; Steigmiller, S.; Reuter, R.; Felekyan, S.; Kudryavtsev, V.; Seidel, C.A.; et al. Proton-powered subunit rotation in single membrane-bound F0F1-ATP synthase. Nat. Struct. Mol. Biol. 2004, 11, 135–141. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Best, R.B.; Depristo, M.A.; Dobson, C.M.; Vendruscolo, M. Simultaneous determination of protein structure and dynamics. Nature 2005, 433, 128–132. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.R.; Zweckstetter, M.; Huang, J.R.; Blackledge, M. Exploring free-energy landscapes of intrinsically disordered proteins at atomic resolution using NMR spectroscopy. Chem. Rev. 2014, 114, 6632–6660. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Maslov, S.; Shakhnovich, E.I. Constraints imposed by non-functional protein-protein interactions on gene expression and proteome size. Mol. Syst. Biol. 2008, 4, 210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levy, E.D.; De, S.; Teichmann, S.A. Cellular crowding imposes global constraints on the chemistry and evolution of proteomes. Proc. Natl. Acad. Sci. USA 2012, 109, 20461–20466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGuffee, S.R.; Elcock, A.H. Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput. Biol. 2010, 6, e1000694. [Google Scholar]
- Tawfik, D.S. Messy biology and the origins of evolutionary innovations. Nat. Chem. Biol. 2010, 6, 692–696. [Google Scholar] [CrossRef] [PubMed]
- Butner, K.A.; Kirschner, M.W. Tau protein binds to microtubules through a flexible array of distributed weak sites. J. Cell. Biol. 1991, 115, 717–730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sigler, P.B. Transcriptional activation. Acid blobs and negative noodles. Nature 1988, 333, 210–212. [Google Scholar] [CrossRef] [PubMed]
- Pricer, R.; Gestwicki, J.E.; Mapp, A.K. From Fuzzy to Function: The New Frontier of Protein-Protein Interactions. Acc. Chem. Res. 2017, 50, 584–589. [Google Scholar] [CrossRef] [PubMed]
- Levy, E.D.; Boeri Erba, E.; Robinson, C.V.; Teichmann, S.A. Assembly reflects evolution of protein complexes. Nature 2008, 453, 1262–1265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, H. Higher-order assemblies in a new paradigm of signal transduction. Cell 2013, 153, 287–292. [Google Scholar] [CrossRef] [PubMed]
- Bienz, M. Signalosome assembly by domains undergoing dynamic head-to-tail polymerization. Trends Biochem. Sci. 2014, 39, 487–495. [Google Scholar] [CrossRef] [PubMed]
- Franzmann, T.M.; Jahnel, M.; Pozniakovsky, A.; Mahamid, J.; Holehouse, A.S.; Nuske, E.; Richter, D.; Baumeister, W.; Grill, S.W.; Pappu, R.V.; et al. Phase separation of a yeast prion protein promotes cellular fitness. Science 2018, 359, 5654. [Google Scholar] [CrossRef] [PubMed]
- Copley, S.D. Shining a light on enzyme promiscuity. Curr. Opin. Struct. Biol. 2017, 47, 167–175. [Google Scholar] [CrossRef] [PubMed]
- Manglik, A.; Kim, T.H.; Masureel, M.; Altenbach, C.; Yang, Z.; Hilger, D.; Lerch, M.T.; Kobilka, T.S.; Thian, F.S.; Hubbell, W.L.; et al. Structural Insights into the Dynamic Process of β2-Adrenergic Receptor Signaling. Cell 2015, 161, 1101–1111. [Google Scholar] [CrossRef] [PubMed]
- Ross, E.D.; Baxa, U.; Wickner, R.B. Scrambled prion domains form prions and amyloid. Mol. Cell. Biol. 2004, 24, 7206–7213. [Google Scholar] [CrossRef] [PubMed]
- Khersonsky, O.; Tawfik, D.S. Enzyme promiscuity: A mechanistic and evolutionary perspective. Annu. Rev. Biochem. 2010, 79, 471–505. [Google Scholar] [PubMed]
- Jeffery, C.J. Moonlighting proteins: Old proteins learning new tricks. Trends Genet. 2003, 19, 415–417. [Google Scholar] [CrossRef]
- Freilich, S.; Spriggs, R.V.; George, R.A.; Al-Lazikani, B.; Swindells, M.; Thornton, J.M. The complement of enzymatic sets in different species. J. Mol. Biol. 2005, 349, 745–763. [Google Scholar] [CrossRef] [PubMed]
- Nam, H.; Lewis, N.E.; Lerman, J.A.; Lee, D.H.; Chang, R.L.; Kim, D.; Palsson, B.O. Network context and selection in the evolution to enzyme specificity. Science 2012, 337, 1101–1104. [Google Scholar] [CrossRef] [PubMed]
- Arnold, F.H.; Wintrode, P.L.; Miyazaki, K.; Gershenson, A. How enzymes adapt: Lessons from directed evolution. Trends Biochem. Sci. 2001, 26, 100–106. [Google Scholar] [CrossRef]
- Tokuriki, N.; Jackson, C.J.; Afriat-Jurnou, L.; Wyganowski, K.T.; Tang, R.; Tawfik, D.S. Diminishing returns and tradeoffs constrain the laboratory optimization of an enzyme. Nat. Commun. 2012, 3, 1257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aharoni, A.; Gaidukov, L.; Khersonsky, O.; Mc, Q.G.S.; Roodveldt, C.; Tawfik, D.S. The ‘evolvability’ of promiscuous protein functions. Nat. Genet. 2005, 37, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Amitai, G.; Gupta, R.D.; Tawfik, D.S. Latent evolutionary potentials under the neutral mutational drift of an enzyme. HFSP J. 2007, 1, 67–78. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- James, L.C.; Roversi, P.; Tawfik, D.S. Antibody multispecificity mediated by conformational diversity. Science 2003, 299, 1362–1367. [Google Scholar] [CrossRef] [PubMed]
- Campbell, E.; Kaltenbach, M.; Correy, G.J.; Carr, P.D.; Porebski, B.T.; Livingstone, E.K.; Afriat-Jurnou, L.; Buckle, A.M.; Weik, M.; Hollfelder, F.; et al. The role of protein dynamics in the evolution of new enzyme function. Nat. Chem. Biol. 2016, 12, 944–950. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.; Karplus, M. Harmonic dynamics of proteins: Normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. USA 1983, 80, 6571–6575. [Google Scholar] [CrossRef] [PubMed]
- Marsh, J.A.; Teichmann, S.A. Parallel dynamics and evolution: Protein conformational fluctuations and assembly reflect evolutionary changes in sequence and structure. Bioessays 2014, 36, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Haliloglu, T.; Bahar, I. Adaptability of protein structures to enable functional interactions and evolutionary implications. Curr. Opin. Struct. Biol. 2015, 35, 17–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smock, R.G.; Gierasch, L.M. Sending signals dynamically. Science 2009, 324, 198–203. [Google Scholar] [CrossRef] [PubMed]
- Nygaard, R.; Zou, Y.; Dror, R.O.; Mildorf, T.J.; Arlow, D.H.; Manglik, A.; Pan, A.C.; Liu, C.W.; Fung, J.J.; Bokoch, M.P.; et al. The dynamic process of beta(2)-adrenergic receptor activation. Cell 2013, 152, 532–542. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P.; Fuxreiter, M. Fuzzy complexes: Polymorphism and structural disorder in protein-protein interactions. Trends Biochem. Sci. 2008, 33, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Raduly, Z.; Miskei, M.; Fuxreiter, M. Fuzzy complexes: Specific binding without complete folding. FEBS Lett. 2015, 589, 2533–2542. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuxreiter, M. Fuzziness in Protein Interactions-A Historical Perspective. J. Mol. Biol. 2018, 430, 2278–2287. [Google Scholar] [CrossRef] [PubMed]
- Hadzi, S.; Mernik, A.; Podlipnik, C.; Loris, R.; Lah, J. The Thermodynamic Basis of the Fuzzy Interaction of an Intrinsically Disordered Protein. Angew Chem. Int. Ed. Engl. 2017, 56, 14494–14497. [Google Scholar] [CrossRef] [PubMed]
- Fuxreiter, M.; Simon, I.; Bondos, S. Dynamic protein-DNA recognition: Beyond what can be seen. Trends Biochem. Sci. 2011, 36, 415–423. [Google Scholar] [CrossRef] [PubMed]
- Buljan, M.; Chalancon, G.; Eustermann, S.; Wagner, G.P.; Fuxreiter, M.; Bateman, A.; Babu, M.M. Tissue-Specific Splicing of Disordered Segments that Embed Binding Motifs Rewires Protein Interaction Networks. Mol. Cell 2012, 46, 871–883. [Google Scholar] [CrossRef] [PubMed]
- Miskei, M.; Gregus, A.; Sharma, R.; Duro, N.; Zsolyomi, F.; Fuxreiter, M. Fuzziness enables context dependence of protein interactions. FEBS Lett. 2017, 591, 2682–2695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toto, A.; Camilloni, C.; Giri, R.; Brunori, M.; Vendruscolo, M.; Gianni, S. Molecular Recognition by Templated Folding of an Intrinsically Disordered Protein. Sci. Rep. 2016, 6, 21994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuxreiter, M. Fold or not to fold upon binding-does it really matter? Curr. Opin. Struct. Biol. 2018, 54, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Warfield, L.; Tuttle, L.M.; Pacheco, D.; Klevit, R.E.; Hahn, S. A sequence-specific transcription activator motif and powerful synthetic variants that bind Mediator using a fuzzy protein interface. Proc. Natl. Acad. Sci. USA 2014, 111, E3506–E3513. [Google Scholar] [CrossRef] [PubMed]
- Tuttle, L.M.; Pacheco, D.; Warfield, L.; Luo, J.; Ranish, J.; Hahn, S.; Klevit, R.E. Gcn4-Mediator Specificity Is Mediated by a Large and Dynamic Fuzzy Protein-Protein Complex. Cell Rep. 2018, 22, 3251–3264. [Google Scholar] [CrossRef] [PubMed]
- Delaforge, E.; Kragelj, J.; Tengo, L.; Palencia, A.; Milles, S.; Bouvignies, G.; Salvi, N.; Blackledge, M.; Jensen, M.R. Deciphering the Dynamic Interaction Profile of an Intrinsically Disordered Protein by NMR Exchange Spectroscopy. J. Am. Chem. Soc. 2018, 140, 1148–1158. [Google Scholar] [CrossRef] [PubMed]
- Kragelj, J.; Palencia, A.; Nanao, M.H.; Maurin, D.; Bouvignies, G.; Blackledge, M.; Jensen, M.R. Structure and dynamics of the MKK7-JNK signaling complex. Proc. Natl. Acad. Sci. USA. 2015, 112, 3409–3414. [Google Scholar] [CrossRef] [PubMed]
- Gogl, G.; Alexa, A.; Kiss, B.; Katona, G.; Kovacs, M.; Bodor, A.; Remenyi, A.; Nyitray, L. Structural Basis of Ribosomal S6 Kinase 1 (RSK1) Inhibition by S100B Protein: Modulation of the extracellular signal-regulated kinase (ERK) signaling cascade in a calcium-dependent way. J. Biol. Chem. 2016, 291, 11–27. [Google Scholar] [CrossRef] [PubMed]
- Lu, A.; Magupalli, V.G.; Ruan, J.; Yin, Q.; Atianand, M.K.; Vos, M.R.; Schroder, G.F.; Fitzgerald, K.A.; Wu, H.; Egelman, E.H. Unified polymerization mechanism for the assembly of ASC-dependent inflammasomes. Cell 2014, 156, 1193–1206. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.M.; Pufall, M.A.; Meeker, C.A.; Kang, H.S.; Graves, B.J.; McIntosh, L.P. The affinity of Ets-1 for DNA is modulated by phosphorylation through transient interactions of an unstructured region. J. Mol. Biol. 2008, 382, 1014–1030. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; McQuade, T.; Siemer, A.B.; Napetschnig, J.; Moriwaki, K.; Hsiao, Y.S.; Damko, E.; Moquin, D.; Walz, T.; McDermott, A.; et al. The RIP1/RIP3 Necrosome Forms a Functional Amyloid Signaling Complex Required for Programmed Necrosis. Cell 2012, 150, 339–350. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davey, N.E.; Cyert, M.S.; Moses, A.M. Short linear motifs-ex nihilo evolution of protein regulation. Cell Commun. Signal. 2015, 13, 43. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Hamkalo, B.; Parseghian, M.H.; Hansen, J.C. Chromatin condensing functions of the linker histone C-terminal domain are mediated by specific amino acid composition and intrinsic protein disorder. Biochemistry 2009, 48, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Ross, E.D.; Edskes, H.K.; Terry, M.J.; Wickner, R.B. Primary sequence independence for prion formation. Proc. Natl. Acad. Sci. USA 2005, 102, 12825–12830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nott, T.J.; Petsalaki, E.; Farber, P.; Jervis, D.; Fussner, E.; Plochowietz, A.; Craggs, T.D.; Bazett-Jones, D.P.; Pawson, T.; Forman-Kay, J.D.; et al. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell 2015, 57, 936–947. [Google Scholar] [CrossRef] [PubMed]
- Milles, S.; Mercadante, D.; Aramburu, I.V.; Jensen, M.R.; Banterle, N.; Koehler, C.; Tyagi, S.; Clarke, J.; Shammas, S.L.; Blackledge, M.; et al. Plasticity of an Ultrafast Interaction between Nucleoporins and Nuclear Transport Receptors. Cell 2015, 163, 734–745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ciuffa, R.; Lamark, T.; Tarafder, A.K.; Guesdon, A.; Rybina, S.; Hagen, W.J.; Johansen, T.; Sachse, C. The selective autophagy receptor p62 forms a flexible filamentous helical scaffold. Cell Rep. 2015, 11, 748–758. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Fuxreiter, M. The Structure and Dynamics of Higher-Order Assemblies: Amyloids, Signalosomes, and Granules. Cell 2016, 165, 1055–1066. [Google Scholar] [CrossRef] [PubMed]
- Burke, K.A.; Janke, A.M.; Rhine, C.L.; Fawzi, N.L. Residue-by-Residue View of In Vitro FUS Granules that Bind the C-Terminal Domain of RNA Polymerase II. Mol. Cell 2015, 60, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.; Lee, H.O.; Jawerth, L.; Maharana, S.; Jahnel, M.; Hein, M.Y.; Stoynov, S.; Mahamid, J.; Saha, S.; Franzmann, T.M.; et al. A Liquid-to-Solid Phase Transition of the ALS Protein FUS Accelerated by Disease Mutation. Cell 2015, 162, 1066–1077. [Google Scholar] [CrossRef] [PubMed]
- Molliex, A.; Temirov, J.; Lee, J.; Coughlin, M.; Kanagaraj, A.P.; Kim, H.J.; Mittag, T.; Taylor, J.P. Phase Separation by Low Complexity Domains Promotes Stress Granule Assembly and Drives Pathological Fibrillization. Cell 2015, 163, 123–133. [Google Scholar] [CrossRef] [PubMed]
- Nagulapalli, M.; Parigi, G.; Yuan, J.; Gsponer, J.; Deraos, G.; Bamm, V.V.; Harauz, G.; Matsoukas, J.; de Planque, M.R.; Gerothanassis, I.P.; et al. Recognition pliability is coupled to structural heterogeneity: A calmodulin intrinsically disordered binding region complex. Structure 2012, 20, 522–533. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Tuu-Szabo, B.; Koczy, L.; Fuxreiter, M. Simulations of Higher-Order Protein Organizations Using a Fuzzy Framework. Complexity 2018, in press. [Google Scholar]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuxreiter, M. Towards a Stochastic Paradigm: From Fuzzy Ensembles to Cellular Functions. Molecules 2018, 23, 3008. https://doi.org/10.3390/molecules23113008
Fuxreiter M. Towards a Stochastic Paradigm: From Fuzzy Ensembles to Cellular Functions. Molecules. 2018; 23(11):3008. https://doi.org/10.3390/molecules23113008
Chicago/Turabian StyleFuxreiter, Monika. 2018. "Towards a Stochastic Paradigm: From Fuzzy Ensembles to Cellular Functions" Molecules 23, no. 11: 3008. https://doi.org/10.3390/molecules23113008
APA StyleFuxreiter, M. (2018). Towards a Stochastic Paradigm: From Fuzzy Ensembles to Cellular Functions. Molecules, 23(11), 3008. https://doi.org/10.3390/molecules23113008