Small Universal Bacteria and Plasmid Computing Systems
Abstract
:1. Introduction
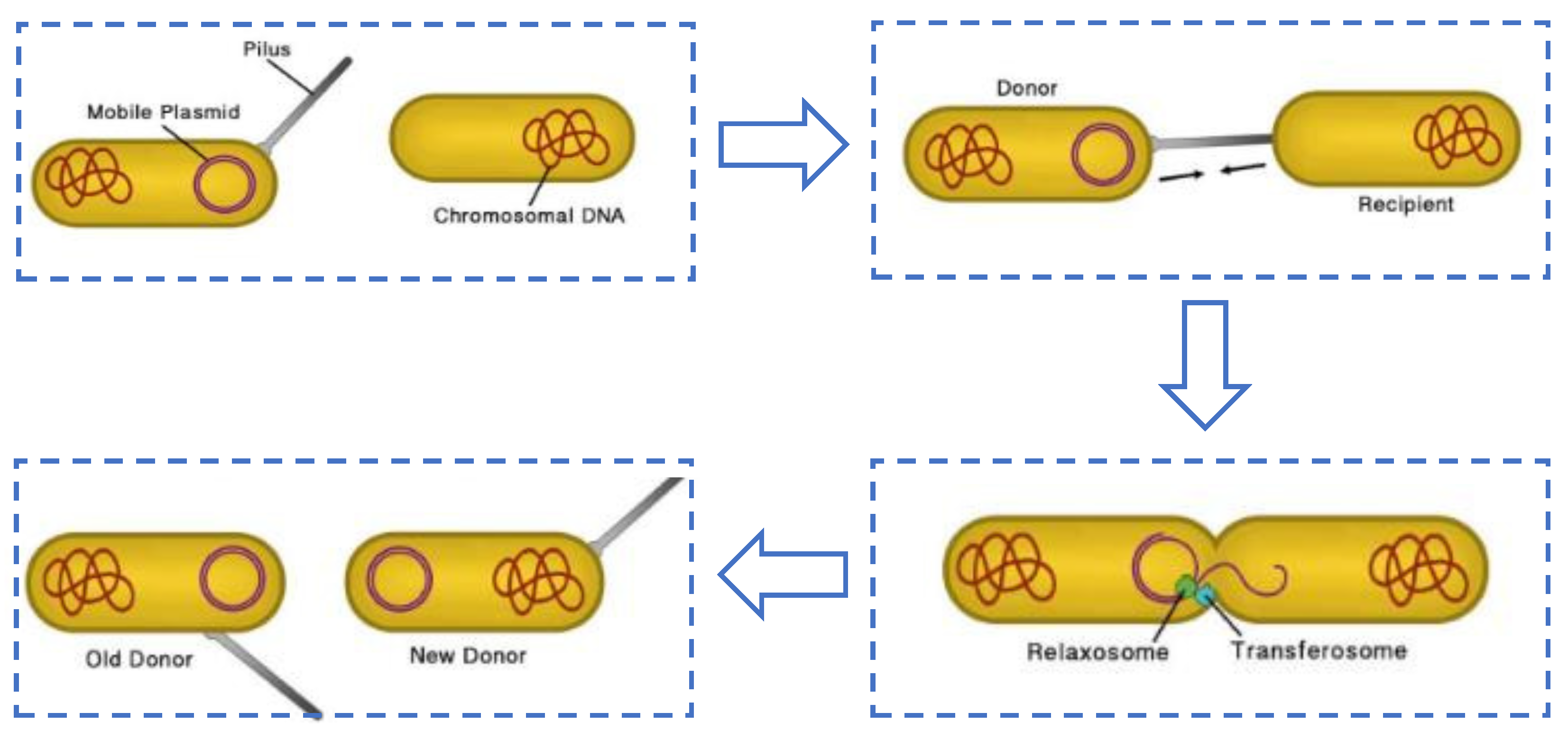
2. The Bacteria and Plasmid System
- –
- a set of bacteria;
- –
- a set of plasmids;
- –
- a set of evolution rules in each bacterium, including conjugation rules and gene-editing (inserting/deleting) rules.
- is a set of genes in the chromosomal DNA of bacteria.
- is a set of plasmids.
- –
- Plasmids in are of the form with , which is used for cutting specific genes.
- –
- Plasmids in are of the form , which takes templates of genes to be inserted.
- –
- Plasmid is of the form for bacteria conjugation.
- Variables are m bacteria of the form , where
- –
- is a set of genes over O initially placed in bacterium ;
- –
- is a set of rules in bacterium of the following forms:
- (1)
- Conjugation rule is of the form , by which ATP in bacterium is consumed and a set of plasmids associated with ATP is transmitted into bacterium .
- (2)
- CRISPR/Cas9 gene inserting rule is of the form , where , , , and and are two neighboring genes. The insertion is operated if and only if and are neighboring genes and plasmids are present in the bacterium.
- (3)
- CRISPR/Cas9 gene deleting rule is of the form with , , and and being two neighboring genes. The rule can be used if and only there exists gene placed between the two neighboring genes.
- Variable is the output bacterium.
3. Universality Results
- ADD (add 1 to register r and then go to one of the instructions with labels and );
- SUB (if register r is non-zero, then subtract 1 from it, and go to the instruction with label ; otherwise, go to the instruction with label );
- HALT (the halt instruction).
3.1. A Small Universal BP System as Function Computing Device
- is set of genes in chromosomal DNA of bacteria.
- is a set of plasmids shown in Table 1, where
- –
- , whose elements associated with the labels of instructions are used for gene cutting;
- –
- are plasmids taking templates of genes to be inserted, which are used for simulating ADD instructions;
- –
- plasmid for bacteria conjugation is used for simulating SUB instructions.
- , where , meaning no initial chromosomal DNA is placed in bacteria ; the set of rules is shown in Table 2.
- , where , indicating the initially placed chromosomal DNA in bacterium ; the set of rules is shown in Table 2.
- , which means bacterium can read signals from the environment, and when the system halts, the computational result is stored in bacterium .
- If instruction is an ADD instruction, then bacterium has the conjugation rule . By using the rule, plasmids and ATP are conjugated to bacterium . In this case, system starts to simulate the proceeding ADD instruction .
- If instruction is a SUB instruction, then bacterium has the conjugation rule , by which plasmids and ATP are transmitted to bacterium . In this case, system starts to simulate the proceeding SUB instruction .
- –
- If there is at least one gene existing between neighboring genes and in chromosomal DNA of bacterium (corresponding to the case that the number stored in register r is ), then the CRISPR/Cas9 deleting rule is used to delete one copy of gene from chromosomal DNA. This simulates the number stored in register r being decreased by 1. By consuming plasmid , bacterium retains plasmid and ATP such that a conjugation rule or is used, which depends on whether the proceeding instruction would be an ADD or a SUB instruction. In this way, plasmids or and ATP are transmitted to bacterium . The system starts to simulate instruction .
- –
- If there is no gene existing between neighboring genes and in chromosomal DNA of bacterium (corresponding to the case that the number stored in register r is 0), then the CRISPR/Cas9 deleting rule cannot be used, but a conjugation rule or is able to be used. Plasmids ( or ) and ATP are conjugated to bacterium , which means the system starts to simulate instruction .
- 2 bacterium for conjugation with each other;
- 22 plasmids for the 22 ADD and SUB instructions with ;
- 9 plasmids for 9 ADD instructions with ;
- 1 plasmid for the 13 SUB instructions;
- 2 plasmids and for the HALT instruction;
- 8 genes for encoding numbers in registers i with ;
- 1 gene for separating gene in chromosomal DNA.
3.2. A Small Universal BP System as a Number Generator
- 2 bacterium for the conjugation with each other;
- 22 plasmids for the 22 ADD and SUB instructions with ;
- 9 plasmids for 9 ADD instructions with ;
- 1 plasmid for the 13 SUB instructions;
- 2 plasmids and for the HALT instruction;
- 8 genes for encoding numbers in registers i with ;
- 1 gene for separating gene in chromosomal DNA.
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gitai, Z. The new bacterial cell biology: Moving parts and subcellular architecture. Cell 2005, 120, 577–586. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, E.; Drlica, K. Regulation of bacterial dna supercoiling: Plasmid linking numbers vary with growth temperature. Proc. Natl. Acad. Sci. USA 1984, 81, 4046–4050. [Google Scholar] [CrossRef] [PubMed]
- Summers, D. The Biology of Plasmids; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Poet, J.L.; Campbell, A.M.; Eckdahl, T.T.; Heyer, L.J. Bacterial computing. XRDS Crossroads ACM Mag. Stud. 2010, 17, 10–15. [Google Scholar] [CrossRef]
- Gupta, V.; Irimia, J.; Pau, I.; Rodríguez-Patón, A. Bioblocks: Programming protocols in biology made easier. ACS Synth. Biol. 2017, 6, 1230–1232. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, M.; Gregorio-Godoy, P.; del Pulgar, G.P.; Munoz, L.E.; Sáez, S.; Rodríguez-Patón, A. A new improved and extended version of the multicell bacterial simulator gro. ACS Synth. Biol. 2017, 6, 1496–1508. [Google Scholar] [CrossRef] [PubMed]
- Adleman, L.M. Molecular computation of solutions to combinatorial problems. Sciences 1994, 266, 1021–1024. [Google Scholar] [CrossRef]
- Carell, T. Molecular computing: Dna as a logic operator. Nature 2011, 469, 45–46. [Google Scholar] [CrossRef] [PubMed]
- Xu, J. Probe machine. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1405–1416. [Google Scholar] [CrossRef] [PubMed]
- Păun, G.; Rozenberg, G.; Salomaa, A. The Oxford Handbook of Nembrane Computing; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Păun, G.; Rozenberg, G. A guide to membrane computing. Theor. Comput. Sci. 2002, 287, 73–100. [Google Scholar] [CrossRef]
- Păun, G. Computing with membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef]
- Freund, R.; Kari, L.; Păun, G. DNA computing based on splicing: The existence of universal computers. Theory Comput. Syst. 1999, 32, 69–112. [Google Scholar] [CrossRef]
- Kari, L.; Păun, G.; Rozenberg, G.; Salomaa, A.; Yu, S. DNA computing, sticker systems, and universality. Acta Inform. 1998, 35, 401–420. [Google Scholar] [CrossRef]
- Martın-Vide, C.; Păun, G.; Pazos, J.; Rodrıguez-Patón, A. Tissue P systems. Theor. Comput. Sci. 2003, 296, 295–326. [Google Scholar] [CrossRef]
- Ionescu, M.; Păun, G.; Yokomori, T. Spiking neural P systems. Fundam. Inform. 2006, 71, 279–308. [Google Scholar]
- Song, T.; Pan, L.; Păun, G. Asynchronous spiking neural p systems with local synchronization. Inform. Sci. 2013, 219, 197–207. [Google Scholar] [CrossRef]
- Ezziane, Z. DNA computing: Applications and challenges. Nanotechnology 2005, 17, R27. [Google Scholar] [CrossRef]
- Chen, X.; Pérez-Jiménez, M.J.; Valencia-Cabrera, L.; Wang, B.; Zeng, X. Computing with viruses. Theor. Comput. Sci. 2016, 623, 146–159. [Google Scholar] [CrossRef]
- Rogozhin, Y. Small universal turing machines. Theor. Comput. Sci. 1996, 168, 215–240. [Google Scholar] [CrossRef]
- Baiocchi, C. Three small universal turing machines. In Machines, Computations, and Universality; Springer: Berlin/Heidelberg, Germany, 2001; pp. 1–10. [Google Scholar]
- Korec, I. Small universal register machines. Theor. Comput. Sci. 1996, 168, 267–301. [Google Scholar] [CrossRef]
- Iirgen Albert, J.; Culik, K., II. A simple universal cellular automaton and its one-way and totalistic version. Complex Syst. 1987, 1, 1–16. [Google Scholar]
- Kudlek, M.; Yu, R. Small universal circular post machines. Comput. Sci. J. Mold. 2001, 9, 25. [Google Scholar]
- Păun, A.; Păun, G. Small universal spiking neural P systems. BioSystems 2007, 90, 48–60. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zeng, X.; Pan, L. Smaller universal spiking neural P systems. Fundam. Inform. 2008, 87, 117–136. [Google Scholar]
- Pan, L.; Zeng, X. A note on small universal spiking neural P systems. Lect. Notes Comput. Sci. 2010, 5957, 436–447. [Google Scholar]
- Păun, A.; Sidoroff, M. Sequentiality induced by spike number in SNP systems: Small universal machines. In Membrane Computing; Springer: Berlin/Heidelberg, Germany, 2012; pp. 333–345. [Google Scholar]
- Song, T.; Jiang, Y.; Shi, X.; Zeng, X. Small universal spiking neural P systems with anti-spikes. J. Comput. Theor. Nanosci. 2013, 10, 999–1006. [Google Scholar] [CrossRef]
- Song, T.; Xu, J.; Pan, L. On the universality and non-universality of spiking neural P systems with rules on synapses. IEEE Trans. Nanobiosci. 2015, 14, 960–966. [Google Scholar] [CrossRef] [PubMed]
- Song, T.; Pan, L. Spiking neural P systems with request rules. Neurocomputing 2016, 193, 193–200. [Google Scholar] [CrossRef]
- Song, T.; Rodríguez-Patón, A.; Gutiérrez, M.; Pan, Z. Computing with bacteria conjugation and crispr/cas9 gene editing operations. Sci. Rep. 2018. sumitted. [Google Scholar]
- Minsky, M.L. Computation: Finite and Infinite Machines; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1967. [Google Scholar]
- Valencia-Cabrera, L.; Orellana-Martín, D.; Martínez-del Amor, M.A.; Riscos-Nú nez, A.; Pérez-Jiménez, M.J. Computational efficiency of minimal cooperation and distribution in polarizationless p systems with active membranes. Fundam. Inform. 2017, 153, 147–172. [Google Scholar] [CrossRef]
- Song, B.; Pérez-Jiménez, M.J.; Pan, L. An efficient time-free solution to qsat problem using p systems with proteins on membranes. Inf. Comput. 2017, 256, 287–299. [Google Scholar] [CrossRef]
- Macías-Ramos, L.F.; Pérez-Jiménez, M.J.; Riscos-Nú nez, A.; Valencia-Cabrera, L. Membrane fission versus cell division: When membrane proliferation is not enough. Theor. Comput. Sci. 2015, 608, 57–65. [Google Scholar] [CrossRef]
- Ma, X.; Sun, F.; Li, H.; He, B. Neural-network-based sliding-mode control for multiple rigid-body attitude tracking with inertial information completely unknown. Inf. Sci. 2017, 400, 91–104. [Google Scholar] [CrossRef]
- Alsaeedan, W.; Menai, M.E.B.; Al-Ahmadi, S. A hybrid genetic-ant colony optimization algorithm for the word sense disambiguation problem. Inf. Sci. 2017, 417, 20–38. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available. |



| Plasmid | Forms of Plasmids | Plasmid | Forms of Plasmids |
|---|---|---|---|
| Sim. | Rules | Bac. |
|---|---|---|
| , , | ||
| , | ||
| , | ||
| , , | ||
| , , | ||
| , | ||
| , , | ||
| , | ||
| , , | ||
| , | ||
| , , | ||
| , , | ||
| , , | ||
| , , | ||
| , , | ||
| , , | ||
| , | ||
| , | ||
| , , | ||
| , , | ||
| , | ||
| , | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zheng, P.; Ma, T.; Song, T. Small Universal Bacteria and Plasmid Computing Systems. Molecules 2018, 23, 1307. https://doi.org/10.3390/molecules23061307
Wang X, Zheng P, Ma T, Song T. Small Universal Bacteria and Plasmid Computing Systems. Molecules. 2018; 23(6):1307. https://doi.org/10.3390/molecules23061307
Chicago/Turabian StyleWang, Xun, Pan Zheng, Tongmao Ma, and Tao Song. 2018. "Small Universal Bacteria and Plasmid Computing Systems" Molecules 23, no. 6: 1307. https://doi.org/10.3390/molecules23061307
APA StyleWang, X., Zheng, P., Ma, T., & Song, T. (2018). Small Universal Bacteria and Plasmid Computing Systems. Molecules, 23(6), 1307. https://doi.org/10.3390/molecules23061307




