Kinetics of Crystallization and Thermal Degradation of an Isotactic Polypropylene Matrix Reinforced with Graphene/Glass-Fiber Filler
Abstract
:1. Introduction
2. Results and Discussion
2.1. Isothermal Crystallization
2.2. Avrami Analysis of Isothermal Crystallization
2.3. Lauritzen–Hoffman Analysis
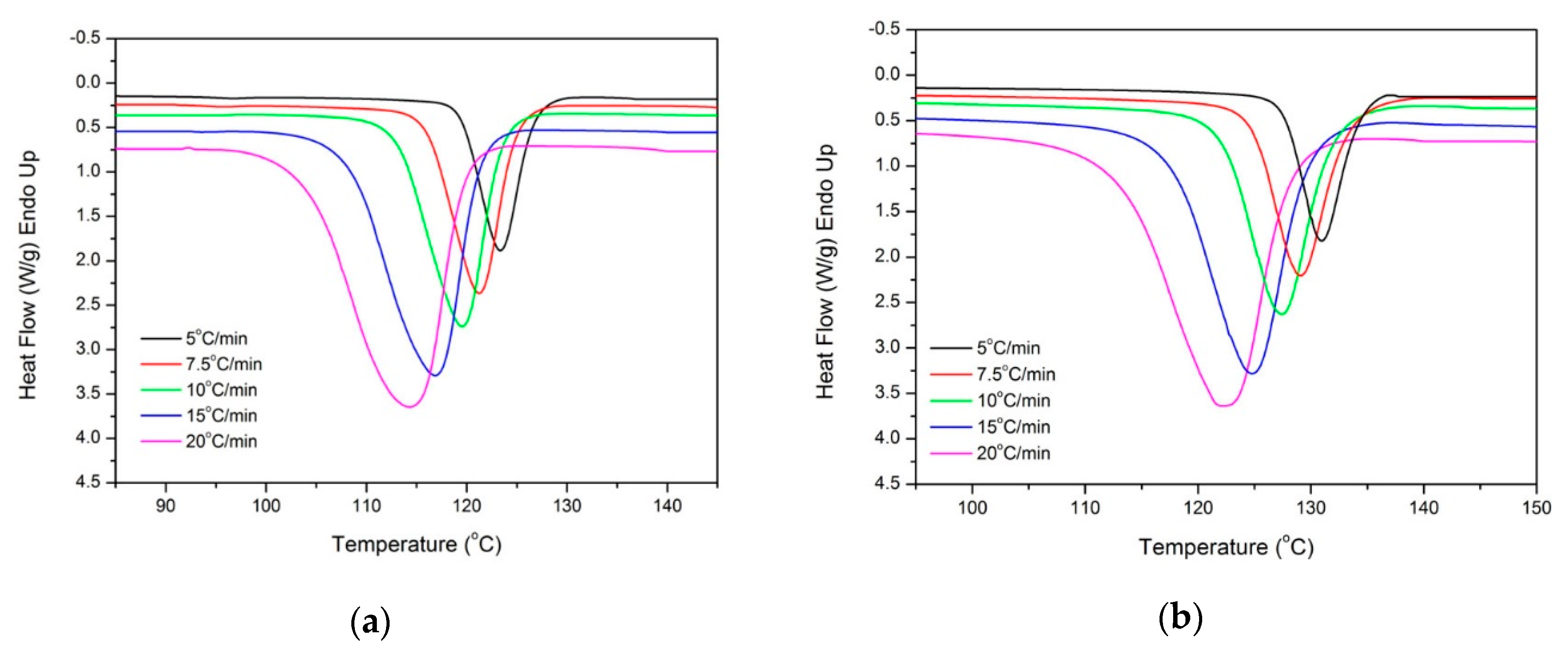
2.4. Melting Behavior after Isothermal Crystallization
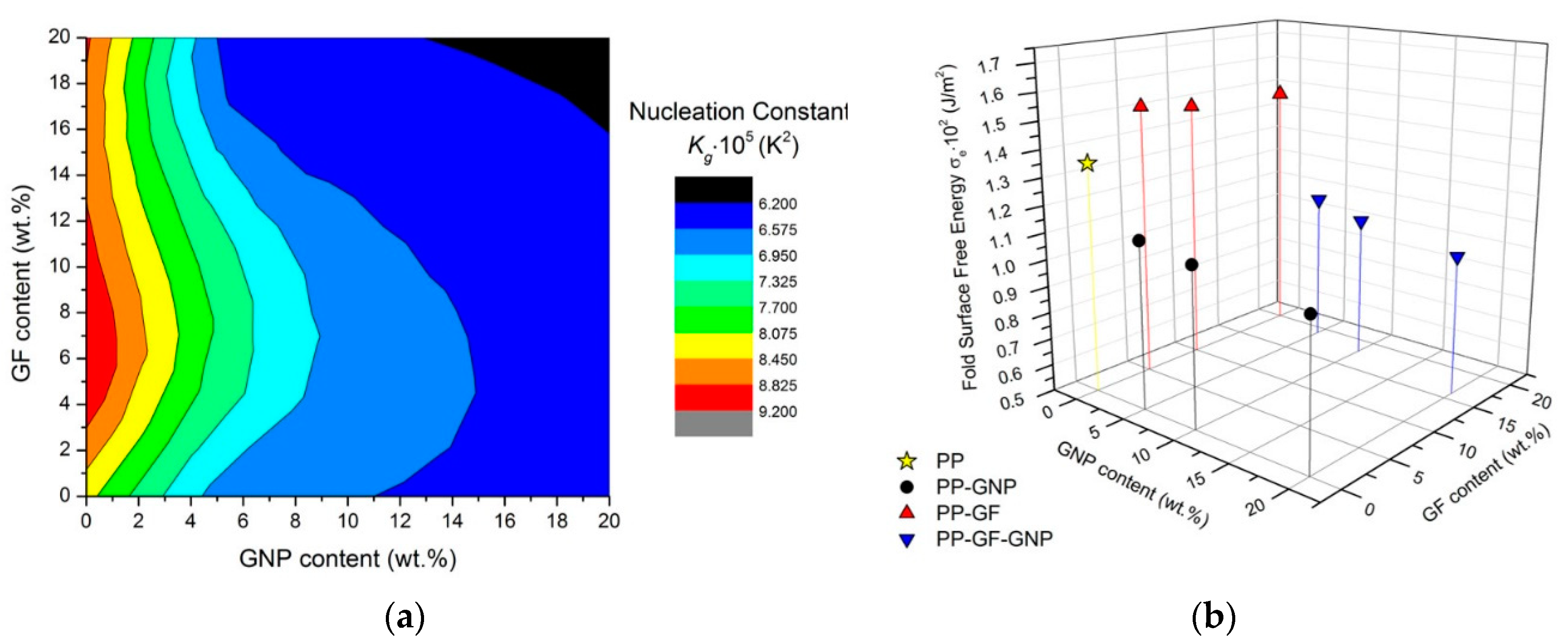
2.5. Nucleation Activity
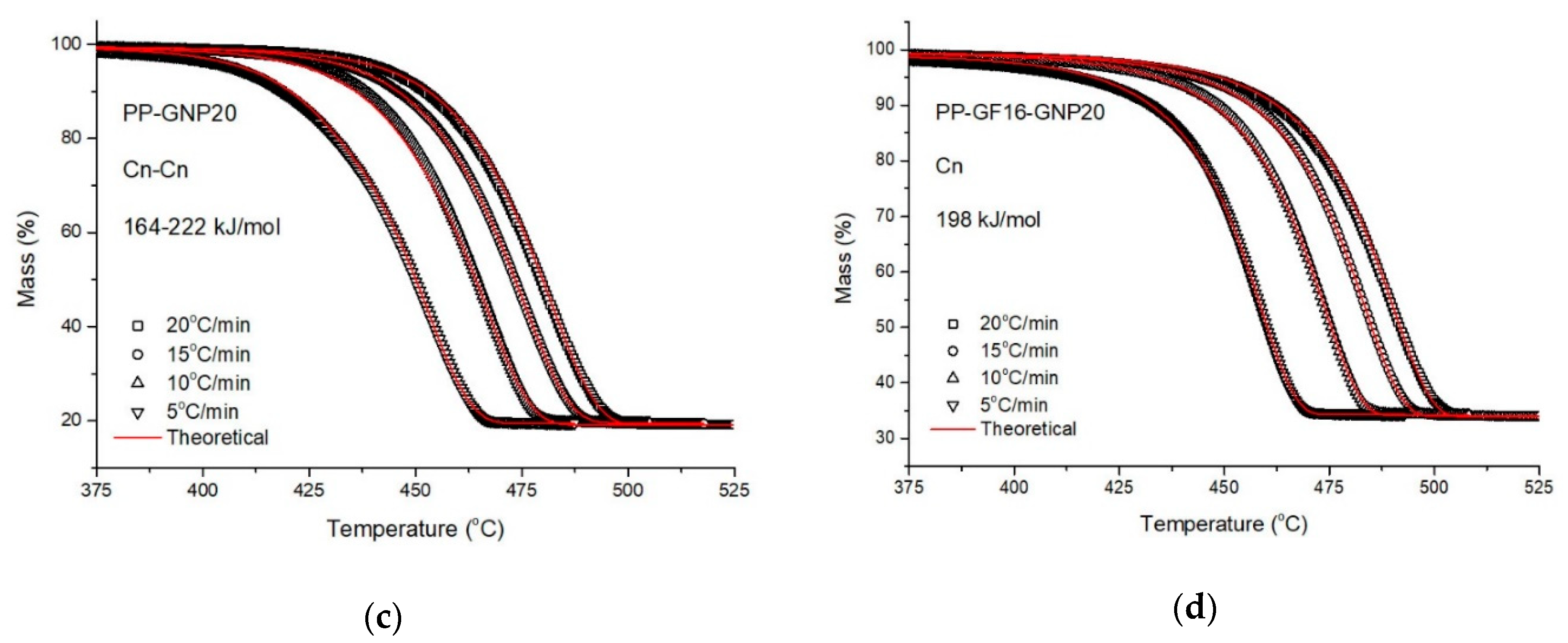
3. Kinetic Analysis Based on Thermogravimetric Data
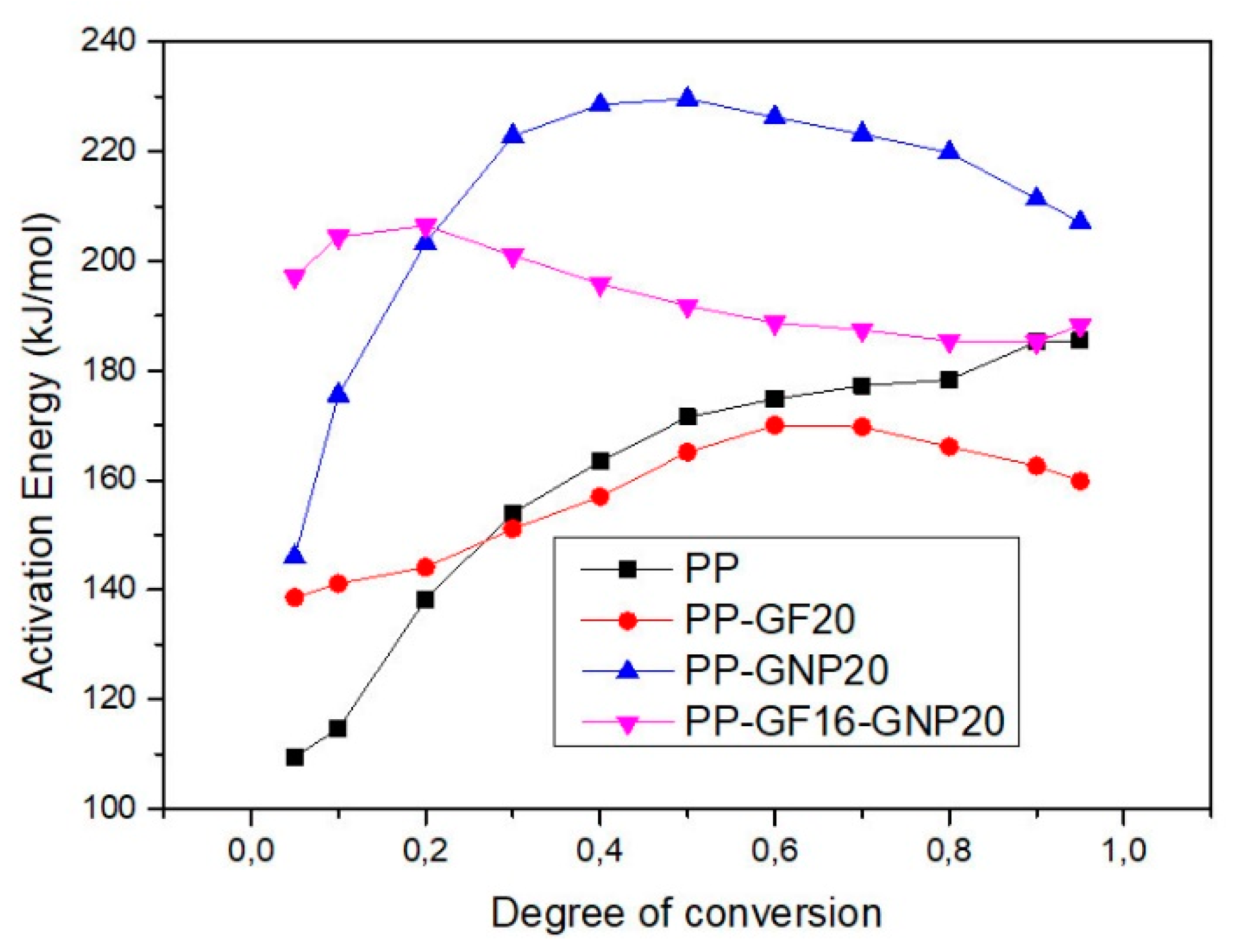
3.1. Isoconversional Methods
3.2. Model-Fitting Procedure
4. Materials and Methods
4.1. Materials
4.2. Differential Scanning Calorimetry (DSC)
4.3. Thermogravimetric Analysis (TGA)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Alexandre, M.; Dubois, P. Polymer-layered silicate nanocomposites: Preparation, properties and uses of a new class of materials. Mat. Sci. Eng. R. 2000, 28, 1–63. [Google Scholar] [CrossRef]
- Valles, C.; Abdelkader, A.M.; Young, R.J.; Kinloch, I.A. Few layer graphene-polypropylene nanocomposites: The role of flake diameter. Faraday Disc. 2014, 173, 379–390. [Google Scholar] [CrossRef]
- Kashiwagi, T.; Grulke, E.; Hilding, J.; Groth, K.; Harris, R.; Butler, K.; Shields, J.; Kharchenko, S.; Douglas, J. Thermal and flammability properties of polypropylene/carbon nanotube nanocomposites. Polymer 2004, 45, 4227–4239. [Google Scholar] [CrossRef]
- Bikiaris, D.N.; Vassiliou, A.; Pavlidou, E.; Karayannidis, G.P. Compatibilisation effect of PP-g-MA copolymer on iPP/SiO2 nanocomposites prepared by melt mixing. Eur. Polym. J. 2005, 41, 1965–1978. [Google Scholar] [CrossRef]
- Bikiaris, D.; Vassiliou, A.; Chrissafis, K.; Paraskevopoulos, K.M.; Jannakoudakis, A.; Docoslis, A. Effect of acid treated multi-walled carbon nanotubes on the mechanical, permeability, thermal properties and thermo-oxidative stability of isotactic polypropylene. Polym. Degrad. Stab. 2008, 93, 952–967. [Google Scholar]
- Gao, S.L.; Mäder, E. Characterisation of interphase nanoscale property variations in glass fibre reinforced polypropylene and epoxy resin composites. Compos. Part A Appl. Sci. Manuf. 2002, 33, 559–576. [Google Scholar] [CrossRef]
- Oever, M.; Peijs, T. Continuous-glass-fibre-reinforced polypropylene composites II. Influence of maleic-anhydride modified polypropylene on fatigue behaviour. Compos. Part A Appl. Sci. Manuf. 1998, 29, 227–239. [Google Scholar] [CrossRef]
- Sanjay, M.; Arpitha, G.; Yogesha, B. Study on mechanical properties of natural-glass fibre reinforced polymer hybrid composites: A review. Mater. Today Proc. 2015, 2, 2959–2967. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. Multifunctional polypropylene composites produced by incorporation of exfoliated graphite nanoplatelets. Carbon 2007, 45, 1446–1452. [Google Scholar] [CrossRef]
- Tarani, E.; Wurm, A.; Schick, C.; Bikiaris, D.N.; Chrissafis, K.; Vourlias, G. Effect of graphene nanoplatelets diameter on non-isothermal crystallization kinetics and melting behavior of high density polyethylene nanocomposites. Thermochim. ACTA 2016, 643, 94–103. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. Mechanical properties and morphological characterization of exfoliated graphite–polypropylene nanocomposites. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1675–1682. [Google Scholar] [CrossRef]
- Tarani, E.; Papageorgiou, D.G.; Valles, C.; Wurm, A.; Terzopoulou, Z.; Bikiaris, D.N.; Schick, C.; Chrissafis, K.; Vourlias, G. Insights into crystallization and melting of high density polyethylene/graphene nanocomposites studied by fast scanning calorimetry. Polym. Test. 2018, 67, 349–358. [Google Scholar] [CrossRef] [Green Version]
- Pedrazzoli, D.; Pegoretti, A.; Kalaitzidou, K. Synergistic effect of graphite nanoplatelets and glass fibers in polypropylene composites. J. Appl. Polym. Sci. 2015, 132, 41682. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Hybrid multifunctional graphene/glass-fibre polypropylene composites. Compos. Sci. Technol. 2016, 137, 44–51. [Google Scholar] [CrossRef] [Green Version]
- Papageorgiou, D.G.; Terzopoulou, Z.; Fina, A.; Cuttica, F.; Papageorgiou, G.Z.; Bikiaris, D.N.; Chrissafis, K.; Young, R.J.; Kinloch, I.A. Enhanced thermal and fire retardancy properties of polypropylene reinforced with a hybrid graphene/glass-fibre filler. Compos. Sci. Technol. 2018, 156, 95–102. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Liu, M.; Li, Z.; Vallés, C.; Young, R.J.; Kinloch, I.A. Hybrid poly(ether ether ketone) composites reinforced with a combination of carbon fibres and graphene nanoplatelets. Compos. Sci. Technol. 2019, 175, 60–68. [Google Scholar] [CrossRef]
- Westerhout, R.W.J.; Waanders, J.; Kuipers, J.A.M.; Van Swaaij, W.P.M. Kinetics of the low-temperature pyrolysis of polyethene, polypropene, and polystyrene modeling, experimental determination, and comparison with literature models and data. Ind. Eng. Chem. Res. 1997, 36, 1955–1964. [Google Scholar] [CrossRef]
- Gao, Z.; Kaneko, T.; Amasaki, I.; Nakada, M. A kinetic study of thermal degradation of polypropylene. Polym. Degrad. Stab. 2003, 80, 269–274. [Google Scholar] [CrossRef]
- Chrissafis, K.; Paraskevopoulos, K.M.; Stavrev, S.Y.; Docoslis, A.; Vassiliou, A.; Bikiaris, D.N. Characterization and thermal degradation mechanism of isotactic polypropylene/carbon black nanocomposites. Thermochim. ACTA 2007, 465, 6–17. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Tzounis, L.; Papageorgiou, G.Z.; Bikiaris, D.N.; Chrissafis, K. β-nucleated propylene–ethylene random copolymer filled with multi-walled carbon nanotubes: Mechanical, thermal and rheological properties. Polymer 2014, 55, 3758–3769. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Bikiaris, D.N.; Chrissafis, K. Effect of crystalline structure of polypropylene random copolymers on Mechanical properties and thermal degradation kinetics. Thermochim. ACTA 2012, 543, 288–294. [Google Scholar] [CrossRef]
- Hay, J.N.; Fitzgerald, P.A.; Wiles, M. Use of differential scanning calorimetry to study polymer crystallization kinetics. Polymer 1976, 17, 1015–1018. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I: General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, Phase Change, and Microstructure Kinetics of Phase Change. III. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Supaphol, P. Application of the Avrami, Tobin, Malkin, and Urbanovici–Segal macrokinetic models to isothermal crystallization of syndiotactic polypropylene. Thermochim. ACTA 2001, 370, 37–48. [Google Scholar] [CrossRef]
- Papageorgiou, G.Z.; Achilias, D.S.; Bikiaris, D.N. Crystallization Kinetics of Biodegradable Poly (butylene succinate) under Isothermal and Non-Isothermal Conditions. Macromol. Chem. Phys. 2007, 208, 1250–1264. [Google Scholar] [CrossRef]
- Ferreira, C.I.; Dal Castel, C.; Oviedo, M.A.S.; Mauler, R.S. Isothermal and non-isothermal crystallization kinetics of polypropylene/exfoliated graphite nanocomposites. Thermochim. ACTA 2013, 553, 40–48. [Google Scholar] [CrossRef]
- Papageorgiou, G.Z.; Achilias, D.S.; Bikiaris, D.N.; Karayannidis, G.P. Crystallization kinetics and nucleation activity of filler in polypropylene/surface-treated SiO2 nanocomposites. Thermochim. ACTA 2005, 427, 117–128. [Google Scholar] [CrossRef]
- Pérez–Camargo, R.A.; Saenz, G.; Laurichesse, S.; Casas, M.T.; Puiggalí, J.; Avérous, L.; Muller, A.J. Nucleation, Crystallization, and Thermal Fractionation of Poly (ε-Caprolactone)-Grafted-Lignin: Effects of Grafted Chains Length and Lignin Content. J. Polym. Sci. B Polym. Phys. 2015, 53, 1736–1750. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Davis, G.T.; Lauritzen, J., Jr. The rate of crystallization of linear polymers with chain folding. In Treatise on Solid State Chemistry; Hannay, N.B., Ed.; Springer: New York, NY, USA, 1976; Volume 3, pp. 497–614. [Google Scholar]
- Huang, J.W. Dispersion crystallization kinetics, and parameters of Hoffman-Lauritzen theory of polypropylene and nanoscale calcium carbonate composites. Polym. Eng. Sci. 2009, 49, 1855–1864. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Miller, R.L. Kinetics of crystallization from the melt and chain folding in polyethylene fractions revisited: Theory and experiment. Polymer 1997, 38, 3151–3212. [Google Scholar] [CrossRef]
- Gaur, U.; Wunderlich, B. Heat capacity and other thermodynamic properties of linear macromolecules. IV. Polypropylene. J. Phys. Chem. Ref. Data 1981, 10, 1051–1064. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Srinivas, S.; Marand, H.; Agarwal, P. Equilibrium melting temperature and undercooling dependence of the spherulitic growth rate of isotactic polypropylene. Macromolecules 1998, 31, 8230–8242. [Google Scholar] [CrossRef]
- Thomas, D.; Staveley, L. A study of the supercooling of drops of some molecular liquids. J. Chem. Soc. 1952, 889, 4569–4577. [Google Scholar] [CrossRef]
- Clark, E.J.; Hoffman, J.D. Regime III crystallization in polypropylene. Macromolecules 1984, 17, 878–885. [Google Scholar] [CrossRef]
- Hikosaka, M.; Seto, T. Order of the molecular chains in isotactic polypropylene crystals. Polym. J. 1973, 5, 111–127. [Google Scholar] [CrossRef]
- De Rosa, C.; Guerra, G.; Napolitano, R.; Petraccone, V.; Pirozzi, B. Conditions for the α1-α2 transition in isotactic polypropylene samples. Eur. Polym. J. 1984, 20, 937–941. [Google Scholar] [CrossRef]
- Nakamura, K.; Shimizu, S.; Umemoto, S.; Thierry, A.; Lotz, B.; Okui, N. Temperature Dependence of Crystal Growth Rate for [alpha] and [beta] Forms of Isotactic Polypropylene. Polym. J. 2008, 40, 915–922. [Google Scholar] [CrossRef]
- Corradini, P.; Napolitano, R.; Oliva, L.; Petraccone, V.; Pirozzi, B.; Guerra, G. A possible structural interpretation of the two DSC melting peaks of isotactic polypropylene in the α-modification. Die Makromol. Chem. Rapid Commun. 1982, 3, 753–756. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Papageorgiou, G.Z.; Bikiaris, D.N.; Chrissafis, K. Crystallization and melting of propylene–ethylene random copolymers. Homogeneous nucleation and β-nucleating agents. Eur. Polym. J. 2013, 49, 1577–1590. [Google Scholar] [CrossRef]
- Naiki, M.; Kikkawa, T.; Endo, Y.; Nozaki, K.; Yamamoto, T.; Hara, T. Crystal ordering of α phase isotactic polypropylene. Polymer 2001, 42, 5471–5477. [Google Scholar] [CrossRef]
- Dobreva, A.; Gutzow, I. Activity of substrates in the catalyzed nucleation of glass-forming melts. I. Theory. J. Non Cryst. Solids 1993, 162, 1–12. [Google Scholar] [CrossRef]
- Weidenfeller, B.; Höfer, M.; Schilling, F.R. Thermal conductivity, thermal diffusivity, and specific heat capacity of particle filled polypropylene. Compos. Part A Appl. Sci. Manuf. 2004, 35, 423–429. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. ACTA 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Determination of pre-exponential factors and of the mathematical functions f(α) or G(α) that describe the reaction mechanism in a model-free way. Thermochim. ACTA 2013, 564, 59–69. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional kinetics. In Handbook of Thermal Analysis and Calorimetry, 1st ed.; Brown, M.E., Gallagher, P.K., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2008; Volume 5, pp. 503–538. [Google Scholar]
- Chen, K.; Wilkie, C.A.; Vyazovkin, S. Nanoconfinement revealed in degradation and relaxation studies of two structurally different polystyrene-clay systems. J. Phys. Chem. B. 2007, 111, 12685–12692. [Google Scholar] [CrossRef]
- Tarani, E.; Terzopoulou, Z.; Bikiaris, D.N.; Kyratsi, T.; Chrissafis, K.; Vourlias, G. Thermal conductivity and degradation behavior of HDPE/graphene nanocomposites. J. Therm. Anal. Calorim. 2017, 129, 1715–1726. [Google Scholar] [CrossRef]
- Terzopoulou, Z.; Tarani, E.; Kasmi, N.; Papadopoulos, L.; Chrissafis, K.; Papageorgiou, D.G.; Papageorgiou, G.Z.; Bikiaris, D.N. Thermal decomposition kinetics and mechanism of in-situ prepared bio-based poly(propylene 2,5-furan dicarboxylate)/graphene nanocomposites. Molecules 2019, 24, 1717. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Arnal, M.L.; Albuerne, J.; Müller, A.J. DSC isothermal polymer crystallization kinetics measurements and the use of the Avrami equation to fit the data: Guidelines to avoid common problems. Polym. Test. 2007, 26, 222–231. [Google Scholar] [CrossRef]







| 1st Step | ||||||
| Sample | Mechanism | E (kJ/mol) | logA (s−1) | N | logKcat | R2 |
| PP | Fn | 115 | 6.3 | 0.4 | - | 0.9998 |
| PP–GF20 | Fn | 140 | 8.5 | 0.6 | - | 0.9998 |
| PP–GNP20 | Cn | 163 | 9.2 | 0.6 | 0.6 | 0.9999 |
| PP–GF16–GNP20 | Cn | 198 | 11.4 | 0.7 | 0.7 | 0.9999 |
| 2nd Step | ||||||
| Sample | Mechanism | E (kJ/mol) | LogA | N | LogKcat | R2 |
| PP | Cn | 175 | 10.3 | 1.0 | 0.3 | 0.9998 |
| PP–GF20 | Cn | 163 | 9.4 | 0.9 | 0.6 | 0.9998 |
| PP–GNP20 | Cn | 222 | 13.5 | 0.8 | 0.2 | 0.9999 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarani, E.; Papageorgiou, G.Z.; Bikiaris, D.N.; Chrissafis, K. Kinetics of Crystallization and Thermal Degradation of an Isotactic Polypropylene Matrix Reinforced with Graphene/Glass-Fiber Filler. Molecules 2019, 24, 1984. https://doi.org/10.3390/molecules24101984
Tarani E, Papageorgiou GZ, Bikiaris DN, Chrissafis K. Kinetics of Crystallization and Thermal Degradation of an Isotactic Polypropylene Matrix Reinforced with Graphene/Glass-Fiber Filler. Molecules. 2019; 24(10):1984. https://doi.org/10.3390/molecules24101984
Chicago/Turabian StyleTarani, Evangelia, George Z. Papageorgiou, Dimitrios N. Bikiaris, and Konstantinos Chrissafis. 2019. "Kinetics of Crystallization and Thermal Degradation of an Isotactic Polypropylene Matrix Reinforced with Graphene/Glass-Fiber Filler" Molecules 24, no. 10: 1984. https://doi.org/10.3390/molecules24101984
APA StyleTarani, E., Papageorgiou, G. Z., Bikiaris, D. N., & Chrissafis, K. (2019). Kinetics of Crystallization and Thermal Degradation of an Isotactic Polypropylene Matrix Reinforced with Graphene/Glass-Fiber Filler. Molecules, 24(10), 1984. https://doi.org/10.3390/molecules24101984









