Relationships between Interaction Energy and Electron Density Properties for Homo Halogen Bonds of the [(A)nY–X···X–Z(B)m] Type (X = Cl, Br, I)
Abstract
:1. Introduction
2. Computational Details
3. Computational Models
4. Results and Discussion
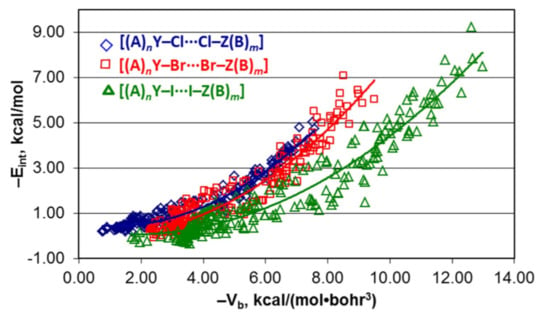
4.1. Whole Set of Structures
4.2. Series [(A)nY–Cl···Cl–Z(B)m], [(A)nY–Br···Br–Z(B)m], and [(A)nY–I···I–Z(B)m]
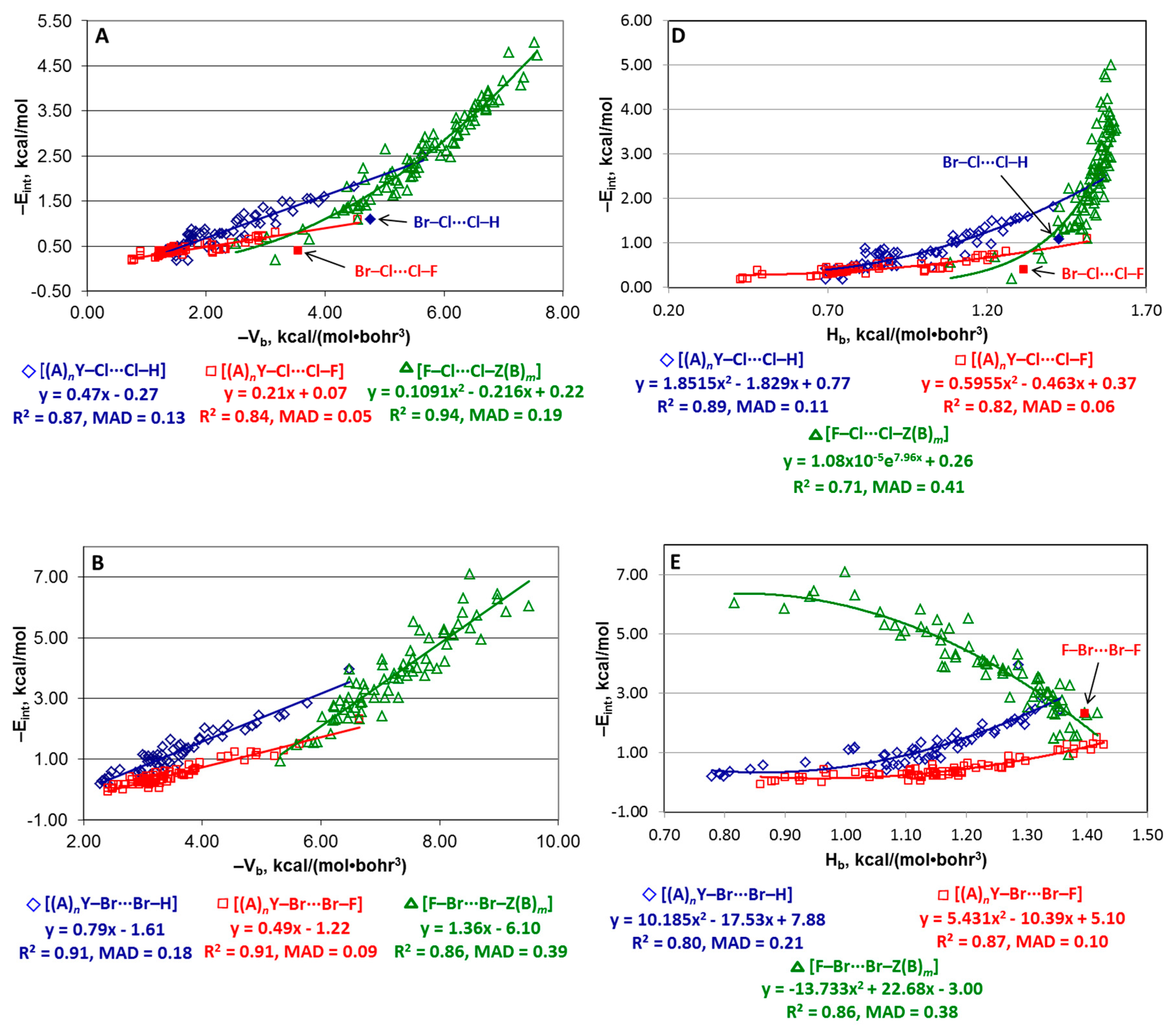
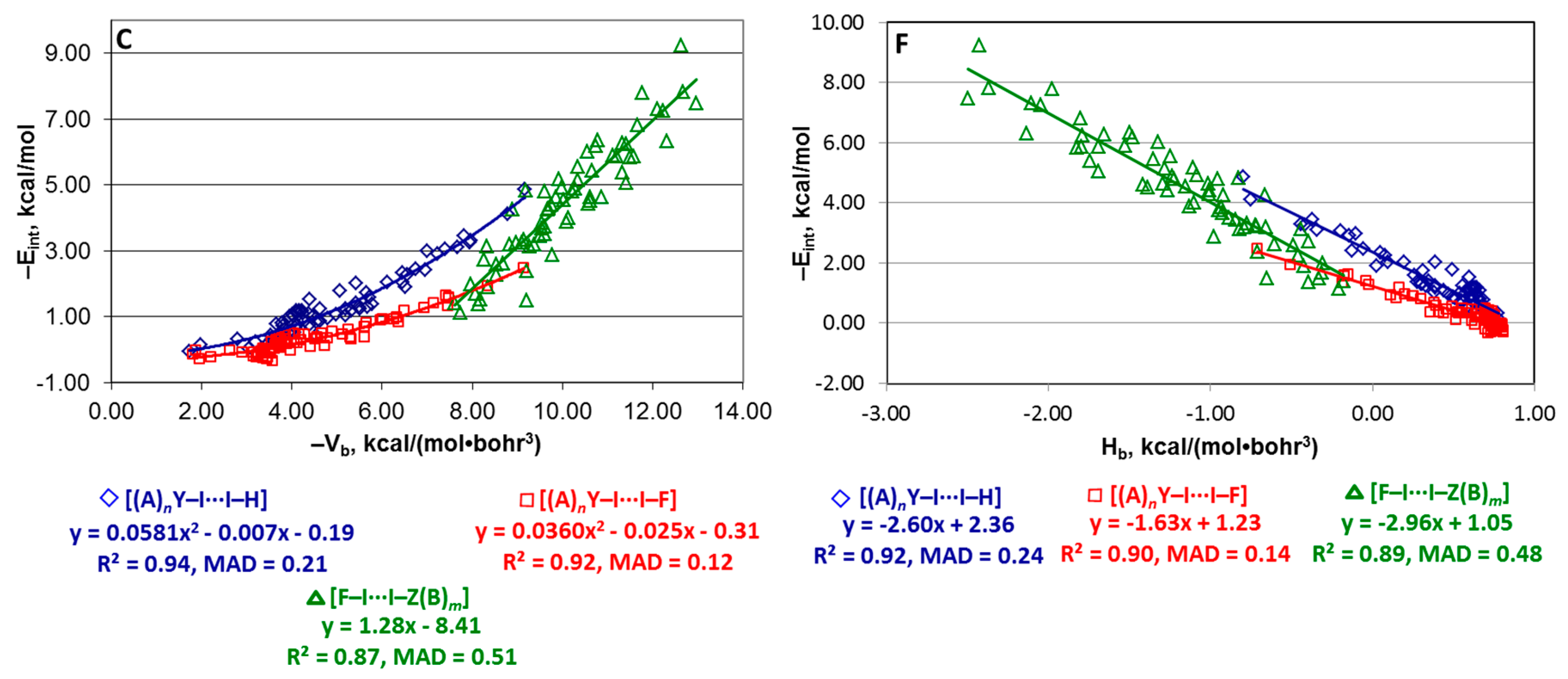
4.3. Series [(A)nY–X···X–H], [(A)nY–X···X–F], and [F–X···X–Z(B)m]
4.4. “Small” Series
4.5. Estimate of Eint from an Integral of Electronic Virial over Interatomic Zero-Flux Surface (IAS)
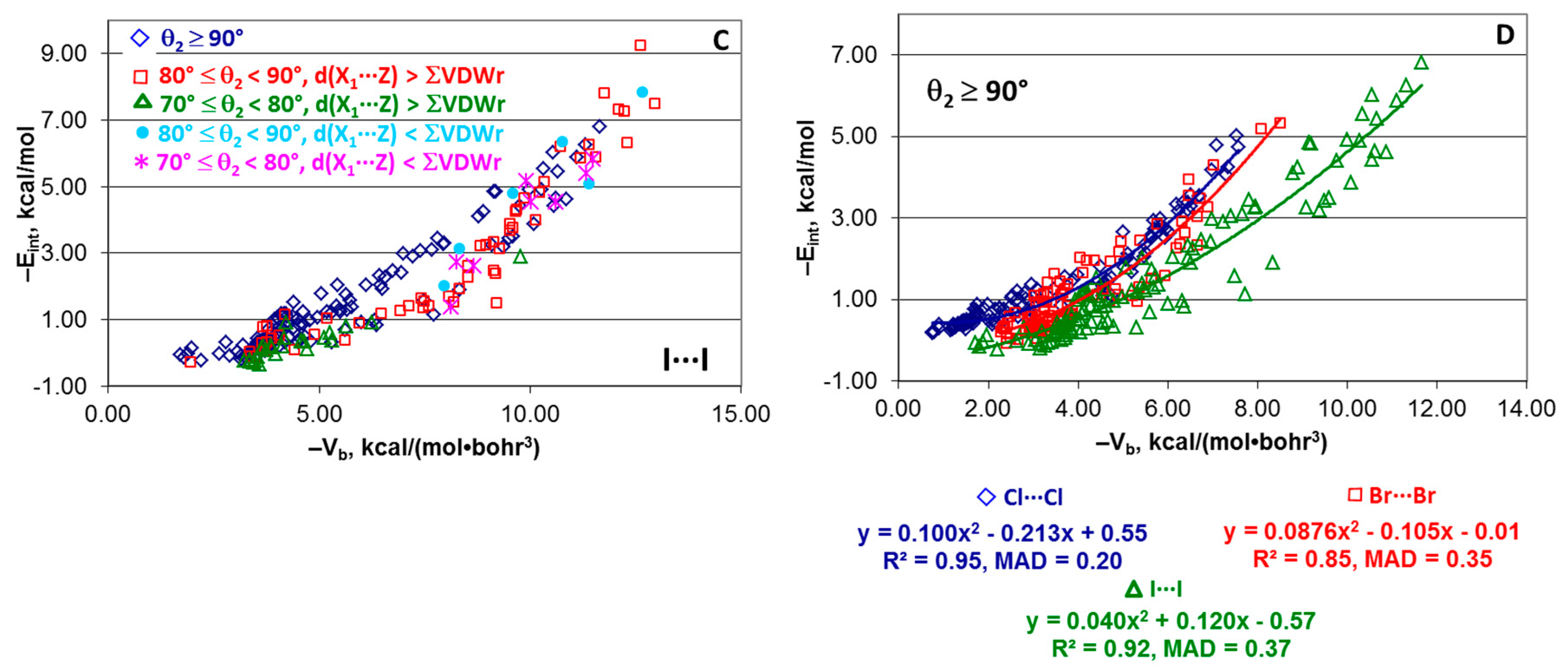
4.6. Effect of Angle θ2
5. Final Remarks
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Metrangolo, P.; Resnati, G. Halogen versus hydrogen. Science 2008, 321, 918–919. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Meyer, F.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen bonding in supramolecular chemistry. Angew. Chem. Int. Ed. 2008, 47, 6114–6127. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Neukirch, H.; Pilati, T.; Resnati, G. Halogen bonding based recognition processes: A world parallel to hydrogen bonding. Acc. Chem. Res. 2005, 38, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen bonding in supramolecular chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef]
- Shirman, T.; Arad, T.; van der Boom, M.E. Halogen bonding: A supramolecular entry for assembling nanoparticles. Angew. Chem. Int. Ed. 2010, 49, 926–929. [Google Scholar] [CrossRef] [PubMed]
- Bayse, C.A.; Rafferty, E.R. Is halogen bonding the basis for iodothyronine deiodinase activity? Inorg. Chem. 2010, 49, 5365–5367. [Google Scholar] [CrossRef] [PubMed]
- Sarwar, M.G.; Dragisic, B.; Salsberg, L.J.; Gouliaras, C.; Taylor, M.S. Thermodynamics of halogen bonding in solution: Substituent, structural, and solvent effects. J. Am. Chem. Soc. 2010, 132, 1646–1653. [Google Scholar] [CrossRef]
- Nelyubina, Y.V.; Antipin, M.Y.; Dunin, D.S.; Kotov, V.Y.; Lyssenko, K.A. Unexpected “amphoteric” character of the halogen bond: The charge density study of the co-crystal of N-methylpyrazine iodide with I2. Chem. Commun. 2010, 46, 5325–5327. [Google Scholar] [CrossRef]
- Koláŕ, M.H.; Hobza, P. Computer modeling of halogen bonds and other σ-hole interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
- Hobza, P.; Müller-Dethlefs, K. Non-Covalent Interactions: Theory and Experiment; Royal Society of Chemistry: Cambridge, UK, 2010. [Google Scholar]
- Natale, D.; Marequerivas, J.C. The combination of transition metal ions and hydrogen-bonding interactions. Chem. Commun. 2008, 425–437. [Google Scholar] [CrossRef] [PubMed]
- Feller, R.K.; Cheetham, A.K. Structural and chemical complexity in multicomponent inorganic–organic framework materials. CrystEngComm 2009, 11, 980–985. [Google Scholar] [CrossRef]
- Corradi, E.; Meille, S.V.; Messina, M.T.; Metrangolo, P.; Resnati, G. Halogen bonding versus hydrogen bonding in driving self-assembly processes. Angew. Chem. Int. Ed. 2000, 39, 1782–1786. [Google Scholar] [CrossRef]
- Desiraju, G.R. Crystal engineering: A holistic view. Angew. Chem. Int. Ed. 2007, 46, 8342–8356. [Google Scholar] [CrossRef] [PubMed]
- Cinčić, D.; Friščić, T.; Jones, W. Structural equivalence of Br and I halogen bonds: A route to isostructural materials with controllable properties. Chem. Mater. 2008, 20, 6623–6626. [Google Scholar] [CrossRef]
- Tepper, R.; Schubert, U.S. Halogen Bonding in Solution: Anion Recognition, Templated Self-Assembly, and Organocatalysis. Angew. Chem. Int. Ed. 2018, 57, 6004–6016. [Google Scholar] [CrossRef] [PubMed]
- Mahmudov, K.T.; Kopylovich, M.N.; Guedes da Silva, M.F.C.; Pombeiro, A.J.L. Non-covalent interactions in the synthesis of coordination compounds: Recent advances. Coord. Chem. Rev. 2017, 345, 54–72. [Google Scholar] [CrossRef]
- Li, B.; Zang, S.-Q.; Wang, L.-Y.; Mak, T.C.W. Halogen bonding: A powerful, emerging tool for constructing high-dimensional metal-containing supramolecular networks. Coord. Chem. Rev. 2016, 308, 1–21. [Google Scholar] [CrossRef]
- Saccone, M.; Cavallo, G.; Metrangolo, P.; Resnati, G.; Priimagi, A. Halogen-Bonded Photoresponsive Materials. In Halogen Bonding II. Topics in Current Chemistry; Metrangolo, P., Resnati, G., Eds.; Springer: Cham, Switzerland, 2014; Volume 359. [Google Scholar]
- Aakeröy, C.B.; Spartz, C.L. Halogen Bonding in Supramolecular Synthesis. In Halogen Bonding I. Topics in Current Chemistry; Metrangolo, P., Resnati, G., Eds.; Springer: Cham, Switzerland, 2014; Volume 358. [Google Scholar]
- Mukherjee, A.; Tothadi, S.; Desiraju, G.R. Halogen bonds in crystal engineering: Like hydrogen bonds yet different. Acc. Chem. Res. 2014, 47, 2514–2524. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, Z.; Liu, Y.; Lu, Y.; Chen, K.; Zhu, W. Halogen bond: Its role beyond drug-target binding affinity for drug discovery and development. J. Chem. Inf. Model. 2014, 54, 69–78. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, T.; Wang, Y.; Yang, H.; Yan, X.; Luo, X.; Jiang, H.; Zhu, W. Halogen bonding—A novel interaction for rational drug design? J. Med. Chem. 2009, 52, 2854–2862. [Google Scholar] [CrossRef] [PubMed]
- Mendez, L.; Henriquez, G.; Sirimulla, S.; Narayan, M. Looking back, looking forward at halogen bonding in drug discovery. Molecules 2017, 22, 1397. [Google Scholar] [CrossRef] [PubMed]
- Fourmigué, M. Halogen Bonding in Conducting or Magnetic Molecular Materials. In Halogen Bonding. Fundamentals and Applications; Metrangolo, P., Resnati, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 126, p. 181. [Google Scholar]
- Atzori, M.; Serpe, A.; Deplano, P.; Schlueter, J.A.; Mercuri, M.L. Tailoring magnetic properties of molecular materials through non-covalent interactions. Inorg. Chem. Front. 2015, 2, 108–115. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Gurbanov, A.V.; Guseinov, F.I.; Guedes da Silva, M.F.C. Noncovalent interactions in metal complex catalysis. Coord. Chem. Rev. 2019, 387, 32–46. [Google Scholar] [CrossRef]
- Szell, P.M.J.; Zablotny, S.; Bryce, D.L. Halogen bonding as a supramolecular dynamics catalyst. Nat. Commun. 2019, 10, 916. [Google Scholar] [CrossRef] [PubMed]
- Schindler, S.; Huber, S.M. Halogen Bonds in Organic Synthesis and Organocatalysis. In Halogen Bonding II. Topics in Current Chemistry; Metrangolo, P., Resnati, G., Eds.; Springer: Cham, Switzerland, 2014; Volume 359. [Google Scholar]
- Cariati, E.; Forni, A.; Biella, S.; Metrangolo, P.; Meyer, F.; Resnati, G.; Righetto, S.; Tordin, E.; Ugo, R. Tuning second-order NLO responses through halogen bonding. Chem. Commun. 2007, 2590–2592. [Google Scholar] [CrossRef]
- Christopherson, J.-C.; Topić, F.; Barrett, C.J.; Friščić, T. Halogen-Bonded Cocrystals as Optical Materials: Next-Generation Control over Light–Matter Interactions. Cryst. Growth Des. 2018, 18, 1245–1259. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, H.-B.; Jia, L.-N.; Mao, Z.-W. Insights into metalloenzyme microenvironments: Biomimetic metal complexes with a functional second coordination sphere. Chem. Soc. Rev. 2013, 42, 8360–8375. [Google Scholar] [CrossRef]
- Ho, P.S. Biomolecular Halogen Bonds. In Halogen Bonding I. Topics in Current Chemistry; Metrangolo, P., Resnati, G., Eds.; Springer: Cham, Switzerland, 2014; Volume 358. [Google Scholar]
- Matter, H.; Nazaré, M.; Güssregen, S.; Will, D.W.; Schreuder, H.; Bauer, A.; Urmann, M.; Ritter, K.; Wagner, M.; Wehner, V. Evidence for C–Cl/C–Br…π Interactions as an Important Contribution to Protein–Ligand Binding Affinity. Angew. Chem. Int. Ed. 2009, 48, 2911–2916. [Google Scholar] [CrossRef]
- Voth, A.R.; Ho, P.S. The role of halogen bonding in inhibitor recognition and binding by protein kinases. Curr. Top. Med. Chem. 2007, 7, 1336–1348. [Google Scholar]
- Wãsik, R.; Łebska, M.; Felczak, K.; Poznański, J.; Shugar, D. Relative Role of Halogen Bonds and Hydrophobic Interactions in Inhibition of Human Protein Kinase CK2α by Tetrabromobenzotriazole and Some C(5)-Substituted Analogues. J. Phys. Chem. B 2010, 114, 10601–10611. [Google Scholar] [CrossRef] [PubMed]
- Cottrell, T.L. The Strengths of Chemical Bonds; Butterworths Publications: London, UK, 1958. [Google Scholar]
- Biedermann, F.; Schneider, H.-J. Experimental binding energies in supramolecular complexes. Chem. Rev. 2016, 116, 5216–5300. [Google Scholar] [CrossRef] [PubMed]
- Musin, R.N.; Mariam, Y.H. An integrated approach to the study of intramolecular hydrogen bonds in malonaldehyde enol derivatives and naphthazarin: Trend in energetic versus geometrical consequences. J. Phys. Org. Chem. 2006, 19, 425–444. [Google Scholar] [CrossRef]
- Fazli, M.; Raissi, H.; Chankandi, B.; Aarabhi, M. The effect of formation of second hydrogen bond in adjacent two-ring resonance-assisted hydrogen bonds—Ab initio and QTAIM studies. J. Mol. Struct. Theochem. 2010, 942, 115–120. [Google Scholar] [CrossRef]
- Szatyłowicz, H. Structural aspects of the intermolecular hydrogen bond strength: H-bonded complexes of aniline, phenol and pyridine derivatives. J. Phys. Org. Chem. 2008, 21, 897–914. [Google Scholar] [CrossRef]
- Hugas, D.; Simon, S.; Duran, M. Electron density topological properties are useful to assess the difference between hydrogen and dihydrogen complexes. J. Chem. Phys. A 2007, 111, 4506–4512. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Properties of a Ring Critical Pointas Measures of Intramolecular H-Bond Strength. Monatsh. Chem. 2002, 133, 1373–1380. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Bilewicz, E. Cooperativity halogen bonding effect—Ab initio calculations on H2CO•••(ClF)n complexes. Chem. Phys. Lett. 2006, 427, 51–55. [Google Scholar] [CrossRef]
- Palusiak, M.; Grabowski, S.J. Characteristics of ring critical point as descriptors of H-bond strength. J. Chem. Res. 2004, 7, 492–493. [Google Scholar] [CrossRef]
- Lipkowski, P.; Grabowski, S.J.; Robinson, T.L.; Leszczynski, J. Properties of the C–H•••H dihydrogen bond: An ab initio and topological analysis. J. Phys. Chem. A 2004, 108, 10865–10872. [Google Scholar] [CrossRef]
- Domagała, M.; Grabowski, S.J. C–H•••N and C–H•••S hydrogen bonds—Influence of hybridization on their strength. J. Phys. Chem. A 2005, 109, 5683–5688. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Hydrogen bonding strength—Measures based on geometric and topological parameters. J. Phys. Org. Chem. 2004, 17, 18–31. [Google Scholar] [CrossRef]
- Rozas, I.; Alkorta, I.; Elguero, J. Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
- Szatyłowicza, H.; Krygowski, T.M. Long distance structural consequences of H-bonding: The case of complexes of para-substituted phenol derivatives. J. Phys. Org. Chem. 2009, 22, 740–746. [Google Scholar] [CrossRef]
- Lyssenko, K.A. Analysis of supramolecular architectures: Beyond molecular packing diagrams. Mendeleev Commun. 2012, 22, 1–7. [Google Scholar] [CrossRef]
- Lyssenko, K.A.; Barzilovich, P.Y.; Nelyubina, Y.V.; Astaf’ev, E.A.; Antipin, M.Y.; Aldoshin, S.M. Charge transfer and hydrogen bond energy in glycinium salts. Izv. Akad. Nauk, Ser. Khim. 2009, 31–40, (Russ. Chem. Bull. Int. Ed. 2009, 58, 31–40). [Google Scholar] [CrossRef]
- Gálvez, O.; Gómez, P.C.; Pacios, L.F. Variation with the intermolecular distance of properties dependent on the electron density in cyclic dimers with two hydrogen bonds. J. Chem. Phys. 2003, 118, 4878–4895. [Google Scholar] [CrossRef]
- Zou, J.W.; Jiang, Y.-J.; Guo, M.; Hu, G.-X.; Zhang, B.; Liu, H.-C.; Yu, Q.-S. Ab initio study of the complexes of halogen-containing molecules RX (X = Cl, Br, and I) and NH3: Towards understanding the nature of halogen bonding and the electron-accepting propensities of covalently bonded halogen atoms. Chem. Eur. J. 2005, 11, 740–751. [Google Scholar] [CrossRef]
- Pacios, L.F. Change with the intermolecular distance of electron properties of hydrogen bond dimers at equilibrium and non-equilibrium geometries. Struct. Chem. 2005, 16, 223–241. [Google Scholar] [CrossRef]
- Raissi, H.; Nadim, E.S.; Yoosefian, M.; Farzad, F.; Ghiamati, E.; Nowroozi, A.R.; Fazli, M.; Amoozadeh, A. The effects of substitutions on structure, electron density, resonance and intramolecular hydrogen bonding strength in 3-mercapto-propenethial. J. Molec. Struct. Theochem. 2010, 960, 1–9. [Google Scholar] [CrossRef]
- Roohi, H.; Bagheri, S. Influence of substitution on the strength and nature of CH•••N hydrogen bond in XCCH•••NH3 complexes. Int. J. Quant. Chem. 2011, 111, 961–969. [Google Scholar] [CrossRef]
- Hayashi, S.; Matsuiwa, K.; Kitamoto, M.; Nakanishi, W. Dynamic behavior of hydrogen bonds from pure closed shell to shared shell interaction regions elucidated by aim dual functional analysis. J. Phys. Chem. A 2013, 117, 1804–1816. [Google Scholar] [CrossRef] [PubMed]
- D’Oria, E.; Novoa, J.J. The strength–length relationship at the light of ab initio computations: Does it really hold? CrystEngComm 2004, 6, 367–376. [Google Scholar] [CrossRef]
- Boyd, R.J.; Choi, S.C. A bond-length-bond-order relationship for intermolecular interactions based on the topological properties of molecular charge distributions. Chem. Phys. Lett. 1985, 120, 80–85. [Google Scholar] [CrossRef]
- Mó, O.; Yáñez, M.; Elguero, J. Cooperative (nonpairwise) effects in water trimers: An ab initio molecular orbital study. J. Chem. Phys. 1992, 97, 6628–6638. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Khorassani, S.M.H.; Delarami, H. Estimation of individual binding energies in some dimers involving multiple hydrogen bonds using topological properties of electron charge density. Chem. Phys. 2009, 365, 18–23. [Google Scholar] [CrossRef]
- Koch, U.; Popelier, P.L.A. Characterization of C–H–O hydrogen bonds on the basis of the charge density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Amezaga, N.J.M.; Pamies, S.C.; Peruchena, N.M.; Sosa, G.L. Halogen bonding: A study based on the electronic charge density. J. Phys. Chem. A 2010, 114, 552–562. [Google Scholar] [CrossRef]
- Grabowski, S.J. What is the covalency of hydrogen bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef]
- Fradera, J.P.X.; Simon, M.S.M.D.S. On the electron-pair nature of the hydrogen bond in the framework of the atoms in molecules theory. Chem. Phys. Lett. 2003, 369, 248–255. [Google Scholar]
- Shi, F.-Q.; An, J.-J.; Yu, J.-Y. Theoretical study on measure of hydrogen bonding strength: R–C≡N•••pyrrole complexes. Chin. J. Chem. 2005, 23, 400–403. [Google Scholar]
- Cubero, E.; Orozco, M.; Hobza, P.; Luque, F.J. Hydrogen bond versus anti-hydrogen bond: A comparative analysis based on the electron density topology. J. Phys. Chem. A 1999, 103, 6394–6401. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Subramanian, V.; Sathyamurthy, N. Hydrogen bonding in phenol, water, and phenol-water clusters. J. Phys. Chem. A 2005, 109, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Wojtulewski, S.; Grabowski, S.J. Unconventional F–H•••π hydrogen bonds—Ab initio and AIM study. J. Molec. Struct. 2002, 605, 235–240. [Google Scholar] [CrossRef]
- Bagheri, S.; Masoodi, H.R.; Abadi, M.N. Estimation of individual NH•••X (X = N, O) hydrogen bonding energies in some complexes involving multiple hydrogen bonds using NBO calculations. Theor. Chem. Acc. 2015, 134, 127. [Google Scholar] [CrossRef]
- Jabłoński, M.; Solà, M. Influence of confinement on hydrogen bond energy. The case of the FH•••NCH dimer. J. Phys. Chem. A 2010, 114, 10253–10260. [Google Scholar] [CrossRef] [PubMed]
- Ayoub, A.T.; Tuszynski, J.; Klobukowski, M. Estimating hydrogen bond energies: Comparison of methods. Theor. Chem. Acc. 2014, 133, 1520. [Google Scholar] [CrossRef]
- Brovarets, O.O.; Yurenko, Y.P.; Hovorun, D.M. Intermolecular CH•••O/N H-bonds in the biologically important pairs of natural nucleobases: A thorough quantum-chemical study. J. Biomol. Struct. Dyn. 2014, 32, 993–1022. [Google Scholar] [CrossRef]
- Martyniak, A.; Majerz, I.; Filarowski, A. Peculiarities of quasi-aromatic hydrogen bonding. RSC Adv. 2012, 2, 8135–8144. [Google Scholar] [CrossRef]
- Vener, M.V.; Egorova, A.N.; Churakov, A.V.; Tsirelson, V.G. Intermolecular hydrogen bond energies in crystals evaluated using electron density properties: DFT computations with periodic boundary conditions. J. Comput. Chem. 2012, 33, 2303–2309. [Google Scholar] [CrossRef]
- Vener, M.V.; Shishkina, A.V.; Rykounov, A.A.; Tsirelson, V.G. Cl•••Cl Interactions in molecular crystals: Insights from the theoretical charge density analysis. J. Phys. Chem. A 2013, 117, 8459–8467. [Google Scholar] [CrossRef] [PubMed]
- Bartashevich, E.V.; Tsirelson, V.G. Interplay between non-covalent interactions in complexes and crystals with halogen bonds. Russ. Chem. Rev. 2014, 83, 1181–1203. [Google Scholar] [CrossRef]
- Ananyev, I.V.; Karnoukhova, V.A.; Dmitrienko, A.O.; Lyssenko, K.A. Toward a rigorous definition of a strength of any interaction between Bader’s atomic basins. J. Phys. Chem. A 2017, 121, 4517–4522. [Google Scholar] [CrossRef] [PubMed]
- Arkhipov, D.E.; Lyubeshkin, A.V.; Volodin, A.D.; Korlyukov, A.A. Molecular Structures, Polymorphism and the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates. Crystals 2019, 9, 242. [Google Scholar] [CrossRef]
- Afonin, A.V.; Vashchenko, A.V.; Sigalov, M.V. Estimating the energy of intramolecular hydrogen bonds from 1H NMR and QTAIM calculations. Org. Biomol. Chem. 2016, 14, 11199–11211. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-H.; Lu, Y.-X.; Zou, J.-W.; Yu, Q.-S. Theoretical investigation on charge-assisted halogen bonding interactions in the complexes of bromocarbons with some anions. Int. J. Quant. Chem. 2008, 108, 90–99. [Google Scholar] [CrossRef]
- Levina, E.O.; Chernyshov, I.Y.; Voronin, A.P.; Alekseiko, L.N.; Stash, A.I.; Vener, M.V. Solving the enigma of weak fluorine contacts in the solid state: A periodic DFT study of fluorinated organic crystals. RSC Adv. 2019, 9, 12520–12537. [Google Scholar] [CrossRef]
- Bartashevich, E.; Matveychuk, Y.; Tsirelson, V. Identification of the Tetrel Bonds between Halide Anions and Carbon Atom of Methyl Groups Using Electronic Criterion. Molecules 2019, 24, 1083. [Google Scholar] [CrossRef]
- Alkorta, I.; Legon, A.C. Nucleophilicities of Lewis bases B and electrophilicities of Lewis acids A determined from the dissociation energies of complexes B···A involving hydrogen bonds, tetrel bonds, pnictogen bonds, chalcogen bonds and halogen bonds. Molecules 2017, 22, 1786. [Google Scholar] [CrossRef]
- Shaw, R.A.; Hill, J.G. A Simple model for halogen bond interaction energies. Inorganics 2019, 7, 19. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Mata, I.; Alkorta, I.; Espinosa, E.; Molins, E. Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields. Chem. Phys. Lett. 2011, 507, 185–189. [Google Scholar] [CrossRef]
- Mata, I.; Molins, E.; Alkorta, I.; Espinosa, E. Effect of an external electric field on the dissociation energy and the electron density properties: The case of the hydrogen bonded dimer HF•••HF*. J. Chem. Phys. 2009, 130, 044104. [Google Scholar] [CrossRef] [PubMed]
- Spackman, M.A. How reliable are intermolecular interaction energies estimated from topological analysis of experimental electron densities? Cryst. Growth Des. 2015, 15, 5624–5628. [Google Scholar] [CrossRef]
- Kuznetsov, M.L. Can halogen bond energy be reliably estimated from electron density properties at bond critical point? The case of the (A)nZ—Y•••X− (X, Y = F, Cl, Br) interactions. Int. J. Quantum. Chem. 2019, 119, e25869. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Kozuch, S.; Martin, J.M.L. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.C.; Muniz, E.P.; Centoducatte, R.; Jorge, F.E. Gaussian basis sets for correlated wave functions. Hydrogen, helium, first-and second-row atoms. J. Mol. Struct. Theochem. 2005, 718, 219–224. [Google Scholar] [CrossRef]
- Camiletti, G.G.; Machado, S.F.; Jorge, F.E. Gaussian basis set of double zeta quality for atoms K through Kr: Application in DFT calculations of molecular properties. J. Comp. Chem. 2008, 29, 2434–2444. [Google Scholar] [CrossRef]
- Barros, C.L.; De Oliveira, P.J.P.; Jorge, F.E.; Neto, A.C.; Campos, M. Gaussian basis set of double zeta quality for atoms Rb through Xe: Application in non-relativistic and relativistic calculations of atomic and molecular properties. Mol. Phys. 2010, 108, 1965–1972. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–556. [Google Scholar] [CrossRef]
- Simon, S.; Duran, M.; Dannenberg, J.J. How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers? J. Chem. Phys. 1996, 105, 11024–11031. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- AIMAll (Version 14.10.27), T.A. Keith, TK Gristmill Software, Overland Park KS, USA. 2014. Available online: aim.tkgristmill.com (accessed on 1 September 2015).
- Metrangolo, P.; Resnati, G. Type II halogen···halogen contacts are halogen bonds. IUCrJ 2014, 1, 5–7. [Google Scholar] [CrossRef] [PubMed]
- Romanova, A.; Lyssenko, K.; Ananyev, I. Estimations of energy of noncovalent bonding from integrals over interatomic zero-flux surfaces: Correlation trends and beyond. J. Comput. Chem. 2018, 39, 1607–1616. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not available. |






| Series | Estimator | Equation |
|---|---|---|
| Whole set | Gb, kcal/(mol•bohr3) | −Eint = 0.128Gb2 − 0.824Gb + 1.66 |
| Cl···Cl | Vb, kcal/(mol•bohr3) | −Eint = 0.1006Vb2 + 0.218Vb + 0.55 |
| Gb, kcal/(mol•bohr3) | −Eint = 0.0841Gb2 − 0.367Gb + 0.84 | |
| ρb, e/Å3 | −Eint = 535.9ρb2 − 31.13ρb + 0.87 | |
| ∇2ρb, e/Å5 | −Eint = 0.09e2.405∇2ρb + 0.17 | |
| λ||,b, e/Å5 | −Eint = 0.099e1.762λ||,b + 0.17 | |
| d(X···X), Å | −Eint = 3.66×109e−6.98d(X···X) + 0.43 | |
| Br···Br | Vb, kcal/(mol•bohr3) | −Eint = 0.0926Vb2 + 0.173Vb + 0.16 |
| Gb, kcal/(mol•bohr3) | −Eint = 0.1178Gb2 − 0.73Gb + 1.50 | |
| ρb, e/Å3 | −Eint = 380.6ρb2 − 24.78ρb + 0.42 | |
| ∇2ρb, e/Å5 | −Eint = 0.07e2.624∇2ρb − 0.10 | |
| λ||,b, e/Å5 | −Eint = 0.30e1.306λ||,b − 0.71 | |
| d(X···X), Å | −Eint = 1.05×109e−6.35d(X···X) + 0.19 | |
| I···I | Vb, kcal/(mol•bohr3) | −Eint = 0.0635Vb2 + 0.217Vb + 0.25 |
| Gb, kcal/(mol•bohr3) | −Eint = 0.1564Gb2 − 1.138Gb + 2.25 | |
| ρb, e/Å3 | −Eint = 305.2ρb2 − 21.78ρb + 0.44 | |
| λ||,b, e/Å5 | −Eint = 0.031e2.818λ||,b − 0.25 | |
| Hb, kcal/(mol•bohr3) | −Eint = −2.35Hb + 1.87 | |
| d(X···X), Å | −Eint = 1.03×108e−5.15d(X···X) + 0.07 |
| Series | Equation |
|---|---|
| [(A)nY–Cl···Cl–H] | −Eint = −0.47Vb − 0.27 |
| [(A)nY–Cl···Cl–F] | −Eint = −0.21Vb + 0.07 |
| [(A)nY–Br···Br–H] | −Eint = −0.79Vb − 1.61 |
| [(A)nY–Br···Br–F] | −Eint = −0.49Vb − 1.22 |
| [(A)nY–I···I–H] | −Eint = 0.0581Vb2 + 0.007Vb − 0.19 |
| [(A)nY–I···I–F] | −Eint = 0.0360Vb2 + 0.025Vb − 0.31 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, M.L. Relationships between Interaction Energy and Electron Density Properties for Homo Halogen Bonds of the [(A)nY–X···X–Z(B)m] Type (X = Cl, Br, I). Molecules 2019, 24, 2733. https://doi.org/10.3390/molecules24152733
Kuznetsov ML. Relationships between Interaction Energy and Electron Density Properties for Homo Halogen Bonds of the [(A)nY–X···X–Z(B)m] Type (X = Cl, Br, I). Molecules. 2019; 24(15):2733. https://doi.org/10.3390/molecules24152733
Chicago/Turabian StyleKuznetsov, Maxim L. 2019. "Relationships between Interaction Energy and Electron Density Properties for Homo Halogen Bonds of the [(A)nY–X···X–Z(B)m] Type (X = Cl, Br, I)" Molecules 24, no. 15: 2733. https://doi.org/10.3390/molecules24152733
APA StyleKuznetsov, M. L. (2019). Relationships between Interaction Energy and Electron Density Properties for Homo Halogen Bonds of the [(A)nY–X···X–Z(B)m] Type (X = Cl, Br, I). Molecules, 24(15), 2733. https://doi.org/10.3390/molecules24152733