Specific Ion Effects of Dodecyl Sulfate Surfactants with Alkali Ions at the Air–Water Interface
Abstract
1. Introduction
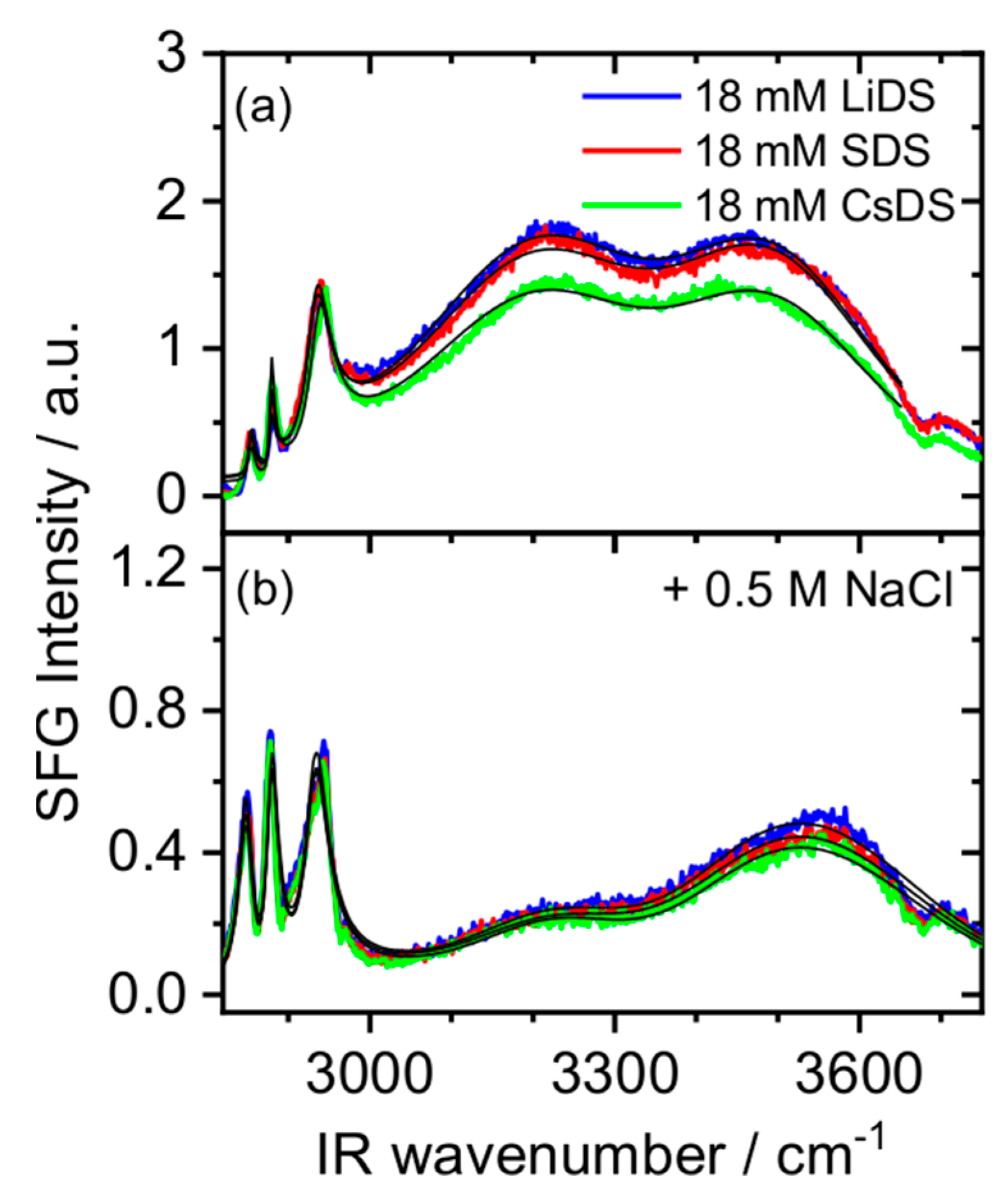
2. Results and Discussion
3. Materials and Methods
3.1. Sample Preparation
3.2. Sum Frequency Generation (SFG)
3.3. Surface Tensiometry
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hofmeister, F. On the understanding of the effects of salts. Arch. Exp. Pathol. Pharmakol. 1888, 24, 247–260. [Google Scholar] [CrossRef]
- Okur, H.I.; Hladílková, J.; Rembert, K.B.; Cho, Y.; Heyda, J.; Dzubiella, J.; Cremer, P.S.; Jungwirth, P. Beyond the Hofmeister Series: Ion-Specific Effects on Proteins and Their Biological Functions. J. Phys. Chem. B 2017, 121, 1997–2014. [Google Scholar] [CrossRef] [PubMed]
- Para, G.; Jarek, E.; Warszynski, P. The surface tension of aqueous solutions of cetyltrimethylammonium cationic surfactants in presence of bromide and chloride counterions. Coll. Surf. A Physicochem. Eng. Asp. 2005, 261, 65–73. [Google Scholar] [CrossRef]
- Para, G.; Jarek, E.; Warszynski, P. The Hofmeister series effect in adsorption of cationic surfactants—Theoretical description and experimental results. Adv. Coll. Int. Sci. 2006, 122, 39–55. [Google Scholar] [CrossRef] [PubMed]
- Warszyński, P.; Lunkenheimer, K.; Czichocki, G. Effect of Counterions on the Adsorption of Ionic Surfactants at Fluid−Fluid Interfaces. Langmuir 2002, 18, 2506–2514. [Google Scholar] [CrossRef]
- Sthoer, A.; Hladílková, J.; Lund, M.; Tyrode, E. Molecular insight into carboxylic acid-alkali metal cations interactions: Reversed affinities and ion-pair formation revealed by non-linear optics and simulations. Phys. Chem. Chem. Phys. 2019, 21, 11329–11344. [Google Scholar] [CrossRef] [PubMed]
- Tyrode, E.; Corkery, R. Charging of Carboxylic Acid Monolayers with Monovalent Ions at Low Ionic Strengths: Molecular Insight Revealed by Vibrational Sum Frequency Spectroscopy. J. Phys. Chem. C 2018, 122, 28775–28786. [Google Scholar] [CrossRef]
- Mukerjee, P.; Mysels, K.; Kapauan, P. Counterion Specificity in the Formation of Ionic Micelles -Size, Hydration, and Hydrophobic Bonding Effects. J. Phys. Chem. 1967, 71, 4166–4175. [Google Scholar] [CrossRef]
- Schelero, N.; von Klitzing, R. Ion specific effects in foam films. Curr. Opin. Colloid Interface Sci. 2015, 20, 124–129. [Google Scholar] [CrossRef]
- Zhao, H. Protein Stabilization and Enzyme Activation in Ionic Liquids: Specific Ion Effects. J. Chem. Technol. Biot. 2016, 91, 25–50. [Google Scholar] [CrossRef]
- Itoh, T. Ionic Liquids as Tool to Improve Enzymatic Organic Synthesis. Chem. Rev. 2017, 117, 10567–10607. [Google Scholar] [CrossRef] [PubMed]
- Khuman, P.; Singh, W.B.K.; Devi, S.D.; Naorem, H. Viscosity-Temperature Behavior of Hydroxypropyl Cellulose Solution in Presence of an Electrolyte or a Surfactant: A Convenient Method to Determine the Cloud Point of Polymer Solutions. J. Polym. Sci. Pol. Chem. 2014, 51, 924–930. [Google Scholar] [CrossRef]
- Weißenborn, E.; Braunschweig, B. Hydroxypropyl cellulose as a green polymer for thermo-responsive aqueous foams. Soft Matter 2019, 15, 2876–2883. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Wickramasinghe, R.; Qian, X. Effects of Salt on the Lower Critical Solution Temperature of Poly (N-Isopropylacrylamide). J. Phys. Chem. B 2010, 114, 16594–16604. [Google Scholar] [CrossRef] [PubMed]
- Bruce, E.E.; Bui, P.T.; Rogers, B.A.; Cremer, P.S.; van der Vegt, N.F.A. Nonadditive Ion Effects Drive Both Collapse and Swelling of Thermoresponsive Polymers in Water. J. Am. Chem. Soc. 2019, 141, 6609–6616. [Google Scholar] [CrossRef]
- Zdrali, E.; Baer, M.D.; Okur, H.I.; Mundy, C.J.; Roke, S. The Diverse Nature of Ion Speciation at the Nanoscale Hydrophobic/Water Interface. J. Phys. Chem. B 2019, 123, 2414–2423. [Google Scholar] [CrossRef] [PubMed]
- Schelero, N.; Hedicke, G.; Linse, P.; Klitzing, R.V. Effects of counterions and co-ions on foam films stabilized by anionic dodecyl sulfate. J. Phys. Chem. B 2010, 114, 15523–15529. [Google Scholar] [CrossRef]
- Schulze-Zachau, F.; Bachmann, S.; Braunschweig, B. Effects of Ca2+ Ion Condensation on the Molecular Structure of Polystyrene Sulfonate at Air-Water Interfaces. Langmuir 2018, 34, 11714–11722. [Google Scholar] [CrossRef]
- Vlachy, N.; Jagoda-Cwiklik, B.; Vácha, R.; Touraud, D.; Jungwirth, P.; Kunz, W. Hofmeister series and specific interactions of charged headgroups with aqueous ions. Adv. Coll. Int. Sci. 2009, 146, 42–47. [Google Scholar] [CrossRef]
- Lukanov, B.; Firoozabadi, A. Specific Ion Effects on the Self-Assembly of Ionic Surfactants: A Molecular Thermodynamic Theory of Micellization with Dispersion Forces. Langmuir 2014, 30, 6373–6383. [Google Scholar] [CrossRef]
- Beierlein, F.R.; Clark, T.; Braunschweig, B.; Engelhardt, K.; Glas, L.; Peukert, W. Carboxylate Ion Pairing with Alkali-Metal Ions for β-Lactoglobulin and Its Role on Aggregation and Interfacial Adsorption. J. Phys. Chem. B 2015, 119, 5505–5517. [Google Scholar] [CrossRef] [PubMed]
- Collins, K.D. Ions from the Hofmeister series and osmolytes: Effects on proteins in solution and in the crystallization process. Methods 2004, 34, 300–311. [Google Scholar] [CrossRef] [PubMed]
- Collins, K.D.; Neilson, G.W.; Enderby, J.E. Ions in water: Characterizing the forces that control chemical processes and biological structure. Biophys. Chem. 2007, 128, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Duignan, T.T.; Parsons, D.F.; Ninham, B.W. Collins’s rule, Hofmeister effects and ionic dispersion interactions. Chem. Phys. Lett. 2014, 608, 55–59. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Nguyen, A.V. New Evidence of Head-to-Tail Complex Formation of SDS-DOH Mixtures Adsorbed at the Air-Water Interface as Revealed by Vibrational Sum Frequency Generation Spectroscopy and Isotope Labelling. Langmuir 2019, 35, 4825–4833. [Google Scholar] [CrossRef] [PubMed]
- Yeon, C.; Kim, G.; Lim, J.W.; Yun, S.J. Highly conductive PEDOT: PSS treated by sodium dodecyl sulfate for stretchable fabric heaters. RSC Adv. 2017, 7, 5888–5897. [Google Scholar] [CrossRef]
- Qiao, B.; Liang, Y.; Wang, T.-J.; Jiang, Y. Surface modification to produce hydrophobic nano-silica particles using sodium dodecyl sulfate as a modifier. Appl. Surf. Sci. 2016, 364, 103–109. [Google Scholar] [CrossRef]
- Fauser, H.; Uhlig, M.; Miller, R.; von Klitzing, R. Surface Adsorption of Oppositely Charged SDS: C(12)TAB Mixtures and the Relation to Foam Film Formation and Stability. J. Phys. Chem. B 2015, 119, 12877–12886. [Google Scholar] [CrossRef] [PubMed]
- Windsor, R.; Neivandt, D.J.; Davies, P.B. Adsorption of Sodium Dodecyl Sulfate in the Presence of Poly(ethylenimine) and Sodium Chloride Studied Using Sum Frequency Vibrational Spectroscopy. Langmuir 2001, 17, 7306–7312. [Google Scholar] [CrossRef]
- Bain, C.D.; Davies, P.B.; Ward, R.N. In-Situ Sum-Frequency Spectroscopy of Sodium Dodecyl Sulfate and Dodecanol Coadsorbed at a Hydrophobic Surface. Langmuir 1994, 10, 2060–2063. [Google Scholar] [CrossRef]
- Gragson, D.E.; McCarty, B.M.; Richmond, G.L. Ordering of Interfacial Water Molecules at the Charged Air/Water Interface Observed by Vibrational Sum Frequency Generation. J. Am. Chem. Soc. 1997, 119, 6144–6152. [Google Scholar] [CrossRef]
- Messmer, M.C.; Conboy, J.C.; Richmond, G.L. Observation of Molecular Ordering at the Liquid-Liquid Interface by Resonant Sum Frequency Generation. J. Am. Chem. Soc. 1995, 117, 8039–8040. [Google Scholar] [CrossRef]
- Hommel, E.L.; Ma, G.; Allen, H.C. Broadband Vibrational Sum Frequency Generation Spectroscopy of a Liquid Surface. Anal. Sci. 2001, 17, 1325–1329. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.M.; Tyrode, E. Study of the adsorption of sodium dodecyl sulfate (SDS) at the air/water interface: Targeting the sulfate headgroup using vibrational sum frequency spectroscopy. Phys. Chem. Chem. Phys. 2005, 7, 2635–2640. [Google Scholar] [CrossRef] [PubMed]
- de Aguiar, H.B.; de Beer, A.G.F.; Strader, M.L.; Roke, S. The interfacial tension of nanoscopic oil droplets in water is hardly affected by SDS surfactant. J. Am. Chem. Soc. 2010, 132, 2122–2123. [Google Scholar] [CrossRef] [PubMed]
- Casson, B.D.; Bain, C.D. Phase transitions in mixed monolayers of sodium dodecyl sulfate and dodecanol at the air/water interface. J. Phys. Chem. B 1998, 102, 7434–7441. [Google Scholar] [CrossRef]
- Conboy, J.C.; Messmer, M.C.; Richmond, G.L. Investigation of surfactant conformation and order at the liquid-liquid interface by total internal reflection sum-frequency vibrational spectroscopy. J. Phys. Chem. 1996, 100, 7617–7622. [Google Scholar] [CrossRef]
- Zdrali, E.; Etienne, G.; Smolentsev, N.; Amstad, E.; Roke, S. The interfacial structure of nano-and micron-sized oil and water droplets stabilized with SDS and Span80. J. Chem. Phys. 2019, 150, 204704. [Google Scholar] [CrossRef]
- Sauerbeck, C. Untersuchung geladener kolloidaler Grenzflächen Mittels Nichtlinearer Lichtstreuung. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2018. [Google Scholar]
- Lu, J.R.; Marrocco, A.; Su, T.J.; Thomas, R.K.; Penfold, J. Adsorption of Dodecyl Sulfate Surfactants with Monovalent Metal Counterions at the Air-Water Interface Studied by Neutron Reflection and Surface Tension. J. Coll. Int. Sci. 1993, 158, 303–316. [Google Scholar] [CrossRef]
- Danov, K.D.; Kralchevsky, P.A.; Ananthapadmanabhan, K.P. Micelle-monomer equilibria in solutions of ionic surfactants and in ionic-nonionic mixtures: A generalized phase separation model. Adv. Coll. Int. Sci. 2014, 206, 17–45. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Boxer, S.G. Vibrational Stark Effect Spectroscopy. J. Am. Chem. Soc. 1995, 117, 1449–1450. [Google Scholar] [CrossRef]
- Fried, S.D.; Boxer, S.G. Measuring electric fields and noncovalent interactions using the vibrational stark effect. Acc. Chem. Res. 2015, 48, 998–1006. [Google Scholar] [CrossRef] [PubMed]
- Hush, N.S.; Reimers, J.R. Vibrational Stark Spectroscopy. 1. Basic Theory and Application to the CO Stretch. J. Phys. Chem. 1995, 99, 15798–15805. [Google Scholar] [CrossRef]
- Zwaschka, G.; Wolf, M.; Campen, R.K.; Tong, Y. A Microscopic Model of the Electrochemical Vibrational Stark Effect: Understanding VSF Spectroscopy of (bi)Sulfate on Pt(111). Surf. Sci. 2018, 678, 78–85. [Google Scholar] [CrossRef]
- Braunschweig, B.; Mukherjee, P.; Dlott, D.D.; Wieckowski, A. Real-time investigations of Pt(111) surface transformations in sulfuric acid solutions. J. Am. Chem. Soc. 2010, 132, 14036–14038. [Google Scholar] [CrossRef]
- Andrews, S.S.; Boxer, S.G. Vibrational Stark Effects of Nitriles I. Methods and Experimental Results. J. Phys. Chem. A 2000, 104, 11853–11863. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Burlington, MA, USA, 2011. [Google Scholar]
- Kunz, W. Specific ion effects in colloidal and biological systems. Curr. Opin. Colloid Interface Sci. 2010, 15, 34–39. [Google Scholar] [CrossRef]
- Gonella, G.; Lütgebaucks, C.; de Beer, A.G.F.; Roke, S. Second Harmonic and Sum-Frequency Generation from Aqueous Interfaces Is Modulated by Interference. J. Phys. Chem. C Nanomater. Interfaces 2016, 120, 9165–9173. [Google Scholar] [CrossRef]
- Ohno, P.E.; Wang, H.-F.; Geiger, F.M. Second-order spectral lineshapes from charged interfaces. Nat. Commun. 2017, 8, 1032. [Google Scholar] [CrossRef]
- García Rey, N.; Weißenborn, E.; Schulze-Zachau, F.; Gochev, G.; Braunschweig, B. Quantifying Double-Layer Potentials at Liquid-Gas Interfaces from Vibrational Sum-Frequency Generation. J. Phys. Chem. C 2019, 123, 1279–1286. [Google Scholar] [CrossRef]
- Exerowa, D.; Zacharieva, M.; Cohen, R.; Platikanov, D. Dependence of the equilibrium thickness and double layer potential of foam films on the surfactant concentration. Colloid Polym. Sci. 1979, 257, 1089–1098. [Google Scholar] [CrossRef]
- Nakahara, H.; Shibata, O.; Moroi, Y. Examination of surface adsorption of sodium chloride and sodium dodecyl sulfate by surface potential measurement at the air/solution interface. Langmuir 2005, 21, 9020–9022. [Google Scholar] [CrossRef] [PubMed]
Sample Available: Not available. |
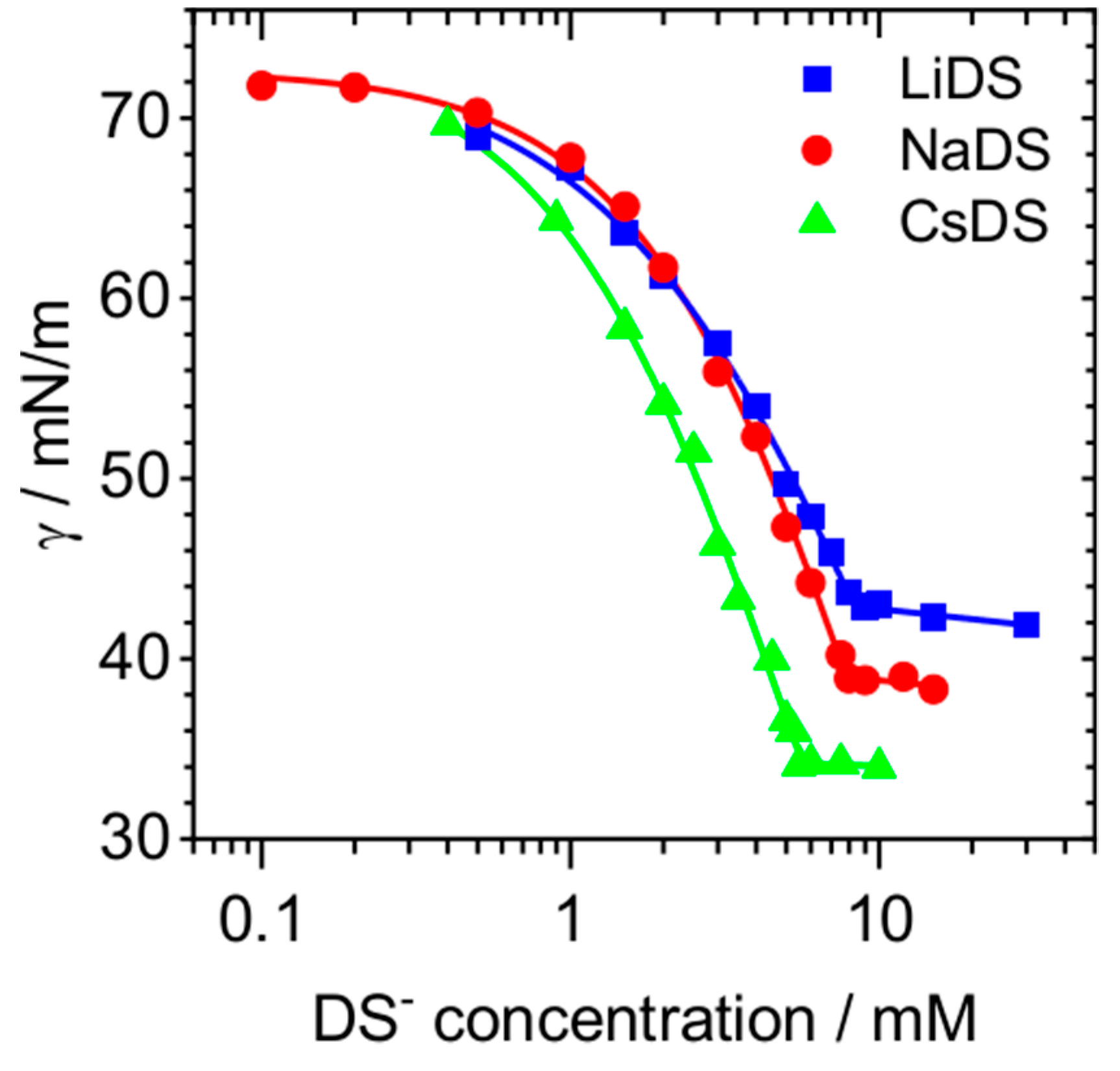

| CMC\mM | |||
|---|---|---|---|
| LiDS | −23.4 | 8.4 | 3.32 |
| LiDS + 25 mM LiCl | −28.2 | 5.3 | |
| SDS | −23.6 | 8.1 | 3.77 |
| SDS + 25 mM NaCl | −28.2 | 3.7 | |
| CsDS | −26.4 | 5.1 | 4.37 |
| CsDS + 25 mM CsCl | −30.7 | 2.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weißenborn, E.; Braunschweig, B. Specific Ion Effects of Dodecyl Sulfate Surfactants with Alkali Ions at the Air–Water Interface. Molecules 2019, 24, 2911. https://doi.org/10.3390/molecules24162911
Weißenborn E, Braunschweig B. Specific Ion Effects of Dodecyl Sulfate Surfactants with Alkali Ions at the Air–Water Interface. Molecules. 2019; 24(16):2911. https://doi.org/10.3390/molecules24162911
Chicago/Turabian StyleWeißenborn, Eric, and Björn Braunschweig. 2019. "Specific Ion Effects of Dodecyl Sulfate Surfactants with Alkali Ions at the Air–Water Interface" Molecules 24, no. 16: 2911. https://doi.org/10.3390/molecules24162911
APA StyleWeißenborn, E., & Braunschweig, B. (2019). Specific Ion Effects of Dodecyl Sulfate Surfactants with Alkali Ions at the Air–Water Interface. Molecules, 24(16), 2911. https://doi.org/10.3390/molecules24162911






