The Dynamics of Hole Transfer in DNA
Abstract
1. Introduction
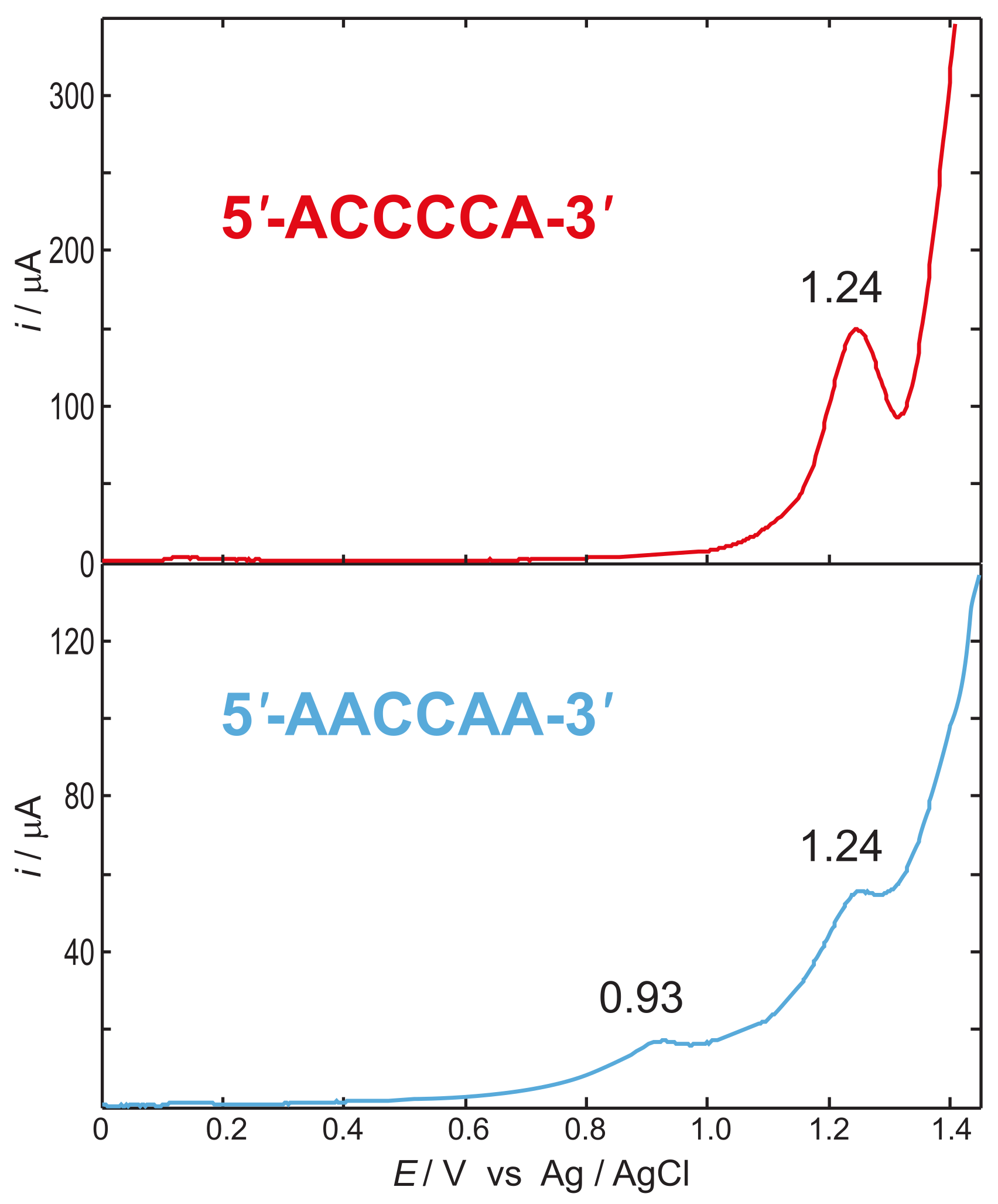
2. Hole Site Energy
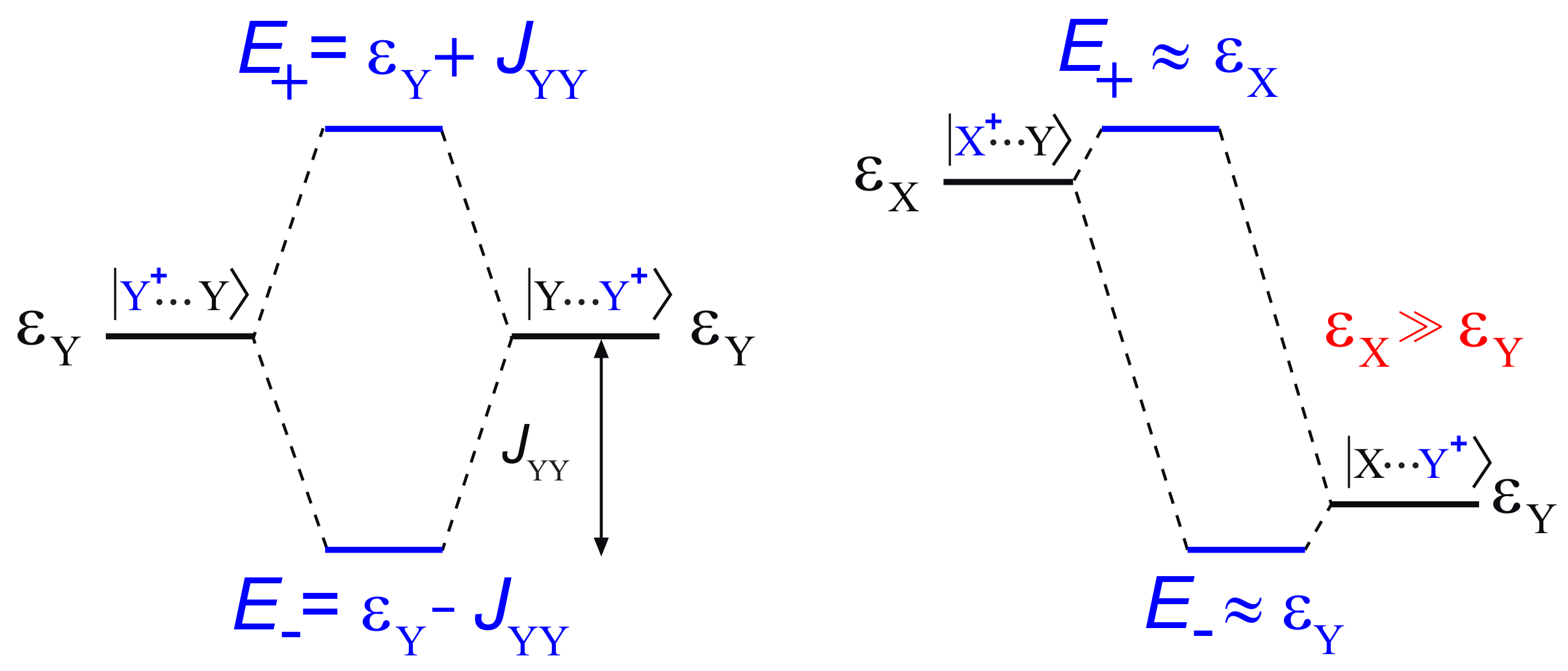
3. Electronic Couplings
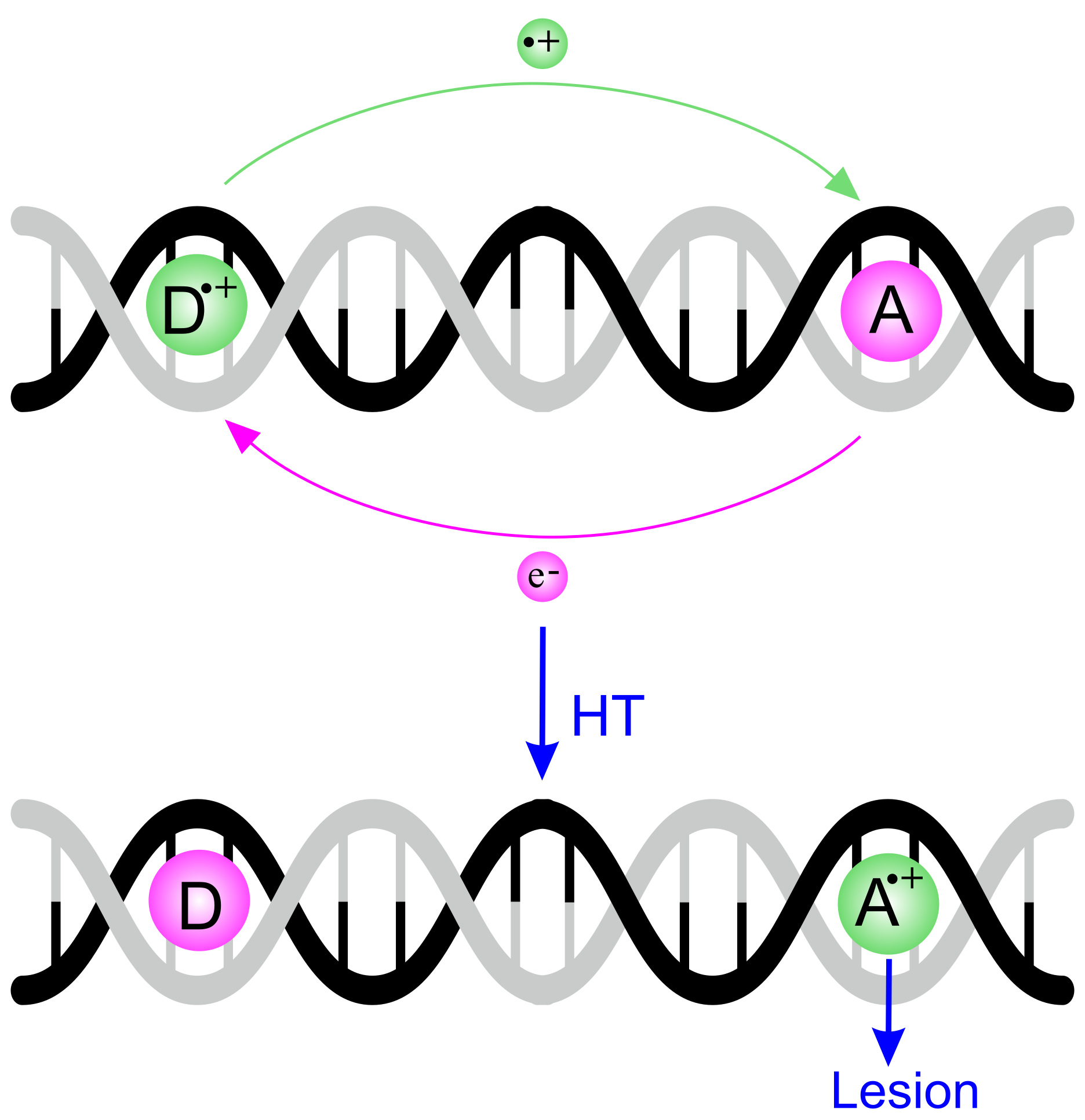
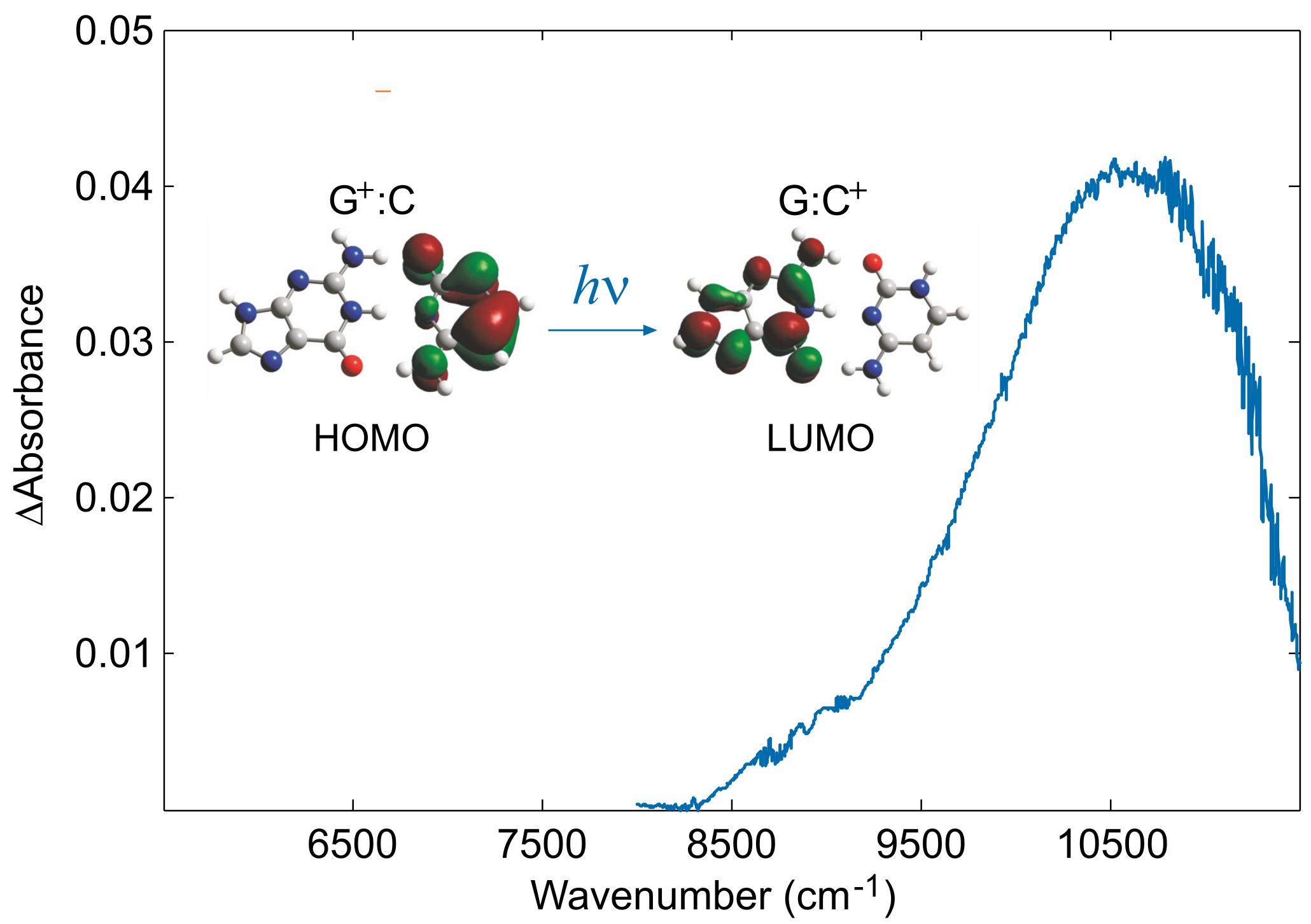
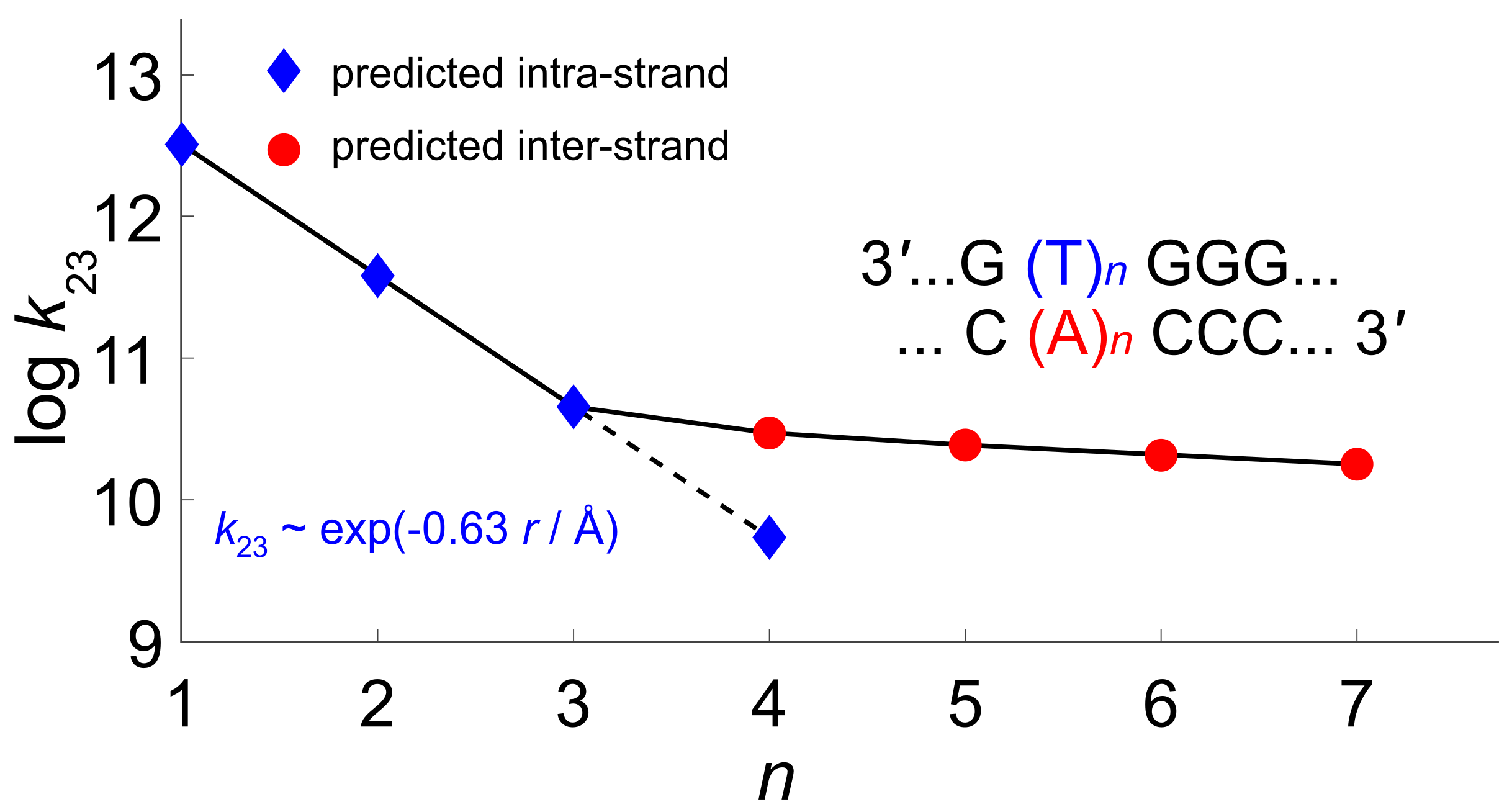
4. The Dynamics of Hole Transfer in DNA
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Eley, D.D.; Spivey, D.I. Semiconductivity of Organic Substances. Part 9. Nucleic Acid in the Dry State. Trans. Faraday Soc. 1962, 58, 411–415. [Google Scholar] [CrossRef]
- Murphy, C.J.; Arkin, M.R.; Jenkins, Y.; Ghatlia, N.D.; Bossmann, S.H.; Turro, N.J.; Barton, J.K. Long-Range Photoinduced Electron Transfer through a DNA Helix. Science 1993, 262, 1025–1029. [Google Scholar] [CrossRef] [PubMed]
- Genereux, J.C.; Barton, J.K. Mechanisms for DNA Charge Transport. Chem. Rev. 2010, 110, 1642–1662. [Google Scholar] [CrossRef] [PubMed]
- Kanvah, S.; Joseph, J.; Schuster, G.B.; Barnett, R.N.; Cleveland, C.L.; Landman, U. Oxidation of DNA: Damage to Nucleobases. Acc. Chem. Res. 2010, 43, 280–287. [Google Scholar] [CrossRef]
- Kawai, K.; Majima, T. Hole Transfer Kinetics of DNA. Acc. Chem. Res. 2013, 46, 2616–2625. [Google Scholar] [CrossRef]
- Cadet, J.; Douki, T.; Ravanat, J.L. Oxidatively Generated Damage to the Guanine Moiety of DNA: Mechanistic Aspects and Formation in Cells. Acc. Chem. Res. 2008, 41, 1075–1083. [Google Scholar] [CrossRef]
- Cooke, M.S.; Evans, M.D.; Dizdaroglu, M.; Lunec, J. Oxidative DNA Damage: Mechanisms, Mutation, and Disease. FASEB J. 2003, 17, 1195–1214. [Google Scholar] [CrossRef]
- Sontz, P.A.; Muren, N.B.; Barton, J.K. DNA Charge Transport for Sensing and Signaling. Acc. Chem. Res. 2012, 45, 1792–1800. [Google Scholar] [CrossRef]
- Zwang, T.J.; Tse, E.C.M.; Barton, J.K. Sensing DNA through DNA Charge Transport. ACS Chem. Biol. 2018, 13, 1799–1809. [Google Scholar] [CrossRef]
- Endres, R.G.; Cox, D.L.; Singh, R.R.P. The Quest for High-Conductance DNA. Rev. Mod. Phys. 2004, 76, 195–214. [Google Scholar] [CrossRef]
- Singh, B.; Sariciftci, N.S.; Grote, J.G.; Hopkins, F.K. Bio-Organic-Semiconductor-Field-Effect-Transistor Based on Deoxyribonucleic Acid Gate Dielectric. J. Appl. Phys. 2006, 100, 024514. [Google Scholar] [CrossRef]
- Zalar, P.; Kamkar, D.; Naik, R.; Ouchen, F.; Grote, J.G.; Bazan, G.C.; Nguyen, T.Q. DNA Electron Injection Interlayers for Polymer Light-Emitting Diodes. J. Am. Chem. Soc. 2011, 133, 11010–11013. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zalar, P.; Kim, C.; Collins, S.; Bazan, G.C.; Nguyen, T.Q. DNA Interlayers Enhance Charge Injection in Organic Field-Effect Transistors. Adv. Mater. 2012, 24, 4255–4260. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Han, S.; Huang, W.; Yu, J. High Mobility Organic Field-Effect Transistor Based on Water-Soluble Deoxyribonucleic Acid via Spray Coating. Appl. Phys. Lett. 2015, 106, 043303. [Google Scholar] [CrossRef]
- Gomez, E.F.; Venkatraman, V.; Grote, J.G.; Steckl, A.J. Exploring the Potential of Nucleic Acid Bases in Organic Light Emitting Diodes. Adv. Mater. 2015, 27, 7552–7562. [Google Scholar] [CrossRef]
- Makarov, V.; Pettitt, B.M.; Feig, M. Solvation and Hydration of Proteins and Nucleic Acids: A Theoretical View of Simulation and Experiment. Acc. Chem. Res. 2002, 35, 376–384. [Google Scholar] [CrossRef]
- Oliveira-Brett, A.M.; Piedade, J.A.P.; Silva, L.A.; Diculescu, V.C. Voltammetric Determination of All DNA Nucleotides. Anal. Biochem. 2004, 332, 321–329. [Google Scholar] [CrossRef]
- O’Neill, M.A.; Barton, J.K. DNA Charge Transport: Conformationally Gated Hopping through Stacked Domains. J. Am. Chem. Soc. 2004, 126, 11471–11483. [Google Scholar] [CrossRef]
- Joseph, J.; Schuster, G.B. Emergent Functionality of Nucleobase Radical Cations in Duplex DNA: Prediction of Reactivity Using Qualitative Potential Energy Landscapes. J. Am. Chem. Soc. 2006, 128, 6070–6074. [Google Scholar] [CrossRef]
- Basko, D.M.; Conwell, E.M. Effect of Solvation on Hole Motion in DNA. Phys. Rev. Lett. 2002, 88, 098102. [Google Scholar] [CrossRef]
- Conwell, E.M.; Bloch, S.M.; McLaughlin, P.M.; Basko, D.M. Duplex Polarons in DNA. J. Am. Chem. Soc. 2007, 129, 9175–9181. [Google Scholar] [CrossRef] [PubMed]
- Capobianco, A.; Caruso, T.; Celentano, M.; La Rocca, M.V.; Peluso, A. Proton Transfer in Oxidized Adenosine Self-Aggregates. J. Chem. Phys. 2013, 139, 145101–145104. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. Proton-Coupled Electron Transfer in DNA on Formation of Radiation-Produced Ion Radicals. Chem. Rev. 2010, 110, 7002–7023. [Google Scholar] [CrossRef] [PubMed]
- Barnett, R.N.; Cleveland, C.L.; Joy, A.; Landman, U.; Schuster, G.B. Charge Migration in DNA: Ion-Gated Transport. Science 2001, 294, 567–571. [Google Scholar] [CrossRef] [PubMed]
- Livshits, G.I.; Stern, A.; Rotem, D.; Borovok, N.; Eidelshtein, G.; Migliore, A.; Penzo, E.; Wind, S.J.; Di Felice, R.; Skourtis, S.S.; et al. Long-Range Charge Transport in Single G-Quadruplex DNA Molecules. Nat. Nanotechnol. 2014, 9, 1040–1046. [Google Scholar] [CrossRef]
- Neidle, S. Quadruplex Nucleic Acids as Novel Therapeutic Targets. J. Med. Chem. 2016, 59, 5987–6011. [Google Scholar] [CrossRef]
- Jortner, J.; Bixon, M.; Langenbacher, T.; Michel-Beyerle, M.E. Charge Transfer and Transport in DNA. Proc. Natl. Acad. Sci. USA 1998, 95, 12759. [Google Scholar] [CrossRef]
- Bixon, M.; Giese, B.; Wessely, S.; Langenbacher, T.; Michel-Beyerle, M.E.; Jortner, J. Long-Range Charge Hopping in DNA. Proc. Natl. Acad. Sci. USA 1999, 96, 11713–11716. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Jortner, J.; Bixon, M.; Rösch, N. Energetic of Hole Transfer in DNA. Chem. Phys. Lett. 2000, 324, 430–434. [Google Scholar] [CrossRef]
- Berlin, Y.A.; Burin, A.L.; Ratner, M.A. Charge Hopping in DNA. J. Am. Chem. Soc. 2001, 123, 260–268. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Jortner, J.; Bixon, M.; Rösch, N. Electronic Coupling between Watson-Crick Pairs for Hole Transfer and Transport in Desoxyribonucleic Acid. J. Chem. Phys. 2001, 114, 5614–5620. [Google Scholar] [CrossRef]
- Troisi, A.; Orlandi, G. Hole Migration in DNA: A Theoretical Analysis of the Role of Structural Fluctuations. J. Phys. Chem. B 2002, 106, 2093–2101. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Grozema, F.C.; Fonseca Guerra, C.; Bickelhaupt, F.M.; Siebbeles, L.D.A. Mapping the Sites for Selective Oxidation of Guanines in DNA. J. Am. Chem. Soc. 2003, 125, 13658–13659. [Google Scholar] [CrossRef] [PubMed]
- Senthilkumar, K.; Grozema, F.C.; Fonseca Guerra, C.; Bickelhaupt, F.M.; Lewis, F.D.; Berlin, Y.A.; Ratner, M.A.; Siebbeles, L.D.A. Absolute Rates of Hole Transfer in DNA. J. Am. Chem. Soc. 2005, 127, 14894–14903. [Google Scholar] [CrossRef]
- Berlin, Y.A.; Kurnikov, I.V.; Beratan, D.; Ratner, M.A.; Burin, A.L. DNA Electron Transfer Processes: Some Theoretical Notions. In Long-Range Charge Transfer in DNA II; Schuster, G.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 237, pp. 1–36. [Google Scholar]
- Grozema, F.C.; Tonzani, S.; Berlin, Y.A.; Schatz, G.C.; Siebbeles, L.D.A.; Ratner, M.A. Effect of Structural Dynamics on Charge Transfer in DNA Hairpins. J. Am. Chem. Soc. 2008, 130, 5157–5166. [Google Scholar] [CrossRef]
- Grozema, F.C.; Tonzani, S.; Berlin, Y.A.; Schatz, G.C.; Siebbeles, L.D.A.; Ratner, M.A. Effect of GC Base Pairs on Charge Transfer through DNA Hairpins: The Importance of Electrostatic Interactions. J. Am. Chem. Soc. 2009, 131, 14204–14205. [Google Scholar] [CrossRef]
- Gollub, C.; Avdoshenko, S.; Gutierrez, R.; Berlin, Y.; Cuniberti, G. Charge Migration in Organic materials: Can Propagating Charges Affect the Key Physical Quantities Controlling Their Motion? Isr. J. Chem. 2012, 52, 452–460. [Google Scholar] [CrossRef]
- Renaud, N.; Berlin, Y.A.; Lewis, F.D.; Ratner, M.A. Between Superexchange and Hopping: An Intermediate Charge-Transfer Mechanism in polyA-polyT DNA Hairpins. J. Am. Chem. Soc. 2013, 135, 3953–3963. [Google Scholar] [CrossRef]
- Kubař, T.; Gutièrrez, R.; Kleinekathöfer, U.; Cuniberti, G.; Elstner, M. Modeling charge transport in DNA Using multi-scale Methods. Phys. Status Solidi B 2013, 250, 2277–2287. [Google Scholar] [CrossRef]
- Lewis, F.D.; Liu, X.; Liu, J.; Hayes, R.T.; Wasielewski, M.R. Dynamics and Equilibria for Oxidation of G, GG, and GGG Sequences in DNA Hairpins. J. Am. Chem. Soc. 2000, 122, 12037–12038. [Google Scholar] [CrossRef]
- Saito, I.; Takayama, M.; Kawanishi, S. Photoactivatable DNA-Cleaving Amino Acids: Highly Sequence- Selective DNA Photocleavage by Novel L-Lysine Derivatives. J. Am. Chem. Soc. 1995, 117, 5590–5591. [Google Scholar] [CrossRef]
- Hall, D.B.; Holmlin, R.E.; Barton, J.K. Oxidative DNA Damage through Long-Range Electron Transfer. Nature 1996, 382, 731–735. [Google Scholar] [CrossRef] [PubMed]
- Yoshioka, Y.; Kitagawa, Y.; Takano, Y.; Yamaguchi, K.; Nakamura, T.; Saito, I. Experimental and Theoretical Studies on the Selectivity of GGG Triplets toward One-Electron Oxidation in B-Form DNA. J. Am. Chem. Soc. 1999, 121, 8712–8719. [Google Scholar] [CrossRef]
- Giese, B.; Amaudrut, J.; Köhler, A.K.; Spormann, M.; Wessely, S. Direct Observation of Hole Transfer through DNA by Hopping between Adenine Bases and by Tunneling. Nature 2001, 412, 318–320. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.A.; Durandin, A.; Dedon, P.C.; Geacintov, N.E.; Shafirovich, V. Oxidation of Guanine in G, GG, and GGG Sequence Contexts by Aromatic Pyrenyl Radical Cations and Carbonate Radical Anions: Relationship between Kinetics and Distribution of Alkali-Labile Lesions. J. Phys. Chem. B 2008, 112, 1834–1844. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Capobianco, A.; Caruso, T.; D’Ursi, A.M.; Fusco, S.; Masi, A.; Scrima, M.; Chatgilialoglu, C.; Peluso, A. Delocalized Hole Domains in Guanine-Rich DNA Oligonucleotides. J. Phys. Chem. B 2015, 119, 5462–5466. [Google Scholar] [CrossRef]
- Genereux, J.C.; Wuerth, S.M.; Barton, J.K. Single-Step Charge Transport through DNA over Long Distances. J. Am. Chem. Soc. 2011, 133, 3863–3868. [Google Scholar] [CrossRef][Green Version]
- Muren, N.B.; Olmon, E.D.; Barton, J.K. Solution, Surface, and Single Molecule Platforms for the Study of DNA-Mediated Charge Transport. Phys. Chem. Chem. Phys. 2012, 14, 13754–13771. [Google Scholar] [CrossRef][Green Version]
- Harris, M.A.; Mishra, A.K.; Young, R.M.; Brown, K.E.; Wasielewski, M.R.; Lewis, F.D. Direct Observation of the Hole Carriers in DNA Photoinduced Charge Transport. J. Am. Chem. Soc. 2016, 138, 5491–5494. [Google Scholar] [CrossRef]
- Paleček, E.; Bartošík, M. Electrochemistry of Nucleic Acids. Chem. Rev. 2012, 112, 3427–3481. [Google Scholar] [CrossRef]
- Troisi, A.; Orlandi, G. The Hole Transfer in DNA: Calculation of Electron Coupling between Close Bases. Chem. Phys. Lett. 2001, 344, 509–518. [Google Scholar] [CrossRef]
- Cramer, T.; Krapf, S.; Koslowski, T. DNA Charge Transfer: An Atomistic Model. J. Phys. Chem. B 2004, 108, 11812–11819. [Google Scholar] [CrossRef]
- Kubař, T.; Woiczikowski, P.B.; Cuniberti, G.; Elstner, M. Efficient Calculation of Charge-Transfer Matrix Elements for Hole Transfer in DNA. J. Phys. Chem. B 2008, 112, 7937–7947. [Google Scholar] [CrossRef] [PubMed]
- Kitoh-Nishioka, H.; Ando, K. Charge-Transfer Matrix Elements by FMO-LCMO Approach: Hole Transfer in DNA with Parameter Tuned Range-Separated DFT. Chem. Phys. Lett. 2015, 621, 96–101. [Google Scholar] [CrossRef]
- Pluharová, E.; Slavíček, P.; Jungwirth, P. Modeling Photoionization of Aqueous DNA and Its Components. Acc. Chem. Res. 2015, 48, 1209–1217. [Google Scholar] [CrossRef] [PubMed]
- Kawai, K.; Wata, Y.; Ichinose, N.; Majima, T. Selective Enhancement of the One-Electron Oxidation of Guanine by Base Pairing with Cytosine. Angew. Chem. Int. Ed. 2000, 39, 4327–4329. [Google Scholar] [CrossRef]
- Seidel, C.A.M.; Schulz, A.; Sauer, M.H.M. Nucleobase-Specific Quenching of Fluorescent Dyes. I. Nucleobase One-Electron Redox Potentials and Their Correlation with Static and Dynamic Quenching Efficiencies. J. Phys. Chem. 1996, 100, 5541–5553. [Google Scholar] [CrossRef]
- Brotons, A.; Mas, L.A.; Metters, J.P.; Banks, C.E.; Iniesta, J. Voltammetric Behaviour of Free DNA Bases, Methylcytosine and Oligonucleotides at Disposable Screen Printed Graphite Electrode Platforms. Analyst 2013, 138, 5239–5249. [Google Scholar] [CrossRef]
- Dryhurst, G.; Elving, P.J. Electrochemical Oxidation of Adenine: Reaction Products and Mechanisms. J. Electrochem. Soc. 1968, 115, 1014–1020. [Google Scholar] [CrossRef]
- Faraggi, M.; Broitman, F.; Trent, J.B.; Klapper, M.H. One-Electron Oxidation Reactions of Some Purine and Pyrimidine Bases in Aqueous Solutions. Electrochemical and Pulse Radiolysis Studies. J. Phys. Chem. 1996, 100, 14751–14761. [Google Scholar] [CrossRef]
- Capobianco, A.; Landi, A.; Peluso, A. Modeling DNA Oxidation in Water. Phys. Chem. Chem. Phys. 2017, 19, 13571–13578. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, C.A.; Pluhařová, E.; Seidel, R.; Schroeder, W.P.; Faubel, M.; Slavíček, P.; Winter, B.; Jungwirth, P.; Bradforth, S.E. Oxidation Half-Reaction of Aqueous Nucleosides and Nucleotides via Photoelectron Spectroscopy Augmented by ab Initio Calculations. J. Am. Chem. Soc. 2015, 137, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Steenken, S.; Jovanovic, S.V. How Easily Oxidizable Is DNA? One-Electron Reduction Potentials of Adenosine and Guanosine Radicals in Aqueous Solution. J. Am. Chem. Soc. 1997, 119, 617–618. [Google Scholar] [CrossRef]
- Orlov, V.M.; Smirnov, A.N.; Varshavsky, Y.M. Ionization Potentials and Electron-Donor Ability of Nucleic Acid Bases and Their Analogues. Tetrahedron Lett. 1976, 48, 4377–4378. [Google Scholar] [CrossRef]
- Abraham, J.; Gosh, A.K.; Schuster, G.B. One-Electron Oxidation of DNA Oligomers That Lack Guanine: Reaction and Strand Cleavage at Remote Thymines by Long-Distance Radical Cation Hopping. J. Am. Chem. Soc. 2006, 128, 5346–5347. [Google Scholar]
- Ghosh, A.; Joy, A.; Schuster, G.B.; Douki, T.; Cadet, J. Selective One-Electron Oxidation of Duplex DNA Oligomers: Reaction at Thymines. Org. Biomol. Chem. 2008, 6, 916–928. [Google Scholar] [CrossRef]
- Joseph, J.; Schuster, G.B. One-Eelectron Oxidation of DNA: Reaction at Thymine. Chem. Commun. 2010, 46, 7872–7878. [Google Scholar] [CrossRef]
- Barnett, R.N.; Joseph, J.; Landman, U.; Schuster, G.B. Oxidative Thymine Mutation in DNA: Water-Wire-Mediated Proton-Coupled Electron Transfer. J. Am. Chem. Soc. 2013, 135, 3904–3914. [Google Scholar] [CrossRef]
- Colson, A.O.; Besler, B.; Sevilla, M.D. Ab Initio Molecular Orbital Calculation of DNA Base Pair Radical Ions: Effects of Base Pairing on Proton Transfer Energies, Electron Affinities and Ionization Potentials. J. Phys. Chem. 1992, 96, 9787–9794. [Google Scholar] [CrossRef]
- Kawai, K.; Wata, Y.; Hara, M.; Toyo, S.; Majima, T. Regulation of One-Electron Oxidation Rate of Guanine by Base Pairing with Cytosine Derivatives. J. Am. Chem. Soc. 2002, 124, 3586–3590. [Google Scholar] [CrossRef] [PubMed]
- Caruso, T.; Carotenuto, M.; Vasca, E.; Peluso, A. Direct Experimental Observation of the Effect of the Base Pairing on the Oxidation Potential of Guanine. J. Am. Chem. Soc. 2005, 127, 15040–15041. [Google Scholar] [CrossRef] [PubMed]
- Kyogoku, Y.; Lord, R.C.; Alexander, R. An infrared study of the hydrogen-bonding specificity of hypoxanthine and other nucleic acid derivatives. Biochim. Biophys. Acta 1969, 179, 10–17. [Google Scholar] [CrossRef]
- Williams, L.D.; Chawla, B.; Shaw, B.R. The hydrogen bonding of cytosine with guanine: Calorimetric and 1H-NMR analysis of the molecular interactions of nucleic acid bases. Biopolymers 1987, 26, 591–603. [Google Scholar] [CrossRef] [PubMed]
- Caruso, T.; Capobianco, A.; Peluso, A. The Oxidation Potential of Adenosine and Adenosine-Thymidine Base-Pair in Chloroform Solution. J. Am. Chem. Soc. 2007, 129, 15347–15353. [Google Scholar] [CrossRef] [PubMed]
- Capobianco, A.; Caruso, T.; Fusco, S.; Terzidis, M.A.; Masi, A.; Chatgilialoglu, C.; Peluso, A. The Association Constant of 5′,8-cyclo-2′-Deoxyguanosine with Cytidine. Front. Chem. 2015, 3, 22. [Google Scholar] [CrossRef]
- Psciuk, B.T.; Lord, R.L.; Munk, B.H.; Schlegel, H.B. Theoretical Determination of One-Electron Oxidation Potentials for Nucleic Acid Bases. J. Chem. Theory Comput. 2012, 12, 5107–5123. [Google Scholar] [CrossRef]
- Capobianco, A.; Carotenuto, M.; Caruso, T.; Peluso, A. The Charge-Transfer Band of an Oxidized Watson-Crick Guanosine-Cytidine Complex. Angew. Chem. Int. Ed. 2009, 48, 9526–9528. [Google Scholar] [CrossRef]
- Capobianco, A.; Caruso, T.; Celentano, M.; D’Ursi, A.M.; Scrima, M.; Peluso, A. Stacking Interactions between Adenines in Oxidized Oligonucleotides. J. Phys. Chem. B 2013, 117, 8947–8953. [Google Scholar] [CrossRef]
- Isaksson, J.; Acharya, S.; Barman, J.; Cheruku, P.; Chattopadhyaya, J. Single-Stranded Adenine-Rich DNA and RNA Retain Structural Characteristics of Their Respective Double-Stranded Conformations and Show Directional Differences in Stacking Pattern. Biochemistry 2004, 43, 15996–16010. [Google Scholar] [CrossRef]
- Zubatiuk, T.A.; Shishkin, O.V.; Gorb, L.; Hovorun, D.M.; Leszczynski, J. B-DNA Characteristics Are Preserved in Double stranded d(A)3·d(T)3 and d(G)3·d(C)3 Mini-Helixes: Conclusions from DFT/M06-2X Study. Phys. Chem. Chem. Phys. 2013, 15, 18155–18166. [Google Scholar] [CrossRef] [PubMed]
- Capobianco, A.; Peluso, A. The Oxidization Potential of AA Steps in Single Strand DNA Oligomers. RSC Adv. 2014, 4, 47887–47893. [Google Scholar] [CrossRef]
- Zubatiuk, T.; Kukuev, M.A.; Korolyova, A.S.; Gorb, L.; Nyporko, A.; Hovorun, D.; Leszczynski, J. Structure and Binding Energy of Double-Stranded A-DNA Mini-helices: Quantum-Chemical Study. J. Phys. Chem. B 2015, 119, 12741–12749. [Google Scholar] [CrossRef] [PubMed]
- Capobianco, A.; Caruso, T.; Peluso, A. Hole Delocalization over Adenine Tracts in Single Stranded DNA Oligonucleotides. Phys. Chem. Chem. Phys. 2015, 17, 4750–4756. [Google Scholar] [CrossRef]
- Capobianco, A.; Velardo, A.; Peluso, A. Single-Stranded DNA Oligonucleotides Retain Rise Coordinates Characteristic of Double Helices. J. Phys. Chem. B 2018, 122, 7978–7989. [Google Scholar] [CrossRef]
- El Hassan, M.A.; Calladine, C.R. Conformational Characteristics of DNA: Empirical Classifications and a Hypothesis for the Conformational Behaviour of Dinucleotide Steps. Philos. Trans. R. Soc. A 1997, 355, 43–100. [Google Scholar] [CrossRef]
- Calladine, C.R.; Drew, H.R.; Luisi, B.F.; Travers, A.A. Understanding DNA, 3rd ed.; Elsevier Academic Press: Oxford, UK, 2004. [Google Scholar]
- Dandliker, P.J.; Holmlin, R.E.; Barton, J.K. Oxidative Thymine Dimer Repair in the DNA Helix. Science 1997, 275, 1465–1468. [Google Scholar] [CrossRef]
- Henderson, P.T.; Jones, D.; Hampikian, G.; Kan, Y.; Schuster, G.B. Long-distance Charge Transport in Duplex DNA: The Phonon-Assisted Polaron-like Hopping Mechanism. Proc. Natl. Acad. Sci. USA 1999, 96, 8353–8358. [Google Scholar] [CrossRef]
- Conwell, E.M.; Rakhamanova, S.V. Polarons in DNA. Proc. Natl. Acad. Sci. USA 2000, 97, 4556–4560. [Google Scholar] [CrossRef]
- Schuster, G.B.; Landman, U. Long-Range Charge Transfer in DNA. II. Top. Curr. Chem. 2004, 236, 139. [Google Scholar]
- Shao, F.; O’Neill, M.A.; Barton, J.K. Long Range Oxidative Damage to Cytosine in Duplex DNA. Proc. Natl. Acad. Sci. USA 2004, 101, 17914–17919. [Google Scholar] [CrossRef] [PubMed]
- Takada, T.; Kawai, K.; Fujitsuka, M.; Majima, T. Rapid Long-Distance Hole Transfer through Consecutive Adenine Sequence. J. Am. Chem. Soc. 2006, 128, 11012–11013. [Google Scholar] [CrossRef] [PubMed]
- Lewis, F.D.; Zhu, H.; Daublain, P.; Cohen, B.; Wasielewski, M.R. Hole Mobility in DNA A Tracts. Angew. Chem. Int. Ed. 2006, 45, 7982–7985. [Google Scholar] [CrossRef] [PubMed]
- Zeidan, T.A.; Carmieli, R.; Kelley, R.F.; Wilson, T.M.; Lewis, F.D.; Wasielewski, M.R. Charge-Transfer and Spin Dynamics in DNA Hairpin Conjugates with Perylenediimide as a Base-Pair Surrogate. J. Am. Chem. Soc. 2008, 130, 13945–13955. [Google Scholar] [CrossRef] [PubMed]
- Vura-Weis, J.; Wasielewski, M.R.; Thazhathveetil, A.K.; Lewis, F.D. Efficient Charge Transport in DNA Diblock Oligomers. J. Am. Chem. Soc. 2009, 131, 9722–9727. [Google Scholar] [CrossRef]
- Blaustein, G.S.; Lewis, F.D.; Burin, A.L. Kinetics of Charge Separation in Poly(A)–Poly(T) DNA Hairpins. J. Phys. Chem. B 2010, 114, 6732–6739. [Google Scholar] [CrossRef]
- Kravec, S.M.; Kinz-Thompson, C.D.; Conwell, E.M. Localization of a Hole on an Adenine-Thymine Radical Cation in B-Form DNA in Water. J. Phys. Chem. B 2011, 115, 6166–6171. [Google Scholar] [CrossRef]
- Kumar, A.; Sevilla, M.D. Density Functional Theory Studies of the Extent of Hole Delocalization in One-Electron Oxidized Adenine And Guanine Base Stacks. J. Phys. Chem. B 2011, 115, 4990–5000. [Google Scholar] [CrossRef]
- Rooman, M.; Wintjens, R. Sequence and Conformation Effects on Ionization Potential and Charge Distribution of Homo-Nucleobase Stacks Using M06-2X Hybrid Density Functional Theory Calculations. J. Biomol. Struct. Dyn. 2014, 32, 532–545. [Google Scholar] [CrossRef]
- Saito, I.; Takayama, M.; Sugiyama, H.; Nakatani, K.; Tsuchida, A.; Yamamoto, M. Photoinduced DNA Cleavage via Electron Transfer: Demonstration that Guanine Residues Located 5′ to Guanine Are the Most Electron-Donating Sites. J. Am. Chem. Soc. 1995, 117, 6406–6407. [Google Scholar] [CrossRef]
- Sugiyama, H.; Saito, I. Theoretical Studies of GG-Specific Photocleavage of DNA via Electron Transfer: Significant Lowering of Ionization Potential and 5′-Localization of HOMO of Stacked GG Bases in B-form DNA. J. Am. Chem. Soc. 1996, 118, 7063–7068. [Google Scholar] [CrossRef]
- Sies, H.; Schulz, W.A.; Steenken, S. Adjacent Guanines as Preferred Sites for Strand Breaks in Plasmid DNA Irradiated with 193 nm and 248 nm UV Laser Light. J. Photochem. Photobiol. B Biol. 1996, 32, 97–102. [Google Scholar] [CrossRef]
- Prat, F.; Houk, K.N.; Foote, C.S. Effect of Guanine Stacking on the Oxidation of 8-Oxoguanine in B-DNA. J. Am. Chem. Soc. 1998, 120, 845–846. [Google Scholar] [CrossRef]
- Saito, I.; Nakamura, T.; Nakatani, K. Mapping of the Hot Spots for DNA Damage by One-Electron Oxidation: Efficacy of GG Doublets and GGG Triplets as a Trap in Long-Range Hole Migration. J. Am. Chem. Soc. 1998, 120, 12686–12687. [Google Scholar] [CrossRef]
- Voityuk, A.A. Are Radical Cation States Delocalized over GG and GGG Hole Traps in DNA? J. Phys. Chem. B 2005, 109, 10793–10796. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. Photoexcitation of Dinucleoside Radical Cations: A Time-Dependent Density Functional Study. J. Phys. Chem. B 2006, 110, 24181–24188. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ito, K.; Inoue, S.; Yamamoto, K.; Kawanishi, S. 8-Hydroxydeoxyguanosine Formation at the 5′ Site of 5′-GG-3′ Sequences in Double-Stranded DNA by UV Radiation with Riboflavin. J. Biol. Chem. 1993, 268, 13221–13227. [Google Scholar]
- Steinbrecher, T.; Koslowski, T.; Case, D.A. Direct Simulation of Electron Transfer Reactions in DNA Radical Cations. J. Phys. Chem. B 2008, 112, 16935–16944. [Google Scholar] [CrossRef]
- Pitterl, F.; Chervet, J.P.; Oberacher, H. Electrochemical Simulation of Oxidation Processes Involving Nucleic Acids Monitored with Electrospray Ionization-Mass Spectrometry. Anal. Bioanal. Chem. 2010, 397, 1203–1215. [Google Scholar] [CrossRef]
- Centore, R.; Fusco, S.; Peluso, A.; Capobianco, A.; Stolte, M.; Archetti, G.; Kuball, H.G. Push-Pull Azo-Chromophores Containing Two Fused Pentatomic Heterocycles and Their Nonlinear Optical Properties. Eur. J. Org. Chem. 2009, 3535–3543. [Google Scholar] [CrossRef]
- Anano, S.; Kurashina, Y.; Anraku, Y.; Mizuno, D. A Possible Recognition of Ribonucleotides by DNA Dependent RNA Polymerase of E. coli. J. Biochem. 1971, 70, 9–20. [Google Scholar] [CrossRef]
- Exinger, F.; Lacroute, F. 6-Azauracil Inhibition of GTP Biosynthesis in Saccharomyces Cerevisiae. Curr. Genet. 1992, 22, 9–11. [Google Scholar] [CrossRef]
- Oyelere, A.K.; Strobel, S.A. Site Specific Incorporation of 6-Azauridine into the Genomic HDV Ribozyme Active Site. Nucleosides Nucleotides Nucleic Acids 2001, 20, 1851–1858. [Google Scholar] [CrossRef]
- Pope, M.; Swenberg, C.E. Electronic Processes in Organic Crystals and Polymers; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Peluso, A.; Del Re, G. On the Occurrence of an Electron-Transfer Step in Aromatic Nitration. J. Phys. Chem. 1996, 100, 5303–5309. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Grozema, F.C.; Bickelhaupt, F.M.; Siebbeles, L.D.A. Charge Transport in Columnar Stacked Triphenylenes: Effects of Conformational Fluctuations on Charge Transfer Integrals and Site Energies. J. Chem. Phys. 2003, 119, 9809–9817. [Google Scholar] [CrossRef]
- Borrelli, R.; Di Donato, M.; Peluso, A. Quantum Dynamics of Electron Transfer from Bacteriochlorophyll to Pheophytin in Bacterial Reaction Centers. J. Chem. Theory Comput. 2007, 3, 673–680. [Google Scholar] [CrossRef]
- Brisker-Klaiman, D.; Peskin, U. Coherent Elastic Transport Contribution to Currents through Ordered DNA Molecular Junctions. J. Phys. Chem. C 2010, 114, 19077–19082. [Google Scholar] [CrossRef]
- Borrelli, R.; Capobianco, A.; Landi, A.; Peluso, A. Vibronic Couplings and Coherent Electron Transfer in Bridged Systems. Phys. Chem. Chem. Phys. 2015, 17, 30937–30945. [Google Scholar] [CrossRef]
- Levine, A.D.; Iv, M.; Peskin, U. Length-Independent Transport Rates in Biomolecules by Quantum Mechanical Unfurling. Chem. Sci. 2016, 7, 1535–1542. [Google Scholar] [CrossRef]
- Borrelli, R.; Peluso, A. Elementary Electron Transfer Reactions: From Basic Concepts to Recent Computational Advances. WIREs Comput. Mol. Sci. 2013, 3, 542–559. [Google Scholar] [CrossRef]
- Zhou, M.; Zhai, Y.; Dong, S. Electrochemical Sensing and Biosensing Platform Based on Chemically Reduced Graphene Oxide. Anal. Chem. 2009, 81, 5603–5613. [Google Scholar] [CrossRef]
- Brotons, A.; Vidal-Iglesias, F.J.; Solla-Gullón, J.; Iniesta, J. Carbon Materials for the Electrooxidation of Nucleobases, Nucleosides and Nucleotides toward Cytosine Methylation Detection: A Review. Anal. Methods 2016, 8, 702–715. [Google Scholar] [CrossRef]
- Renger, T.; Marcus, R.A. Variable Range Hopping Electron Transfer Through Disordered Bridge States: Application to DNA. J. Phys. Chem. A 2003, 107, 8404–8419. [Google Scholar] [CrossRef]
- Bixon, M.; Jortner, J. Incoherent Charge Hopping and Conduction in DNA and Long Molecular Chains. Chem. Phys. 2005, 319, 273–282. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Balaeff, A.; Skourtis, S.S.; Beratan, D.N. Biological Charge Transfer via Flickering Resonance. Proc. Natl. Acad. Sci. USA 2014, 111, 10049–10054. [Google Scholar] [CrossRef]
- Levine, A.D.; Iv, M.; Peskin, U. Formulation of Long-Range Transport Rates through Molecular Bridges: From Unfurling to Hopping. J. Phys. Chem. Lett. 2018, 9, 4139–4145. [Google Scholar] [CrossRef]
- Parson, W.W. Vibrational Relaxations and Dephasing in Electron-Transfer Reactions. J. Phys. Chem. B 2016, 120, 11412–11418. [Google Scholar] [CrossRef]
- Parson, W.W. Effects of Free Energy and Solvent on Rates of Intramolecular Electron Transfer in Organic Radical Anions. J. Phys. Chem. A 2017, 121, 7297–7306. [Google Scholar] [CrossRef]
- Parson, W.W. Electron-Transfer Dynamics in a Zn-Porphyrin-Quinone Cyclophane: Effects of Solvent, Vibrational Relaxations, and Conical Intersections. J. Phys. Chem. B 2018, 122, 854–3863. [Google Scholar] [CrossRef]
- Parson, W.W. Temperature Dependence of the Rate of Intramolecular Electron Transfer. J. Phys. Chem. B 2018, 122, 8824–8833. [Google Scholar] [CrossRef]
- Landi, A.; Borrelli, R.; Capobianco, A.; Peluso, A. Transient and Enduring Electronic Resonances Drive Coherent Long Distance Charge Transport in Molecular Wires. J. Phys. Chem. Lett. 2019, 10, 1845–1851. [Google Scholar] [CrossRef]
- Jimenez, R.; Fleming, G.R.; Kumar, P.V.; Maroncelli, M. Femtosecond Solvation Dynamics of Water. Nature 1994, 369, 471–473. [Google Scholar] [CrossRef]
- Fleming, G.R.; Cho, M. Chromophore-Solvent Dynamics. Annu. Rev. Phys. Chem. 1996, 47, 109–134. [Google Scholar] [CrossRef]
- Kobayashi, K.; Tagawa, S. Direct Observation of Guanine Radical Cation Deprotonation in Duplex DNA Using Pulse Radiolysis. J. Am. Chem. Soc. 2003, 125, 10213–10218. [Google Scholar] [CrossRef]
- Rokhlenko, Y.; Cadet, J.; Geacintov, N.E.; Shafirovich, V. Mechanistic Aspects of Hydration of Guanine Radical Cations in DNA. J. Am. Chem. Soc. 2014, 136, 5956–5962. [Google Scholar] [CrossRef]
- Candeias, L.P.; Steenken, S. Structure and Acid-Base Properties of One-Electron-Oxidized Deoxyguanosine, Guanosine, and 1-Methylguanosine. J. Am. Chem. Soc. 1989, 111, 1094–1099. [Google Scholar] [CrossRef]
- Chatgilialoglu, C.; Caminal, C.; Guerra, M.; Mulazzani, Q.G. Tautomers of One-Electron-Oxidized Guanosine. Angew. Chem. Int. Ed. 2005, 44, 6030–6032. [Google Scholar] [CrossRef]
- Chatgilialoglu, C.; Caminal, C.; Altieri, A.; Vougioukalakis, G.C.; Mulazzani, Q.G.; Gimisis, T.; Guerra, M. Tautomerism in the Guanyl Radical. J. Am. Chem. Soc. 2006, 128, 13796–13805. [Google Scholar] [CrossRef]
- Borrelli, R.; Capobianco, A.; Peluso, A. Hole Hopping Rates in Single Strand Oligonucleotides. Chem. Phys. 2014, 440, 25–30. [Google Scholar] [CrossRef]
- Velardo, A.; Borrelli, R.; Capobianco, A.; La Rocca, M.V.; Peluso, A. First Principle Analysis of Charge Dissociation and Charge Recombination Processes in Organic Solar Cells. J. Phys. Chem. C 2015, 119, 18870–18876. [Google Scholar] [CrossRef]
- Macía, E. Electrical Conductance in Duplex DNA: Helical Effects and Low-Frequency Vibrational Coupling. Phys. Rev. B 2007, 76, 245123. [Google Scholar] [CrossRef]
- Li, G.; Govind, N.; Ratner, M.A.; Cramer, C.J.; Gagliardi, L. Influence of Coherent Tunneling and Incoherent Hopping on the Charge Transfer Mechanism in Linear Donor-Bridge-Acceptor Systems. J. Phys. Chem. Lett. 2015, 6, 4889–4897. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron Transfer Reactions in Chemistry. Theory and Experiment. Rev. Mod. Phys. 1993, 65, 599–610. [Google Scholar] [CrossRef]
- Borrelli, R.; Gelin, M.F. Quantum Eelectron-Vibrational Dynamics at Finite Temperature: Thermo Field Dynamics Approach. J. Chem. Phys. 2016, 145, 224101. [Google Scholar] [CrossRef]
- Wu, J.; Meng, Z.; Lu, Y.; Shao, F. Efficient Long-Range Hole Transport Through G-Quadruplexes. Chem. Eur. J. 2017, 23, 13980–13985. [Google Scholar] [CrossRef]








| I(N) | (Ns) | (N) | (Nt) | (Ns) | (Ns) e | (N) | |
|---|---|---|---|---|---|---|---|
| A | +0.41 | +0.5 | +0.27 | +0.30 | +0.47 | +0.15 | +0.49 |
| C | +0.74 | +0.8 | +0.61 | +0.57 | +0.65 | +0.38 | +0.91 |
| T | +0.75 | +0.8 | +0.45 | +0.52 | +0.62 | +0.31 | +1.10 |
| Y | |||||
|---|---|---|---|---|---|
| G | 0.00 | 0.09 | 0.15 | 0.23 | 0.14 |
| A | 0.43 | 0.15 | 0.24 | 0.16 | 0.08 |
| C | 0.68 | 0.23 | 0.16 | 0.12 | 0.12 |
| T | 0.70 | 0.14 | 0.08 | 0.12 | 0.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peluso, A.; Caruso, T.; Landi, A.; Capobianco, A. The Dynamics of Hole Transfer in DNA. Molecules 2019, 24, 4044. https://doi.org/10.3390/molecules24224044
Peluso A, Caruso T, Landi A, Capobianco A. The Dynamics of Hole Transfer in DNA. Molecules. 2019; 24(22):4044. https://doi.org/10.3390/molecules24224044
Chicago/Turabian StylePeluso, Andrea, Tonino Caruso, Alessandro Landi, and Amedeo Capobianco. 2019. "The Dynamics of Hole Transfer in DNA" Molecules 24, no. 22: 4044. https://doi.org/10.3390/molecules24224044
APA StylePeluso, A., Caruso, T., Landi, A., & Capobianco, A. (2019). The Dynamics of Hole Transfer in DNA. Molecules, 24(22), 4044. https://doi.org/10.3390/molecules24224044







