Linear Response Functions of Densities and Spin Densities for Systematic Modeling of the QM/MM Approach for Mono- and Poly-Nuclear Transition Metal Systems
Abstract
:1. Introduction
2. Theoretical Background
2.1. Linear Response Function of Density and Spin Density
2.2. Spin Density as an Indicator of Correlation Effects in Kohn-Sham DFT
3. Results and Discussion
3.1. Heme System~Reaction Center of P450
3.1.1. The Target System
3.1.2. Linear Response Functions of Electron Density of P450
3.1.3. Linear Response Functions of Spin Density of P450
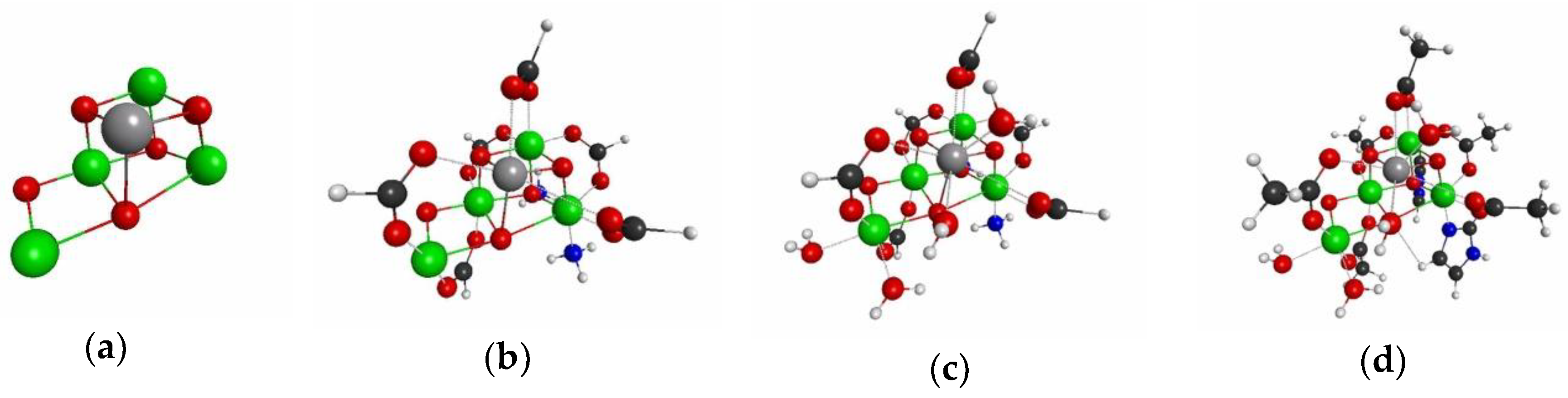
3.1.4. QM Cluster and QM/MM Calculations for Several Models of P450
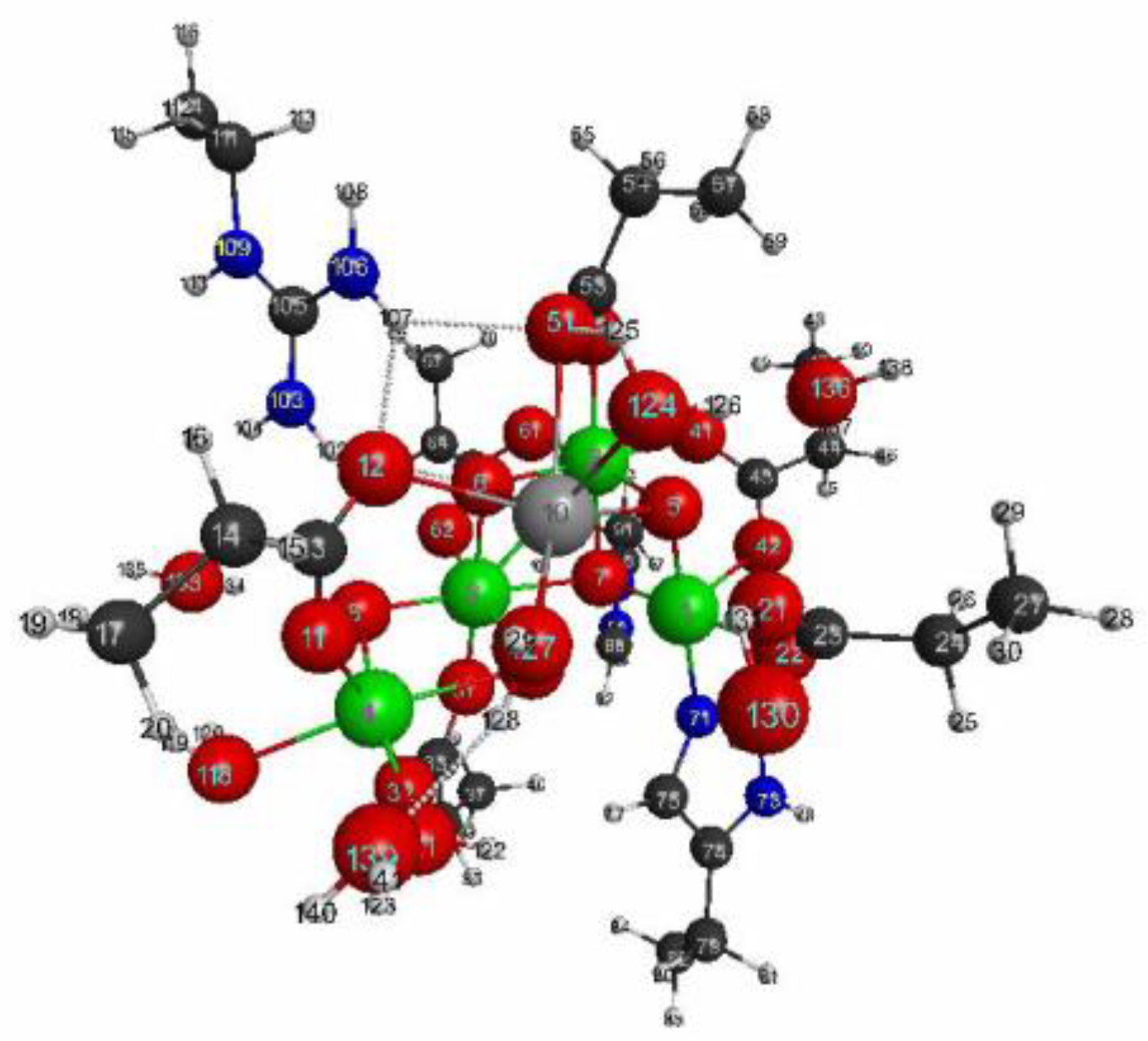
3.2. Oxygen Evolving Complex of Photosystem II.
3.2.1. The Target System
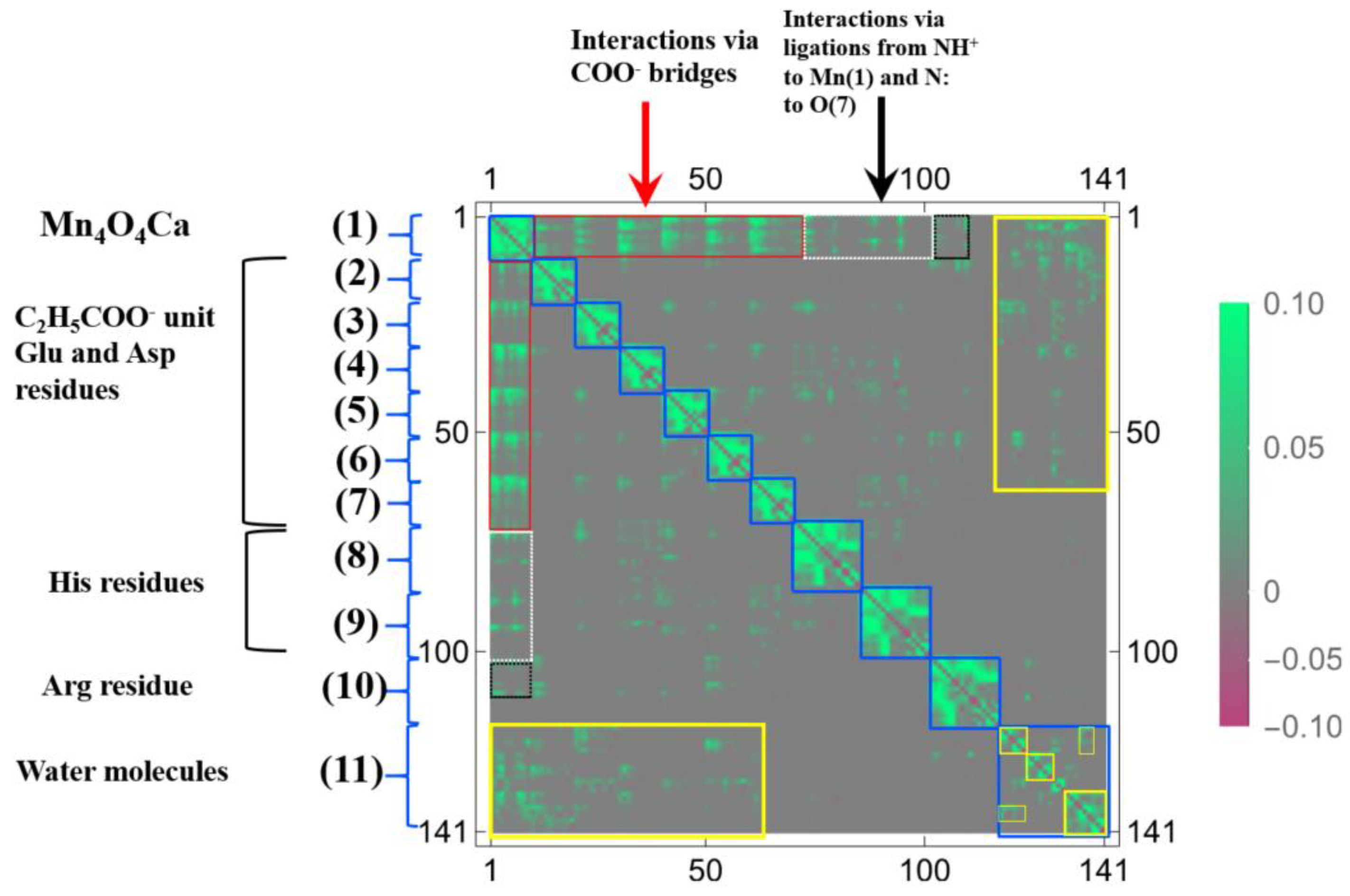
3.2.2. Linear Response Functions of Electron Density of OEC
3.2.3. Linear Response Functions of Spin Density of OEC
3.2.4. QM Cluster and QM/MM Calculations for Several Models of OEC
4. Materials and Methods
4.1. Numerical Details for Computations of “Condensed” Versions of the Linear Response Function
4.2. Computational Details of Transition Metal Complexes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Warshel, A.; Karplus, M. Calculation of ground and excited state potential surfaces of conjugated molecules. I. Formulation and parametrization. J. Am. Chem. Soc. 1972, 94, 5612–5625. [Google Scholar] [CrossRef]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Vreven, T.; Morokuma, K.; Farkas, O.; Schlegel, H.B.; Frisch, M.J. Geometry optimization with QM/MM, ONIOM, and other combined methods. I. Microiterations and constraints. J. Comp. Chem. 2003, 24, 760–769. [Google Scholar] [CrossRef] [PubMed]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.; Herrera, L.B.; Chehelamirani, M.; Hostas, J.; Jalife, S.; Salahub, D.R. Multiscale modeling of enzymes: QM-cluster, QM/MM, and QM/MM/MD: A tutorial review. Int. J. Quantum Chem. 2018, 118, e25558. [Google Scholar] [CrossRef] [Green Version]
- Bash, P.A.; Field, M.J.; Davenport, R.C.; Petsko, G.A.; Ringe, D.; Karplus, M. Computer Simulation and Analysis of the Reaction Pathway of Triosephosphate Isomerase. Biochemistry 1991, 30, 5826–5832. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.-Z.; Thiel, W. Convergence in the QM-only and QM/MM modeling of enzymatic reactions: A case study for acetylene hydratase. J. Comput. Chem. 2013, 34, 2389–2397. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Söderhjelm, P.; Ryde, U. On the Convergence of QM/MM Energies. J. Chem. Theory Comput. 2011, 7, 761–777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kulik, H.J.; Zhang, J.; Klinman, J.P.; Martínez, T.J. How Large Should the QM Region Be in QM/MM Calculations? The Case of Catechol O-Methyltransferase. J. Phys. Chem. B 2016, 120, 11381–11394. [Google Scholar] [CrossRef] [PubMed]
- Karelina, M.; Kulik, H.J. Systematic Quantum Mechanical Region Determination in QM/MM Simulation. J. Chem. Theory Comput. 2017, 13, 563–576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sumner, S.; Söderhjelm, P.; Ryde, U. Effect of Geometry Optimizations on QM-Cluster and QM/MM Studies of Reaction Energies in Proteins. J. Chem. Theory Comput. 2013, 9, 4205–4214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jindal, G.; Warshel, A. Exploring the Dependence of QM/MM Calculations of Enzyme Catalysis on the Size of the QM Region. J. Phys. Chem. B 2016, 120, 9913–9921. [Google Scholar] [CrossRef] [PubMed]
- Benediktsson, B.; Bjornsson, R. QM/MM Study of the Nitrogenase MoFe Protein Resting State: Broken-Symmetry States, Protonation States, and QM Region Convergence in the FeMoco Active Site. Inorg. Chem. 2017, 56, 13417–13429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, S.; Nam, K.; Major, D.T. Rapid Convergence of Energy and Free Energy Profiles with Quantum Mechanical Size in Quantum Mechanical−Molecular Mechanical Simulations of Proton Transfer in DNA. J. Chem. Theory Comput. 2018, 14, 1695–1705. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Mehmood, R.; Wang, M.; Qi, H.W.; Steeves, A.H.; Kulik, H.J. Revealing quantum mechanical effects in enzyme catalysis with large-scale electronic structure simulation. React. Chem. Eng. 2019, 4, 298–315. [Google Scholar] [CrossRef]
- Senet, P.J. Nonlinear electronic responses, Fukui functions and hardnesses as functionals of the ground state electronic density. J. Chem. Phys. 1996, 105, 6471–6489. [Google Scholar] [CrossRef]
- Contreras, R.R.; Fuentealba, P.; Galván, M.; Pérez, P. A direct evaluation of regional Fukui functions in molecules. Chem. Phys. Lett. 1999, 304, 405–413. [Google Scholar] [CrossRef]
- Yamanaka, S.; Yonezawa, Y.; Nakata, K.; Nishihara, S.; Okumura, M.; Takada, T.; Yamaguchi, K.; Nakamura, H. Locality and nonlocality of electronic structures of molecular systems: Toward QM/MM and QM/QM approaches. AIP Conf. Proc. 2012, 1504, 916–919. [Google Scholar]
- Ueda, K.; Yamanaka, S.; Nakata, K.; Ehara, M.; Okumura, M.; Yamaguchi, K.; Nakamura, H. Linear response function approach for the boundary problem of QM/MM methods. Int. J. Quantum Chem. 2013, 113, 336–341. [Google Scholar] [CrossRef]
- Mitsuta, Y.; Yamanaka, S.; Yamaguchi, K.; Okumura, M.; Nakamura, H. Theoretical Investigation on Nearsightedness of Finite Model and Molecular Systems based on Linear response analysis. Molecules 2014, 19, 13358–13373. [Google Scholar] [CrossRef] [PubMed]
- Mitsuta, Y.; Yamanaka, S.; Saito, T.; Kawakami, K.; Yamaguchi, K.; Okumura, M.; Nakamura, H. Nearsightedness-related indices of finite systems based on linear response function: One-dimensional cases. Mol. Phys. 2016, 114, 380–388. [Google Scholar] [CrossRef]
- Berkowitz, M.; Parr, R.G. Molecular hardness and softness, local hardness and softness, hardness and softness kernels, and relations among these quantities. J. Chem. Phys. 1988, 88, 2554–2557. [Google Scholar] [CrossRef]
- Geerlings, P.; Proft, F.D.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef] [PubMed]
- Geerlings, P.; FIas, S.; Boisdenghien, Z.; De Proft, F. Conceptual DFT: Chemistry from the linear response function. Chem. Soc. Rev. 2014, 43, 4989–5008. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.-J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Prodan, E.; Kohn, W. Nearsightedness of electronic matter. Proc. Natl. Acad. Sci. USA 2005, 112, 11635–11638. [Google Scholar] [CrossRef] [PubMed]
- Handbook of Metalloprotein; Messerschmidt, A.; Huber, R.; Poulos, T.; Wieghardt, K. (Eds.) John Willey & Sons: New Jersey, NJ, USA, 2001; Volume 1. [Google Scholar]
- Nakamura, A.; Ueyama, N.; Yamaguchi, K. Organometallic Conjugation: Structures, Reactions and Functions of d-d and d-π Conjugated Systems; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003. [Google Scholar]
- Itoh, K.; Kinoshita, M. (Eds.) Molecular Magnetism; Gordon & Breach: New York, NY, USA, 2000. [Google Scholar]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules. In Horizons of Quantum Chemistry; Springer, Dordrecht: New York, NY, USA, 1989. [Google Scholar]
- Perdew, J.P.; Ernzherof, M.; Burke, K.; Savin, A. On-top pair-density interpretation of spin density functional theory, with applications to magnetism. Int. J. Quantum Chem. 1997, 61, 197–205. [Google Scholar] [CrossRef]
- Takeda, R.; Yamanaka, S.; Yamaguchi, K. CAS-DFT based on odd-electron density and radical density. Chem. Phys. Lett. 2002, 366, 321–328. [Google Scholar] [CrossRef]
- Yamaguchi, K. Self-Consistent Field Theory and Applications; Carbo, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 727–757. [Google Scholar]
- Yamanaka, S.; Kanda, K.; Saito, T.; Umena, Y.; Kawakami, K.; Shen, J.-R.; Kamiya, N.; Nakamura, H.; Yamaguchi, K. Electronic and spin structures of the CaMn4O5(H2O)4 cluster in OEC of PS II refined to 1.9 Å X-ray resolution. Adv. Quantum Chem. 2012, 64, 121–187. [Google Scholar]
- Feynmann, R.P. Forces in molecules. Phys. Rev. 1939, 56, 340–343. [Google Scholar] [CrossRef]
- Fias, S.; Boisdenghien, Z.; Proft, F.D.; Geerlings, P. The spin polarized linear response from density functional theory: Theory and application to atoms. J. Chem. Phys. 2014, 141, 184107. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, S.; Kawakami, T.; Nagao, H.; Yamaguchi, K. Effective exchange integrals for open-shell species by density functional methods. Chem. Phys. Lett. 1994, 231, 25–33. [Google Scholar] [CrossRef]
- Yamaguchi, K. General Molecular Orbital Theories of organic reaction mechanisms. Chem. Phys. 1978, 29, 117–139. [Google Scholar] [CrossRef]
- Kishi, R.; Ochi, S.; Izumi, S.; Makino, A.; Nagami, T.; Fujiyoshi, J.; Nakano, N. Diradical Character Tuning for the Third-Order Nonlinear Optical Properties of Quinoidal Oligothiophenes by Introducing Thiophene-S,S-dioxide Rings. Chem. Eur. J. 2016, 22, 1493–1500. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Heme, T.L. Enzyme Structure and Function, Poulos. Chem. Rev. 2014, 114, 3919–3962. [Google Scholar]
- Gober, J.G.; Ghodge, S.V.; Bogart, J.W.; Wever, W.J.; Watkins, R.R.; Brustad, E.M.; Bowers, A.A. P450-Mediated Non-natural Cyclopropanation of Dehydroalanine-Containing Thiopeptides. ACS Chem. Biol. 2017, 12, 1726–1731. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, K.; Kawakami, T.; Yamaki, D. Theory of Molecular Magnetism. In Molecular Magnetism, Molecular Magnetism; Gordon & Breach: New York, NY, USA, 2000; pp. 9–48. [Google Scholar]
- Whittaker, J.W. Non-heme manganese catalase--the ‘other’ catalase. Arch. Biochem. Biophys. 2012, 525, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Holley, A.K.; Baktthavatchalu, V.; Velez-Roman, J.M.; St. Clair, D.K. SOD Manganese Superoxide Dismutase: Guardian of the Powerhouse. Int. J. Mol. Sci. 2011, 12, 7114–7162. [Google Scholar] [CrossRef] [PubMed]
- Umena, Y.; Kawakami, K.; Shen, J.R.; Kamiya, N. Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 Å. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanaka, A.; Fukushima, Y.; Kamiya, N. Two Different Structures of the Oxygen-Evolving Complex in the Same Polypeptide Frameworks of Photosystem II. J. Am. Chem. Soc. 2017, 139, 1718–1721, A chain (pdb entry: 5b66). [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, K.; Shoji, M.; Isobe, H.; Yamanaka, S.; Umena, Y.; Kawakami, K.; Kamiya, N. On the guiding principles for understanding of geometrical structures of the CaMn4O5 cluster in oxygen-evolving complex of photosystem II. Proposal of estimation formula of structural deformations via the Jahn–Teller effects. Mol. Phys. 2016, 115, 636–666. [Google Scholar] [CrossRef]
- Shoji, M.; Isobe, H.; Tanaka, A.; Fukushima, Y.; Kawakami, K.; Umena, Y.; Kamiya, N.; Nakajima, T.; Yamaguchi, K. Understanding Two Different Structures in the Dark Stable State of the Oxygen-Evolving Complex of Photosystem II: Applicability of the Jahn–Teller Deformation Formula. ChemPhotoChem 2018, 2, 257–270. [Google Scholar] [CrossRef] [PubMed]
- Siegbahn, P.E.M.; Blomberg, M.R.A. Density functional theory of biologically relevant metal centers. Annu. Rev. Phys. Chem. 1999, 50, 221–249. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, S.; Kanda, K.; Saito, T.; Kitagawa, Y.; Kawakami, T.; Ehara, M.; Okumura, M.; Nakamura, H.; Yamaguchi, K. Does B3LYP correctly describe magnetism of manganese complexes. Chem. Phys. Lett. 2012, 519–520, 134–140. [Google Scholar] [CrossRef]
- Eduardo, M.; Sproviero, E.M.; Gascon, J.A.; McEvoy, J.P.; Brudvig, G.W.; Batista, V.S. Characterization of synthetic oxomanganese complexes and the inorganic core of the O2-evolving complex in photosystemII: Evaluation of the DFT/B3LYP level of theory. J. Inorg. Biochem. 2006, 100, 786–800. [Google Scholar]
- Yamanaka, S.; Kanda, K.; Saito, T.; Kitagawa, Y.; Kawakami, T.; Ehara, M.; Okumura, M.; Nakamura, H.; Yamaguchi, K. Density Functional Study of Manganese Complexes: Protonation Effects on Geometry and Magnetism. In Progress in Theoretical Chemistry and Physics; Kiyoshi Nishikawa, K., Maruani, J., Brändas, E.J., Delgado-Barrio, G., Piecuch, P., Eds.; Springer Business Media Dordrecht: New York, NY, USA, 2013; pp. 21–26. [Google Scholar]
- Smith, F.J. Quadrature Methods based on the Euler-Maclaurin Formula and on the Clenshaw-Curtis Method of Integration. Numer. Math. 1965, 7, 406–411. [Google Scholar] [CrossRef]
- Lebedev, V.I. Spherical quadrature formulas exact to orders 25–29. Siberian Math. J. 1977, 18, 99–107. [Google Scholar] [CrossRef]
- Becke, A. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Wachters, J.H. Gaussian basis set for molecular wavefunctions containing third-row atoms. J. Chem. Phys. 1970, 52, 1033–1036. [Google Scholar] [CrossRef]
- Bauschlicher, C.W., Jr.; Langhoff, S.R.; Barnes, L.A. Theoretical studies of the first-and second-row transition-metal methyls and their positive ions. J. Chem. Phys. 1989, 91, 2399–2411. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. GAUSSIAN 09, Revision C 0.1. Available online: http://gaussian.com/g09_c01/ (accessed on 25 February 2018).
- Bode, B.M.; Gordon, M.S. MacMolPlt: A graphical user interface for GAMESS. J. Mol. Graphics Mod. 1998, 16, 133–138. [Google Scholar] [CrossRef]
- Mathematica Ver. 11, Wolfram Research: Champaign, IL, USA. Available online: http: //www.wolfram.com /mathematica (accessed on 30 December 2018).
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds not available. |
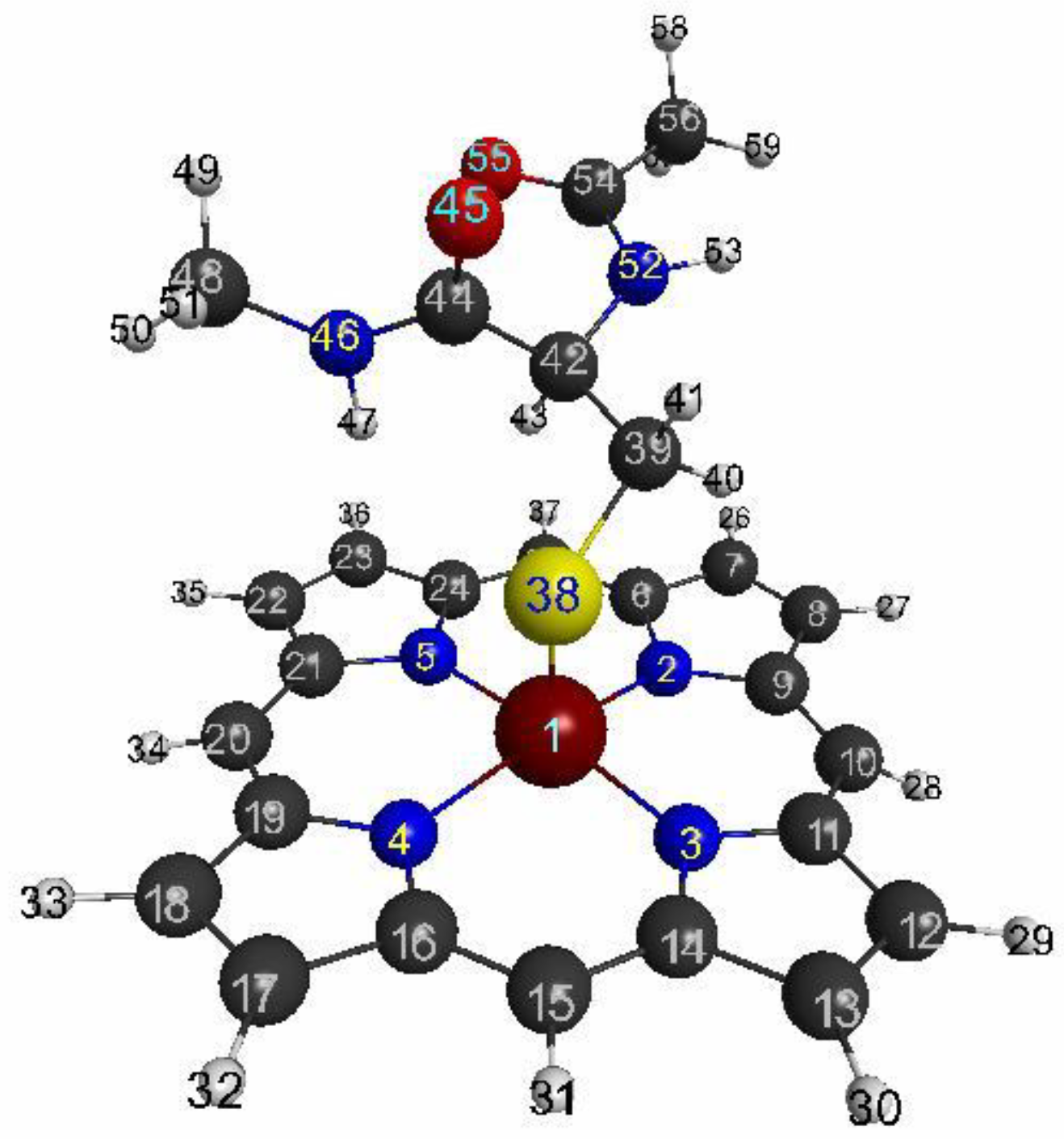

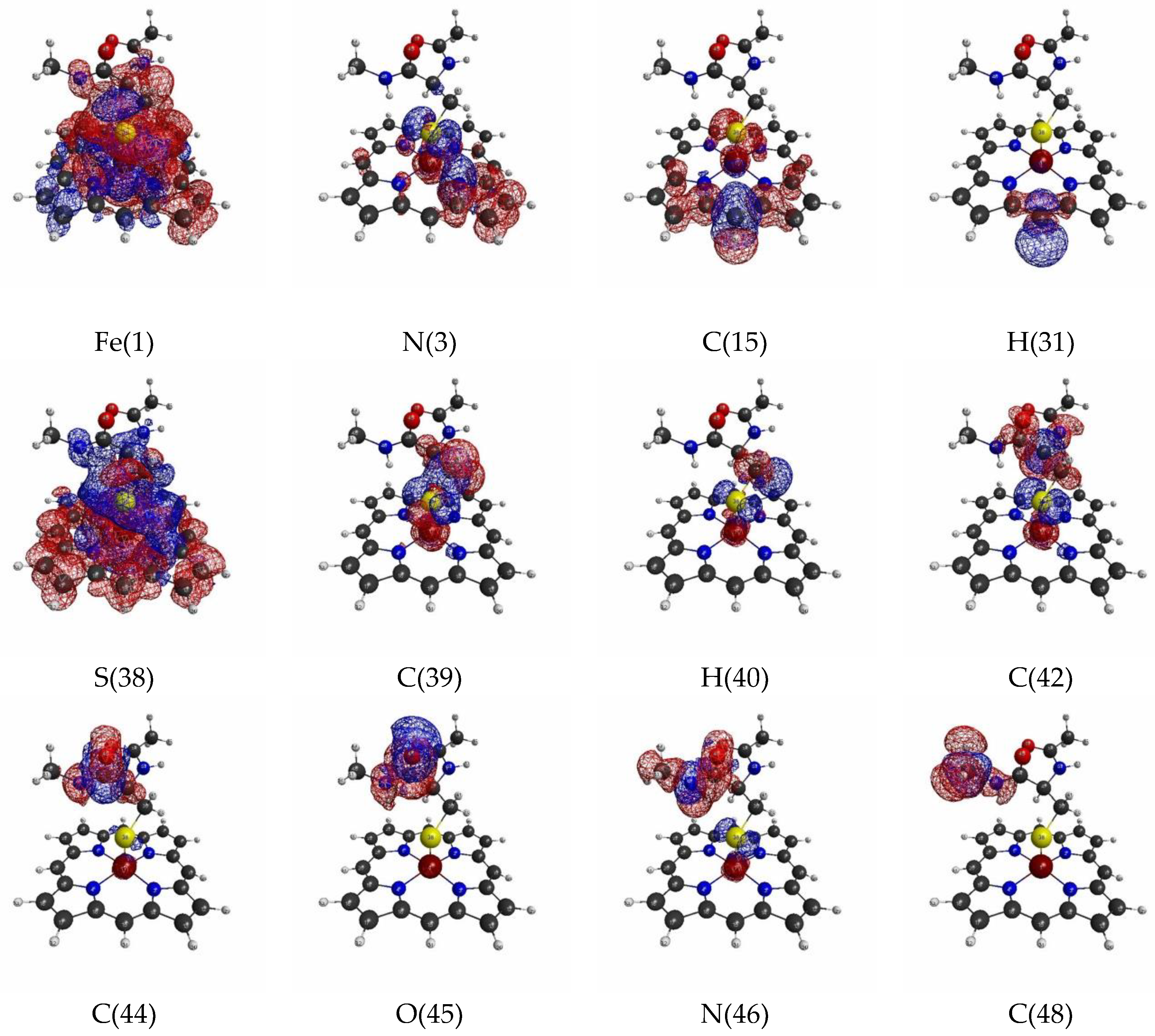
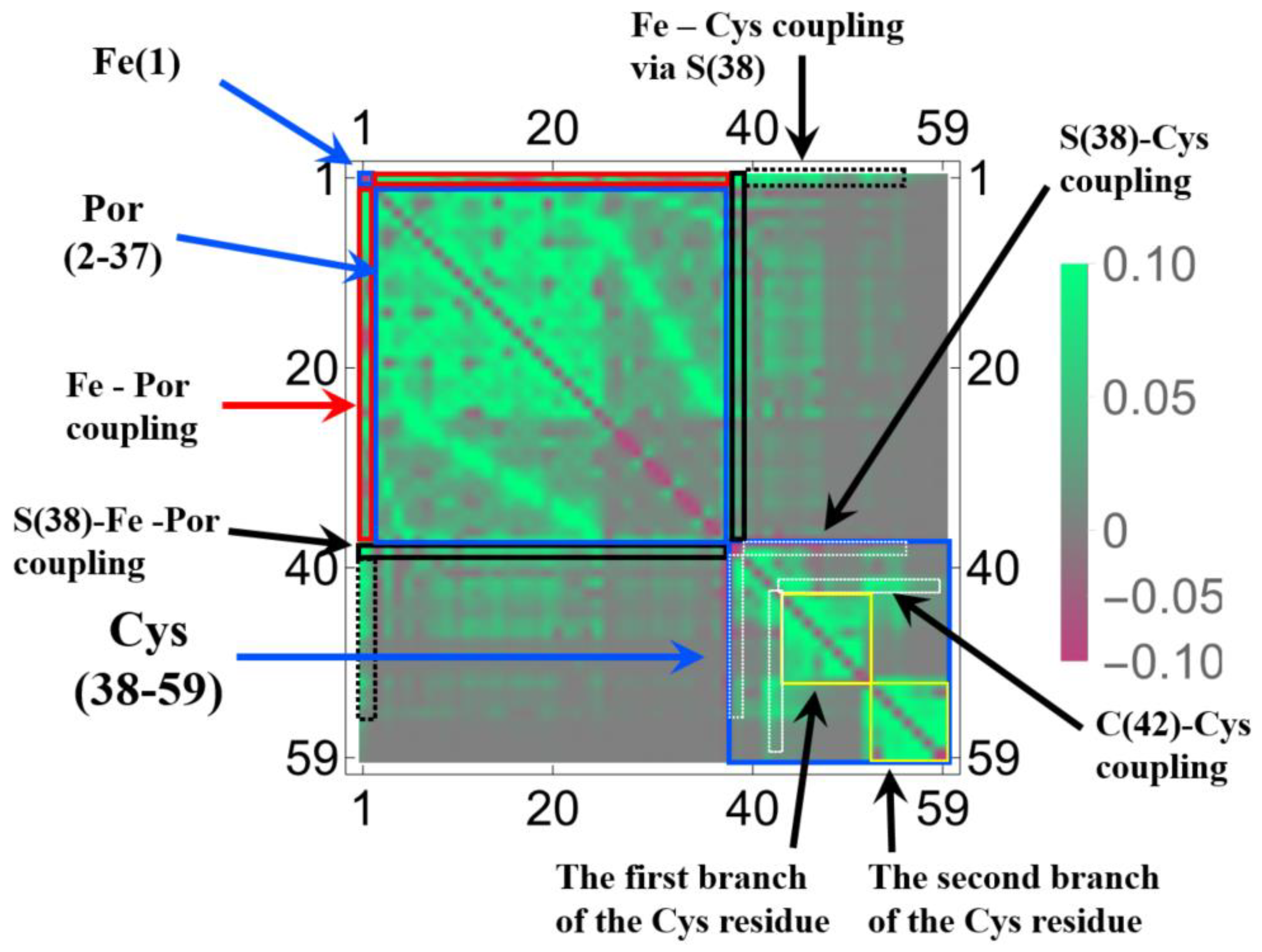
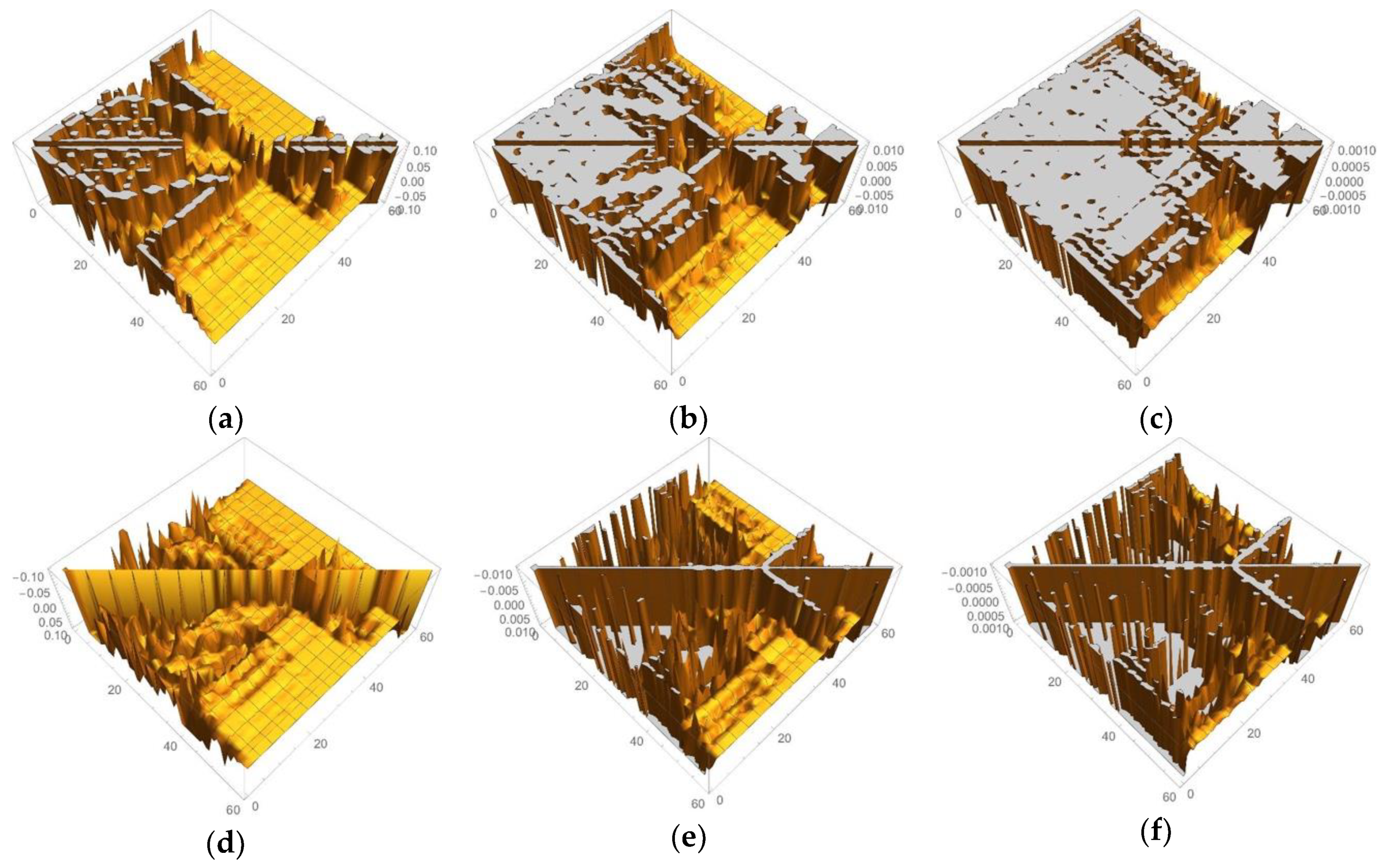
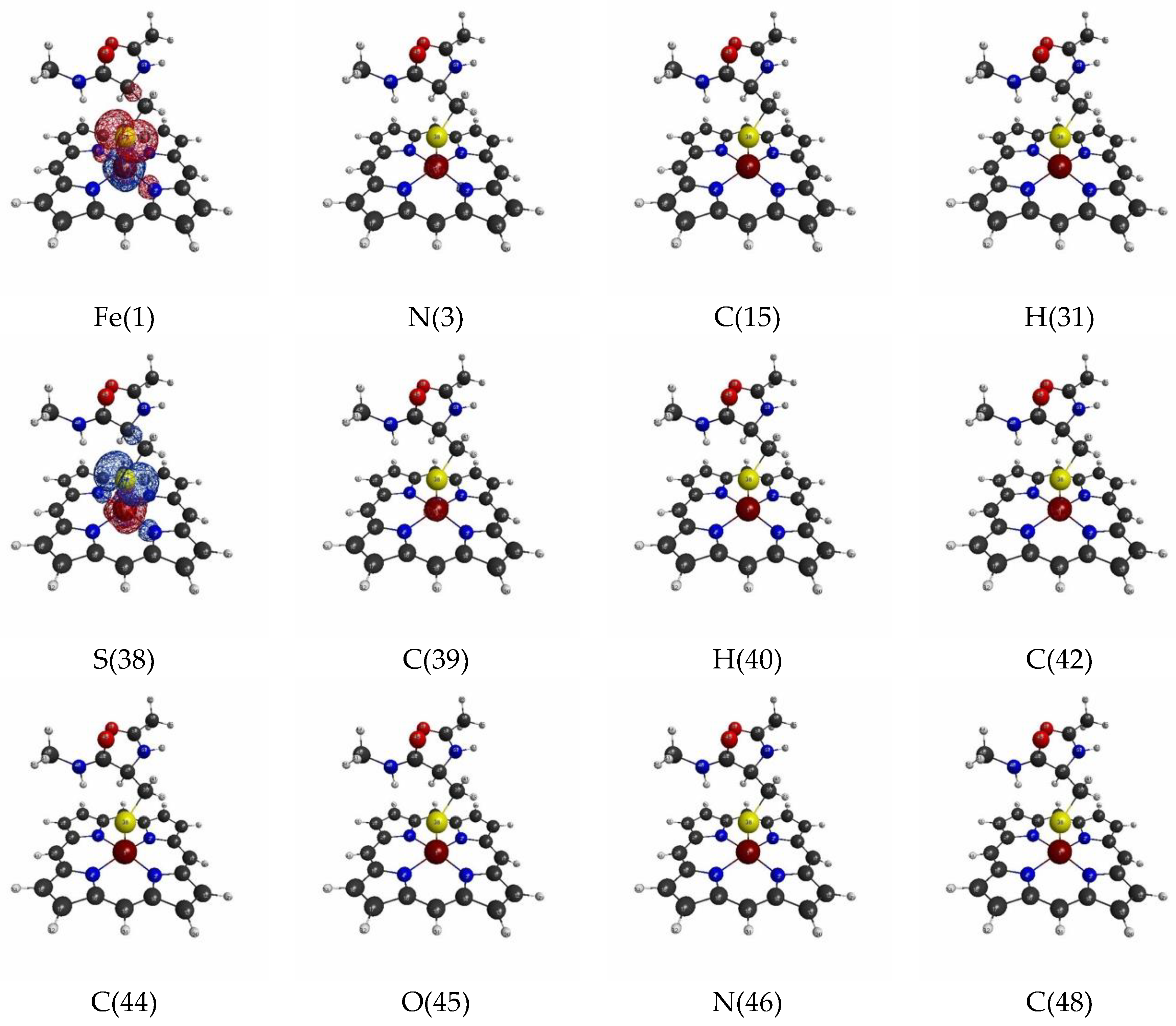
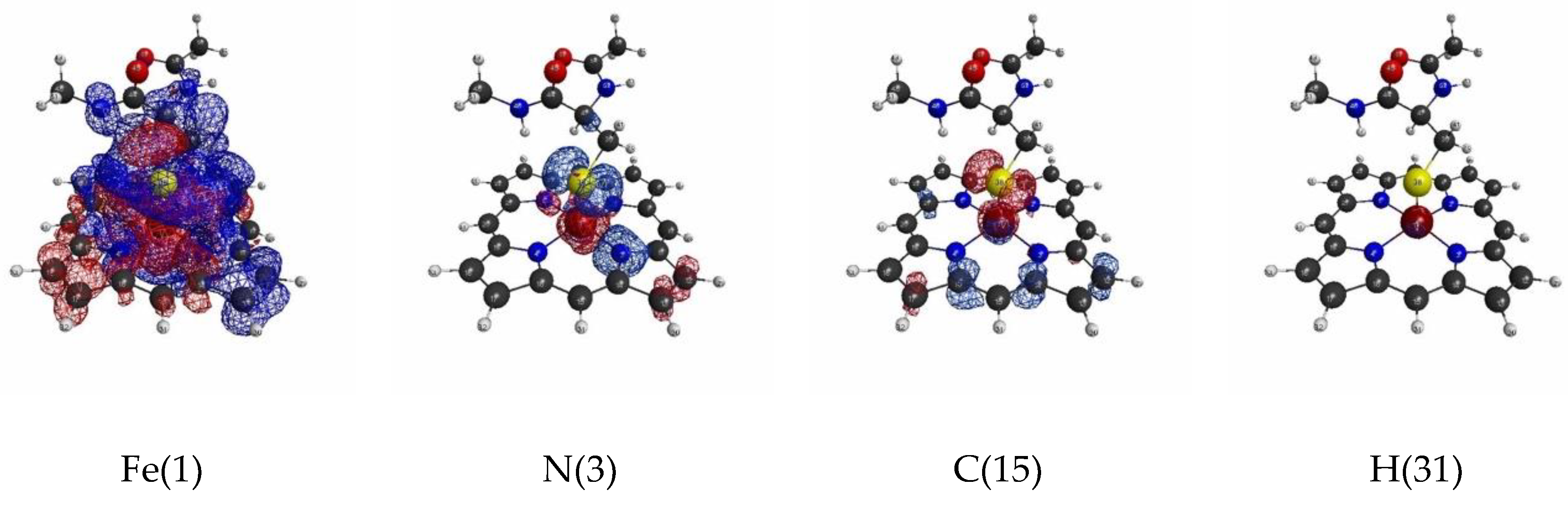
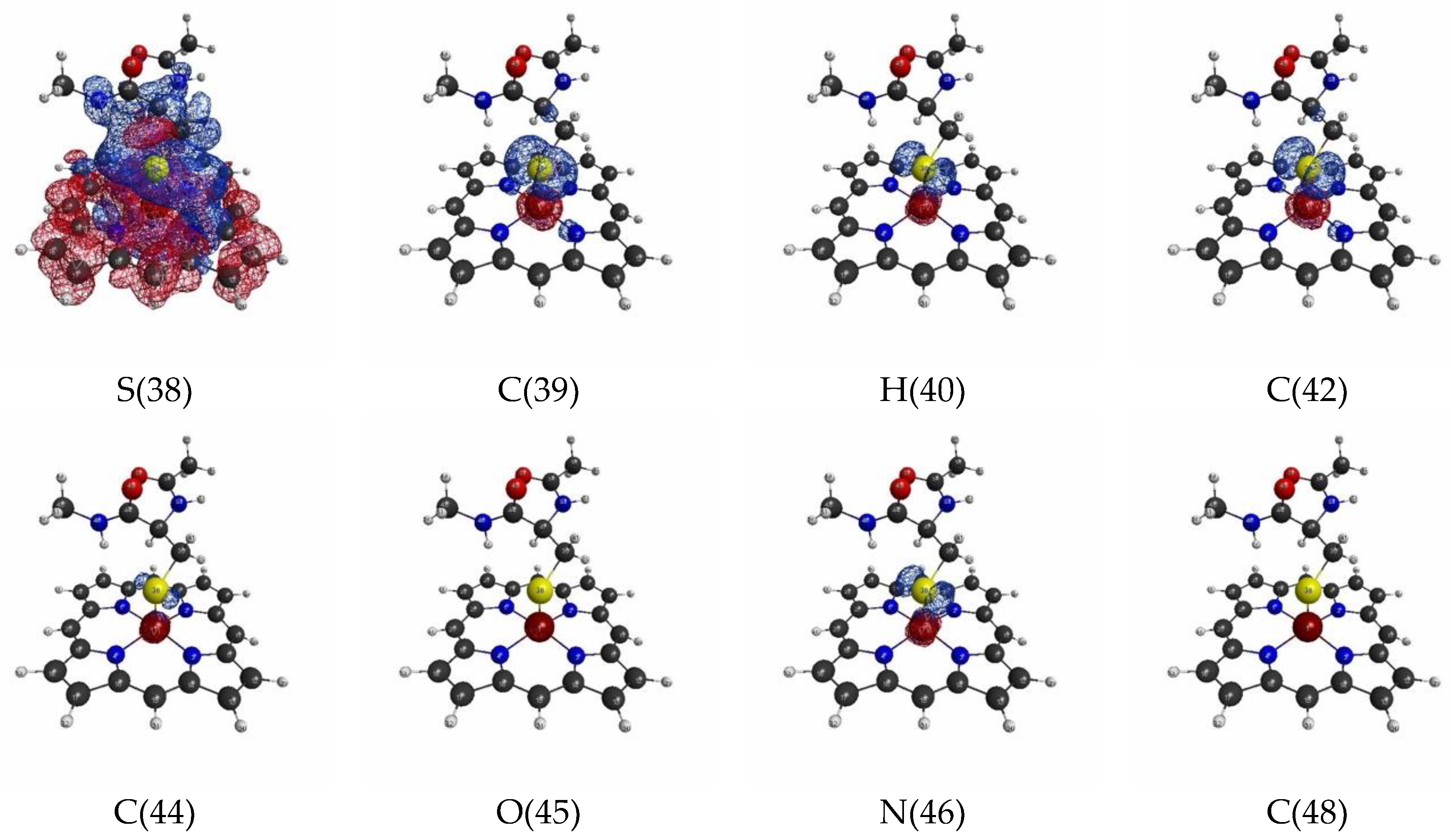


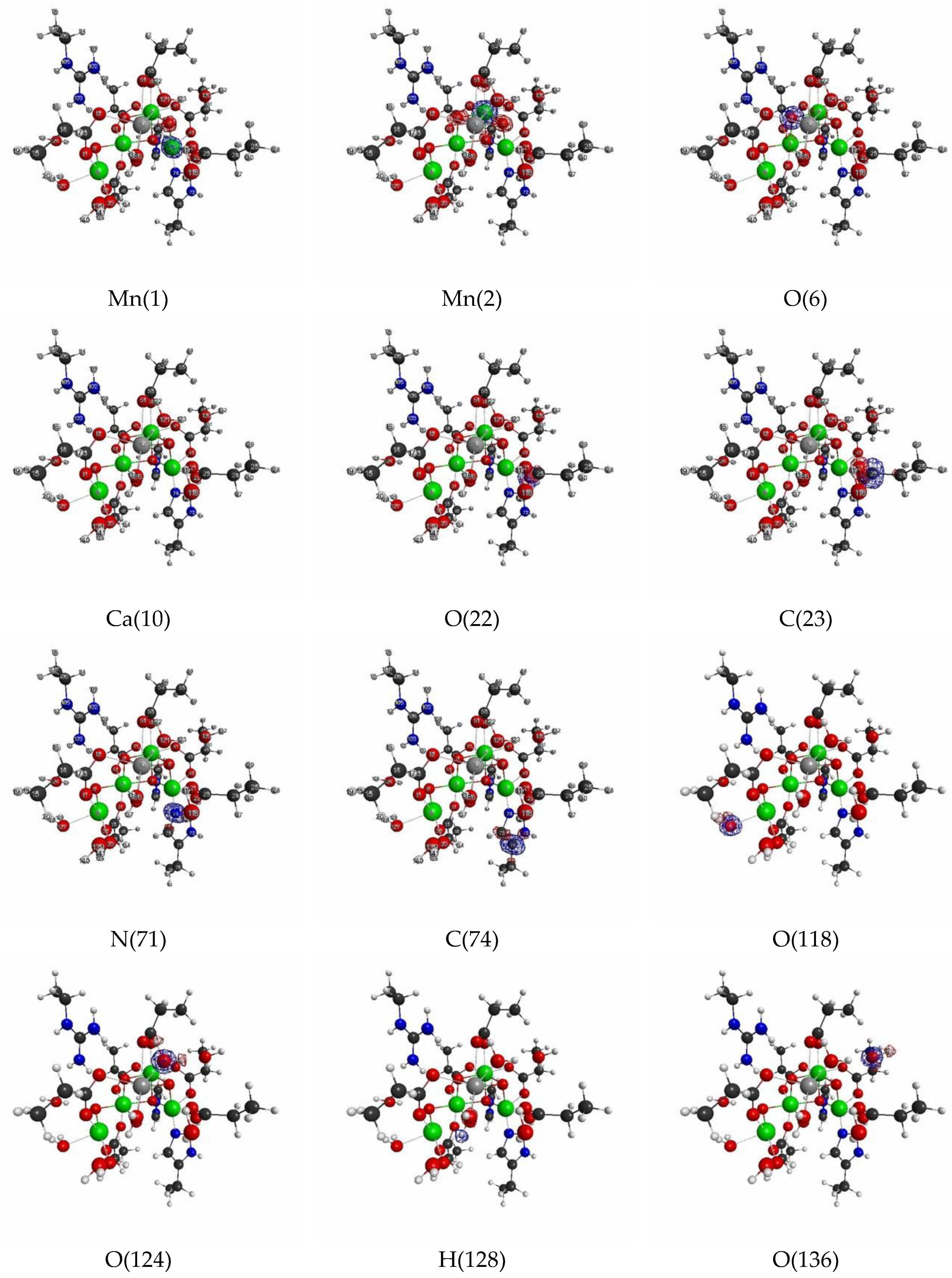
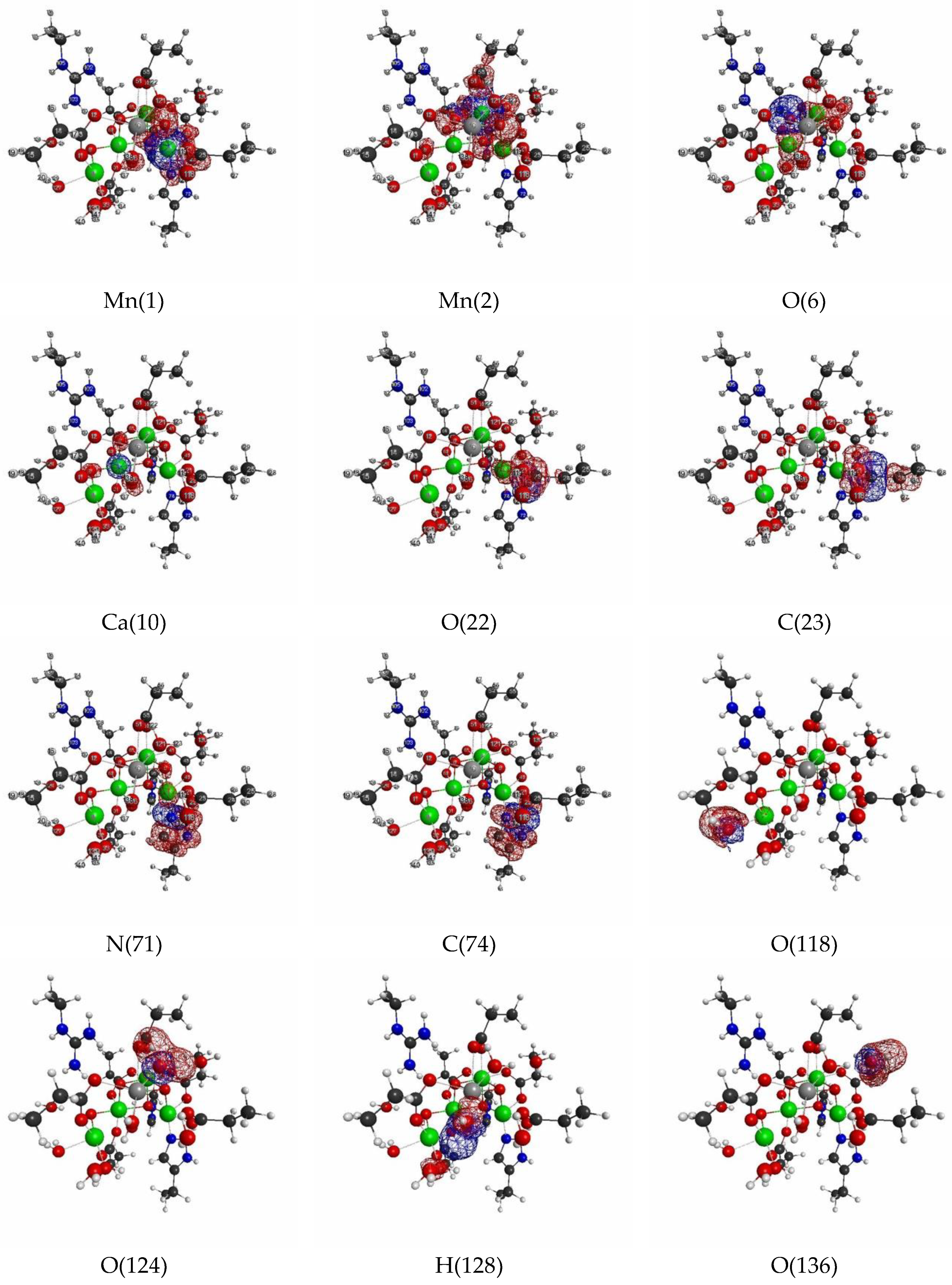
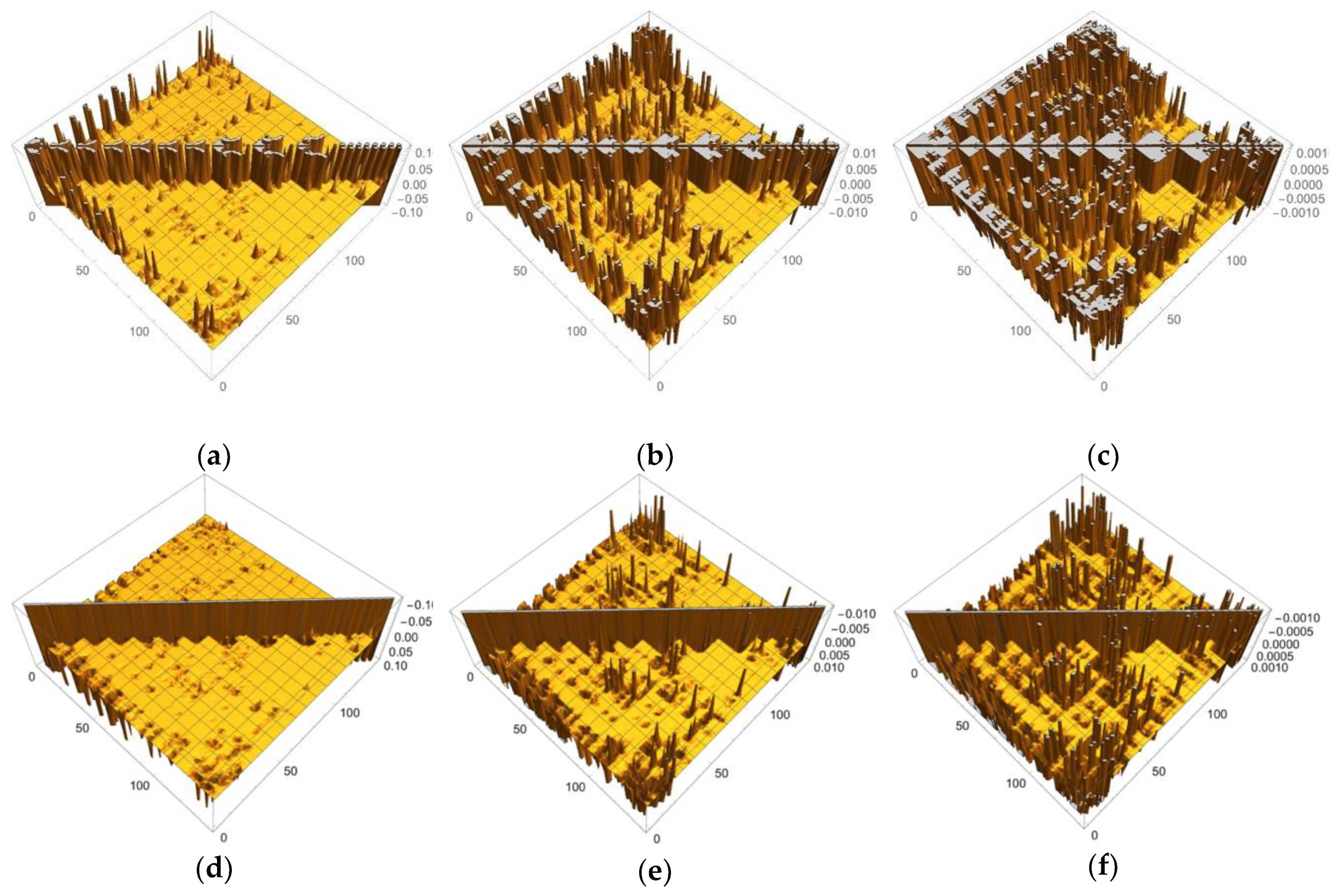
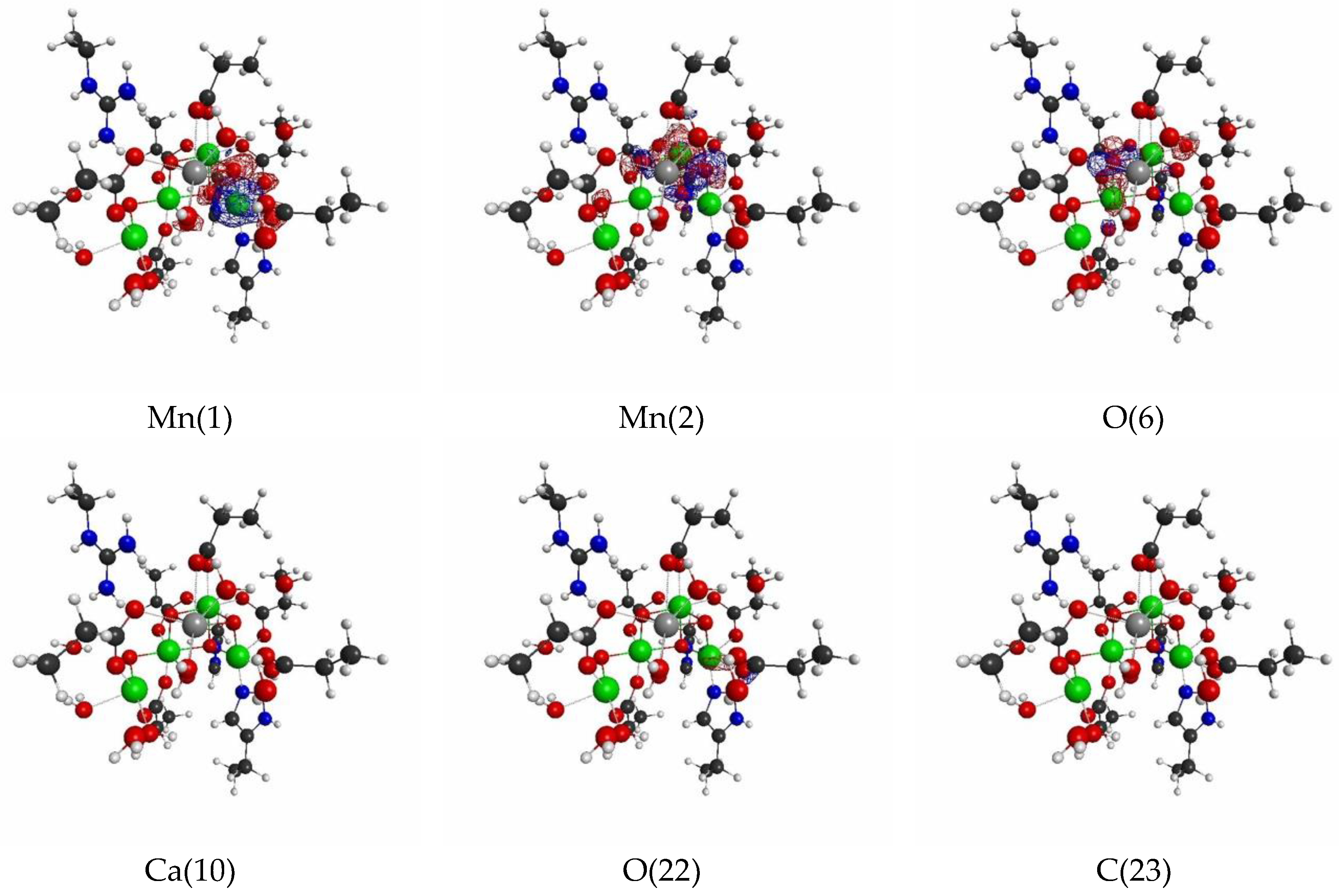
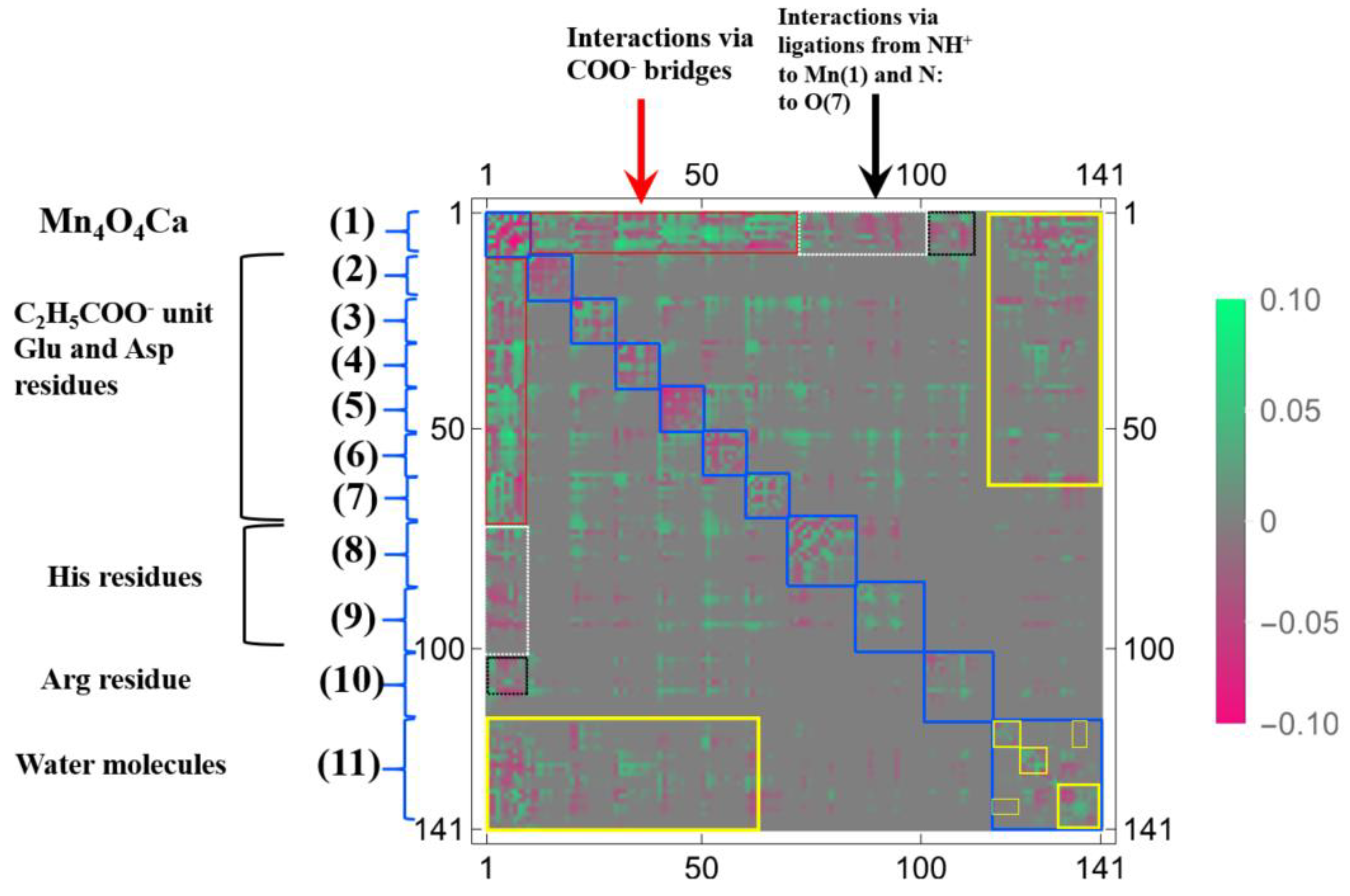
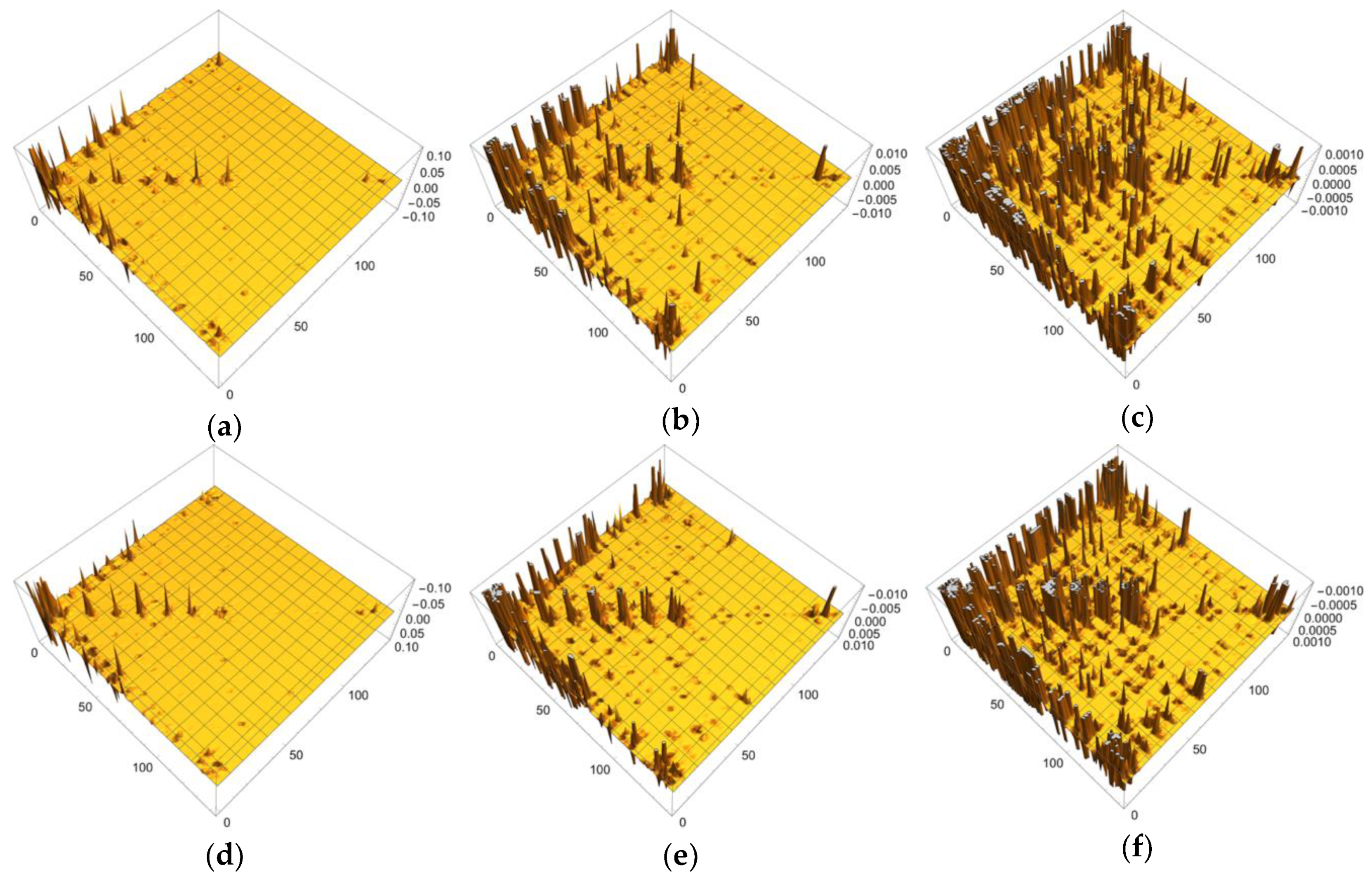
| Atom | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|
| QM | QM/MM | QM | QM/MM | QM | QM/MM | |
| Fe | 0.069 | 0.099 | −0.006 | −0.013 | 0.001 | 0.014 |
| N | 0.025 | 0.034 | 0.001 | 0.001 | 0.000 | −0.001 |
| N | 0.020 | 0.029 | 0.000 | 0.000 | 0.000 | 0.000 |
| N | 0.017 | 0.028 | 0.000 | 0.001 | 0.000 | −0.001 |
| N | 0.020 | 0.027 | 0.004 | 0.003 | 0.000 | −0.003 |
| S | 0.082 | -0.018 | −0.006 | 0.033 | −0.001 | −0.015 |
| Atom | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|
| QM | QM/MM | QM | QM/MM | QM | QM/MM | |
| Fe | 0.023 | −0.070 | 0.007 | 0.017 | −0.002 | −0.016 |
| N | 0.015 | 0.002 | 0.002 | 0.005 | −0.001 | −0.004 |
| N | 0.018 | 0.004 | 0.000 | 0.002 | 0.000 | −0.002 |
| N | 0.013 | −0.002 | 0.000 | 0.001 | 0.000 | −0.001 |
| N | 0.025 | 0.014 | −0.001 | 0.000 | 0.000 | −0.001 |
| S | −0.113 | 0.024 | −0.018 | −0.039 | 0.003 | 0.035 |
| Atom | Model 1 | Model 2 | Model 3 | Model 4 | ||||
|---|---|---|---|---|---|---|---|---|
| QM | QM/MM | QM | QM/MM | QM | QM/MM | QM | QM/MM | |
| Mn(1) | 0.941 | 1.069 | 0.051 | 0.032 | 0.041 | 0.025 | 0.004 | 0.005 |
| Mn(2) | 0.835 | 1.050 | 0.036 | 0.026 | 0.030 | 0.021 | 0.017 | 0.014 |
| Mn(3) | 0.571 | 0.687 | 0.041 | 0.013 | 0.024 | −0.001 | 0.019 | 0.001 |
| Mn(4) | 1.071 | 1.134 | 0.237 | 0.365 | 0.026 | 0.043 | 0.009 | 0.024 |
| O(5) | 0.185 | 0.192 | −0.003 | 0.024 | −0.001 | 0.025 | −0.013 | 0.005 |
| O(6) | 0.230 | 0.158 | 0.036 | −0.006 | 0.042 | −0.003 | 0.037 | −0.014 |
| O(7) | 0.236 | 0.033 | −0.015 | −0.034 | −0.019 | −0.036 | −0.008 | −0.007 |
| O(8) | 0.380 | 0.178 | 0.071 | 0.021 | 0.021 | −0.002 | 0.011 | −0.016 |
| O(9) | 0.224 | 0.153 | −0.004 | 0.002 | −0.009 | 0.002 | −0.011 | 0.004 |
| Ca(10) | 1.158 | 1.175 | 0.364 | 0.412 | 0.022 | 0.004 | 0.014 | −0.005 |
| Atom | Model 1 | Model 2 | Model 3 | Model 4 | ||||
|---|---|---|---|---|---|---|---|---|
| QM | QM/MM | QM | QM/MM | QM | QM/MM | QM | QM/MM | |
| Mn(1) | 0.321 | 0.305 | −0.012 | −0.015 | −0.012 | −0.015 | −0.003 | −0.002 |
| Mn(2) | −0.858 | −0.634 | −0.012 | −0.026 | −0.026 | −0.033 | −0.020 | −0.004 |
| Mn(3) | 0.267 | 0.272 | −0.010 | 0.027 | −0.027 | 0.015 | −0.033 | 0.008 |
| Mn(4) | −0.630 | −0.507 | −0.162 | −0.141 | −0.007 | −0.001 | −0.006 | 0.000 |
| O(5) | 0.112 | 0.148 | −0.005 | 0.004 | −0.002 | 0.005 | 0.000 | 0.002 |
| O(6) | 0.224 | 0.157 | 0.012 | 0.003 | 0.033 | 0.014 | 0.031 | 0.004 |
| O(7) | 0.167 | 0.116 | −0.017 | −0.015 | −0.008 | −0.011 | −0.004 | −0.001 |
| O(8) | 0.627 | 0.306 | 0.092 | 0.036 | 0.019 | −0.006 | 0.021 | 0.001 |
| O(9) | −0.111 | −0.048 | −0.040 | −0.060 | 0.021 | −0.016 | 0.026 | −0.011 |
| Ca(10) | −0.003 | −0.001 | 0.002 | 0.000 | 0.001 | 0.000 | 0.001 | 0.000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kitakawa, C.K.; Maruyama, T.; Oonari, J.; Mitsuta, Y.; Kawakami, T.; Okumura, M.; Yamaguchi, K.; Yamanaka, S. Linear Response Functions of Densities and Spin Densities for Systematic Modeling of the QM/MM Approach for Mono- and Poly-Nuclear Transition Metal Systems. Molecules 2019, 24, 821. https://doi.org/10.3390/molecules24040821
Kitakawa CK, Maruyama T, Oonari J, Mitsuta Y, Kawakami T, Okumura M, Yamaguchi K, Yamanaka S. Linear Response Functions of Densities and Spin Densities for Systematic Modeling of the QM/MM Approach for Mono- and Poly-Nuclear Transition Metal Systems. Molecules. 2019; 24(4):821. https://doi.org/10.3390/molecules24040821
Chicago/Turabian StyleKitakawa, Colin K., Tomohiro Maruyama, Jinta Oonari, Yuki Mitsuta, Takashi Kawakami, Mitsutaka Okumura, Kizashi Yamaguchi, and Shusuke Yamanaka. 2019. "Linear Response Functions of Densities and Spin Densities for Systematic Modeling of the QM/MM Approach for Mono- and Poly-Nuclear Transition Metal Systems" Molecules 24, no. 4: 821. https://doi.org/10.3390/molecules24040821
APA StyleKitakawa, C. K., Maruyama, T., Oonari, J., Mitsuta, Y., Kawakami, T., Okumura, M., Yamaguchi, K., & Yamanaka, S. (2019). Linear Response Functions of Densities and Spin Densities for Systematic Modeling of the QM/MM Approach for Mono- and Poly-Nuclear Transition Metal Systems. Molecules, 24(4), 821. https://doi.org/10.3390/molecules24040821






