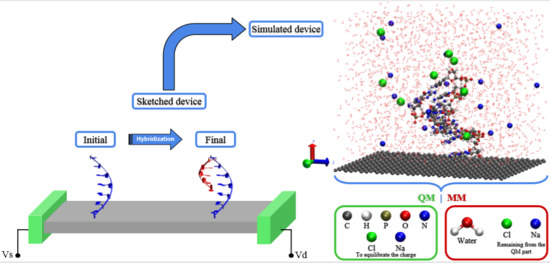
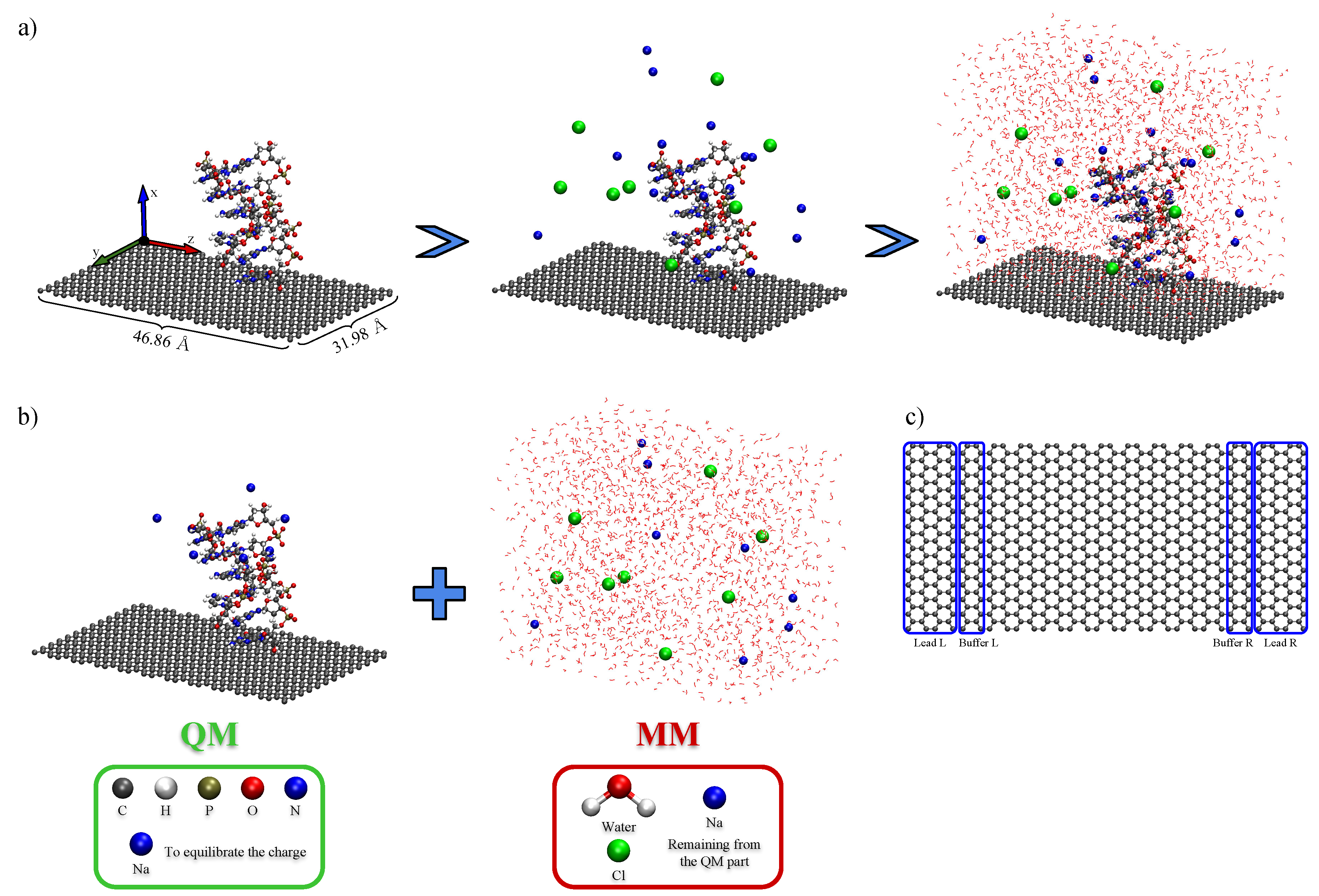
Simulating DNA Chip Design Using All-Electronic Graphene-Based Substrates
Abstract
:1. Introduction
2. Methodology
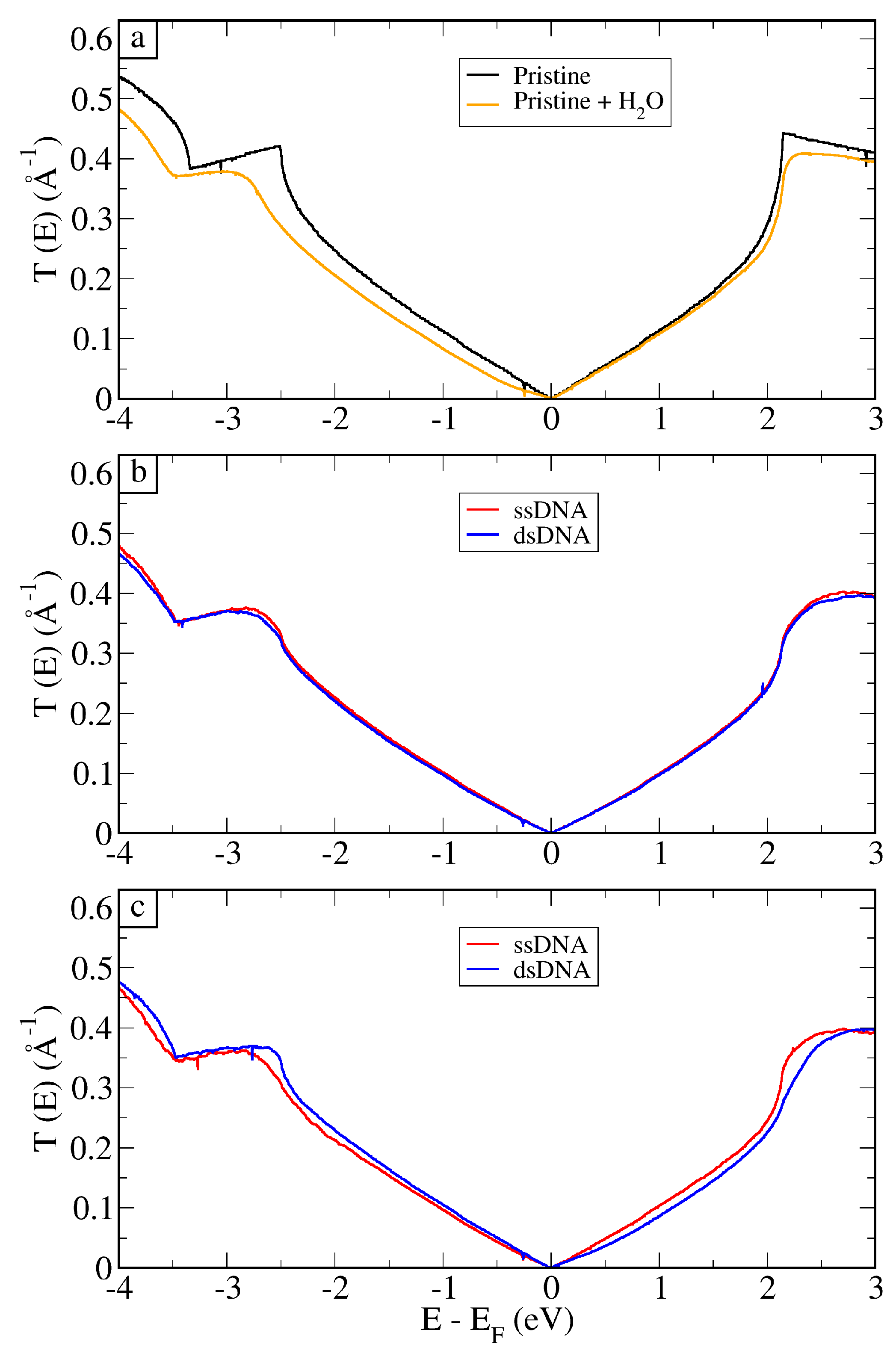
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DNA | Deoxyribonucleic acid |
| ssDNA | Single-stranded DNA |
| dsDNA | Double-stranded DNA |
| DFT | Density functional theory |
| NEGF | Non-equilibrium Green’s functions |
| QM/MM | Quantum mechanics/molecular mechanics |
| MD | Molecular dynamics |
| NPT | Isothermal-isobaric ensemble |
| NVT | Canonical ensemble |
| SPC | Simple point-charge |
| PBC | Periodic boundary conditions |
| RMSD | Root mean square deviation |
| SD | Standard deviation |
References
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Abedin, M.I.; Hassan, A. A novel approach to label-free detection of DNA hybridization based on graphene quantum capacitance dependent frequency/wireless readout. In Proceedings of the 2015 International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 21–23 May 2015. [Google Scholar] [CrossRef]
- Liang, L.; Shen, J.W.; Zhang, Z.; Wang, Q. DNA sequencing by two-dimensional materials: As theoretical modeling meets experiments. Biosens. Bioelectron. 2017, 89, 280–292. [Google Scholar] [CrossRef] [PubMed]
- Shendure, J.; Balasubramanian, S.; Church, G.M.; Gilbert, W.; Rogers, J.; Schloss, J.A.; Waterston, R.H. DNA sequencing at 40: Past, present and future. Nature 2017, 550, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Ansorge, W.J. Next-generation DNA sequencing techniques. New Biotechnol. 2009, 25, 195–203. [Google Scholar] [CrossRef] [PubMed]
- Metzker, M.L. Sequencing technologies the next generation. Nat. Rev. Genet. 2010, 11, 31–46. [Google Scholar] [CrossRef] [PubMed]
- Buermans, H.P.J.; Dunnen, J.T.D.; Metzker, M.L.; Goodwin, S.; McPherson, J.D.; McCombie, W.R.; Levy, S.E.; Myers, R.M. Coming of age: Ten years of next-generation sequencing technologies. Nat. Rev. Genet. 2016, 17, 95–115. [Google Scholar] [CrossRef]
- Cost per Megabase of DNA Sequence. Available online: https://www.genome.gov/sequencingcostsdata/ (accessed on 13 October 2018).
- Di Ventra, M.; Taniguchi, M. Decoding DNA, RNA and peptides with quantum tunnelling. Nature Nanotechnol. 2016, 11, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Sivaraman, G.; Amorim, R.G.; Scheicher, R.H.; Fyta, M. Diamondoid-functionalized gold nanogaps as sensors for natural, mutated, and epigenetically modified DNA nucleotides. Nanoscale 2016, 8, 10105–10112. [Google Scholar] [CrossRef] [PubMed]
- Fyta, M. Threading DNA through nanopores for biosensing applications. J. Phys. Condens. Matter 2015, 27, 273101. [Google Scholar] [CrossRef] [PubMed]
- Růžička, M.; Kulhánek, P.; Radová, L.; Čechová, A.; Špačková, N.; Fajkusová, L.; Réblová, K. DNA mutation motifs in the genes associated with inherited diseases. PLoS ONE 2017, 12, e0182377. [Google Scholar] [CrossRef]
- Heerema, S.J.; Dekker, C. Graphene nanodevices for DNA sequencing. Nat. Nanotechnol. 2016, 11, 127–136. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Katsnelson, M.; Geim, A. Electron scattering on microscopic corrugations in graphene. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2008, 366, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Feliciano, G.T.; Sanz-Navarro, C.; Coutinho-Neto, M.D.; Ordejón, P.; Scheicher, R.H.; Rocha, A.R. Capacitive DNA Detection Driven by Electronic Charge Fluctuations in a Graphene Nanopore. Phys. Rev. Appl. 2015, 3, 034003. [Google Scholar] [CrossRef]
- Feliciano, G.T.; Sanz-Navarro, C.; Coutinho-Neto, M.D.; Ordejón, P.; Scheicher, R.H.; Rocha, A.R. Addressing the Environment Electrostatic Effect on Ballistic Electron Transport in Large Systems: A QM/MM-NEGF Approach. J. Phys. Chem. B 2018, 122, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Jang, H.D.; Kim, S.K.; Chang, H.; Choi, J.W. 3D label-free prostate specific antigen (PSA) immunosensor based on graphene–gold composites. Biosens. Bioelectron. 2015, 63, 546–551. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Javadi, A.; Li, H.; Gong, S. Ultrasensitive immunosensor for the detection of cancer biomarker based on graphene sheet. Biosens. Bioelectron. 2010, 26, 560–565. [Google Scholar] [CrossRef] [PubMed]
- Pumera, M. Graphene in biosensing. Mater. Today 2011, 14, 308–315. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, S.; Xu, T.; Zhang, T.; Mo, Y.; Liu, J.; Yan, L.; Xing, F. Ultra-sensitive and ultra-fast detection of whole unlabeled living cancer cell responses to paclitaxel with a graphene-based biosensor. Sens. Actuators B Chem. 2018, 263, 417–425. [Google Scholar] [CrossRef]
- Singh, J.; Rathi, A.; Rawat, M.; Gupta, M. Graphene: From synthesis to engineering to biosensor applications. Front. Mater. Sci. 2018, 12, 1–20. [Google Scholar] [CrossRef]
- Prasongkit, J.; de Freitas Martins, E.; de Souza, F.A.L.; Scopel, W.L.; Amorim, R.G.; Amornkitbamrung, V.; Rocha, A.R.; Scheicher, R.H. Topological Line Defects Around Graphene Nanopores for DNA Sequencing. J. Phys. Chem. C 2018, 122, 7094–7099. [Google Scholar] [CrossRef]
- Prasongkit, J.; Feliciano, G.T.; Rocha, A.R.; He, Y.; Osotchan, T.; Ahuja, R.; Scheicher, R.H. Theoretical assessment of feasibility to sequence DNA through interlayer electronic tunneling transport at aligned nanopores in bilayer graphene. Sci. Rep. 2015, 5, 17560. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Scheicher, R.H.; Pandey, R.; Rocha, A.R.; Sanvito, S.; Grigoriev, A.; Ahuja, R.; Karna, S.P. Functionalized Nanopore-Embedded Electrodes for Rapid DNA Sequencing. J. Phys. Chem. C 2008, 112, 3456–3459. [Google Scholar] [CrossRef]
- Amorim, R.G.; Rocha, A.R.; Scheicher, R.H. Boosting DNA Recognition Sensitivity of Graphene Nanogaps through Nitrogen Edge Functionalization. J. Phys. Chem. C 2016, 120, 19384–19388. [Google Scholar] [CrossRef]
- Nelson, T.; Zhang, B.; Prezhdo, O.V. Detection of Nucleic Acids with Graphene Nanopores: Ab Initio Characterization of a Novel Sequencing Device. Nano Lett. 2010, 10, 3237–3242. [Google Scholar] [CrossRef] [PubMed]
- Sanz-Navarro, C.F.; Grima, R.; García, A.; Bea, E.A.; Soba, A.; Cela, J.M.; Ordejón, P. An efficient implementation of a QM-MM method in SIESTA. Theor. Chem. Acc. 2011, 128, 825–833. [Google Scholar] [CrossRef]
- Rothlisberger, U.; Carloni, P. Drug-Target Binding Investigated by Quantum Mechanical/Molecular Mechanical (QM/MM) Methods; Springer: Berlin/Heidelberg, Germany, 2006; Volume 1, p. 449. [Google Scholar]
- Büttiker, M.; Imry, Y.; Landauer, R.; Pinhas, S. Generalized many-channel conductance formula with application to small rings. Phys. Rev. B 1985, 31, 6207–6215. [Google Scholar] [CrossRef]
- Brandbyge, M.; Mozos, J.L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 2002, 65, 165401. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems, 1st ed.; Cambridge University Press: Cambridge, UK, 1995; pp. 57–88. [Google Scholar]
- Rocha, A.; García-Suárez, V.; Bailey, S.; Lambert, C.; Ferrer, J.; Sanvito, S. Spin and molecular electronics in atomically generated orbital landscapes. Phys. Rev. B 2006, 73, 085414. [Google Scholar] [CrossRef]
- Rocha, A.R.; García-Suárez, V.M.; Bailey, S.W.; Lambert, C.J.; Ferrer, J.; Sanvito, S. Towards Molecular Spintronics. Nat. Mater. 2005, 4, 335–339. [Google Scholar] [CrossRef]
- Karimi, H.; Yusof, R.; Rahmani, R.; Hosseinpour, H.; Ahmadi, M.T. Development of solution-gated graphene transistor model for biosensors. Nanoscale Res. Lett. 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins Struct. Funct. Bioinform. 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J.; Pullman, B. (Eds.) Intermolecular Forces. The Jerusalem Symposia on Quantum Chemistry and Biochemistry; Chapter Interaction Models for Water in Relation to Protein Hydration; Springer: Holland, Dordrecht, 1981; Volume 14. [Google Scholar]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Soler, M.; Artacho, E.; Gale, J.D.; Garc, A.; Junquera, J.; Ordej, P.; Daniel, S. The SIESTA method for ab initio order-N materials. J. Phys. Condens. Matter 2002, 2745, 2745–2779. [Google Scholar] [CrossRef]
- Crespo, A.; Scherlis, D.A.; Martí, M.A.; Ordejón, P.; Roitberg, A.E.; Estrin, D.A. A DFT-Based QM-MM Approach Designed for the Treatment of Large Molecular Systems: Application to Chorismate Mutase. J. Phys. Chem. B 2003, 107, 13728–13736. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef]
- Troullier, N. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Haug, H.; Jauho, A.P. Quantum Kinetics in Transport and Optics of Semiconductors; Springer Verlag: New York, NY, USA, 1999; pp. 1–362. [Google Scholar]
- Landauer, R. Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction. IBM J. Res. Dev. 1957, 1, 223–231. [Google Scholar] [CrossRef]
- Landauer, R. Conductance from Transmission: Common Sense Points. Phys. Scr. 1992, 1992, 110. [Google Scholar] [CrossRef]
- Caroli, C.; Combescot, R.; Nozieres, P.; Saint-James, D. Direct calculation of the tunneling current. J. Phys. C Solid State Phys. 1971, 4, 916–929. [Google Scholar] [CrossRef]
- Schneider, G.F.; Xu, Q.; Hage, S.; Luik, S.; Spoor, J.N.H.; Malladi, S.; Zandbergen, H.; Dekker, C. Tailoring the hydrophobicity of graphene for its use as nanopores for DNA translocation. Nat. Commun. 2013, 4, 2619. [Google Scholar] [CrossRef] [PubMed]
- Gowtham, S.; Scheicher, R.H.; Ahuja, R.; Pandey, R.; Karna, S.P. Physisorption of nucleobases on graphene: Density-functional calculations. Phys. Rev. B 2007, 76, 033401. [Google Scholar] [CrossRef]
Sample Availability: Structural data for molecular dynamics simulations, as well as inputs for all simulations can be obtained from the authors. |


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Freitas Martins, E.; Troiano Feliciano, G.; Hendrik Scheicher, R.; Reily Rocha, A. Simulating DNA Chip Design Using All-Electronic Graphene-Based Substrates. Molecules 2019, 24, 951. https://doi.org/10.3390/molecules24050951
de Freitas Martins E, Troiano Feliciano G, Hendrik Scheicher R, Reily Rocha A. Simulating DNA Chip Design Using All-Electronic Graphene-Based Substrates. Molecules. 2019; 24(5):951. https://doi.org/10.3390/molecules24050951
Chicago/Turabian Stylede Freitas Martins, Ernane, Gustavo Troiano Feliciano, Ralph Hendrik Scheicher, and Alexandre Reily Rocha. 2019. "Simulating DNA Chip Design Using All-Electronic Graphene-Based Substrates" Molecules 24, no. 5: 951. https://doi.org/10.3390/molecules24050951
APA Stylede Freitas Martins, E., Troiano Feliciano, G., Hendrik Scheicher, R., & Reily Rocha, A. (2019). Simulating DNA Chip Design Using All-Electronic Graphene-Based Substrates. Molecules, 24(5), 951. https://doi.org/10.3390/molecules24050951